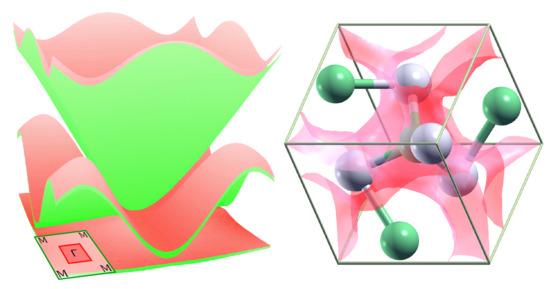
Optical Response of Chiral Multifold Semimetal PdGa
Abstract
1. Introduction
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yan, B.; Felser, C. Topological Materials: Weyl Semimetals. Annu. Rev. Condens. Matter Phys. 2017, 8, 337–354. [Google Scholar] [CrossRef]
- Murakami, S. Phase transition between the quantum spin Hall and insulator phases in 3D: Emergence of a topological gapless phase. New J. Phys. 2007, 9, 356. [Google Scholar] [CrossRef]
- Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef]
- Burkov, A.A.; Balents, L. Weyl Semimetal in a Topological Insulator Multilayer. Phys. Rev. Lett. 2011, 107, 127205. [Google Scholar] [CrossRef] [PubMed]
- Šmejkal, L.; Jungwirth, T.; Sinova, J. Route towards Dirac and Weyl antiferromagnetic spintronics. Phys. Status Solidi RRL 2017, 11, 1700044. [Google Scholar] [CrossRef]
- Šmejkal, L.; Mokrousov, Y.; Yan, B.; MacDonald, A.H. Topological antiferromagnetic spintronics. Nat. Phys. 2018, 14, 242–251. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, M.; Wu, J. A spin filter transistor made of topological Weyl semimetal. Appl. Phys. Lett. 2015, 107, 102403. [Google Scholar] [CrossRef]
- Grushin, A.G.; Bardarson, J.H. How to Make Devices with Weyl Materials. Physics 2017, 10, 63. [Google Scholar] [CrossRef]
- Hills, R.D.Y.; Kusmartseva, A.; Kusmartsev, F.V. Current-voltage characteristics of Weyl semimetal semiconducting devices, Veselago lenses, and hyperbolic Dirac phase. Phys. Rev. B 2017, 95, 214103. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, F.; Meng, Y.; Yuan, X.; Xiu, F.; Luo, H.; Wang, Y.; Li, J.; Lv, X.; He, L.; et al. A robust and tuneable mid-infrared optical switch enabled by bulk Dirac fermions. Nat. Commun. 2017, 8, 1–7. [Google Scholar] [CrossRef]
- Sun, Y.; Meng, Y.; Jiang, H.; Qin, S.; Yang, Y.; Xiu, F.; Shi, Y.; Zhu, S.; Wang, F. Dirac semimetal saturable absorber with actively tunable modulation depth. Opt. Lett. 2019, 44, 582–585. [Google Scholar] [CrossRef] [PubMed]
- Müchler, L.; Zhang, H.; Chadov, S.; Yan, B.; Casper, F.; Kübler, J.; Zhang, S.C.; Felser, C. Topological Insulators from a Chemist’s Perspective. Angew. Chem. Int. Ed. 2012, 51, 7221–7225. [Google Scholar] [CrossRef] [PubMed]
- Kong, D.; Cui, Y. Opportunities in chemistry and materials science for topological insulators and their nanostructures. Nat. Chem. 2011, 3, 845–849. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhu, W.; Xiao, D.; Zhang, Z. CO Oxidation Facilitated by Robust Surface States on Au-Covered Topological Insulators. Phys. Rev. Lett. 2011, 107, 056804. [Google Scholar] [CrossRef]
- Yan, B.; Stadtmüller, B.; Haag, N.; Jakobs, S.; Seidel, J.; Jungkenn, D.; Mathias, S.; Cinchetti, M.; Aeschlimann, M.; Felser, C. Topological states on the gold surface. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef]
- Xiao, J.; Kou, L.; Yam, C.Y.; Frauenheim, T.; Yan, B. Toward Rational Design of Catalysts Supported on a Topological Insulator Substrate. ACS Catal. 2015, 5, 7063–7067. [Google Scholar] [CrossRef]
- Lv, B.Q.; Weng, H.M.; Fu, B.B.; Wang, X.P.; Miao, H.; Ma, J.; Richard, P.; Huang, X.C.; Zhao, L.X.; Chen, G.F.; et al. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X 2015, 5, 031013. [Google Scholar] [CrossRef]
- Weng, H.; Fang, C.; Fang, Z.; Bernevig, B.A.; Dai, X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Phys. Rev. X 2015, 5, 011029. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Y.; Felser, C.; Yan, B. Strong Intrinsic Spin Hall Effect in the TaAs Family of Weyl Semimetals. Phys. Rev. Lett. 2016, 117, 146403. [Google Scholar] [CrossRef]
- Aroyo, M.I. International Tables for Crystallography, Volume A, 6th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Sohncke, L. Entwicklung einer Theorie der Kristallstruktur; B. G. Teubner: Leipzig, Germany, 1879. [Google Scholar]
- Bradlyn, B.; Cano, J.; Wang, Z.; Vergniory, M.G.; Felser, C.; Cava, R.J.; Bernevig, B.A. Beyond Dirac and Weyl fermions: Unconventional quasiparticles in conventional crystals. Science 2016, 353. [Google Scholar] [CrossRef]
- Sanchez, D.S.; Belopolski, I.; Cochran, T.A.; Xu, X.; Yin, J.X.; Chang, G.; Xie, W.; Manna, K.; Süß, V.; Huang, C.Y.; et al. Topological chiral crystals with helicoid-arc quantum states. Nature 2019, 567, 500–505. [Google Scholar] [CrossRef] [PubMed]
- Schröter, N.B.M.; Pei, D.; Vergniory, M.G.; Sun, Y.; Manna, K.; de Juan, F.; Krieger, J.A.; Süss, V.; Schmidt, M.; Dudin, P.; et al. Chiral topological semimetal with multifold band crossings and long Fermi arcs. Nat. Phys. 2019, 15, 759–765. [Google Scholar] [CrossRef]
- Chang, G.; Xu, S.Y.; Wieder, B.J.; Sanchez, D.S.; Huang, S.M.; Belopolski, I.; Chang, T.R.; Zhang, S.; Bansil, A.; Lin, H.; et al. Unconventional Chiral Fermions and Large Topological Fermi Arcs in RhSi. Phys. Rev. Lett. 2017, 119, 206401. [Google Scholar] [CrossRef] [PubMed]
- Rao, Z.; Li, H.; Zhang, T.; Tian, S.; Li, C.; Fu, B.; Tang, C.; Wang, L.; Li, Z.; Fan, W.; et al. Observation of unconventional chiral fermions with long Fermi arcs in CoSi. Nature 2019, 567, 496–499. [Google Scholar] [CrossRef] [PubMed]
- Tang, P.; Zhou, Q.; Zhang, S.C. Multiple Types of Topological Fermions in Transition Metal Silicides. Phys. Rev. Lett. 2017, 119, 206402. [Google Scholar] [CrossRef]
- Takane, D.; Wang, Z.; Souma, S.; Nakayama, K.; Nakamura, T.; Oinuma, H.; Nakata, Y.; Iwasawa, H.; Cacho, C.; Kim, T.; et al. Observation of Chiral Fermions with a Large Topological Charge and Associated Fermi-Arc Surface States in CoSi. Phys Rev. Lett. 2019, 122, 076402. [Google Scholar] [CrossRef]
- Sessi, P.; Fan, F.R.; Küster, F.; Manna, K.; Schröter, N.B.M.; Ji, J.R.; Stolz, S.; Krieger, J.A.; Pei, D.; Kim, T.K.; et al. Handedness-dependent quasiparticle interference in the two enantiomers of the topological chiral semimetal PdGa. Nat. Commun. 2020, 11, 3507. [Google Scholar] [CrossRef]
- Schröter, N.B.M.; Stolz, S.; Manna, K.; de Juan, F.; Vergniory, M.G.; Krieger, J.A.; Pei, D.; Schmitt, T.; Dudin, P.; Kim, T.K.; et al. Observation and control of maximal Chern numbers in a chiral topological semimetal. Science 2020, 369, 179. [Google Scholar] [CrossRef]
- De Juan, F.; Grushin, A.G.; Morimoto, T.; Moore, J.E. Quantized circular photogalvanic effect in Weyl semimetals. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef]
- Le, C.; Zhang, Y.; Felser, C.; Sun, Y. Ab initio study of quantized circular photogalvanic effect in chiral multifold semimetals. Phys. Rev. B 2020, 102, 121111. [Google Scholar] [CrossRef]
- Rees, D.; Manna, K.; Lu, B.; Morimoto, T.; Borrmann, H.; Felser, C.; Moore, J.E.; Torchinsky, D.H.; Orenstein, J. Helicity-dependent photocurrents in the chiral Weyl semimetal RhSi. Sci. Adv. 2020, 6, eaba0509. [Google Scholar] [CrossRef] [PubMed]
- Ni, Z.; Wang, K.; Zhang, Y.; Pozo, O.; Xu, B.; Han, X.; Manna, K.; Paglione, J.; Felser, C.; Grushin, A.G.; et al. Giant topological longitudinal circular photo-galvanic effect in the chiral multifold semimetal CoSi. Nat. Commun. 2021, 12, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Maulana, L.Z.; Manna, K.; Uykur, E.; Felser, C.; Dressel, M.; Pronin, A.V. Optical conductivity of multifold fermions: The case of RhSi. Phys. Rev. Res. 2020, 2, 023018. [Google Scholar] [CrossRef]
- Neubauer, D.; Carbotte, J.P.; Nateprov, A.A.; Löhle, A.; Dressel, M.; Pronin, A.V. Interband optical conductivity of the [001]-oriented Dirac semimetal Cd3As2. Phys. Rev. B 2016, 93, 121202. [Google Scholar] [CrossRef]
- Schilling, M.B.; Schoop, L.M.; Lotsch, B.V.; Dressel, M.; Pronin, A.V. Flat Optical Conductivity in ZrSiS due to Two-Dimensional Dirac Bands. Phys. Rev. Lett. 2017, 119, 187401. [Google Scholar] [CrossRef]
- Hütt, F.; Yaresko, A.; Schilling, M.B.; Shekhar, C.; Felser, C.; Dressel, M.; Pronin, A.V. Linear-in-Frequency Optical Conductivity in GdPtBi due to Transitions near the Triple Points. Phys. Rev. Lett. 2018, 121, 176601. [Google Scholar] [CrossRef]
- Biswas, A.; Iakutkina, O.; Wang, Q.; Lei, H.C.; Dressel, M.; Uykur, E. Spin-Reorientation-Induced Band Gap in Fe3Sn2: Optical Signatures of Weyl Nodes. Phys. Rev. Lett. 2020, 125, 076403. [Google Scholar] [CrossRef]
- Shao, Y.; Sun, Z.; Wang, Y.; Xu, C.; Sankar, R.; Breindel, A.J.; Cao, C.; Fogler, M.M.; Millis, A.J.; Chou, F.; et al. Optical signatures of Dirac nodal lines in NbAs2. Proc. Natl. Acad. Sci. USA 2019, 116, 1168–1173. [Google Scholar] [CrossRef]
- Hosur, P.; Parameswaran, S.A.; Vishwanath, A. Charge Transport in Weyl Semimetals. Phys. Rev. Lett. 2012, 108, 046602. [Google Scholar] [CrossRef]
- Bácsi, A.; Virosztek, A. Low-frequency optical conductivity in graphene and in other scale-invariant two-band systems. Phys. Rev. B 2013, 87, 125425. [Google Scholar] [CrossRef]
- Polatkan, S.; Goerbig, M.O.; Wyzula, J.; Kemmler, R.; Maulana, L.Z.; Piot, B.A.; Crassee, I.; Akrap, A.; Shekhar, C.; Felser, C.; et al. Magneto-Optics of a Weyl Semimetal beyond the Conical Band Approximation: Case Study of TaP. Phys. Rev. Lett. 2020, 124, 176402. [Google Scholar] [CrossRef] [PubMed]
- Mohelský, I.; Dubroka, A.; Wyzula, J.; Slobodeniuk, A.; Martinez, G.; Krupko, Y.; Piot, B.A.; Caha, O.; Humlíček, J.; Bauer, G.; et al. Landau level spectroscopy of Bi2Te3. Phys. Rev. B 2020, 102. [Google Scholar] [CrossRef]
- Akrap, A.; Hakl, M.; Tchoumakov, S.; Crassee, I.; Kuba, J.; Goerbig, M.O.; Homes, C.C.; Caha, O.; Novák, J.; Teppe, F.; et al. Magneto-Optical Signature of Massless Kane Electrons in Cd3As2. Phys. Rev. Lett. 2016, 117, 136401. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, D.; Tsirlin, A.A.; Biesner, T.; Ueno, T.; Takahashi, T.; Kobayashi, K.; Dressel, M.; Uykur, E. Two Linear Regimes in Optical Conductivity of a Type-I Weyl Semimetal: The Case of Elemental Tellurium. Phys. Rev. Lett. 2020, 124, 136402. [Google Scholar] [CrossRef] [PubMed]
- Uykur, E.; Li, W.; Kuntscher, C.A.; Dressel, M. Optical signatures of energy gap in correlated Dirac fermions. NPJ Quantum Mater. 2019, 4, 1–8. [Google Scholar] [CrossRef]
- Xu, B.; Fang, Z.; Sánchez-Martínez, M.Á.; Venderbos, J.W.F.; Ni, Z.; Qiu, T.; Manna, K.; Wang, K.; Paglione, J.; Bernhard, C.; et al. Optical signatures of multifold fermions in the chiral topological semimetal CoSi. Proc. Natl. Acad. Sci. USA 2020, 117, 27104–27110. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.; Kvasnicka, D.; Luitz, J.; Laskowski, R.; Tran, F.; Marks, L.D. Wien2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties; Schwarz, K., Ed.; Vienna University of Technology: Vienna, Austria, 2019; ISBN 3-9501031-1-2. [Google Scholar]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.H.; Marks, L.D. WIEN2k: An APW+lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef]
- Rarita, W.; Schwinger, J. On a Theory of Particles with Half-Integral Spin. Phys. Rev. 1941, 60, 61. [Google Scholar] [CrossRef]
- Ambrosch-Draxl, C.; Sofo, J. Linear optical properties of solids within the full-potential linearized augmented planewave method. Comput. Phys. Commun. 2006, 175, 1–14. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polatkan, S.; Uykur, E. Optical Response of Chiral Multifold Semimetal PdGa. Crystals 2021, 11, 80. https://doi.org/10.3390/cryst11020080
Polatkan S, Uykur E. Optical Response of Chiral Multifold Semimetal PdGa. Crystals. 2021; 11(2):80. https://doi.org/10.3390/cryst11020080
Chicago/Turabian StylePolatkan, Sascha, and Ece Uykur. 2021. "Optical Response of Chiral Multifold Semimetal PdGa" Crystals 11, no. 2: 80. https://doi.org/10.3390/cryst11020080
APA StylePolatkan, S., & Uykur, E. (2021). Optical Response of Chiral Multifold Semimetal PdGa. Crystals, 11(2), 80. https://doi.org/10.3390/cryst11020080