Molecular Dynamics Simulations of the Tensile Mechanical Responses of Selective Laser-Melted Aluminum with Different Crystalline Forms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Interatomic Potential
2.2. Modeling Methods
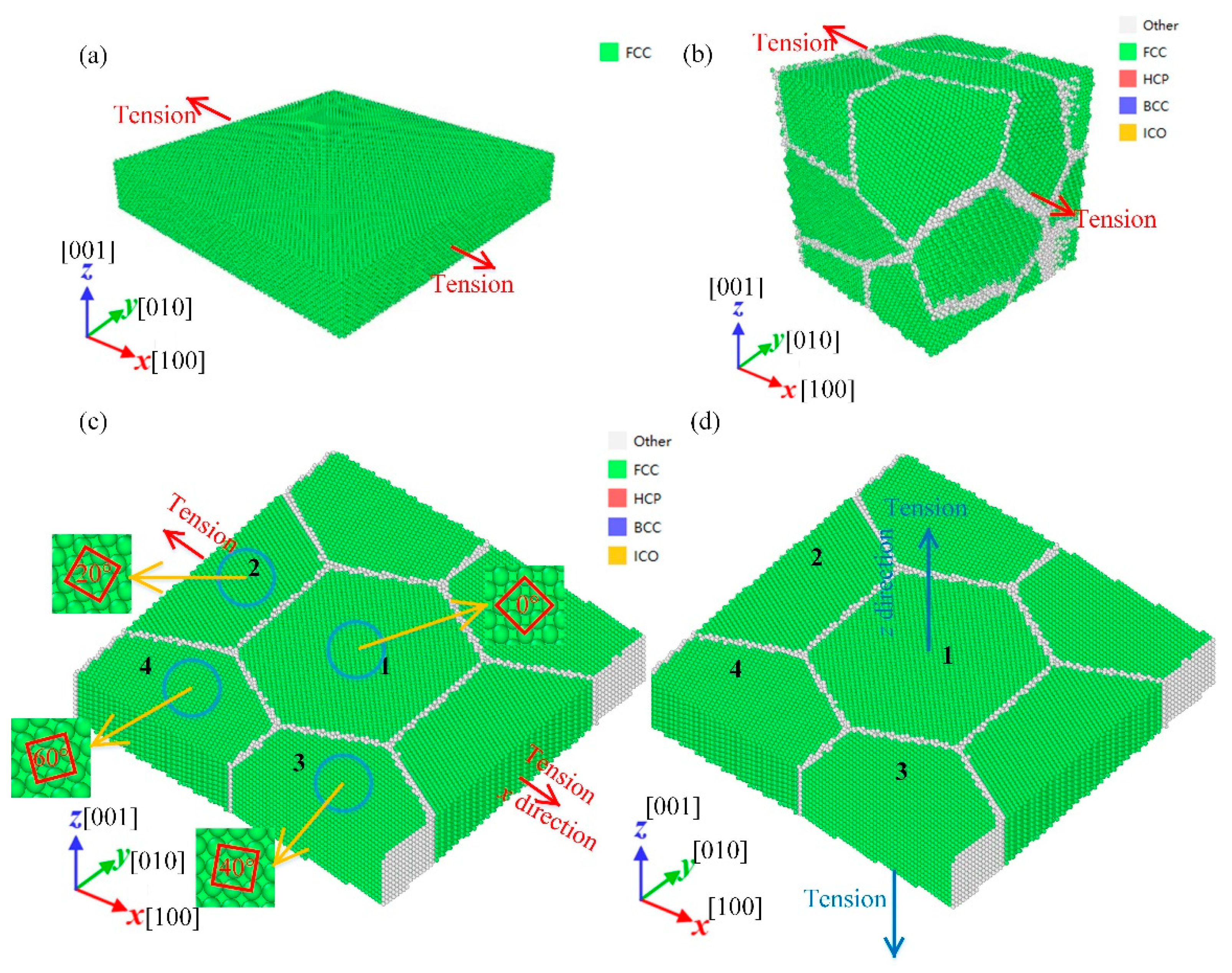
2.2.1. Different Crystalline State Models
2.2.2. Models of Columnar Grains with Different Grain Orientations
3. Results and Discussion
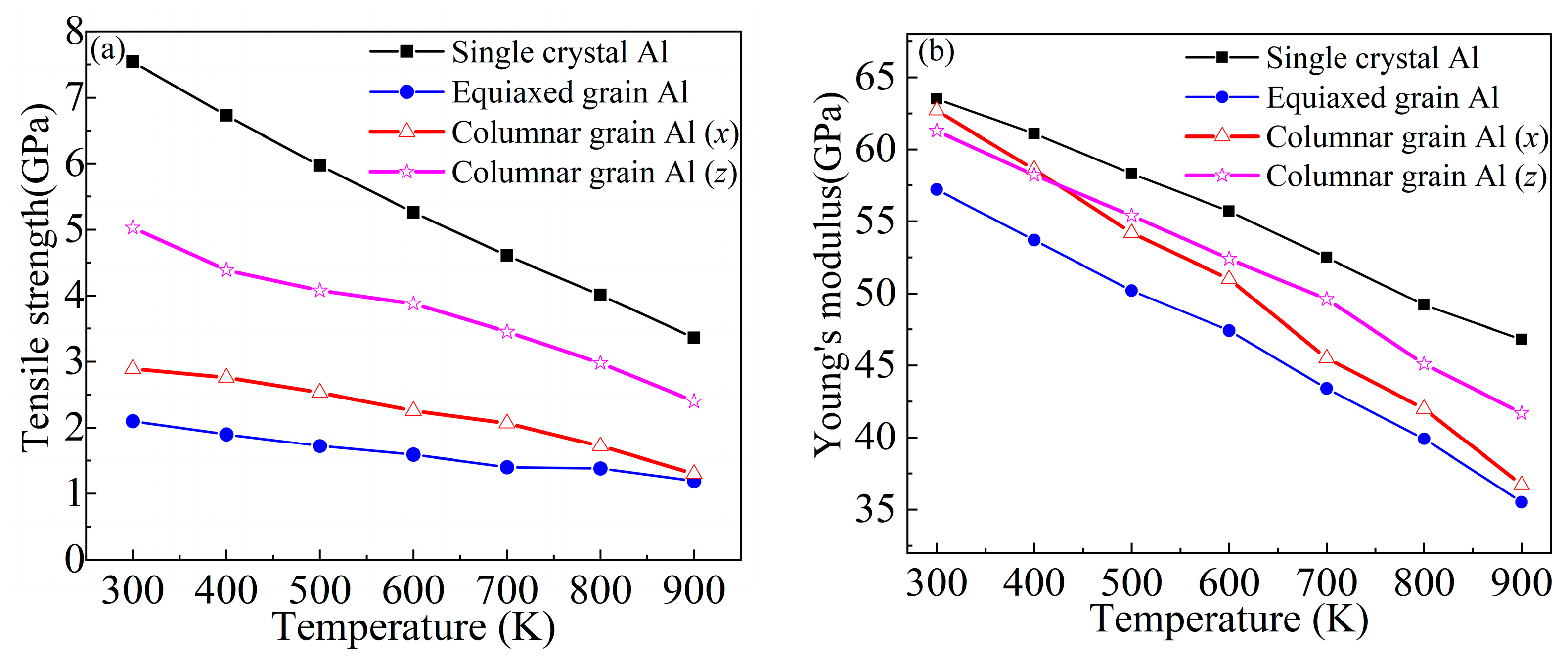
3.1. Effect of Temperature on the Mechanical Properties of Aluminum with Different Crystal Structures
3.2. Mechanical Properties of Columnar Grains with Different Orientations
4. Conclusions
- (1)
- The Young’s modulus, yield strength, and tensile strength of SLM aluminum decreased with increasing temperature. The tensile strength of SLM aluminum with columnar grains at different temperatures was lower than that of single-crystal aluminum, but greater than that of aluminum with equiaxed grains.
- (2)
- The tensile strength and Young’s modulus both decreased approximately linearly with increasing temperature. The tensile strength of SLM aluminum with columnar grains was more sensitive to temperature than aluminum with equiaxed grains, but less sensitive than single-crystal aluminum. The sensitivity of the Young’s modulus of SLM aluminum with columnar grains stretched along the x-axis was the greatest, but the sensitivity of the Young’s modulus of SLM aluminum with columnar grains stretched along the z-axis was greater than that of single-crystal aluminum, but less sensitive than that of aluminum with equiaxed grains.
- (3)
- The deformation mechanisms of equiaxed and columnar grain were dislocation slip, grain boundary migration, and torsion. The deformation mechanisms of single crystals were stacking fault formation and amorphization.
- (4)
- The Young’s modulus was almost independent of the grain orientation, but the tensile strength was greatly affected by the orientation of columnar grains. Reasonable control of the grain orientation can improve the tensile strength of SLM aluminum.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Bandyopadhyay, A.; Traxel, K.D. Invited review article: Metal-additive manufacturing—Modeling strategies for application-optimized designs. Addit. Manuf. 2018, 22, 758–774. [Google Scholar] [CrossRef]
- Guo, N.; Leu, M.C. Additive manufacturing: Technology, applications and research needs. Front. Mech. Eng. 2013, 8, 215–243. [Google Scholar] [CrossRef]
- Tofail, S.A.M.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; O’Donoghue, L.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2018, 21, 22–37. [Google Scholar] [CrossRef]
- Zaretsky, E.; Stern, A.; Frage, N. Dynamic response of AlSi10Mg alloy fabricated by selective laser melting. Mater. Sci. Eng. A 2017, 688, 375–380. [Google Scholar] [CrossRef]
- Larrosa, N.O.; Wang, W.; Read, N.; Loretto, M.H.; Evans, C.; Carr, J.; Tradowsky, U.; Attallah, M.M.; Withers, P.J. Linking microstructure and processing defects to mechanical properties of selectively laser melted AlSi10Mg alloy. Theor. Appl. Fract. Mec. 2018, 98, 123–133. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Li, S.; Liu, J.; Zhang, A.; Zhou, Y.; Wei, Q.; Yan, C.; Shi, Y. Effect of heat treatment on AlSi10Mg alloy fabricated by selective laser melting: Microstructure evolution, mechanical properties and fracture mechanism. Mater. Sci. Eng. A 2016, 663, 116–125. [Google Scholar] [CrossRef]
- Takata, N.; Liu, M.; Kodaira, H.; Suzuki, A.; Kobashi, M. Anomalous strengthening by supersaturated solid solutions of selectively laser melted Al–Si-based alloys. Addit. Manuf. 2020, 33, 101152. [Google Scholar] [CrossRef]
- Takata, N.; Kodaira, H.; Sekizawa, K.; Suzuki, A.; Kobashi, M. Change in microstructure of selectively laser melted AlSi10Mg alloy with heat treatments. Mater. Sci. Eng. A 2017, 704, 218–228. [Google Scholar] [CrossRef]
- Thijs, L.; Kempen, K.; Kruth, J.P.; Humbeeck, J.V. Fine-structured aluminium products with controllable texture by selective laser melting of pre-alloyed AlSi10Mg powder. Acta Mater. 2013, 61, 1809–1819. [Google Scholar] [CrossRef] [Green Version]
- Ben, D.D.; Ma, Y.R.; Yang, H.J.; Meng, L.X.; Shao, X.H.; Liu, H.Q.; Wang, S.G.; Duan, Q.Q.; Zhang, Z.F. Heterogeneous microstructure and voids dependence of tensile deformation in a selective laser melted AlSi10Mg alloy. Mater. Sci. Eng. A 2020, 798, 140109. [Google Scholar] [CrossRef]
- Chen, B.; Moon, S.K.; Yao, X.; Bi, G.; Shen, J.; Umeda, J.; Kondoh, K. Strength and strain hardening of a selective laser melted AlSi10Mg alloy. Scripta Mater. 2017, 141, 45–49. [Google Scholar] [CrossRef]
- Kurian, S.; Mirzaeifar, R. Deformation mechanisms of the subgranular cellular structures in selective laser melted 316L stainless steel. Mech. Mater. 2020, 148, 103478. [Google Scholar] [CrossRef]
- Mei, A.B.; Kindlund, H.; Broitman, E.; Hultman, L.; Petrov, I.; Greene, J.E.; Sangiovanni, D.G. Adaptive hard and tough mechanical response in single-crystal B1 VNx ceramics via control of anion vacancies. Acta Mater. 2020, 192, 78–88. [Google Scholar] [CrossRef]
- Ghaffarian, H.; Taheri, A.K.; Kang, K.; Ryu, S. Molecular dynamics simulation study of the effect of temperature and grain size on the deformation behavior of polycrystalline cementite. Scripta Mater. 2015, 95, 23–26. [Google Scholar] [CrossRef]
- Husain, A.; La, P.; Yue, H.; Sheng, J. Influence of temperature on mechanical properties of nanocrystalline 316L stainless steel investigated via molecular dynamics simulations. Materials 2020, 13, 2803. [Google Scholar] [CrossRef]
- Zepeda-Ruiz, L.A.; Stukowski, A.; Oppelstrup, T.; Bertin, N.; Barton, N.R.; Freitas, R.; Bulatov, V.V. Atomistic insights into metal hardening. Nat. Mater. 2020, 20, 315–320. [Google Scholar] [CrossRef]
- Branco, D.D.C.; Vasconcelos, L.; An, L.; Zhao, K.; Cheng, G.J. Ultrastrong pure aluminum structure with gradient via selective pulsed laser melting: Computation framework and experiments. J. Mech. Phys. Solids 2021, 151, 104391. [Google Scholar] [CrossRef]
- Qi, Y.; Krajewski, P.E. Molecular dynamics simulations of grain boundary sliding: The effect of stress and boundary misorientation. Acta Mater. 2007, 55, 1555–1563. [Google Scholar] [CrossRef]
- Yamakov, V.; Wolf, D.; Phillpot, S.; Mukherjee, A.K.; Gleiter, H. Dislocation processes in the deformation of nanocrystalline aluminium by molecular-dynamics simulation. Nature Mater. 2002, 1, 45–49. [Google Scholar] [CrossRef]
- Li, S.F.; Wang, G. Introduction to Micromechanics and Nanomechanics; World Scientific Publishing Company: Singapore, 2008. [Google Scholar]
- Zhu, H.; Chen, J.; Chen, H.Q.; Fang, L.; Sun, K. Loading direction-dependent mechanical properties of columnar polycrystal: A molecular dynamics study. J. Mater. Eng. Perform. 2021, 30, 1970–1980. [Google Scholar] [CrossRef]
- Mishin, Y.; Farkas, D.; Mehl, M.J.; Papaconstantopoulos, D.A. Interatomic potentials for monoatomic metals from experimental data and ab initio calculations. Phys. Rev. B 1999, 59, 3393–3407. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phy. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.C.; Jiang, W.G.; Zhou, Y. Molecular dynamics simulation of the tensile mechanical response of single crystal/polycrystalline nickel, Rare. Metal. Mat. Eng. 2020, 49, 2372–2379. [Google Scholar]
- Wen, Y.H.; Zhu, Z.Z.; Zhu, R.Z. Molecular dynamics study of the mechanical behavior of nickel nanowire: Strain rate effects. Comp. Mater. Sci. 2008, 41, 553–560. [Google Scholar] [CrossRef] [Green Version]
- Evans, D.J.; Holian, B.L. The Nose-Hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—the open visualization tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 2154–2162. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Finney, J.L. A procedure for the construction of voronoi polyhedral. J. Comput. Phys. 1979, 32, 137–143. [Google Scholar] [CrossRef]
- Bertolino, G.; Ruda, M.; Pasianot, R.; Farkas, D. Atomistic simulation of the tension/compression response of textured nanocrystalline HCP Zr. Comp. Mater. Sci. 2017, 130, 172–182. [Google Scholar] [CrossRef]
- Rajput, A.; Paul, S.K. Cyclic plastic deformation response of nanocrystalline BCC iron. Met. Mater. Int. 2021, 27, 825–837. [Google Scholar] [CrossRef]
- Zhang, L.; Shibuta, Y.; Huang, X.; Lu, C.; Liu, M. Grain boundary induced deformation mechanisms in nanocrystalline Al by molecular dynamics simulation: From interatomic potential perspective. Comp. Mater. Sci. 2019, 156, 421–433. [Google Scholar] [CrossRef] [Green Version]
- Suk, M.E. Effect of the nanotube radius and the volume fraction on the mechanical properties of carbon nanotube-reinforced aluminum metal matrix composites. Molecules 2021, 26, 3947. [Google Scholar] [CrossRef] [PubMed]
- Haque, M.A.; Saif, M.T.A. Mechanical behavior of 30–50 nm thick aluminum films under uniaxial tension. Scripta Mater. 2002, 47, 863–867. [Google Scholar] [CrossRef]
- Matli, P.R.; Ubaid, F.; Shakoor, R.A.; Parande, G.; Gupta, M. Improved properties of Al–Si3N4 nanocomposites fabricated through a microwave sintering and hot extrusion process. RSC Adv. 2017, 7, 34401–34410. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Q.; Wang, L.; Jiang, W. Molecular Dynamics Simulations of the Tensile Mechanical Responses of Selective Laser-Melted Aluminum with Different Crystalline Forms. Crystals 2021, 11, 1388. https://doi.org/10.3390/cryst11111388
Zeng Q, Wang L, Jiang W. Molecular Dynamics Simulations of the Tensile Mechanical Responses of Selective Laser-Melted Aluminum with Different Crystalline Forms. Crystals. 2021; 11(11):1388. https://doi.org/10.3390/cryst11111388
Chicago/Turabian StyleZeng, Qiang, Lijuan Wang, and Wugui Jiang. 2021. "Molecular Dynamics Simulations of the Tensile Mechanical Responses of Selective Laser-Melted Aluminum with Different Crystalline Forms" Crystals 11, no. 11: 1388. https://doi.org/10.3390/cryst11111388






