Numerical Analysis of Micro-Rotation Effect on Nanofluid Flow for Vertical Riga Plate
Abstract
:1. Introduction
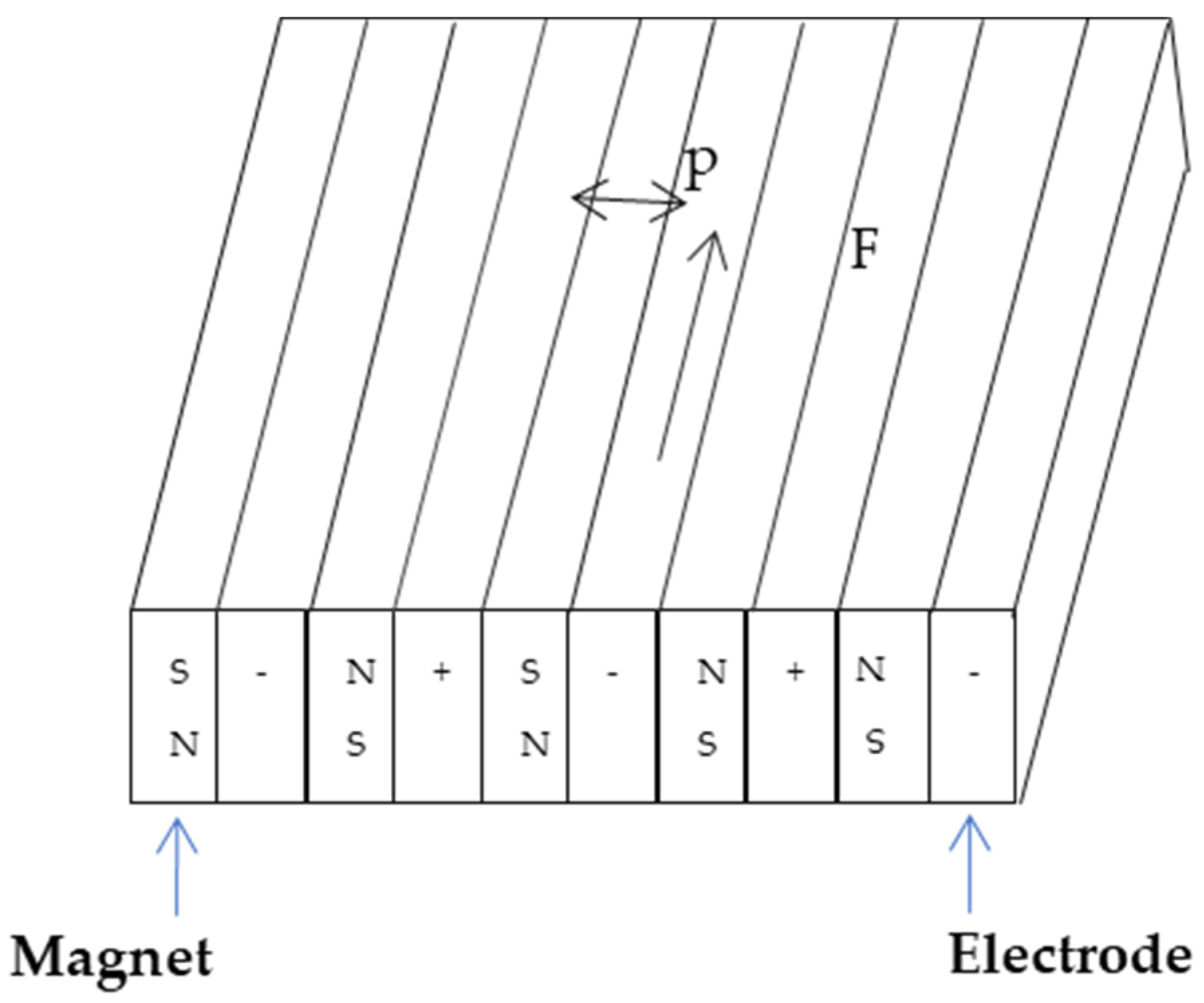
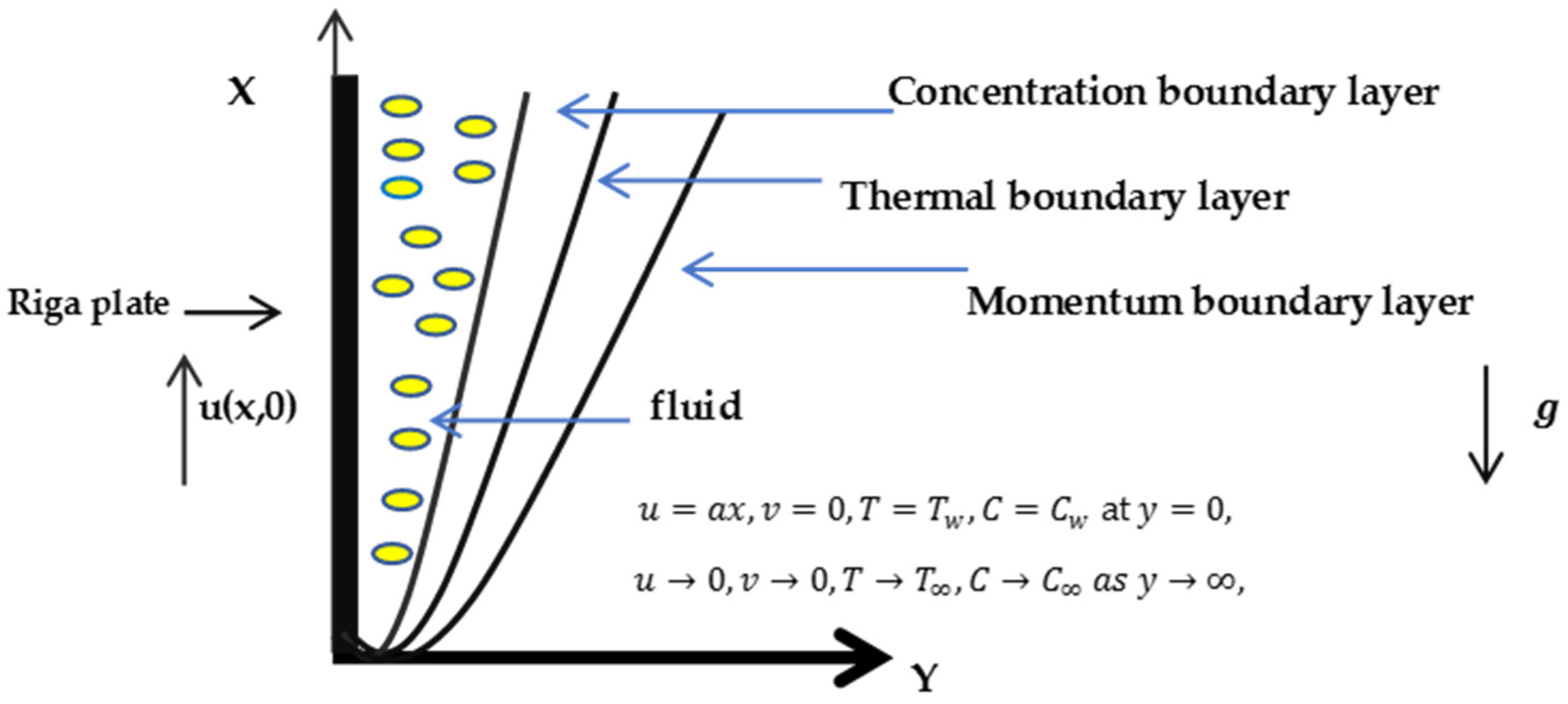
2. Materials and Methods
3. Results
4. Conclusions
- The increment in modified Hartmann number boosts the energy and mass flux rates.
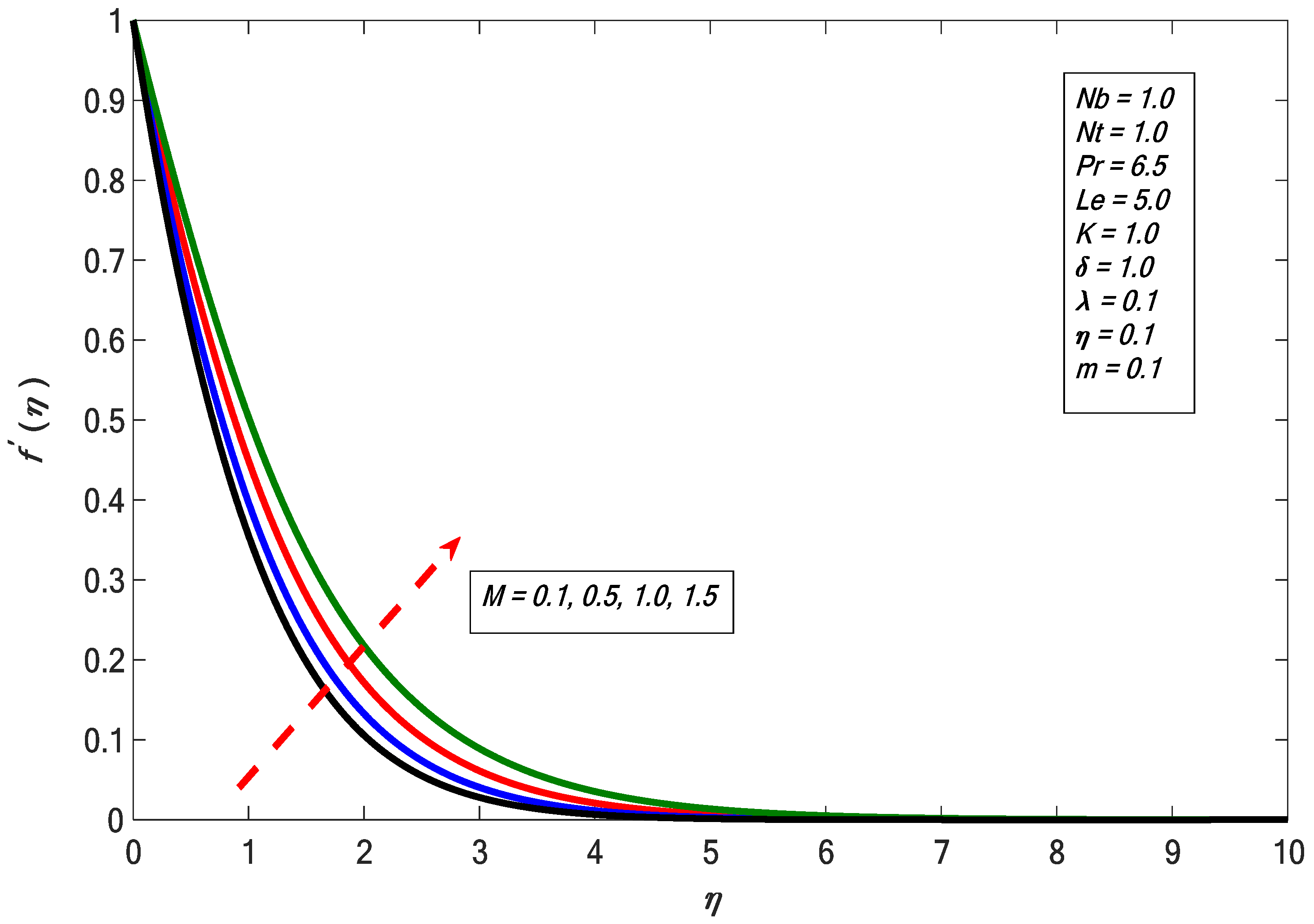
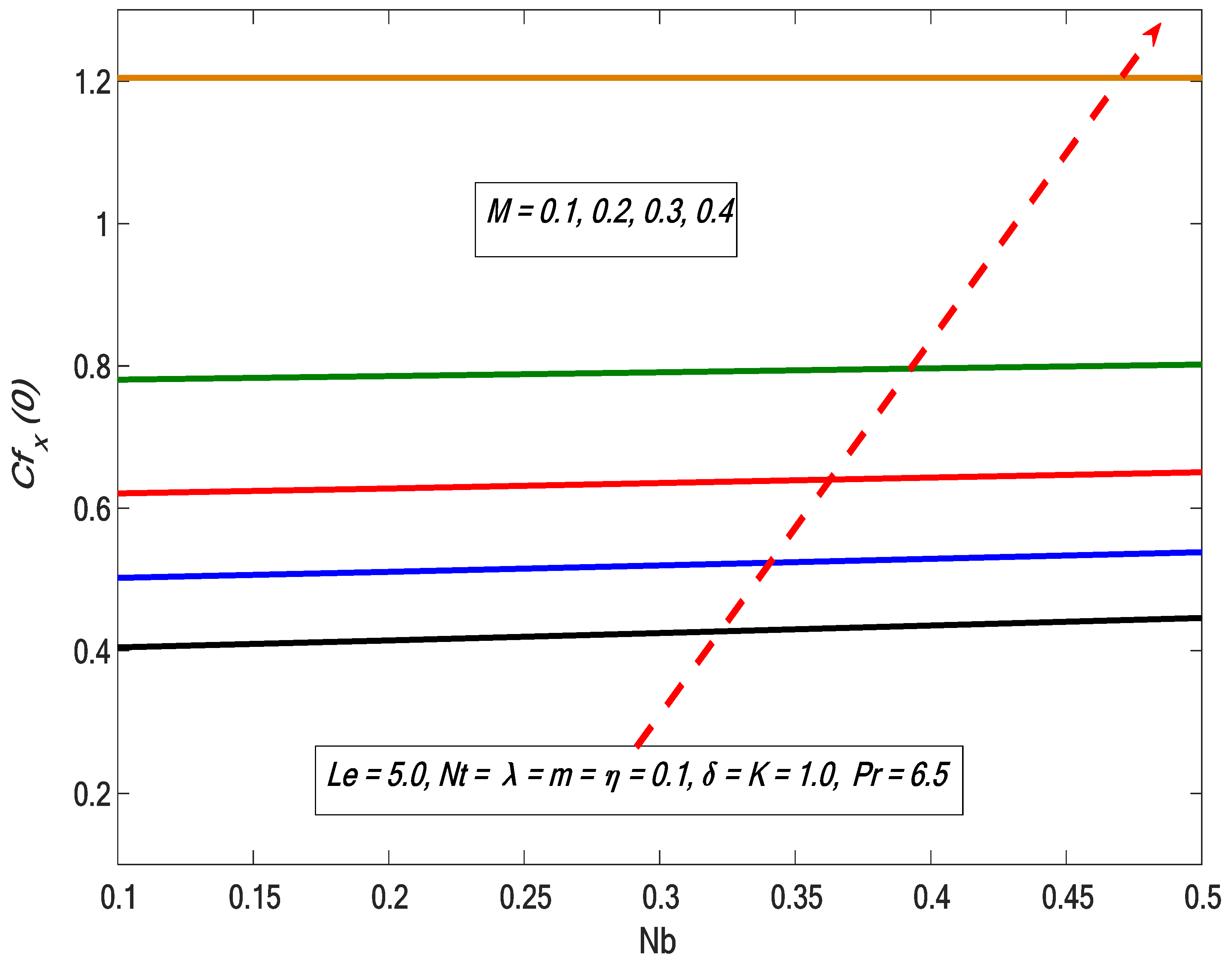
- Skin friction increases with the increase in modified Hartmann number.
- Mixed convection improves the energy and mass transport rates.
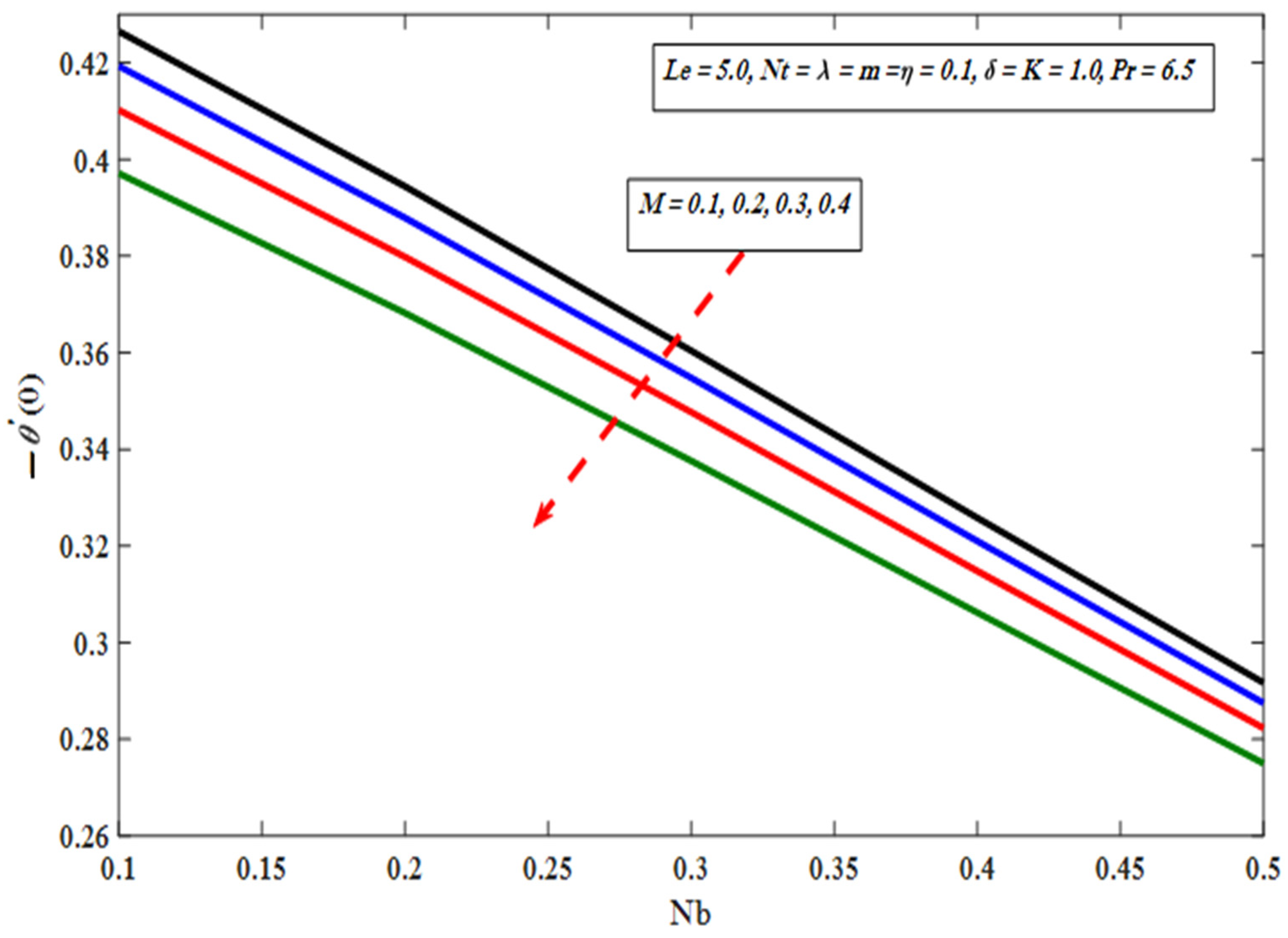
- Nusselt number graph declines by increasing Brownian motion and modified Hartmann number parameters.
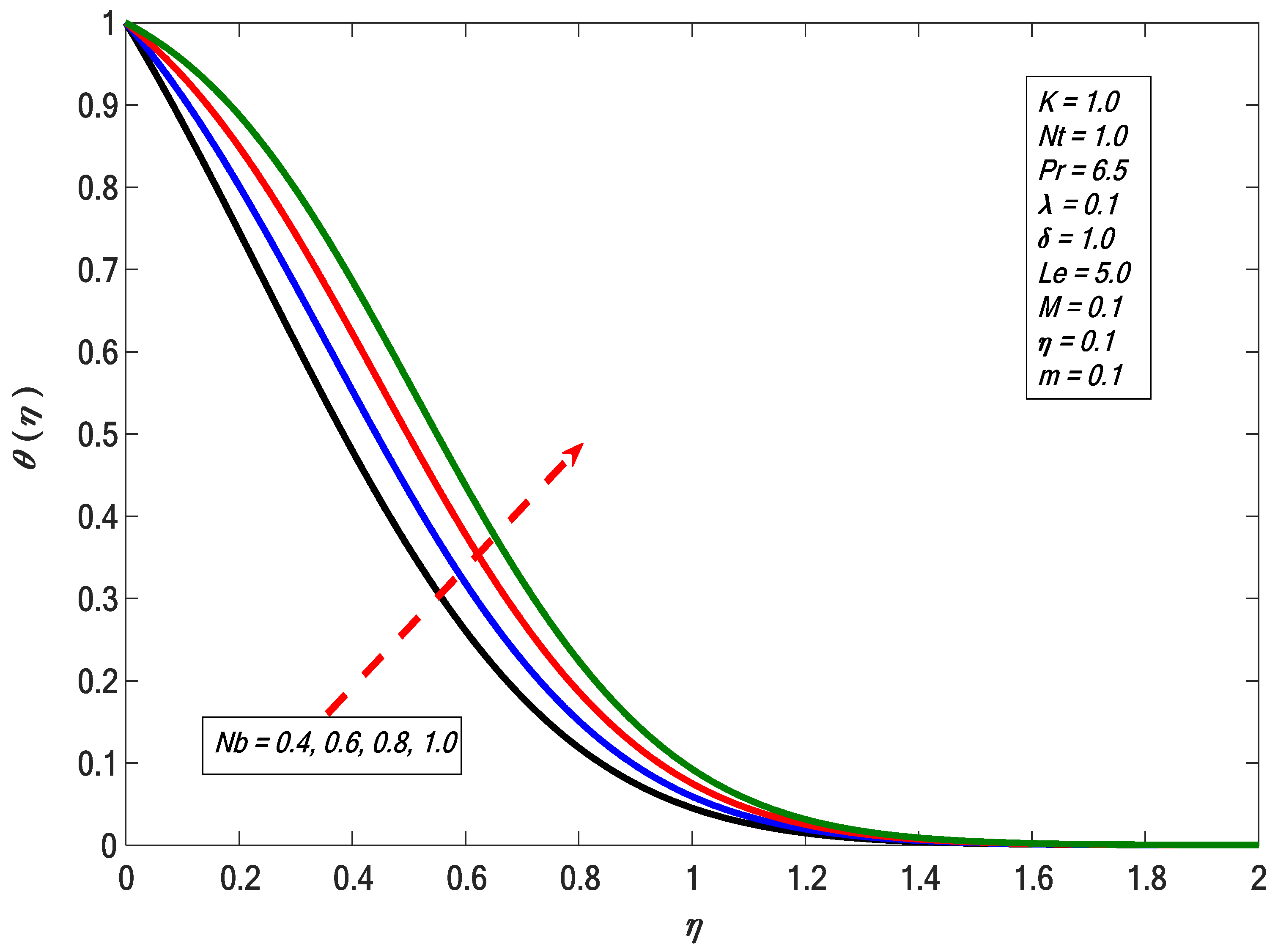
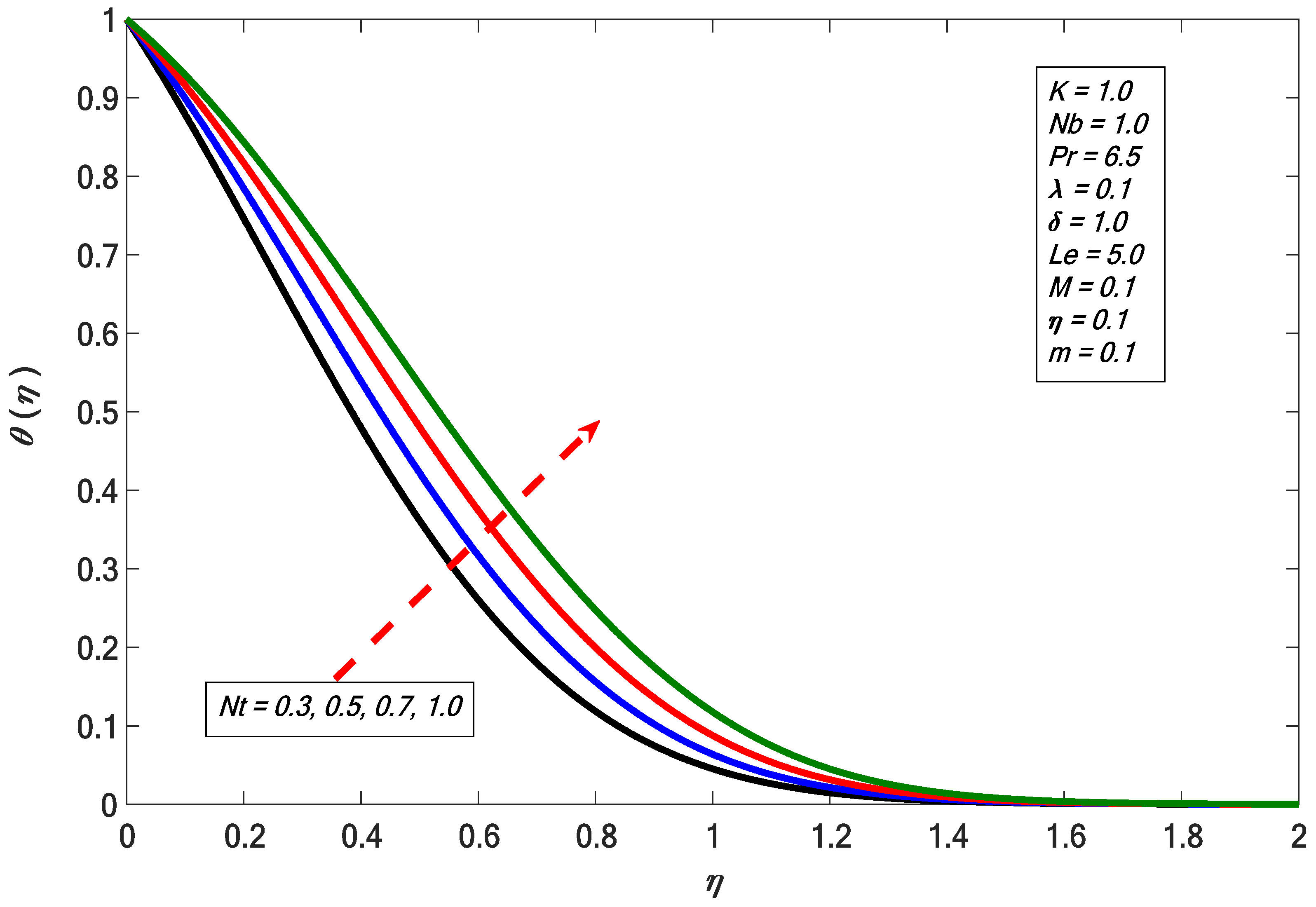
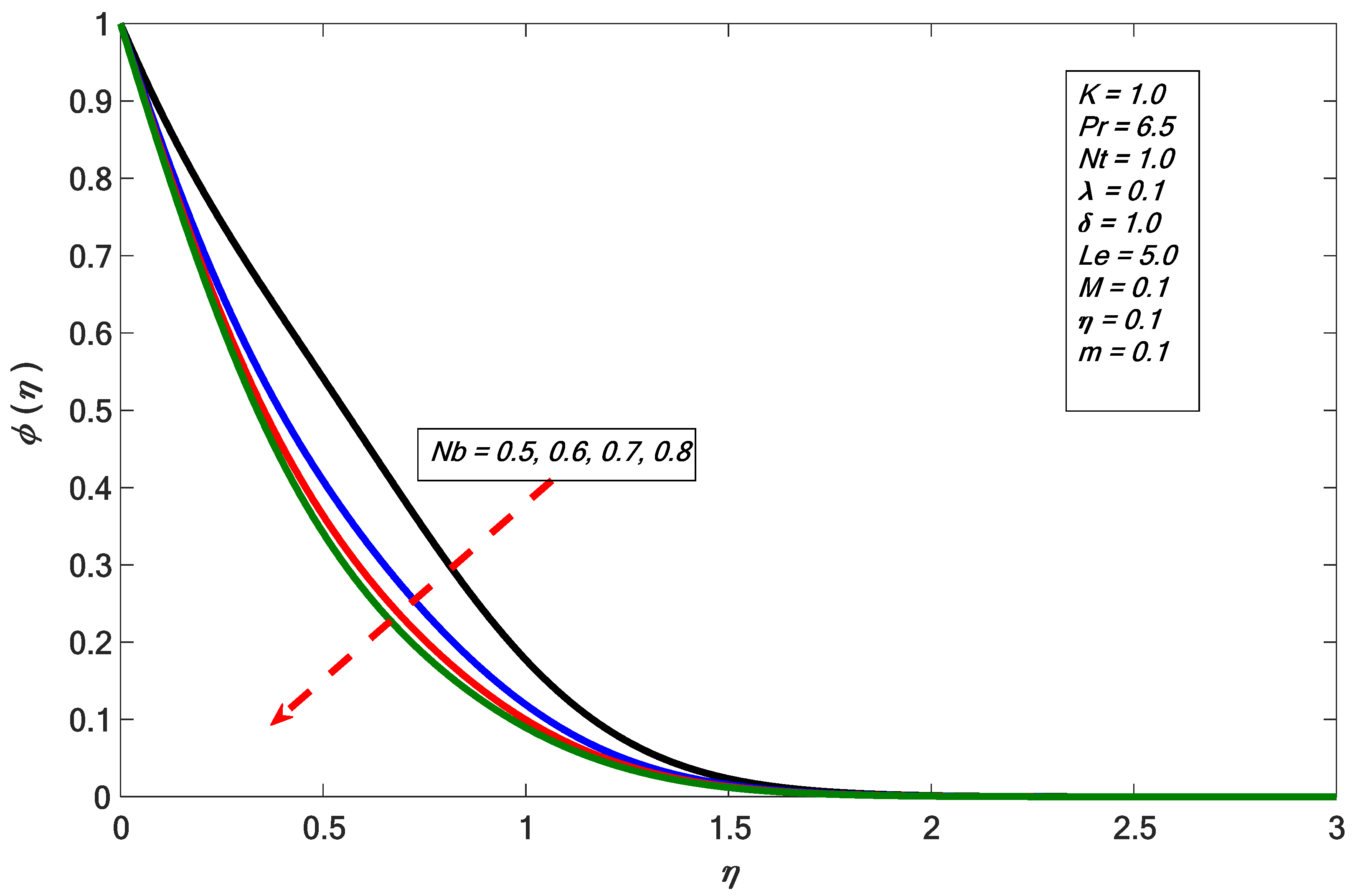
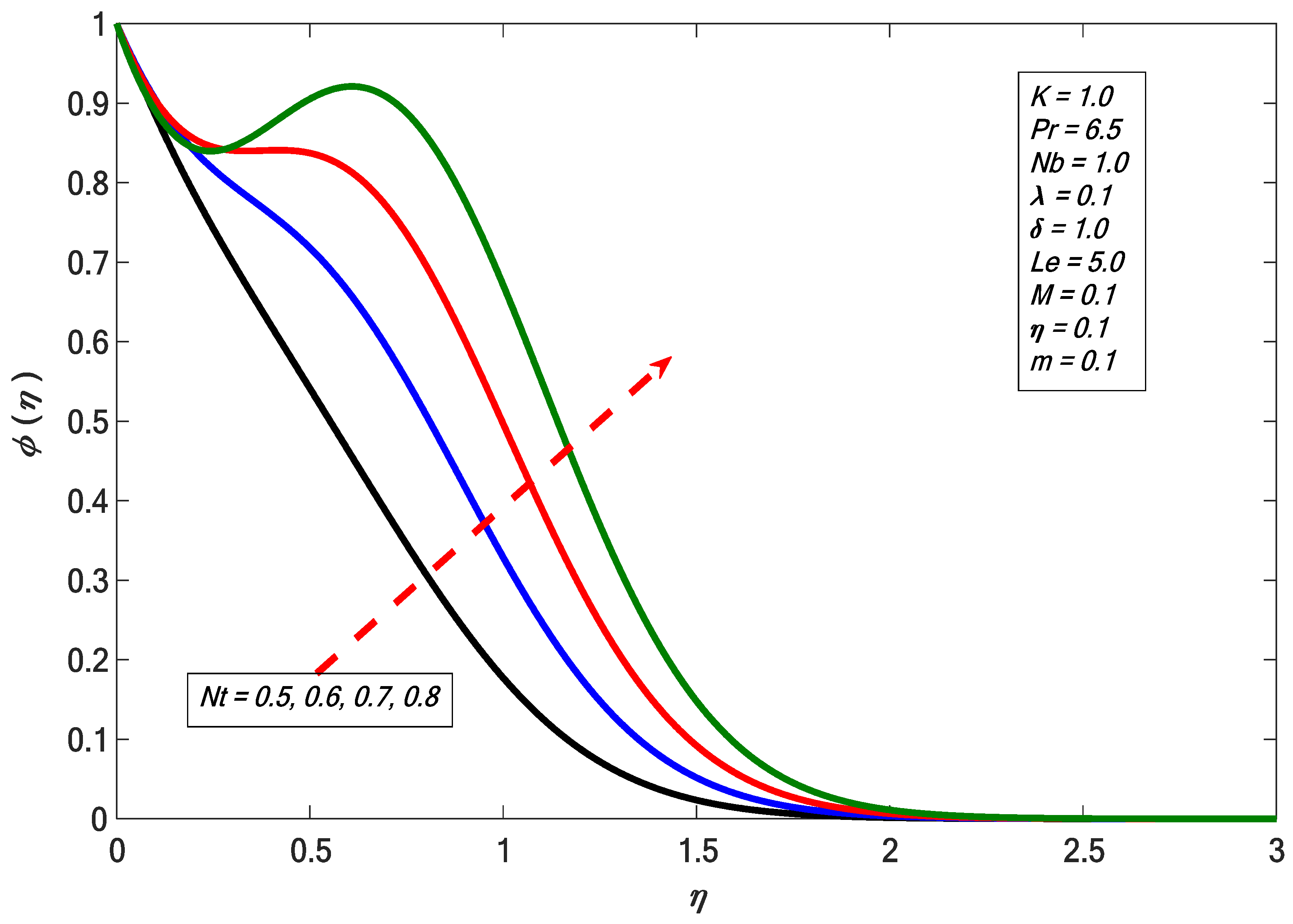
- The temperature distribution increases, whereas concentration distribution diminishes for larger values of Brownian motion. It is also found that concentration distribution shows a direct relation with thermophoretic impact.
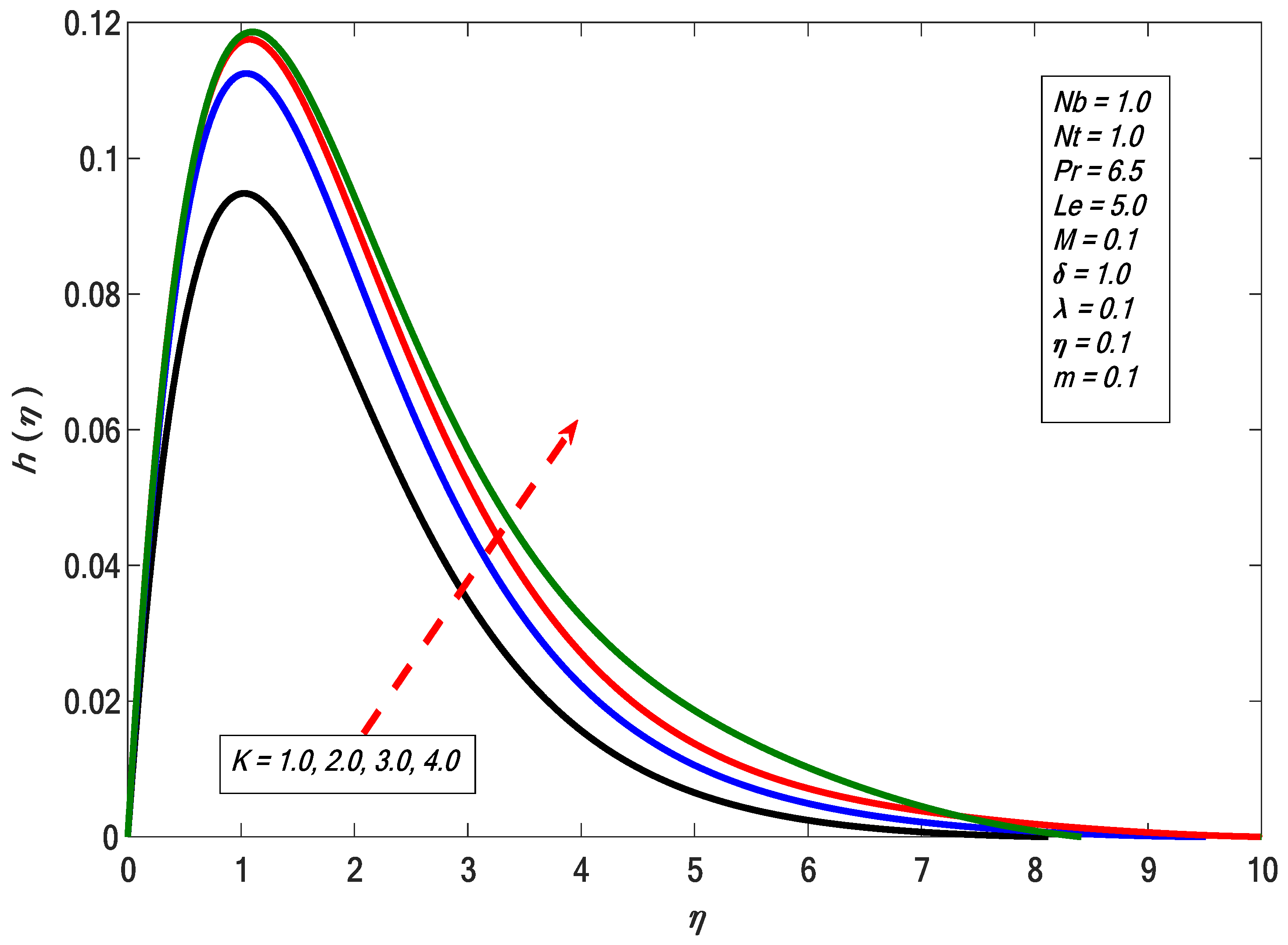
- Material parameter enhances the angular velocity profile.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Explanation | Symbols | Explanation | Symbols | Explanation |
| Fluid concentration | Electrodes and magnets width | Applied density | |||
| Coefficient of Skin friction | Thermal diffusivity | Lewis number | |||
| Stretching rate | Sherwood number | Thermophoretic factor | |||
| Surface volume fraction | liquid temperature | Nusselt number | |||
| Specific heat at constant pressure | Brownian motion factor | Gravitational acceleration | |||
| Brownian diffusion coefficient | Wall temperature | Ambient condition | |||
| Thermophoretic diffusion coefficient | Condition at the wall | Prandtl number | |||
| Dynamic viscosity | Ambient temperature | ambient velocity | |||
| Dimensionless Parameter | Kinematic viscosity | Spin gradient viscosity | |||
| Dimensionless solid volume fraction | Similarity function for velocity | wall velocity | |||
| Local Grashof number | Thermal expansion coefficient | Concentration expansion coefficient | |||
| Electric conductivity | Velocity in direction | Vertex viscosity | |||
| Micro inertia per unit mass | Material parameter | Differentiation with respect to | |||
| Similarity variable | Thermal conductivity | Cartesian coordinate | |||
| Liquid density | magnetization of variable permanent magnets | direction velocity | |||
| angular velocity | magnetic field strength | ||||
| Modified Grashof number | Reynolds number | Ambient volume fraction |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; (No. ANL/MSD/CP-84938; CONF-951135-29); Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Rafique, K.; Alotaibi, H.; Nofal, T.A.; Anwar, M.I.; Misiran, M.; Khan, I. Numerical Solutions of Micropolar Nanofluid over an Inclined Surface Using Keller Box Analysis. J. Math. 2020, 2020, 6617652. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif, E.-S.M.; Sooppy Nisar, K. Keller-box simulation for the buongiorno mathematical model of micropolar nanofluid flow over a nonlinear inclined surface. Processes 2019, 7, 926. [Google Scholar] [CrossRef] [Green Version]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Asjad, M.I. Energy and mass transport of micropolar nanofluid flow over an inclined surface with Keller-Box simulation. Heat Transf. 2020, 49, 4592–4611. [Google Scholar] [CrossRef]
- Alotaibi, H.; Althubiti, S.; Eid, M.R.; Mahny, K.L. Numerical treatment of MHD flow of casson nanofluid via convectively heated non-linear extending surface with viscous dissipation and suction/injection effects. Comput. Mater. Contin. 2020, 66, 229–245. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif ES, M.; Nisar, K.S. Brownian motion and thermophoretic diffusion effects on micropolar type nanofluid flow with Soret and Dufour impacts over an inclined sheet: Keller-box simulations. Energies 2019, 12, 4191. [Google Scholar] [CrossRef] [Green Version]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow towards a stagnation point on a stretching/shrinking cylinder. Sci. Rep. 2020, 10, 9296. [Google Scholar] [CrossRef] [PubMed]
- Khashi’ie, N.S.; Waini, I.; Zainal, N.A.; Hamzah, K.; Mohd Kasim, A.R. Hybrid Nanofluid Flow Past a Shrinking Cylinder with Prescribed Surface Heat Flux. Symmetry 2020, 12, 1493. [Google Scholar] [CrossRef]
- Rashad, A.M.; Khan, W.A.; EL-Kabeir, S.M.; EL-Hakiem, A. Mixed convective flow of micropolar nanofluid across a horizontal cylinder in saturated porous medium. Appl. Sci. 2019, 9, 5241. [Google Scholar] [CrossRef] [Green Version]
- Reddy, P.S.; Sreedevi, P.; Chamkha, A.J. MHD natural convection boundary layer flow of nanofluid over a vertical cone with chemical reaction and suction/injection. Comput. Therm. Sci. Int. J. 2017, 9, 1663–1668. [Google Scholar]
- Rasool, G.; Zhang, T.; Chamkha, A.J.; Shafiq, A.; Tlili, I.; Shahzadi, G. Entropy generation and consequences of binary chemical reaction on MHD Darcy–Forchheimer Williamson nanofluid flow over non-linearly stretching surface. Entropy 2020, 22, 18. [Google Scholar] [CrossRef] [Green Version]
- Hazarika, S.; Ahmed, S.; Chamkha, A.J. Investigation of nanoparticles Cu, Ag and Fe3O4 on thermophoresis and viscous dissipation of MHD nanofluid over a stretching sheet in a porous regime: A numerical modeling. Math. Comput. Simul. 2021, 182, 819–837. [Google Scholar] [CrossRef]
- Gailitis, A. On the possibility to reduce the hydrodynamic drag of a plate in an electrolyte. Appl. Magnetohydrodyn. Rep. Inst. Phys. Riga 1961, 13, 143–146. [Google Scholar]
- Ramzan, M.; Bilal, M.; Chung, J.D. Radiative Williamson nanofluid flow over a convectively heated Riga plate with chemical reaction-A numerical approach. Chin. J. Phys. 2017, 55, 1663–1673. [Google Scholar] [CrossRef]
- Iqbal, Z.; Azhar, E.; Mehmood, Z.; Maraj, E.N. Melting heat transport of nanofluidic problem over a Riga plate with erratic thickness: Use of Keller Box scheme. Results Phys. 2017, 7, 3648–3658. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Md Arifin, N.; Pop, I. Mixed convective stagnation point flow towards a vertical riga plate in hybrid Cu-Al2O3/water nanofluid. Mathematics 2020, 8, 912. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, T.; Ayub, M.; Farooq, M.; Alsaedi, A. Flow of nanofluid due to convectively heated Riga plate with variable thickness. J. Mol. Liq. 2016, 222, 854–862. [Google Scholar] [CrossRef]
- Nadeem, S.; Malik, M.Y.; Abbas, N. Heat transfer of three-dimensional micropolar fluid on a Riga plate. Can. J. Phys. 2020, 98, 32–38. [Google Scholar] [CrossRef]
- Ahmad, R.; Mustafa, M.; Turkyilmazoglu, M. Buoyancy effects on nanofluid flow past a convectively heated vertical Riga-plate: A numerical study. Int. J. Heat Mass Transf. 2017, 111, 827–835. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Hussanan, A. Second law analysis of dissipative flow over a riga plate with non-linear Rosseland thermal radiation and variable transport properties. Entropy 2018, 20, 615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mollah, M.T. EMHD laminar flow of Bingham fluid between two parallel Riga plates. Int. J. Heat Tech. 2019, 37, 641–648. [Google Scholar] [CrossRef] [Green Version]
- Khatun, S.; Islam, M.M.; Mollah, M.T.; Poddar, S.; Alam, M.M. EMHD radiating fluid flow along a vertical Riga plate with suction in a rotating system. SN Appl. Sci. 2021, 3, 452. [Google Scholar] [CrossRef]
- Wakif, A.; Chamkha, A.; Animasaun, I.L.; Zaydan, M.; Waqas, H.; Sehaqui, R. Novel physical insights into the thermodynamic irreversibilities within dissipative EMHD fluid flows past over a moving horizontal riga plate in the coexistence of wall suction and joule heating effects: A comprehensive numerical investigation. Arab. J. Sci. Eng. 2020, 45, 9423–9438. [Google Scholar] [CrossRef]
- Modather, M. CHAMKHA: A An analytical study of MHD heat and mass transfer oscillatory flow of a micropolar fluid over a vertical permeable plate in a porous medium. Turk. J. Eng. Environ. Sci. 2010, 33, 245–258. [Google Scholar]
- Ibrahim, W. MHD boundary layer flow and heat transfer of micropolar fluid past a stretching sheet with second order slip. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 791–799. [Google Scholar] [CrossRef]
- Yasmin, A.; Ali, K.; Ashraf, M. Study of heat and mass transfer in MHD flow of micropolar fluid over a curved stretching sheet. Sci. Rep. 2020, 10, 4581. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Sherif ES, M.; Seikh, A.H. Magnetohydrodynamic (MHD) flow of micropolar fluid with effects of viscous dissipation and Joule heating over an exponential shrinking sheet: Triple solutions and stability analysis. Symmetry 2020, 12, 142. [Google Scholar] [CrossRef] [Green Version]
- Abbas, N.; Saleem, S.; Nadeem, S.; Alderremy, A.A.; Khan, A.U. On stagnation point flow of a micro polar nanofluid past a circular cylinder with velocity and thermal slip. Results Phys. 2018, 9, 1224–1232. [Google Scholar] [CrossRef]
- Uddin, M.S.; Bhattacharyya, K.; Shafie, S. Micropolar fluid flow and heat transfer over an exponentially permeable shrinking sheet. Propuls. Power Res. 2016, 5, 310–317. [Google Scholar]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Anjum, A.; Mir, N.A.; Farooq, M.; Javed, M.; Ahmad, S.; Malik, M.Y.; Alshomrani, A.S. Physical aspects of heat generation/absorption in the second grade fluid flow due to Riga plate: Application of Cattaneo-Christov approach. Results Phys. 2018, 9, 955–960. [Google Scholar] [CrossRef]
- Ganesh, N.V.; Al-Mdallal, Q.M.; Al Fahel, S.; Dadoa, S. Riga–Plate flow of γ Al2O3-water/ethylene glycol with effective Prandtl number impacts. Heliyon 2019, 5, e01651. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| Nt | Nb | Current Results | Khan and Pop [30] | ||
|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.9524 | 2.1294 | 0.9524 | 2.1294 |
| 0.2 | 0.2 | 0.3654 | 2.5152 | 0.3654 | 2.5152 |
| 0.3 | 0.3 | 0.1355 | 2.6088 | 0.1355 | 2.6088 |
| 0.4 | 0.4 | 0.0495 | 2.6038 | 0.0495 | 2.6038 |
| 0.5 | 0.5 | 0.0179 | 2.5731 | 0.0179 | 2.5731 |
| Nb | Nt | Pr | Le | M | K | λ | δ | m | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 0.1 | 1.0 | 0.1 | 1.0 | 1.1488 | 1.2659 | 0.7564 |
| 0.4 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 0.1 | 1.0 | 0.1 | 1.0 | 0.3633 | 1.7258 | 0.8366 |
| 0.1 | 0.4 | 6.5 | 5.0 | 0.1 | 1.0 | 0.1 | 1.0 | 0.1 | 1.0 | 0.6376 | 1.5645 | 0.5416 |
| 0.1 | 0.1 | 10.0 | 5.0 | 0.1 | 1.0 | 0.1 | 1.0 | 0.1 | 1.0 | 1.1865 | 1.2812 | 0.7506 |
| 0.1 | 0.1 | 6.5 | 10.0 | 0.1 | 1.0 | 0.1 | 1.0 | 0.1 | 1.0 | 1.0219 | 2.2157 | 0.8756 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.3 | 1.0 | 0.1 | 1.0 | 0.1 | 1.0 | 1.1627 | 1.3111 | 0.4994 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 2.0 | 0.1 | 1.0 | 0.1 | 1.0 | 1.1549 | 1.2849 | 0.9665 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 0.3 | 1.0 | 0.1 | 1.0 | 1.1511 | 1.2702 | 0.6935 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 0.1 | 2.0 | 0.1 | 1.0 | 1.1646 | 1.2986 | 0.3694 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 0.1 | 1.0 | 0.3 | 1.0 | 1.1473 | 1.2608 | 0.7824 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 0.1 | 1.0 | 0.1 | 1.0 | 1.1480 | 1.2633 | 0.7699 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alotaibi, H.; Rafique, K. Numerical Analysis of Micro-Rotation Effect on Nanofluid Flow for Vertical Riga Plate. Crystals 2021, 11, 1315. https://doi.org/10.3390/cryst11111315
Alotaibi H, Rafique K. Numerical Analysis of Micro-Rotation Effect on Nanofluid Flow for Vertical Riga Plate. Crystals. 2021; 11(11):1315. https://doi.org/10.3390/cryst11111315
Chicago/Turabian StyleAlotaibi, Hammad, and Khuram Rafique. 2021. "Numerical Analysis of Micro-Rotation Effect on Nanofluid Flow for Vertical Riga Plate" Crystals 11, no. 11: 1315. https://doi.org/10.3390/cryst11111315
APA StyleAlotaibi, H., & Rafique, K. (2021). Numerical Analysis of Micro-Rotation Effect on Nanofluid Flow for Vertical Riga Plate. Crystals, 11(11), 1315. https://doi.org/10.3390/cryst11111315






