Multivariate Analysis Applications in X-ray Diffraction
Abstract
1. Introduction
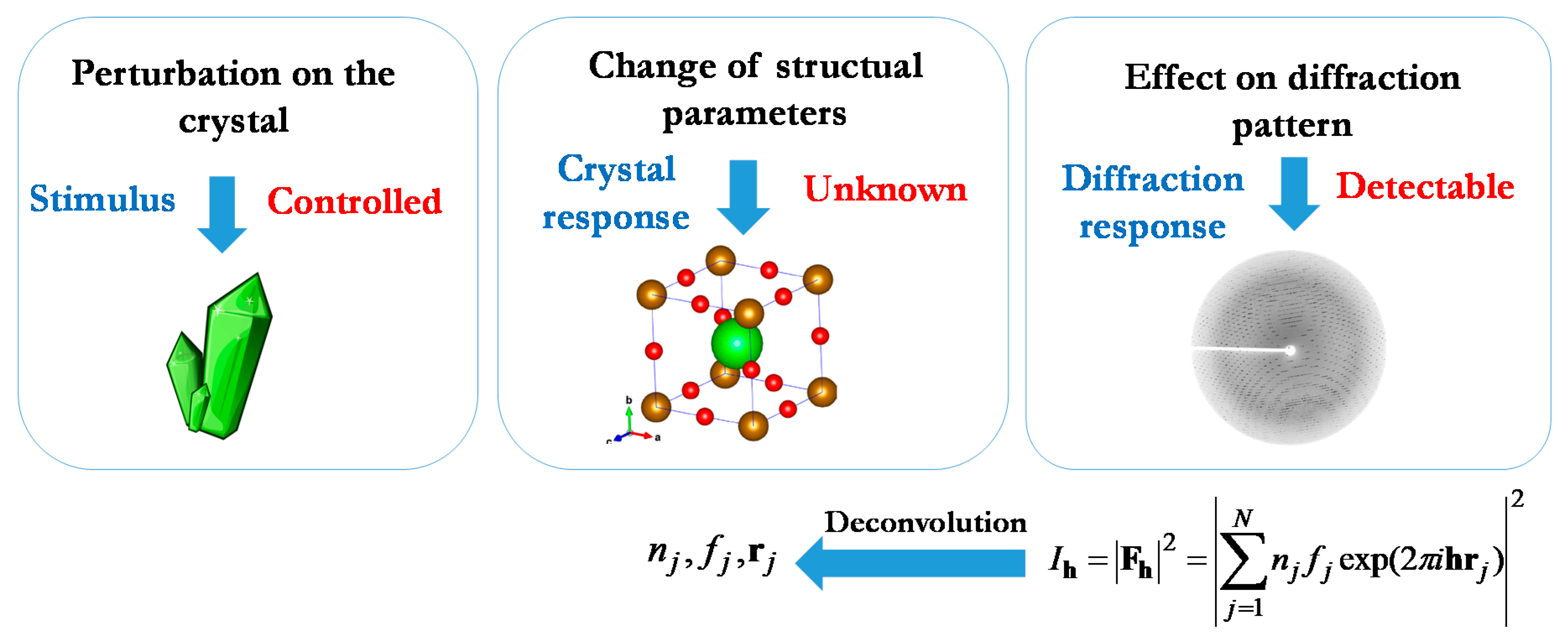
2. Multivariate Methods
2.1. High Dimension and Overfitting
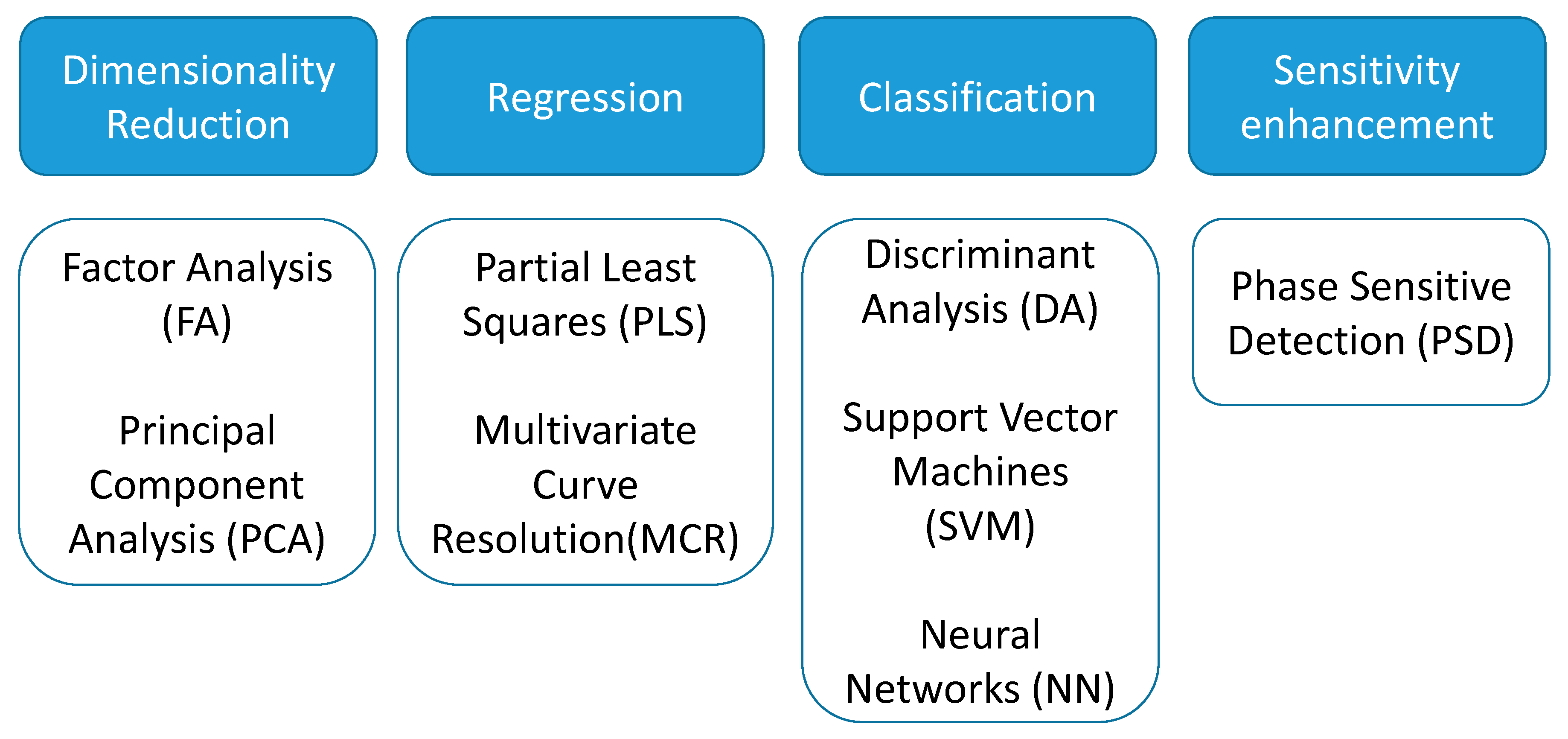
2.2. Dimensionality Reduction Methods
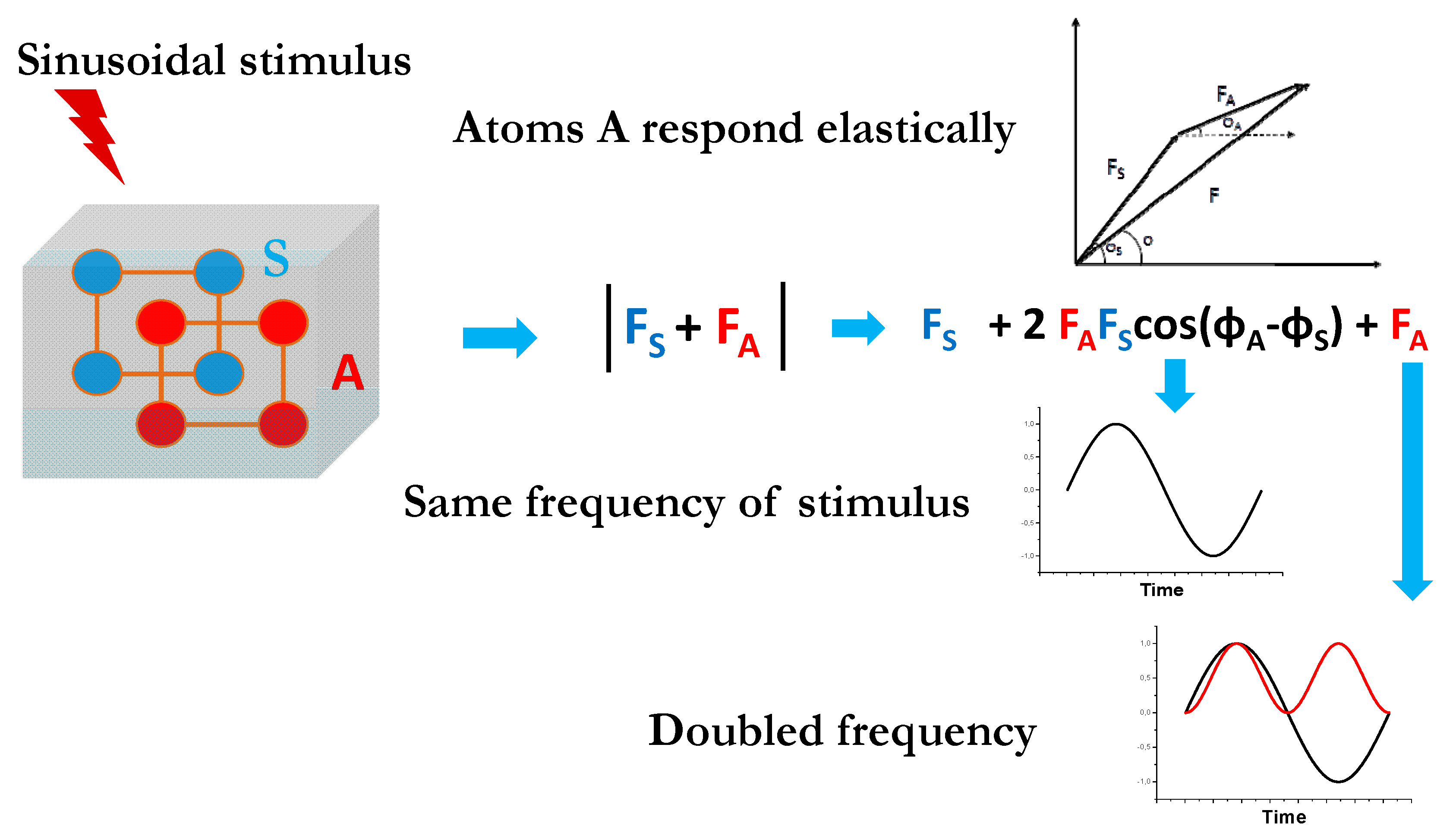
3. Modulated Enhanced Diffraction
Deconvolution Methods
4. Applications in Powder X-ray Diffraction
4.1. Kinetic Studies by Single or Multi-Probe Experiments
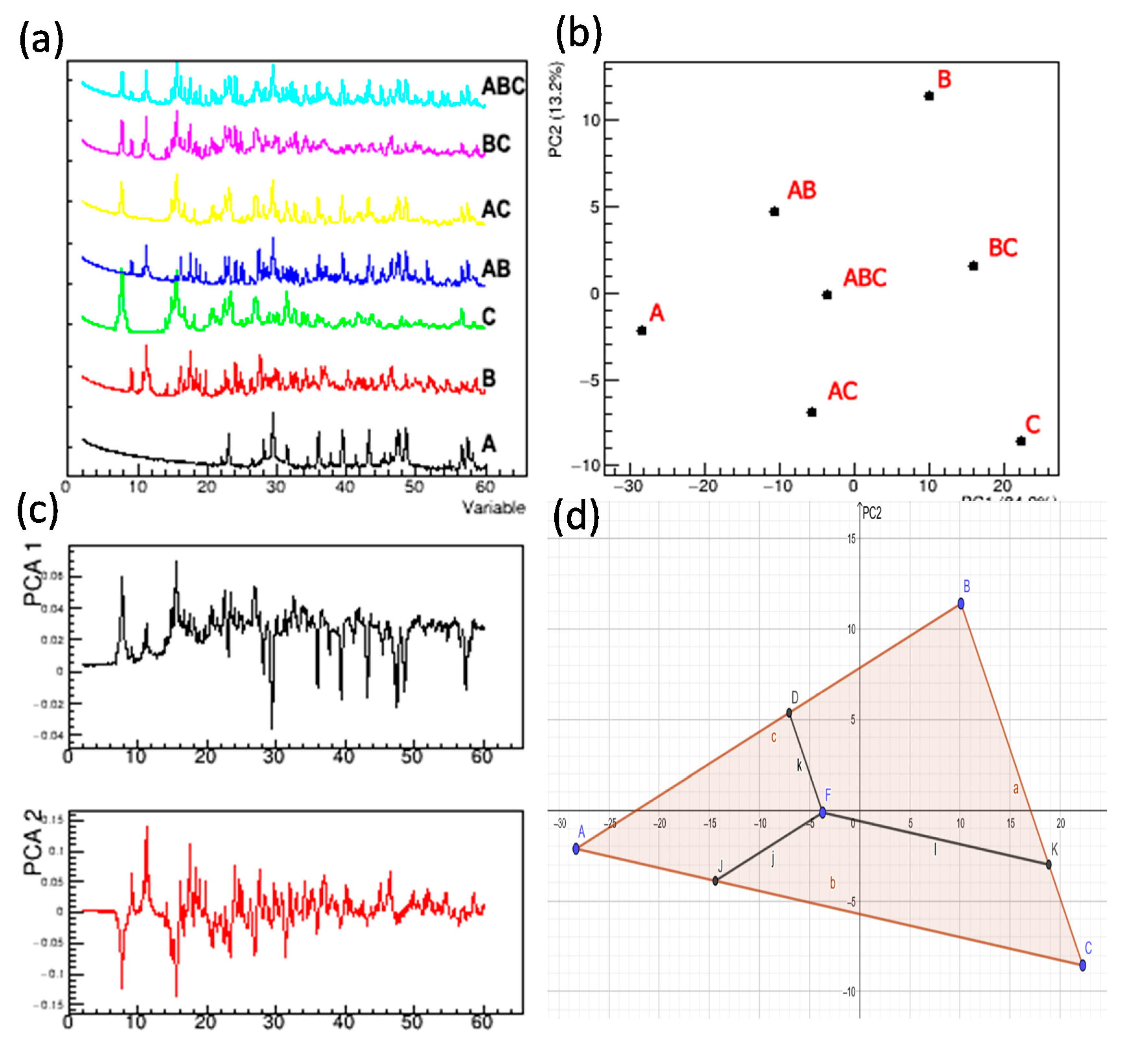
4.2. Qualitative and Quantitative Studies
5. Applications in Single-Crystal X-ray Diffraction
5.1. Multivariate Approaches to Solve the Phase Problem
5.2. Merging of Single-Crystal Datasets
5.3. Crystal Monitoring
6. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Pearson, K.; Yule, G.U.; Blanchard, N.; Lee, A. The Law of Ancestral Heredity. Biometrika 1903, 2, 211–236. [Google Scholar] [CrossRef]
- Yule, G.U. On the Theory of Correlation. J. R. Stat. Soc. 1897, 60, 812–854. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Components Analysis, 2nd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Brereton, R.G. The evolution of chemometrics. Anal. Methods 2013, 5, 3785–3789. [Google Scholar] [CrossRef]
- Massart, D.L. The use of information theory for evaluating the quality of thin-layer chromatographic separations. J. Chromatogr. A 1973, 79, 157–163. [Google Scholar] [CrossRef]
- Child, D. The Essentials of Factor Analysis, 3rd ed.; Bloomsbury Academic Press: London, UK, 2006. [Google Scholar]
- Bro, R.; Smilde, A.K. Principal Component Analysis. Anal. Methods 2014, 6, 2812–2831. [Google Scholar] [CrossRef]
- De Juan, A.; Jaumot, J.; Tauler, R. Multivariate Curve Resolution (MCR). Solving the mixture analysis problem. Anal. Methods 2014, 6, 4964–4976. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Hellberg, S.; Sjöström, M.; Wold, S. The prediction of bradykinin potentiating potency of pentapeptides, an example of a peptide quantitative structure–activity relationship. Acta Chem. Scand. B 1986, 40, 135–140. [Google Scholar] [CrossRef]
- Di Profio, G.; Salehi, S.M.; Caliandro, R.; Guccione, P. Bioinspired Synthesis of CaCO3 Superstructures through a Novel Hydrogel Composite Membranes Mineralization Platform: A Comprehensive View. Adv. Mater. 2015, 28, 610–616. [Google Scholar] [CrossRef]
- Ballabio, D.; Consonni, V. Classification tools in chemistry: Part 1: Linear models. PLS-DA. Anal. Methods 2013, 5, 3790–3798. [Google Scholar] [CrossRef]
- Xu, Y.; Zomer, S.; Brereton, R. Support vector machines: A recent method for classification in chemometrics. Crit. Rev. Anal. Chem. 2006, 36, 177–188. [Google Scholar] [CrossRef]
- Ellis, D.L.; Brewster, V.L.; Dunn, W.B.; Allwood, J.W.; Golovanov, A.P.; Goodacrea, R. Fingerprinting food: Current technologies for the detection of food adulteration and contamination. Chem. Soc. Rev. 2012, 41, 5706–5727. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Guerra, M.; Ballabio, D.; Amigo, J.M.; Viguri, J.R.; Bro, R. A chemometric approach to the environmental problem of predicting toxicity in contaminated sediments. J. Chemom. 2009, 24, 379–386. [Google Scholar] [CrossRef]
- Heinemann, J.; Mazurie, A.; Lukaszewska, M.T.; Beilman, G.L.; Bothner, B. Application of support vector machines to metabolomics experiments with limited replicates. Metabolomics 2014, 10, 1121–1128. [Google Scholar] [CrossRef]
- Huang, S.; Cai, N.; Pacheco, P.P.; Narandes, S.; Wang, Y.; Xu, W. Applications of SVM Learning Cancer Genomics. Cancer Genom. Proteom. 2018, 15, 41–51. [Google Scholar]
- Schwaighofer, A.; Ferfuson-Miller, S.; Naumann, R.L.; Knoll, W.; Nowak, C. Phase-sensitive detection in modulation excitation spectroscopy applied to potential induced electron transfer in crytochrome c oxidase. Appl. Spectrosc. 2014, 68, 5–13. [Google Scholar] [CrossRef]
- Izenmann, A.J. Introduction to Manifold Learning. WIREs Comput. Stat. 2012, 4, 439–446. [Google Scholar] [CrossRef]
- Jaumot, J.; Tauler, R.; Gargallo, R. Exploratory data analysis of DNA microarrays by multivariate curve resolution. Anal. Biochem. 2006, 358, 76–89. [Google Scholar] [CrossRef]
- Culhane, A.C.; Thioulouse, J.; Perrière, G.; Higgins, D.G. MADE4: An R package for multivariate analysis of gene expression data. Bioinformatics 2005, 21, 2789–2790. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning, 8th ed.; Casella, G., Fienberg, S., Olkin, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; p. 204. [Google Scholar]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L. A Practical Approach to Feature Selection. In Proceedings of the Ninth International Workshop on Machine Learning, Aberdeen, UK, 1–3 July 1992; pp. 249–256. [Google Scholar]
- Kumar, A.P.; Valsala, P. Feature Selection for high Dimensional DNA Microarray data using hybrid approaches. Bioinformation 2013, 9, 824–828. [Google Scholar] [CrossRef]
- Giannopoulou, E.G.; Garbis, S.D.; Vlahou, A.; Kossida, S.; Lepouras, G.; Manolakos, E.S. Proteomic feature maps: A new visualization approach in proteomics analysis. J. Biomed. Inform. 2009, 42, 644–653. [Google Scholar] [CrossRef] [PubMed]
- Lualdi, M.; Fasano, M. Statistical analysis of proteomics data: A review on feature selection. J. Proteom. 2019, 198, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Anton, H.; Rorres, C. Elementary Linear Algebra (Applications Version), 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Stasiak, J.; Koba, M.; Gackowski, M.; Baczek, T. Chemometric Analysis for the Classification of some Groups of Drugs with Divergent Pharmacological Activity on the Basis of some Chromatographic and Molecular Modeling Parameters. Comb. Chem. High Throughput Screen. 2018, 21, 125–137. [Google Scholar] [CrossRef] [PubMed]
- Harshman, R.A.; Hong, S.; Lundy, M.E. Shifted factor analysis—Part I: Models and properties. J. Chemometr. 2003, 17, 363–378. [Google Scholar] [CrossRef]
- Hong, S. Warped factor analysis. J. Chemom. 2009, 23, 371–384. [Google Scholar] [CrossRef]
- Zhou, Y.; Wilkinson, D.; Schreiber, R.; Pan, R. Large-Scale Parallel Collaborative Filtering for the Netflix Prize. In Algorithmic Aspects in Information and Management; Springer: Berlin/Heidelberg, Germany, 2008; pp. 337–348. [Google Scholar]
- Chernyshov, D.; Van Beek, W.; Emerich, H.; Milanesio, M.; Urakawa, A.; Viterbo, D.; Palin, L.; Caliandro, R. Kinematic diffraction on a structure with periodically varying scattering function. Acta Cryst. A 2011, 67, 327–335. [Google Scholar] [CrossRef]
- Urakawa, A.; Van Beek, W.; Monrabal-Capilla, M.; Galán-Mascarós, J.R.; Palin, L.; Milanesio, M. Combined, Modulation Enhanced X-ray Powder Diffraction and Raman Spectroscopic Study of Structural Transitions in the Spin Crossover Material [Fe(Htrz)2(trz)](BF4)]. J. Phys. Chem. C 2011, 115, 1323–1329. [Google Scholar] [CrossRef]
- Uschmajew, A. Local Convergence of the Alternating Least Square Algorithm for Canonical Tensor Approximation. J. Matrix Anal. Appl. 2012, 33, 639–652. [Google Scholar] [CrossRef]
- Comona, P.; Luciania, X.; De Almeida, A.L.F. Tensor decompositions, alternating least squares and other tales. J. Chemom. 2009, 23, 393–405. [Google Scholar] [CrossRef]
- Malinowski, E.R. Theory of the distribution of error eigenvalues resulting from principal component analysis with applications to spectroscopic data. J. Chemom. 1987, 1, 33–40. [Google Scholar] [CrossRef]
- Malinowski, E.R. Statistical F-tests for abstract factor analysis and target testing. J. Chemom. 1989, 3, 49–60. [Google Scholar] [CrossRef]
- Guttman, L. Some necessary conditions for common factor analysis. Psychometrika 1954, 19, 149–161. [Google Scholar] [CrossRef]
- Kaiser, H.F. The application of electronic computers to factor analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Caliandro, R.; Guccione, P.; Nico, G.; Tutuncu, G.; Hanson, J.C. Tailored Multivariate Analysis for Modulated Enhanced Diffraction. J. Appl. Cryst. 2015, 48, 1679–1691. [Google Scholar] [CrossRef]
- Silverman, B.W. Smoothed functional principal components analysis by choice of norm. Ann. Stat. 1996, 24, 1–24. [Google Scholar] [CrossRef]
- Chen, Z.-P.; Liang, Y.-Z.; Jiang, J.-H.; Li, Y.; Qian, J.-Y.; Yu, R.-Q. Determination of the number of components in mixtures using a new approach incorporating chemical information. J. Chemom. 1999, 13, 15–30. [Google Scholar] [CrossRef]
- Dharmayat, S.; Hammond, R.B.; Lai, X.; Ma, C.; Purba, E.; Roberts, K.J.; Chen, Z.-P.; Martin, E.; Morris, J.; Bytheway, R. An Examination of the Kinetics of the Solution-Mediated Polymorphic Phase Transformation between α- and β-Forms of l-Glutamic Acid as Determined Using Online Powder X-ray Diffraction. Cryst. Growth Des. 2008, 8, 2205–2216. [Google Scholar] [CrossRef]
- Turner, T.D.; Caddick, S.; Hammond, R.B.; Roberts, K.J.; Lai, X. Kinetics of the Aqueous-Ethanol Solution Mediated Transformation between the Beta and Alpha Polymorphs of p-Aminobenzoic Acid. Cryst. Growth Des. 2018, 18, 1117–1125. [Google Scholar] [CrossRef]
- Caliandro, R.; Chernyshov, D.; Emerich, H.; Milanesio, M.; Palin, L.; Urakawa, A.; Van Beek, W.; Viterbo, D. Patterson selectivity by modulation-enhanced diffraction. J. Appl. Cryst. 2012, 45, 458–470. [Google Scholar] [CrossRef]
- Palin, L.; Caliandro, R.; Viterbo, D.; Milanesio, M. Chemical selectivity in structure determination by the time dependent analysis of in situ XRPD data: A clear view of Xe thermal behavior inside a MFI zeolite. Phys. Chem. Chem. Phys. 2015, 17, 17480–17493. [Google Scholar] [CrossRef] [PubMed]
- Guccione, P.; Palin, L.; Milanesio, M.; Belviso, B.D.; Caliandro, R. Improved multivariate analysis for fast and selective monitoring of structural dynamics by in situ X-ray powder diffraction. Phys. Chem. Chem. Phys. 2018, 20, 2175–2187. [Google Scholar] [CrossRef] [PubMed]
- Chernyshov, D.; Dovgaliuk, I.; Dyadkin, V.; Van Beek, W. Principal Component Analysis (PCA) for Powder Diffraction Data: Towards Unblinded Applications. Crystals 2020, 10, 581. [Google Scholar] [CrossRef]
- Conterosito, E.; Palin, L.; Caliandro, R.; Van Beek, W.; Chernyshov, D.; Milanesio, M. CO2 adsorption in Y zeolite: A structural and dynamic view by a novel principal-component-analysis-assisted in situ single-crystal X-ray diffraction experiment. Acta Cryst. A 2019, 75, 214–222. [Google Scholar] [CrossRef] [PubMed]
- Lopresti, M.; Palin, L.; Alberto, G.; Cantamessa, S.; Milanesio, M. Epoxy resins composites for X-ray shielding materials additivated by coated barium sulfate with improved dispersibility. Mater. Today Commun. 2020, 20, 101888. [Google Scholar] [CrossRef]
- Palin, L.; Milanesio, M.; Van Beek, W.; Conterosito, E. Understanding the Ion Exchange Process in LDH Nanomaterials by Fast In Situ XRPD and PCA-Assisted Kinetic Analysis. J. Nanomater. 2019, 2019, 4612493. [Google Scholar] [CrossRef]
- Kumar, S.; Carniato, F.; Arrais, A.; Croce, G.; Boccaleri, E.; Palin, L.; Van Beek, W.; Milanesio, M. Investigating Surface vs Bulk Kinetics in the Formation of a Molecular Complex via Solid-State Reaction by Simultaneous Raman/X-ray Powder Diffraction. Cryst. Growth Des. 2009, 9, 3396–3404. [Google Scholar] [CrossRef]
- Matos, C.R.S.; Xavier, M.J.; Barreto, L.S.; Costa, N.B.; Gimenez, I.F. Principal Component Analysis of X-Ray Diffraction Patterns to Yield Morphological Classification of Brucite Particles. Anal. Chem. 2007, 75, 2091–2095. [Google Scholar] [CrossRef]
- Guccione, P.; Palin, L.; Belviso, B.D.; Milanesio, M.; Caliandro, R. Principal component analysis for automatic extraction of solid-state kinetics from combined in situ experiments. Phys. Chem. Chem. Phys. 2018, 20, 19560–19571. [Google Scholar] [CrossRef]
- Conterosito, E.; Lopresti, M.; Palin, L. In Situ X-Ray Diffraction Study of Xe and CO2 Adsorption in Y Zeolite: Comparison between Rietveld and PCA-Based Analysis. Crystals 2020, 10, 483. [Google Scholar] [CrossRef]
- Rodriguez, M.A.; Keenan, M.R.; Nagasubramanian, G. In situ X-ray diffraction analysis of (CFx)n batteries: Signal extraction by multivariate analysis. J. Appl. Cryst. 2007, 40, 1097–1104. [Google Scholar] [CrossRef]
- Taris, A.; Grosso, M.; Brundu, M.; Guida, V.; Viani, A. Reaction Monitoring of Cementing Materials through Multivariate Techniques Applied to In Situ Synchrotron X-Ray Diffraction Data. Comput. Aided Chem. Eng. 2015, 37, 1535–1540. [Google Scholar]
- Taris, A.; Grosso, M.; Brundu, M.; Guida, V.; Viani, A. Application of combined multivariate techniques for the description of time-resolved powder X-ray diffraction data. J. Appl. Cryst. 2017, 50, 451–461. [Google Scholar] [CrossRef]
- Caliandro, R.; Altamura, D.; Belviso, B.D.; Rizzo, A.; Masi, S.; Giannini, C. Investigating temperature-induced structural changes of lead halide perovskites by in situ X-ray powder diffraction. J. Appl. Cryst. 2019, 52, 1104–1118. [Google Scholar] [CrossRef]
- Caliandro, R.; Toson, V.; Palin, L.; Conterosito, E.; Aceto, M.; Boccaleri, E.; Gianotti, V.; Dooryhee, E.; Milanesio, M. New hints on Maya Blue formation process by PCA-assisted in situ XRPD/PDF and optical spectroscopy. Chem. Eur. J. 2019, 25, 11503–11511. [Google Scholar] [CrossRef]
- Rizzuti, A.; Caliandro, R.; Gallo, V.; Mastrorilli, P.; Chita, G.; Latronico, M. A combined approach for characterisation of fresh and brined vine leaves by X-ray powder diffraction, NMR spectroscopy and direct infusion high resolution mass spectrometry. Food Chem. 2013, 141, 1908–1915. [Google Scholar] [CrossRef] [PubMed]
- Fomina, E.; Kozlov, E.; Bazai, A. Factor Analysis of XRF and XRPD Data on the Example of the Rocks of the Kontozero Carbonatite Complex (NW Russia). Part I: Algorithm. Crystals 2020, 10, 874. [Google Scholar] [CrossRef]
- Kozlov, E.; Fomina, E.; Khvorov, P. Factor Analysis of XRF and XRPD Data on the Example of the Rocks of the Kontozero Carbonatite Complex (NW Russia). Part II: Geological Interpretation. Crystals 2020, 10, 873. [Google Scholar] [CrossRef]
- Goodpaster, A.M.; Kennedy, M.A. Quantification and statistical significance analysis of group separation in NMR-based metabonomics studies. Chemom. Intell. Lab. Syst. 2011, 109, 162–170. [Google Scholar] [CrossRef]
- Worley, B.; Halouska, S.; Powers, R. Utilities for Quantifying Separation in PCA/PLS-DA Scores Plots. Anal. Biochem. 2013, 433, 102–104. [Google Scholar] [CrossRef] [PubMed]
- Caliandro, R.; Belviso, B.D. RootProf: Software for multivariate analysis of unidimensional profiles. J. Appl. Cryst. 2014, 47, 1087–1096. [Google Scholar] [CrossRef]
- Cornell, J.A. Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Caliandro, R.; Di Profio, G.; Nicolotti, O. Multivariate analysis of quaternary carbamazepine-saccharin mixtures by X-ray diffraction and infrared spectroscopy. J. Pharm. Biomed. Anal. 2013, 78–79, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-W.; Park, W.B.; Lee, J.H.; Sing, S.P.; Sohn, K.-S. A deep-learning technique for phase identification in multiphase inorganic compounds using synthetic XRD powder patterns. Nat. Commun. 2020, 11, 86. [Google Scholar] [CrossRef] [PubMed]
- Pannu, N.S.; McCoy, A.J.; Read, R.J. Application of the complex multivariate normal distribution to crystallographic methods with insights into multiple isomorphous replacement phasing. Acta Cryst. D 2003, 59, 1801–1808. [Google Scholar] [CrossRef] [PubMed]
- Hauptman, H.; Karle, J. The Solution of the Phase Problem. I: The Centrosymmetric Crystal; ACA Monograph No. 3; American Crystallographic Association: New York, NY, USA, 1953. [Google Scholar]
- Shmueli, U.; Weiss, G.H. Probabilistic Methods in Crystal Structure Analysis. J. Am. Stat. Assoc. 1990, 85, 6–19. [Google Scholar] [CrossRef]
- Giacovazzo, C. Direct Methods in Crystallography; Oxford University Press: Oxford, UK, 1980. [Google Scholar]
- Giacovazzo, C. Phasing in Crystallography; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Skubák, P.; Murshudov, G.N.; Pannu, N.S. Direct incorporation of experimental phase information in model refinement. Acta Cryst. D 2004, 60, 2196–2201. [Google Scholar] [CrossRef]
- Read, R.J. Pushing the boundaries of molecular replacement with maximum likelihood. Acta Cryst. D 2001, 57, 1373–1382. [Google Scholar] [CrossRef]
- David, C.C.; Jacobs, D.J. Principal component analysis: A method for determining the essential dynamics of proteins. Methods Mol. Biol. 2014, 1084, 193–226. [Google Scholar]
- Herranz-Trillo, F.; Groenning, M.; Van Maarschalkerweerd, A.; Tauler, R.; Vestergaard, B.; Bernardò, P. Structural Analysis of Multi-component Amyloid Systems by Chemometric SAXS Data Decomposition. Structure 2017, 25, 5–15. [Google Scholar] [CrossRef]
- Foadi, J.; Aller, P.; Alguel, Y.; Cameron, A.; Axford, D.; Owen, R.L.; Armour, W.; Waterman, D.G.; Iwata, S.; Evans, G. Clustering procedures for the optimal selection of data sets from multiple crystals in macromolecular crystallography. Acta Cryst. D 2013, 69, 1617–1632. [Google Scholar] [CrossRef]
- Winter, G.; Waterman, D.G.; Parkhurst, J.M.; Brewster, A.S.; Gildea, R.J.; Gerstel, M.; Fuentes-Montero, L.; Vollmar, M.; Michels-Clark, T.; Young, I.D.; et al. DIALS: Implementation and evaluation of a new integration package. Acta Cryst. D 2018, 74, 85–97. [Google Scholar] [CrossRef] [PubMed]
- Beilsten-Edmands, J.; Winter, G.; Gildea, R.; Parkhurst, J.; Waterman, D.; Evans, G. Scaling diffraction data in the DIALS software package: Algorithms and new approaches for multi-crystal scaling. Acta Cryst. D 2020, 76, 385–399. [Google Scholar] [CrossRef] [PubMed]
- Gavira, J.A.; Otálora, F.; González-Ramírez, L.A.; Melero, E.; Driessche, A.E.; García-Ruíz, J.M. On the Quality of Protein Crystals Grown under Diffusion Mass-transport Controlled Regime (I). Crystals 2020, 10, 68. [Google Scholar] [CrossRef]
- Berntson, A.; Stojanoff, V.; Takai, H. Application of a neural network in high-throughput protein crystallography. J. Synchrotron Radiat. 2003, 10, 445–449. [Google Scholar] [CrossRef] [PubMed]
- Bruno, A.E.; Charbonneau, P.; Newman, J.; Snell, E.H.; So, D.R.; Vanhoucke, V.; Watkins, C.J.; Williams, S.; Wilson, J. Classification of crystallization outcomes using deep convolutional neural networks. PLoS ONE 2018, 13, e0198883. [Google Scholar] [CrossRef]
- Mele, K.; Lekamge, B.M.T.; Fazio, V.J.; Newman, J. Using Time Courses to Enrich the Information Obtained from Images of Crystallization Trials. Cryst. Growth Des. 2014, 14, 261–269. [Google Scholar] [CrossRef]
- Snell, E.H.; Nagel, R.M.; Wojtaszcyk, A.; O’Neill, H.; Wolfley, J.L.; Luft, J.R. The application and use of chemical space mapping to interpret crystallization screening results. Acta Cryst. D 2008, 64, 1240–1249. [Google Scholar] [CrossRef]
- Available online: http://www.ba.ic.cnr.it/softwareic/rootprof/ (accessed on 24 December 2020).
- Available online: https://mcrals.wordpress.com/download/mcr-als-2-0-toolbox/ (accessed on 24 December 2020).



| Sample | Geometric Estimation from PC Scores | Regression | |||||
|---|---|---|---|---|---|---|---|
| Phase 1 | Phase 2 | Phase 3 | Phase 1 | Phase 2 | Phase 3 | ||
| 0 | 1.00 | 0.00 | 0.00 | 1.000 | 0.000 | 0.000 | |
| 1 | 0.00 | 1.00 | 0.00 | 0.000 | 1.000 | 0.000 | |
| 2 | 0.00 | 0.00 | 1.00 | 0.000 | 0.000 | 1.000 | |
| 3 | 0.53 | 0.49 | 0.00 | 0.538 | 0.462 | 0.000 | |
| 4 | 0.58 | 0.00 | 0.53 | 0.507 | 0.000 | 0.493 | |
| 5 | 0.00 | 0.51 | 0.49 | 0.000 | 0.522 | 0.478 | |
| 6 | 0.45 | 0.28 | 0.27 | 0.425 | 0.301 | 0.274 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guccione, P.; Lopresti, M.; Milanesio, M.; Caliandro, R. Multivariate Analysis Applications in X-ray Diffraction. Crystals 2021, 11, 12. https://doi.org/10.3390/cryst11010012
Guccione P, Lopresti M, Milanesio M, Caliandro R. Multivariate Analysis Applications in X-ray Diffraction. Crystals. 2021; 11(1):12. https://doi.org/10.3390/cryst11010012
Chicago/Turabian StyleGuccione, Pietro, Mattia Lopresti, Marco Milanesio, and Rocco Caliandro. 2021. "Multivariate Analysis Applications in X-ray Diffraction" Crystals 11, no. 1: 12. https://doi.org/10.3390/cryst11010012
APA StyleGuccione, P., Lopresti, M., Milanesio, M., & Caliandro, R. (2021). Multivariate Analysis Applications in X-ray Diffraction. Crystals, 11(1), 12. https://doi.org/10.3390/cryst11010012









