Factor Analysis of XRF and XRPD Data on the Example of the Rocks of the Kontozero Carbonatite Complex (NW Russia). Part I: Algorithm
Abstract
1. Introduction
2. Theory
3. Materials and Methods
3.1. Sample Description
3.2. Analytical Techniques
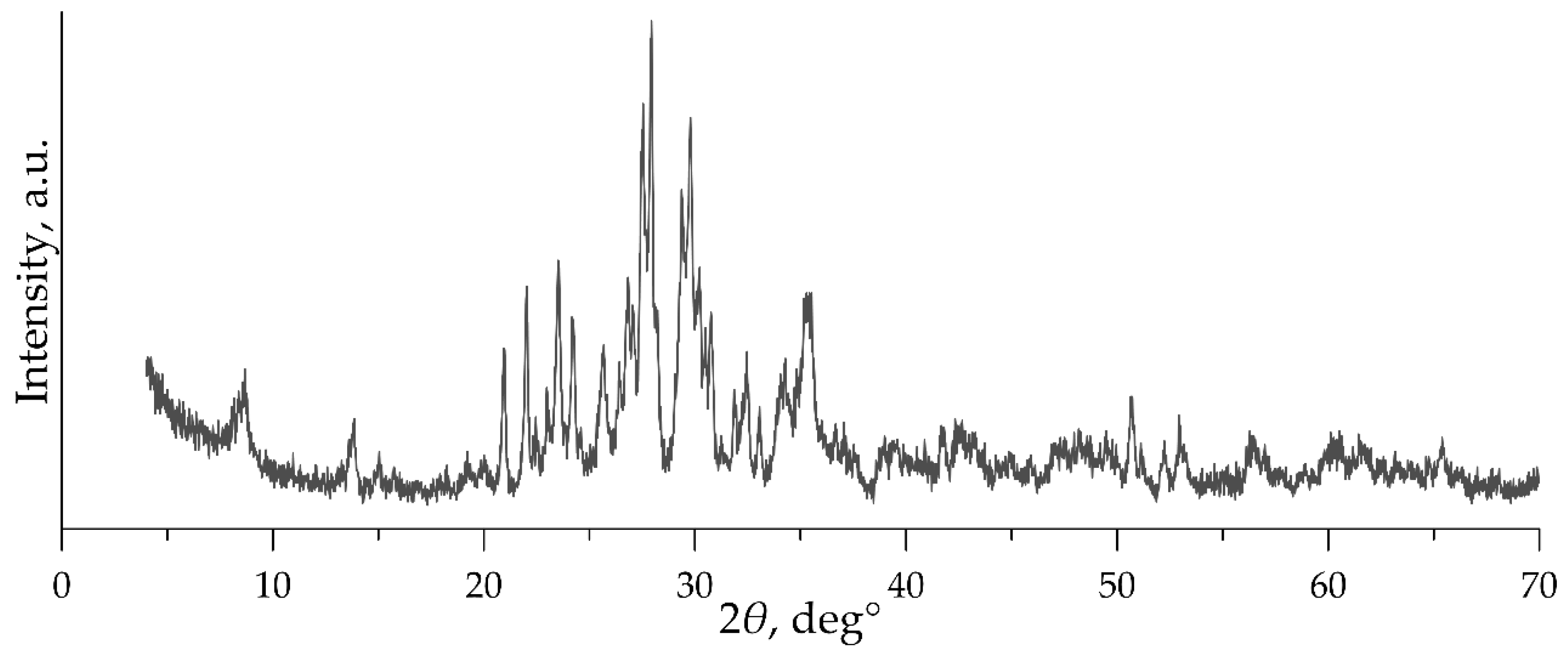
3.2.1. XRPD
3.2.2. XRF
3.3. Data Processing
4. Results and Discussions
4.1. Types of the Extracted Factors
4.2. Evaluation of the Stability of the Factor Solution
- Raw X-ray diffraction patterns not subjected to any spectral operations;
- Raw diffraction patterns subjected to baseline correction;
- Smoothed diffraction patterns subjected to baseline correction (the data used in the method of [13]).
- The subset of carbonatites sensu stricto selected according to the formal principle “SiO2 < 20 wt %”, commonly used for the classification of carbonatites [36]—99 observations;
- The cumulative subset of all other rocks of the collection (silicocarbonatites and carbonate-bearing silicate rocks)—99 observations;
- The entire set of samples from the Kontozero collection—198 observations.
4.3. Interpretation of the Results of Factor Analysis
4.4. The Algorithm for the Selection of Representative Samples
- XRPD and XRF analysis and primary data processing, including baseline corrections and removal of zero values. The output of this step is a database suitable for FA (an example is shown in the supplementary Table S3);
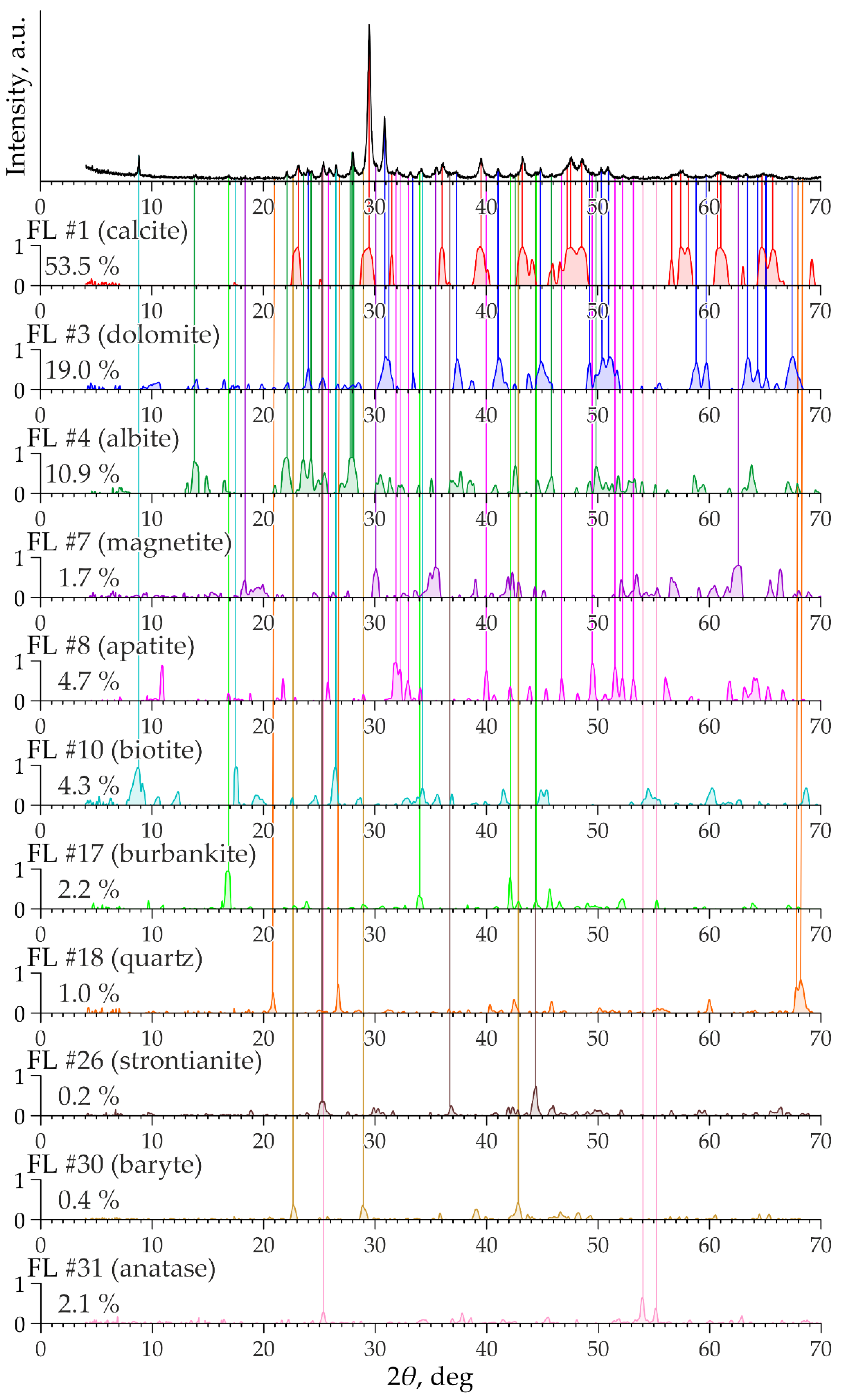
- Factor analysis of the obtained results. The outputs are (a) tables of FL values for XRPD and XRF variables (see Supplementary Table S4), (b) graphs of factor loadings for XRPD variables (e.g., Figure 5), and (c) factor scores for each sample (see Supplementary Table S5);
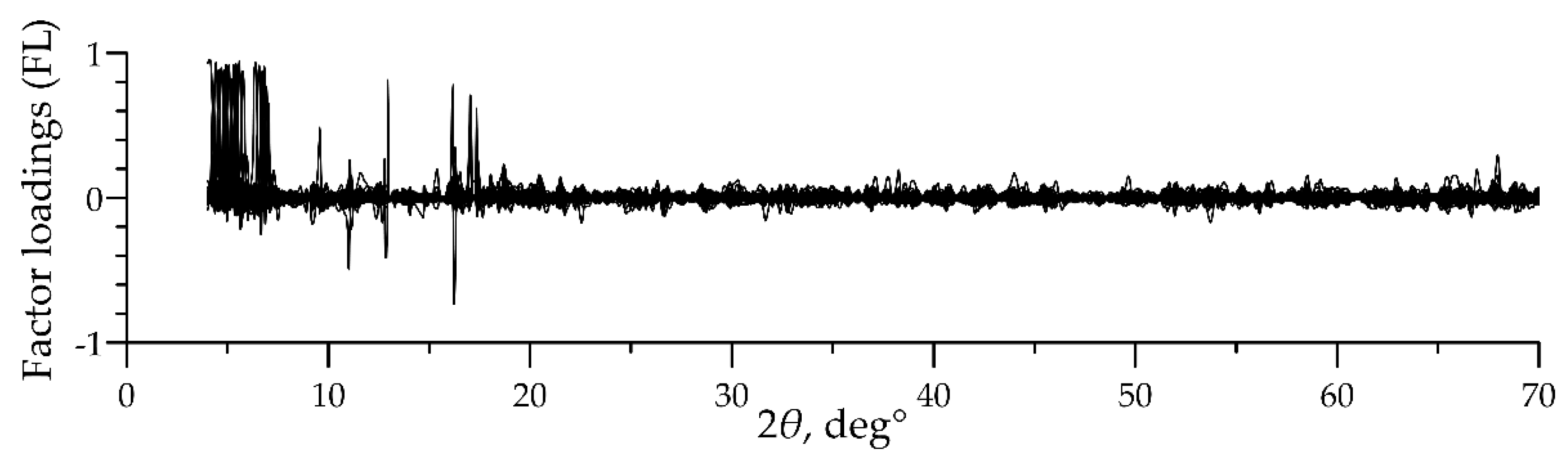
- Compilation and examination of all FL graphs on a single chart. The output is the rejection of all non-interpreted noise factors (see Figure 3);
- Interpretation of the easily interpretable factors by combining the two proposed techniques (Figure 10). The output is a highly confident mineralogical explanation of these factors;
- Interpretation of difficult-to-interpret factors by searching for the mineral (s) according to the position of the most intense peaks in the AMCSD database. The output is an assumption about the nature of these factors;
- Routine mineralogical (optical microscopy, SEM + EPMA, Raman) examination of the samples with the highest FSs. The output is a verification of the FA results, a collection of the most representative samples, an idea of the mineral composition of all studied rocks at the level of main, minor, and most accessory minerals, all within a reasonably short time.
5. Conclusions and Future Perspectives
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Olympus. XRF and XRD Analyzers. Available online: https://www.olympus-ims.com/en/innovx-xrf-xrd/ (accessed on 19 August 2020).
- Xu, X.; Liang, T.; Zhu, J.; Zheng, D.; Sun, T. Review of classical dimensionality reduction and sample selection methods for large-scale data processing. Neurocomputing 2019, 328, 5–15. [Google Scholar] [CrossRef]
- Mirzaei-Paiaman, A.; Asadolahpour, S.R.; Saboorian-Jooybari, H.; Chen, Z.; Ostadhassan, M. A new framework for selection of representative samples for special core analysis. Pet. Res. 2020. [Google Scholar] [CrossRef]
- Barr, G.; Dong, W.; Gilmore, C.J. PolySNAP: A computer program for analysing high-throughput powder diffraction data. J. Appl. Crystallogr. 2004, 37, 658–664. [Google Scholar] [CrossRef]
- Barr, G.; Dong, W.; Gilmore, C. PolySNAP3: A computer program for analysing and visualizing high-throughput data from diffraction and spectroscopic sources. J. Appl. Crystallogr. 2009, 42, 965–974. [Google Scholar] [CrossRef]
- Butler, B.M.; Palarea-Albaladejo, J.; Shepherd, K.D.; Nyambura, K.M.; Towett, E.K.; Sila, A.M.; Hillier, S. Mineral–nutrient relationships in African soils assessed using cluster analysis of X-ray powder diffraction patterns and compositional methods. Geoderma 2020, 375, 114474. [Google Scholar] [CrossRef]
- Butler, B.M.; Sila, A.M.; Shepherd, K.D.; Nyambura, M.; Gilmore, C.J.; Kourkoumelis, N.; Hillier, S. Pre-treatment of soil X-ray powder diffraction data for cluster analysis. Geoderma 2019, 337, 413–424. [Google Scholar] [CrossRef]
- Chen, Z.P.; Morris, J.; Martin, E.; Hammond, R.; Lai, X.; Ma, C.; Purba, E.; Roberts, K.J.; Bytheway, R. Enhancing the Signal-to-Noise Ratio of X-ray Diffraction Profiles by Smoothed Principal Component Analysis. Anal. Chem. 2005, 77, 6563–6570. [Google Scholar] [CrossRef]
- Wasserman, S.R.; Allen, P.G.; Shuh, D.K.; Bucher, J.J.; Edelstein, N.M. EXAFS and principal component analysis: A new shell game. J. Synchrotron Radiat. 1999, 6, 284–286. [Google Scholar] [CrossRef]
- Liu, P.; Zhou, X.; Li, Y.; Li, M.; Yu, D.; Liu, J. The application of principal component analysis and non-negative matrix factorization to analyze time-resolved optical waveguide absorption spectroscopy data. Anal. Methods 2013, 5, 4454–4459. [Google Scholar] [CrossRef]
- Frenkel, A.I.; Kleifeld, O.; Wasserman, S.R.; Sagi, I. Phase speciation by extended X-ray absorption fine structure spectroscopy. J. Chem. Phys. 2002, 116, 9449–9456. [Google Scholar] [CrossRef]
- Burley, J.C.; O’Hare, D.; Williams, G.R. The application of statistical methodology to the analysis of time-resolved X-ray diffraction data. Anal. Methods 2011, 3, 814. [Google Scholar] [CrossRef]
- Fomina, E.; Kozlov, E.; Ivashevskaja, S. Study of diffraction data sets using factor analysis: A new technique for comparing mineralogical and geochemical data and rapid diagnostics of the mineral composition of large collections of rock samples. Powder Diffr. 2019, 34, S59–S70. [Google Scholar] [CrossRef]
- George, D. IBM SPSS Statistics 23 Step by Step; Routledge: New York, NY, SUA, 2016; ISBN 9781315545899. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Ford, W. The Singular Value Decomposition. In Numerical Linear Algebra with Applications Using MATLAB; Ford, W., Ed.; Academic Press: Boston, MA, USA, 2015; pp. 299–320. ISBN 978-0-12-394435-1. [Google Scholar]
- Klug, H.P.; Alexander, L.E. X-ray Diffraction Procedures for Polycrystalline and Amorphous Materials; John Wiley & Sons, Inc.: New York, NY, USA, 1954. [Google Scholar]
- Jenkins, R.; Snyder, R.L. Introduction to X-ray Powder Diffractometry; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996; ISBN 9781118520994. [Google Scholar]
- MAUD Software. Available online: http://maud.radiographema.eu/ (accessed on 3 July 2020).
- Lutterotti, L.; Matthies, S.; Wenk, H.-R. MAUD: A friendly Java program for materials analysis using diffraction. Int. Union Crystallogr. Comm. Powder Diffr. Newsl. 1999, 21, 14–15. [Google Scholar]
- Downes, H.; Balaganskaya, E.; Beard, A.; Liferovich, R.; Demaiffe, D. Petrogenetic processes in the ultramafic, alkaline and carbonatitic magmatism in the Kola Alkaline Province: A review. Lithos 2005, 85, 48–75. [Google Scholar] [CrossRef]
- Bulakh, A.; Ivanikov, V.; Orlova, M.; Wall, F. Overview of carbonatite-phoscorite complexes of the Kola Alkaline Province in the context of a Scandinavian North Atlantic Alkaline Province. In Phoscorites and Carbonatites from Mantle to Mine; Wall, F., Zaitsev, A.N., Eds.; Mineralogical Society of Great Britain and Ireland: London, UK, 2004; pp. 1–43. [Google Scholar]
- Kramm, U.; Kogarko, L.; Kononova, V.; Vartiainen, H. The Kola Alkaline Province of the CIS and Finland: Precise Rb-Sr ages define 380–360 Ma age range for all magmatism. Lithos 1993, 30, 33–44. [Google Scholar] [CrossRef]
- Arzamastsev, A.A.; Petrovsky, M.N. Alkaline volcanism in the Kola Peninsula, Russia: Paleozoic Khibiny, Lovozero and Kontozero calderas. Proc. MSTU 2012, 15, 277–299. [Google Scholar]
- Petrovsky, M.N.; Savchenko, E.A.; Kalachev, V.Y. Formation of eudialyte-bearing phonolite from Kontozero carbonatite paleovolcano, Kola Peninsula. Geol. Ore Deposits 2012, 54, 540–556. [Google Scholar] [CrossRef]
- Website of IM UB RAS (Miass, Russia). Available online: http://www.mineralogy.ru (accessed on 3 July 2020).
- Amosova, A.A.; Panteeva, S.V.; Chubarov, V.M.; Finkelshtein, A.L. Determination of major elements by wavelength-dispersive X-ray fluorescence spectrometry and trace elements by inductively coupled plasma mass spectrometry in igneous rocks from the same fused sample (110 mg). Spectrochim. Acta Part B At. Spectrosc. 2016, 122, 62–68. [Google Scholar] [CrossRef]
- Website of IG SB RAS (Irkutsk, Russia). Available online: http://www.igc.irk.ru (accessed on 3 July 2020).
- Qualx2 Software. Available online: http://www.ba.ic.cnr.it/softwareic/qualx/ (accessed on 3 July 2020).
- Altomare, A.; Corriero, N.; Cuocci, C.; Falcicchio, A.; Moliterni, A.G.G.; Rizzi, R. QUALX2.0: A qualitative phase analysis software using the freely available database POW_COD. J. Appl. Crystallogr. 2015, 48, 598–603. [Google Scholar] [CrossRef]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Downs, R.T.; Hall-Wallace, M. The American Mineralogist crystal structure database. Am. Mineral. 2003, 88, 247–250. [Google Scholar]
- Gražulis, S.; Daškevič, A.; Merkys, A.; Chateigner, D.; Lutterotti, L.; Quirós, M.; Serebryanaya, N.R.; Moeck, P.; Downs, R.T.; Le Bail, A. Crystallography Open Database (COD): An open-access collection of crystal structures and platform for world-wide collaboration. Nucleic Acids Res. 2011, 40, D420–D427. [Google Scholar] [CrossRef] [PubMed]
- Gates-Rector, S.; Blanton, T.N. The Powder Diffraction File: A quality materials characterization database. Powder Diffr. 2019, 34, 352–360. [Google Scholar] [CrossRef]
- Fomina, E.; Kozlov, E. Application of the method of statistical comparison of XRD- and XRF-data for identification of the most representative rоск samples: Case study of a large collection of carbonatites and aluminosilicate rocks of the Kontozero alkaline complex (Kola Peninsula, NW Russia). IOP Conf. Ser. Earth Environ. Sci. 2020, in press. [Google Scholar]
- Le Maitre, R.W.; Streckeisen, A.; Zanettin, B.; Le Bas, M.J.; Bonin, B.; Bateman, P.; Bellieni, G.; Dudek, A.; Efremova, S.; Keller, J.; et al. Igneous Rocks, 2nd ed.; Le Maitre, R.W., Streckeisen, A., Zanettin, B., Le Bas, M.J., Bonin, B., Bateman, P., Eds.; Cambridge University Press: Cambridge, UK, 2002; ISBN 9780511535581. [Google Scholar]
- Lafuente, B.; Downs, R.T.; Yang, H.; Stone, N.L. The power of databases: The RRUFF project. In Highlights in Mineralogical Crystallography; Armbruster, T., Danisi, R.M., Eds.; De Gruyter: Berlin/München, Germany, 2016; pp. 1–30. ISBN 9783110417104. [Google Scholar]
- Kozlov, E.; Fomina, E.; Khvorov, P. Factor Analysis of XRF- and XRPD-data on the Example of the Rocks of the Kontozero Carbonatite Complex (NW Russia). Part II: Geological Interpretation. Crystals 2020, 10, 873. [Google Scholar] [CrossRef]
- Cattell, R.B. The Scree Test For The Number Of Factors. Multivariate Behav. Res. 1966, 1, 245–276. [Google Scholar] [CrossRef]


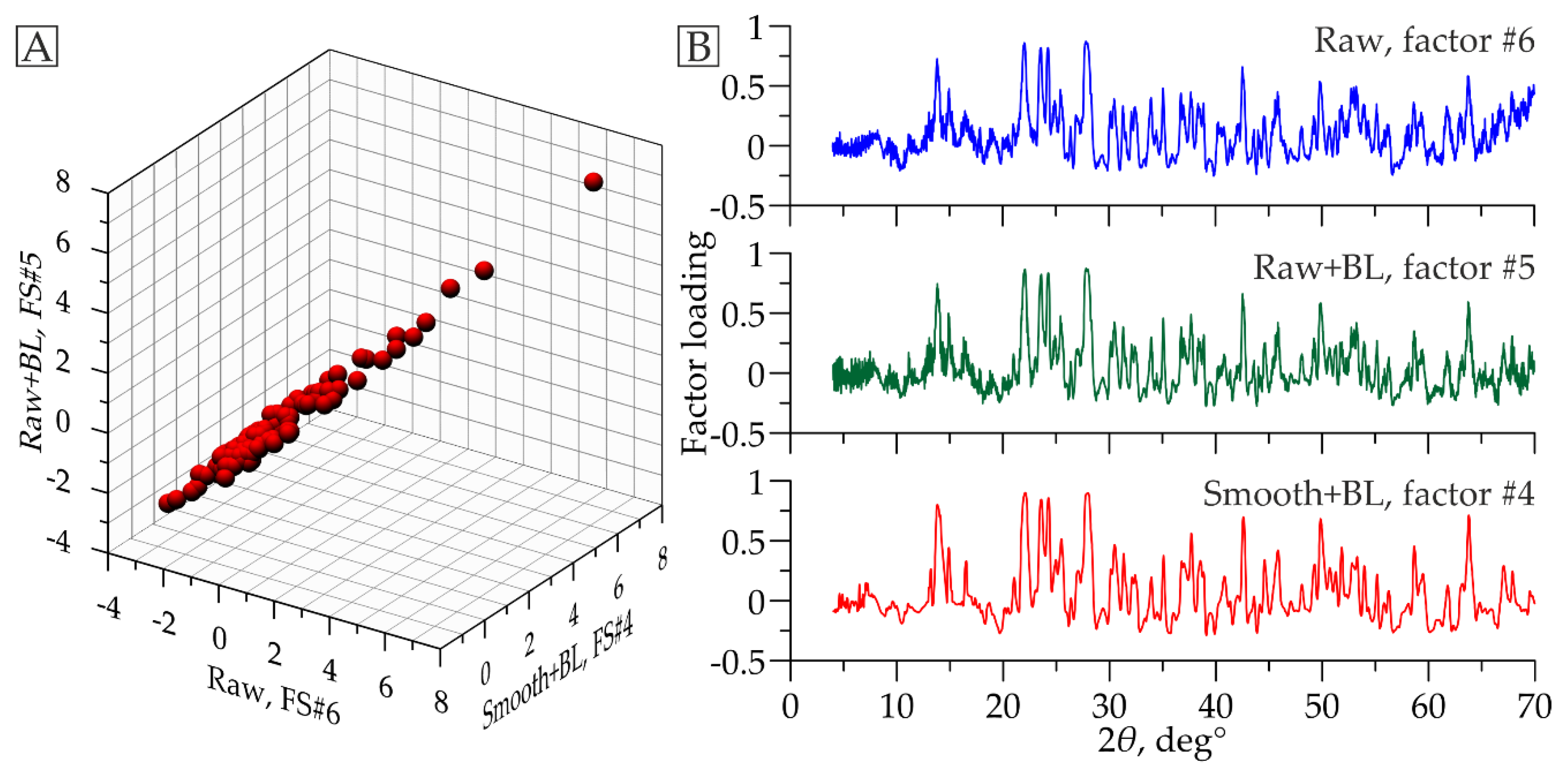
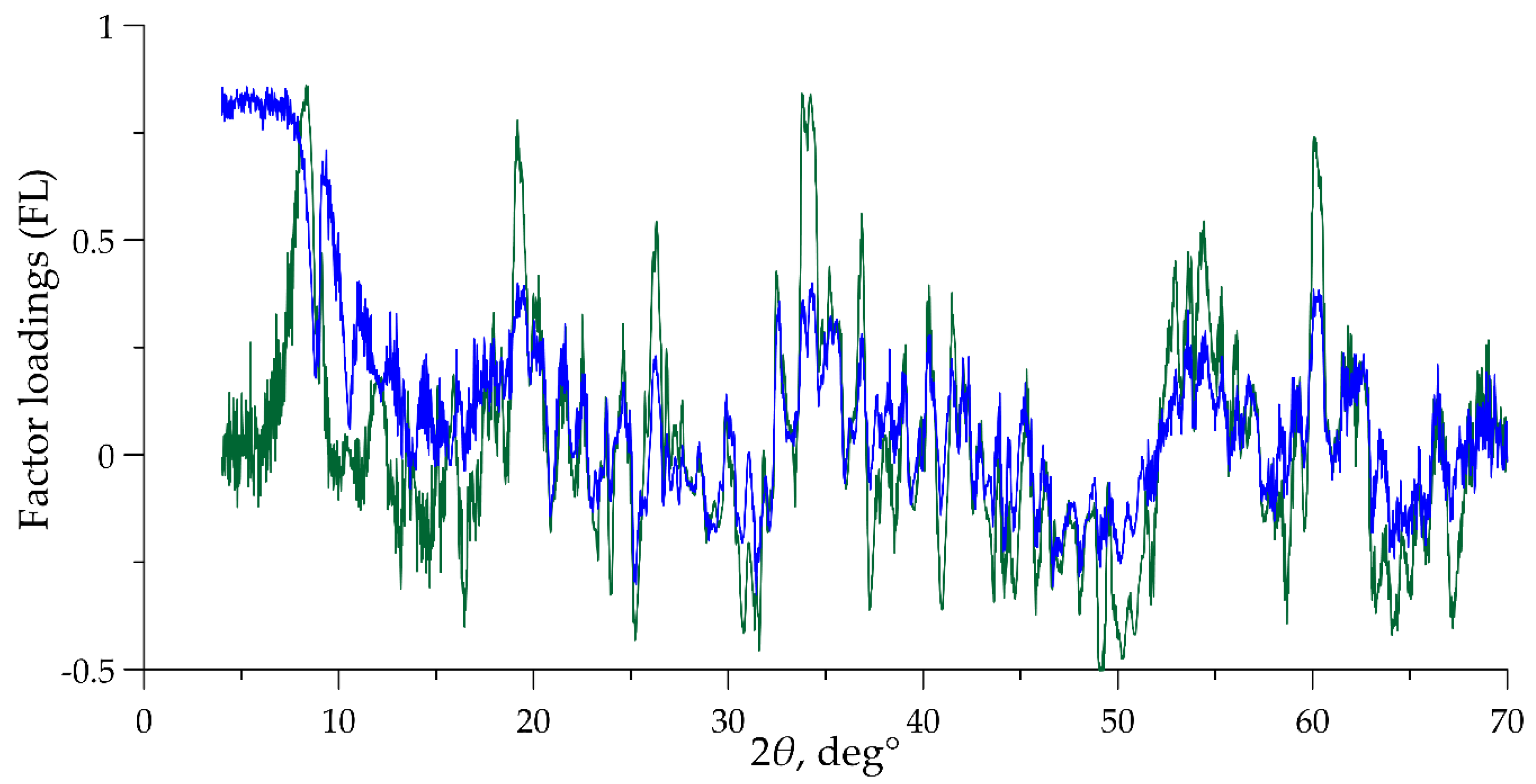
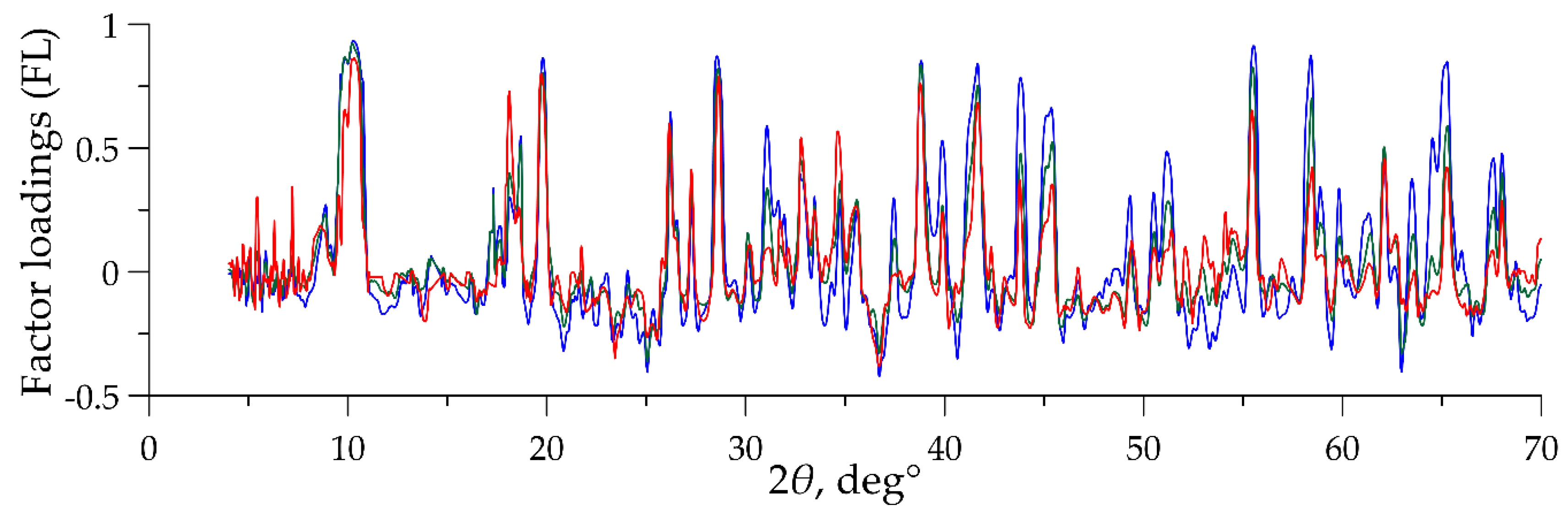
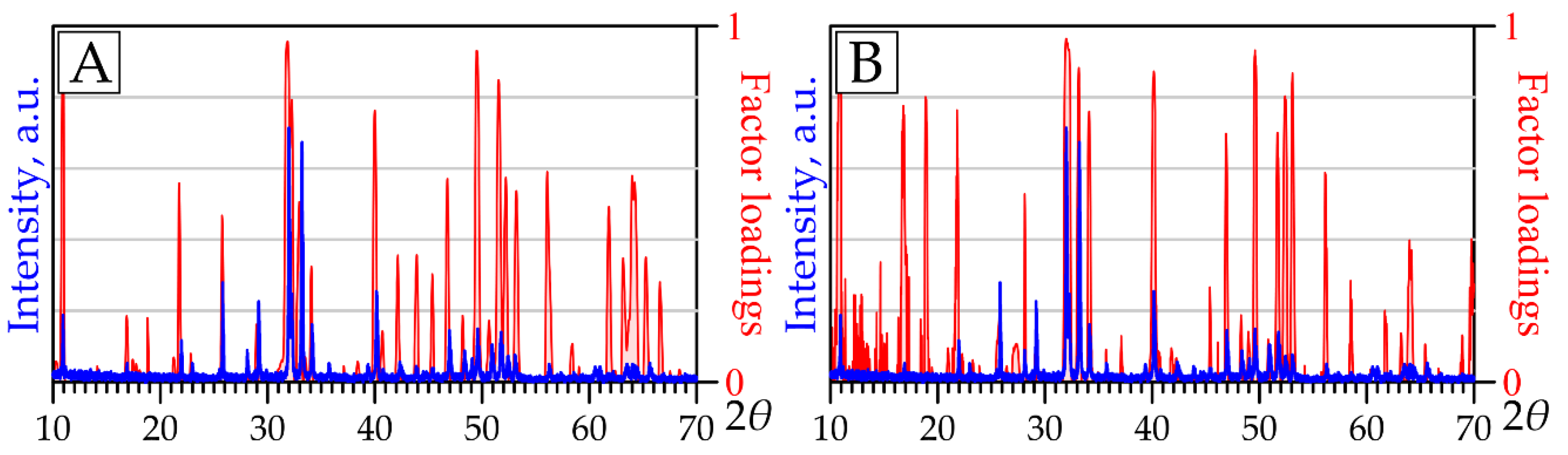



| Raw data (factors #): | 1 * | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Raw data + baseline (factors #): | 1 | 2 | 3 | 4 | 7 | 5 | 6 | 8 | 9 |
| Correlation coefficient between FSs: | 0.91 | 0.94 | 0.43 | 0.97 | 0.97 | 0.97 | 0.94 | 0.97 | 0.97 |
| Raw data (factors #): | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Smoothed data + baseline (factors #): | 1 | 2 | 11 | 5 | 6 | 4 | 7 | 9 | 8 |
| Correlation coefficient between FSs: | 0.76 | 0.89 | 0.20 | 0.94 | 0.96 | 0.95 | 0.87 | 0.94 | 0.95 |
| 1 * | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 17 | 22 | 24 | 26 | 30 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cal ** | Adr + Srp | Dol | Ab | Amp | Anl | Di + Mag | Ap | Or | Bt | Bur | Py | Ilm | Str | Brt | Ant | |
| Si | −0.71 | 0.19 | −0.15 | 0.29 | 0.14 | 0.24 | 0.22 | −0.15 | 0.24 | 0.11 | −0.05 | 0.05 | 0.08 | −0.05 | −0.05 | 0.03 |
| Ti | −0.67 | 0.24 | −0.14 | 0.05 | −0.02 | 0.17 | 0.05 | −0.24 | 0.04 | 0.23 | −0.07 | 0.10 | 0.20 | −0.04 | −0.05 | 0.15 |
| Zr | −0.30 | −0.09 | −0.09 | 0.29 | −0.11 | 0.48 | −0.05 | 0.19 | 0.34 | −0.01 | −0.05 | 0.15 | 0.13 | −0.07 | −0.04 | 0.08 |
| Al | −0.53 | 0.00 | −0.15 | 0.53 | −0.11 | 0.38 | −0.04 | −0.15 | 0.35 | 0.07 | 0.00 | 0.05 | 0.08 | −0.05 | −0.04 | 0.06 |
| Ca | 0.83 | −0.09 | 0.01 | −0.19 | −0.17 | −0.16 | −0.21 | 0.13 | −0.13 | −0.14 | 0.05 | −0.05 | −0.07 | 0.06 | 0.06 | −0.04 |
| Sr | 0.59 | −0.23 | 0.01 | −0.01 | −0.24 | −0.10 | −0.29 | −0.05 | −0.08 | −0.18 | 0.22 | −0.08 | −0.03 | 0.36 | 0.06 | −0.08 |
| Mg | −0.55 | 0.32 | 0.07 | −0.29 | 0.32 | −0.10 | 0.35 | −0.08 | −0.21 | 0.17 | −0.07 | 0.01 | 0.02 | −0.05 | −0.04 | −0.01 |
| Fe | −0.78 | 0.19 | −0.13 | −0.04 | 0.08 | 0.06 | 0.41 | 0.04 | −0.06 | 0.10 | −0.07 | 0.03 | 0.04 | −0.12 | −0.08 | 0.02 |
| Mn | −0.55 | 0.07 | −0.08 | −0.12 | 0.21 | −0.09 | 0.23 | 0.08 | −0.13 | 0.04 | 0.09 | −0.07 | −0.13 | 0.02 | −0.02 | −0.20 |
| Ba | −0.19 | −0.14 | −0.10 | 0.03 | −0.13 | 0.04 | −0.25 | −0.12 | 0.15 | −0.03 | 0.08 | −0.04 | −0.03 | 0.20 | 0.25 | −0.04 |
| K | −0.47 | −0.13 | −0.20 | 0.13 | −0.05 | 0.12 | −0.05 | −0.15 | 0.66 | 0.19 | −0.09 | 0.06 | 0.04 | −0.06 | −0.03 | 0.07 |
| Na | −0.51 | −0.19 | 0.08 | 0.56 | 0.26 | 0.42 | −0.01 | −0.07 | 0.02 | 0.04 | 0.07 | 0.00 | 0.07 | −0.09 | −0.03 | 0.04 |
| P | −0.07 | −0.08 | −0.08 | −0.13 | −0.07 | −0.02 | −0.06 | 0.95 | −0.07 | −0.02 | 0.06 | 0.09 | −0.01 | −0.05 | −0.02 | −0.01 |
| S | −0.20 | −0.14 | 0.16 | 0.05 | −0.19 | −0.05 | −0.29 | 0.24 | 0.02 | −0.03 | −0.11 | 0.67 | −0.01 | −0.05 | −0.02 | 0.01 |
| L.O.I. | 0.75 | −0.27 | 0.26 | −0.12 | −0.07 | −0.20 | −0.25 | −0.09 | −0.10 | −0.13 | 0.06 | −0.02 | −0.14 | −0.08 | 0.00 | 0.07 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fomina, E.; Kozlov, E.; Bazai, A. Factor Analysis of XRF and XRPD Data on the Example of the Rocks of the Kontozero Carbonatite Complex (NW Russia). Part I: Algorithm. Crystals 2020, 10, 874. https://doi.org/10.3390/cryst10100874
Fomina E, Kozlov E, Bazai A. Factor Analysis of XRF and XRPD Data on the Example of the Rocks of the Kontozero Carbonatite Complex (NW Russia). Part I: Algorithm. Crystals. 2020; 10(10):874. https://doi.org/10.3390/cryst10100874
Chicago/Turabian StyleFomina, Ekaterina, Evgeniy Kozlov, and Ayya Bazai. 2020. "Factor Analysis of XRF and XRPD Data on the Example of the Rocks of the Kontozero Carbonatite Complex (NW Russia). Part I: Algorithm" Crystals 10, no. 10: 874. https://doi.org/10.3390/cryst10100874
APA StyleFomina, E., Kozlov, E., & Bazai, A. (2020). Factor Analysis of XRF and XRPD Data on the Example of the Rocks of the Kontozero Carbonatite Complex (NW Russia). Part I: Algorithm. Crystals, 10(10), 874. https://doi.org/10.3390/cryst10100874






