Characterization of Accumulated B-Integral of Regenerative Amplifier Based CPA Systems
Abstract
1. Introduction
2. Materials and Methods
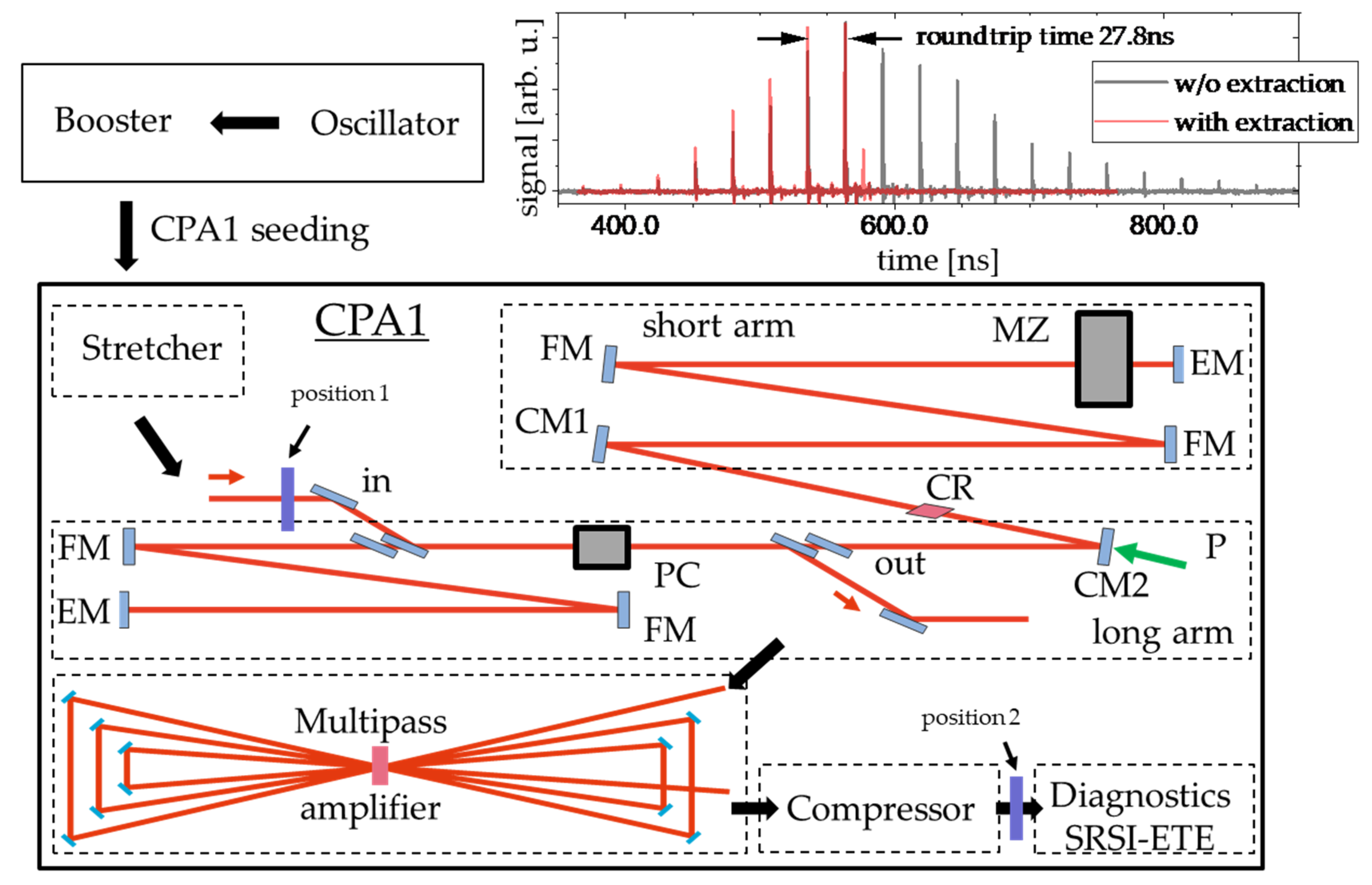
2.1. Experimental Setup
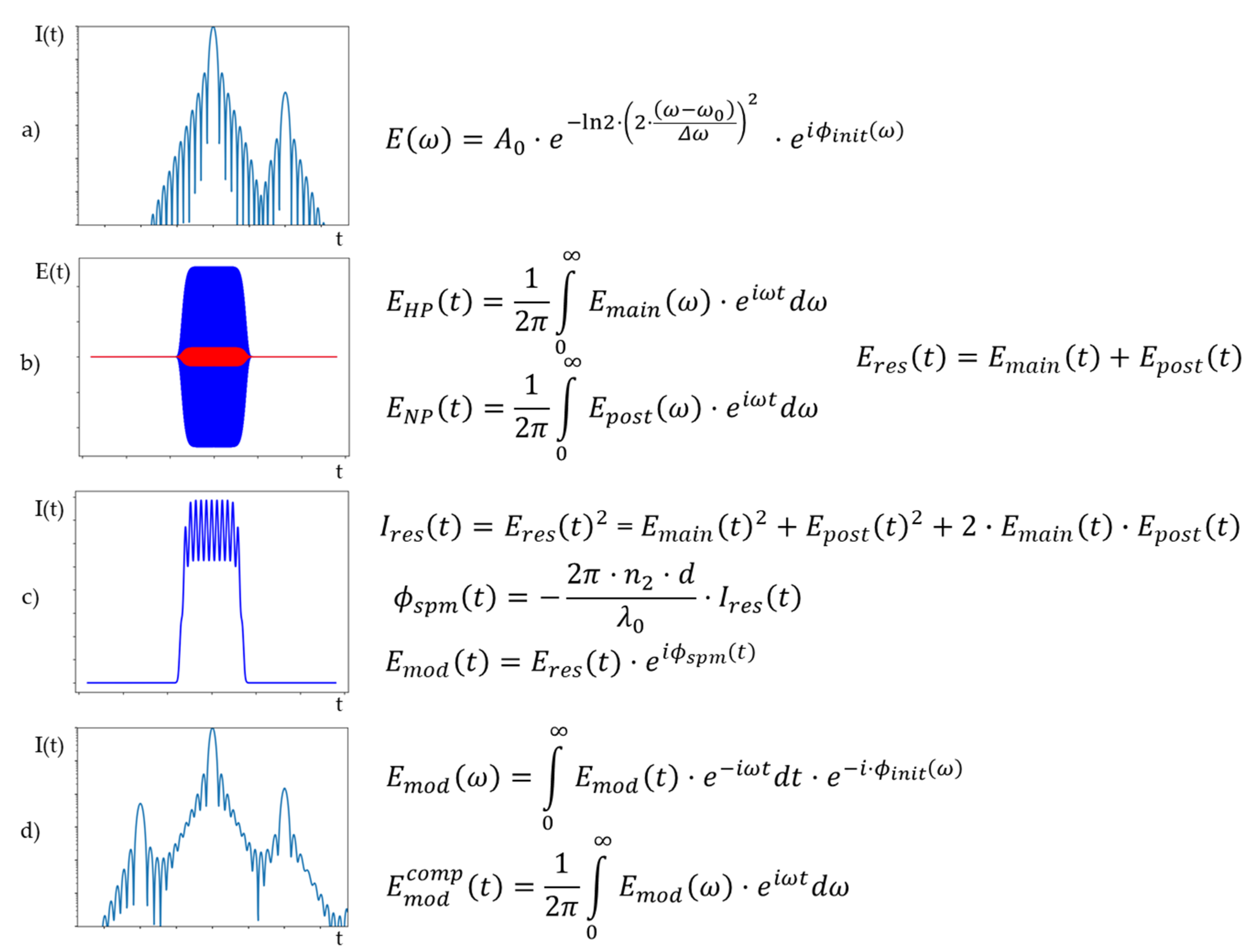
2.2. Numerical Model
2.3. Amplification Modelling for B-Integral Estimation
3. Results
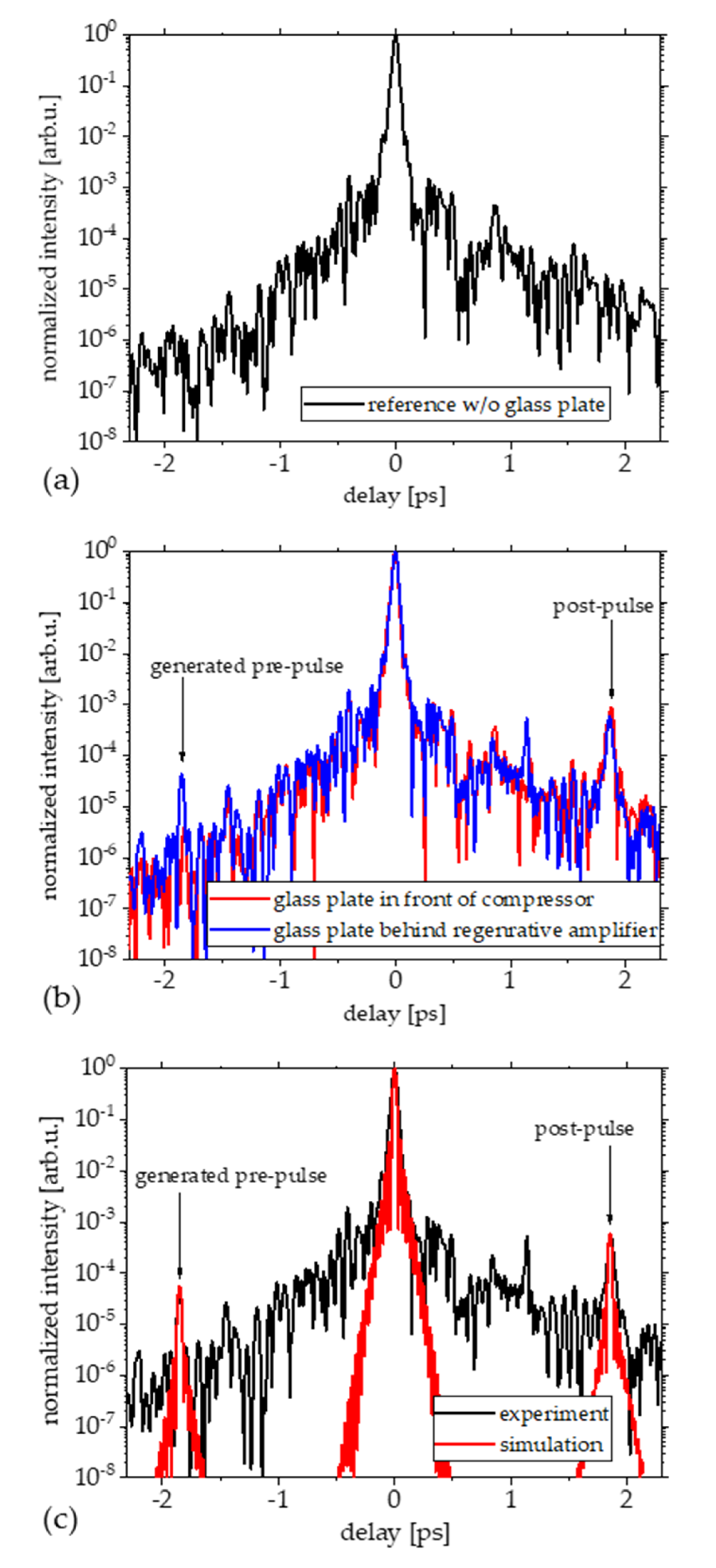
3.1. B-integral Measurement under Normal Operational Conditions
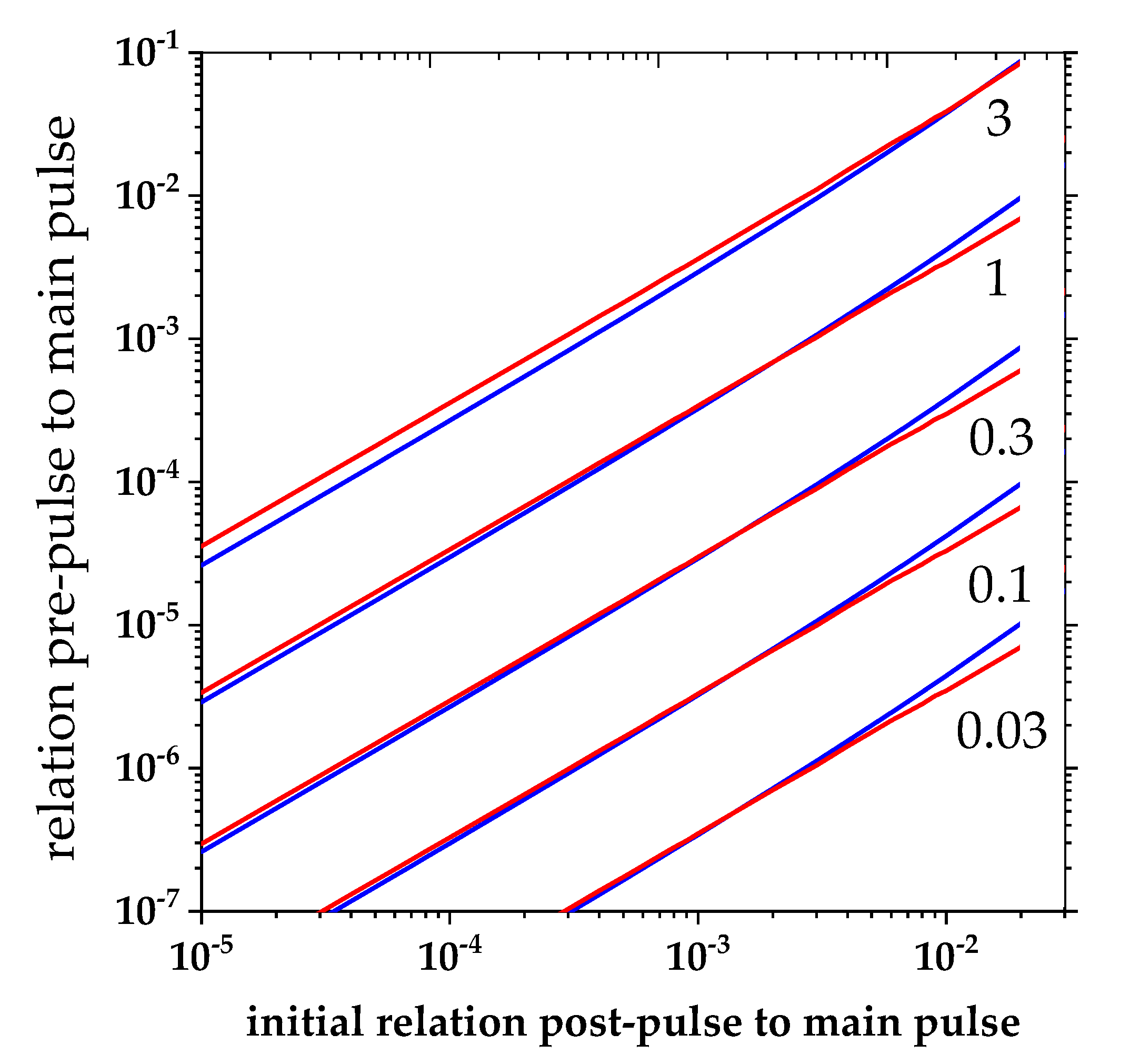
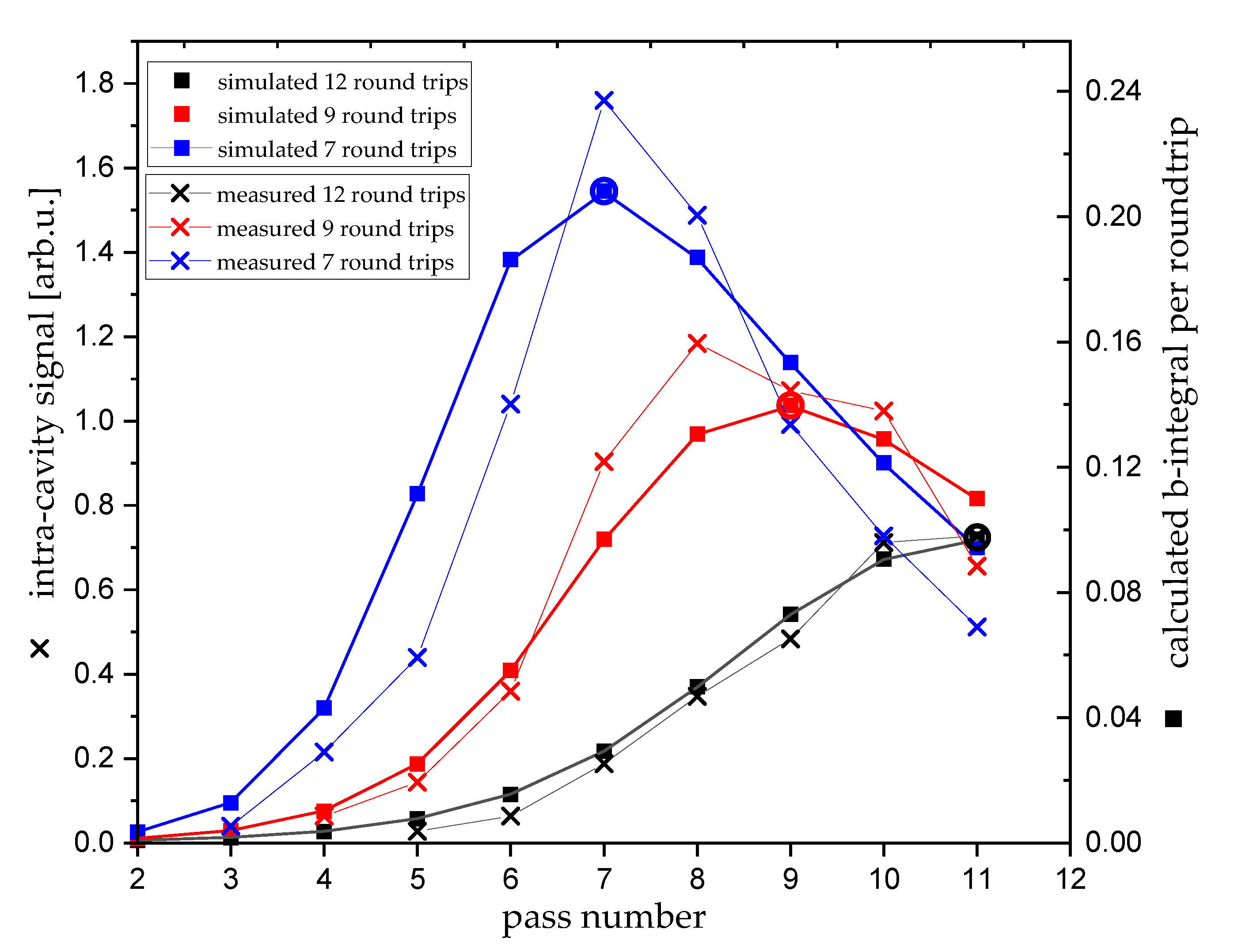
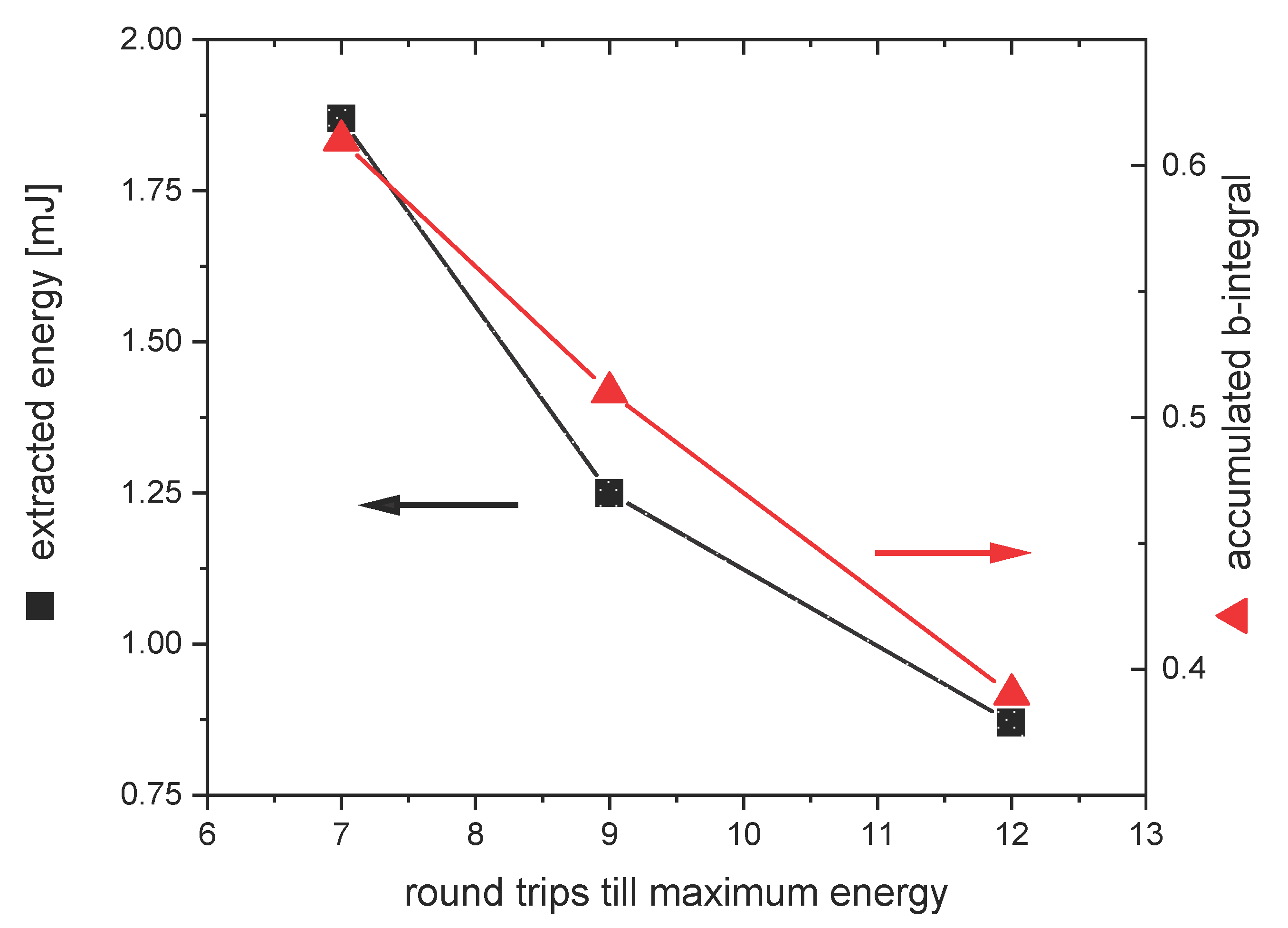
3.2. Influence of Number of Roundtrips and Gain Saturation on Accumulated B-Integral
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Downer, M.C.; Zgadzaj, R.; Debus, A.; Schramm, U.; Kaluza, M.C. Diagnostics for plasma-based electron accelerators. Rev. Mod. Phys. 2018, 90, 035002. [Google Scholar] [CrossRef]
- Macchi, A.; Borghesi, M.; Passoni, M. Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 2013, 85, 751. [Google Scholar] [CrossRef]
- Esarey, E.; Schroeder, C.B.; Leemans, W.P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 2009, 81, 1229. [Google Scholar] [CrossRef]
- Schramm, U.; Bussmann, M.; Irman, A.; Siebold, M.; Zeil, K.; Albach, D.; Bernert, C.; Bock, S.; Brack, F.; Branco, J.; et al. First results with the novel Petawatt laser acceleration facility in Dresden. J. Phys. Conf. Ser. 2017, 874, 012028. [Google Scholar] [CrossRef]
- Kaluza, M.; Schreiber, J.; Santala, M.I.K.; Tsakiris, G.D.; Eidmann, K.; Meyer-ter-Vehn, J.; Witte, K.J. Influence of the laser prepulse on proton acceleration in thin-foil experiments. Phys. Rev. Lett. 2004, 93, 045003. [Google Scholar] [CrossRef] [PubMed]
- Poole, P.L.; Obst, L.; Cochran, G.E.; Metzkes, J.; Schlenvoigt, H.-P.; Prencipe, I.; Kluge, T.; Cowan, T.E.; Schramm, U.; Schumacher, D.W.; et al. Laser-driven ion acceleration via target normal sheath accelerationin the relativistic transparency regime. New J. Phys. 2018, 20, 013019. [Google Scholar] [CrossRef]
- Obst, L.; Göde, S.; Rehwald, M.; Brack, F.E.; Branco, J.; Bock, S.; Bussmann, M.; Cowan, T.E.; Curry, C.B.; Fiuza, F.; et al. Efficient laser-driven proton acceleration from cylindrical and planar cryogenic hydrogen jets. Sci. Rep. 2017, 7, 10248. [Google Scholar] [CrossRef]
- Obst, L.; Metzkes-Ng, J.; Bock, S.; Cochran, G.E.; Cowan, T.E.; Oksenhendler, T.; Poole, P.L.; Prencipe, I.; Rehwald, M.; Rödel, C.; et al. On-shot characterization of single plasma mirror temporal contrast improvement. Plasma Phys. Control. Fusion 2018, 60, 054007. [Google Scholar] [CrossRef]
- Cerchez, M.; Prasad, R.; Aurand, B.; Giesecke, A.L.; Spickermann, S.; Brauckmann, S.; Aktan, E.; Swantusch, M.; Toncian, M.; Toncian, T.; et al. ARCTURUS laser: A versatile high-contrast, high-power multi-beam laser system. High Power Laser Sci. Eng. 2019, 7, e37. [Google Scholar] [CrossRef]
- Ziegler, T.; Bernert, C.; Bock, S.; Brack, F.-E.; Cowan, T.E.; Dover, N.P.; Garten, M.; Gaus, L.; Gebhardt, R.; Helbig, U.; et al. PW-class laser-driven proton acceleration optimization by application of temporally asymmetric pulse shapes. arXiv 2020, arXiv:2007.11499v1. [Google Scholar]
- Kiriyama, H.; Pirozhkov, A.S.; Nishiuchi, M.; Fukuda, Y.; Ogura, K.; Sagisaka, A.; Miyasaka, Y.; Mori, M.; Sakaki, H.; Dover, N.P.; et al. High-contrast high-intensity repetitivepetawatt laser. Opt. Lett. 2018, 43, 2595–2598. [Google Scholar] [CrossRef] [PubMed]
- Khodakovsky, N.; Kalashnikov, M.; Gontier, E.; Falcoz, F.; Paul, P.-M. Degradation of picosecond temporal contrast of Ti:sapphire lasers with coherent pedestals. Opt. Lett. 2016, 41, 4441–4444. [Google Scholar] [CrossRef] [PubMed]
- Kalashnikov, M.; Osvay, K.; Sandner, W. High-power Ti:Sapphire lasers: Temporal contrast and spectral narrowing. Laser Part. Beams 2007, 219–223. [Google Scholar] [CrossRef]
- Nantel, M.; Itatani, J.; Tien, A.-C.; Faure, J.; Kaplan, D.; Bouvier, M.; Buma, T.; Van Rompay, P.; Nees, J.; Pronko, P.P.; et al. Temporal contrast in Ti:sapphire lasers: Characterization and control. IEEE J. Sel. Top. Quantum Electron. 1998, 4, 449–458. [Google Scholar] [CrossRef]
- Didenko, N.V.; Konyashchenko, A.V.; Lutsenko, A.P.; Tenyakov, S.Y. Contrast degradation in a chirped-pulse amplifier due to generation of prepulses by postpulses. Opt. Express 2008, 16, 3178–3190. [Google Scholar] [CrossRef] [PubMed]
- Keppler, S.; Honrung, M.; Bödefeld, R.; Kahle, M.; Hein, J.; Kaluza, M.C. All-reflective, highly accurate polarization rotator for high-power short-pulse laser systems. Opt. Express 2012, 20, 20742–20747. [Google Scholar] [CrossRef]
- Kiriyama, H.; Miyasaka, Y.; Sagisaka, A.; Ogura, K.; Nishiuchi, M.; Pirozhkov, A.S.; Fukuda, Y.; Kando, M.; Kondo, K. Experimental investigation on the temporal contrast of pre-pulses by post-pulses in a petawatt laser facility. Opt. Lett. 2020, 45, 1100–1103. [Google Scholar] [CrossRef]
- Kogelnik, H.; Ippen, E.P.; Dienes, A.; Shank, C.V. Astigmatically compensated cavities for CW dye lasers. IEEE J. Quantum Electron. 1972, 8, 373–379. [Google Scholar] [CrossRef]
- Barty, C.P.J.; Korn, G.; Raksi, F.; Rose-Petruck, C.; Squier, J.; Tien, A.-C.; Wilson, K.R.; Yakovlev, V.V.; Yamakawa, K. Regenerative pulse shaping and amplification of ultrabroadband optical pulses. Opt. Lett. 1996, 21, 219–221. [Google Scholar] [CrossRef] [PubMed]
- Oksenhendler, T.; Kaplan, D.; Tournois, P.; Greetham, G.M. Intracavity acousto-optic programmable gain control for ultra-wide-band regenerative amplifiers. Appl. Phys. B 2006, 83, 491. [Google Scholar] [CrossRef]
- Oksenhendler, T.; Bizouard, P.; Albert, O.; Bock, S.; Schramm, U. High dynamic, high resolution and wide range single shot temporal pulse contrast measurement. Opt. Express 2017, 25, 12588–12600. [Google Scholar] [CrossRef] [PubMed]
- Kon, A.; Nishiuchi, M.; Kiriyama, H.; Kando, M.; Bock, S.; Ziegler, T.; Pueschel, T.; Zeil, K.; Schramm, U.; Kondo, K. Single-shot measurement of post-pulse-generated pre-pulse in high-power laser systems. Crystals 2020, 10, 657. [Google Scholar] [CrossRef]
- Kiriyama, H.; Pirozhkov, A.S.; Nishiuchi, M.; Fukuda, Y.; Ogura, K.; Sagisaka, A.; Miyasaka, Y.; Sakaki, H.; Dover, N.P.; Kondo, K.; et al. Status and progress of the J-KAREN-P high intensity laser system at QST. High Energy Density Phys. 2020, 36, 100771. [Google Scholar] [CrossRef]
- Cheriaux, G.; Rousseau, P.; Salin, F.; Chambaret, J.P.; Walker, B.; Dimauro, L.F. Aberration-free stretcher design for ultrashort-pulse amplification. Opt. Lett. 1996, 21, 414–416. [Google Scholar] [CrossRef] [PubMed]
- Tournois, P. Acousto-optic programmable dispersive filter for adaptive compensation of group delay time dispersion in laser systems. Opt. Commun. 1997, 140, 245–249. [Google Scholar] [CrossRef]
- Kaplan, D.; Tournois, P. Theory and performance of the acousto optic programmable dispersive filter used for femtosecond laser pulse shaping. Phys. IV Fr. 2002, 12, 69–75. [Google Scholar] [CrossRef]
- Oksenhendler, T.; Coudreau, S.; Forget, N.; Crozatier, V.; Grabielle, S.; Herzog, R.; Gobert, O.; Kaplan, D. Self-referneced spectral interferometry. Appl. Phys. B 2010, 99, 7–12. [Google Scholar] [CrossRef]
- Moulet, A.; Grabielle, S.; Cornaggia, C.; Forget, N.; Oksenhendler, T. Single-shot, high-dynamic-range measurement of sub-15 fs pulses by self-referenced spectral interferometry. Opt. Lett. 2010, 35, 3856–3858. [Google Scholar] [CrossRef]
- Frantz, L.M.; Nodvik, J.S. Theory of pulse propagation in a laser amplifier. J. Appl. Phys. 1963, 34, 2346–2349. [Google Scholar] [CrossRef]
- Jeong, J.; Cho, S.; Yu, T.J. Numerical extension of Frantz-Nodvik equation for double-pass amplifiers with pulse overlap. Opt. Express 2017, 25, 3946–3953. [Google Scholar] [CrossRef]
- Rivera, V.A.G.; Manzani, D. Technological advances in tellurite glasses. In Springer Series in Material Science, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Forget, N.; (Fastlite, Antibes, France). Personal communication, 2020.
- Major, A.; Yoshino, F.; Nikolakakos, I.; Aitchison, J.S.; Smith, P.W.E. Dispersion of the nonlinear refractive index in sapphire. Opt. Lett. 2004, 29, 602–604. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Li, T.; Wang, S.; Wang, J.; Wang, Z.; Xu, X.; Zhang, F. Study on nonlinear refractive properties of KDP and DKDP crystals. RSC Adv. 2016, 6, 14490–14495. [Google Scholar] [CrossRef]
- Wang, D.; Li, T.; Wang, S.; Wang, J.; Shen, C.; Ding, J.; Li, W.; Huang, P.; Lu, C. Characteristics of nonlinear optical absorption and refraction for KDP and DKDP crystals. Opt. Mater. Express 2017, 7, 533–541. [Google Scholar] [CrossRef]
- Al-Salami, A.E. Thermal stability, linear and nonlinear refractive indices of heavy ternary tellurite glass. J. Ovonic Res. 2016, 12, 309–316. [Google Scholar]
- Kim, S.H.; Yoko, T.; Sakka, S. Linear and nonlinear optical properties of TeO2 glass. J. Am. Ceram. Soc. 1993, 76, 2486–2490. [Google Scholar] [CrossRef]
- Kim, S.H.; Yoko, T. Nonlinear optical properties of TeO2-based glasses: MOx-TeO2 (M = Sc, Ti, V, Nb, Mo, Ta, and W) binary glasses. J. Am. Ceram. Soc. 1995, 78, 1061–1065. [Google Scholar] [CrossRef]
- RefractiveIndex.info. Available online: https://refractiveindex.info (accessed on 7 July 2020).
- Konoplev, O.A.; Meyerhofer, D.D. Cancellation of B-integral accumulation for CPA lasers. IEEE J. Sel. Top. Quantum Electron. 1998, 4, 459–469. [Google Scholar] [CrossRef]
- Sung, J.H.; Yu, T.J.; Lee, S.K.; Jeong, T.M.; Choi, I.W.; Ko, D.-K.; Lee, J. Design of a femtosecond Ti:sapphire laser for generation and temporal optimization of 0.5-PW laser pulses at a 0.1-Hz repetition rate. J. Opt. Soc. Korea 2009, 13, 53–59. [Google Scholar] [CrossRef]
| Material | n2 [m²/W] | Individual Nonlinearity [m/W] |
|---|---|---|
| TeO2 [31,32] | 4.48 × 10−19 | 4.4 × 10−15 |
| Sapphire [33] | 3 × 10−20 | 9 × 10−16 |
| DKDP [34,35] | 1 × 10−19 | 5 × 10−16 |
| Roundtrips Till Gain Saturation | Relative Value of Generated Pre-Pulse | B-Integral from Fit | B-Integral Derived from Amplification Simulation |
|---|---|---|---|
| 12 | 4.3 × 10−5 | 0.41 | 0.39 |
| 9 | 8.9 × 10−5 | 0.69 | 0.73 |
| 7 | 2.65 × 10−4 | 0.97 | 1.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bock, S.; Herrmann, F.M.; Püschel, T.; Helbig, U.; Gebhardt, R.; Lötfering, J.J.; Pausch, R.; Zeil, K.; Ziegler, T.; Irman, A.; et al. Characterization of Accumulated B-Integral of Regenerative Amplifier Based CPA Systems. Crystals 2020, 10, 847. https://doi.org/10.3390/cryst10090847
Bock S, Herrmann FM, Püschel T, Helbig U, Gebhardt R, Lötfering JJ, Pausch R, Zeil K, Ziegler T, Irman A, et al. Characterization of Accumulated B-Integral of Regenerative Amplifier Based CPA Systems. Crystals. 2020; 10(9):847. https://doi.org/10.3390/cryst10090847
Chicago/Turabian StyleBock, Stefan, Franziska Marie Herrmann, Thomas Püschel, Uwe Helbig, René Gebhardt, Jakob Johannes Lötfering, Richard Pausch, Karl Zeil, Tim Ziegler, Arie Irman, and et al. 2020. "Characterization of Accumulated B-Integral of Regenerative Amplifier Based CPA Systems" Crystals 10, no. 9: 847. https://doi.org/10.3390/cryst10090847
APA StyleBock, S., Herrmann, F. M., Püschel, T., Helbig, U., Gebhardt, R., Lötfering, J. J., Pausch, R., Zeil, K., Ziegler, T., Irman, A., Oksenhendler, T., Kon, A., Nishuishi, M., Kiriyama, H., Kondo, K., Toncian, T., & Schramm, U. (2020). Characterization of Accumulated B-Integral of Regenerative Amplifier Based CPA Systems. Crystals, 10(9), 847. https://doi.org/10.3390/cryst10090847






