Tunable Non-Volatile Memory by Conductive Ferroelectric Domain Walls in Lithium Niobate Thin Films
Abstract
1. Introduction
2. Materials and Methods
3. Results
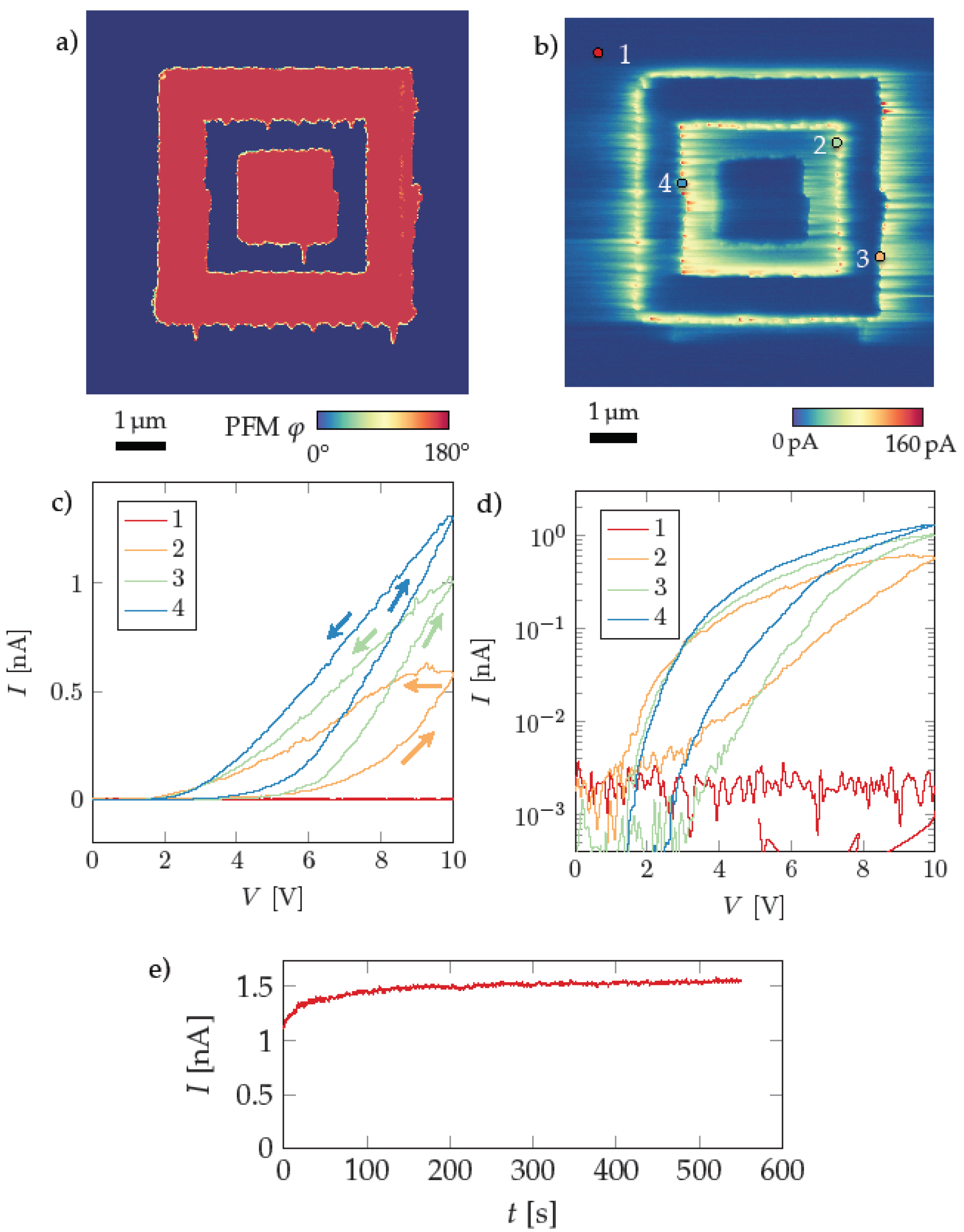
3.1. Conductive AFM Investigation
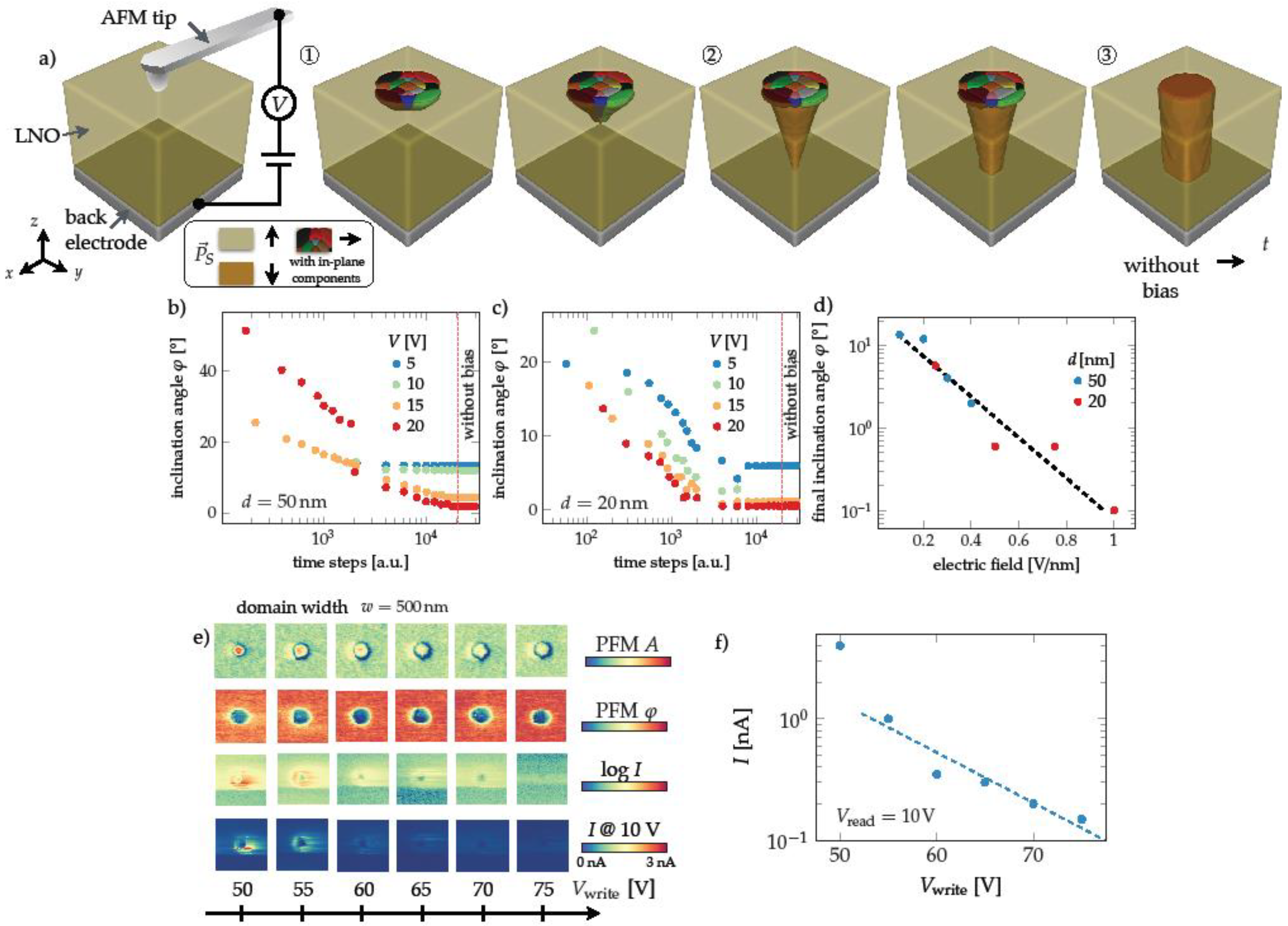
3.2. Phase-Field Simulation
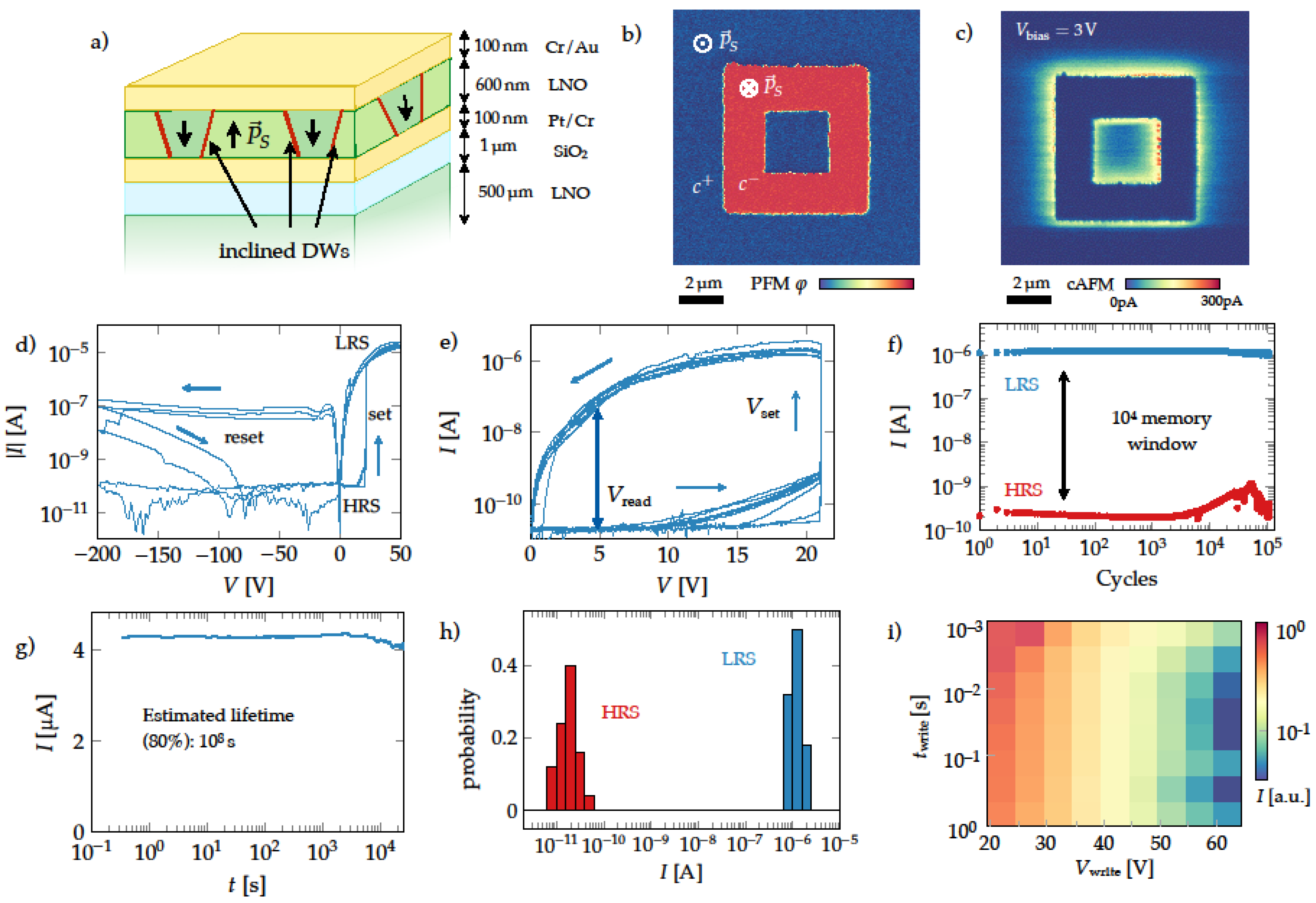
3.3. Resistive Switching Investigations
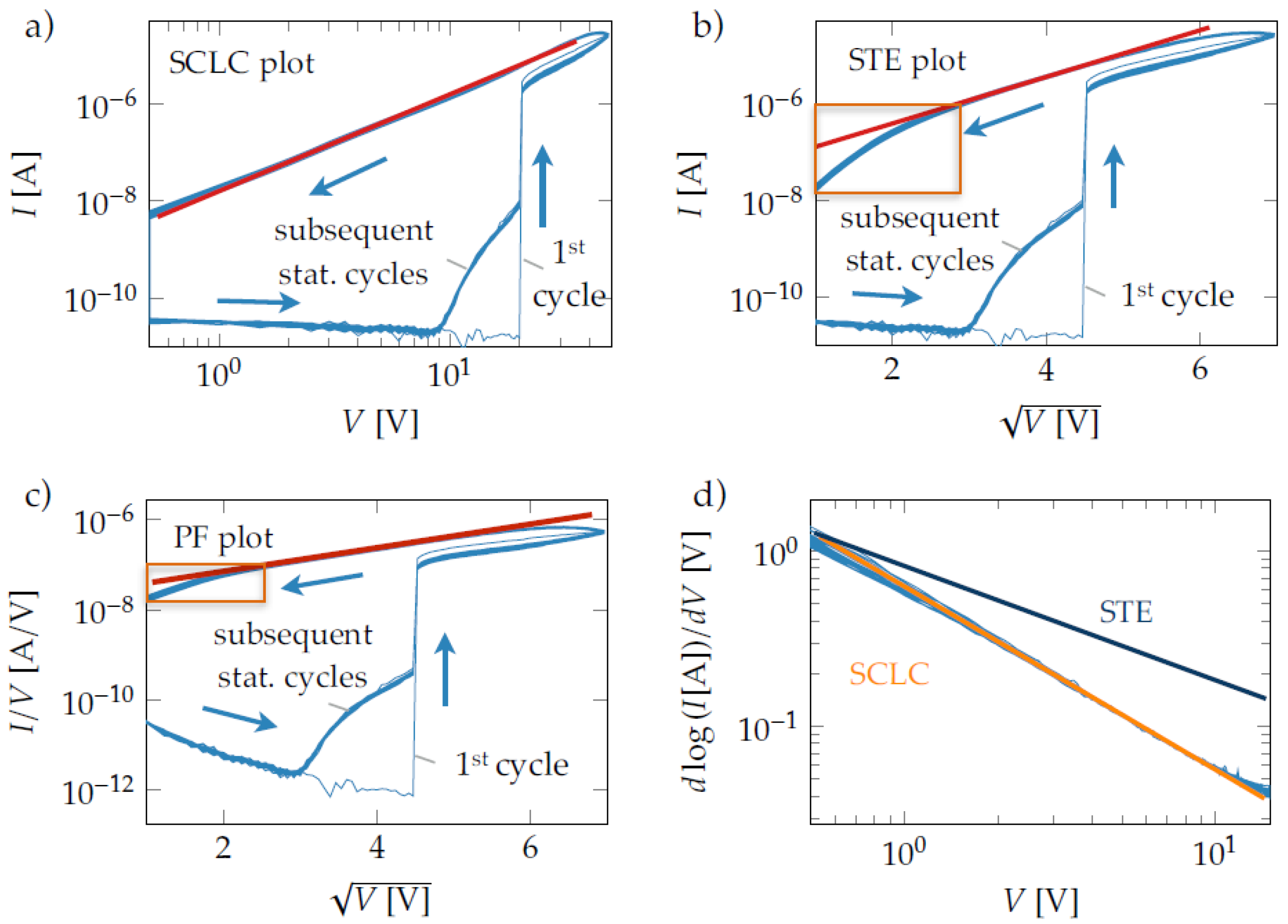
3.4. Conductance Type Extraction
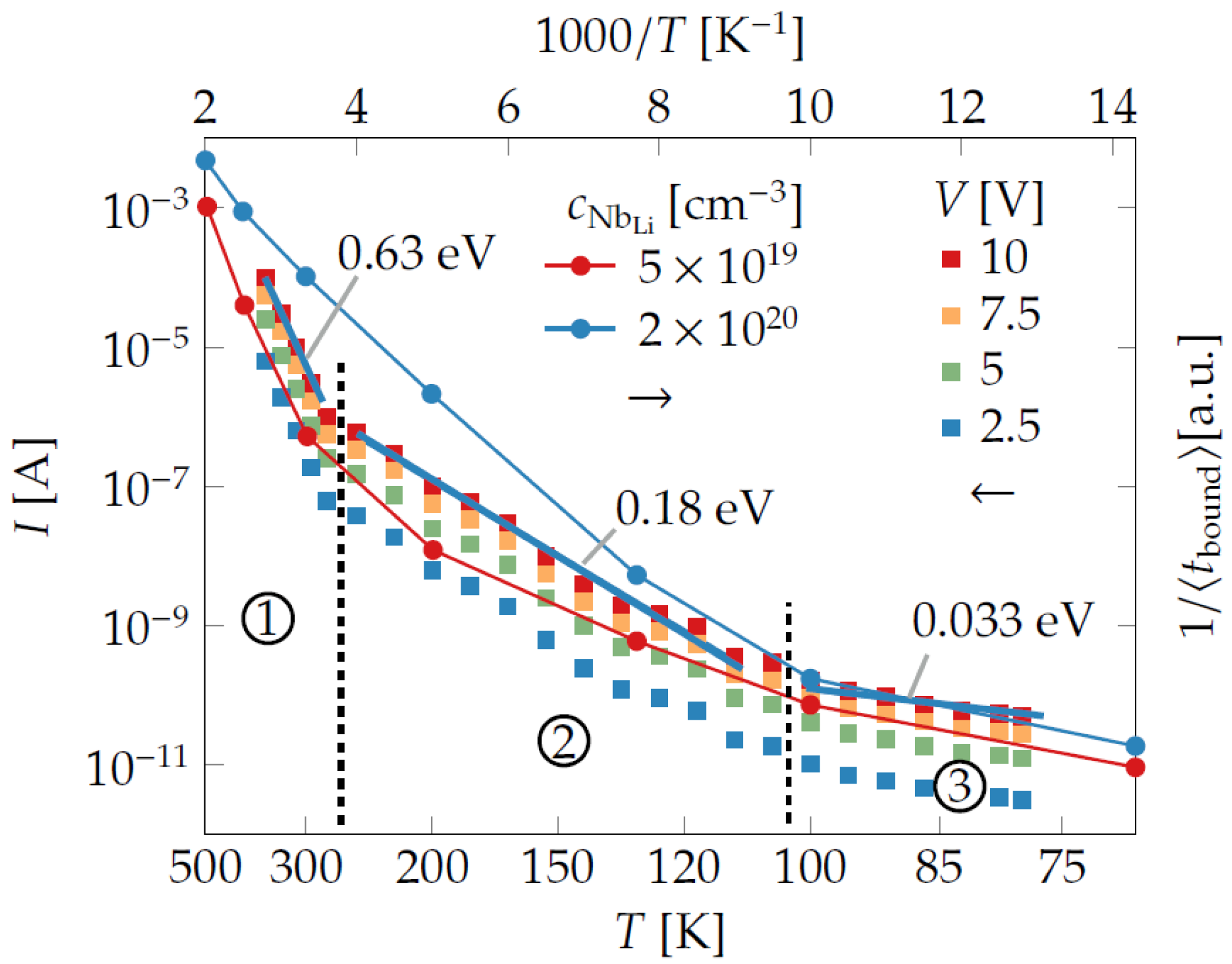
3.5. Temperature Dependent Conductance
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seidel, J.; Martin, L.W.; He, Q.; Zhan, Q.; Chu, Y.-H.; Rother, A.; Hawkridge, M.E.; Maksymovych, P.; Yu, P.; Gajek, M.; et al. Conduction at domain walls in oxide multiferroics. Nat. Mater. 2009, 8, 229–234. [Google Scholar] [CrossRef] [PubMed]
- Guyonnet, J.; Gaponenko, I.; Gariglio, S.; Paruch, P. Conduction at domain walls in insulating Pb (Zr0.2Ti0.8)O3 thin films. Adv. Mater. 2011, 23, 5377. [Google Scholar] [CrossRef] [PubMed]
- Gaponenko, I.; Tückmantel, P.; Karthik, J.; Martin, L.W.; Paruch, P. Towards reversible control of domain wall conduction in Pb (Zr0.2Ti0.8)O3 thin films. Appl. Phys. Lett. 2015, 106, 162902. [Google Scholar] [CrossRef]
- Lu, H.; Tan, Y.; McConville, J.P.V.; Ahmadi, Z.; Wang, B.; Conroy, M.; Moore, K.; Bangert, U.; Shield, J.E.; Chen, L.-Q.; et al. Electrical Tunability of Domain Wall Conductivity in LiNbO3 Thin Films. Adv. Mater. 2019, 31, 1902890. [Google Scholar] [CrossRef]
- Volk, T.R.; Gainutdinov, R.V.; Zhang, H.H. Domain-wall conduction in AFM-written domain patterns in ion-sliced LiNbO3 films. Appl. Phys. Lett. 2017, 110, 132905. [Google Scholar] [CrossRef]
- Rojac, T.; Bencan, A.; Drazic, G.; Sakamoto, N.; Ursic, H.; Jancar, B.; Tavcar, G.; Makarovic, M.; Walker, J.; Malic, B.; et al. Domain-wall conduction in ferroelectric BiFeO3 controlled by accumulation of charged defects. Nat. Mater. 2017, 16, 322–327. [Google Scholar] [CrossRef]
- Eliseev, E.A.; Morozovska, A.N.; Svechnikov, G.S.; Gopalan, V.; Shur, V.Y. Static conductivity of charged domain walls in uniaxial ferroelectric semiconductors. Phys. Rev. B 2011, 83, 235313. [Google Scholar] [CrossRef]
- Xiao, S.Y.; Kämpfe, T.; Jin, Y.M.; Haußmann, A.; Lu, X.M.; Eng, L.M. Dipole-Tunneling Model from Asymmetric Domain-Wall Conductivity in LiNbO3 Single Crystals. Phys. Rev. Appl. 2018, 10, 034002. [Google Scholar] [CrossRef]
- Sturman, B.; Podivilov, E.; Stepanov, M.; Tagantsev, A.; Setter, N. Quantum properties of charged ferroelectric domain walls. Phys. Rev. B 2015, 92, 21. [Google Scholar] [CrossRef]
- Godau, C.; Kämpfe, T.; Thiessen, A.; Eng, L.M.; Haußmann, A. Enhancing the domain wall conductivity in lithium niobate single crystals. ACS Nano 2017, 11, 5. [Google Scholar]
- Werner, C.S.; Herr, S.J.; Buse, K.; Sturman, B.; Soergel, E.; Razzaghi, C.; Breunig, I. Large and accessible conductivity of charged domain walls in lithium niobate. Sci. Rep. 2017, 7, 9862. [Google Scholar] [CrossRef] [PubMed]
- Pawlik, A.-S.; Kämpfe, T.; Haußmann, A.; Woike, T.; Treske, U.; Knupfer, M.; Büchner, B.; Soergel, E.; Streubel, R.; Koitzsch, A.; et al. Polarization driven conductance variations at charged ferroelectric domain walls. Nanoscale 2017, 9, 30. [Google Scholar] [CrossRef] [PubMed]
- Kirbus, B.; Godau, C.; Wehmeier, L.; Beccard, H.; Beyreuther, E.; Haußmann, A.; Eng, L.M. Real-Time 3D Imaging of Nanoscale Ferroelectric Domain Wall Dynamics in Lithium Niobate Single Crystals under Electric Stimuli: Implications for Domain-Wall-Based Nanoelectronic Devices. ACS Appl. Nanomater. 2019, 2, 5787–5794. [Google Scholar] [CrossRef]
- Xia, Q.; Yang, J.J. Memristive crossbar arrays for brain-inspired computing. Nat. Mater. 2019, 18, 309–323. [Google Scholar] [CrossRef] [PubMed]
- Schröder, M.; Haußmann, A.; Thiessen, A.; Soergel, E.; Woike, T.; Eng, L.M. Conducting domain walls in lithium niobate single crystals. Adv. Funct. Mater. 2012, 22, 3936. [Google Scholar] [CrossRef]
- Schröder, M.; Chen, X.; Haußmann, A.; Thiessen, A.; Poppe, J.; Bonnell, D.A.; Eng, L.M. Nanoscale and macroscopic electrical ac transport along conductive domain walls in lithium niobate single crystals. Mater. Res. Express 2014, 1, 035012. [Google Scholar] [CrossRef]
- Kämpfe, T.; Reichenbach, P.; Schröder, M.; Haußmann, A.; Eng, L.M.; Woike, T.; Soergel, E. Optical three-dimensional profiling of charged domain walls in ferroelectrics by Cherenkov second-harmonic generation. Phys. Rev. B 2014, 89, 035314. [Google Scholar] [CrossRef]
- Kämpfe, T.; Reichenbach, P.; Haußmann, A.; Woike, T.; Soergel, E.; Eng, L.M. Real-time three-dimensional profiling of ferroelectric domain walls. Appl. Phys. Lett. 2015, 107, 152905. [Google Scholar] [CrossRef]
- Wehmeier, L.; Kämpfe, T.; Haußmann, A.; Eng, L.M. In situ 3D observation of the domain wall dynamics in a triglycine sulfate single crystal upon ferroelectric phase transitio. Phys. Stat. Solidi RRL 2017, 11, 1700267. [Google Scholar] [CrossRef]
- Reichenbach, P.; Kämpfe, T.; Thiessen, A.; Haußmann, A.; Woike, T.; Eng, L.M. Multiphoton photoluminescence contrast in switched Mg: LiNbO3 and Mg: LiTaO3 single crystals. Appl. Phys. Lett. 2014, 105, 22906. [Google Scholar] [CrossRef]
- Reichenbach, P.; Kämpfe, T.; Thiessen, A.; Schröder, M.; Haußmann, A.; Woike, T.; Eng, L.M. Conducting domain walls in lithium niobate single crystals. J. Appl. Phys. 2014, 115, 213509. [Google Scholar] [CrossRef]
- Reichenbach, P.; Kämpfe, T.; Haußmann, A.; Thiessen, A.; Woike, T.; Steudtner, R.; Kocsor, L.; Szaller, Z.; Kovács, L.; Eng, L.M. Polaron-Mediated Luminescence in Lithium Niobate and Lithium Tantalate and Its Domain Contrast. Crystals 2018, 8, 214. [Google Scholar] [CrossRef]
- Haußmann, A.; Kirsten, L.; Schmidt, S.; Cimalla, P.; Wehmeier, L.; Koch, E.; Eng, L.M. Three-Dimensional, Time-Resolved Profiling of Ferroelectric Domain Wall Dynamics by Spectral-Domain Optical Coherence Tomography. Ann. Phys. 2017, 529, 1700139. [Google Scholar] [CrossRef]
- Haußmann, A.; Gemeinhardt, A.; Schröder, M.; Kämpfe, T.; Eng, L.M. Bottom-up assembly of molecular nanostructures by means of ferroelectric lithography. Langmuir 2017, 33, 475–484. [Google Scholar] [CrossRef]
- Gonnissen, J.; Batuk, D.; Nataf, G.F.; Jones, L.; Abakumov, A.M.; van Aert, S.; Schryvers, D.; Salje, E.K.H. Direct Observation of Ferroelectric Domain Walls in LiNbO3: Wall-Meanders, Kinks, and Local Electric Charges. Adv. Funct. Mater. 2016, 26, 42. [Google Scholar] [CrossRef]
- Conroy, M.; Moore, K.; O’Connell, E.N.; McConville, J.P.V.; Lu, H.; Chaudhary, P.; Lipatov, A.; Sinitskii, A.; Gruverman, A.; Gregg, J.M.; et al. Atomic-Scale Characterization of Ferro-Electric Domains in Lithium Niobate-revealing the Electronic Properties of Domain Wall. Microsc. Microanal. 2019, 25, 576–577. [Google Scholar] [CrossRef]
- Poberaj, G.; Hu, H.; Sohler, W.; Günter, P. Lithium niobate on insulator (LNOI) for micro-photonic devices. Laser Photonics Rev. 2012, 6, 488–503. [Google Scholar] [CrossRef]
- Chen, L.Q. Phase-field models for microstructure evolution. Ann. Rev. Mat. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef]
- Scrymgeour, D.; Gopalan, V.; Itagi, A.; Saxena, A.; Swart, P. Phenomenological theory of a single domain wall in uniaxial trigonal ferroelectrics: Lithium niobate and lithium tantalite. Phys. Rev. B 2005, 71, 184110. [Google Scholar] [CrossRef]
- Kämpfe, T. Charged Domain Walls in Ferroelectric Single Crystals. Ph.D. Thesis, Dresden University of Technology, Dresden, Germany, 2017. [Google Scholar]
- Maksymovych, P.; Pan, M.; Yu, P.; Ramesh, R.; Baddorf, A.P.; Kalinin, S.V. Scaling and disorder analysis of local I–V curves from ferroelectric thin films of lead zirconate titanate. Nanotechnology 2011, 22, 254031. [Google Scholar] [CrossRef]
- Ding, N.; Xu, J.; Yao, Y.X.; Wegner, G.; Fang, X.; Chen, C.H.; Lieberwirth, I. Determination of the diffusion coefficient of lithium ions in nano-Si. Solid State Ion. 2009, 180, 222–225. [Google Scholar] [CrossRef]
- Mott, N.F.; Gurney, R.W. Electronic Processes in Ionic Crystals; The Clarendon Press: Oxford, UK, 1940. [Google Scholar]
- Kämpfe, T.; Haußmann, A.; Eng, L.M.; Reichenbach, P.; Thiessen, A.; Woike, T.; Steudtner, R. Time-resolved photoluminescence spectroscopy of Nb Nb 4+ and O− polarons in LiNbO3 single crystals. Phys. Rev. B 2016, 93, 74116. [Google Scholar] [CrossRef]
- Mhaouech, I.; Guilbert, L. Temperature dependence of small polaron population decays in iron-doped lithium niobate by Monte Carlo simulations. Solid State Sci. 2016, 60, 28–36. [Google Scholar] [CrossRef]
- Sanson, A.; Zaltron, A.; Argiolas, N.; Sada, C.; Bazzan, M.; Schmidt, W.G.; Sanna, S. Polaronic deformation at the Fe2+/3+ impurity site in Fe: LiNbO3 crystals. Phys. Rev. B 2015, 91, 094109. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Imlau, M.; Merschjann, C.; Schoke, B. Electron small polarons and bipolarons in LiNbO3. J Phys. Cond. Matter 2009, 21, 23201. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kämpfe, T.; Wang, B.; Haußmann, A.; Chen, L.-Q.; Eng, L.M. Tunable Non-Volatile Memory by Conductive Ferroelectric Domain Walls in Lithium Niobate Thin Films. Crystals 2020, 10, 804. https://doi.org/10.3390/cryst10090804
Kämpfe T, Wang B, Haußmann A, Chen L-Q, Eng LM. Tunable Non-Volatile Memory by Conductive Ferroelectric Domain Walls in Lithium Niobate Thin Films. Crystals. 2020; 10(9):804. https://doi.org/10.3390/cryst10090804
Chicago/Turabian StyleKämpfe, Thomas, Bo Wang, Alexander Haußmann, Long-Qing Chen, and Lukas M. Eng. 2020. "Tunable Non-Volatile Memory by Conductive Ferroelectric Domain Walls in Lithium Niobate Thin Films" Crystals 10, no. 9: 804. https://doi.org/10.3390/cryst10090804
APA StyleKämpfe, T., Wang, B., Haußmann, A., Chen, L.-Q., & Eng, L. M. (2020). Tunable Non-Volatile Memory by Conductive Ferroelectric Domain Walls in Lithium Niobate Thin Films. Crystals, 10(9), 804. https://doi.org/10.3390/cryst10090804







