In Situ Electric-Field Study of Surface Effects in Domain Engineered Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 Relaxor Crystals by Grazing Incidence Diffraction
Abstract
1. Introduction
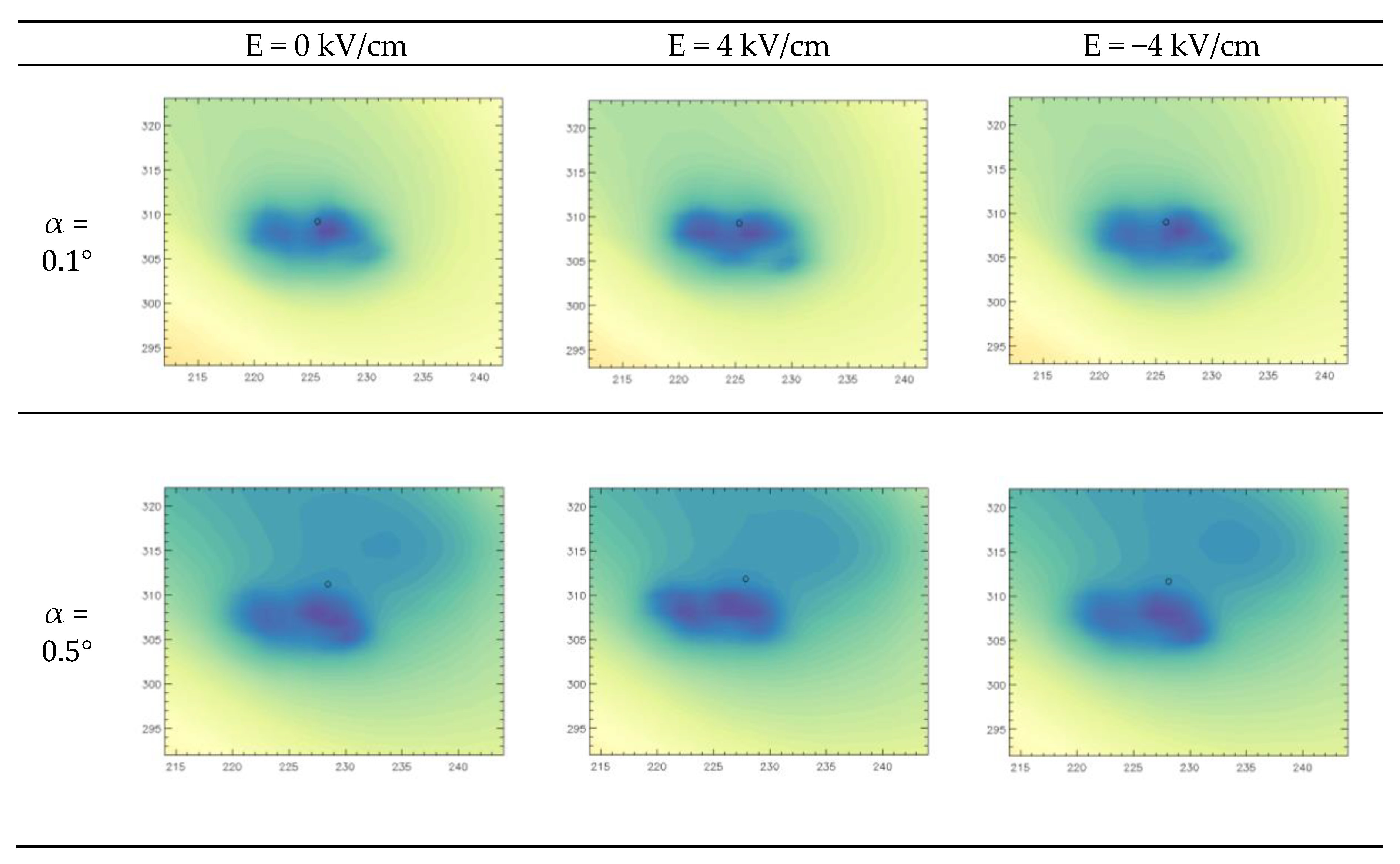
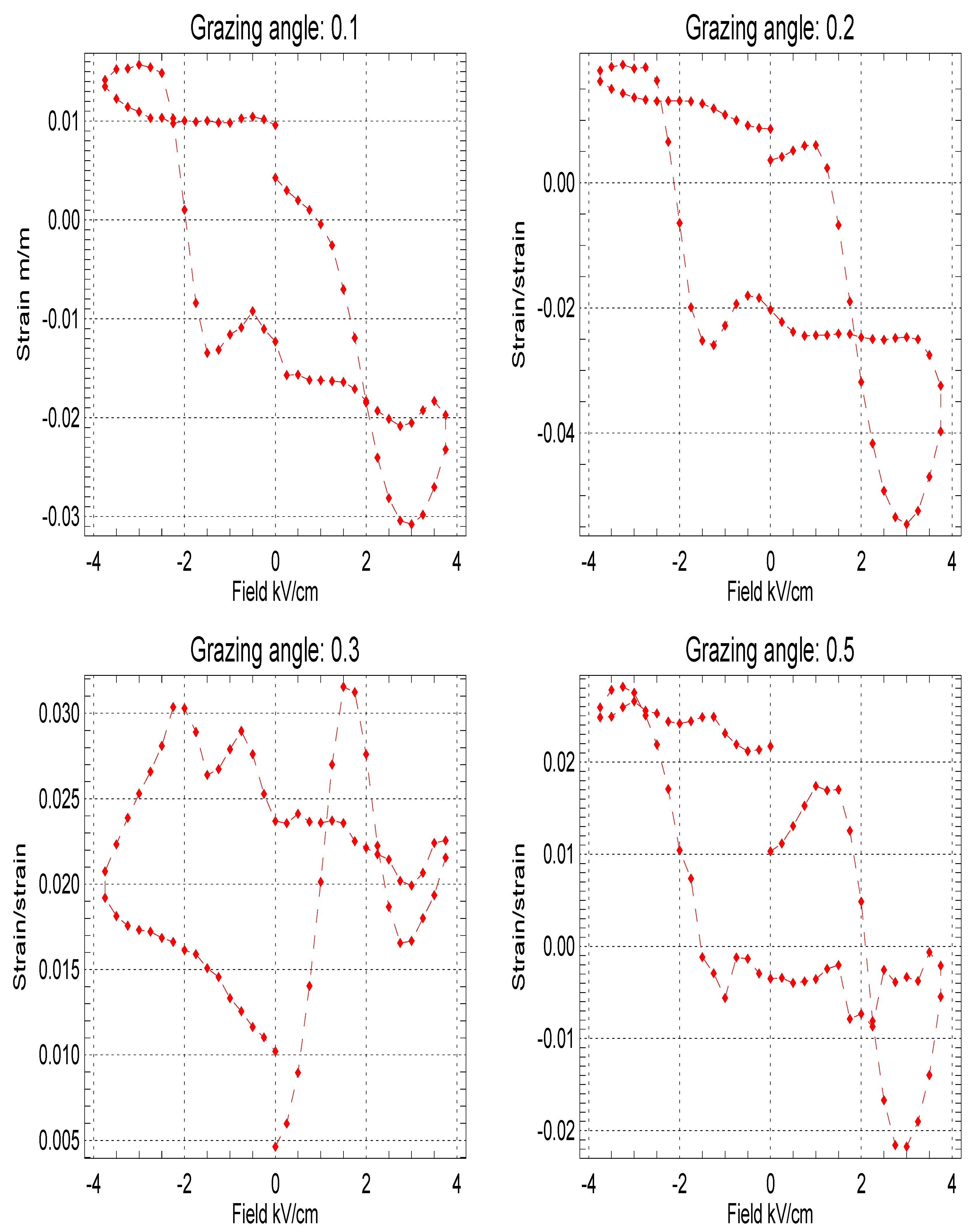
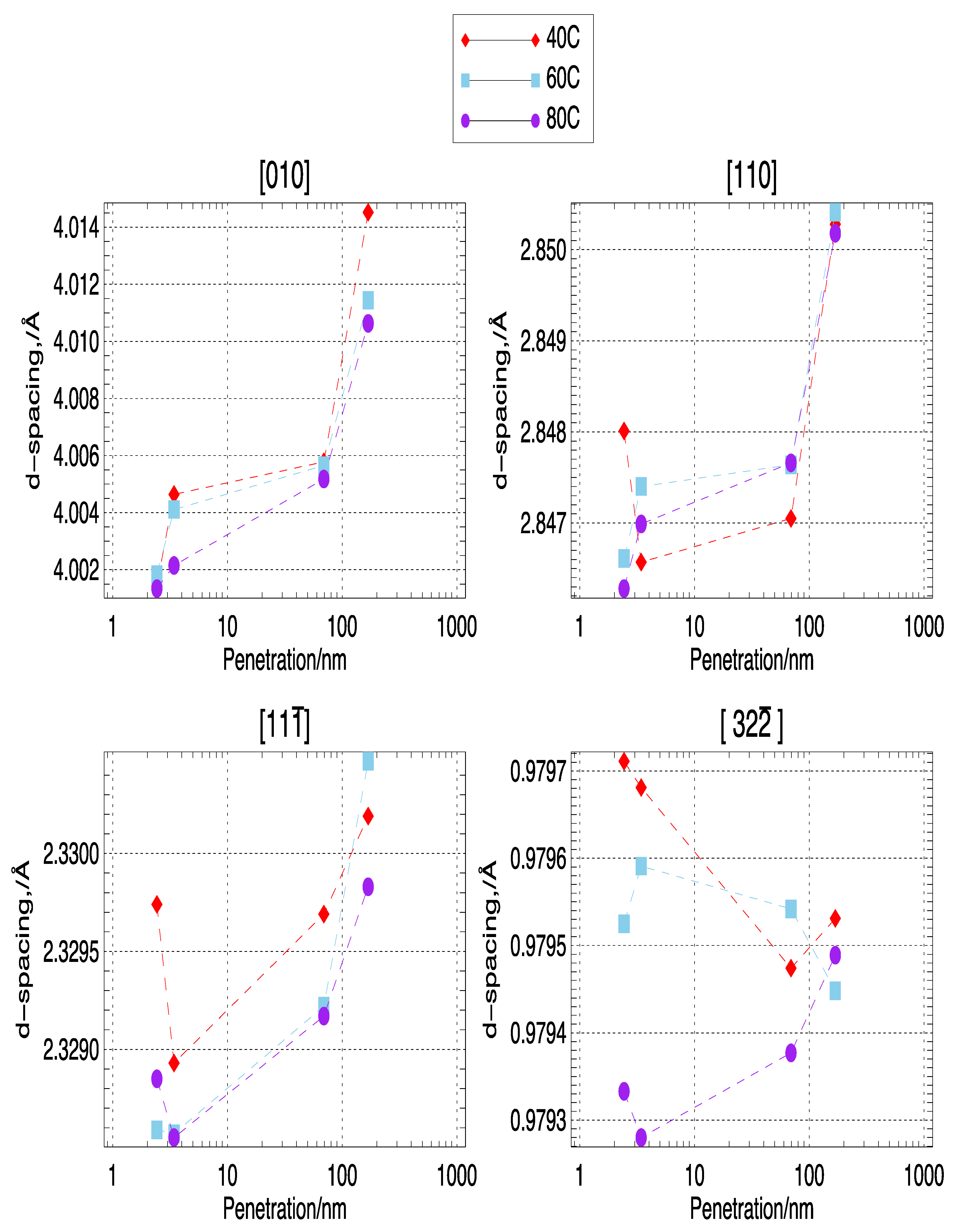
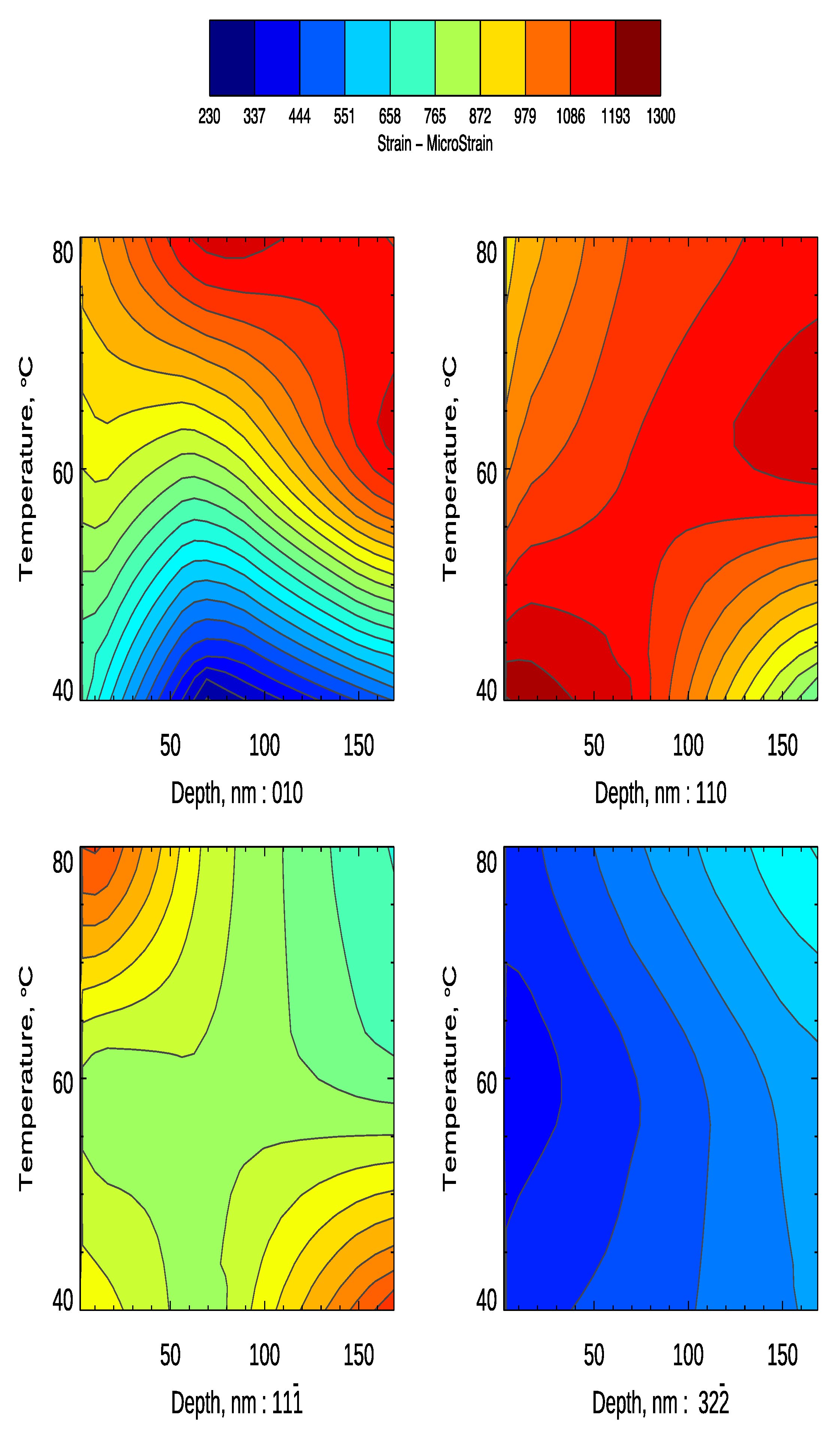
2. Results and Discussion
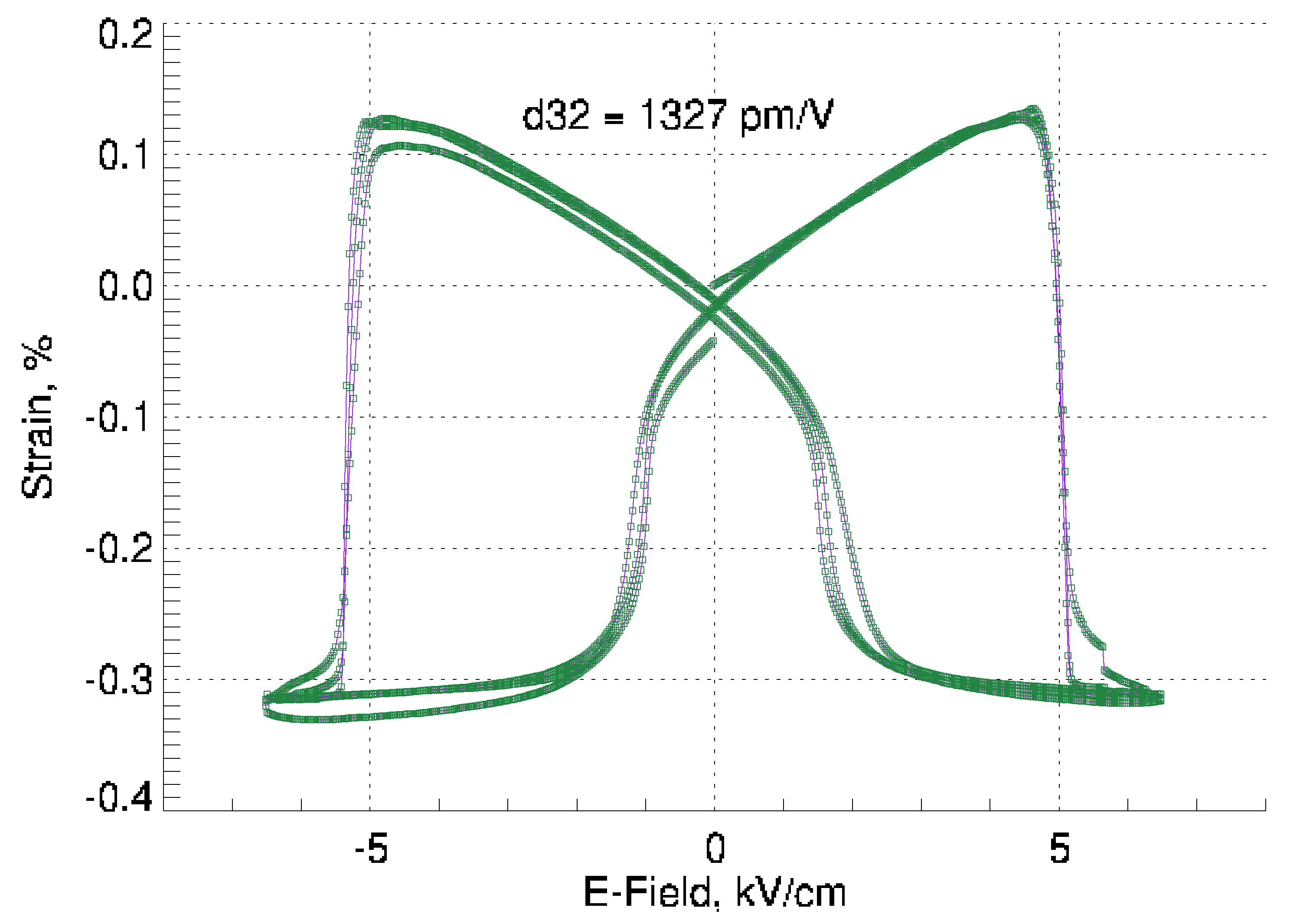
2.1. Results
2.2. Discussion
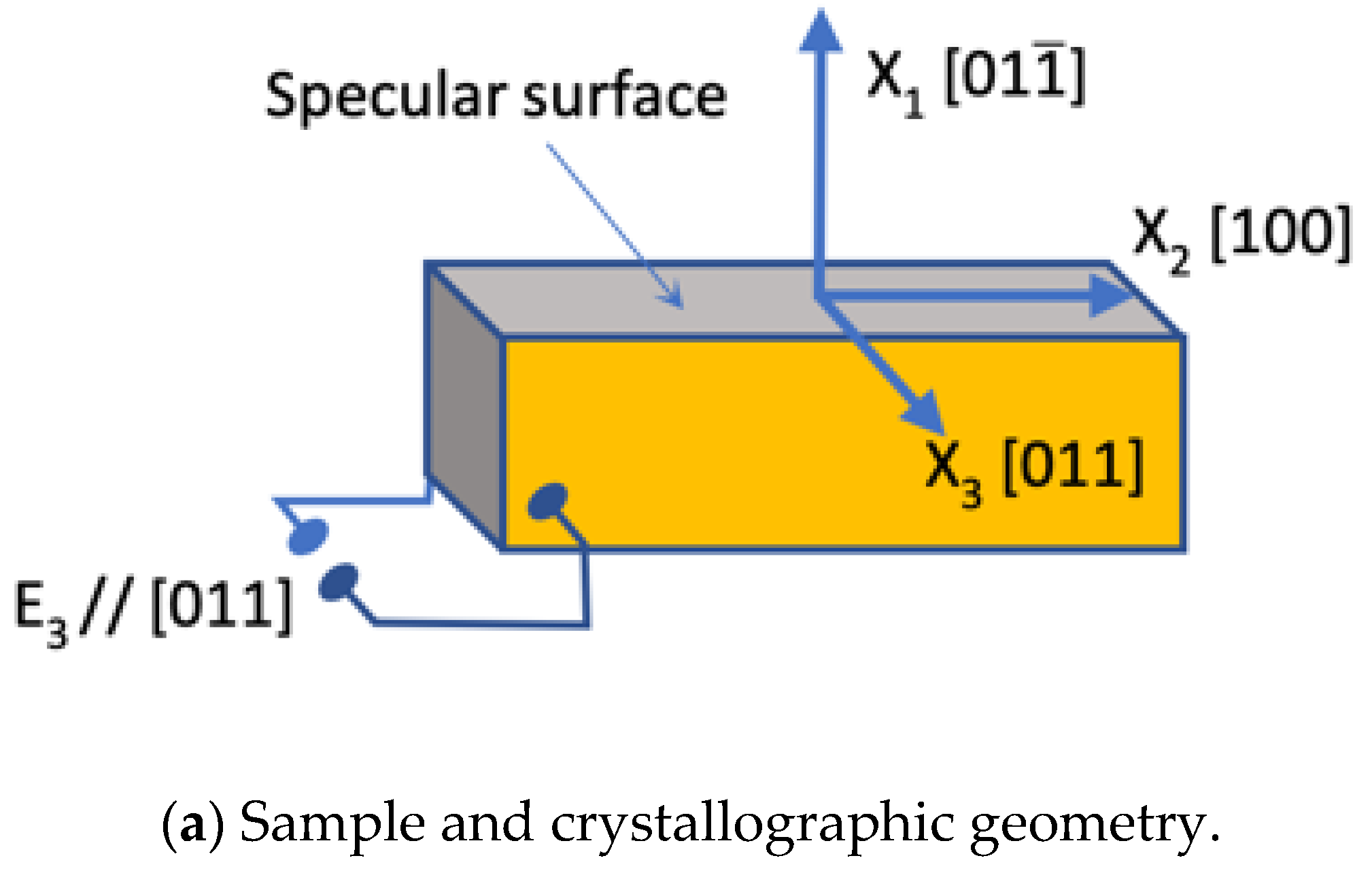
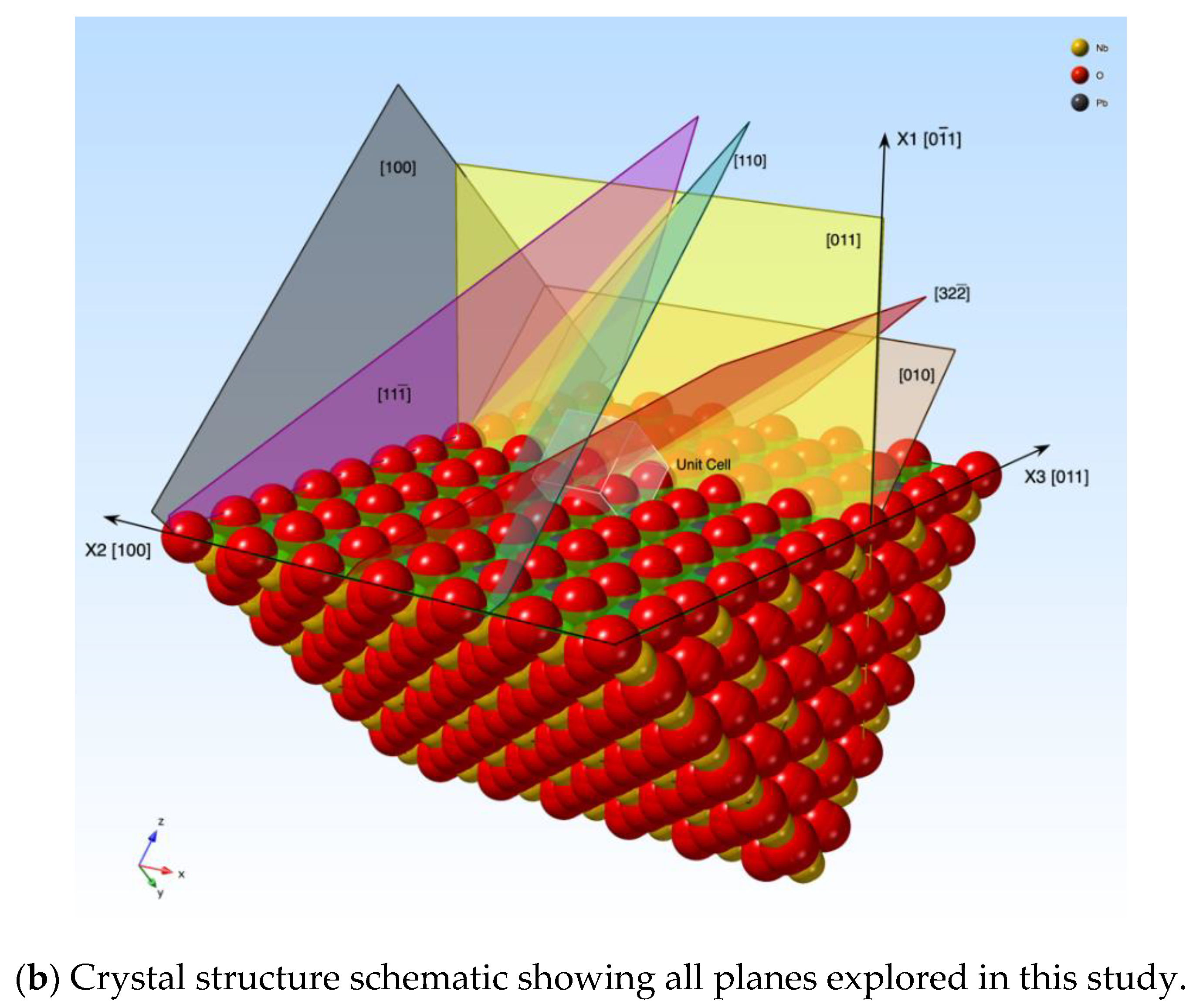
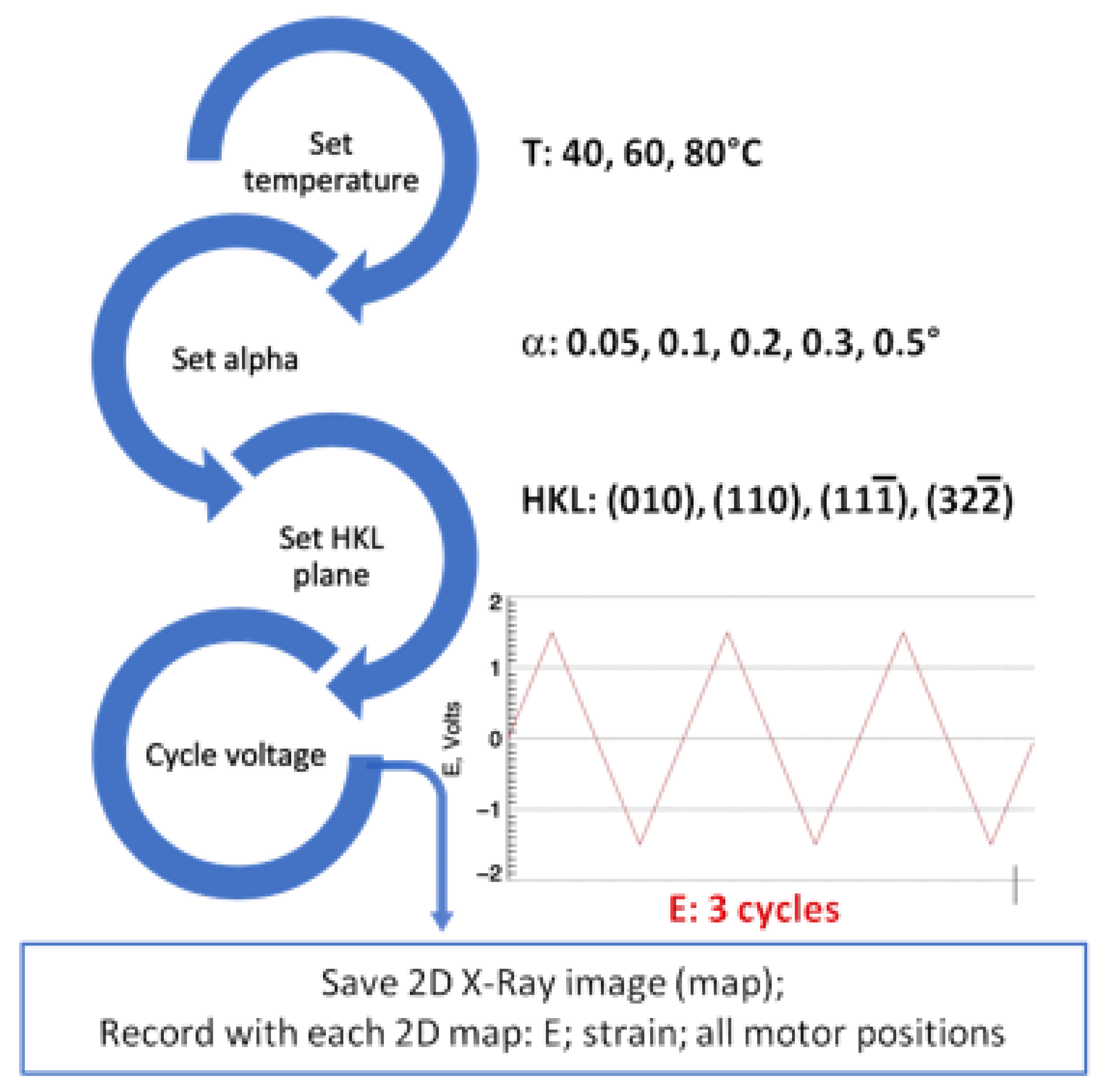
3. Experimental Section
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Park, S.E.E.; Hackenberger, W. High performance single crystal piezoelectrics: Applications and issues. Curr. Opin. Solid State Mater. Sci. 2002, 6, 11–18. [Google Scholar] [CrossRef]
- Zhang, S.; Shrout, T. Relaxor-PT single crystals: Observations and developments. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2010, 57, 2138–2146. [Google Scholar] [CrossRef] [PubMed]
- Sun, E.; Cao, W. Relaxor-based ferroelectric single crystals: Growth, domain engineering, characterization and applications. J. Prog. Mater. Sci. 2014, 65, 124–210. [Google Scholar] [CrossRef] [PubMed]
- Hosono, Y.; Yamashita, Y. Piezoelectric ceramics and single crystals for ultrasonic medical transducers. J. Electroceram 2006, 17, 577–583. [Google Scholar] [CrossRef]
- Li, F.; Zhang, S.; Luo, J.; Geng, X.; Xu, Z.; Shrout, T.R. [111]-oriented PIN-PMN-PT crystals with ultrahigh dielectric permittivity and high frequency constant for high-frequency transducer applications. J. Appl. Phys. 2016, 120, 074105. [Google Scholar] [CrossRef]
- Qiao, H.; He, C.; Wang, Z.; Li, X.; Liu, Y.; Tailor, H.; Long, X. Orientation-dependent electrical property and domain configuration of Mn-doped Pb(In 0.5Nb 0.5)O 3-PbTiO 3single crystal. J. Am. Ceram. Soc. 2018, 102, 79–84. [Google Scholar] [CrossRef]
- Li, F.; Zhang, S.; Xu, Z.; Wei, X.; Luo, J.; Shrout, T.R. Investigation of Electromechanical Properties and Related Temperature Characteristics in Domain-Engineered Tetragonal Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 Crystals. J. Am. Ceram. Soc. 2010, 93, 2731–2734. [Google Scholar] [CrossRef]
- Bell, A.J. Ferroelectrics: The role of ceramic science and engineering. J. Eur. Ceram. Soc. 2008, 28, 1307–1317. [Google Scholar] [CrossRef]
- Damjanovic, D.; Brem, F.; Setter, N. Crystal orientation dependence of the piezoelectric d[sub 33] coefficient in tetragonal BaTiO[sub 3] as a function of temperature. Appl. Phys. Lett. 2002, 80, 652. [Google Scholar] [CrossRef]
- Damjanovic, D. Contributions to the Piezoelectric Effect in Ferroelectric Single Crystals and Ceramics. J. Am. Ceram. Soc. 2005, 88, 2663–2676. [Google Scholar] [CrossRef]
- Damjanovic, D. A morphotropic phase boundary system based on polarization rotation and polarization extension. Appl. Phys. Lett. 2010, 97, 062906. [Google Scholar] [CrossRef]
- Finkel, P.; Staruch, M.; Amin, A.; Ahart, M.; Lofland, S.E. Simultaneous Stress and Field Control of Sustainable Switching of Ferroelectric Phases. Sci. Rep. 2015. [Google Scholar] [CrossRef] [PubMed]
- Nan, C.-W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Noheda, B.; Cox, D.; Shirane, G.; Gonzalo, J.; Cross, L.; Park, S. A monoclinic ferroelectric phase in the Pb (ZrTi) O solid solution. Appl. Phys. Lett. 1999, 74, 2059. [Google Scholar] [CrossRef]
- Fu, H.; Cohen, R. Polarization rotation mechanism for ultrahigh electromechanical response in single-crystal piezoelectrics. Nature 2000, 403, 281–283. [Google Scholar] [CrossRef]
- Park, S.-E.; Shrout, T.R. Ultrahigh strain and piezoelectric behavior in relaxor based ferroelectric single crystals. J. Appl. Phys. 1997, 82, 1804. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Yuan, G.; Ma, H.; Xu, F.; Li, J.; Viehland, D.; Gehring, P.M. Fragile morphotropic phase boundary and phase stability in the near-surface region of the relaxor ferroelectric (1-x) Pb (Z n1 /3N b2 /3) O3-x PbTi O3: [001] field-cooled phase diagrams. Phys. Rev. B 2016, 94, 174103. [Google Scholar] [CrossRef]
- Xu, G.; Gehring, P.M.; Stock, C.; Conlon, K. The anomalous skin effect in single crystal relaxor ferroelectric PZN-x PT and PMN-x PT. Phase Transit. 2006, 79, 135–152. [Google Scholar] [CrossRef]
- Cowley, R.A.; Gvasaliya, S.N.; Lushnikov, S.G.; Roessli, B.; Rotaru, G.M. Relaxing with relaxors: A review of relaxor ferroelectrics. Adv. Phys. 2011, 60, 229–327. [Google Scholar]
- Phelan, D.; Rodriguez, E.E.; Gao, J.; Bing, Y.; Ye, Z.G.; Huang, Q.; Wen, J.; Xu, G.; Stock, C.; Matsuura, M.; et al. Phase diagram of the relaxor ferroelectric (1-x) Pb(Mg1/3Nb2/3)O3+xPbTiO3 revisited: A neutron powder diffraction study of the relaxor skin effect. Phase Transit. 2015, 88, 283–305. [Google Scholar] [CrossRef]
- Xu, G.; Zhong, Z.; Bing, Y.; Ye, Z.G.; Stock, C.; Shirane, G. Ground state of the relaxor ferroelectric Pb(Zn1/3Nb2/3)O3. Phys. Rev. B Condens. Matter 2003, 67, 1804–1805. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, G.; Luo, H.; Li, J.; Viehland, D. Phase Transition in the Near-Surface Region of Ternary Pb(In1/2Nb1/2)O3−Pb(Mg1/3Nb2/3)O3−PbTiO3Relaxor Ferroelectric Crystals. Phys. Rev. Appl. 2017, 8, 034032. [Google Scholar] [CrossRef]
- Feidenhans’l, R. Surface structure determination by X-ray diffraction. Surf. Sci. Rep. 1989, 10, 105–188. [Google Scholar] [CrossRef]
- Lee, H.J.; Zhang, S.; Luo, J.; Li, F.; Shrout, T.R. Thickness-Dependent Properties of Relaxor-PbTiO3 Ferroelectrics for Ultrasonic Transducers. Adv. Funct. Mater. 2010, 20, 3154–3162. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zeng, K. Domain structure, local surface potential distribution and relaxation of Pb(Zn1/3Nb2/3)O3-9%PbTiO3 (PZN-9%PT) single crystals. J. Mater. 2016, 2, 309–315. [Google Scholar] [CrossRef]
- Qi, X.; Zhao, Y.; Sun, E.; Du, J.; Li, K.; Sun, Y.; Yang, B.; Zhang, R.; Cao, W. Large electrostrictive effect and high energy storage performance of Pr3+-doped PIN-PMN-PT multifunctional ceramics in the ergodic relaxor phase. J. Eur. Ceram. Soc. 2019, 39, 4060–4069. [Google Scholar] [CrossRef]
- Vlasov, E.O.; Chezganov, D.S.; Gimadeeva, L.V.; Ushakov, A.D.; Hu, Q.; Wei, X.; Shur, V.Y. Domain structure imaging in PMN-PT crystals using channelling-contrast backscattered electron microscopy. IOP Conf. Ser. Mater. Sci. Eng. 2018, 443, 012038. [Google Scholar] [CrossRef]
- Herdier, R.; Leclerc, G.; Poullain, G.; Bouregba, R.; Remiens, E.D.; Dogheche, E. Investigation of Piezoelectric and Electrostrictive Properties of (Pb 1-3 y/2,La y) (Zr x,Ti 1-x)O 3Ferroelectric Thin Films Using a Doppler Laser Vibrometer. Ferroelectrics 2010, 362, 145–151. [Google Scholar] [CrossRef]
- He, W.; Li, Q.; Xi, X.; Yan, Q. High temperature-insensitive ferro-/piezoelectric properties and nanodomain structures of Pb(In 1/2Nb 1/2)O 3-PbZrO 3-Pb(Mg 1/3Nb 2/3)O 3-PbTiO 3relaxor single crystals. J. Am. Ceram. Soc. 2017, 101, 1236–1244. [Google Scholar] [CrossRef]
- Detalle, M.; Herdier, R.; Wang, G.S.; Remiens, D.; Roussel, P.; Fribourg-Blanc, E. Electrostrictive and Piezoelectric Behavior of PMN-PT Thin Films. Ferroelectrics 2007, 351, 15–24. [Google Scholar] [CrossRef]
- Patterson, E.A.; Staruch, M.; Matis, B.R.; Young, S.; Lofland, S.E.; Antonelli, L.; Blackmon, F.; Damjanovic, D.; Cain, M.G.; Thompson, P.B.J.; et al. Dynamic piezoelectric response of relaxor single crystal under electrically driven inter-ferroelectric phase transformations. Appl. Phys. Lett. 2020, 116, 222903. [Google Scholar] [CrossRef]
- Cain, M.G. Springer series in measurement science and technology. In Characterisation of Ferroelectric Bulk Materials and Thin Films; Springer: Berlin, Germany, 2014. [Google Scholar]
- Vecchini, C.; Thompson, P.; Stewart, M.; Muniz-Piniella, A.; McMitchell, S.R.C.; Wooldridge, J.; Lepadatu, S.; Bouchenoire, L.; Brown, S.; Wermeille, D.; et al. Simultaneous dynamic electrical and structural measurements of functional materials. Rev. Sci. Instrum. 2015, 86, 103901. [Google Scholar] [CrossRef] [PubMed]
- Solé, V.A.; Papillon, E.; Cotte, M.; Walter, P.; Susini, J. A multiplatform code for the analysis of energy-dispersive X-ray fluorescence spectra. Spectrochim. Acta Part. B At. Spectrosc. 2007, 62, 63–68. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cain, M.G.; Staruch, M.; Thompson, P.; Lucas, C.; Wermeille, D.; Kayser, Y.; Beckhoff, B.; Lofland, S.E.; Finkel, P. In Situ Electric-Field Study of Surface Effects in Domain Engineered Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 Relaxor Crystals by Grazing Incidence Diffraction. Crystals 2020, 10, 728. https://doi.org/10.3390/cryst10090728
Cain MG, Staruch M, Thompson P, Lucas C, Wermeille D, Kayser Y, Beckhoff B, Lofland SE, Finkel P. In Situ Electric-Field Study of Surface Effects in Domain Engineered Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 Relaxor Crystals by Grazing Incidence Diffraction. Crystals. 2020; 10(9):728. https://doi.org/10.3390/cryst10090728
Chicago/Turabian StyleCain, Markys G., Margo Staruch, Paul Thompson, Christopher Lucas, Didier Wermeille, Yves Kayser, Burkhard Beckhoff, Sam E. Lofland, and Peter Finkel. 2020. "In Situ Electric-Field Study of Surface Effects in Domain Engineered Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 Relaxor Crystals by Grazing Incidence Diffraction" Crystals 10, no. 9: 728. https://doi.org/10.3390/cryst10090728
APA StyleCain, M. G., Staruch, M., Thompson, P., Lucas, C., Wermeille, D., Kayser, Y., Beckhoff, B., Lofland, S. E., & Finkel, P. (2020). In Situ Electric-Field Study of Surface Effects in Domain Engineered Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 Relaxor Crystals by Grazing Incidence Diffraction. Crystals, 10(9), 728. https://doi.org/10.3390/cryst10090728





