Nowotny Chimney Ladder Phases with Group 5 Metals: Crystal and Electronic Structure and Relations to the CrSi2 Structure Type
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis
2.2. Powder X-ray Diffraction
2.3. Energy Dispersive X-ray Analysis
2.4. Crystal Structure Investigation
2.5. Electronic Strcuture Calculations
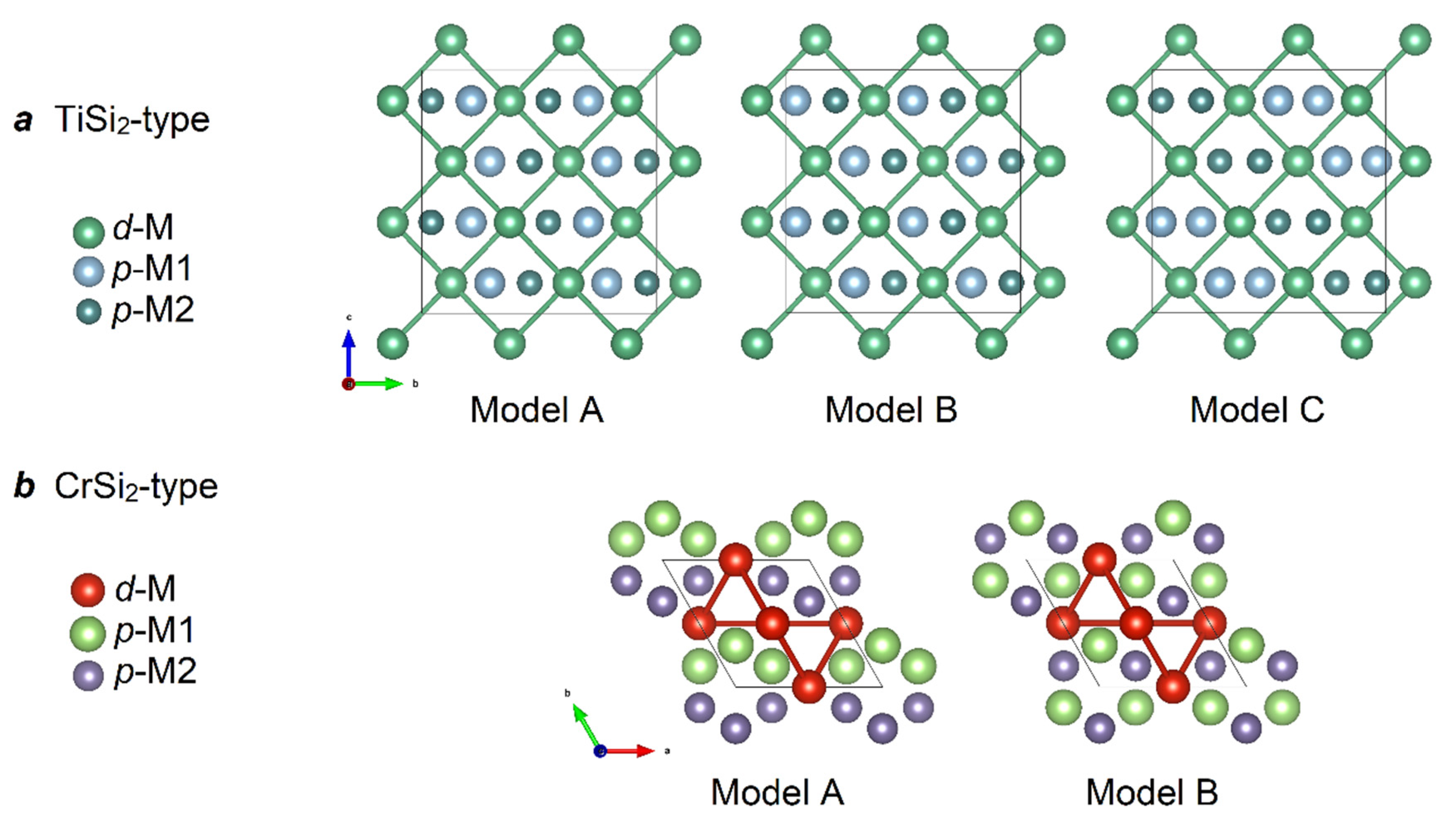
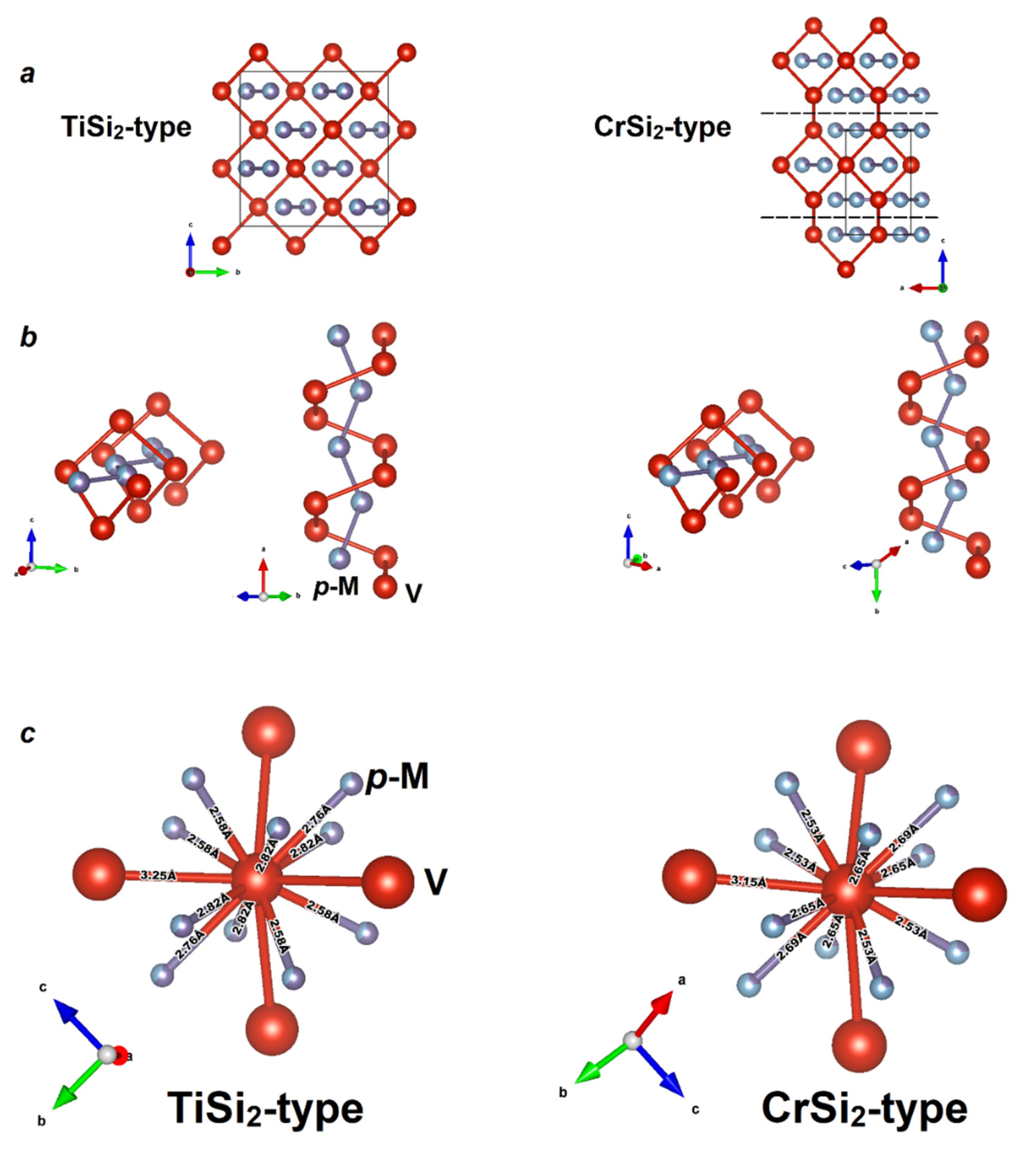
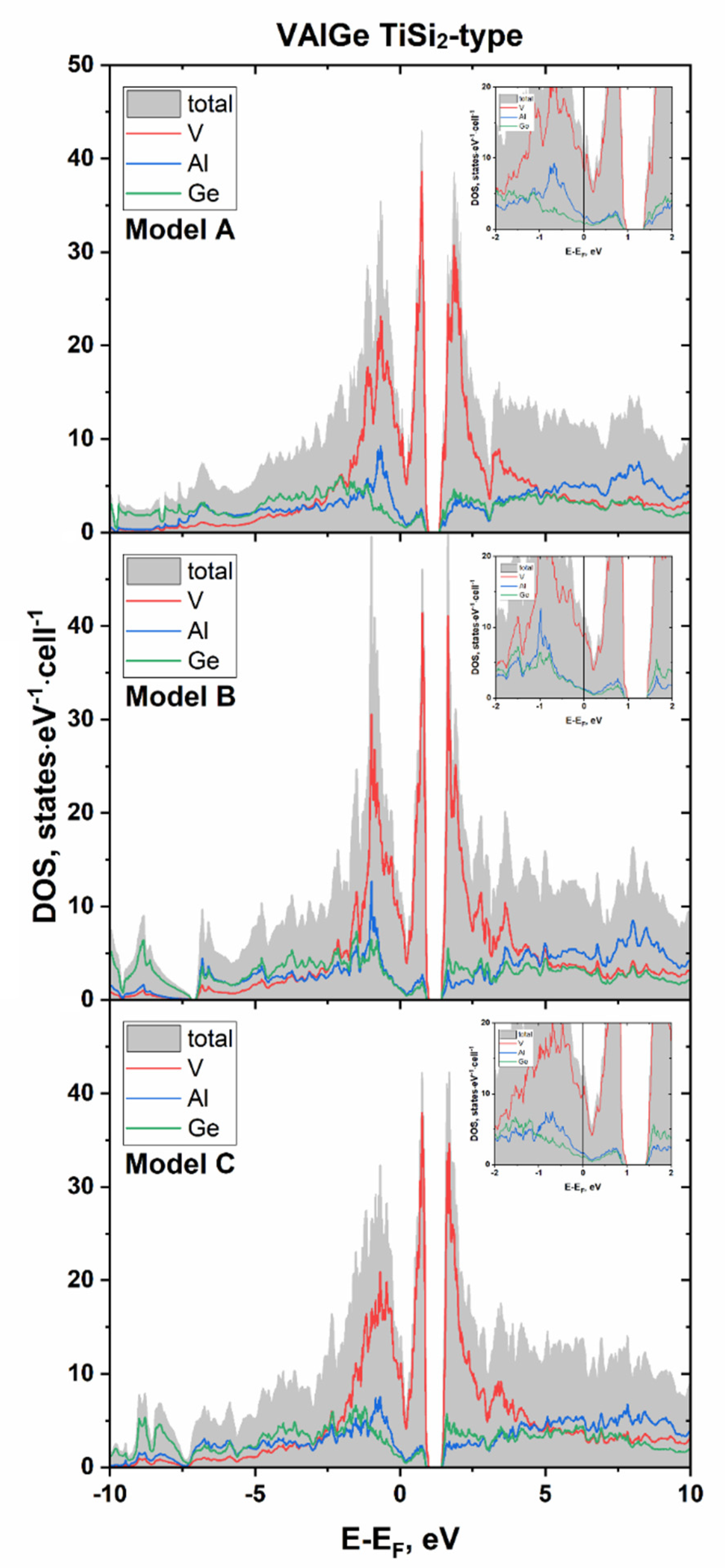
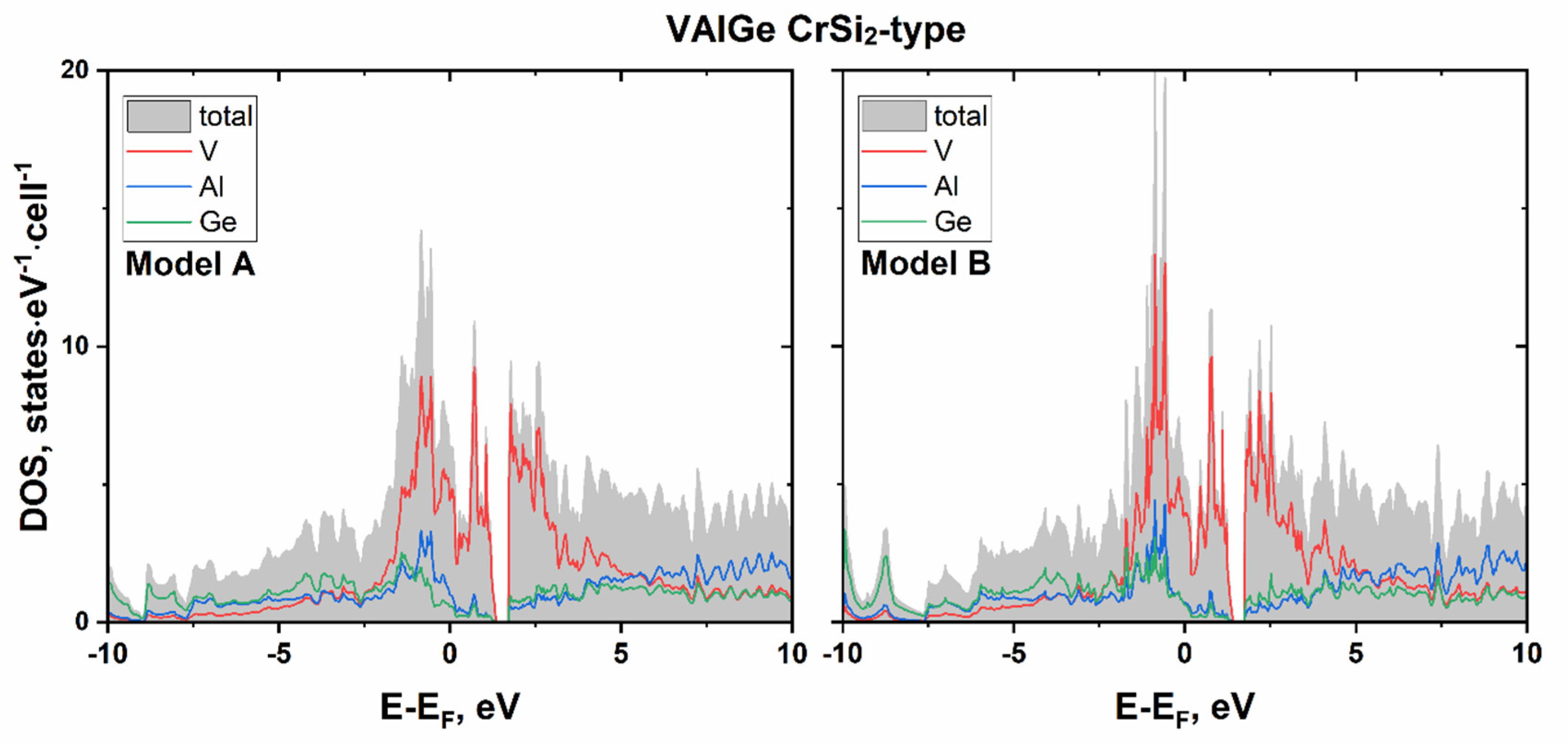
3. Results and Discussion
3.1. VAl2−xGex: Phase Equilibria, and Crystal and Electronic Structure
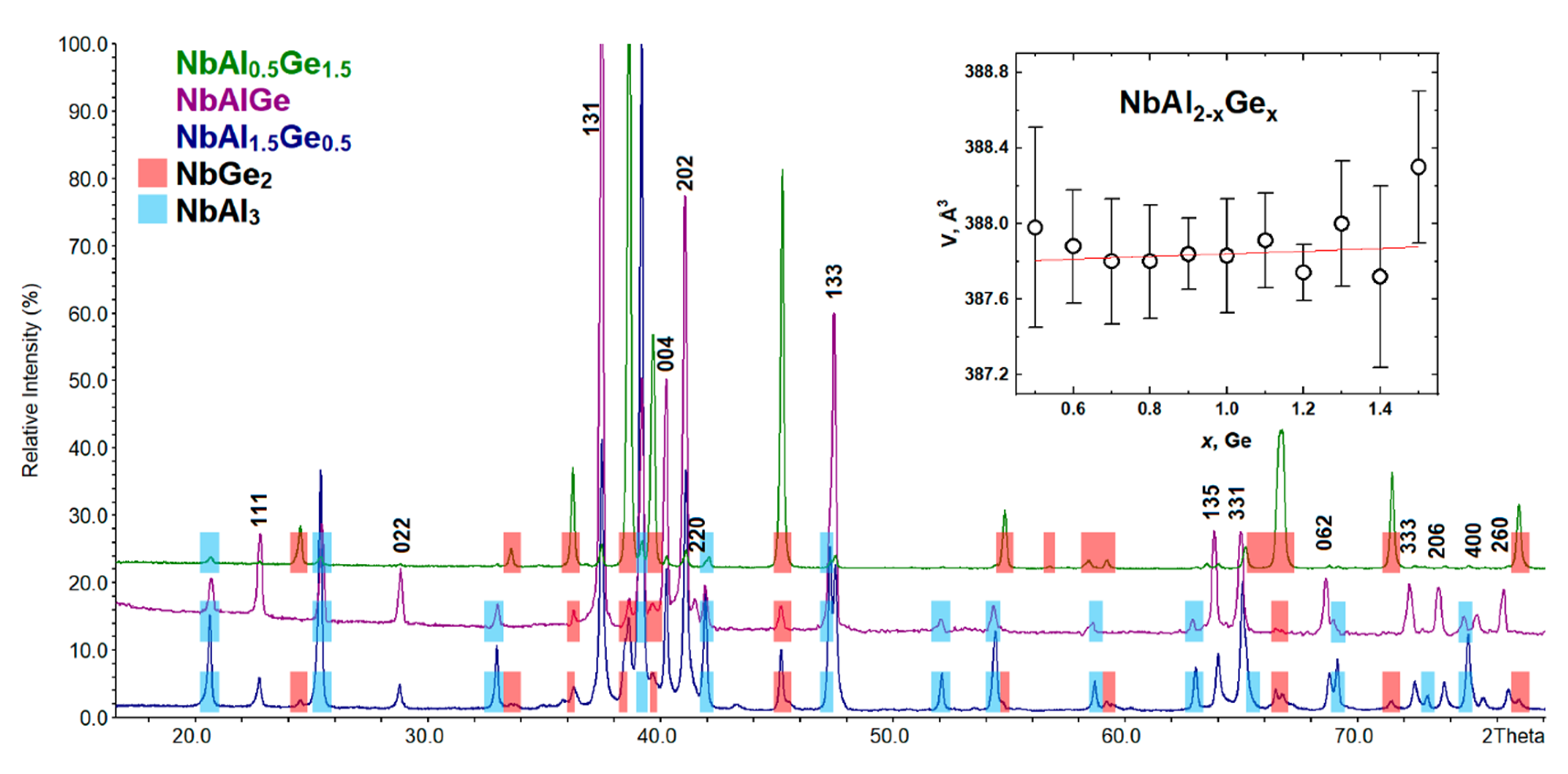
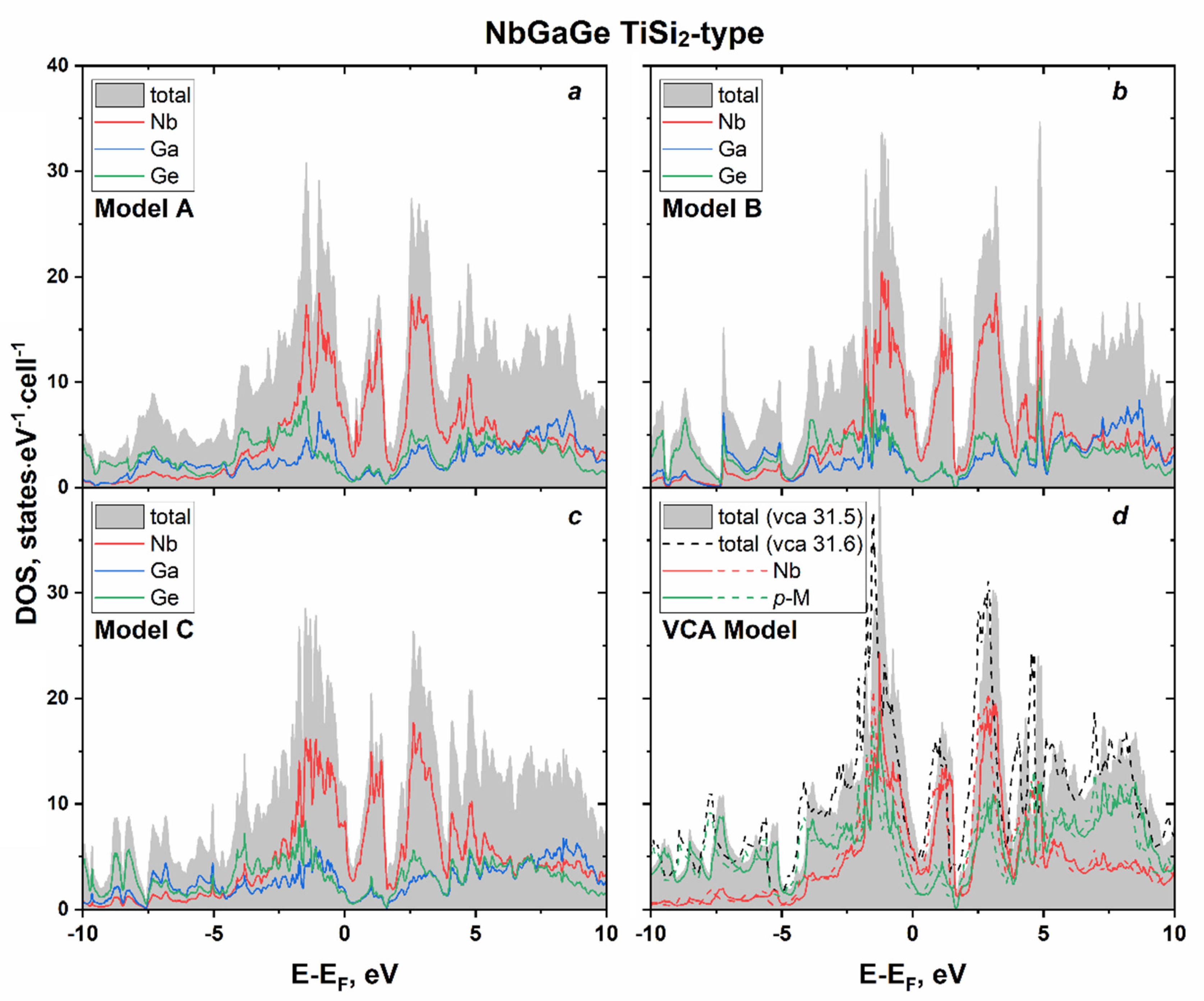
3.2. NbE2−xGex (E = Al, Ga): Phase Equilibria, Crystal and Electronic Structure
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Steurer, W.; Dshemuchadse, J. Intermetallics: Structures, Properties, and Statistics; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Akhmetshina, T.G.; Blatov, V.A.; Proserpio, D.M.; Shevchenko, A.P. Topology of intermetallic structures: From statistics to rational design. Acc. Chem. Res. 2018, 51, 21–30. [Google Scholar] [CrossRef]
- Oliynyk, A.O.; Mar, A. Discovery of intermetallic compounds from traditional to machine-learning approaches. Acc. Chem. Res. 2018, 51, 59–68. [Google Scholar] [CrossRef]
- Buschow, K.H.J. The importance of ternary intermetallic compounds in science and technology. J. Alloys Compd. 1993, 193, 223–230. [Google Scholar] [CrossRef]
- Fredrickson, D.C.; Miller, G.J. Intermetallic Chemistry: New Advances in Humanity’s Age-Old Exploration of Metals and Alloys. Acc. Chem. Res. 2018, 51, 213. [Google Scholar] [CrossRef]
- Fredrickson, D.C. Parallels in Structural Chemistry between the Molecular and Metallic Realms Revealed by Complex Intermetallic Phases. Acc. Chem. Res. 2018, 51, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Mizutani, U. Hume-Rothery Rules for Structurally Complex Alloy Phases; CRC Press: New York, NY, USA, 2010. [Google Scholar]
- Shevelkov, A.V.; Kovnir, K. Zintl Clathrates: Structure and Bonding; Springer: Berlin/Heidelberg, Germany, 2011; Volume 139, pp. 97–142. [Google Scholar]
- Imai, Y.; Watanabe, A. Consideration of the validity of the 14 valence electron rule for semiconducting chimney-ladder phase compounds. Intermetallics 2005, 13, 233–241. [Google Scholar] [CrossRef]
- Verchenko, V.Y.; Wei, Z.; Tsirlin, A.A.; Callaert, C.; Jesche, A.; Hadermann, J.; Dikarev, E.V.; Shevelkov, A.V. Crystal growth of the Nowotny chimney ladder phase Fe2Ge3: Exploring new Fe-based narrow-gap semiconductor with promising thermoelectric performance. Chem. Mater. 2017, 29, 9954–9963. [Google Scholar] [CrossRef]
- Sato, N.; Ouchi, H.; Takagiwa, Y.; Kimura, K. Glass-like Lattice Thermal Conductivity and Thermoelectric Properties of Incommensurate Chimney-Ladder Compound FeGeγ. Chem. Mater. 2016, 28, 529–533. [Google Scholar] [CrossRef]
- Terada, T.; Ishibe, T.; Watanabe, K.; Nakamura, Y. Growth of epitaxial FeGeγ nanocrystals with incommensurate Nowotny chimney-ladder phase on Si substrate. Jpn. J. Appl. Phys. 2018, 57, 08NB01. [Google Scholar] [CrossRef]
- Boström, M.; Lind, H.; Lidin, S.; Niewa, R.; Grin, Y. Synthesis, crystal structure, phase relations and chemical bonding analysis of the new Nowotny chimney-ladder compound ZrBi1.62. Solid State Sci. 2006, 8, 1173–1180. [Google Scholar] [CrossRef]
- Jeitschko, W. Refinement of the crystal structure of TiSi2 and some comments on bonding in TiSi2 and related compounds. Acta Crystallogr. B 1977, 33, 2347–2348. [Google Scholar] [CrossRef]
- Fredrickson, D.C.; Lee, S.; Hoffmann, R. The Nowotny chimney ladder phases: Whence the 14 electron rule? Inorg. Chem. 2004, 43, 6159–6167. [Google Scholar] [CrossRef] [PubMed]
- Fredrickson, D.C.; Lee, S.; Hoffmann, R.; Lin, J. The Nowotny chimney ladder phases: Following the cpseudo clue toward an explanation of the 14 electron rule. Inorg. Chem. 2004, 43, 6151–6158. [Google Scholar] [CrossRef] [PubMed]
- Milyan, V.V.; Kuzma, Y.B. Phase equilibria in the Cr-Al-Ge system. Russ. Metall. 1987, 4, 191–193. [Google Scholar]
- Kusma, J.B.; Nowotny, H. Untersuchungen im Dreistoff: Mn-Al-Si. Monatsh. Chem. 1964, 95, 1266–1271. [Google Scholar] [CrossRef]
- Nowotny, H.; Benesovsky, F.; Brukl, C.E. Der Dreistoff: Niob-Aluminium-Silicium. Monatsh. Chem. 1961, 92, 193–196. [Google Scholar] [CrossRef]
- Kuzma, Y.B.; Milyan, V.V. New compounds in the system Mo-Al-Ge. Inorg. Mater. 1979, 15, 11–13. [Google Scholar]
- Brukl, C.E.; Nowotny, H.; Schob, O.; Benesovsky, F. Die Kristallstrukturen von TiSi, Ti(Al,Si)2 und Mo(Al,Si)2. Monatsh. Chem. 1961, 92, 781–788. [Google Scholar] [CrossRef]
- Völlenkle, H.; Wittmann, A.; Nowotny, H. Abkömmlinge der TiSi2-Struktur—Ein neues Bauprinzip. Monatsh. Chem. 1966, 97, 506–516. [Google Scholar] [CrossRef]
- Miyazaki, Y.; Nakajo, T.; Kikuchi, Y.; Hayashi, K. Crystal structure and thermoelectric properties of the incommensurate chimney–ladder compound RhGeγ (γ ~ 1.293). J. Mater. Res. 2015, 30, 2611–2617. [Google Scholar] [CrossRef]
- Larchev, V.I.; Popova, S.V. The new chimney ladder phases Co2Si3 and Re4Ge7 formed by treatment at high temperatures and pressures. J. Less-Common Met. 1982, 84, 87–91. [Google Scholar] [CrossRef]
- Yannello, V.J.; Fredrickson, D.C. Orbital origins of helices and magic electron counts in the Nowotny chimney ladders: The 18-n rule and a path to incommensurability. Inorg. Chem. 2014, 53, 10627–10631. [Google Scholar] [CrossRef] [PubMed]
- Yannello, V.J.; Fredrickson, D.C. Generality of the 18-n rule: Intermetallic structural chemistry explained through isolobal analogies to transition metal complexes. Inorg. Chem. 2015, 54, 11385–11398. [Google Scholar] [CrossRef] [PubMed]
- Hamada, H.; Kikuchi, Y.; Hayashi, K.; Miyazaki, Y. Crystal structure and thermoelectric properties of the incommensurate chimney–ladder compound VGeγ (γ ~ 1.82). J. Electron. Mater. 2016, 45, 1365–1368. [Google Scholar] [CrossRef]
- Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic computing system JANA2006: General features. Z. Kristallogr. Cryst. Mater. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Bruker. SAINT (Version 8.38A); Bruker AXS Inc.: Madison, WI, USA, 2017. [Google Scholar]
- Krause, L.; Herbst-Irmer, R.; Sheldrick, G.M.; Stalke, D. Comparison of Silver and Molybdenum Microfocus X-ray Sources for Single-crystal Structure Determination. J. Appl. Cryst. 2015, 48, 3–10. [Google Scholar] [CrossRef]
- Bruker. SADABS v. 2014/5; Bruker AXS Inc.: Madison, WI, USA, 2015. [Google Scholar]
- Palatinus, L.; Chapuis, G. Superflip—A computer program for the solution of crystal structures by charge flipping in arbitrary dimensions. J. Appl. Crystallogr. 2007, 40, 786–790. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal Structure Refinement with SHELXL. Acta Crystallogr. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA|3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Koepernik, K.; Eschrig, H. Full-Potential Nonorthogonal Local-Orbital Minimum-Basis Band-Structure Scheme. Phys. Rev. B 1999, 59, 1743. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B 1994, 49, 16223. [Google Scholar] [CrossRef] [PubMed]
- Takizawa, H.; Sato, T.; Endo, T.; Shimada, M. High-Pressure Synthesis and Crystal Structure of VGe2 and Cr4Ge7. J. Solid State Chem. 1988, 73, 427–432. [Google Scholar] [CrossRef]
- Rudometkina, M.V.; Seropegin, Y.D.; Schvyryaeva, E.E. Investigation of the Zr-V-Ge system alloys. J. Less-Common Met. 1988, 138, 263–269. [Google Scholar] [CrossRef]
- Maas, J.; Bastin, G.F.; Van Loo, F.J.J.; Metselaar, R. The Texture in Diffusion-Grown Layers of Trialuminides MeAl3 (Me = Ti, V, Ta, Nb, Zr, Hf) and VNi3. Z. Metallkd. 1983, 74, 294–299. [Google Scholar]
- Brukl, C.E.; Nowotny, H.; Benesovsky, F. Untersuchungen in den Dreistoffsystemen: V-Al-Si, Nb-Al-Si, Cr-Al-Si, Mo-Al-Si bzw. Cr(Mo)-Al-Si. Monatsh. Chem. 1961, 92, 967–980. [Google Scholar] [CrossRef]
- Tanaka, K.; Nawata, K.; Inui, H.; Yamaguchi, M.; Koiwa, M. Refinement of Crystallographic Parameters in Refractory Metal Disilicides. Mater. Res. Soc. Symp. Proc. 2000, 646, N4.3.1. [Google Scholar] [CrossRef]
- Rudometkina, M.V.; Seropegin, Y.D.; Gribanov, A.V.; Gusei, L.S. Phase equilibria in the Ti-Nb-Ge system at 1170K. J. Less-Common Met. 1989, 147, 239–247. [Google Scholar] [CrossRef]
- Kubiak, R.; Horyn, R.; Broda, H.; Lukaszewicz, K. Refinement of the Crystal Structure of NbSi2, NbGe2 and TaGe2. Bull. Acad. Pol. Sci. (Ser. Sci. Chim.) 1972, 20, 429–436. [Google Scholar]
- Mattheiss, L.F. Calculated structural properties of CrSi2, MoSi2, and WSi2. Phys. Rev. B Condens. Matter Mater. Phys. 1992, 45, 3252–3259. [Google Scholar] [CrossRef]
- Baykov, V.I.; Jerlerud Perez, R.; Korzhavyi, P.A.; Sundman, B.; Johansson, B. Structural stability of intermetallic phases in the Zr-Sn system. Scr. Mater. 2006, 55, 485–488. [Google Scholar] [CrossRef]
- Kotur, B.Y. The Sc-Hf-Ge phase diagram for 1070K. Russ. Metall. (Engl. Transl.) 1991, 3, 211–214. [Google Scholar]
- Jongste, J.F.; Loopstra, O.B.; Janssen, G.C.A.M.; Radelaar, S. Elastic constants and thermal expansion coefficient of metastable C49 TiSi2. J. Appl. Phys. 1993, 73, 2816–2820. [Google Scholar] [CrossRef]
- Setton, M.; Van Der Spiegel, J. Structural and electrical properties of ZrSi2 and Zr2CuSi4 formed by rapid thermal processing. J. Appl. Phys. 1991, 70, 193–197. [Google Scholar] [CrossRef]
- Weitzer, F.; Rogl, P.; Noel, H. The ternary system: Hafnium-silicon-uranium. J. Alloys Compd. 2005, 387, 246–250. [Google Scholar] [CrossRef]
- Mudryk, Y.S.; Romaka, L.P.; Stadnyk, Y.V.; Bodak, O.I.; Fruchart, D. X-ray investigation of the R-Fe-Sn ternary systems (R = Y, Gd). J. Alloys Compd. 2004, 383, 162–165. [Google Scholar] [CrossRef]
- Dasgupta, T.; Etourneau, J.; Chevalier, B.; Matar, S.F.; Umarji, A.M. Structural, thermal, and electrical properties of CrSi2. J. Appl. Phys. 2008, 103, 113516. [Google Scholar] [CrossRef]
- Lue, C.S.; Su, T.H.; Xie, B.X.; Cheng, C. Comparative NMR study of hybridization effect and structural stability in D022-type NbAl3 and NbGa3. Phys. Rev. B 2006, 74, 094101. [Google Scholar] [CrossRef]
- Kilduff, B.J.; Yanello, V.J.; Fredrickson, D.C. Defusing Complexity in Intermetallics: How Covalently Shared Electron Pairs Stabilize the FCC Variant Mo2CuxGa6–x (x ≈ 0.9). Inorg. Chem. 2015, 54, 8103–8110. [Google Scholar] [CrossRef]



| Sample | VAl2−xGex | NbGa2−xGex |
|---|---|---|
| Nominal composition | VAl0.7Ge1.3 | NbGa0.8Ge1.2 |
| Refinement composition | VAl0.72(2)Ge1.28(2) | NbGa0.8Ge1.2 * |
| Molar mass, g/mol | 163.4 | 235.80 |
| Structure type | TiSi2 | TiSi2 |
| Space group | Fddd | Fddd |
| Z | 8 | 8 |
| a, Å | 4.87415(5) | 5.05858(3) |
| b, Å | 8.33502(9) | 8.61295(6) |
| c, Å | 8.70267(9) | 8.92618(6) |
| V, Å3 | 353.556(7) | 388.907(4) |
| dcalc, g/cm3 | 6.140 | 8.054 |
| Temperature, K | 293 | 293 |
| Radiation, λ, Å | Synchrotron, 0.35451 | Synchrotron, 0.35451 |
| 2θ range, ° | 1–37.914 | 1–37.914 |
| Total No. of reflections | 287 | 318 |
| No. of refined parameters | 32 | 27 |
| R1 | 0.0441 | 0.0807 |
| wR2 | 0.0602 | 0.0817 |
| Rprof | 0.0637 | 0.0871 |
| wRprof | 0.1435 | 0.1728 |
| GoF | 2.94 | 2.89 |
| Sample | VAl2−xGex |
|---|---|
| Refinement composition | VAl1.534(3)Ge0.466(3) |
| Molar mass, g/mol | 126.18 |
| Structure type | CrSi2 |
| Space group | P6422 |
| Z | 3 |
| a, Å | 4.6178(2) |
| c, Å | 6.4218(4) |
| V, Å3 | 118.593(13) |
| dcalc, g/cm3 | 5.300 |
| Temperature, K | 100 |
| μ, mm−1 | 15.168 |
| Radiation, λ, Å | Mo Kα, 0.71073 |
| Absorption correction | Multiscan |
| θ range, ° | 3.172–38.571 |
| Index ranges | −8 ≤ h ≤ 8; −8 ≤ k ≤ 8; −11 ≤ l ≤ 11 |
| No. of reflections collected | 4776 |
| No. unique/no. observed [I > 2σ(I)] | 227/224 |
| Tmin/Tmax | 0.186/0.320 |
| No. of refined parameters | 12 |
| R1 [I > 2σ(I)] | 0.0156 |
| wR2 [I > 2σ(I)] | 0.0463 |
| GoF | 1.616 |
| Atom | Wyckoff Site | x/a | y/b | z/c | Uiso, Å2 | Occupancy |
|---|---|---|---|---|---|---|
| V1 | 8a | 0.125 | 0.125 | 0.125 | 0.0093(12) | 1 |
| p-M1 | 16f | 0.125 | 0.4562(3) | 0.125 | 0.0068(5) | 0.36(2)Al + 0.64(2)Ge |
| Atom | Wyckoff Site | x/a | y/b | z/c | Ueq, Å2 | Occupancy |
|---|---|---|---|---|---|---|
| V1 | 3c | 0.5 | 0 | 0 | 0.00121(12) | 1.000 |
| p-M1 | 6i | 0.16358(2) | 0.32716(5) | 0 | 0.00066(15) | 0.767(2)Al + 0.233(2)Ge |
| Atom. | Wyckoff Site | x/a | y/b | z/c | Uiso, Å2 | Occupancy |
|---|---|---|---|---|---|---|
| Nb1 | 8a | 0.125 | 0.125 | 0.125 | 0.0024(4) | 1 |
| p-M1 | 16f | 0.125 | 0.4604(2) | 0.125 | 0.0066(4) | 0.4Ga + 0.6Ge * |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Likhanov, M.S.; Sytov, N.V.; Wei, Z.; Dikarev, E.V.; Shevelkov, A.V. Nowotny Chimney Ladder Phases with Group 5 Metals: Crystal and Electronic Structure and Relations to the CrSi2 Structure Type. Crystals 2020, 10, 670. https://doi.org/10.3390/cryst10080670
Likhanov MS, Sytov NV, Wei Z, Dikarev EV, Shevelkov AV. Nowotny Chimney Ladder Phases with Group 5 Metals: Crystal and Electronic Structure and Relations to the CrSi2 Structure Type. Crystals. 2020; 10(8):670. https://doi.org/10.3390/cryst10080670
Chicago/Turabian StyleLikhanov, Maxim S., Nikita V. Sytov, Zheng Wei, Evgeny V. Dikarev, and Andrei V. Shevelkov. 2020. "Nowotny Chimney Ladder Phases with Group 5 Metals: Crystal and Electronic Structure and Relations to the CrSi2 Structure Type" Crystals 10, no. 8: 670. https://doi.org/10.3390/cryst10080670
APA StyleLikhanov, M. S., Sytov, N. V., Wei, Z., Dikarev, E. V., & Shevelkov, A. V. (2020). Nowotny Chimney Ladder Phases with Group 5 Metals: Crystal and Electronic Structure and Relations to the CrSi2 Structure Type. Crystals, 10(8), 670. https://doi.org/10.3390/cryst10080670








