Next Article in Journal
Magnetic Field-Induced Phase Transition
Next Article in Special Issue
Revealing the Bonding Nature in an ALnZnTe3-Type Alkaline-Metal (A) Lanthanide (Ln) Zinc Telluride by Means of Experimental and Quantum-Chemical Techniques
Previous Article in Journal
Processing of Functional Composite Resins Using Deep Eutectic Solvent
Previous Article in Special Issue
Nowotny Chimney Ladder Phases with Group 5 Metals: Crystal and Electronic Structure and Relations to the CrSi2 Structure Type
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 10
Issue 10
10.3390/cryst10100865
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

First Principles Density Functional Theory Prediction of the Crystal Structure and the Elastic Properties of Mo2ZrB2 and Mo2HfB2

by
Rachid Stefan Touzani
* and
Manja Krüger
Institute of Materials and Joining Technology, Otto-von-Guericke University Magdeburg, P.O. Box 4120, D-39016 Magdeburg, Germany
*
Author to whom correspondence should be addressed.
Crystals 2020, 10(10), 865; https://doi.org/10.3390/cryst10100865
Submission received: 11 September 2020 / Revised: 21 September 2020 / Accepted: 22 September 2020 / Published: 24 September 2020
(This article belongs to the Special Issue Intermetallic)
Browse Figures
Versions Notes

Abstract

:
The Molybdenum rich ternary alloys Mo-M-B (M = Zr, Hf) contain, next to the Mo solid solution (bcc Mo with small amounts of Zr or Hf as substitutional atoms), the binary borides Mo2B, MB and MB2. Recently, it was found that there is also ternary Mo2MB2, but the crystal structure and further properties are currently unknown. Density functional theory (DFT) calculations were used not only to predict the crystal structure of the Mo2MB2 phases, but also to estimate the isotropic and anisotropic elastic properties like bulk, shear and Young’s modulus, as well as the Vickers hardness of these new borides. Several known crystal structures that fulfill the criterion of the chemical composition were investigated, and the AlMn2B2 type structure seems to be the most stable crystal structure for Mo2HfB2 and Mo2ZrB2 as there are no signs of electronic or dynamic instability. Regarding the elastic properties, it was found that Mo2HfB2 shows higher elastic moduli and is less elastically anisotropic than Mo2ZrB2.

Graphical Abstract

1. Introduction

There is a significant demand for new high-performance materials for technically challenging applications, e.g., in the metal processing industry, or in the energy generation and the aviation sectors. It is well-accepted that the materials capability affects the performance of machines, like turbines [1]. State-of-the-art materials for heavily stressed structural components are single-crystalline nickel-based superalloys. However, beyond ~1100 °C, the strength of these materials drops significantly and, thus, they become unusable for structural components.
The most challenging goal is to develop new high-temperature materials that provide balanced properties in a wide temperature range, i.e., sufficient fracture toughness at low and ambient temperatures, as well as creep strength and appropriate oxidation resistance at ultra-high temperatures. This target could be met by tailored refractory metal alloys, e.g., those based on molybdenum [2,3,4,5]. Mostly, the alloying strategy is due to the formation of temperature and oxidation-resistant intermetallic phases in a molybdenum solid solution matrix, like different silicides [6,7]. Recently, systems that incorporate borides as strengthening phases were described in terms of their microstructural evolution and mechanical properties, namely the ternary systems Mo-Hf-B and Mo-Zr-B [8,9,10]. It could be shown that this class of materials is very attractive in terms of a promising combination of high fracture toughness and outstanding creep resistance. The borides especially, e.g., ZrB, HfB or Mo2B, and the respective ternary borides that form in Mo-rich alloys, provide excellent creep resistance. Since boride phases, as well as the molybdenum solid solution phase, show a loss of environmental resistance at intermediate temperatures, a coating strategy based on Si-N and Si-O ceramic phases was already developed [11].
However, there is a lack of data on the properties of the ternary phases, especially their thermodynamic stability within the ternary systems Mo-Hf-B and Mo-Zr-B. The latest versions of the respective phase diagrams were published by Rogl, which do not contain the Mo-rich ternary intermetallic phases [12,13]. In our preliminary work so far, we found undescribed ternary phases, which were provisionally named Mo2HfBx and Mo2ZrBx in previous publications [9,10]. More precise information on the exact chemical composition of the phases was derived from Atom Probe Tomography (APT) measurements [14,15]. These results give evidence on the type of phases to be Mo2MB2 (M = Zr, Hf), but the crystal structure and stability of the phases is still unclear.
The prediction of the crystal structure of new materials or of known crystals at extreme conditions is an ongoing research topic. Diverse methods exist, e.g., Random Sampling [16], Simulated Annealing [17] and Evolutionary Algorithms [18], often in combination with Density Functional Theory (DFT) calculations. One drawback of using these methods, however, can be the high demand of calculation power and/or time. To overcome these drawbacks, a different approach was used to predict the crystal structure of Mo2MB2 (M = Zr, Hf) by simply using known crystals structures of intermetallics with the 2-1-2 or 3-2 chemical composition within our DFT calculations.

2. Materials and Methods

Based on the measured chemical composition 2-1-2 for Mo, M (M = Zr, Hf) and B, respectively, for the new compounds [14,15], we took 50 crystal structures of already known 2-1-2 and 3-2 intermetallics that fulfill the above-mentioned criterion of composition. Of those 50 types of crystal structures, the nine that showed the lowest total energy were those of the AlMn2B2-type [19], the Mo2FeB2-type [20], the Nb2OsB2-type (a superstructure variant of the Mo2FeB2-type) [21], the U2Pt2Sn-type [22] (also a superstructure variant of the Mo2FeB2-type, but no boride is currently known), the CeAl2Ga2-type (e.g., the known boride DyCo2B2 [23]), the β-Cr2IrB2-type [24], the Mo2IrB2-type [25], the HoNi2B2-type [26] and the W2CoB2-type [27]. First-principles calculation were carried out with Quickstep [28], as implemented in the CP2K version 5.1 program package, for a first structural relaxation and a quick estimation of the total energy [29]. Using the Gaussian plane wave method (GPW) [30], for Mo, Zr, Hf and B, the DZVP-MOLOPT-SR-GTH basis was set [31] and GTH-pseudopotentials were chosen [32,33,34]. Cell shape and volume variations were allowed during the structural optimization until a total energy self-consistency of 10−8 Ha and until the self-consistency for the forces and maximum geometry change of 10−6 Ha/Bohr and 10−6 Bohr, respectively, were achieved. The energy cut-off for the plane waves on the grid was 600 Ha, and the k-meshes were sampled via the Monkhorst–Pack algorithm [35]. Exchange and correlation in this density functional theory (DFT)-based method were treated with the generalized gradient approximation (GGA) functional as parameters by Perdew, Burke and Ernzerhof (PBE-GGA) [36]. Additionally, the PHONOPY program [37] was used to check for the dynamically most stable structure, similar to an approach made in Ref. [38].
The Density-Of-States calculation was done on the most stable energy ground-state structure using the tight-binding, linear muffin-tin orbitals with the atomic spheres approximation (TB-LMTO-ASA) [39,40] as implemented in the TB-LMTO 4.7 program. The Fermi level (EF) was set to 0 eV. The Monkhorst–Pack algorithm generated k-mesh was 27 × 27 × 27. Exchange and correlation were treated with the PW91-GGA functional by Perdew et al. [41]. The bonding analysis was done by calculation of the crystal orbital Hamilton population (COHP) [42] and its integrals (ICOHP). The ICOHP can be seen as a semi-quantitative bonding energy that measures covalent contributions in solids.
For the calculation of the elastic properties, a further structure optimization of the most stable crystal structure was carried out with Quantum ESPRESSO [43,44] using PAW pseudopotentials [45] from the PSLibrary version 1.0.0 [46]. The kinetic energy cut-off of the plane waves was set to 100 Ry, while the cut-off for the charge of density and potential was set to 400 Ry. The structural relaxation stopped until a total energy convergence of 10−6 Ry and a force convergence of 10−5 Ry/Bohr were reached. The Marzari–Vanderbilt cold smearing [47] and a Gaussian spreading of 0.01 Ry were chosen to account for the Brillouin-zone integration in metals. The k-mesh was divided by 20 × 4 × 20 using the aforementioned Monkhorst–Pack algorithm. Exchange and correlation in this density functional theory (DFT) based method were again treated with PBE-GGA. The elastic properties were determined with thermo_pw [48], a Fortran program using Quantum ESPRESSO routines as the underlying engine. In order to get the Voight–Reuss–Hill [49,50,51] approximated bulk, shear and Young’s modulus, the standard algorithm and frozen ions were used. To calculate the Vickers hardness, Tian et al.’s formula [52] was used. The formulas for the anisotropic bulk and Young’s modulus were taken from Ref. [53], while the formula for the anisotropic shear modulus is based from the formula given in [54]. Because of the usage of directional cosines of the elastic constants along the x-, y-, z-, xy-, xz- and yz-directions (see Ref. [53]), the elastic moduli along the crystallographic {111} direction is the average of the {111} directions within the ab-c-, ac-b- and bc-a-plane, which is spanned by the vectors along {110} & {001}, {101} & {010} and {011} & {100}, respectively.
The elastic anisotropy was determined in two ways: First, we calculated the Universal Elastic Anisotropy Index using the Voigt and Reuss bulk and shear moduli [55]. Second, as there are maxima and minima of the anisotropic elastic moduli, one can make another estimation of the anisotropy for the bulk, shear and Young’s modulus as well as the Vickers hardness using the following Formula (1) [56]:
E M A I = E M m a x E M m i n .
EMAI: Elastic modulus anisotropy index; EMmax: Maximum of the elastic modulus; EMmin: Minimum of the elastic modulus.
If EMAI = 0, then the elastic modulus is isotropic; a higher EMAI should display a more anisotropic elastic modulus.

3. Results and Discussion

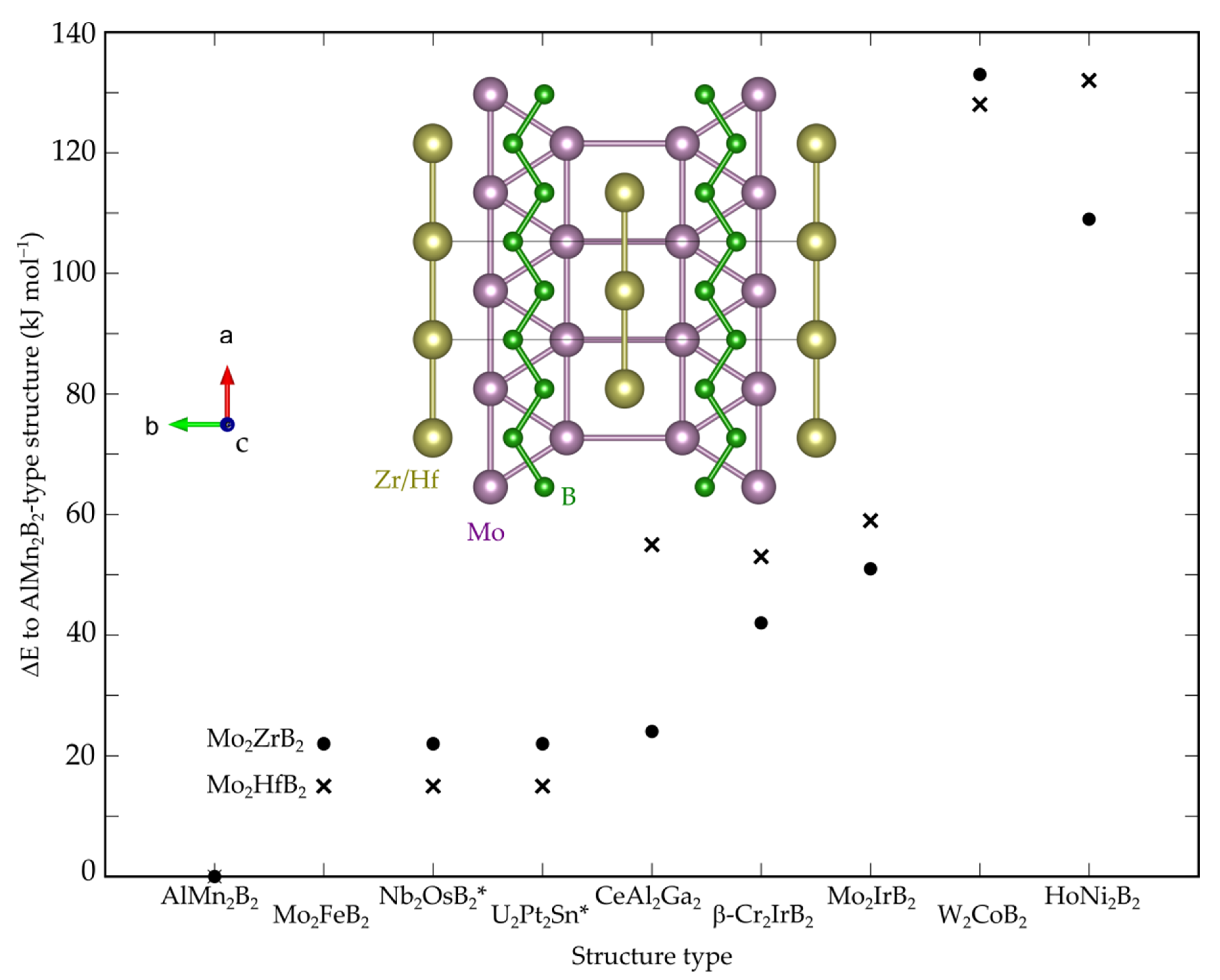
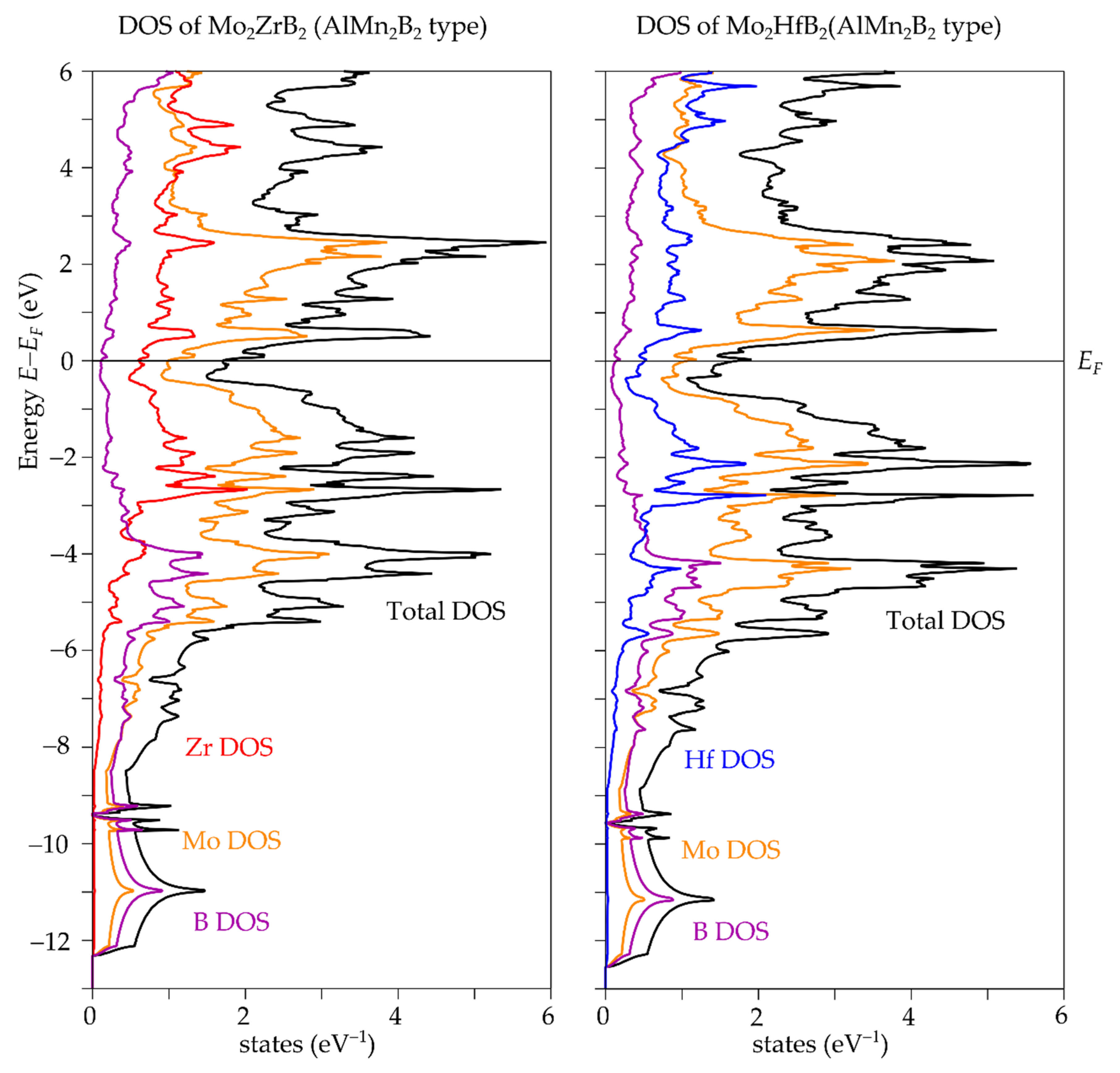
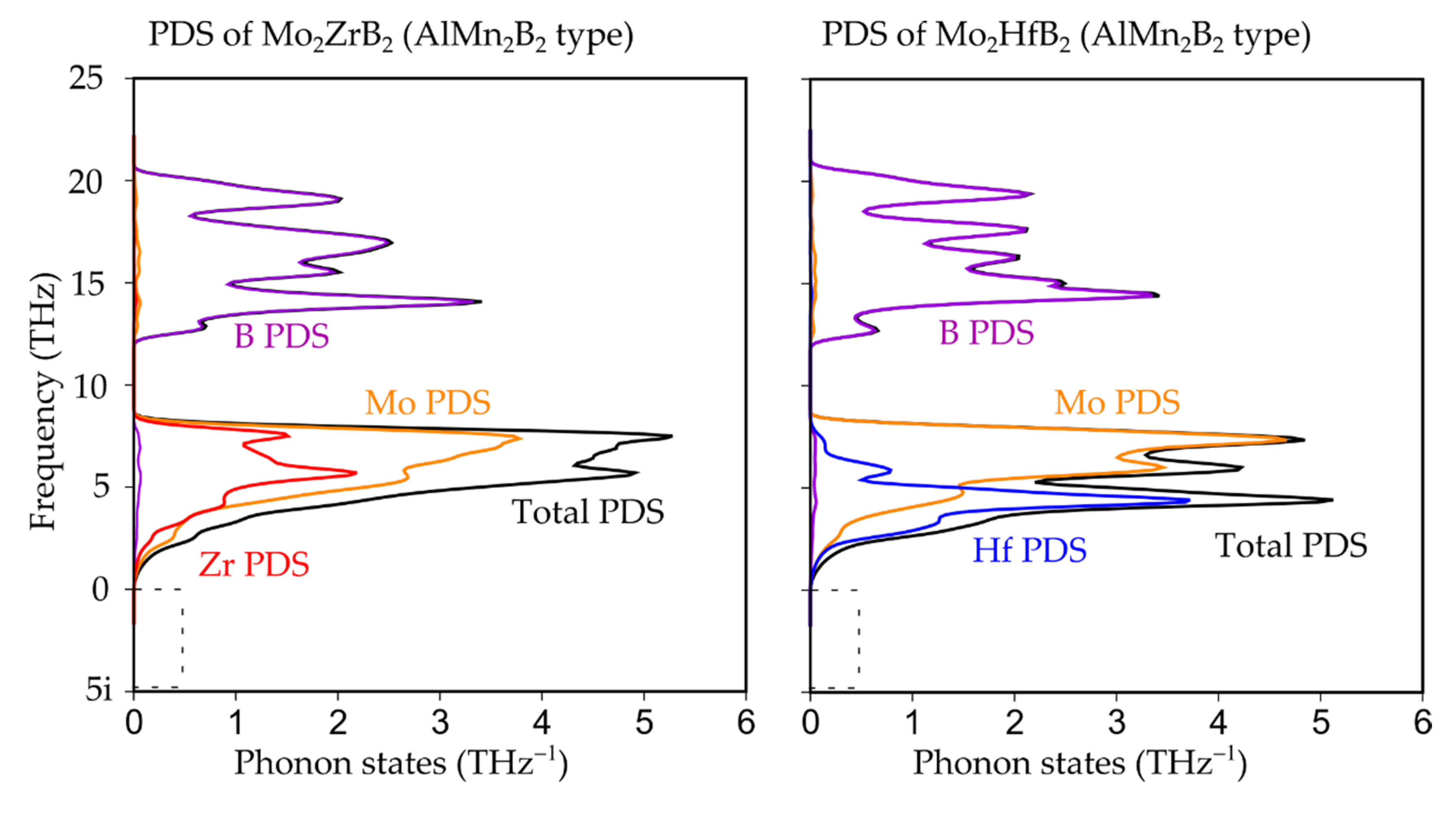
3.1. Crystal, Electronic and Phonon Structure

To predict the crystal structure of a compound, the total energy per formula unit is the main decision criterion. Here, nine crystal structure candidates for Mo2MB2 (M = Zr, Hf) and their total energy difference to the energetically most stable structure type will be presented: the AlMn2B2-type [19], the Mo2FeB2-type [20], the Nb2OsB2-type (a superstructure variant of the Mo2FeB2-type) [21], the U2Pt2Sn-type [22] (also a superstructure variant of the Mo2FeB2-type, but no boride is currently known), the CeAl2Ga2-type (e.g., the known boride DyCo2B2 [23]), the β-Cr2IrB2-type [24], the Mo2IrB2-type [25], the HoNi2B2-type [26] and the W2CoB2-type [27].
Their calculated energy differences are shown in Figure 1. It is obvious that the AlMn2B2-type structure (see inlay of Figure 1) is the most stable one of all investigated structures for Mo2ZrB2 and Mo2HfB2. The AlMn2B2-type is a structure variant within the orthorhombic spacegroup Cmmm. The Mo2FeB2-type structure for Mo2ZrB2 (Mo2HfB2) is less stable with an energy difference of +23 kJ/mol (+15 kJ/mol). The Nb2OsB2 and U2Pt2Sn types are structurally unstable as they both changed towards the Mo2FeB2-type during the cell optimization. The CeRu2Al2-type, β-Cr2IrB2-type, Mo2IrB2-type, HoNi2B2-type and W2CoB2-type are even more unstable with energy differences of +24 kJ/mol (+55 kJ/mol), +42 kJ/mol (+54 kJ/mol), +51 kJ/mol (+60 kJ/mol), +109 kJ/mol (+132 kJ/mol) and +134 kJ/mol (+129 kJ/mol), respectively.
To check if the AlMn2B2 type is electronically and dynamically stable, we also calculated the electronic Density-Of-States (DOS, Figure 2) and the Phonon-Density-of-States (PDS, Figure 3). In Figure 2 (left), the DOS of Mo2ZrB2 shows no signs of electronic instabilities as the Fermi level lies in the vicinity of a local DOS minimum. However, the Fermi level of Mo2HfB2 (see Figure 2, right) lies close to a small maximum of the DOS, which might indicate the formation of boron vacancies, but is no serious sign of an instability of the crystal structure. Because of the non-vanishing DOS at the Fermi level, Mo2ZrB2 and Mo2HfB2 should be metals.
The PDS of Mo2ZrB2 with the AlMn2B2 type structure in Figure 3 (left) contains no occupied imaginary frequencies and, hence, no dynamic instability is found. The same is valid for the PDS of Mo2HfB2 (Figure 3, right).
In terms of geometry, the lattice parameters of Mo2ZrB2 and of Mo2HfB2 after the cell optimization with CP2k are presented in Table 1. After a further structural optimization for the subsequent calculation of the elastic properties (see Section 3.2) with Quantum ESPRESSO, the lattice parameters of Mo2ZrB2 and Mo2HfB2 do not change much (see also Table 1 for the respective volumes).
Because of the similar atomic radius in crystals of Zr and Hf (both 155 pm according to Slater [57]), the lattice parameters a and c of Mo2ZrB2 and Mo2HfB2 differ by less than 1%, while the difference for the lattice parameter b is about 2%. The difference might come from the slightly different chemical behavior of Zr and Hf.
In conclusion, the AlMn2B2-type is found to be the most energetic, electronic and dynamic stable structure for both Mo2ZrB2 and Mo2HfB2.

3.2. Elastic Properties

3.2.1. Isotropic Elastic Properties

In this section, the isotropic bulk, shear and Young’s modulus along with the Vickers hardness of Mo2ZrB2 and Mo2HfB2 will be discussed (see also Table 2).
It is clear that all the isotropic elastic moduli and the Vickers hardness of Mo2HfB2 are higher than those of Mo2ZrB2.
The Universal Elastic Anisotropy Index [52] of Mo2ZrB2 and Mo2HfB2 was also calculated and while it is slightly larger for Mo2ZrB2 than for Mo2HfB2, it is very small for both compounds. A deeper analysis of the anisotropic elastic properties is presented in the next subsection.

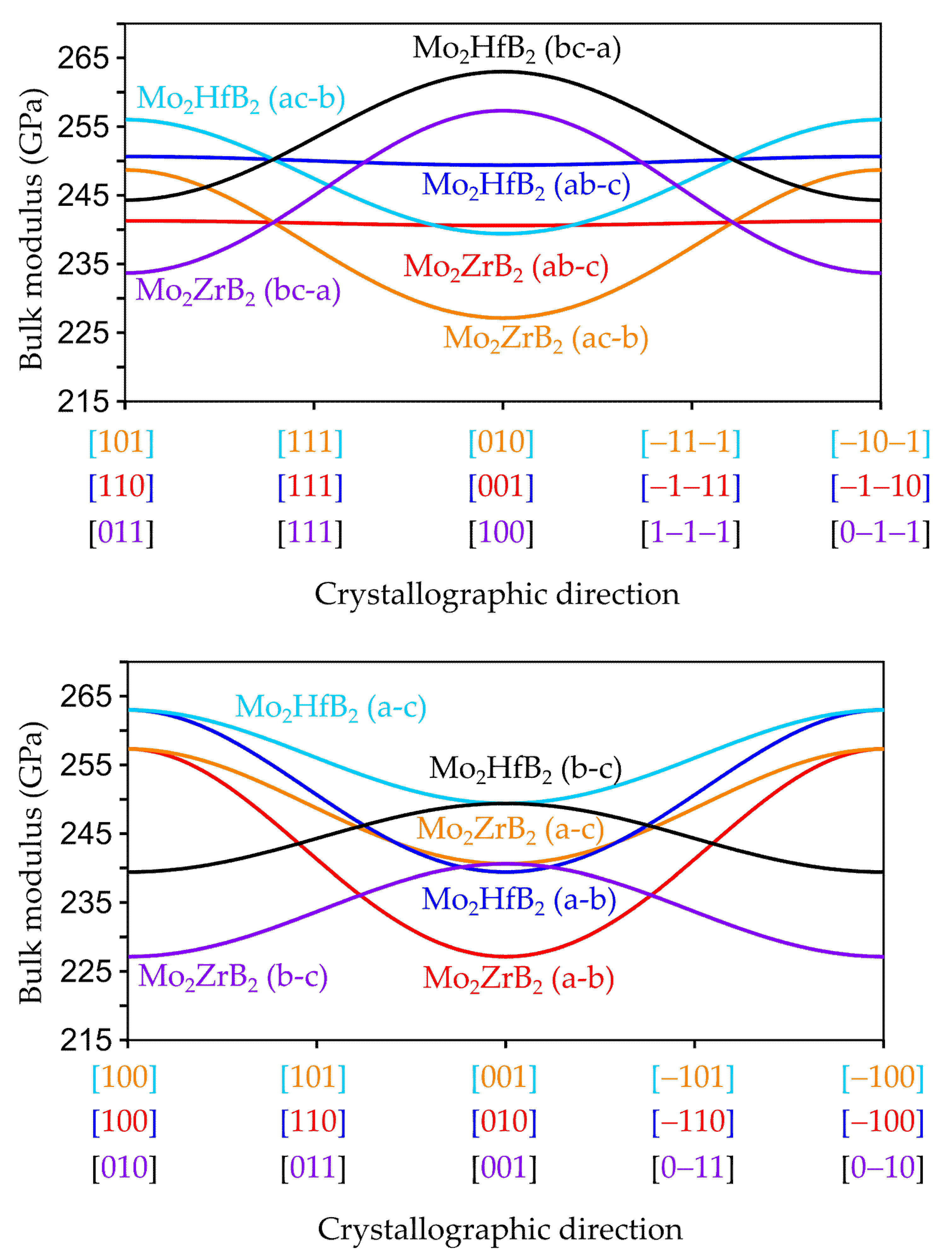
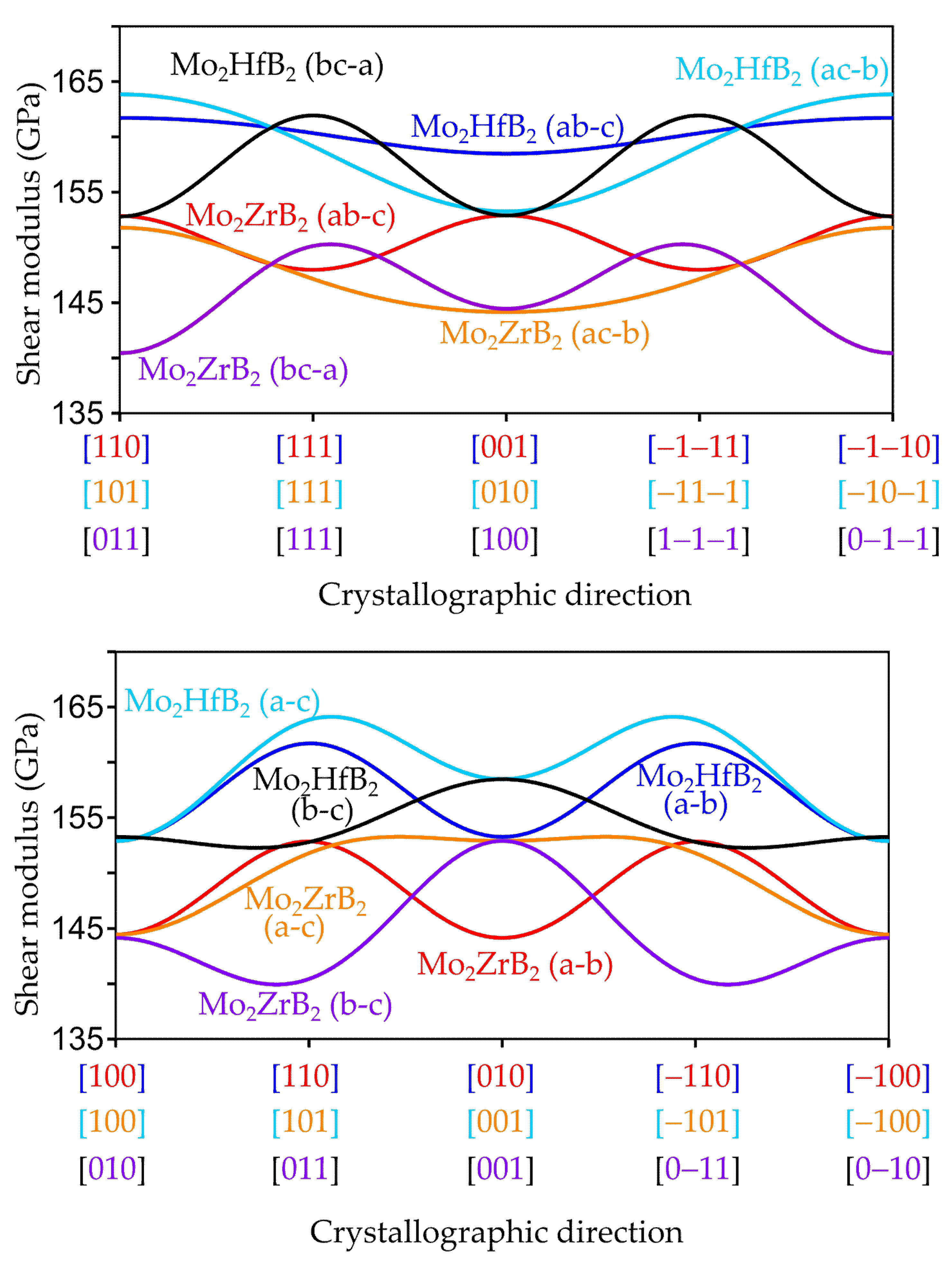
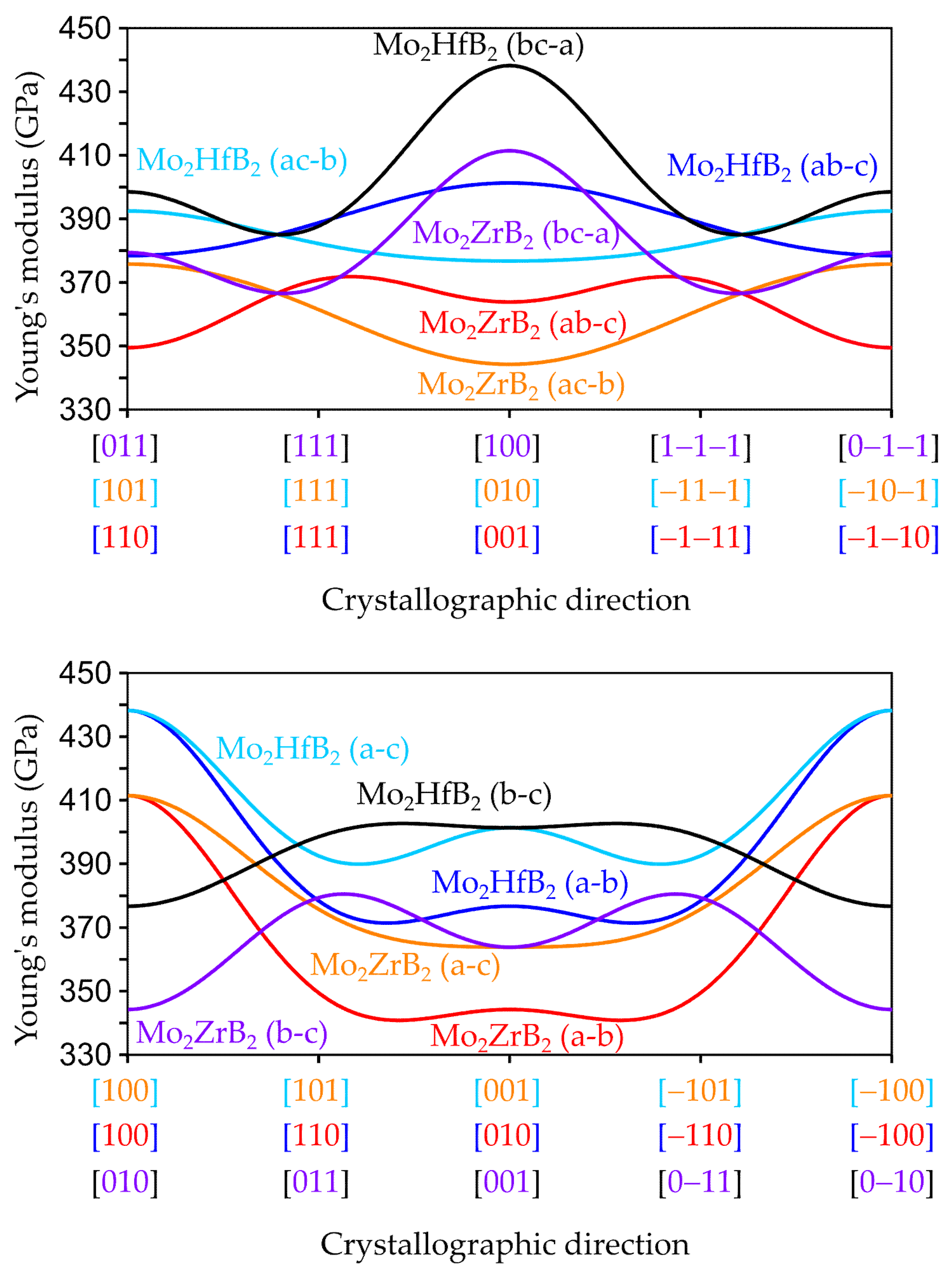
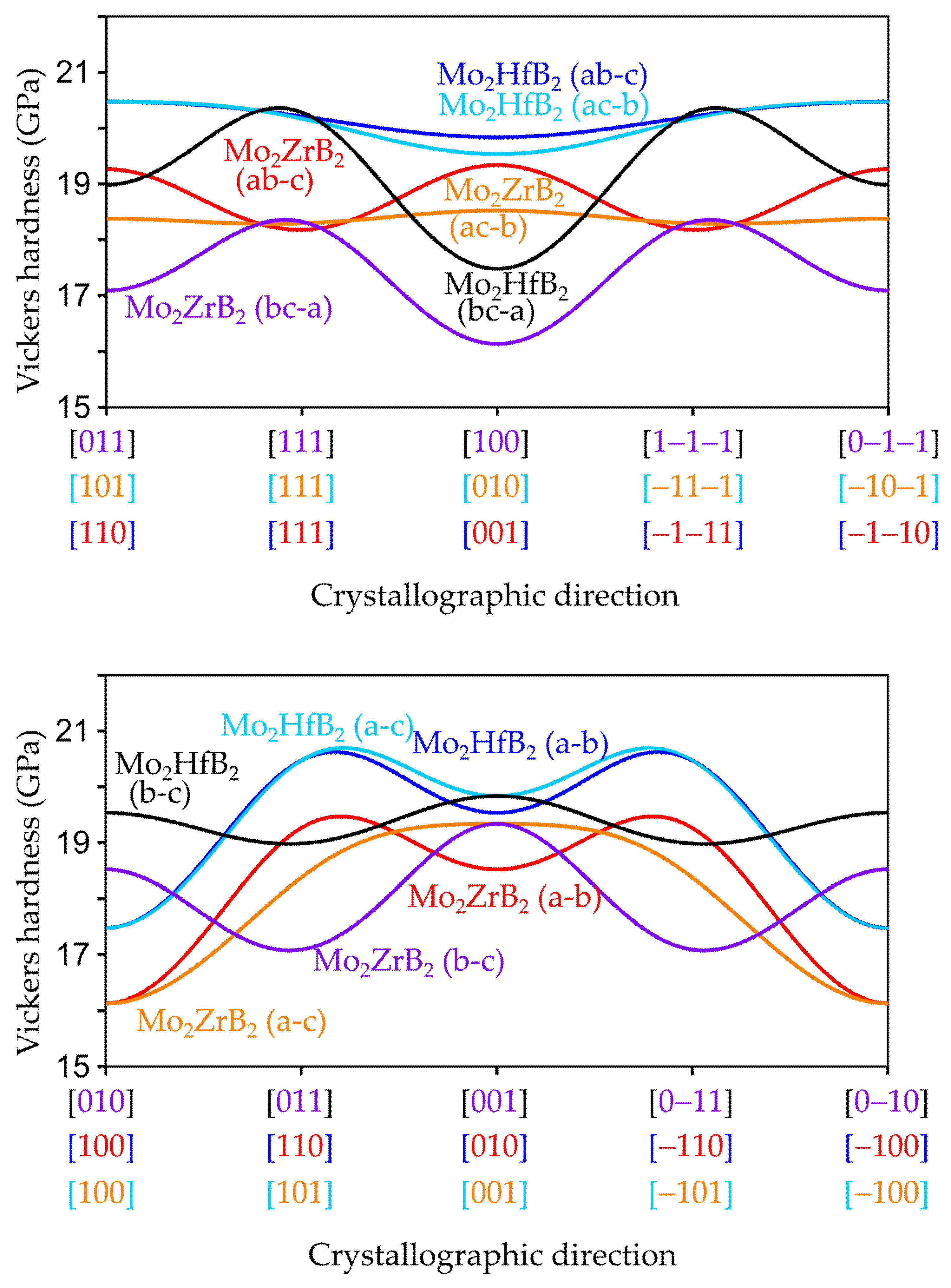
3.2.2. Anisotropic Elastic Properties

In this section, the anisotropic elastic moduli bulk, shear and Young’s modulus, along with the Vickers hardness of Mo2ZrB2 and Mo2HfB2, will be discussed. The discussion starts with the anisotropic bulk modulus shown in Figure 4.
The minimum of the anisotropic bulk modulus of Mo2ZrB2 and Mo2HfB2 is 227.14 GPa and 239.41 GPa, respectively, and can be found along the {010} direction. Along the {100}, the bulk modulus of Mo2ZrB2 and Mo2HfB2 is 257.32 GPa and 263.00 GPa, respectively, which is the maximum.
Taking into account the maximum and minimum of the elastic moduli of Mo2ZrB2 and Mo2HfB2, one can make an assumption of the anisotropy (see Table 3): For the bulk modulus, the anisotropy is 0.13 and 0.10 for Mo2ZrB2 and Mo2HfB2, respectively.
The anisotropic shear modulus G is shown in Figure 5.
The shear modulus near the {011} direction in the b-c plane of Mo2ZrB2 and Mo2HfB2 is 139.93 GPa and 152.27 GPa, respectively, and it is the minimum. The maximum of the shear modulus is observed near the {101} direction in the a-c plane, as it is 153.26 GPa and 164.12 GPa, for Mo2ZrB2 and Mo2HfB2, respectively.
The anisotropic shear modulus of Mo2ZrB2 and Mo2HfB2 within the ab-c plane, as well as the a-c plane, behaves differently. While within the ab-c plane, G of Mo2HfB2 is only slightly changing, while G of Mo2ZrB2 shows clear a clear minimum near the {111} direction and maxima near {110} and {001}. Within the a-c plane, G of Mo2ZrB2 is almost constant between the {101} and {001} directions, while G of Mo2HfB2 shows clear minima and maxima between these directions. This different behavior of the shear modulus of Mo2ZrB2 and Mo2HfB2 also effects the Young’s modulus and Vickers hardness in the same planes.
Using the maximum and minimum shear modulus of Mo2ZrB2 and Mo2HfB2, the anisotropy of G is 0.10 and 0.08 for Mo2ZrB2 and Mo2HfB2, respectively (see also Table 3).
The anisotropic Young’s modulus is shown in Figure 6.
The Young’s modulus of Mo2ZrB2 and Mo2HfB2 near the {110} direction in the a-b-plane is the minimum, as Y is 340.83 GPa and 371.43 GPa, respectively. The maximum of the Young’s modulus of Mo2ZrB2 and Mo2HfB2 is 411.43 GPa and 438.21 GPa, respectively, and it is found along the {100} direction.
Taking into account the maximum and minimum Young’s modulus of Mo2ZrB2 and Mo2HfB2, the anisotropy of Y is 0.21 and 0.18 for Mo2ZrB2 and Mo2HfB2, respectively (see also Table 3).
In Figure 7 the anisotropic Vickers hardness HV of Mo2ZrB2 and Mo2HfB2 is shown.
The anisotropic Vickers hardness was calculated using the bulk and shear modulus according to the formula of Tian et al. [52]. The minimum of the Vickers hardness of Mo2ZrB2 and Mo2HfB2 is along the {100} direction, as HV is 16.13 GPa and 17.48 GPa, respectively. However, the maximum of the Vickers hardness of Mo2ZrB2 and Mo2HfB2 is along different crystallographic directions. Near the {110} direction in the a-b plane, the maximum Vickers hardness of Mo2ZrB2 is 19.47 GPa, while for the same direction, the HV of Mo2HfB2 is 20.62 GPa, which is not the maximum HV of Mo2HfB2. The maximum Vickers hardness of Mo2HfB2 is near the {101} direction in the a-c plane as HV is 20.70 GPa. In the same direction, HV of Mo2ZrB2 is 18.85 GPa. The experimental Vickers hardness of Mo2ZrB2 is 19.50 GPa [10,14]; thus, the DFT calculated numbers of the anisotropic Vickers hardness are in very good agreement with the experiment. Unfortunately for Mo2HfB2, no experimental Vickers hardness is currently known.
Taking into account the maximum and minimum Vickers hardness of Mo2ZrB2 and Mo2HfB2, the anisotropy of HV is 0.21 and 0.18 for Mo2ZrB2 and Mo2HfB2, respectively, which is similar to the one of Y (see also Table 3).
In summary, the anisotropic bulk, shear and Young’s modulus as well as the Vickers hardness of Mo2HfB2 are for the same directions in the same plane higher than the elastic moduli of Mo2ZrB2, which might be due to their respective interatomic bonding conditions. This hypothesis will be investigated in Section 3.3. The maxima of the bulk and Young’s modulus of Mo2ZrB2 and Mo2HfB2 were observed for the {100} direction, while the maximum of the shear modulus of Mo2ZrB2 and Mo2HfB2 was found near the {101} direction. The maximum of the Vickers hardness of Mo2ZrB2 was found near the {110} direction, while the maximum of the Vickers hardness of Mo2HfB2 is near the {101} direction. The minimum of the bulk modulus of Mo2ZrB2 and Mo2HfB2 is along the {010} direction, while the minimum of the shear modulus of these borides is along the {011} direction. The minimum of the Young’s modulus of Mo2ZrB2 and Mo2HfB2 is along the {110} direction, while for the Vickers hardness the minimum is along the {100} direction.
Also, the elastic moduli of Mo2HfB2 are less anisotropic than the elastic moduli of Mo2ZrB2. To better compare this with the Universal Anisotropy Index AU, one can also define a B and G averaged anisotropy index and for Mo2HfB2; this is 0.09 (AU = 0.02), while for Mo2ZrB2 it is 0.12 (AU = 0.03). The similarity of the calculated B and G averaged anisotropy index and the Universal Anisotropy Index indicates that both indexes can be used to determine the elastic anisotropy, and that Mo2ZrB2 and Mo2HfB2 show only slightly elastic anisotropic behavior.

3.3. Influence of the Chemical Bonding on the Elastic Properties

In this section, we will use the integrated crystal orbital Hamilton population (ICOHP) as a measure for the strength of the chemical bonding to explain the differences of the elastic properties between Mo2ZrB2 and Mo2HfB2. The respective ICOHPs per bond type are presented in Table 4.
The ICOHP of the bonds B-B short and long M-M (M = Zr, Hf), Mo-M and longest Mo-Mo are higher in Mo2HfB2 than in Mo2ZrB2, while in Mo2ZrB2, the short and long Mo-B bonds and the short, medium and long Mo-Mo bonds are stronger than in Mo2HfB2. If one sums up these ICOHPs, it becomes clear that the chemical bonding in Mo2HfB2 is stronger than in Mo2ZrB2. This might be the explanation why the elastic moduli of Mo2HfB2 are larger than the elastic moduli of Mo2ZrB2. A similar correlation of ICOHP per formula unit and the elastic moduli were also found in other A2MB2 borides (A = Nb, Ta; M = Fe, Ru, Os) [56,58].
However, the ICOHPs of individual bonds alone are not sufficient to explain the different behavior of the anisotropic shear modulus G of Mo2ZrB2 and Mo2HfB2 within the ab-c and a-c plane. A closer look at the bonding situation reveals that the Mo-Mo, Mo-M and M-M bonds are along the a, c, ab and ab-c directions and, thus, for the directions, the different behavior of G was observed. The DOSs of Mo and Zr in Mo2ZrB2 differ from the DOSs of Mo and Hf in Mo2HfB2, especially in the area between −5 eV and 0 eV (see Figure 2). Taking a look on the Phonon-Density-of-States of Mo2ZrB2 and Mo2HfB2 (Figure 3), the PDSs of Mo and Zr show a similar dispersion between 5 THz and 8 THz, while, because of the higher atomic weight, the PDS of Hf is mainly at lower frequencies below 5 THz and shows no similar dispersion like the PDS of Mo. Therefore, these differences in the DOSs and the PDSs might explain the different anisotropic behavior of the shear modulus of Mo2ZrB2 and Mo2HfB2. The influence of the electronic structure on the shear modulus was also observed in other A2MB2 borides (A = Nb, Ta; M = Fe, Ru, Os) [56,58].

4. Conclusions

In this work, we predicted the crystal structure of Mo2ZrB2 and Mo2HfB2 to be of the AlMn2B2 type structure, as there are no signs of electronic or dynamical instability found in the DOS and the PDS, respectively. Further, we investigated the elastic properties of these ternary borides and the isotropic and anisotropic elastic moduli like the bulk, shear and Young’s modulus, as well as the Vickers hardness, which of Mo2HfB2 are higher than those of Mo2ZrB2 because of the chemical bonding situation. Also, it was shown that Mo2HfB2 is less elastically anisotropic than Mo2ZrB2.

Author Contributions

Conceptualization, R.S.T. and M.K.; methodology, R.S.T.; investigation, R.S.T.; writing—original draft preparation, R.S.T. and M.K.; writing—review and editing, R.S.T. and M.K.; visualization, R.S.T.; funding acquisition, M.K. All authors have read and agreed to the published version of the manuscript.

Funding

The financial support by the German Research Foundation (DFG) in the framework of project 438070774 is greatly acknowledged.

Acknowledgments

We thank V. Bolbut for fruitful discussions on the existence and stability of phases in the systems Mo-Hf-B and Mo-Zr-B. R.T. also thanks the URZ OVGU Magdeburg for calculation power and time.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Dimiduk, D.M.; Perepezko, J.H. Mo-Si-B Alloys: Developing a Revolutionary Turbine-Engine Material. MRS Bull. 2003, 28, 639–645. [Google Scholar] [CrossRef]
  2. Kruzic, J.J.; Schneibel, J.H.; Ritchie, R.O. Ambient- to elevated-temperature fracture and fatigue properties of Mo-Si-B alloys: Role of microstructure. Metall. Mater. Trans. A 2005, 36, 2393–2402. [Google Scholar] [CrossRef]
  3. Yu, X.J.; Kumar, K.S. The tensile response of Mo, Mo-Re and Mo-Si solid solutions. Int. J. Refract. Hard Met. 2013, 41, 329–338. [Google Scholar] [CrossRef]
  4. Perepezko, J.H. The hotter the engine, the better. Science 2009, 326, 1068–1069. [Google Scholar] [CrossRef]
  5. Rioult, F.A.; Imhoff, S.D.; Sakidja, R.; Perepezko, J.H. Transient oxidation of Mo-Si-B alloys: Effect of the microstructure size scale. Acta Mater. 2009, 57, 4600–4613. [Google Scholar] [CrossRef]
  6. Krüger, M.; Jain, P.; Kumar, K.S.; Heilmaier, M. Correlation between microstructure and properties of fine grained Mo-Mo3Si-Mo5SiB2 alloys. Intermetallics 2014, 48. [Google Scholar] [CrossRef]
  7. Schliephake, D.; Azim, M.; von Klinski-Wetzel, K.; Gorr, B.; Christ, H.J.; Bei, H.; George, E.P.; Heilmaier, M. High-temperature creep and oxidation behavior of Mo-Si-B alloys with high Ti contents. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2014, 45, 1102–1111. [Google Scholar] [CrossRef]
  8. Bolbut, V.; Seils, S.; Boll, T.; Chassaing, D.; Krüger, M. Controversial discussion on the existence of the Hf and Zr monoborides and experimental proof by atom probe tomography. Materialia 2019, 6, 100322. [Google Scholar] [CrossRef]
  9. Bolbut, V.; Bogomol, I.; Loboda, P.; Krüger, M. Microstructure and mechanical properties of a directionally solidified Mo-12Hf-24B alloy. J. Alloys Compd. 2018, 735, 2324–2330. [Google Scholar] [CrossRef]
  10. Bolbut, V.; Bogomol, I.; Bauer, C.; Krüger, M. Gerichtet erstarrte Mo-Zr-B-Legierungen/ Directionally solidified Mo-Zr-B alloys. Materialwissenschaft und Werkstofftechnik 2017, 48, 1113–1124. [Google Scholar] [CrossRef]
  11. Smokovych, I.; Bolbut, V.; Krüger, M.; Scheffler, M. Tailored Oxidation Barrier Coatings for Mo-Hf-B and Mo-Zr-B Alloys. Materials 2019, 12, 2215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  12. Rogl, B. Boron-Molybdenum-Zirconium. In Numerical Data and Functional Relationships in Science and Technology; Effenberg, G., Madelung, O., Eds.; Springer: Berlin, Germany, 2010; pp. 72–82. [Google Scholar]
  13. Rogl, P. Boron-Hafnium-Molybdenum. In Refractory Metal Systems; Martienssen, W., Effenberg, G., Ilyenko, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 695–707. [Google Scholar]
  14. Bolbut, V. Development of Mo-Hf-B and Mo-Zr-B Alloys for High Temperature Application. Ph.D. Thesis, Otto-von-Guericke University Magdeburg, Magdeburg, Germany, 2018. [Google Scholar]
  15. Bolbut, V.; Seils, S.; Chassaing, D.; Boll, T.; Krüger, M. Assessment of ternary borides in the Mo-Hf-B and Mo-Zr-B systems and new description on phase equilibria. Unpublished work.
  16. Schmidt, M.U.; Englert, U. Prediction of crystal structures. J. Chem. Soc. Dalton Trans. 1996, 10, 2077–2082. [Google Scholar] [CrossRef]
  17. Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
  18. Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  19. Becher, H.J.; Krogmann, K.; Peisker, E. Über das ternäre Borid Mn2AlB2. Z. Anorg. Allg. Chem. 1966, 344, 140–147. (In German) [Google Scholar] [CrossRef]
  20. Rieger, W.; Nowotny, H.; Benesovsky, F. Die Kristallstruktur von Mo2FeB2. Monatsh. Chem. 1964, 95, 1502–1503. (In German) [Google Scholar] [CrossRef]
  21. Mbarki, M.; Touzani, R.S.; Fokwa, B.P.T. Nb2OsB2, with a new twofold superstructure of the U3Si2 type: Synthesis, crystal chemistry and chemical bonding. J. Sol. Sta. Chem. 2013, 203, 304–309. [Google Scholar] [CrossRef]
  22. Gravereau, P.; Mirambet, F.; Chevalier, B.; Weill, F.; Fournès, L.; Laffargue, D.; Bourée, F.; Etourneau, J. Crystal structure of U2Pt2Sn: A new derivative of the tetragonal U3Si2-type structure. J. Mater. Chem. 1994, 4, 1893–1895. [Google Scholar] [CrossRef]
  23. Rogl, P. Über SE-Metall-Kobaltboride. Monatsh. Chem. 1973, 104, 1623–1631. (In German) [Google Scholar] [CrossRef]
  24. Kotzott, D.; Ade, M.; Hillebrecht, H. Synthesis and Crystal Structures of alpha- and beta-Modifications of Cr2IrB2 containing B4-Chains, τ-Borides Cr23−xIrxB6 and Cr2B. Sol. Sta. Sci. 2008, 10, 291–302. [Google Scholar] [CrossRef]
  25. Rogl, P.; Beneshovsky, F.; Nowotny, H. Über einige Komplexboride mit Platinmetallen. Monatsh. Chem. 1972, 103, 965–989. (In German) [Google Scholar] [CrossRef]
  26. Bruskov, V.A.; Gubich, I.B.; Kuz’ma, Y.B. Crystal structure of a new boride HoNi2B2. Kristallografiya 1991, 36, 1123–1125. [Google Scholar]
  27. Rieger, W.; Nowotny, H.; Benesovsky, F. Die Kristallstruktur von W2CoB2 und isotypen Phasen. Monatsh. Chem. 1966, 97, 378–382. (In German) [Google Scholar] [CrossRef]
  28. Vande Vondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Commun. Comput. Phys. 2005, 167, 103–128. [Google Scholar] [CrossRef] [Green Version]
  29. Hutter, J.; Ianuzzi, M.; Schiffmann, F.; Vande Vondele, J. CP2k: Atomistic Simulations of Condensed Matter System. WIRES Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef] [Green Version]
  30. Lippert, G.; Hutter, J.; Parrinello, M. A hybrid Gaussian and plane wave density functional scheme. Mol. Phys. 1997, 92, 477–488. [Google Scholar] [CrossRef]
  31. Vande Vondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef] [Green Version]
  32. Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef] [Green Version]
  33. Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar] [CrossRef] [Green Version]
  34. Krack, M. Pseudopotentials for H to Kr optimized for gradient-corrected exchange-correlation functionals. Theor. Chem. Acc. 2005, 114, 145–152. [Google Scholar] [CrossRef] [Green Version]
  35. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  36. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  37. Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scripta Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
  38. Touzani, R.S.; Mbarki, M.; Chen, X.; Fokwa, B.P.T. Peierls-Distorted Ru-Chains and Boron Dumbbells in Nb2RuB2 and Ta2RuB2 from First-Principles Calculations and Experiments. Eur. J. Inorg. Chem. 2016, 25, 4104–4110. [Google Scholar] [CrossRef]
  39. Andersen, O.K.; Skriver, H.L.; Nohl, H.; Johansson, B. Electronic structure of transition metal compounds; ground-state properties of the 3d-monoxides in the atomic sphere approximation. Pure Appl. Chem. 1980, 52, 93–118. [Google Scholar] [CrossRef]
  40. Andersen, O.K.; Jepsen, O. Explicit, First-Principles Tight-Binding Theory. Phys. Rev. Lett. 1984, 53, 2571–2574. [Google Scholar] [CrossRef]
  41. Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
  42. Dronskowski, R.; Blöchl, P. Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
  43. Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
  44. Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
  45. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
  46. Dal Corso, A. Pseudopotentials periodic table: From H to Pu. Comput. Mat. Sci. 2014, 95, 337–350. [Google Scholar] [CrossRef]
  47. Marzari, N.; Vanderbilt, D.; De Vita, A.; Payne, M.C. Thermal Contraction and Disordering of the Al(110) Surface. Phys. Rev. Lett. 1999, 82, 3296–3299. [Google Scholar] [CrossRef] [Green Version]
  48. Thermo_pw is an Extension of the Quantum ESPRESSO (QE) Package Which Provides an Alternative Organization of the QE Work-flow for the Most Common Tasks. Available online: https://dalcorso.github.io/thermo_pw/ (accessed on 17 August 2020).
  49. Voigt, W. Lehrbuch der Kristallphysik; Springer: Berlin/Leipzig, Germany, 1928. (In German) [Google Scholar]
  50. Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew Math. Mech. 1929, 9, 49–58. (In German) [Google Scholar] [CrossRef]
  51. Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
  52. Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
  53. Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: New York, NY, USA, 1985. [Google Scholar]
  54. Wu, D.-H.; Wang, H.-C.; Wei, L.-T.; Pan, R.-K.; Tang, B.-Y. First-principles study of structural stability and elastic properties of MgPd3 and its hydride. J. Magnes. Alloy 2014, 2, 165–174. [Google Scholar] [CrossRef] [Green Version]
  55. Ranganathan, S.I.; Ostoja-Starzewski, M. Universal Elastic Anisotropy Index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [Green Version]
  56. Touzani, R.S. Quantenchemische Untersuchung der Elastischen und Magnetischen Eigenschaften Einiger Übergangsmetallboride. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2016. (In German). [Google Scholar]
  57. Slater, J.C. Atomic Radii in Crystals. J. Chem. Phys. 1964, 41, 3199–3204. [Google Scholar] [CrossRef]
  58. Touzani, R.S.; Rehorn, C.W.G.; Fokwa, B.P.T. Influence of chemical bonding and mahnetism on elastic properties of the A2MB2 borides (A = Nb, Ta; M = Fe, Ru, Os) from first-principles calculations. Comput. Mater. Sci. 2015, 104, 52–59. [Google Scholar] [CrossRef]
Crystals 10 00865 g001 550
Figure 1. The calculated energy differences of the phases Mo2ZrB2 and Mo2HfB2 per formula unit with the different types of crystal structures. *: Unstable crystal structures, which turn to the Mo2FeB2 type during the structural relaxation.
Figure 1. The calculated energy differences of the phases Mo2ZrB2 and Mo2HfB2 per formula unit with the different types of crystal structures. *: Unstable crystal structures, which turn to the Mo2FeB2 type during the structural relaxation.
Crystals 10 00865 g001
Crystals 10 00865 g002 550
Figure 2. Electronic density of states (DOS) of Mo2ZrB2 (left) and Mo2HfB2 (right) both with AlMn2B2-type structure.
Figure 2. Electronic density of states (DOS) of Mo2ZrB2 (left) and Mo2HfB2 (right) both with AlMn2B2-type structure.
Crystals 10 00865 g002
Crystals 10 00865 g003 550
Figure 3. Phonon-Density-of-States (PDS) of Mo2ZrB2 (left) and Mo2HfB2 (right) both with AlMn2B2-type structure. The dashed boxes show that there are no imaginary phonon frequencies for Mo2ZrB2 and Mo2HfB2.
Figure 3. Phonon-Density-of-States (PDS) of Mo2ZrB2 (left) and Mo2HfB2 (right) both with AlMn2B2-type structure. The dashed boxes show that there are no imaginary phonon frequencies for Mo2ZrB2 and Mo2HfB2.
Crystals 10 00865 g003
Crystals 10 00865 g004 550
Figure 4. Anisotropic bulk modulus in the a-b, a-c and b-c-plane (lower part) and the ab-c, ac-b and bc-a-plane (upper part) of Mo2ZrB2 (red, orange and purple) and Mo2HfB2 (blue, cyan and black), respectively, both with the AlMn2B2-type structure.
Figure 4. Anisotropic bulk modulus in the a-b, a-c and b-c-plane (lower part) and the ab-c, ac-b and bc-a-plane (upper part) of Mo2ZrB2 (red, orange and purple) and Mo2HfB2 (blue, cyan and black), respectively, both with the AlMn2B2-type structure.
Crystals 10 00865 g004
Crystals 10 00865 g005 550
Figure 5. Anisotropic shear modulus in the a-b, a-c and b-c-plane (lower part) and the ab-c, ac-b and bc-a-plane (upper part) of Mo2ZrB2 (red, orange and purple) and Mo2HfB2 (blue, cyan and black), respectively, both with the AlMn2B2-type structure.
Figure 5. Anisotropic shear modulus in the a-b, a-c and b-c-plane (lower part) and the ab-c, ac-b and bc-a-plane (upper part) of Mo2ZrB2 (red, orange and purple) and Mo2HfB2 (blue, cyan and black), respectively, both with the AlMn2B2-type structure.
Crystals 10 00865 g005
Crystals 10 00865 g006 550
Figure 6. Anisotropic Young’s modulus in the a-b, a-c and b-c-plane (lower part) and the ab-c, ac-b and bc-a-plane (upper part) of Mo2ZrB2 (red, orange and purple) and Mo2HfB2 (blue, cyan and black), respectively, both with the AlMn2B2-type structure.
Figure 6. Anisotropic Young’s modulus in the a-b, a-c and b-c-plane (lower part) and the ab-c, ac-b and bc-a-plane (upper part) of Mo2ZrB2 (red, orange and purple) and Mo2HfB2 (blue, cyan and black), respectively, both with the AlMn2B2-type structure.
Crystals 10 00865 g006
Crystals 10 00865 g007 550
Figure 7. Anisotropic Vickers hardness in the a-b, a-c and b-c-plane (lower part) and the ab-c, ac-b and bc-a-plane (upper part) of Mo2ZrB2 (red, orange and purple) and Mo2HfB2 (blue, cyan and black), respectively, both with the AlMn2B2-type structure.
Figure 7. Anisotropic Vickers hardness in the a-b, a-c and b-c-plane (lower part) and the ab-c, ac-b and bc-a-plane (upper part) of Mo2ZrB2 (red, orange and purple) and Mo2HfB2 (blue, cyan and black), respectively, both with the AlMn2B2-type structure.
Crystals 10 00865 g007
Table
Table 1. Lattice parameters a, b, c and volumes of Mo2ZrB2 and Mo2HfB2 as calculated with CP2k (Quantum ESPRESSO).
Table 1. Lattice parameters a, b, c and volumes of Mo2ZrB2 and Mo2HfB2 as calculated with CP2k (Quantum ESPRESSO).
Compounda (Å)b (Å)c (Å)V (Å3)
Mo2ZrB23.145 (3.146)12.59 (12.60)3.208 (3.208)127.1 (127.2)
Mo2HfB23.143 (3.141)12.33 (12.35)3.213 (3.212)124.6 (124.6)
Table
Table 2. Isotropic bulk modulus B, shear modulus G, Young’s modulus Y, Vickers hardness HV and the Universal Elastic Anisotropy Index AU of Mo2ZrB2 and Mo2HfB2.
Table 2. Isotropic bulk modulus B, shear modulus G, Young’s modulus Y, Vickers hardness HV and the Universal Elastic Anisotropy Index AU of Mo2ZrB2 and Mo2HfB2.
CompoundB (GPa)G (GPa)Y (GPa)HV (GPa)AU ( )
Mo2ZrB2241.19148.34369.3018.240.03
Mo2HfB2250.31158.73393.1119.810.02
Table
Table 3. Anisotropy of the bulk, shear and Young’s modulus as well as the Vickers hardness of Mo2ZrB2 and Mo2HfB2.
Table 3. Anisotropy of the bulk, shear and Young’s modulus as well as the Vickers hardness of Mo2ZrB2 and Mo2HfB2.
CompoundB Anisotropy Index ( )G Anisotropy Index ( )Y Anisotropy Index ( )HV Anisotropy Index ( )B and G Averaged Anisotropy Index ( )
Mo2ZrB20.130.100.210.210.12
Mo2HfB20.100.080.180.180.09
Table
Table 4. Integrated crystal orbital Hamilton population (ICOHPs) per formula unit of the Mo-Mo, Mo-M, Mo-B M-M, M-B and B-B bonds (M = Zr, Hf) in Mo2ZrB2 and Mo2HfB2.
Table 4. Integrated crystal orbital Hamilton population (ICOHPs) per formula unit of the Mo-Mo, Mo-M, Mo-B M-M, M-B and B-B bonds (M = Zr, Hf) in Mo2ZrB2 and Mo2HfB2.
Bonds (Number)Direction Along AxisICOHP of the Bonds in Mo2ZrB2 (eV)ICOHP of the Bonds in Mo2HfB2 (eV)
B-B (2×)ab−6.56−6.67
M-B (2×)b−2.51−2.79
Mo-B, short (4×)ac−9.09−8.92
Mo-B, long (2×)bc−3.80−3.74
M-M, short (2×)a−1.54−1.66
M-M, long (2×)c−1.51−1.58
Mo-M (4×)ab-c−5.24−5.62
Mo-Mo, short (2×)ab−2.23−2.13
Mo-Mo, medium (2×)a−1.65−1.63
Mo-Mo, long (2×)c−1.29−1.24
Mo-Mo, longest (1×)b−0.26−0.36
Sum −35.68−36.33

Share and Cite

MDPI and ACS Style

Touzani, R.S.; Krüger, M. First Principles Density Functional Theory Prediction of the Crystal Structure and the Elastic Properties of Mo2ZrB2 and Mo2HfB2. Crystals 2020, 10, 865. https://doi.org/10.3390/cryst10100865

AMA Style

Touzani RS, Krüger M. First Principles Density Functional Theory Prediction of the Crystal Structure and the Elastic Properties of Mo2ZrB2 and Mo2HfB2. Crystals. 2020; 10(10):865. https://doi.org/10.3390/cryst10100865

Chicago/Turabian Style

Touzani, Rachid Stefan, and Manja Krüger. 2020. "First Principles Density Functional Theory Prediction of the Crystal Structure and the Elastic Properties of Mo2ZrB2 and Mo2HfB2" Crystals 10, no. 10: 865. https://doi.org/10.3390/cryst10100865

APA Style

Touzani, R. S., & Krüger, M. (2020). First Principles Density Functional Theory Prediction of the Crystal Structure and the Elastic Properties of Mo2ZrB2 and Mo2HfB2. Crystals, 10(10), 865. https://doi.org/10.3390/cryst10100865

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop