Application of Artificial Neural Networks in Crystal Growth of Electronic and Opto-Electronic Materials
Abstract
1. Introduction
2. Crystal Growth Challenges and AI Potential
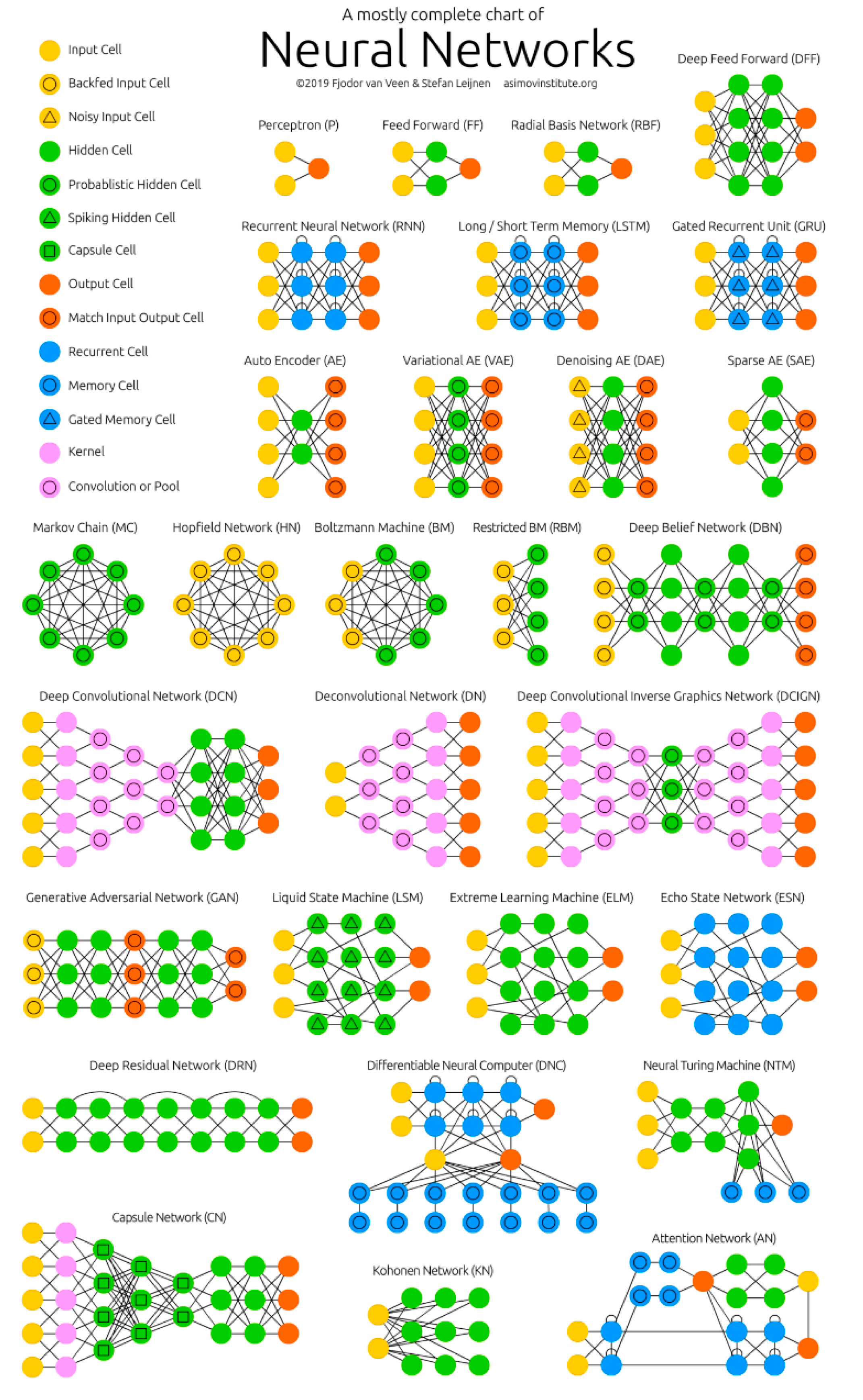
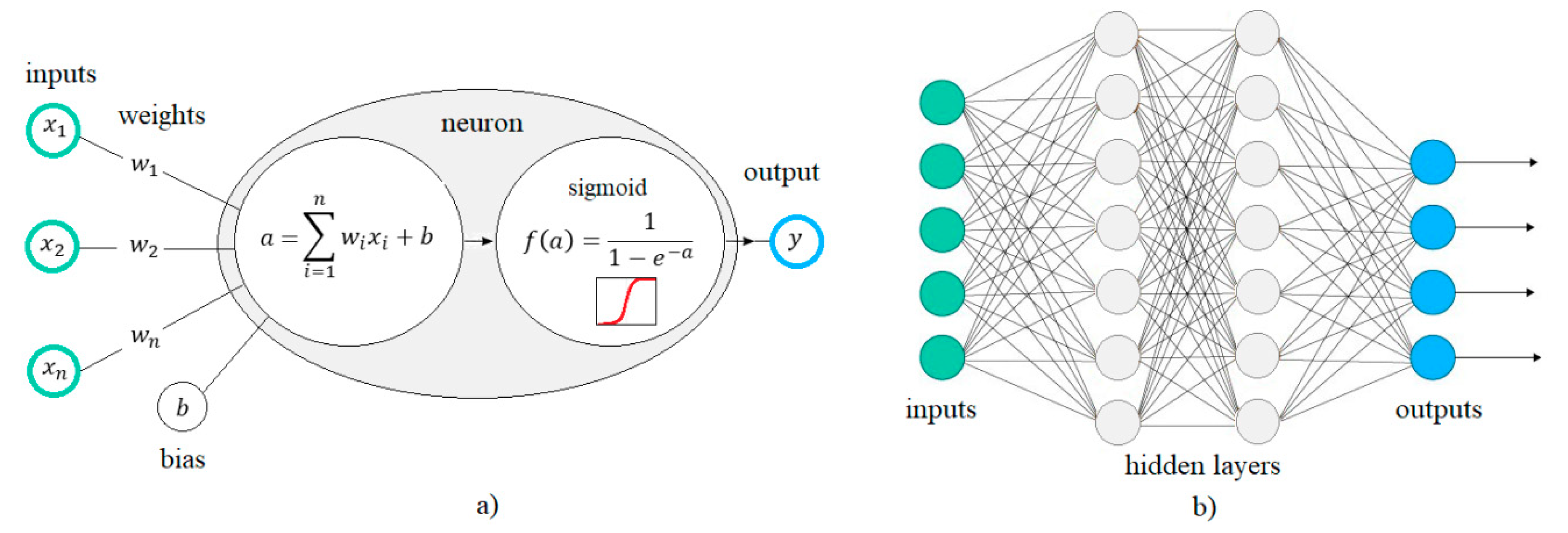
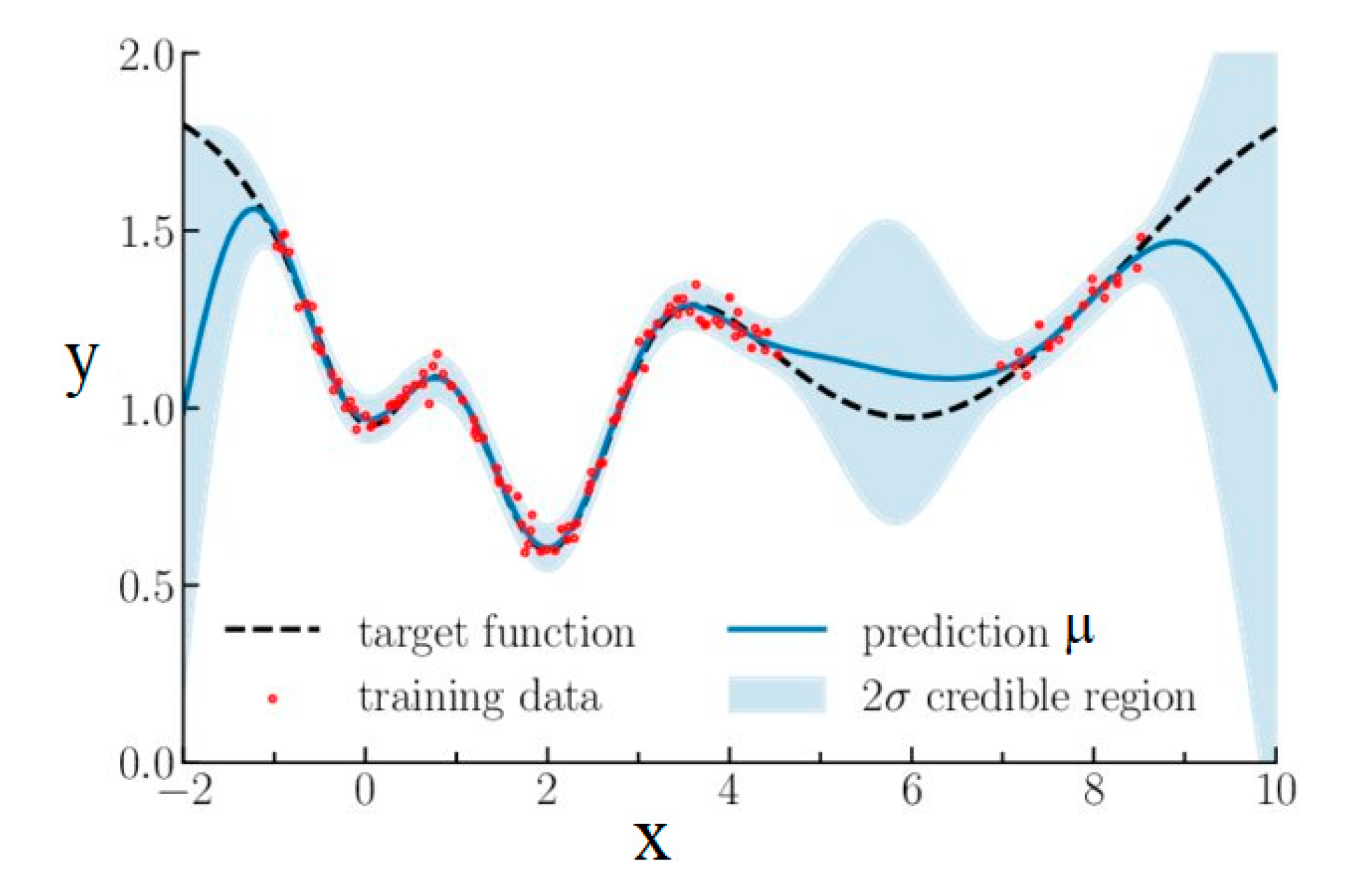
3. Artificial Neural Networks Overview
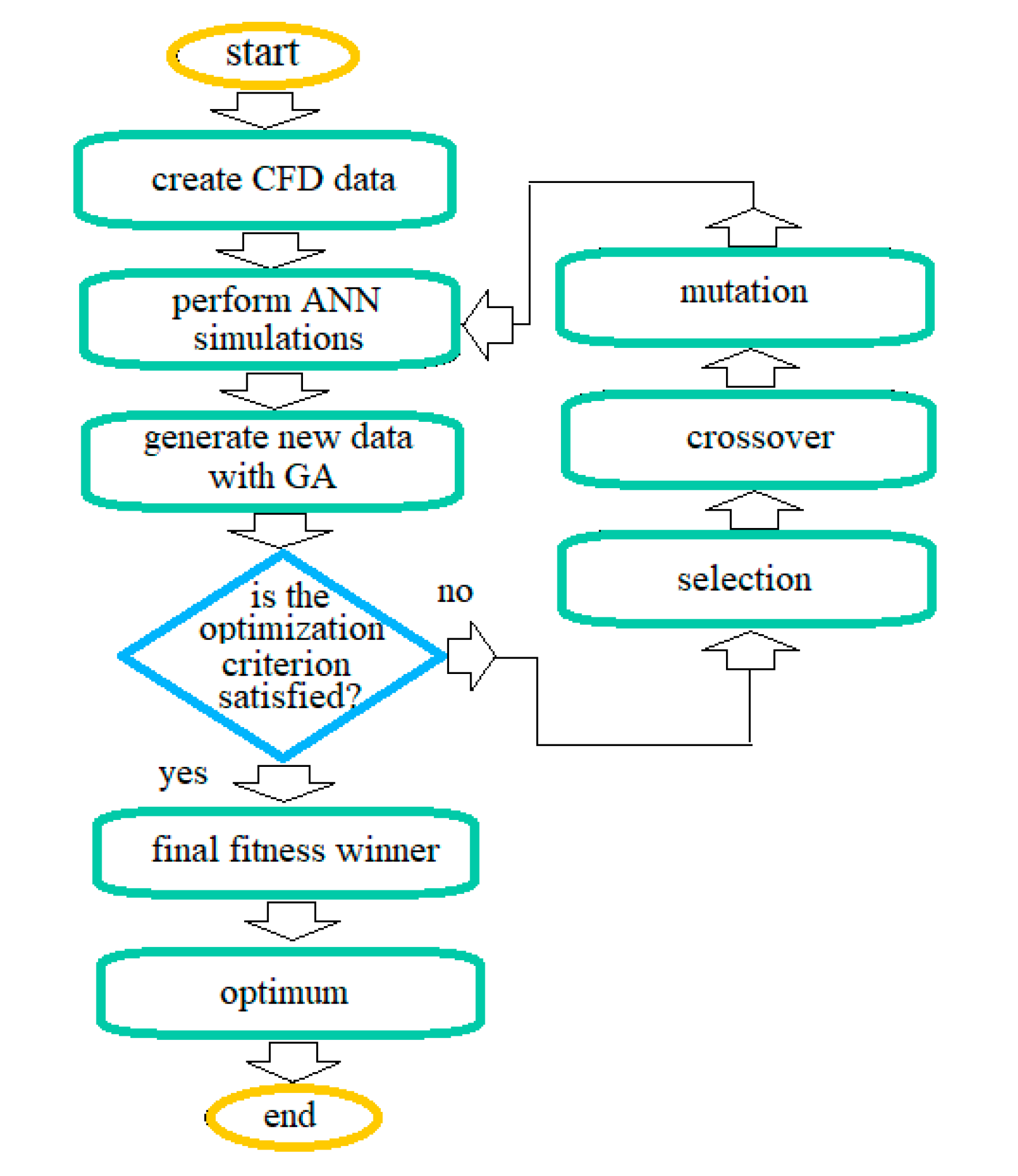
4. AI Applications in Crystal Growth: State of the Art
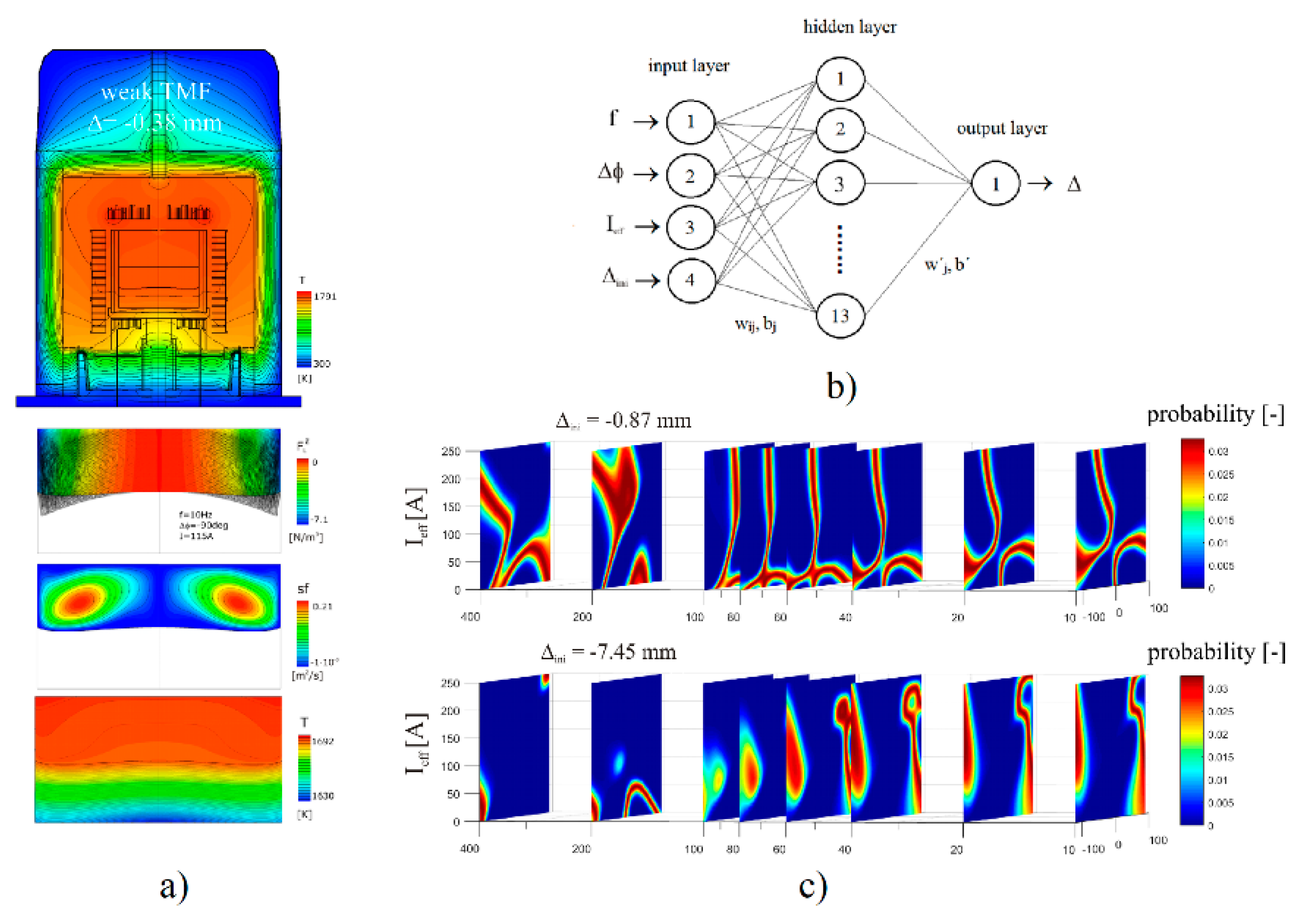
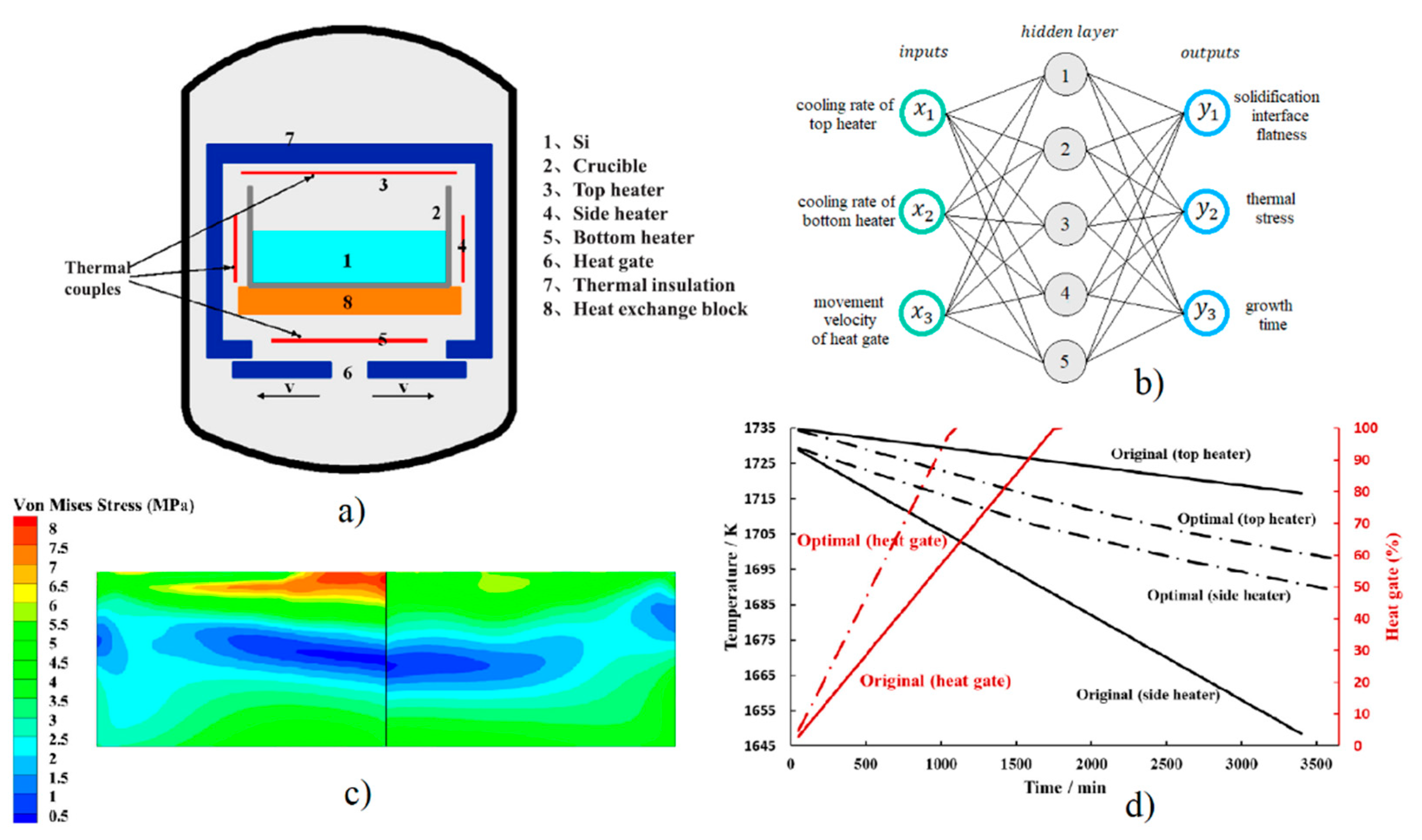
4.1. Static ANN Applications
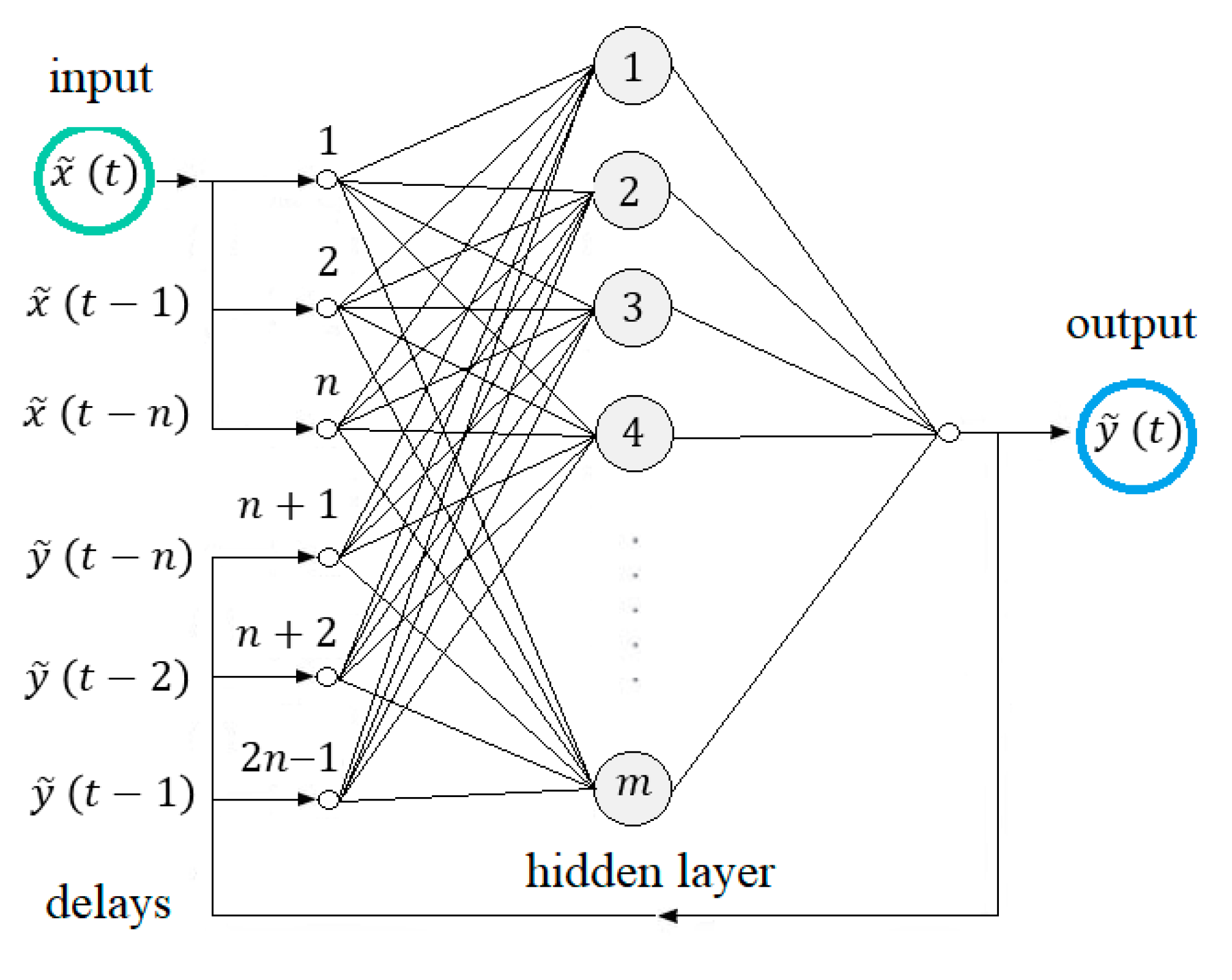
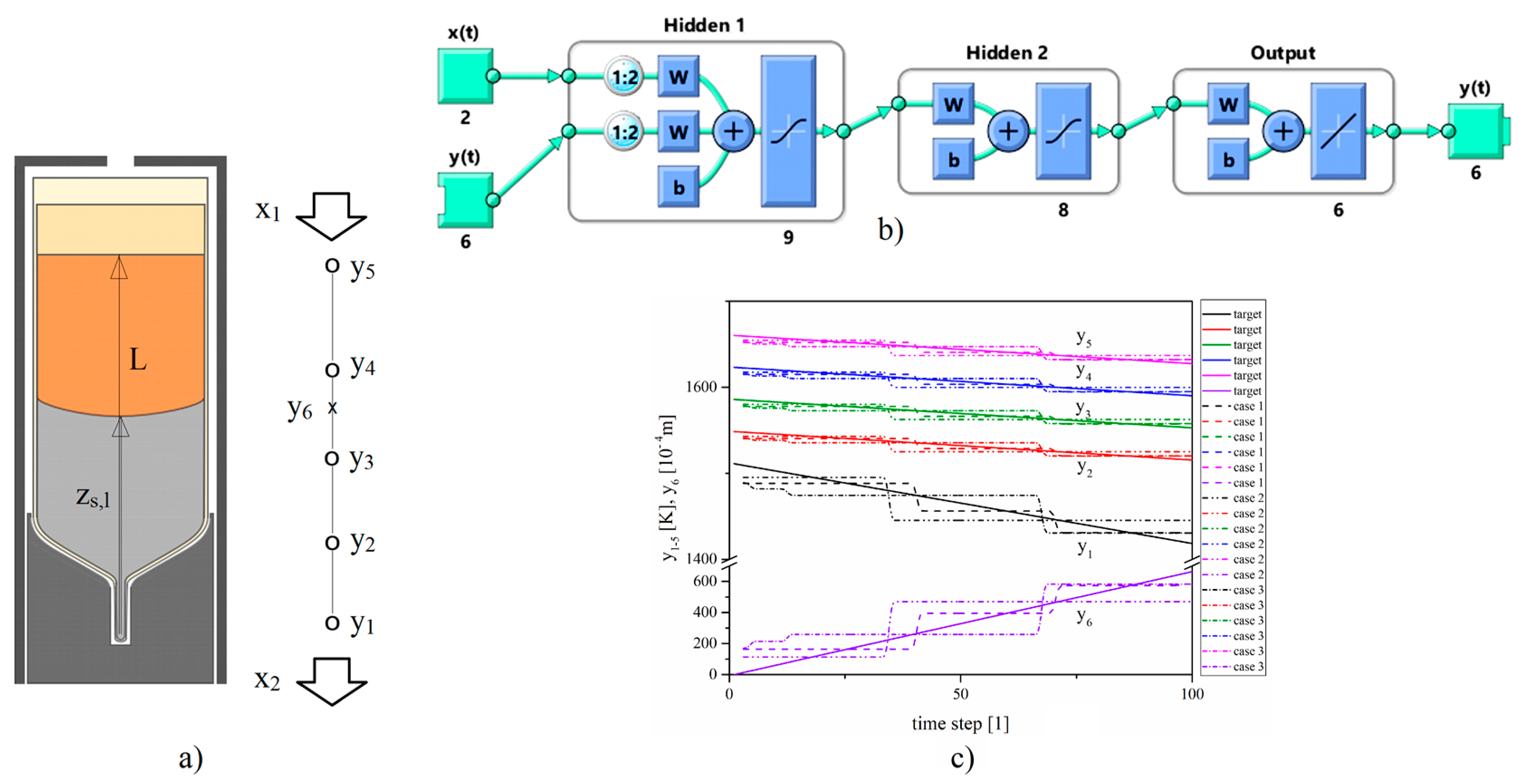
4.2. Dynamic Applications
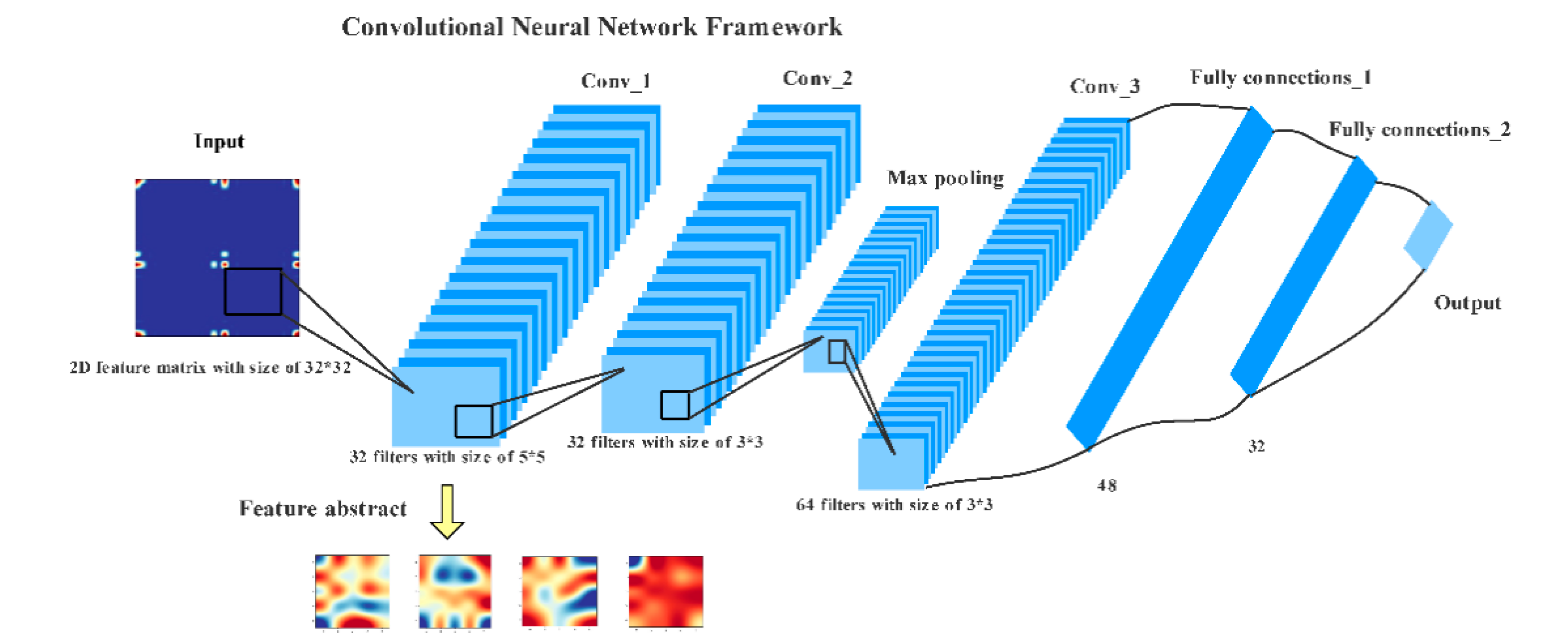
4.3. Image Processing Applications
5. Conclusions and Outlook
Funding
Conflicts of Interest
References
- Scheel, H.J. The Development of Crystal Growth Technology. In Crystal Growth Technology; Scheel, H.J., Fukuda, T., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Capper, P. Bulk Crystal Growth—Methods and Materials. In Springer Handbook of Electronic and Photonic Materials; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Chen, X.; Liu, J.; Pang, Y.; Chen, J.; Chi, L.; Gong, C. Developing a new mesh quality evaluation method based on convolutional neural network. Eng. Appl. Comput. Fluid Mech. 2020, 14, 391–400. [Google Scholar] [CrossRef]
- Duffar, T. Crystal Growth Processes Based on Capillarity: Czochralski, Floating Zone, Shaping and Crucible Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Schmidt, J.; Marques, M.R.G.; Botti, S.; Marques, M.A.L. Recent advances and applications of machine learning in solid-state materials science. npj Comput. Mater. 2019, 5. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.S.; Nebgen, B.T.; Zubatyuk, R.; Lubbers, N.; Devereux, C.; Barros, K.; Tretiak, S.; Isayev, O.; Roitberg, A. Outsmarting Quantum Chemistry through Transfer Learning. ChemRxiv 2018. [Google Scholar]
- Rojas, R. Neural Networks: A Systematic Introduction; Springer: Berlin, Germany, 1996. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design; PWS Publishing: Boston, MA, USA, 2014; Chapters 11 and 12. [Google Scholar]
- Leijnen, S.; Van Veen, F. The Neural Network Zoo. Proceedings 2020, 47, 9. [Google Scholar] [CrossRef]
- Picard, R.; Cook, D. Cross-Validation of Regression Models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
- Gupta, M.; Jin, L.; Homma, N. Static and Dynamic Neural Networks: From Fundamentals to Advanced Theory; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Leontaritis, I.J.; Billings, S.A. Input-output parametric models for non-linear systems Part I: Deterministic non-linear systems. Int. J. Control 1985, 41, 303–328. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S.A.; Grant, P.M. Non-linear system identification using neural networks. Int. J. Control 1990, 51, 1191–1214. [Google Scholar] [CrossRef]
- Narendra, K.; Parthasarathy, K. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cao, Z.; Dan, Y.; Xiong, Z.; Niu, C.; Li, X.; Qian, S.; Hu, J. Convolutional Neural Networks for Crystal Material Property Prediction Using Hybrid Orbital-Field Matrix and Magpie Descriptors. Crystals 2019, 9, 191. [Google Scholar] [CrossRef]
- Asadian, M.; Seyedein, S.; Aboutalebi, M.; Maroosi, A. Optimization of the parameters affecting the shape and position of crystal–melt interface in YAG single crystal growth. J. Cryst. Growth 2009, 311, 342–348. [Google Scholar] [CrossRef]
- Baerns, M.; Holena, M. Combinatorial Development of Solid Catalytic Materials. Design of High Throughput Experiments, Data Analysis, Data Mining; Imperial College Press: London, UK, 2009. [Google Scholar]
- Landín, M.; Rowe, R.C. Artificial neural networks technology to model, understand, and optimize drug formulations. In Formulation Tools for Pharmaceutical Development; Elsevier: Amsterdam, The Netherlands, 2013; pp. 7–37. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Leclercq, F. Bayesian optimisation for likelihood-free cosmological inference. Phys. Rev. D 2018, 98, 063511. [Google Scholar] [CrossRef]
- Kumar, K.V. Neural Network Prediction of Interfacial Tension at Crystal/Solution Interface. Ind. Eng. Chem. Res. 2009, 48, 4160–4164. [Google Scholar] [CrossRef]
- Sun, X.; Tang, X. Prediction of the Crystal’s Growth Rate Based on BPNN and Rough Sets. In Proceedings of the Second International Conference on Computational Intelligence and Natural Computing (CINC), Wuhan, China, 14 September 2010; pp. 183–186. [Google Scholar]
- Srinivasan, S.; Saghir, M.Z. Modeling of thermotransport phenomenon in metal alloys using artificial neural networks. Appl. Math. Model. 2013, 37, 2850–2869. [Google Scholar] [CrossRef]
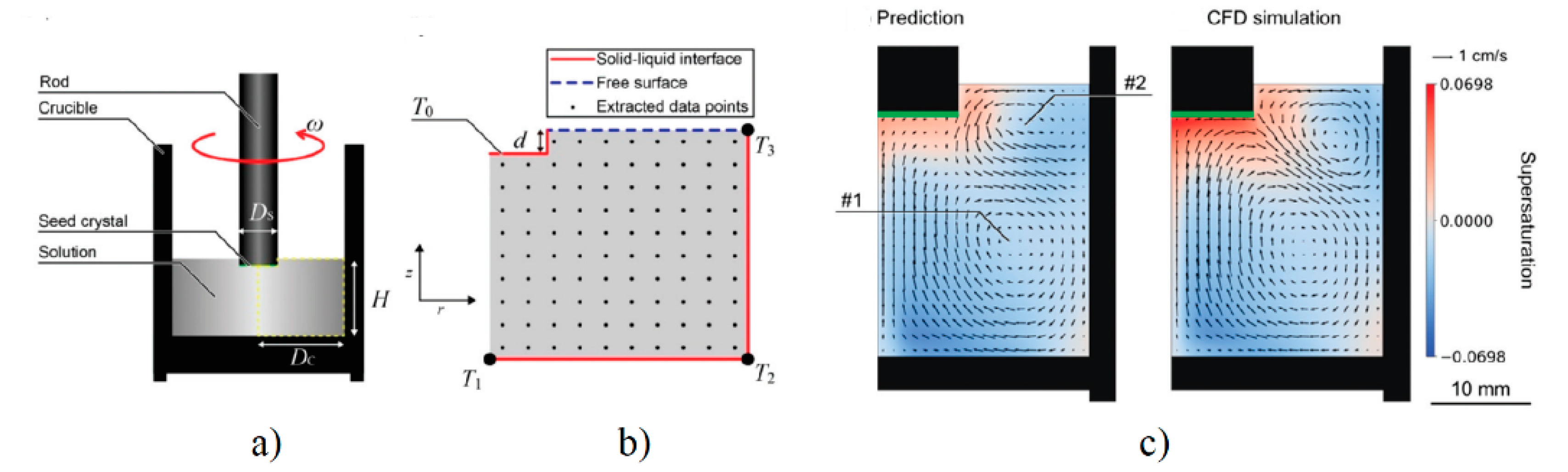
- Tsunooka, Y.; Kokubo, N.; Hatasa, G.; Harada, S.; Tagawa, M.; Ujihara, T. High-speed prediction of computational fluid dynamics simulation in crystal growth. CrystEngComm 2018, 20, 6546–6550. [Google Scholar] [CrossRef]
- Tang, Q.W.; Zhang, J.; Lui, D. Diameter Model Identification of CZ Silicon Single Crystal Growth Process. In Proceedings of the International Symposium on Industrial Electronics (IEEE) 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 2069–2073. [Google Scholar] [CrossRef]
- Dropka, N.; Holena, M.; Ecklebe, S.; Frank-Rotsch, C.; Winkler, J. Fast forecasting of VGF crystal growth process by dynamic neural networks. J. Cryst. Growth 2019, 521, 9–14. [Google Scholar] [CrossRef]
- Dropka, N.; Holena, M. Optimization of magnetically driven directional solidification of silicon using artificial neural networks and Gaussian process models. J. Cryst. Growth 2017, 471, 53–61. [Google Scholar] [CrossRef]
- Dropka, N.; Holena, M.; Frank-Rotsch, C. TMF optimization in VGF crystal growth of GaAs by artificial neural networks and Gaussian process models. In Proceedings of the XVIII International UIE-Congress on Electrotechnologies for Material Processing, Hannover, Germany, 6–9 June 2017; pp. 203–208. [Google Scholar]
- Dang, Y.; Liu, L.; Li, Z. Optimization of the controlling recipe in quasi-single crystalline silicon growth using artificial neural network and genetic algorithm. J. Cryst. Growth 2019, 522, 195–203. [Google Scholar] [CrossRef]
- Ujihara, T.; Tsunooka, Y.; Endo, T.; Zhu, C.; Kutsukake, K.; Narumi, T.; Mitani, T.; Kato, T.; Tagawa, M.; Harada, S. Optimization of growth condition of SiC solution growth by the predication model constructed by machine learning for larger diameter. Jpn. Soc. Appl. Phys. 2019. [Google Scholar]
- Ujihara, T.; Tsunooka, Y.; Hatasa, G.; Kutsukake, K.; Ishiguro, A.; Murayama, K.; Narumi, T.; Harada, S.; Tagawa, M. The Prediction Model of Crystal Growth Simulation Built by Machine Learning and Its Applications. Vac. Surf. Sci. 2019, 62, 136–140. [Google Scholar] [CrossRef]
- Velásco-Mejía, A.; Vallejo-Becerra, V.; Chávez-Ramírez, A.; Torres-González, J.; Reyes-Vidal, Y.; Castañeda, F. Modeling and optimization of a pharmaceutical crystallization process by using neural networks and genetic algorithms. Powder Technol. 2016, 292, 122–128. [Google Scholar] [CrossRef]
- Paengjuntuek, W.; Thanasinthana, L.; Arpornwichanop, A. Neural network-based optimal control of a batch crystallizer. Neurocomputing 2012, 83, 158–164. [Google Scholar] [CrossRef]
- Samanta, G. Application of machine learning to a MOCVD process. In Proceedings of the Program and Abstracts Ebook of ICCGE-19/OMVPE-19/AACG Conference, Keystone, CO, USA, 28 July–9 August 2019; pp. 203–208. [Google Scholar]
- Boucetta, A.; Kutsukake, K.; Kojima, T.; Kudo, H.; Matsumoto, T.; Usami, N. Application of artificial neural network to optimize sensor positions for accurate monitoring: An example with thermocouples in a crystal growth furnace. Appl. Phys. Express 2019, 12, 125503. [Google Scholar] [CrossRef]
- Daikoku, H.; Kado, M.; Seki, A.; Sato, K.; Bessho, T.; Kusunoki, K.; Kaidou, H.; Kishida, Y.; Moriguchi, K.; Kamei, K. Solution growth on concave surface of 4H-SiC crystal. Cryst. Growth Des. 2016, 1256–1260. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations ICLR, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
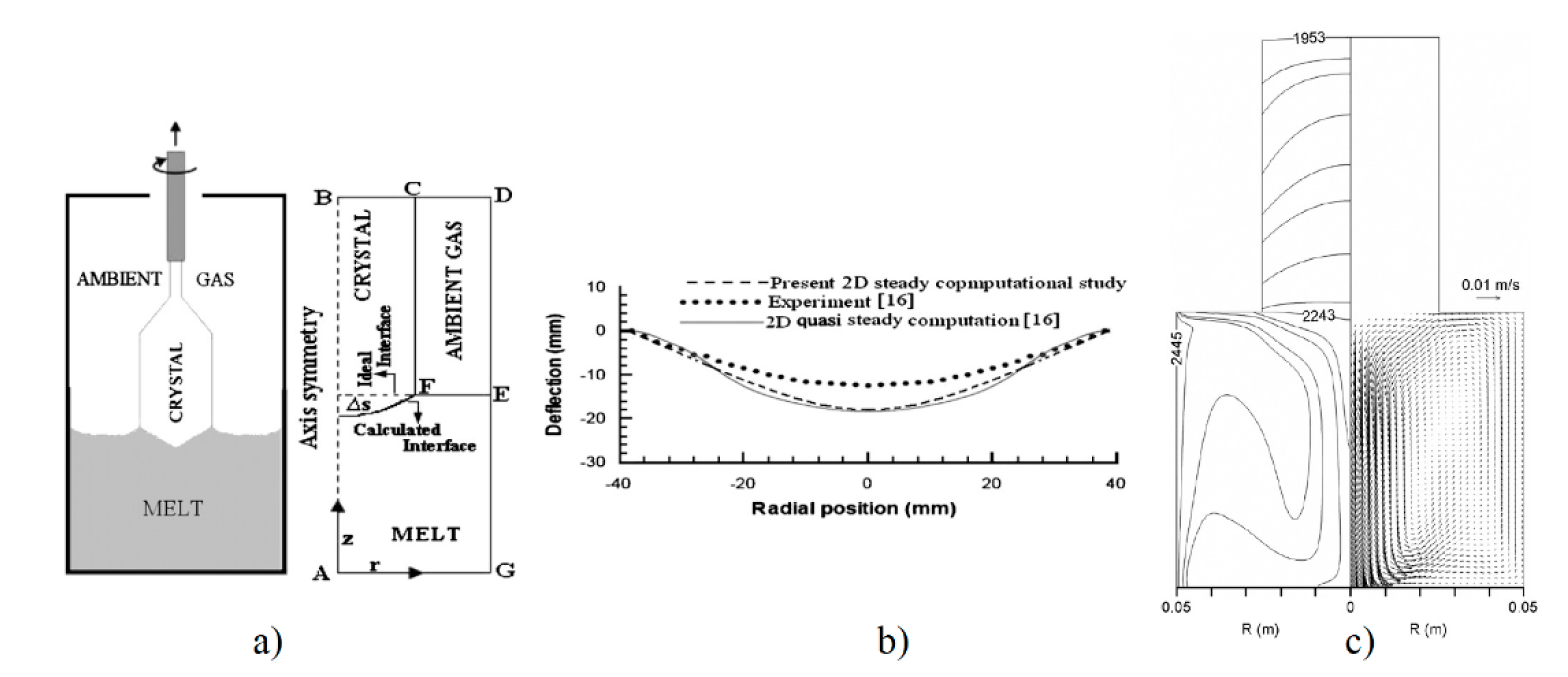
- Yakovlev, E.V.; Kalaev, V.V.; Bystrova, E.N.; Smirnova, O.V.; Makarov, Y.N.; Frank-Rotsch, C.; Neubert, M.; Rudolph, P. Modeling analysis of liquid encapsulated Czochralski growth of GaAs and InP crystals. Cryst. Res. Technol. 2003, 38, 506–514. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence Modeling in the Age of Data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Isayev, O.; Oses, C.; Toher, C.; Gossett, E.; Curtalolo, S.; Tropsha, A. Universal fragment descriptors for predicting properties of inorganic crystals. Nat. Commun. 2017, 8, 15679. [Google Scholar] [CrossRef]
- Xie, T.; Grossman, J.C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef]
- Carrete, J.; Li, W.; Mingo, N.; Wang, S.; Curtalolo, S. Finding Unprecedentedly Low-Thermal-Conductivity Half-Heusler Semiconductors via High-Throughput Materials Modeling. Phys. Rev. X 2014, 4, 011019. [Google Scholar] [CrossRef]
- Seko, A.; Maekawa, T.; Tsuda, K.; Tanaka, I. Machine learning with systematic density-functional theory calculations: Application to melting temperatures of single- and binary-component solids. Phys. Rev. B 2014, 89, 054303. [Google Scholar] [CrossRef]
- Gaultois, M.W.; Oliynyk, A.O.; Mar, A.; Sparks, T.D.; Mulholland, G.; Meredig, B. Perspective: Web-based machine learning models for real-time screening of thermoelectric materials properties. APL Mater. 2016, 4, 53213. [Google Scholar] [CrossRef]
- Ziatdinov, M.; Dyck, O.; Maksov, A.; Li, X.; Sang, X.; Xiao, K.; Unocic, R.R.; Vasudevan, R.; Jesse, S.; Kalinin, S.V. Deep Learning of Atomically Resolved STEM Images: Chemical Identification and Tracking Local Transformations. ACS Nano 2017, 11, 12742–12752. [Google Scholar] [CrossRef] [PubMed]
- Guven, G.; Oktay, A.B. Nanoparticle detection from TEM images with deep learning. In Proceedings of the 26th Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; pp. 1–4. [Google Scholar]
- Gal, Y.; Islam, R.; Ghahramani, Z. Deep Bayesian Active Learning with Image Data. arXiv. 2017. Available online: https://arxiv.org/abs/1703.02910 (accessed on 25 July 2020).
- Huang, S.-J.; Zhao, J.-W.; Liu, Z.-Y. Cost-Effective Training of Deep CNNs with Active Model Adaptation. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1580–1588. [Google Scholar] [CrossRef]
- Kandemir, M. Variational closed-Form deep neural net inference. Pattern Recognit. Lett. 2018, 112, 145–151. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, W.; Li, X. Training data reduction in ddeep neural networks with partial mutual information based feature selection and correlation matching based active learning. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5 March 2017; pp. 2362–2366. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. NIPS 2014, 3104–3112. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dropka, N.; Holena, M. Application of Artificial Neural Networks in Crystal Growth of Electronic and Opto-Electronic Materials. Crystals 2020, 10, 663. https://doi.org/10.3390/cryst10080663
Dropka N, Holena M. Application of Artificial Neural Networks in Crystal Growth of Electronic and Opto-Electronic Materials. Crystals. 2020; 10(8):663. https://doi.org/10.3390/cryst10080663
Chicago/Turabian StyleDropka, Natasha, and Martin Holena. 2020. "Application of Artificial Neural Networks in Crystal Growth of Electronic and Opto-Electronic Materials" Crystals 10, no. 8: 663. https://doi.org/10.3390/cryst10080663
APA StyleDropka, N., & Holena, M. (2020). Application of Artificial Neural Networks in Crystal Growth of Electronic and Opto-Electronic Materials. Crystals, 10(8), 663. https://doi.org/10.3390/cryst10080663





