Extraordinary Response of H-Charged and H-Free Coherent Grain Boundaries in Nickel to Multiaxial Loading
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
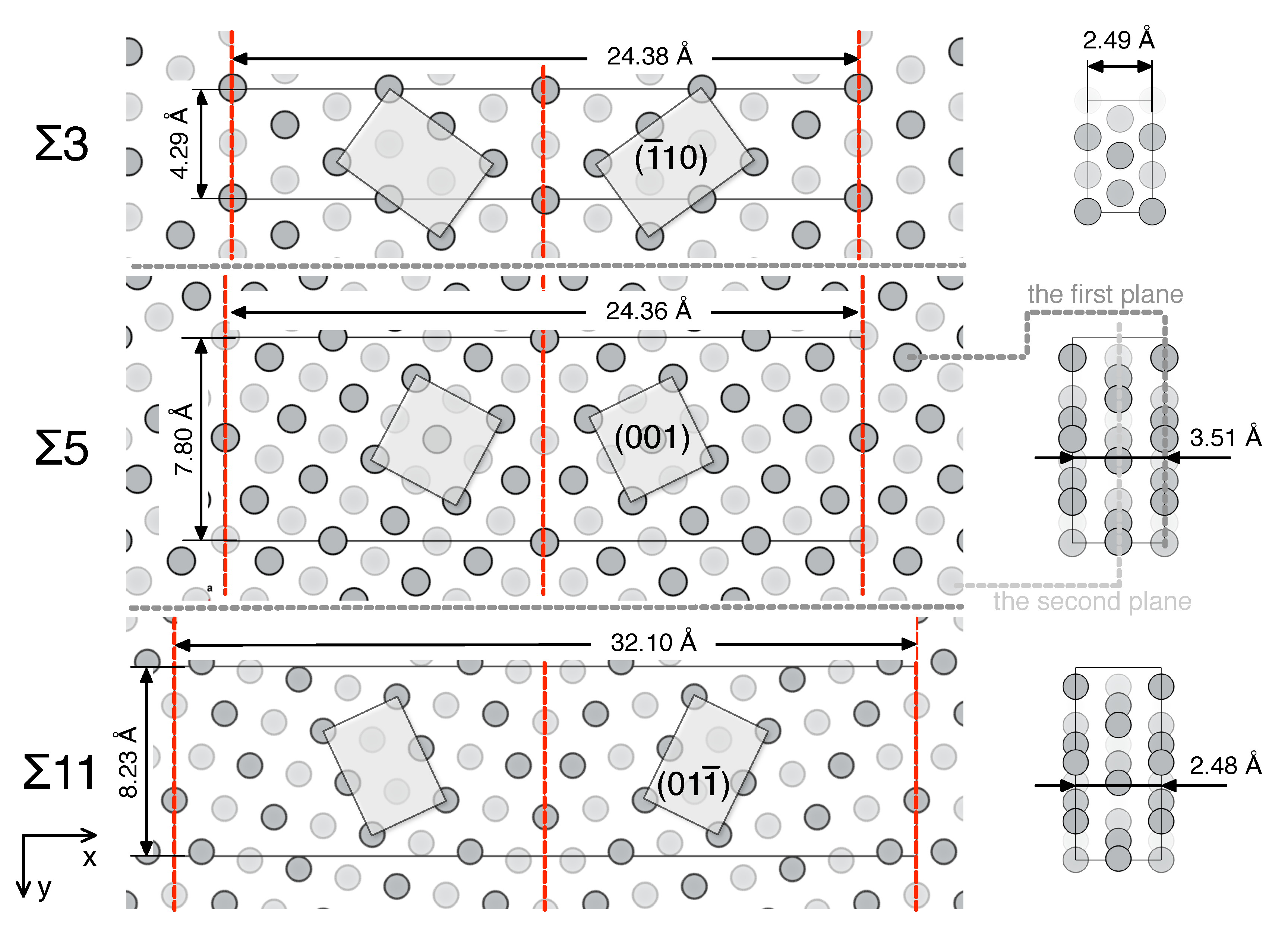
3.1. Structure Parameters of 3, 5, and 11 GBs
3.1.1. Clean Grain Boundaries
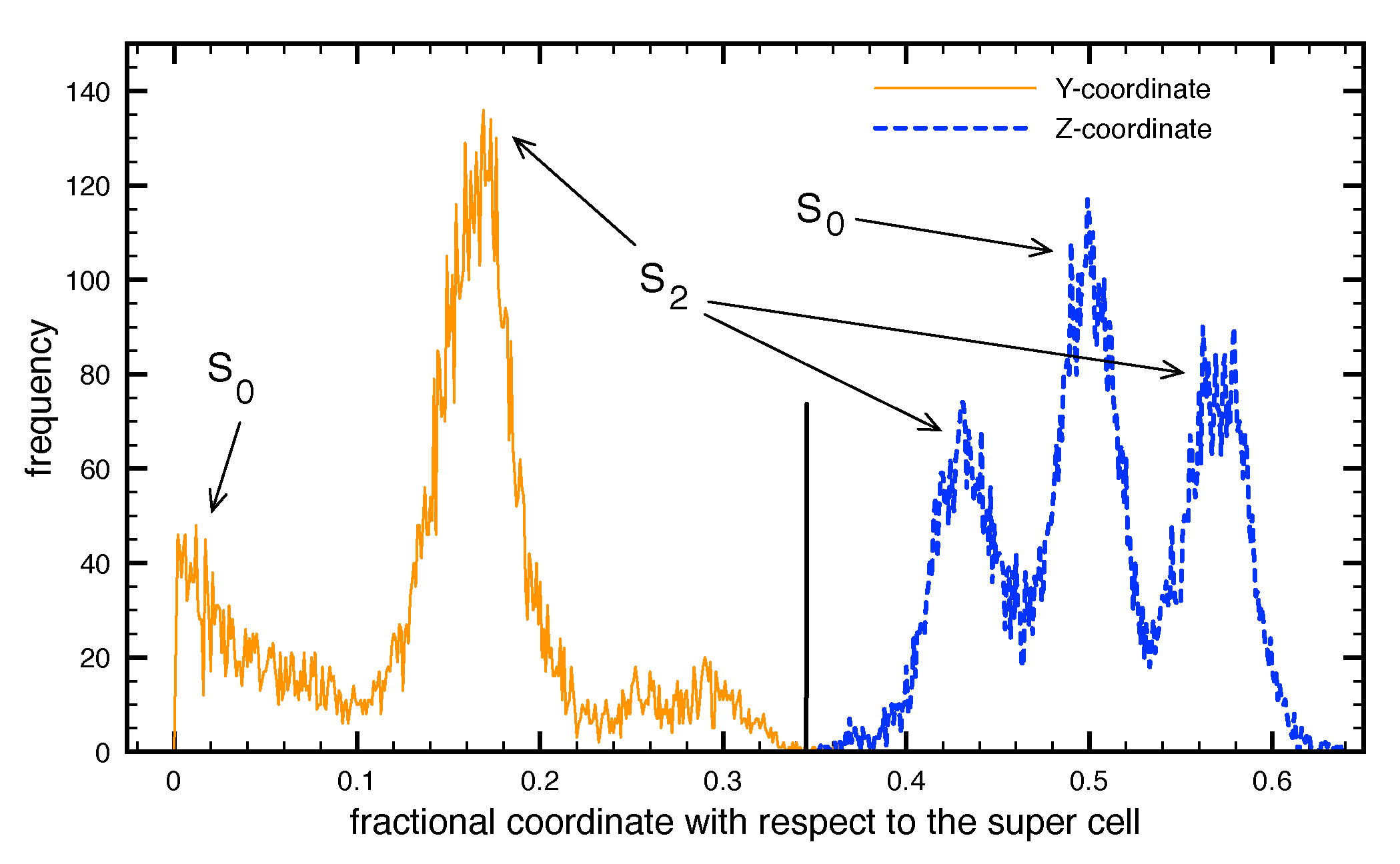
3.1.2. H-Charged Grain Boundaries
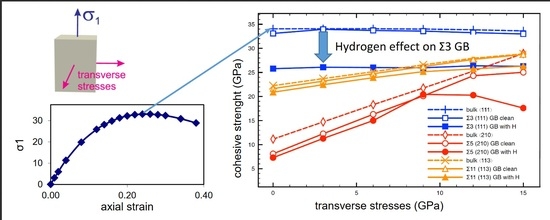
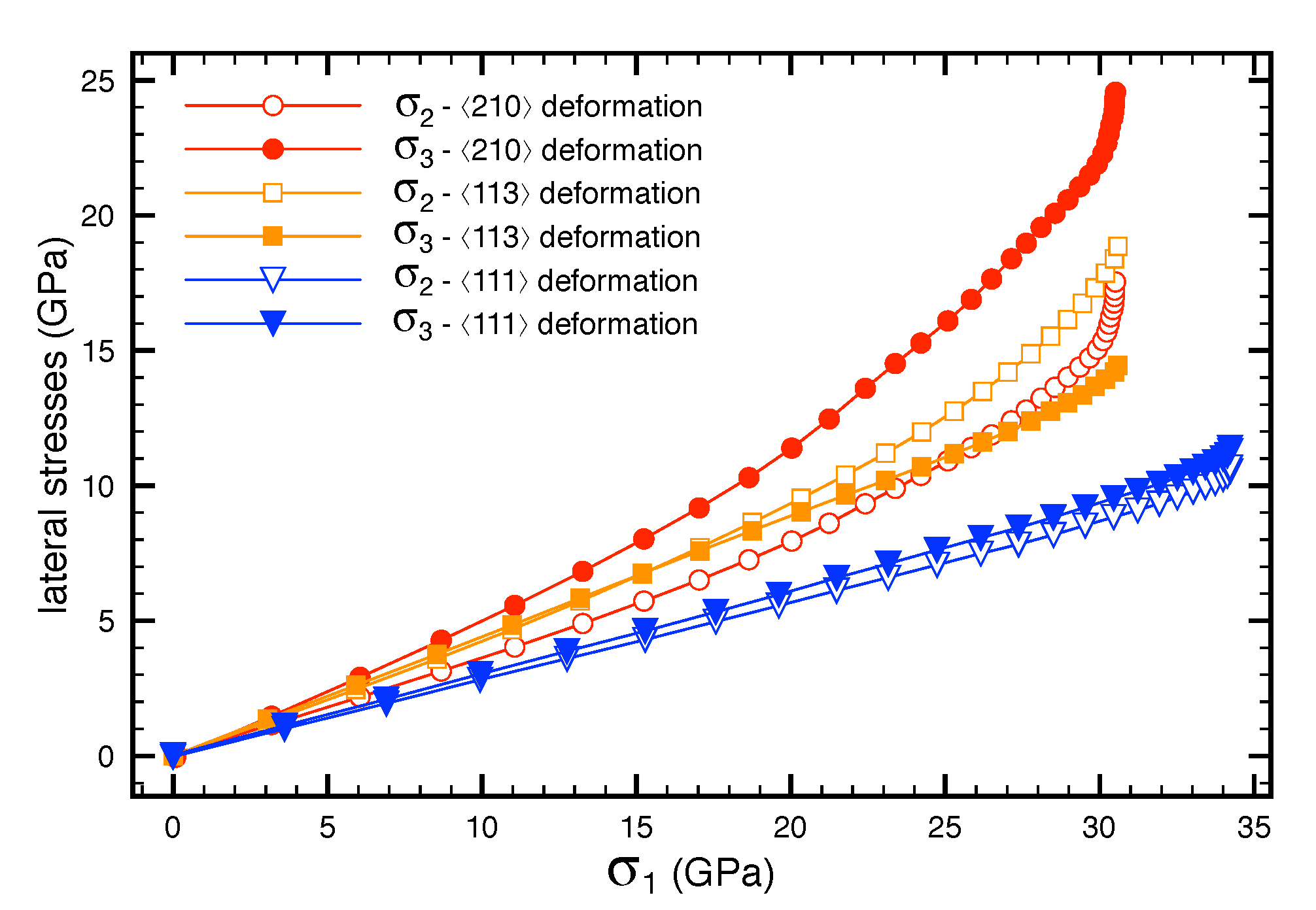
3.2. Cohesive Strength of Hydrogen-Free GBs
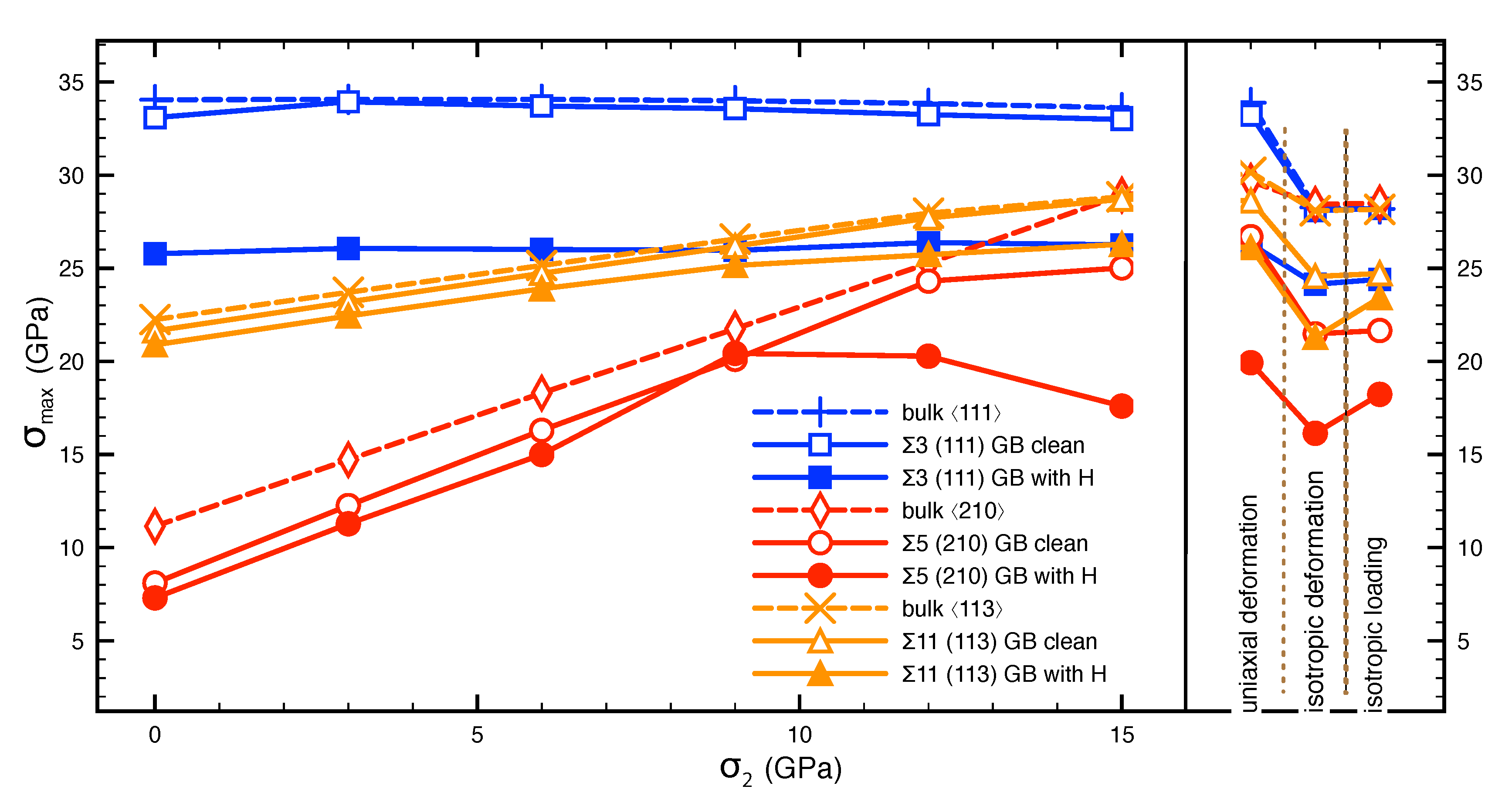
3.3. Cohesive Strength of Hydrogen-Charged GBs
3.4. Work of Separation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Seita, M.; Hanson, J.P.; Gradečak, S.; Demkowicz, M.J. The dual role of coherent twin boundaries in hydrogen embrittlement. Nat. Commun. 2015, 6, 6164. [Google Scholar] [CrossRef] [PubMed]
- Koyama, M.; Tasan, C.C.; Akiyama, E.; Tsuzaki, K.; Raabe, D. Hydrogen-assisted decohesion and localized plasticity in dual-phase steel. Acta Mater. 2014, 70, 174–187. [Google Scholar] [CrossRef]
- Geng, W.T.; Freeman, A.J.; Wu, R.; Geller, C.B.; Raynolds, J.E. Embrittling and strengthening effects of hydrogen, boron, and phosphorus on a Σ5 nickel grain boundary. Phys. Rev. B 1999, 60, 7149–7155. [Google Scholar] [CrossRef]
- Xu, X.; Wen, M.; Hu, Z.; Fukuyama, S.; Yokogawa, K. Atomistic process on hydrogen embrittlement of a single crystal of nickel by the embedded atom method. Comput. Mater. Sci. 2002, 23, 131–138. [Google Scholar] [CrossRef]
- Wen, M.; Xu, X.J.; Omura, Y.; Fukuyama, S.; Yokogawa, K. Modeling of hydrogen embrittlement in single crystal Ni. Comput. Mater. Sci. 2004, 30, 202–211. [Google Scholar] [CrossRef]
- Tahir, A.; Janisch, R.; Hartmaier, A. Hydrogen embrittlement of a carbon segregated symmetrical tilt grain boundary in α-Fe. Mater. Sci. Eng. A 2014, 612, 462–467. [Google Scholar] [CrossRef]
- Di Stefano, D.; Mrovec, M.; Elsässer, C. First-principles investigation of hydrogen trapping and diffusion at grain boundaries in nickel. Acta Mater. 2015, 98, 306–312. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Shiga, M.; Kaburaki, H. First-Principles Study on Segregation Energy and Embrittling Potency of Hydrogen in NiΣ5(012) Tilt Grain Boundary. J. Phys. Soc. Jpn. 2004, 73, 441–449. [Google Scholar] [CrossRef]
- Yu, H.; Olsen, J.S.; Alvaro, A.; Olden, V.; He, J.; Zhang, Z. A uniform hydrogen degradation law for high strength steels. Eng. Fract. Mech. 2016, 157, 56–71. [Google Scholar] [CrossRef]
- Alvaro, A.; Jensen, I.T.; Kheradmand, N.; Løvvik, O.; Olden, V. Hydrogen embrittlement in nickel, visited by first principles modeling, cohesive zone simulation and nanomechanical testing. Int. J. Hydrog. Energy 2015, 40, 16892–16900. [Google Scholar] [CrossRef]
- Chen, J.; Dongare, A.M. Role of grain boundary character on oxygen and hydrogen segregation-induced embrittlement in polycrystalline Ni. J. Mater. Sci. 2017, 52, 30–45. [Google Scholar] [CrossRef]
- Tehranchi, A.; Curtin, W.A. Atomistic study of hydrogen embrittlement of grain boundaries in nickel: II. Decohesion. Modell. Simul. Mater. Sci. Eng. 2017, 25, 075013. [Google Scholar] [CrossRef]
- He, S.; Ecker, W.; Pippan, R.; Razumovskiy, V.I. Hydrogen-enhanced decohesion mechanism of the special Sigma5(012)[100] grain boundary in Ni with Mo and C solutes. Comput. Mater. Sci. 2019, 167, 100–110. [Google Scholar] [CrossRef]
- Oriani, R.A. A mechanistic theory of hydrogen embrittlement of steels. Berichte Bunsenges. Phys. Chem. 1972, 76, 848–857. [Google Scholar] [CrossRef]
- Birnbaum, H.; Sofronis, P. Hydrogen-enhanced localized plasticity—A mechanism for hydrogen-related fracture. Mater. Sci. Eng. A 1994, 176, 191–202. [Google Scholar] [CrossRef]
- Yu, H.; Olsen, J.S.; He, J.; Zhang, Z. Hydrogen-microvoid interactions at continuum scale. Int. J. Hydrog. Energy 2018, 43, 10104–10128. [Google Scholar] [CrossRef]
- Zhao, K.; He, J.; Mayer, A.; Zhang, Z. Effect of hydrogen on the collective behavior of dislocations in the case of nanoindentation. Acta Mater. 2018, 148, 18–27. [Google Scholar] [CrossRef]
- Všianská, M.; Šob, M. The effect of segregated sp-impurities on grain-boundary and surface structure, magnetism and embrittlement in nickel. Prog. Mater. Sci. 2011, 56, 817–840. [Google Scholar] [CrossRef]
- Černý, M.; Šesták, P.; Řehák, P.; Všianská, M.; Šob, M. Ab initio tensile tests of grain boundaries in the fcc crystals of Ni and Co with segregated sp-impurities. Mater. Sci. Eng. A 2016, 669, 218–225. [Google Scholar] [CrossRef]
- Tahir, A.M.; Janisch, R.; Hartmaier, A. Ab initio calculation of traction separation laws for a grain boundary in molybdenum with segregated C impurites. Modell. Simul. Mater. Sci. Eng. 2013, 21, 075005. [Google Scholar] [CrossRef]
- Janisch, R.; Ahmed, N.; Hartmaier, A. Ab initio tensile tests of Al bulk crystals and grain boundaries: Universality of mechanical behavior. Phys. Rev. B 2010, 81, 184108. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Bean, J.J.; McKenna, K.P. Origin of differences in the excess volume of copper and nickel grain boundaries. Acta Mater. 2016, 110, 246–257. [Google Scholar] [CrossRef]
- Shiga, M.; Yamaguchi, M.; Kaburaki, H. Structure and energetics of clean and hydrogenated Ni surfaces and symmetrical tilt grain boundaries using the embedded-atom method. Phys. Rev. B 2003, 68, 245402. [Google Scholar] [CrossRef]
- Černý, M.; Pokluda, J. Ideal tensile strength of cubic crystals under superimposed transverse biaxial stresses from first principles. Phys. Rev. B 2010, 82, 174106. [Google Scholar] [CrossRef]
- Černý, M.; Šesták, P.; Řehák, P.; Všianská, M.; Šob, M. Atomistic approaches to cleavage of interfaces. Modell. Simul. Mater. Sci. Eng. 2019, 27, 035007. [Google Scholar] [CrossRef]
- Tran, R.; Xu, Z.; Radhakrishnan, B.; Winston, D.; Sun, W.; Persson, K.A.; Ong, S.P. Surface energies of elemental crystals. Sci. Data 2016, 3, 160080. [Google Scholar] [CrossRef]
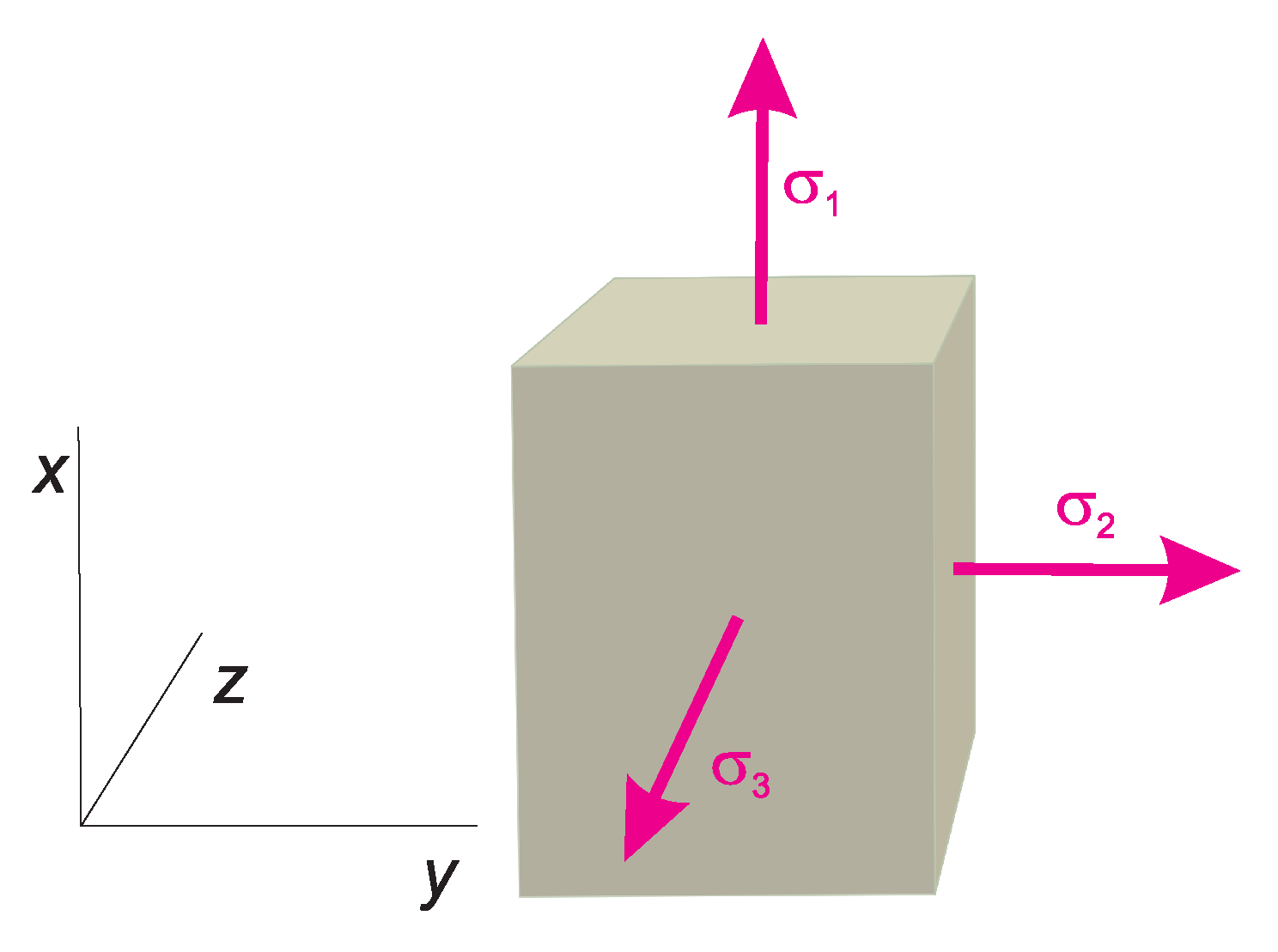

| uniaxial loading | |
| uniaxial deformation | 0 |
| triaxial loading | |
| isotropic deformation | |
| isotropic loading |
| GB | Plane | Rotation | Rotation | k-Points Grid | N | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Axis | Angle | (Å) | (J/m) | (Å) | (Å) | (Å) | |||||
| 3 | present | 109.5° | 0.02 | 0.06 | 24.4 | 4.29 | 2.49 | 1 × 6 × 10 | 24 | ||
| Reference [7] | 0.05 | 0.18 | 24.5 | 4.32 | 2.50 | 1 × 6 × 10 | 24 | ||||
| Reference [26] | 0.01 | 0.04 | - | - | - | 1 × 3 × 3 | - | ||||
| Reference [11] | −0.11 | 0.09 | 24.3 | 4.73 | 4.94 | 1 × 4 × 4 | 48 | ||||
| 5 | present | 36.9° | 0.26 | 1.26 | 24.4 | 7.81 | 3.49 | 1 × 3 × 7 | 60 | ||
| Reference [7] | 0.38 | 1.29 | 16.4 | 7.93 | 3.55 | 2 × 4 × 8 | 40 | ||||
| Reference [18] | - | 1.23 | 23.6 | 7.87 | 3.52 | 2 × 6 × 18 | 60 | ||||
| Reference [26] | 0.35 | 1.23 | - | - | - | 1 × 3 × 3 | - | ||||
| Reference [11] | 0.45 | 1.30 | 22.9 | 7.82 | 6.80 | 1 × 3 × 3 | - | ||||
| 11 | present | 50.5° | 0.08 | 0.43 | 32.1 | 8.23 | 2.48 | 1 × 3 × 10 | 60 | ||
| Reference [11] | 0.06 | 0.47 | 21.7 | 8.22 | 4.93 | 1 × 4 × 4 | 80 |
| GB | Unrelaxed | Relaxed | ||
|---|---|---|---|---|
| Clean | With H | Clean | With H | |
| 3(111) | 3.78 | 2.77 | 3.76 | 2.34 |
| 5(210) | 4.00 | 3.41 | 3.59 | 1.82 |
| 11(311) | 4.35 | 3.76 | 4.15 | 3.37 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šesták, P.; Černý, M.; Zhang, Z.; Pokluda, J. Extraordinary Response of H-Charged and H-Free Coherent Grain Boundaries in Nickel to Multiaxial Loading. Crystals 2020, 10, 590. https://doi.org/10.3390/cryst10070590
Šesták P, Černý M, Zhang Z, Pokluda J. Extraordinary Response of H-Charged and H-Free Coherent Grain Boundaries in Nickel to Multiaxial Loading. Crystals. 2020; 10(7):590. https://doi.org/10.3390/cryst10070590
Chicago/Turabian StyleŠesták, Petr, Miroslav Černý, Zhiliang Zhang, and Jaroslav Pokluda. 2020. "Extraordinary Response of H-Charged and H-Free Coherent Grain Boundaries in Nickel to Multiaxial Loading" Crystals 10, no. 7: 590. https://doi.org/10.3390/cryst10070590
APA StyleŠesták, P., Černý, M., Zhang, Z., & Pokluda, J. (2020). Extraordinary Response of H-Charged and H-Free Coherent Grain Boundaries in Nickel to Multiaxial Loading. Crystals, 10(7), 590. https://doi.org/10.3390/cryst10070590