Abstract
The thermal response of a magnetic solid to an applied magnetic field constitutes magnetocaloric effect. The maximum magnetic entropy change (MMEC) is one of the quantitative parameters characterizing this effect, while the magnetic solids exhibiting magnetocaloric effect have great potential in magnetic refrigeration technology as they offer a green solution to the known pollutant-based refrigerants. In order to determine the MMEC of doped manganite and the influence of dopants on the magnetocaloric effect of doped manganite compounds, this work developed a grid search (GS)-based extreme learning machine (ELM) and hybrid gravitational search algorithm (GSA)-based support vector regression (SVR) for estimating the MMEC of doped manganite compounds using ionic radii and crystal lattice parameters as descriptors. Based on the root-mean-square error (RMSE), the developed GSA-SVR-radii model performs better than the existing genetic algorithm (GA)-SVR-ionic model in the literature by 27.09%, while the developed GSA-SVR-crystal model performs better than the existing GA-SVR-lattice model in the literature by 38.34%. Similarly, the developed ELM-GS-crystal model performs better than the existing GA-SVR-ionic model with a performance enhancement of 14.39% and 20.65% using the mean absolute error (MAE) and RMSE, respectively, as performance measuring parameters. The developed models also perform better than the existing models using correlation coefficient as the performance measuring parameter when validated with experimentally measured MMEC. The superior performance of the present models coupled with easy accessibility of the descriptors definitely will facilitate the synthesis of doped manganite compounds with a high magnetocaloric effect without experimental stress.
1. Introduction
Magnetocaloric compounds are of technological and scientific interest mainly because of their significance in magnetic refrigeration, which has shown high potential in replacing the conventional compression–expansion cycle of a gas cooling system [1,2,3,4]. These compounds are significant in magnetic refrigeration technology since they serve as the refrigerants and the major component of the cooling system characterized with lower noise, a high degree of compactness, high cooling efficiency and environmental friendliness as they do not require ozone-depleting gases [5,6]. Before the discovery of manganite-based compounds as a potential source of a high magnetocaloric effect (which is a physical phenomenon that measures the change in internal temperature of a compound when subjected to adiabatic magnetization), gadolinium was among the well-explored elements with significant magnetocaloric effect near room temperature [7,8]. However, magnetocaloric effect can be observed in many compounds, while the application of these compounds in magnetic refrigeration technology is hindered by the appearance of the magnetocaloric effect at relatively high magnetic fields and/or at transition temperatures differing greatly from room temperature. Manganite-based compounds combine many unique features that make them fit well into magnetic refrigeration technology [9]. They demonstrate a high magnetocaloric effect at low applied magnetic fields, relatively cheap elemental compositions, high stability (especially in some corrosive environments) and physical parameters that can be easily tuned through doping mechanisms [5,10,11]. Doping concentration plays a crucial role in altering the magnetocaloric effect as well as the maximum magnetic entropy change (MMEC) of manganite-based compounds, since A-site average ionic radius, ratio of Mn4+ and Mn3+ ions and A-site disorder are strongly affected by the nature as well as the concentration of dopants [12,13,14]. A-site average ionic radius contributes mainly to magnetic properties of doped manganite through an energy bandwidth of electron alteration that is related to the observed double-exchange interaction, while A-site disorder measures A-site ionic distribution variance [15,16]. The present work developed models through which the maximum magnetic entropy change (MMEC) of manganite compounds could be influenced by the introduction of dopants into the parent manganite compound.
The observed physical properties in manganite-based compounds come from strong competition among antiferromagnetic superexchange interactions, ferromagnetic double-exchange interaction and spin–phonon coupling [17,18]. Zener’s double-exchange theory explains the importance of Mn4+ and Mn3+ ions to the ferromagnetic feature of these compounds, while the exhibition of magnetic properties is well captured within electron–phonon interaction described in Jahn–Teller formalism [4]. Doping of sites in the parent manganite compound with divalent alkaline–earth ions, monovalent alkaline or any other transition metals induces distortion in the lattice and changes the Mn4+ and Mn3+ ion network that, in turn, alters the magnetocaloric effect as well as the maximum magnetic entropy change (MMEC) of manganite-based compounds. Identifying the relationship between the nature as well as the concentration of the dopants supports the understanding of their physical properties, while the synthesis of new manganite-based compounds having multifunctional applications becomes possible. Some screening approaches to developing and identifying materials with a large magnetocaloric effect have been proposed in the literature [19], [20]. However, machine learning techniques have been identified as effective and efficient tools for determining the influence of dopants on the physical properties (such as magnetic ordering temperature, relative cooling power and magnetocaloric effect) of doped manganite-based compounds [6,21,22,23,24,25]. The proposed grid search-based extreme learning machine (GS-ELM) and hybrid gravitational search-based support vector regression model the relationship between lattice distortion as well as elemental compositions on the MMEC when dopants are incorporated into the crystal structure of the parent manganite-based compounds.
Support vector regression (SVR) is a type of machine learning technique developed using statistical learning theory [26]. It acquires support vectors linking the descriptors with the desired target at the training phase while the acquired vectors are further validated. The algorithm maintains a high level of precision and accuracy while dealing with many real-life as well as complex problems [27,28,29,30]. The robustness and effectiveness of an SVR-based model have been attributed to its non-convergence to local minima, sound mathematical background and proper tuning of its user-defined hyperparameters [31,32]. As such, the SVR algorithm and its hybrid have been extensively applied to many problems in science and engineering. A gravitational search algorithm (GSA) was used in this research work for SVR hyperparameter optimization. GSA is a population-based optimization algorithm that is capable of navigating potential solutions in the search space using Newtonian mechanical principles [33]. Its fast convergence to a global solution, avoidance of premature convergence and dependence of its convergence on a limited number of parameters contribute to its uniqueness that required its implementation in this work.
The extreme learning machine (ELM) is a computational intelligence algorithm in which a single-hidden-layer feedforward network is trained in a unique way that ensures a very fast speed together with significant computational scalability [34,35,36]. Three different layers are associated with the ELM; these layers include the input layer, the hidden or latent layer and the output layer. The parameters of the hidden layer are generated randomly and kept unchanged throughout the training phase of model development. Another stronghold of the ELM algorithm is the implementation of the least-square method for solving the optimization problem instead of obtaining partial derivatives of model parameters through the chain rule; thus, output weights are obtained analytically [37]. With the stochastic latent layer weights, the ELM still maintains universal approximation strength in acquiring the relationship between descriptors and targets. These unique capacities of the ELM algorithm are explored in the present work for modeling the MMEC of doped manganite compounds using lattice parameters and ionic radii as descriptors.
The results of modeling and simulation of the MMEC of doped manganite compounds show that the developed GSA-SVR-radii model, which employs the ionic radii and the concentrations of dopants as descriptors, performs better than the existing genetic algorithm( GA)-SVR-ionic model [38] in the literature by 27.09% on the basis of the root-mean-square error (RMSE), while the developed GSA-SVR-crystal model, which utilizes crystal lattice parameters of the compound, performs better than the existing GA-SVR-lattice model [38] in the literature by 38.34% using RMSE as a performance measuring parameter. The superior performance demonstrated by the proposed model definitely helps identify the manganite compounds with a high magnetocaloric effect and ultimately hastens the practical implementation of magnetic refrigeration technology.
The remaining part of this manuscript is organized as follows: Section 2 describes the mathematical formulation of the support vector regression algorithm, gravitational search algorithm and extreme learning machine. Section 3 discusses the computational strategies employed for model development. The description of the dataset used for modeling and simulation is also presented in the section. Section 4 presents the results and compares the present work with the existing models. Section 5 concludes the manuscript.
2. Mathematical Formulation of the Proposed Models
The mathematical background and formulation of the proposed techniques are presented in this section. The algorithms described include support vector regression, gravitational search algorithm and extreme learning machine.
2.1. Description of the Support Vector Regression Algorithm
The support vector regression algorithm is a learning computational algorithm that acquires useful information and intricacies linking the descriptors with the desired target so as to ultimately attain excellent generalization [39,40]. The algorithm was first developed using the structural risk minimization inductive principle that aims at minimizing Vapnik–Chervonenkis dimension and empirical risk simultaneously. The algorithm acquires relevant and highly informative patterns from the training set of data and constructs a regression model that governs future predictions. The regression equation can be generalized as presented in Equation (1):
where is the estimated maximum magnetic entropy change; represents the descriptors, which are the crystal lattice parameters and the applied magnetics field for the GSA-SVR-crystal model, whereas it represents the concentration of the dopants, ionic radii and the applied magnetic field for the GSA-SVR-ionic model; is the dot product and is the input pattern space.
Prior to the construction of the regression function in either the ordinary or the high dimensional feature space, the optimization problem depicted in Equation (2) is solved with a special consideration given to the constraints in Equation (3) [41,42,43]:
where represents the Euclidian norm, stands for the measured maximum magnetic entropy change, are the slack variables and is the maximum allowable deviation of all training data points from the measured values.
Deviations of data points from the measured values are penalized or regularized in the SVR algorithm. The parameter C in Equation (2) measures the degree of penalty and is referred to as the penalty factor. In addition, the slack variables are introduced into the constraint equation presented in Equation (3) purposely to eradicate or minimize the possibility of data points falling outside
. Mapping of data points that could not be solved in ordinary space to the high dimensional feature space was done in the present work using the Gaussian kernel function presented in Equation (4):
where represents the kernel option.
The final regression equation after transformation is presented in Equation (5):
where and are the Lagrange multipliers.
The performance of the SVR-based model is strongly influenced by the model hyperparameters which include [44,45,46]. Therefore, in order to develop a robust model that is characterized with a high degree of precision, these hyperparameters must be tuned to optimum values. The hyperparameters are tuned in this work using the gravitational search algorithm.
2.2. Physical Principles of the Gravitational Search Algorithm
The gravitational search algorithm (GSA) is a class of heuristic population-based algorithms employed for solving optimization problems [33]. Its fundamental principle of navigating through a search space of possible solutions is Newtonian mechanical formalism. In this approach, the solution search space is explored and exploited by the agents, which are known as objects in Newtonian description. The interaction of these agents with one another is controlled by the value of their masses as well as gravitational pull [27,47,48]. An agent with heavy mass corresponds to a good or global solution and moves very slowly in the solution space, whereas agents of lighter masses are attracted towards heavy agents. A stepwise description of the algorithm operational principles goes as follows:
Step 1: Agent initialization. For q-number of initial population of agents, initialize the position of the agents randomly. Evaluate the fitness of each of the agents using a defined objective function. The fitness of the agents in this work was evaluated using the root-mean-square error between the measured MMEC and predicted values obtained from objective function implementation. specifies the position of agent where .
Step II: Calculation of agents’ masses. Using the minimum and maximum values of the fitness of the entire population, the mass of each of the agents is computed at the iteration through the implementation of Equations (6) and (7):
where , and represent the fitness of the agent, the minimum fitness of the entire population and the maximum fitness of the entire population, respectively.
Step III: Computation of Newtonian gravitational force. The Newtonian gravitational attraction between the and agents is depicted in Equation (8), where and are defined, respectively, in Equations (9) and (10) [49]:
where , and stand for the Euclidian distance between the k and z agents, the gravitational constant defined as and the random number spanning in the range of 0 to 1, respectively. Similarly, , and represent the active gravitational mass of the agent, the maximum iteration and a small constant value, respectively.
Step IV: Calculation of the acceleration with which each of the agents is navigating. The acceleration of the agents is calculated using Equation (11):
Step V: Calculation of the position and velocity of the agents. Equations (12) and (13) present the expression for calculating the position and velocity of the agents in the population, respectively.
Step VI: Stopping criteria of the algorithm. Steps I to V are repeated until the maximum number of iterations is reached.
2.3. Mathematical Background of the Extreme Learning Machine
The extreme learning machine is a novel learning algorithm of training a single-hidden-layer feedforward neural network [34,50]. The algorithm analytically determines the output weights using the Moore–Penrose generalized inverse method, while the input weights as well as the hidden biases are randomly chosen. Suppose a single-hidden-layer feedforward neural network is to be trained with the aid of number of hidden neurons coupled with the nonlinear activation function and number of training samples so that and (where and represent the number of data points for output and input layers, respectively). The operational principle of the ELM algorithm transforms the nonlinear system to a linear system using the transformation relation presented in Equation (14) [51].
where , is the hidden neuron output with respect to =, = weight vector, linking the hidden neuron to the input neurons, = bias of the hidden neuron, , the output weight matrix
, the weight vector linking the hidden neuron to the output neurons and is the matrix containing the descriptors.
The value of the MMEC of the doped manganite compound was estimated using the least-square method with the minimum norm relation presented in Equation (15) after the implementation of the linearization process of Equation (14):
where = Moore–Penrose generalized inverse of matrix .
3. Dataset Description and Computational Implementation of the Proposed Models
This section describes the computational method employed for the hybridization of the gravitational search algorithm with the support vector regression algorithm. The computational details of the proposed ELM-based model are also presented as well as the description of the dataset. The chemical formula of the manganite compound, whose MMEC the developed models can effectively estimate, is also described and presented.
3.1. Dataset Description and Chemical Formula of the Doped Manganite that Can be Incorporated into the Developed Models
The proposed models in this work were developed using one hundred experimentally measured MMEC of different manganite-based compounds extracted from the literature [7,8,11,15,18,52,53,54,55,56,57,58,59,60,61,62,63,64]. The descriptors to the model are two sets of data. The descriptors to the proposed GSA-SVR-crystal model are the lattice distortions (as measured by the crystal lattice parameters) suffered by the manganite crystal structure due to the introduction of dopants into the parent manganite [54,65,66,67,68,69,70,71,72]. The applied magnetic field is also included as a descriptor. The significance of lattice distortion to magnetic properties of the manganite-based compound can be inferred from the influence of lattice distortion that accompanied doping on the Mn4+ and Mn3+ ion network. Similarly, since ionic radii of the dopants have a strong influence on the magnetic properties of manganite-based compounds, these ionic radii and the concentrations of dopants serve as the descriptors to the developed GSA-SVR-radii model. This model also employs the value of the applied field as a descriptor. The chemical formula that explains the implementation of the proposed GSA-SVR-radii model on manganite-based compounds is presented in Equation (16).
where R and A represent the rare-earth element and alkaline-earth element, respectively, while B and C are any dopant of choice. The concentrations of the dopants are represented by the lower case of the dopant symbols. Implementation of the proposed GSA-SVR-radii model helps in determining the nature and the concentration of dopants that give the desired value of the MMEC, and the outcome of the model can be verified experimentally. The GSA-SVR-radii model is robust in the sense that it can easily incorporate four different dopants including the rare-earth elements at various concentrations. This is advantageous as a variety of dopants can be explored as quickly as possible. During model implementation, the dopant that is absent in the chemical structure is assigned a zero value. Suppose that the model is to be implemented to determine the MMEC of the Pr0.6Ca 0.1Sr 0.3Mn0.8Fe0.2O3 compound; the descriptors are the ionic radii of elements Pr, Ca, Sr and Fe, while a, b and c are 0.1, 0.3 and 0.2, respectively. Table 1 shows the results of statistical analysis conducted on the dataset. This is insightful in determining the content and the nature of the dataset employed for modeling and simulation. The correlation coefficients between the descriptors and the target clearly show an insignificant degree of linear relationship between them. Therefore, the need for nonlinear modeling techniques such as those presented in this work becomes necessary.

Table 1.
Statistical analysis of the dataset.
3.2. Computational Hybridization of the Gravitational Search and Support Vector Regression Algorithms
The computational part of this work was carried out within the MATLAB computing environment. The available data points for modeling and simulation were partitioned into training and testing sets after being randomized to ensure uniformity and prevent uneven distribution of the data points. The hyperparameters of the SVR algorithm optimized using the GSA include the regularization factor, epsilon and kernel option of the best kernel function, while the hyperparameter that controls the hyperplanes was maintained as 1E−7. Step-by-step procedures for the computational hybridization of GSA with the SVR algorithm are detailed as follows:
Step I: Data division. The 100 available data points were divided into training and testing sets in the ratio of 8:2. The descriptors in each of the partitions consisted of nine different descriptors for the GSA-SVR-radii model, while four descriptors were attributed to the GSA-SVR-crystal model. The developed GSA-SVR-radii model employs the ionic radii of the dopants as well as their concentrations, while the developed GSA-SVR-crystal model utilizes the crystal lattice distortion of the manganite-based compound due to the introduction of dopants into the crystal lattice structure of the parent manganite.
Step II: Hyperparameter initialization. The agents were populated within the Newtonian description of the gravitational search algorithm. Each agent encodes the regularization factor, epsilon and kernel option of a chosen function. For K-number of agents in a search space, each agent position is represented as where and represents the current agent position in the Dth dimension. In the present work, the dimension is three since there are three parameters to be optimized.
Step III: Rating of fitness of each of the agents in the population. The fitness of each of the agents was determined using the root-mean-square error (RMSE) between the model estimates and the measured values of the MMEC. The agent in the testing set of the data, which is characterized by the lowest RMSE, has the best fitness, while the agent with the highest RMSE becomes the worst agent in the population.
Step IV: Inertial mass of the agents in the population and gravitational pull computation. The inertial mass is computed using Equations (6) and (7). The Newtonian gravitation pull is computed using Equation (8).
Step V: Computation of acceleration, position and velocity of the agents in the population. The acceleration, position and velocity of each of the agents in the population were computed using Equations (11)–(13), respectively.
Step VI: Stopping condition. After each iteration, Steps II to V are repeated, while the position of each of the agents in the population is updated until the algorithm attains a global solution. The global solution is indicated by a zero value of RMSE or the same value of RMSE for fifty consecutive numbers of iteration.
3.3. Computational Implementation of the Grid Search-Based Extreme Learning Machine
The extreme learning machine is an efficient and robust algorithm that adequately trains a single-hidden-layer feedforward network and ultimately achieves a high degree of precision as well as reduced computational time. The ELM algorithm has one parameter (i.e., the number of hidden nodes) and a nonlinear function that must be tuned and optimized in order to enhance the precision of the algorithm. This parameter and the function are optimized in this work using a grid search (GS) approach. The number of hidden nodes was sought within a specified range for each of the available activation functions. Before the computational implementation of the ELM-GS model, the dataset was partitioned and randomized in a similar manner to the approach used in developing the GSA-SVR models. In this case also, two different models were developed. The developed ELM-GS-radii model uses ionic radii and concentrations of dopants as descriptors similar to the descriptors of the GSA-SVR-radii model, whereas the developed ELM-GS-crystal model employs lattice parameters as descriptors. Of course, all the developed models in this work include the applied magnetic field during magnetization measurement to the descriptors. The details of the computational strategies employed in developing the two ELM-GS-based models are described step by step as follows:
Step I: Data randomization and partition. The datasets used for developing the GSA-SVR-based models were also employed here. This allows a fair comparison between the generalization and predictive strength of the developed models.
Step II: Generation of input weights and biases using pseudorandom number generator. Using the pseudorandom number generator (seeding) in the MATLAB computing environment, input weights and biases were generated. With the Mersenne Twister generator using seed N [rng(N)], these weights and biases were optimized by searching for values of N between 0 to 100 that result in the lowest RMSE between the measured and estimated MMEC. The optimum initial weights and biases were saved and implemented for the rest of the modeling and simulation stages.
Step III: Computation of hidden-layer output matrix . For the selected activation function from the pool of available functions (Sine (sin), sigmoidal (sig), radial basis (radbas), hardlim (hardlim) and triangular basis (tribas) functions), compute the hidden-layer output weights for each of the hidden nodes, which spans between (1,100) using the training set of data.
Step IV: Determination of output weights and computation of the MMEC. Compute the output weights and calculate the MMEC for each of the manganite-based compounds using the Moore–Penrose generalized inverse matrix for each of the hidden nodes in Step III.
Step V: Selection of the best model for each of the activation functions. Using the obtained input weights, biases and output weights for each of the number of nodes, determine the RMSE between the measured MMEC and the estimated values and select the model with the lowest RMSE using the testing set of data. The number of nodes and the activation function corresponding to the best model are also saved.
Step VI: Selection of the overall best model. Repeat Steps III to V and select the overall best model. The input weights, biases, output weights, activation function and the number of nodes corresponding to the best models are saved for future implementation.
4. Results and Discussion
This section discusses the outcome of the research work. The dependence of the convergence of the GSA-SVR-based model on the initial number of agents exploiting and exploring the population is discussed and presented. The comparison between the results of this work and the existing models is also presented in this section.
4.1. Searching for the Optimum Hyperparameters of the Developed Models
The dependence of the convergence of the developed GSA-SVR-radii and GSA-SVR-crystal models to the initial number of agents exploring and exploiting the search space are presented in Figure 1 and Figure 2, respectively. For the convergence of the GSA-SVR–radii model presented in Figure 1, the convergence to local minima was observed when ten, thirty and fifty agents explored the search space, while the model converged to a global solution when the number of agents was increased to seventy. Above this value, no further minimization of the objective function was possible. Similarly, Figure 2 presents the convergence for the GSA-SVR-crystal model that employs the crystal lattice parameters and the applied magnetic field as descriptors. The developed GSA-SVR-crystal model converged to a local solution when ten agents were exploring and exploiting the search space. The global solution was reached by thirty agents, while the increase in the number of initial agents returned the model to a local solution convergence. The optimum values of the SVR hyperparameters for the GSA-SVR-radii and GSA-SVR-crystal models are presented in Table 2. The table also presents the optimum activation functions and the number of hidden nodes for the developed ELM-GS-radii and ELM-GS-crystal models.
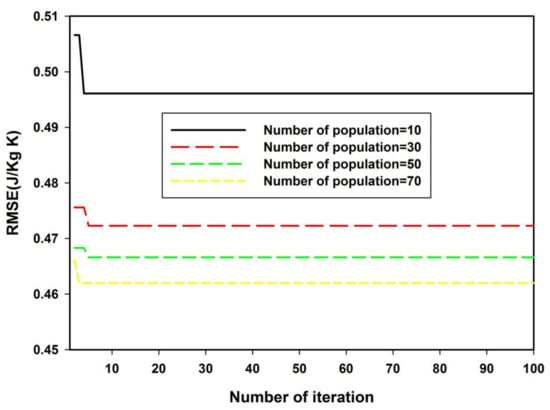
Figure 1.
Dependence of convergence of GSA-SVR-radii model on the density of search space.
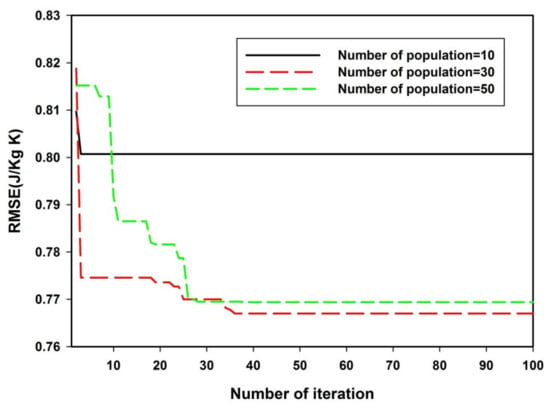
Figure 2.
Dependence of convergence of GSA-SVR-crystal model on the density of search space.

Table 2.
Optimum hyperparameters of support vector regression (SVR)-based models as obtained using a gravitational search algorithm (GSA) and extreme learning machine (ELM)-based models as obtained using grid search (GS).
4.2. Generalization and Predictive Strength Comparison Between the SVR- and ELM-Based Models
The generalization and predictive strengths of the developed models are compared using three different performance measuring parameters, which include correlation coefficient (CC), mean absolute error (MAE) and root-mean-square error (RMSE). Figure 3 and Figure 4 compare the training and testing stages of the GSA-SVR-radii and GSA-SVR crystal models using CC and MAE performance measuring parameters, respectively.
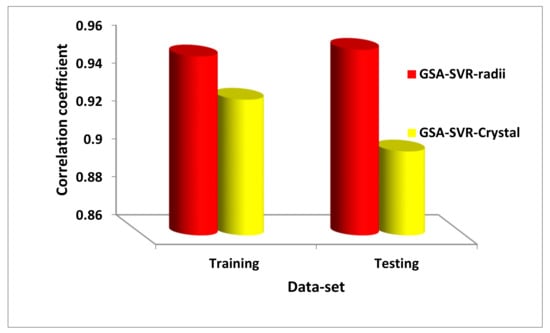
Figure 3.
Comparison between the GSA-SVR-radii and GSA-SVR-Crystal models on the basis of the correlation coefficient.
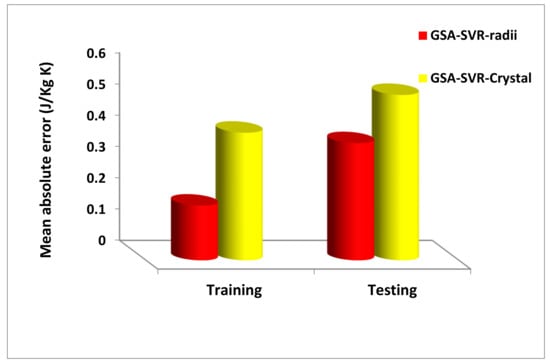
Figure 4.
Comparison between the GSA-SVR-radii and GSA-SVR-crystal models on the basis of the mean absolute error.
The training stage of the GSA-SVR-radii model demonstrates better performance than that of the GSA-SVR-crystal model with a performance improvement of 2.39%, whereas a percentage enhancement of 5.59% was achieved on the testing set of data using CC as the performance measuring parameter.
Using MAE as the yardstick for measuring the generalization and future estimation capacity as presented in Figure 4, the developed GSA-SVR-radii model shows a better performance as compared to the GSA-SVR crystal model with a performance enhancement of 56.86% and 29.04% during the training and testing stages, respectively.
A similar improvement is presented in Figure 5 using RMSE as the performance measuring parameter. The prediction capacity of the developed GSA-SVR-radii model for the training dataset performs better than that of the GSA-SVR-crystal model with a performance improvement of 19.32%. while an improvement of 39.77% was obtained for the testing dataset. It should be noted that the testing stage of the developed GSA-SVR-radii model shows a better performance than the training phase of model development. This shows the robustness and uniqueness of the developed model in generalizing well to an unseen dataset. Another advantage of the developed GSA-SVR-radii model over the developed GSA-SVR-crystal model, aside from a better and excellent performance, is the ease of its descriptors. The descriptors for the developed GSA-SVR-radii model can be easily acquired without any prior experimental measurement, whereas XRD analysis must be performed before extracting the descriptors for the developed GSA-SVR-crystal model. Hence, the developed GSA-SVR-radii model allows pre-lab simulation and ultimately saves experimental time as well as other valuable resources.
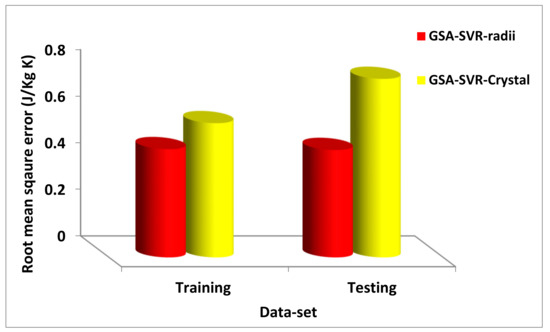
Figure 5.
Comparison between the GSA-SVR-radii and GSA-SVR-crystal models on the basis of the root-mean-square error.
Figure 6 presents the comparison between the ELM-GS-radii and ELM-GS-crystal models at the training and testing stages of model development using correlation coefficient as the measure of performance strength. The developed ELM-GS-crystal model performs better than the ELM-GS-radii model with a performance improvement of 5.29%, whereas, at the validation stage, the developed ELM-GS-radii model performs better than the ELM-GS-crystal model with a performance improvement of 5.07%. The comparison between the models is presented in Figure 7 with the mean absolute error as the performance measuring parameter. A similar trend of performance improvement is observed at the training and testing phases of model development.
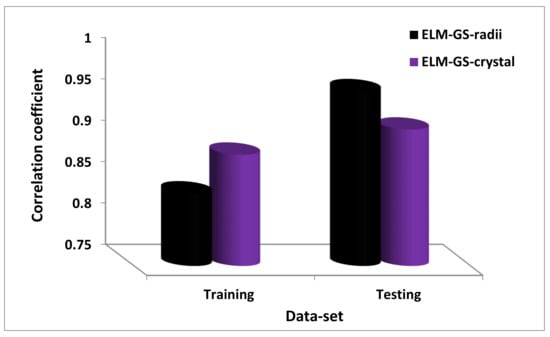
Figure 6.
Comparison between the ELM-GS-radii and ELM-GS-crystal models on the basis of the correlation coefficient.
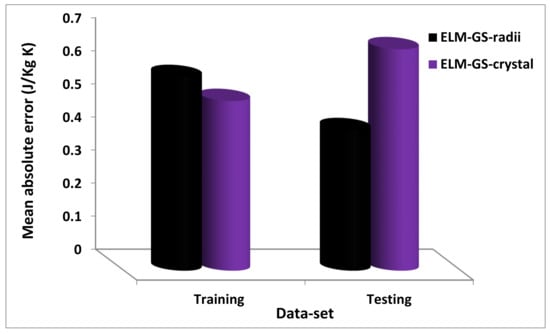
Figure 7.
Comparison between the ELM-GS-radii and ELM-GS-crystal models on the basis of the mean absolute error.
The developed ELM-GS-crystal model shows an improvement of 14.08% as compared to the ELM-GS-radii model at the training stage, whereas the latter performs better than the former with a percentage improvement of 36.44% at the testing stage of model development. In Figure 8, which presents the comparison on the basis of RMSE, the ELM-GS-crystal model shows a percentage improvement of 19.11% over the developed ELM-GS-radii model at the training stage, whereas the ELM-GS-radii model demonstrates a better performance of 39.35% at the testing stage. The actual values of each of the performance measuring parameters at different stages of model development are presented in Table 3. It is worth mentioning that although the developed ELM-GS-crystal model shows a better performance at the training phase, the excellent performance of the ELM-GS-radii model at the testing phase is more meritorious since the testing stage shows the future estimating capacity of the model.
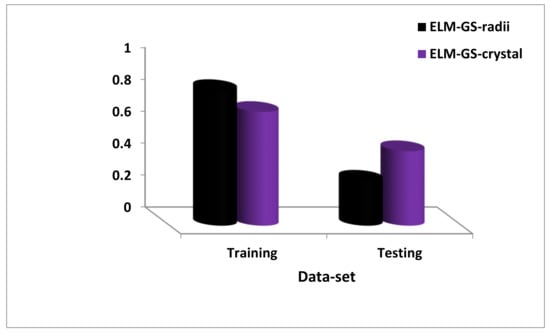
Figure 8.
Comparison between the ELM-GS-radii and ELM-GS-crystal models on the basis of the root-mean-square error.

Table 3.
Performance measuring parameters for the four developed models at different stages of model development.
The correlation cross-plots between the measured and predicted MMEC for training and testing sets of data are preesented in Figure 9 and Figure 10, respectively. The values of the correlation coefficient for each of the developed models are also presented in the cross-plot for easy comparison. A direct impression about the precision and quality of the developed models can be easily inferred from the distribution and the alignment of the data points in the cross-plots.
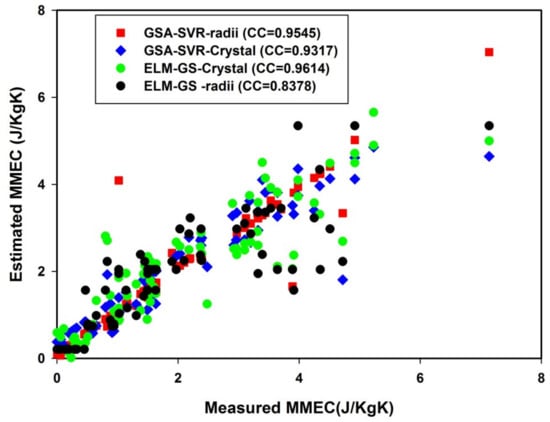
Figure 9.
Correlation cross-plot between the measured and estimated MMEC for all developed models using the training set of data.
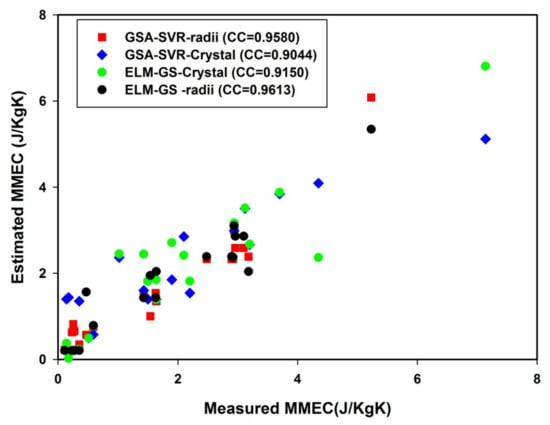
Figure 10.
Correlation cross-plot between the measured and estimated MMEC for all developed models using the testing set of data.
4.3. Superiority of the Present Models as Compared to the Existing Models in the Literature
The generalization and predictive strength of the present models are compared with the existing models using mean absolute error and root-mean-square error metrics. The comparison between the performance of the present and existing models that employ the ionic radii and the concentrations of dopants as descriptors is presented in Figure 11 on the basis of the mean absolute error, while Figure 12 presents the same finding using the root-mean-square error as the performance measuring parameter.
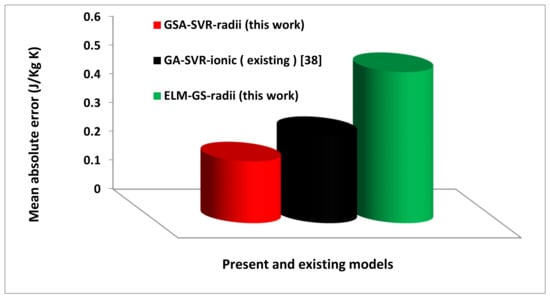
Figure 11.
Comparison between the present and existing ionic radii-based models using the mean absolute error metric.
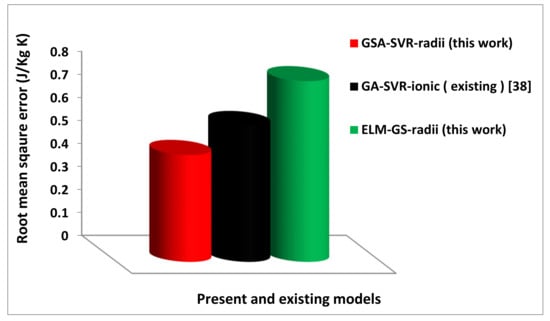
Figure 12.
Comparison between the present and existing ionic radii-based models using the root-mean-square error metric.
The developed GSA-SVR-radii model performs better than the existing GA-SVR-ionic model [38] with a performance improvement of 28.85% as can be observed from Figure 11. The developed GSA-SVR-radii model also performs better than the developed ELM-GS-radii model with a performance of 58.86%. The superior performance demonstrated by the developed GSA-SVR-radii model can be attributed to the uniqueness of the Newtonian-based optimization algorithm in effectively selecting optimum hyperparameters of the SVR algorithm. Following a similar trend, the developed GSA-SVR-radii model performs better than the existing GA-SVR-ionic model [38] and the present ELM-GS-radii model with a performance improvement of 27.09% and 40.85%, respectively, on the basis of RMSE as presented in Figure 12.
Figure 13 and Figure 14 present the comparison between the present and existing models that employ crystal lattice distortions as well as the applied magnetic field as the descriptors. The comparison presented in Figure 13 is based on the mean absolute error, whereas that of Figure 14 is based on the root-mean-square error. Table 4 also presents the actual values of each of the performance measuring parameters for the present and existing models.
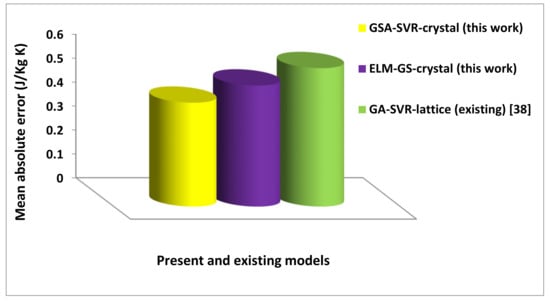
Figure 13.
Comparison between the present and existing crystal lattice distortion-based models using the mean absolute error metric.
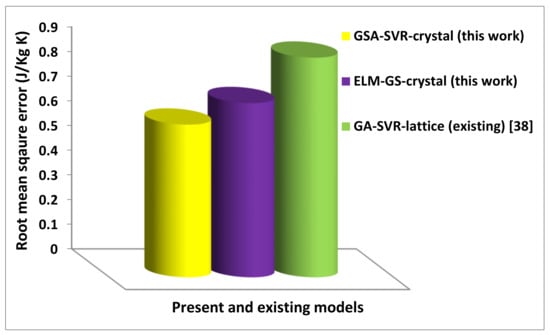
Figure 14.
Comparison between the present and existing crystal lattice distortion-based models using the root-mean-square error metric.

Table 4.
Performance comparison between the present and existing models.
The developed GSA-SVR-crystal model performs better than the existing GA-SVR-lattice model [38] with a performance improvement of 33.35% and 38.34% on the basis of MAE and RMSE, respectively. The developed ELM-GS-crystal model also performs better than the existing GA-SVR-ionic model with a performance enhancement of 14.39% and 20.65% using MAE and RMSE as performance measuring parameters, respectively. The observed precision of the developed crystal lattice distortion-based models over the existing model can be attributed to the strong mathematical background of the developed models as well as the excellent power of hybridization.
4.4. Investigating the Doping Effect of Fe on the Value of the MMEC of the Pr0.6Ca 0.1Sr 0.3Mn 1-xFexO3 Manganite Compound Using the Developed GSA-SVR-Crystal Model
The influence of Fe dopants on the MMEC of the Pr0.6Ca 0.1Sr 0.3Mn 1-xFexO3 manganite compound is presented in Table 5. It was observed that an increase in the concentration of Fe lowers the value of the MMEC. This observation as obtained using the developed GSA-SVR-crystal model conforms to the experimental observation [70]. The effect of the partial substitution of Fe in the Mn site in the Pr0.6Ca 0.1Sr 0.3Mn 1-xFexO3 manganite compound lowers the value of the MMEC because the incorporation of Fe particles modifies the Mn/Fe-O distance and Mn-O-Mn angle, which subsequently leads to a weakening of the double-exchange interaction at the expense of the superexchange interaction [38].

Table 5.
Comparison between the results of the developed GSA-SVR-crystal model and the measured values of the MMEC for different classes of manganite-based compounds.
4.5. Implementation of the Developed Model for Determining the Maximum Magnetic Entropy Change of Different Classes of Doped Manganite
In order to further investigate the generalization and predictive strength of the developed model in determining the MMEC of manganite-based compounds, the developed GSA-SVR-crystal model was employed in determining the MMEC of several classes of manganite-based compounds and the obtained results were compared with the experimental values. The comparison is presented in Table 5. It is worth mentioning that the developed GSA-SVR-crystal model was only supplied with the descriptors, whereas the model implements the support vectors that it acquired during the training phase for its estimation. The results of the developed model agree well with the experimentally measured values. It has been reported that the experimental values of the MMEC suffer from an experimental uncertainty of approximately at least 5% [78] and that this may explain deviations of the results of the developed model from the measured values.
5. Conclusions and Recommendations
This work developed a grid search (GS)-based extreme learning machine (ELM) and hybrid gravitational search algorithm (GSA)-based support vector regression (SVR) for estimating the maximum magnetic entropy change (MMEC) of doped manganite-based compounds. The developed GSA-SVR-radii and ELM-GS-radii models employ ionic radii and concentrations of dopants at a specific value of an applied magnetic field as descriptors, whereas the developed GSA-SVR-crystal and ELM-GS-crystal models utilize the crystal lattice distortions due to the incorporation of dopants into the crystal lattice structure of the parent manganite compound as well as the value of the applied magnetic field as descriptors. The developed models perform better than the existing models in the literature using RMSE and MAE as performance measuring parameters. The better performance of the present models as compared to the existing models can be attributed to the sound mathematical background as well as the intrinsic ability of the models to precisely acquire all the intricacies, information and patterns linking the descriptors with the target. The precision of the developed models offers a green solution to the known pollutant-based refrigerants and opens up ways by which manganite-based compounds of the desired maximum magnetic entropy change can be predicted for possible laboratory fabrication and implementation.
Author Contributions
All authors have read and agreed to the published version of the manuscript. T.O.O. conceived, involved in data curation and wrote the original draft while S.M.I.S. designed the experiment, performed the experiment, analyzed the data, interpreted the data, involved in reviewing and editing. Both authors provided the materials for the experiment.
Funding
This research received no external funding.
Acknowledgments
The support provided by the University of Hafr Al Batin and Adekunle Ajasin University is acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hamdi, R.; Tozri, A.; Dhahri, E.; Bessais, L. Magnetocaloric properties and Landau theory of Dy0.5(Sr1−xCax)0.5MnO3 (0≤ x≤0.3) manganites at cryogenic temperatures. Chem. Phys. Lett. 2017, 680, 94–100. [Google Scholar] [CrossRef]
- Sellami-Jmal, E.; Ezaami, A.; Cheikhrouhou-Koubaa, W.; Cheikhrouhou, A. Investigation on physical properties in lanthanum vacancy of La0.65Ca0.35MnO3 elaborated at high temperature. J. Magn. Magn. Mater. 2018, 465, 762–767. [Google Scholar] [CrossRef]
- Ayadi, F.; Ammar, S.; Nowak, S.; Cheikhrouhou-Koubaa, W.; Regaieg, Y.; Koubaa, M.; Monnier, J.; Sicard, L. Importance of the synthesis and sintering methods on the properties of manganite ceramics: The example of La 0.7 Ca 0.3 MnO 3. J. Alloys Compd. 2018, 759, 52–59. [Google Scholar] [CrossRef]
- Das, K.; Banik, S.; Das, I. Large magnetocaloric effect in geometrically frustrated polycrystalline ErMnO 3 compound at cryogenic temperature. Phys. B Condens. Matter 2018, 533, 46–49. [Google Scholar] [CrossRef]
- Guorui, X..; Wei, H.; Peiqi, C.; Xiaowei, W. Effect of Nd-substitution on the structural, magnetic and magnetocaloric properties of La0.67-xNdxCa0.13Ba0.2MnO3 manganites. J. Magn. Magn. Mater. 2019, 491, 133–142. [Google Scholar]
- Owolabi, T.O.; Akande, K.O.; Olatunji, S.O.; Aldhafferi, N.; Alqahtani, A. Support Vector Regression Ensemble for Effective Modeling of Magnetic Ordering Temperature of Doped Manganite in Magnetic Refrigeration. J. Low Temp. Phys. 2019, 195, 179–201. [Google Scholar] [CrossRef]
- Linh, D.C.; Ha, N.T.; Duc, N.H.; Nam, L.H.G.; Bau, L.V.; An, N.M.; Yu, S.-C.; Tran, D.T. Na-doped La 0.7 Ca 0.3 MnO 3 compounds exhibiting a large magnetocaloric effect near room temperature. Phys. B Condens. Matter 2018, 532, 155–160. [Google Scholar] [CrossRef]
- Das, S.; Roychowdhury, P.; De, S.; Roy, A.; Chatterjee, S.; De, K. Magnetic and electrical transport of the cation-deficient LaMnO 3: Common origin for both Sr-doping and self-doping effects. Phys. B Condens. Matter 2018, 544, 17–22. [Google Scholar] [CrossRef]
- Yen, P.D.H.; Dung, N.T.; Tran, D.T.; Yu, S.-C. Magnetic properties and magnetocaloric effect of Sr-doped Pr0.7Ca0.3MnO3 compounds. Curr. Appl. Phys. 2018, 18, 1280–1288. [Google Scholar] [CrossRef]
- Aziz, F.; Chandra, M.; Das, S.; Prajapat, M.; Mavani, K. Structural and metamagnetic transitions in thin films of Ce-doped Pr0.5Ca0.5MnO3 manganites. Thin Solid Films 2016, 615, 338–344. [Google Scholar] [CrossRef]
- Sudakshina, B.; Arun, B.; Chandrasekhar, K.D.; Yang, H.D.; Vasundhara, M. Structural and magnetic properties of Nd 0.67 Ba 0.33 MnO 3 manganites with partial replacement of Fe and Cu at Mn-site. Phys. B Condens. Matter 2018, 539, 14–20. [Google Scholar] [CrossRef]
- Asmira, N.; Ibrahim, N.; Mohamed, Z.; Yahya, A. Effect of Cr 3+ substitution at Mn-site on electrical and magnetic properties of charge ordered Bi 0.3 Pr 0.3 Ca 0.4 MnO 3 manganites. Phys. B Condens. Matter 2018, 544, 34–46. [Google Scholar] [CrossRef]
- Kataria, B.; Solanki, P.; Pandya, D.; Solanki, P.; Shah, N. Role of antimony in the charge transport mechanisms for La 0.67 Ca 0.33 Mn 1–x Sb x O 3 manganites. Phys. B Condens. Matter 2018, 541, 43–49. [Google Scholar] [CrossRef]
- Poojary, T.; Babu, P.; Sanil, T.; Daivajna, M.D. Effect of gadolinium dopant on structural, magneto-transport, magnetic and thermo-power of Pr 0.8 Sr 0.2 MnO 3. Solid State Commun. 2018, 275, 35–42. [Google Scholar] [CrossRef]
- Makni-Chakroun, J.; M’Nassri, R.; Cheikhrouhou-Koubaa, W.; Koubaa, M.; Chniba-Boudjada, N.; Cheikhrouhou, A. Effect of A-site deficiency on investigation of structural, magnetic and magnetocaloric behaviors for (LaSr)-lacunar manganites. Chem. Phys. Lett. 2018, 707, 61–70. [Google Scholar] [CrossRef]
- Akça, G.; Çetin, S.K.; Güneş, M.; Ekicibil, A. Magnetocaloric properties of (La1−xPrx)0.85K0.15MnO3 (x=0.0, 0.1, 0.3 and 0.5) perovskite manganites. Ceram. Int. 2016, 3, 3–10. [Google Scholar] [CrossRef]
- Selmi, A.; M’Nassri, R.; Cheikhrouhou-Koubaa, W.; Boudjada, N.C.; Cheikhrouhou, A. Effects of partial Mn-substitution on magnetic and magnetocaloric properties in Pr0.7Ca0.3Mn0.95X0.05O3 (Cr, Ni, Co and Fe) manganites. J. Alloys Compd. 2015, 619, 627–633. [Google Scholar] [CrossRef]
- Vadnala, S.; Asthana, S. Magnetocaloric effect and critical field analysis in Eu substituted La0.7-xEuxSr0.3MnO3(x = 0.0, 0.1, 0.2, 0.3) manganites. J. Magn. Magn. Mater. 2018, 446, 68–79. [Google Scholar] [CrossRef]
- Bocarsly, J.D.; Levin, E.E.; Garcia, C.A.C.; Schwennicke, K.; Wilson, S.D.; Seshadri, R. A Simple Computational Proxy for Screening Magnetocaloric Compounds. Chem. Mater. 2017, 29, 1613–1622. [Google Scholar] [CrossRef]
- Zarkevich, N.; Johnson, D.D. Reliable thermodynamic estimators for screening caloric materials. J. Alloys Compd. 2019, 802, 712–722. [Google Scholar] [CrossRef]
- Owolabi, T.; Akande, K.O.; Olatunji, S.O.; Alqahtani, A.; Aldhafferi, N. Estimation of Curie temperature of manganite-based materials for magnetic refrigeration application using hybrid gravitational based support vector regression. AIP Adv. 2016, 6, 105009. [Google Scholar] [CrossRef]
- Owolabi, T.; Oloore, L.E.; Akande, K.O.; Olatunji, S.O. Modeling of magnetic cooling power of manganite-based materials using computational intelligence approach. Neural Comput. Appl. 2017, 31, 1291–1298. [Google Scholar] [CrossRef]
- Owolabi, T.; Akande, K.O.; Olatunji, S.O.; Alqahtani, A.; Aldhafferi, N. Incorporation of GSA in SBLLM-based neural network for enhanced estimation of magnetic ordering temperature of manganite. J. Intell. Fuzzy Syst. 2017, 33, 1225–1233. [Google Scholar] [CrossRef]
- Owolabi, T.; Akande, K.O.; Olatunji, S.O.; Alqahtani, A.; Aldhafferid, N. Modeling of Curie temperature of manganite for magnetic refrigeration application using manual search and hybrid gravitational-based support vector regression. Soft Comput. 2017, 22, 3023–3032. [Google Scholar] [CrossRef]
- Owolabi, T.; Akande, K.O.; Olatunji, S.O.; Aldhafferi, N.; Alqahtani, A. Ensemble-Based Support Vector Regression with Gravitational Search Algorithm Optimization for Estimating Magnetic Relative Cooling Power of Manganite Refrigerant in Magnetic Refrigeration Application. J. Supercond. Nov. Magn. 2018, 32, 2107–2118. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory; Wiley-Interscience: New York, NY, USA, 1998. [Google Scholar]
- Oloore, L.; Owolabi, T.; Fayose, S.; Adegoke, M.; Akande, K.; Olatunji, S. Modeling of semiconductors refractive indices using hybrid chemometric model. Model. Meas. Control. A 2018, 91, 95–103. [Google Scholar] [CrossRef]
- Owolabi, T.; Akande, K.O.; Olatunji, S.O. Estimation of average surface energies of transition metal nitrides using computational intelligence technique. Soft Comput. 2016, 21, 6175–6182. [Google Scholar] [CrossRef]
- Zhang, H.-R.; Zhang, Y.; Dai, D.-B.; Cao, M.; Shen, W.-F. Modelling and optimization of the superconducting transition temperature. Mater. Des. 2016, 92, 371–377. [Google Scholar] [CrossRef]
- Cai, C.; Xiao, T.; Tang, J.; Huang, S. Analysis of process parameters in the laser deposition of YBa2Cu3O7 superconducting films by using SVR. Phys. C Supercond. 2013, 493, 100–103. [Google Scholar] [CrossRef]
- Motamedi, S.; Shamshirband, S.; Hashim, R.; Petković, D.; Roy, C. RETRACTED: Estimating unconfined compressive strength of cockle shell–cement–sand mixtures using soft computing methodologies. Eng. Struct. 2015, 98, 49–58. [Google Scholar] [CrossRef]
- Behnood, A.; Verian, K.P.; Modiri-Gharehveran, M. Evaluation of the splitting tensile strength in plain and steel fiber-reinforced concrete based on the compressive strength. Constr. Build. Mater. 2015, 98, 519–529. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Yan, C.; Qi, J.; Ma, J.; Tang, H.; Zhang, T.; Li, H. Determination of carbon and sulfur content in coal by laser induced breakdown spectroscopy combined with kernel-based extreme learning machine. Chemom. Intell. Lab. Syst. 2017, 167, 226–231. [Google Scholar] [CrossRef]
- Owolabi, T.; Gondal, M. Development of hybrid extreme learning machine based chemo-metrics for precise quantitative analysis of LIBS spectra using internal reference pre-processing method. Anal. Chim. Acta 2018, 1030, 33–41. [Google Scholar] [CrossRef]
- Wang, Y.G.; Cao, F.; Yuan, Y. A study on effectiveness of extreme learning machine. Neurocomputing 2011, 74, 2483–2490. [Google Scholar] [CrossRef]
- Owolabi, T. Modeling the magnetocaloric effect of manganite using hybrid genetic and support vector regression algorithms. Phys. Lett. A 2019, 383, 1782–1790. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the 5th Annual ACM Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Basak, D.; Pal, S.; Patranabis, D.C. Support Vector Regression. Neural Inf. Process. Lett. Rev. 2007, 11, 203–224. [Google Scholar]
- Peng, J.; Li, L. Support vector regression in sum space for multivariate calibration. Chemom. Intell. Lab. Syst. 2014, 130, 14–19. [Google Scholar] [CrossRef]
- Aldhafferi, N.; Owolabi, T.O.; Akande, K.O.; Olatunji, S.O.; Alqahtani, A. Support vector regression approach of modeling the superconducting transition temperature of borocarbide-based superconductors. ARPN J. Eng. Appl. Sci. 2018, 13, 1900–1905. [Google Scholar]
- Owolabi, T.; Akande, K.O.; Olatunji, S.O. Estimation of surface energies of hexagonal close packed metals using computational intelligence technique. Appl. Soft Comput. 2015, 31, 360–368. [Google Scholar] [CrossRef]
- Owolabi, T.; Suleiman, M.A.; Adeyemo, H.; Akande, K.O.; Alhiyafi, J.; Olatunji, S.O. Estimation of minimum ignition energy of explosive chemicals using gravitational search algorithm based support vector regression. J. Loss Prev. Process. Ind. 2019, 57, 156–163. [Google Scholar] [CrossRef]
- Adeyemo, H.B.; Owolabi, T.O.; Suleiman, M.A.; Akande, A.J.; Fayose, S.; Olatuji, S.O. Heliyon Hybrid chemometric approach for estimating the heat of detonation of aromatic energetic compounds. Heliyon 2019, 5, 1–8.
- Owolabi, T. Determination of the Velocity of Detonation of Primary Explosives Using Genetically Optimized Support Vector Regression. Propellants Explos. Pyrotech. 2019, 1–12. [Google Scholar] [CrossRef]
- Yildiz, B.S.; Lekesiz, H.; Yildiz, A.R.; Yıldız, B.S. Structural design of vehicle components using gravitational search and charged system search algorithms. Mater. Test. 2016, 58, 79–81. [Google Scholar] [CrossRef]
- Sabri, N.M.; Puteh, M.; Mahmood, M.R. A review of gravitational search algorithm. Int. J. Adv. Soft Comput. Appl. 2013, 5. [Google Scholar]
- Owolabi, T.; Gondal, M.A. A hybrid intelligent scheme for estimating band gap of doped titanium dioxide semiconductor using crystal lattice distortion. Comput. Mater. Sci. 2017, 137, 249–256. [Google Scholar] [CrossRef]
- Huang, G.-B.; Chen, L. Convex incremental extreme learning machine. Neurocomputing 2007, 70, 3056–3062. [Google Scholar] [CrossRef]
- Owolabi, T.; Gondal, M.A. Quantitative analysis of LIBS spectra using hybrid chemometric models through fusion of extreme learning machines and support vector regression. J. Intell. Fuzzy Syst. 2018, 1–10. [Google Scholar] [CrossRef]
- ElGhoul, A.; Krichene, A.; Boudjada, N.C.; Boujelben, W. Rare earth effect on structural, magnetic and magnetocaloric properties of La0.75Ln0.05Sr0.2MnO3 manganites. Ceram. Int. 2018, 44, 12723–12730. [Google Scholar] [CrossRef]
- Koubaa, M.; Regaieg, Y.; Koubaa, W.C.; Cheikhrouhou, A.; Ammar-Merah, S.; Herbst, F. Magnetic and magnetocaloric properties of lanthanum manganites with monovalent elements doping at A-site. J. Magn. Magn. Mater. 2011, 323, 252–257. [Google Scholar] [CrossRef]
- Nedelko, N.; Lewińska, S.; Pashchenko, A.; Radelytskyi, I.; Diduszko, R.; Zubov, É.E.; Lisowski, W.; Sobczak, J.; Dyakonov, K.; Ślawska-Waniewska, A.; et al. Magnetic properties and magnetocaloric effect in La0.7Sr0.3−xBixMnO3 manganites. J. Alloys Compd. 2015, 640, 433–439. [Google Scholar] [CrossRef]
- Arun, B.; Athira, M.; Akshay, V.R.; Sudakshina, B.; Mutta, G.R.; Vasundhara, M. Investigation on the structural, magnetic and magnetocaloric properties of nanocrystalline Pr-deficient Pr1−xSrxMnO3−δmanganites. J. Magn. Magn. Mater. 2018, 448, 322–331. [Google Scholar] [CrossRef]
- Saleh, J.A.; Sarsari, I.A.; Kameli, P.; Salamati, H. Influence of Al-doping on the structural, magnetic, and electrical properties of La0.8Ba0.2Mn1−xAlxO3(0 ≤ x ≤ 0.25) manganites. J. Magn. Magn. Mater. 2018, 465, 339–347. [Google Scholar] [CrossRef]
- Choudhary, Y.; Mangavati, S.; Patil, S.; Rao, A.; Nagaraja, B.; Thomas, R.; Okram, G.; Kini, S.G. Effect of rare-earth substitution at La-site on structural, electrical and thermoelectric properties of La0.7−xRExSr0.3MnO3 compounds (x = 0, 0.2, 0.3; RE = Eu, Gd, Y). J. Magn. Magn. Mater. 2018, 451, 110–120. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, W.; Zhou, K.; Yan, J. Effect of Cu doping on the structural, magnetic and magnetocaloric properties of La0.7Sr0.25Na0.05Mn1−xCuxO3 manganites. Ceram. Int. 2018, 44, 2797–2802. [Google Scholar] [CrossRef]
- Ben Khlifa, H.; Othmani, S.; Chaaba, I.; Tarhouni, S.; Cheikhrouhou-Koubaa, W.; Koubaa, M.; Cheikhrouhou, A.; Hlil, E. Effect of K-doping on the structural, magnetic and magnetocaloric properties of Pr0.8Na0.2–K MnO3 (0 ≤ x ≤ 0.15) manganites. J. Alloys Compd. 2016, 680, 388–396. [Google Scholar] [CrossRef]
- Iqbal, M.; Khan, M.N.; Khan, A.A. Structural, magnetic, magnetocaloric and critical behavior studies in the vicinity of the paramagnetic to ferromagnetic phase transition temperature in LaMnO3+δcompound. J. Magn. Magn. Mater. 2018, 465, 670–677. [Google Scholar] [CrossRef]
- Snini, K.; Ben Jemaa, F.; Mohamed, E.; Hlil, E. Structural, magnetic and magnetocaloric investigations in Pr0.67Ba0.22Sr0.11Mn1-xFexO3 (0 ≤ x ≤ 0.15) manganite oxide. J. Alloys Compd. 2018, 739, 948–954. [Google Scholar] [CrossRef]
- Tejaswini, B.P.; Daivajna, M.D. Thrupthi Structural, electrical, magnetic and thermal properties of Pr0.8-xDyxSr0.2MnO3 with (x = 0, 0.2 and 0.25). J. Alloys Compd. 2018, 741, 97–105. [Google Scholar] [CrossRef]
- Hira, U.; Sher, F. Structural, magnetic and high-temperature thermoelectric properties of La0.4Bi0.4Ca0.2Mn1−Co O3 (0 ≤ x ≤ 0.3) perovskites. J. Magn. Magn. Mater. 2018, 452, 64–72. [Google Scholar] [CrossRef]
- Elyana, E.; Mohamed, Z.; Kamil, S.; Supardan, S.; Chen, S.; Yahya, A. Revival of ferromagnetic behavior in charge-ordered Pr0.75Na0.25MnO3 manganite by ruthenium doping at Mn site and its MR effect. J. Solid State Chem. 2018, 258, 191–200. [Google Scholar] [CrossRef]
- Ghodhbane, S.; Tka, E.; Dhahri, J.; Hlil, E. A large magnetic entropy change near room temperature in La0.8Ba0.1Ca0.1Mn0.97Fe0.03O3 perovskite. J. Alloys Compd. 2014, 600, 172–177. [Google Scholar] [CrossRef]
- Selmi, A.; M’Nassri, R.; Cheikhrouhou-Koubaa, W.; Boudjada, N.C.; Cheikhrouhou, A. Influence of transition metal doping (Fe, Co, Ni and Cr) on magnetic and magnetocaloric properties of Pr0.7Ca0.3MnO3 manganites. Ceram. Int. 2015, 41, 10177–10184. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, J. Magnetic entropy change in perovskite manganites La0.7A0.3MnO3 La0.7A0.3Mn0.9Cr0.1O3 (A = Sr, Ba, Pb) and Banerjee criteria on phase transition. Solid State Sci. 2013, 18, 36–41. [Google Scholar] [CrossRef]
- Selmi, A.; M’Nassri, R.; Cheikhrouhou-Koubaa, W.; Boudjada, N.C.; Cheikhrouhou, A. The effect of Co doping on the magnetic and magnetocaloric properties of Pr0.7Ca0.3Mn1−xCoxO3 manganites. Ceram. Int. 2015, 41, 7723–7728. [Google Scholar] [CrossRef]
- Oumezzine, E.; Hcini, S.; Hlil, E.-K.; Dhahri, E.; Oumezzine, M. Effect of Ni-doping on structural, magnetic and magnetocaloric properties of La 0.6 Pr 0.1 Ba 0.3 Mn 1− x Ni x O 3 nanocrystalline manganites synthesized by Pechini sol–gel method. J. Alloys Compd. 2014, 615, 553–560. [Google Scholar] [CrossRef]
- Mahjoub, S.; Baazaoui, M.; M’Nassri, R.; Rahmouni, H.; Boudjada, N.C.; Oumezzine, M. Effect of iron substitution on the structural, magnetic and magnetocaloric properties of Pr0.6Ca0.1Sr0.3Mn1−xFexO3 (0 ≤ x ≤ 0.075) manganites. J. Alloys Compd. 2014, 608, 191–196. [Google Scholar] [CrossRef]
- Mleiki, A.; Othmani, S.; Cheikhrouhou-Koubaa, W.; Koubaa, A.; Cheikhrouhou, A.; Hlil, E.K. Effect of praseodymium doping on the structural, magnetic and magnetocaloric properties of Sm0.55Sr0.45MnO3 manganite. J. Alloys Compd. 2015, 645, 559–565. [Google Scholar] [CrossRef]
- Kossi, S.E.; Ghodhbane, S.; Dhahri, J.; Hlil, E.K. The impact of disorder on magnetocaloric properties in Ti-doped manganites of La0.7Sr0.25Na0.05Mn(1-x)TixO3 (0≤x ≤0.2). J. Magn. Magn. Mater. 2015, 395, 134–142. [Google Scholar] [CrossRef]
- Taboada-Moreno, C.; Jesús, F.S.-D.; Pedro-García, F.; Cortés-Escobedo, C.; Betancourt-Cantera, J.; Ramírez-Cardona, M.; Bolarín-Miró, A. Large magnetocaloric effect near to room temperature in Sr doped La0.7Ca0.3MnO3. J. Magn. Magn. Mater. 2020, 496, 165887. [Google Scholar] [CrossRef]
- Xiao, G.; He, W.; Yang, T.; Huang, G.; Wang, T.; Huang, J. Effect of Co-doping on structural, magnetic and magnetocaloric properties of La 0.67 Ca 0.13 Ba 0.2 Mn 1-x Co x O 3 (x = 0, 0.02, 0.04, 0.06, 0.08, 0.1) manganites. Curr. Appl. Phys. 2019, 19, 424–435. [Google Scholar] [CrossRef]
- Bouzaiene, E.; Dhahri, A.; Dhahri, J.; Hlil, E.; Bajahzar, A. Effect of A-site-substitution on structural, magnetic and magnetocaloric properties in La0.7Sr0.3 Mn0.9Cu0.1O3 manganite. J. Magn. Magn. Mater. 2019, 491, 165540. [Google Scholar] [CrossRef]
- Hassayoun, O.; Baazaoui, M.; Laouyenne, M.; Hosni, F.; Hlil, E.; Oumezzine, M.; Farah, K. Magnetocaloric effect and electron paramagnetic resonance studies of the transition from ferromagnetic to paramagnetic in La0.8Na0.2Mn1-xNixO3 (0≤x≤0.06). J. Phys. Chem. Solids 2019, 135, 109058. [Google Scholar] [CrossRef]
- Mahjoub, S.; M’Nassri, R.; Baazaoui, M.; Hlil, E.; Oumezzine, M. Tuning magnetic and magnetocaloric properties around room temperature via chromium substitution in La0.65Nd0.05Ba0.3MnO3 system. J. Magn. Magn. Mater. 2019, 481, 29–38. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A. Magnetocaloric effect from indirect measurements: Magnetization and heat capacity. J. Appl. Phys. 1999, 565. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).