Intersubband Transition Engineering in the Conduction Band of Asymmetric Coupled Ge/SiGe Quantum Wells
Abstract
1. Introduction
2. Materials and Methods
3. Results
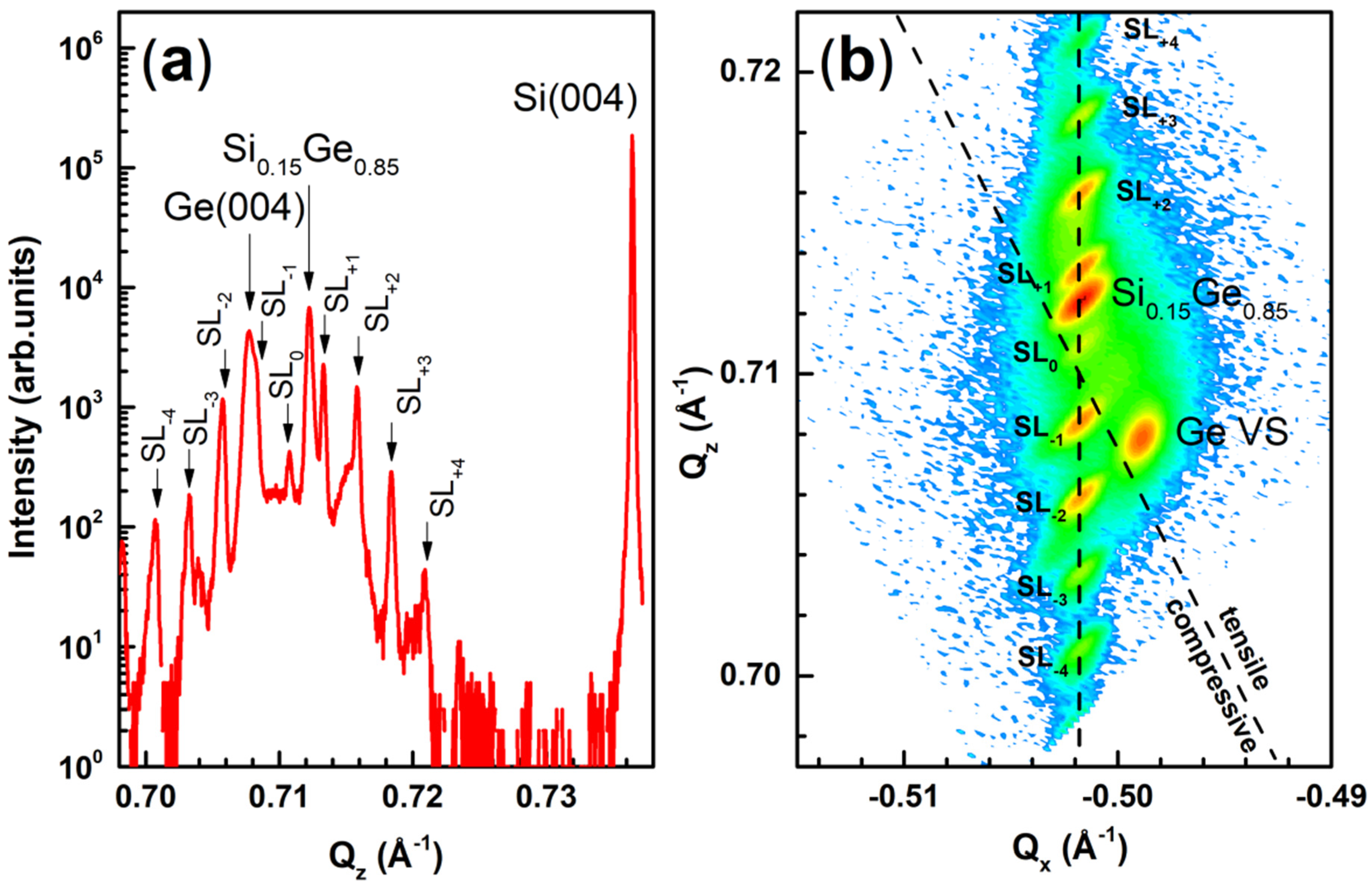
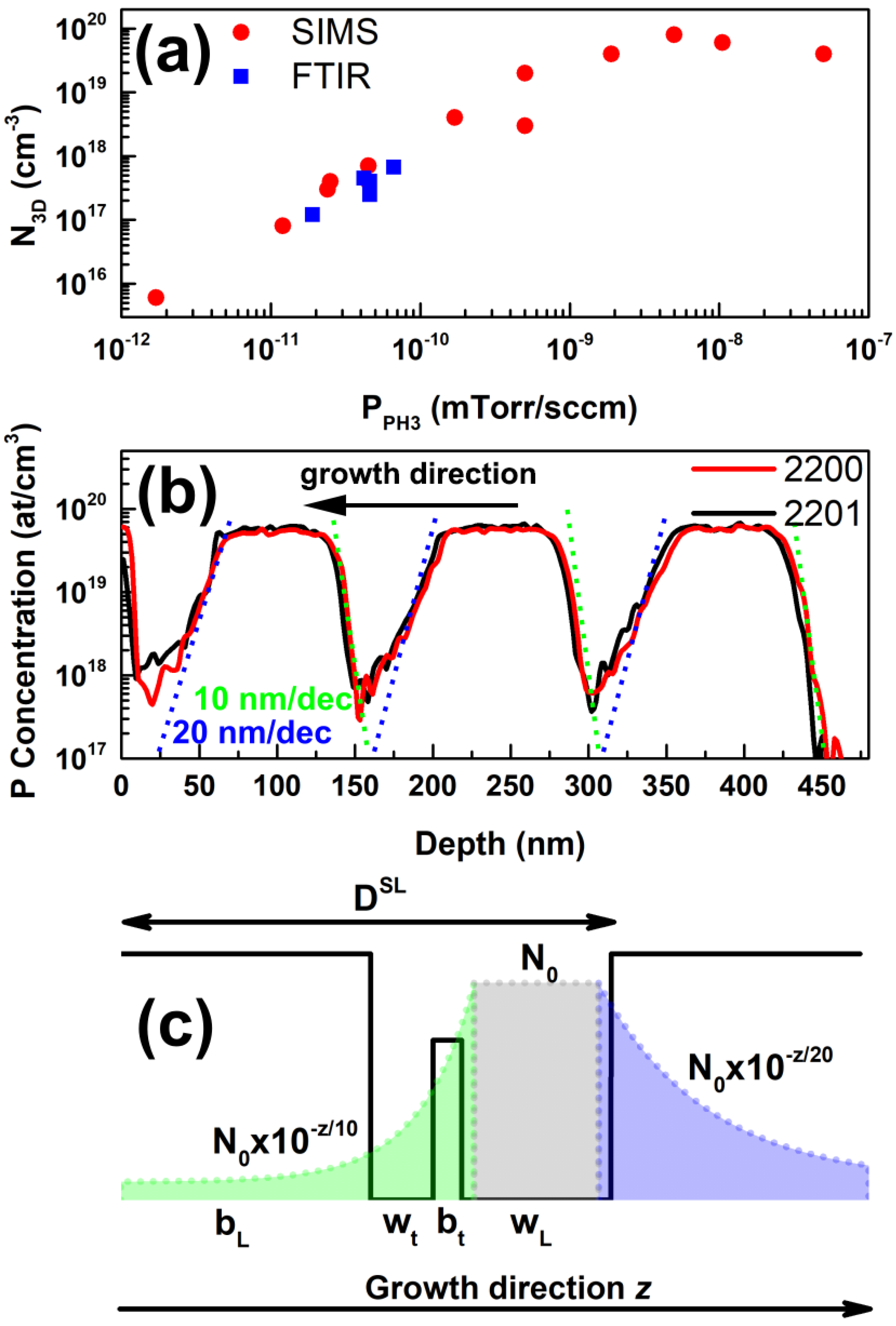
3.1. Structural Characterization
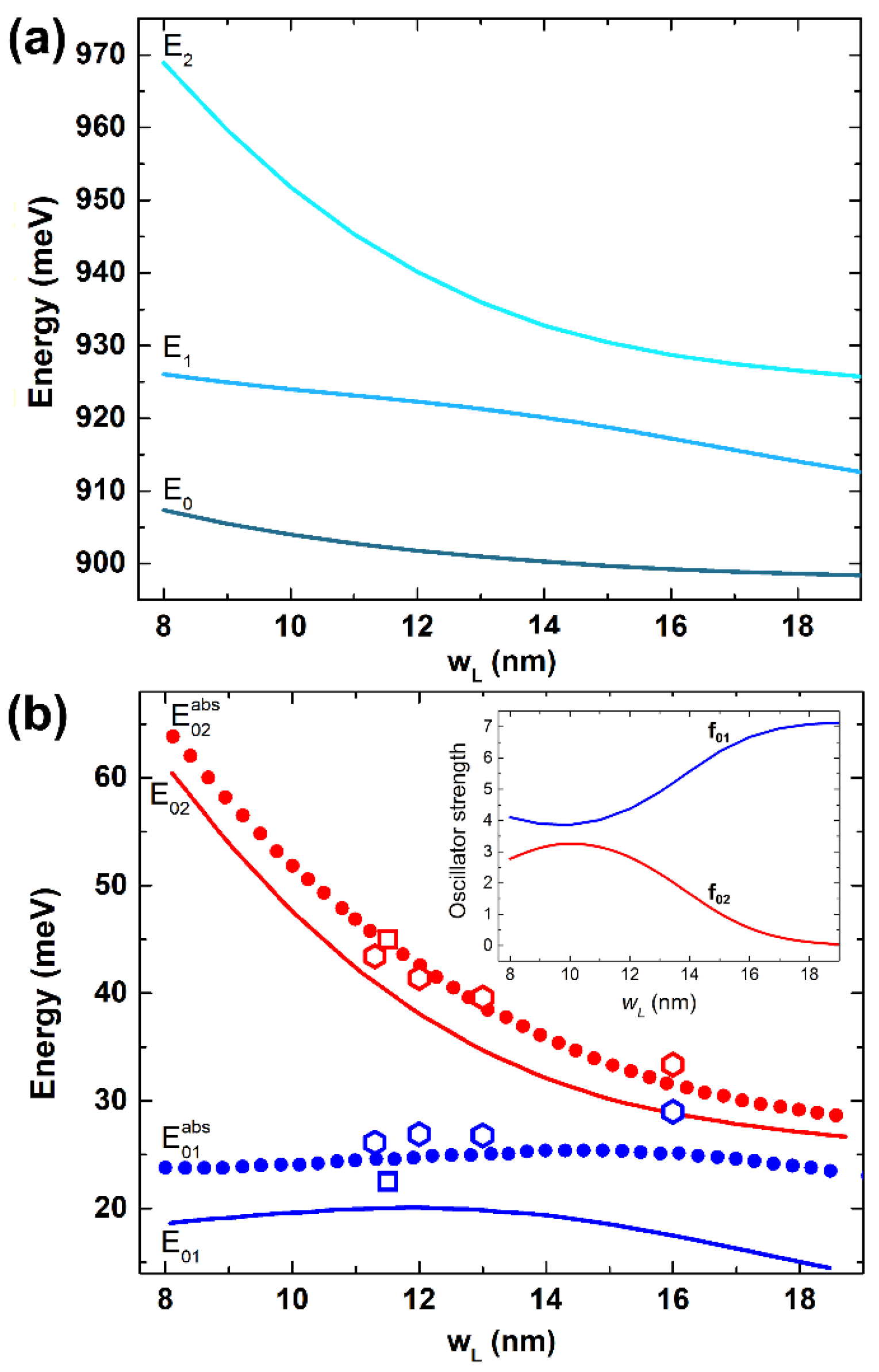
3.2. Optical Absorption Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Bastard, G. Wave Mechanics Applied to Semiconductor Heterostructures; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Fox, M.; Ispasoiu, R. Quantum Wells, Superlattices, and Band-Gap Engineering. In Springer Handbook of Electronic and Photonic Materials; Kasap, S., Capper, P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; p. 1. [Google Scholar] [CrossRef]
- Barnham, K.W.J.; Ballard, I.; Connolly, J.P.; Ekins-Daukes, N.J.; Kluftinger, B.G.; Nelson, J.; Rohr, C. Quantum well solar cells. Phys. E Low Dimens. Syst. Nanostructures 2002, 14, 27–36. [Google Scholar] [CrossRef]
- Almosni, S.; Delamarre, A.; Jehl, Z.; Suchet, D.; Cojocaru, L.; Giteau, M.; Behaghel, B.; Julian, A.; Ibrahim, C.; Tatry, L.; et al. Material challenges for solar cells in the twenty-first century: Directions in emerging technologies. Sci. Technol. Adv. Mater. 2018, 19, 336–369. [Google Scholar] [CrossRef] [PubMed]
- Welser, R.E.; Polly, S.J.; Kacharia, M.; Fedorenko, A.; Sood, A.K.; Hubbard, S.M. Design and Demonstration of High-Efficiency Quantum Well Solar Cells Employing Thin Strained Superlattices. Sci. Rep. 2019, 9, 13955. [Google Scholar] [CrossRef] [PubMed]
- Köhler, R.; Tredicucci, A.; Beltram, F.; Beere, H.E.; Linfield, E.H.; Davies, A.G.; Ritchie, D.A.; Iotti, R.C.; Rossi, F. Terahertz semiconductor-heterostructure laser. Nature 2002, 417, 156–159. [Google Scholar] [CrossRef] [PubMed]
- Williams, B.S. Terahertz quantum-cascade lasers. Nat. Photonics 2007, 1, 517–525. [Google Scholar] [CrossRef]
- Vitiello, M.S.; Scalari, G.; Williams, B.; De Natale, P. Quantum cascade lasers: 20 years of challenges. Opt. Express 2015, 23, 5167–5182. [Google Scholar] [CrossRef]
- Giorgioni, A.; Paleari, S.; Cecchi, S.; Vitiello, E.; Grilli, E.; Isella, G.; Jantsch, W.; Fanciulli, M.; Pezzoli, F. Strong confinement-induced engineering of the g factor and lifetime of conduction electron spins in Ge quantum wells. Nat. Commun. 2016, 7, 13886. [Google Scholar] [CrossRef]
- Hendrickx, N.W.; Franke, D.P.; Sammak, A.; Scappucci, G.; Veldhorst, M. Fast two-qubit logic with holes in germanium. Nature 2020, 577, 487–491. [Google Scholar] [CrossRef]
- Faist, J.; Capasso, F.; Sivco, D.L.; Sirtori, C.; Hutchinson, A.L.; Cho, A.Y. Quantum Cascade Laser. Science 1994, 264, 553. [Google Scholar] [CrossRef]
- Gauthier-Lafaye, O.; Julien, F.H.; Cabaret, S.; Lourtioz, J.M.; Strasser, G.; Gornik, E.; Helm, M.; Bois, P. High-power GaAs/AlGaAs quantum fountain unipolar laser emitting at 14.5 μm with 2.5% tunability. Appl. Phys. Lett. 1999, 74, 1537–1539. [Google Scholar] [CrossRef]
- Paul, D.J. The progress towards terahertz quantum cascade lasers on silicon substrates. Laser Photonics Rev. 2010, 4, 610–632. [Google Scholar] [CrossRef]
- Grange, T.; Stark, D.; Scalari, G.; Faist, J.; Persichetti, L.; Di Gaspare, L.; De Seta, M.; Ortolani, M.; Paul, D.J.; Capellini, G.; et al. Room temperature operation of n-type Ge/SiGe terahertz quantum cascade lasers predicted by non-equilibrium Green’s functions. Appl. Phys. Lett. 2019, 114, 111102. [Google Scholar] [CrossRef]
- Sabbagh, D.; Schmidt, J.; Winnerl, S.; Helm, M.; Di Gaspare, L.; De Seta, M.; Virgilio, M.; Ortolani, M. Electron Dynamics in Silicon–Germanium Terahertz Quantum Fountain Structures. ACS Photonics 2016, 3, 403–414. [Google Scholar] [CrossRef]
- Ciano, C.; Virgilio, M.; Bagolini, L.; Baldassarre, L.; Pashkin, A.; Helm, M.; Montanari, M.; Persichetti, L.; Di Gaspare, L.; Capellini, G.; et al. Terahertz Absorption-Saturation and Emission from Electron-doped Germanium Quantum Wells. Opt. Express 2020, 28, 7245–7258. [Google Scholar] [CrossRef]
- Sun, G.; Cheng, H.H.; Menéndez, J.; Khurgin, J.B.; Soref, R.A. Strain-free Ge/GeSiSn quantum cascade lasers based on L-valley intersubband transitions. Appl. Phys. Lett. 2007, 90, 251105. [Google Scholar] [CrossRef]
- Sun, G.; Soref, R.A.; Cheng, H.H. Design of a Si-based lattice-matched room-temperature GeSn/GeSiSn multi-quantum-well mid-infrared laser diode. Opt. Express 2010, 18, 19957–19965. [Google Scholar] [CrossRef]
- Virgilio, M.; Ortolani, M.; Teich, M.; Winnerl, S.; Helm, M.; Sabbagh, D.; Capellini, G.; De Seta, M. Combined effect of electron and lattice temperatures on the long intersubband relaxation times of Ge/SixGe1−x quantum wells. Phys. Rev. B 2014, 89, 045311. [Google Scholar] [CrossRef]
- Ciano, C.; Virgilio, M.; Bagolini, L.; Baldassarre, L.; Rossetti, A.; Pashkin, A.; Helm, M.; Montanari, M.; Persichetti, L.; Di Gaspare, L.; et al. Electron Population Dynamics in Optically Pumped Asymmetric Coupled Ge/SiGe Quantum Wells: Experiment and Models. Photonics 2019, 7, 2. [Google Scholar] [CrossRef]
- Ciano, C.; Virgilio, M.; Montanari, M.; Persichetti, L.; Di Gaspare, L.; Ortolani, M.; Baldassarre, L.; Zoellner, M.H.; Skibitzki, O.; Scalari, G.; et al. Control of Electron-State Coupling in Asymmetric Ge/SiGe Quantum Wells. Phys. Rev. Appl. 2019, 11, 014003. [Google Scholar] [CrossRef]
- Driscoll, K.; Paiella, R. Design of n-type silicon-based quantum cascade lasers for terahertz light emission. J. Appl. Phys. 2007, 102, 093103. [Google Scholar] [CrossRef]
- Valavanis, A.; Dinh, T.V.; Lever, L.J.M.; Ikonić, Z.; Kelsall, R.W. Material configurations for $n$-type silicon-based terahertz quantum cascade lasers. Phys. Rev. B 2011, 83, 195321. [Google Scholar] [CrossRef]
- Montanari, M.; Virgilio, M.; Manganelli, C.L.; Zaumseil, P.; Zoellner, M.H.; Hou, Y.; Schubert, M.A.; Persichetti, L.; Di Gaspare, L.; De Seta, M.; et al. Photoluminescence study of interband transitions in few-layer, pseudomorphic, and strain-unbalanced Ge/GeSi multiple quantum wells. Phys. Rev. B 2018, 98, 195310. [Google Scholar] [CrossRef]
- De Seta, M.; Capellini, G.; Ortolani, M.; Virgilio, M.; Grosso, G.; Nicotra, G.; Zaumseil, P. Narrow intersubband transitions in n-type Ge/SiGe multi-quantum wells: Control of the terahertz absorption energy trough the temperature dependent depolarization shift. Nanotechnol 2012, 23, 465708. [Google Scholar] [CrossRef] [PubMed]
- Helm, M. The basic physics of intersubband transitions. In Intersubband Transition in Quantum Wells: Physics and Device Applications I. Semiconductors and Semimetals; Liu, H.C., Ed.; Academic: San Diego, CA, USA, 2000; pp. 1–99. [Google Scholar]
- Busby, Y.; De Seta, M.; Capellini, G.; Evangelisti, F.; Ortolani, M.; Virgilio, M.; Grosso, G.; Pizzi, G.; Calvani, P.; Lupi, S.; et al. Near- and far-infrared absorption and electronic structure of Ge-SiGe multiple quantum wells. Phys. Rev. B 2010, 82, 205317. [Google Scholar] [CrossRef]
- Tersoff, J. Dislocations and strain relief in compositionally graded layers. Appl. Phys. Lett. 1993, 62, 693–695. [Google Scholar] [CrossRef]
- Montalenti, F.; Rovaris, F.; Bergamaschini, R.; Miglio, L.; Salvalaglio, M.; Isella, G.; Isa, F.; Von Känel, H. Dislocation-Free SiGe/Si Heterostructures. Crystals 2018, 8, 257. [Google Scholar] [CrossRef]
- Grange, T.; Mukherjee, S.; Capellini, G.; Montanari, M.; Persichetti, L.; Di Gaspare, L.; Birner, S.; Attiaoui, A.; Moutanabbir, O.; Virgilio, M.; et al. Atomic-scale insights into diffuse heterointerfaces: From three-dimensional roughness analysis to a generalized theory of interface scattering. arXiv 2020, arXiv:2002.00851. [Google Scholar]
- Capellini, G.; De Seta, M.; Zaumseil, P.; Kozlowski, G.; Schroeder, T. High temperature x ray diffraction measurements on Ge/Si(001) heterostructures: A study on the residual tensile strain. J. Appl. Phys. 2012, 111, 073518. [Google Scholar] [CrossRef]
- Virgilio, M.; Sabbagh, D.; Ortolani, M.; Di Gaspare, L.; Capellini, G.; De Seta, M. Physical mechanisms of intersubband-absorption linewidth broadening in s-Ge/SiGe quantum wells. Phys. Rev. B 2014, 90, 155420. [Google Scholar] [CrossRef]
- Among our samples, the lowest interwell interaction is obtained in 2224, which features the thickest tunnel barrier, and where, consistently with wL = 12.0 nm, we observe the strongest amplitude of L1 in the narrow well, see Figure 4m.


| Sample | wL (nm) | bt (nm) | xGe | DSL (nm) | n2D (× 1011 cm−2) |
|---|---|---|---|---|---|
| 2216 | 12.0 | 2.3 | 0.87 | 41.6 [40.3] | 7.2 |
| 2217 | 13.0 | 2.3 | 0.87 | 42.8 [41.3] | 9.0 |
| 2218 | 11.3 | 2.3 | 0.87 | 40.6 [39.6] | 7.8 |
| 2219 | 11.5 | 2.3 | 0.87 | 40.6 [39.8] | 1.0 |
| 2221 | 12.0 | 3.3 | 0.81 | 42.4 [41.3] | 6.0 |
| 2222 | 12.0 | 4.0 | 0.81 | 43.0 [42.0] | 4.6 |
| 2223 | 12.0 | 2.3 | 0.87 | 39.5 [40.3] | undoped |
| 2224 | 12.0 | 5.0 | 0.81 | 43.9 [43.0] | 1.5 |
| 2267 | 16.0 | 2.3 | 0.81 | [44.3] | 3.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Persichetti, L.; Montanari, M.; Ciano, C.; Di Gaspare, L.; Ortolani, M.; Baldassarre, L.; Zoellner, M.; Mukherjee, S.; Moutanabbir, O.; Capellini, G.; et al. Intersubband Transition Engineering in the Conduction Band of Asymmetric Coupled Ge/SiGe Quantum Wells. Crystals 2020, 10, 179. https://doi.org/10.3390/cryst10030179
Persichetti L, Montanari M, Ciano C, Di Gaspare L, Ortolani M, Baldassarre L, Zoellner M, Mukherjee S, Moutanabbir O, Capellini G, et al. Intersubband Transition Engineering in the Conduction Band of Asymmetric Coupled Ge/SiGe Quantum Wells. Crystals. 2020; 10(3):179. https://doi.org/10.3390/cryst10030179
Chicago/Turabian StylePersichetti, Luca, Michele Montanari, Chiara Ciano, Luciana Di Gaspare, Michele Ortolani, Leonetta Baldassarre, Marvin Zoellner, Samik Mukherjee, Oussama Moutanabbir, Giovanni Capellini, and et al. 2020. "Intersubband Transition Engineering in the Conduction Band of Asymmetric Coupled Ge/SiGe Quantum Wells" Crystals 10, no. 3: 179. https://doi.org/10.3390/cryst10030179
APA StylePersichetti, L., Montanari, M., Ciano, C., Di Gaspare, L., Ortolani, M., Baldassarre, L., Zoellner, M., Mukherjee, S., Moutanabbir, O., Capellini, G., Virgilio, M., & De Seta, M. (2020). Intersubband Transition Engineering in the Conduction Band of Asymmetric Coupled Ge/SiGe Quantum Wells. Crystals, 10(3), 179. https://doi.org/10.3390/cryst10030179






