Abstract
We report a first-principles study of hybrid organic–inorganic perovskites with formula [A]Cu(H2POO)3 (A = triazolium (Trz) and guanidinium (Gua), and H2POO− = hypophosphite), and [HIm]Cu(HCO2)3 (HIm = imidazolium cation, = formate). The triazolium hypophosphite and the formate have been suggested as possible ferroelectrics. We study the fully relaxed structures with different magnetic orderings and possible phonon instabilities. For the [Trz]Cu hypophosphite, the Trz cation is shown to induce large octahedral distortions due to the Jahn-Teller effect, with Cu-O long-bond ordering along two perpendicular directions, which is correlated with antiferromagnetic ordering and strongly one-dimensional. We find that the structure is dynamically stable with respect to zone-center distortions, but instabilities appear along high symmetry lines in the Brillouin zone. On the other hand, for the [HIm]Cu formate, large octahedral distortions are found, with large Cu-O bonds present in half of the octahedra, in this case along a single direction, and correspondingly, the magnetism is almost two-dimensional.
1. Introduction
Metal-organic frameworks (MOFs), where metal centers or clusters are linked by organic ligands, have received intense research interest recently. The denser MOFs, in particular with ABX3 perovskite topology, where the X− and/or A-site of simple perovskites are substituted by polyatomic ions, have shown fascinating ferroelectric, magnetic, and multiferroic properties [1,2,3], similar to their inorganic counterparts [4,5]. Theoretical studies of this family of compounds using density functional theory calculations [6] have matched well with experimental results, which highlights the predictive power of computation [7,8].
Recently, hybrid organic-inorganic perovskites based on the hypophosphite ligand have been synthesized [9]. Both formate and hypophosphite ligands produce intermediate-size cubic interstices, allowing for a choice of several different amine cations on the A site.
A recent group-theoretical analysis [10] showed that the number of possible distortions is greatly enhanced in molecular perovskites due to the additional kinds of symmetry-breaking degrees of freedom allowed, including unconventional octahedral rotations [11,12,13], columnar shifts [11,14], and multipolar order of the organic cations [15]. This allows more flexibility for different functionalities. The symmetry analysis [10] of the distortions present in synthesized Mn compounds, triazolium manganese hypophosphite [9] or imidazolium manganese formate [16], has suggested that the respective Cu analogues could be ferroelectric, due to the propensity of the Cu octahedra to show Jahn–Teller distortions in combination with the distortion modes available for hybrid perovskites already present in the Mn compounds. This motivated us to study Cu-based organic-inorganic perovskites using first-principles density functional theory calculations. For the hypophosphites, besides the suggested triazolium hypophosphite, we have also considered guanidinium as an organic cation. The structures considered in this work are shown in Figure 1.

Figure 1.
Unit cells of the considered materials. (a) [Trz]Cu(H2POO)3, with space group P21/c. (b) [Gua]Cu(H2POO)3, with space group . (c) [HIm]Cu(HCO2)3, with space group P21/c. Color code: The orange octahedra are Cu centered, with oxygen (black) at the vertices; P—gray; C—brown; H—white; N—blue.
We find that the different Cu compounds have both 1D and 2D magnetism, with small couplings in the spin exchange paths which involve the long Cu-O bonds, but we do not find significant structural instabilities with respect to the centrosymmetric group of the Mn analogues.
2. Methods
We have used the Vienna Ab-initio Simulation Package, VASP (VASP Software GmbH, Vienna, Austria) [17] for density functional calculations, which uses a plane wave basis set and the projector augmented-wave (PAW) method [18]. We considered the GGA-PBE (generalized gradient approximation, Perdew-Burke-Erzernhof) exchange-correlation functional [19] and added an effective Coulomb repulsion U to Cu 3d orbitals, according to the simplified approach of Dudarev et al. [20]. For Cu oxides, values of U = 4 eV may be most appropriate, but it is difficult to choose an appropriate U value that correctly describes different properties [21]. Here, we studied the variation of U from 0 to 5 eV. For the PBE (U = 0) cases, we also applied the DFT-D3 (BJ) method [22,23] to take van der Waals corrections into consideration. The following settings were used, except when stated otherwise: a 3 × 3 × 2 k-points mesh for the hypophosphites and a 2 × 2 × 1 mesh for the formate; the energy cutoff for the plane waves was 600 eV for the [Trz]Cu(H2POO)3 and 520 eV for the other two compounds; the full relaxations (atomic positions, cell shape, and volume) did not use symmetry, and stopped when the maximum residual force components were less than 0.005 eV/A. The FINDSYM program (Brigham Young University, Provo, UT, USA) [24,25] was used to find the symmetry of the optimized structure, the VESTA software for analysis and structural representation [26], and PHONOPY to post-process VASP results and calculate phonons.
3. Triazolium Cu Hypophosphite
3.1. Magnetism
We started from the structural data for [Trz]Mn hypophosphite given by Wu et al. [9], wherein the compound adopts the space group P21/c and subsequently replaces the Mn atoms by Cu. We performed a series of full structural optimizations with the ferromagnetic and the three antiferromagnetic orders obtained by the different combinations of up/down spins in the unit cell. These can be called A, C, and G-type antiferromagnetism (AFM) [27], considering that the Cu framework is cubic-like (even if the framework is distorted from ideal cubes by columnar shifts).
Figure 2 shows the total energies obtained for the optimized structures as a function of U. There is a clear separation between two pairs of states; the A and G-type AFM are always lowest in energy, while the C-type AFM and FM are highest. This separation decreases with U, as expected from the increased localization of states, but it is always much larger than between each pair. These degeneracies between states with different (F/AF) in-plane interactions suggest that the in-plane exchange interaction is very weak. On the other hand, the states where the out-of-plane magnetic ordering switches from F to AF are separated by large energy differences; thus, the out-of-plane exchange must be much stronger (particularly for low U values and AFM). The A-AFM state is slightly lower in energy than the G-AFM state, with the difference slightly larger for lower U values, suggesting a small in-plane ferromagnetic (FM) coupling, while the C and F states remain almost degenerate. Thus, this compound presents a quasi-1D magnetism, particularly for lower U values, with very weakly coupled 1D antiferromagnetic chains. This unusual property has previously been shown in another Cu metal–organic framework perovskite [28], dimethylammonium copper formate ([DMA]Cu[HCO2]3), and it could be understood on the basis of Jahn–Teller distortions in the CuO6 octahedra. We will show in the following structural analysis that strong octahedral distortions are also present in our compound. Indications of low-dimensional magnetism were also seen in guanidinium Cu formate [29], which is consistent with first-principles calculations that have shown a dominant 1D interaction [7]. We also used the DFT-D3(BJ) method to check the influence of dispersion corrections, parametrized for GGA (U = 0), shown in the rightmost set of points of Figure 2. The FM/AFM out-of-plane difference corresponds to intermediate values of U, while the A/G and particularly C/F states are now more separated, indicating higher in-plane exchange, but dominant 1D magnetism is still seen.
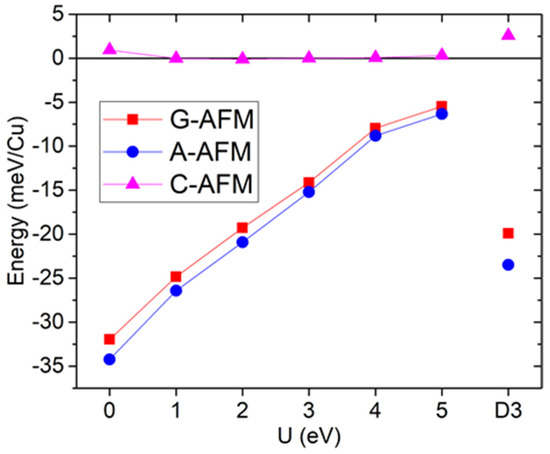
Figure 2.
[Trz]Cu(H2POO)3 GGA+U total energies, as a function of U, and GGA+D3(BJ) total energies, relative to the ferromagnetic state.
The calculated Cu moments are in the range between 0.6 and 0.8 μB, and the total moment per cell is 1 μB/Cu for the FM state. The values are consistent with the Cu2+ S = 1/2 Jahn-Teller state. Considering the cubic-like framework of Cu ions, we can use the same model as in Ref. [28] to map the density functional theory (DFT)total energies to a Heisenberg model and obtain three exchange interactions between spins: intra-chain nearest-neighbor (J1), interchain in-plane (J2), and interchain out-of-plane (J3). The interactions are shown in Table 1. (For comparison with the previous work, we follow the convention where AFM interactions are positive.) As it can be seen by comparison of the two rightmost columns, the exchange interactions in our compound are qualitatively similar to [DMA]Cu[HCO2]3 for the same U value, with an AFM intrachain larger by far than the interchain interactions J2 + J3 (overall weakly ferromagnetic). Therefore, similar experimental signatures of 1D magnetism should be found. The AFM intrachain spin exchange J1 is slightly weaker in our case, but so is the interchain exchange (J2 + J3), such that the dimensionless ratio J1/(J2 + J3) is −38 for [Trz]Cu(H2POO)3 and −35 for [DMA]Cu(HCO2)3.

Table 1.
Spin exchange interactions (in K) for H = 1/2∑ijJij Si Sj, with S = 1/2, calculated with GGA, GGA+U, GGA+D3(BJ), and comparison with another quasi-1D Cu MOF.
3.2. Structure
Concerning the structure, while the Mn analogue at room temperature has a measured volume of 277.22 Å3/Mn, for the Cu compound, our calculations (after full relaxation and without use of symmetry) result in 279.29 to 285.91 Å3/Cu, depending on UCu, with smaller volumes for larger U. For G/A-AFM orders, the changes in volume are similar and come mostly from the change of U. There is a small expansion in any case, as could be expected on the basis of a slightly larger Cu2+ ionic radius relative to Mn2+ [30]. Concerning the transition metal–oxygen bonds, in the synthesized Mn compound, the Mn-O bonds vary between 2.11 and 2.24 Å, with an average bond length of 2.18 Å, while for the Cu compound, our predictions for U = 0 (U = 5) show a much more distorted octahedron, consisting of a Cu-O square with “equatorial” bonds 1.95–1.99 (1.96–1.99) Å, while the other two “axial” distances are much larger, 2.62 (2.42) and 2.94 (2.76) Å. These distances are almost the same for A and G-type orders. The strong AFM coupling between ab-planes can be related to the Cu-O bonds along the c direction connecting planes, which are all the smaller equatorial ones, while in the ab-plane, half of the bonds are the long axial bonds. The very large Cu-O 2.94 (2.76) Å distance in particular, alternating direction in half of the in-plane framework edges, must considerably weaken the Cu-Cu super-exchange path through the O atoms, disrupting the formation of long-range magnetic order in the plane. For increasing U values, the two axial distances decrease, so the distortion of the Cu-O octahedra is not so large; nevertheless, the in-plane magnetic coupling is lower due to the enhanced localization.
The comparison of structural parameters between GGA with and without D3 corrections and U is shown in Table 2. The D3 corrections cause a large decrease in volume (10.6%) corresponding to the decrease of in-plane lattice parameters a and b by 3.0 and 7.0%. The effect of U = 5 eV is much smaller, and the small decrease in volume is mostly caused by a decrease in b by 1.5%. Looking at the Cu-O octahedral distances, the equatorial bonds remain in the range 1.95–1.99 Å, and the difference caused by the dispersion corrections is smaller axial distances, now 2.39 and 2.63 Å, compared with 2.62 and 2.94 Å with GGA, respectively. In this case, GGA+U also produces a considerable decrease in the axial bonds to 2.49 and 2.76 Å, although it is not as great as D3. Thus, the effect of both corrections is a less distorted octahedron.

Table 2.
Structural parameters a, b, c (Å), β (°), Volume V (Å3/fu), and Cu–O equatorial and axial distances (Å) for different approximations: GGA, GGA+D3(BJ), and GGA+U (UCu = 5 eV).
We looked at the symmetry of the optimized structures, and, except for small (below 0.01 Å) tolerances in atomic positions and lattice parameters, the structure remains with the initial space group, P21/c, which is centrosymmetric. Using the structure found at U = 0 with the A-AFM order, we searched for possible dynamical instabilities using the VASP software by calculating the Hessian matrix (with central differences and a step size of 0.015 Å) and corresponding zone-center (Γ point) vibrational frequencies. The 297 (3N−3, where N = 100 is the number of atoms) non-translational modes are all real, showing that the P21/c structure is stable with respect to zone-center distortions, and thus, this compound will likely not be a proper ferroelectric. For example, the five lowest mode frequencies are 34, 46, 47, 48, and 51 cm−1. However, this does not exclude other possibilities such as hybrid improper ferroelectricity [31], where the polarization would be induced by other modes. Therefore, we also calculated phonons in other regions of the reciprocal space, using density functional perturbation theory to calculate the force constants [32] and then post-processing using the PHONOPY code [33] to calculate the phonon dispersion in high symmetry lines of the Brillouin zone. The resulting phonon band structure plot is shown in Figure 3. Instabilities are seen in many lines in the Brillouin zone, which are shown as negative frequencies in the plot, but with small magnitudes (≈33 cm−1). Although a more extensive check is in order here, the calculations are already too computationally expensive using the original cell.
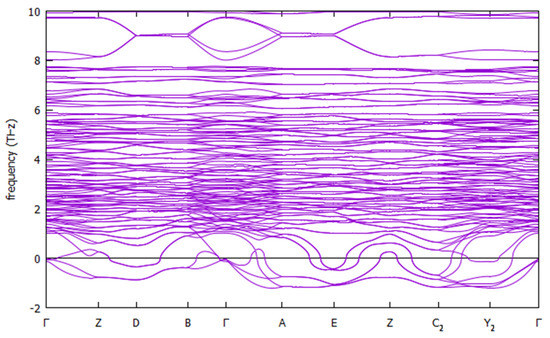
Figure 3.
[Trz]Cu(H2POO)3 phonon band structure (THz) for high-symmetry directions of the Brillouin zone.
There are imaginary frequencies (negative in the plot) in all the studied lines. In addition to the three lowest (acoustic) modes, two more modes (optic) get imaginary frequencies near the E point (A–E and E–Z directions), and near C2 (Z–C2 and C2–Y2 directions) there is one more, with six total imaginary modes.
To further explore these instabilities, we have looked at the eigenvectors of the phonons in some high-symmetry points (Z, D, E, C2), and constructed modulated supercell structures with the displacements given by weighted eigenvectors. Then, these structures were optimized, as before, and the symmetry and energies of the optimized structures were analyzed. For the Z point, the modulated structure, as well as the optimized final structure, have P1 symmetry, although it remains P21/c within tolerances of 10−3 Å in lattice and 10−2 Å in atomic positions or larger, which shows that the distortions are small. The energy lowering with respect to the initial P21/c structure is only a 0.30 meV/formula unit. For the D and E points, the initial modulated and optimized structures have symmetry (for D, the structure remains P21/c symmetry for tolerances 10−3 Å in lattice and 10−2 Å in atomic positions or larger; for E, the structure remains P21/c symmetry for tolerances 10−4 Å in lattice and 10−2 Å in atomic positions or larger), and the energies are lower by 1.00 and 0.82 meV/Cu, respectively. These energy and structural differences are indeed small but due to the computational cost of the calculations, we did not explore this point further.
4. Guanidinium Cu Hypophosphite
We studied another compound of the Cu hypophosphite family with the Guanidinium cation (C(NH2)3±) at the A site. For this system, we also started with the structure from the Mn analogue synthesized by Wu et al. [9]. In this case, we used the low temperature structure [9]. Due to the low symmetry, the only possible symmetry-lowering distortion is the break of inversion symmetry. We considered the FM and the three AFM states supported by the four Cu atoms in the triclinic unit cell. In this case, the + + − − state (where + (−) refers to the sign of projection of the spin moment on a given Cu atom along the quantization axis, considered as a z-axis, and the order corresponds to Cu atoms with z coordinates approximately 0.25, 0.75, 0.5, and 0), corresponds to the G-AFM alternating state for the pseudo-cubic framework, while the + − + − and − + + − cases correspond to double-layered AFM states for ferromagnetic (001) triclinic planes (corresponding to (111) pseudo-cubic planes), as shown in Figure 4. Furthermore, the initial calculations in some cases converged to a ferrimagnetic state of the type + + − +, suggesting that this is also a competing state; therefore, we also included it in our analysis.
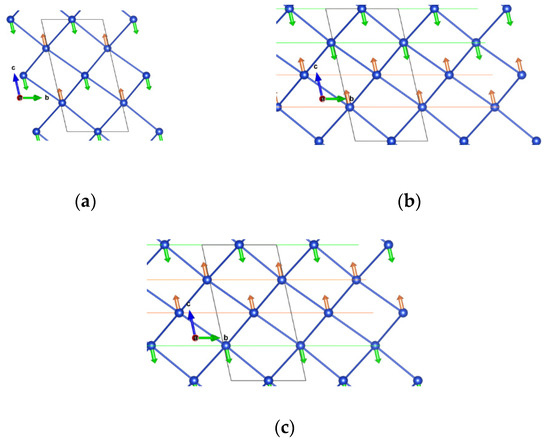
Figure 4.
Description of the antiferromagnetism (AFM) orders supported by the triclinic unit cell (dark lines). (a) + + − − (G-AFM type) order. (b) + − + −, and (c) − + + −: double-layered AFM orders, with (001) FM triclinic planes (equivalent to (111) pseudocubic planes).
Figure 5 shows the total energies obtained for the optimized structures of these five states as a function of U, where FM is taken as the zero-energy state. Indeed, for low values of U (<4 eV), the ferrimagnetic state (+ + − +) turns out to be the lowest energy state among those considered. In the range U > 3 eV, which may be most appropriate, the G-AFM state becomes the ground state.
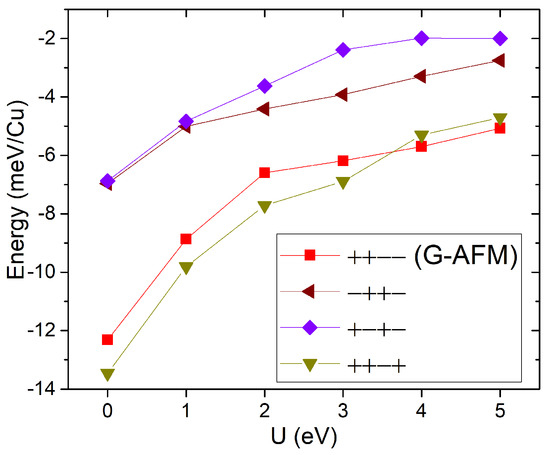
Figure 5.
[Gua]Cu(H2POO)3 GGA+U total energies relative to the ferromagnetic state as a function of U.
5. Imidazolium Cu Formate
5.1. Magnetism
We started from the Mn analogue structure, which was also previously synthesized and characterized [16]. The low-temperature ordered structure has the same space group (P21/c) as [Trz]Mn(H2PO2)3, but the HIm cations order such that there are now two crystallographically inequivalent cations and metal centers in 4e Wyckoff positions, and thus, the cell is approximately doubled with respect to the previous hypophosphites.
Figure 6 shows the energies for the three simple AFM orders, relative to FM, as a function of U. In this case, due to the larger cell, other orders could have been investigated, but we will focus on the G/C/A/F orders considering c as the out-of-plane axis. For example, the A-AFM order consists of ferromagnetic ab-planes with antiferromagnetic stacking along the c axis. In this case, the C/G states are much lower in energy than A/F; both pairs near degenerate, meaning that the out-of-plane coupling must be much weaker than the in-plane coupling, and there is a quasi-two-dimensional antiferromagnetism, particularly for low values of U.
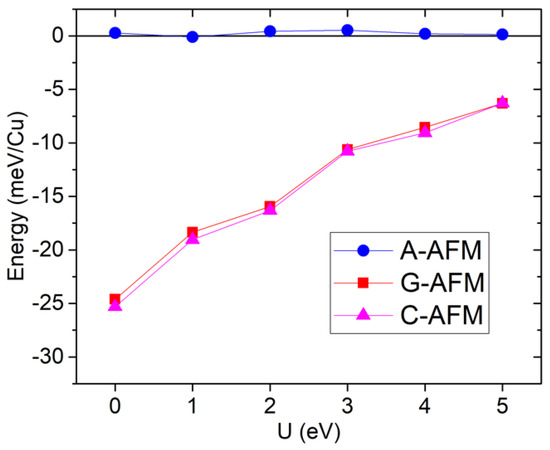
Figure 6.
[HIm]Cu(HCO2)3 GGA+U total energies as a function of U, relative to the ferromagnetic state.
We can use the same model as before to calculate the exchange interactions: J2 is the in-plane interaction, while J1 is the vertical out-of-plane interaction, and J3 is the diagonal one. Table 3 shows the calculated exchange interactions. As seen for [Trz]Cu(H2PO2)3, the main exchange interaction decreases with U. In the dimethylammonium Cu formate case, the DFT values were much closer to experiment for the higher U values calculations [28], which indicates that for this Cu compound, the U = 5 eV results, with overall ≈75 K AF interaction, are also more reasonable than U = 0 eV. In this case, the degree of 2D magnetism can be estimated by J2/(J1 + J3) = −22 for U = 5 eV, i.e., the AFM in-plane interaction is much larger than the out-of-plane ones (overall weakly ferromagnetic). Note that there are two times more octahedral in-plane than out-of-plane bonds, so the overall exchange interactions, here dominated by J2 (in-plane), are of similar magnitude to the ones in the hypophosphite (where the dominant out-of-plane J1 = 780 K for U = 0 eV and 141 K for U = 5 eV, approximately double the in-plane interactions here), and to the ones in the previously studied DMA Cu formate (J1 = 214 K for U = 5 eV) [28].

Table 3.
Spin exchange interactions (in K) for H = 1/2∑ijJij Si Sj, with S = 1/2, calculated with GGA and GGA+U.
5.2. Structure
In this case, there are two inequivalent octahedra. Half of the octahedra have four bonds with 2 Å, one with 2.5 Å, and one with 2.9 Å, while the other half have four bonds with 2 Å, one with 2.4 Å, and one with 2.6 Å. As in the [Trz] Cu hypophosphite, long 2.9 Å bonds should reduce the magnetic interactions. In the [Him]Cu formate, these bonds are only along the c out-of-plane direction, decreasing the coupling in this direction.
Using the FINDSYM program to check the symmetry group of the optimized structures, we found the P21 polar space group for the ferromagnetic calculation, U = 4 eV for small tolerances (10−3 Å for lattice and position parameters), while increasing the positions tolerance (to 10−2 Å), the centrosymmetric P21/c space group is found instead. Nevertheless, this indicated the possible stability of the polar phase. In order to quantify a possible energy lowering, we performed relaxations with the symmetry constraints of both P21 and P21/c space groups (using the initial structures found with different tolerances) to well converged values for the more stable magnetic orders (C and G cases), with U = 4 eV. However, after converging the calculations to more stringent parameters (energy cutoff of 600 eV and forces threshold of 2 meV/fu), the energy difference is found to be 0.03 meV/fu for the C magnetic order, meaning that P21 and P21/c are almost degenerate in energy, and it is also almost vanishing for the G order, −0.006 meV/fu. In this case, we could not try to calculate phonons, due to the larger size of the system.
6. Conclusions
Starting from the Mn analogues, we have explored the possible compounds triazolium/guanidinium Cu hypophosphites and imidazolium Cu formate. We could not find significant energy-lowering distortions with respect to the P21/c space group of the Mn analogues, which suggests these compounds are not ferroelectric. We have shown that [Trz]Cu hypophosphite and [HIm]Cu formate exhibit strong, almost ideal 1D and 2D magnetism, respectively, highlighting the role of strong octahedral distortions in combination with different periodic orderings of the organic cations. We hope that our study motivates the synthesis and characterization of these compounds.
Author Contributions
Conceptualization, A.S.; methodology, A.S. and J.N.G.; investigation, J.N.G.; writing—original draft preparation, J.N.G.; validation, J.N.G., A.E.P., W.L. and A.S.; writing—review and editing, all authors. All authors have read and agreed to the published version of the manuscript.
Funding
The work has been performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme. In part (J.N.G.), this work was developed within the scope of the project CICECO-Aveiro Institute of Materials (UIDB/50011/2020 & UIDP/50011/2020), financed by national funds through the FCT/MEC, Portugal. A.E.P and A.S. thank the Royal Society (UK) for support from an International Exchange (IES\R1\180034).
Acknowledgments
J.N.G. gratefully acknowledges the computer resources/technical support provided by CINECA. J.N.G. acknowledges the kind hospitality by CNR-SPIN c/o Department of Chemical and Physical Science of University of L’Aquila (Italy) during the visiting period from 3 November 2019 to 21 December2019 and from 7 January 2020 to 15 February 2020. A.S. thanks Professor Anthony K. Cheetham for useful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tian, Y.; Stroppa, A.; Chai, Y.S.; Yan, L.Q.; Wang, S.; Barone, P.; Picozzi, S.; Sun, Y. Cross coupling between electric and magnetic orders in a multiferroic metal–organic framework. Sci. Rep. 2015, 4, 6062. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Aguirre, L.C.; Pato-Doldán, B.; Mira, J.; Castro-García, S.; Señarís-Rodríguez, M.A.; Sánchez-Andújar, M.; Singleton, J.; Zapf, V.S. Magnetic Ordering-Induced Multiferroic Behavior in [CH3NH3][Co(HCOO)3] Metal–Organic Framework. J. Am. Chem. Soc. 2016, 138, 1122–1125. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, Z.; Deschler, F.; Gao, S.; Friend, R.H.; Cheetham, A.K. Chemically diverse and multifunctional hybrid organic–inorganic perovskites. Nat. Rev. Mater. 2017, 2, 16099. [Google Scholar] [CrossRef]
- Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.; Tokura, Y. Magnetic control of ferroelectric polarization. Nature 2003, 426, 55–58. [Google Scholar] [CrossRef]
- Wang, J.; Neaton, B.; Zheng, H.; Nagarajan, V.; Ogale, S.B.; Liu, B.; Viehland, D.; Vaithyanathan, V.; Schlom, D.G.; Waghmare, U.V.; et al. Epitaxial BiFeO3 multi-ferroic thin film heterostructures. Science 2003, 299, 1719–1722. [Google Scholar] [CrossRef]
- Tian, Y.; Stroppa, A.; Chai, Y.S.; Barone, P.; Perez-Mato, M.; Picozzi, S.; Sun, Y. High-temperature ferro-electricity and strong magnetoelectric effects in a hybrid organic-inorganic perovskite framework, physica status solidi. Rapid Res. Lett. 2015, 9, 62–67. [Google Scholar]
- Stroppa, A.; Jain, P.; Barone, P.; Marsman, M.; Perez-Mato, J.M.; Cheetham, A.K.; Kroto, H.W.; Picozzi, S. Electric Control of Magnetization and Interplay between Orbital Ordering and Ferroelectricity in a Multiferroic Metal-Organic Framework. Angew. Chem. Int. Ed. 2011, 50, 5847–5850. [Google Scholar] [CrossRef]
- Stroppa, A.; Barone, P.; Jain, P.K.; Perez-Mato, J.M.; Picozzi, S. Hybrid Improper Ferroelectricity in a Multiferroic and Magnetoelectric Metal-Organic Framework. Adv. Mater. 2013, 25, 2284–2290. [Google Scholar] [CrossRef]
- Wu, Y.; Shaker, S.; Brivio, F.; Murugavel, R.; Bristowe, P.D.; Cheetham, A.K. [Am]Mn(H2POO)3: A New Family of Hybrid Perovskites Based on the Hypophosphite Ligand. J. Am. Chem. Soc. 2017, 139, 16999–17002. [Google Scholar] [CrossRef]
- Boström, H.L.B.; Senn, M.S.; Goodwin, A.L. Recipes for improper ferroelectricity in molecular perovskites. Nat. Commun. 2018, 9, 1–7. [Google Scholar] [CrossRef]
- Wu, Y.; Binford, T.; Hill, J.A.; Shaker, S.; Wang, J.; Cheetham, A.K. Hypophosphite hybrid perovskites: A platform for unconventional tilts and shifts. Chem. Commun. 2018, 54, 3751–3754. [Google Scholar] [CrossRef]
- Hill, J.A.; Thompson, A.L.; Goodwin, A.L. Di-cyanometallates as model extended frameworks. J. Am. Chem. Soc. 2016, 138, 5886–5896. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.; Li, W.; Butler, K.T.; Feng, G.; Howard, C.J.; Carpenter, M.P.; Lu, P.; Walsh, A.; Cheetham, A.K. An Unusual Phase Transition Driven by Vibrational Entropy Changes in a Hybrid Organic-Inorganic Perovskite. Angew. Chem. Int. Ed. 2018, 57, 8932–8936. [Google Scholar] [CrossRef] [PubMed]
- Boström, H.L.B.; Hill, J.A.; Goodwin, A.L. Columnar shifts as symmetry-breaking degrees of freedom in molecular perovskites. Phys. Chem. Chem. Phys. 2016, 18, 31881–31894. [Google Scholar] [CrossRef] [PubMed]
- Evans, N.L.; Thygesen, P.M.M.; Boström, H.L.B.; Reynolds, E.M.; Collings, I.E.; Phillips, A.E.; Goodwin, A.L. Control of Multipolar and Orbital Order in Perovskite-like [C(NH2)3]CuxCd1–x(HCOO)3 Metal–Organic Frameworks. J. Am. Chem. Soc. 2016, 138, 9393–9396. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.Q.; Yan, H.-B.; Huang, Z.Q.; Zhang, Z. Reversible high-temperature phase transition of a manganese(II) formate framework with imidazolium cations. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2013, 69, 616–619. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. 1996, 54, 11169. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. 1994, 50, 17953. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Wang, L.; Maxisch, T.; Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. 2006, 73, 195107. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Stokes, H.T.; Hatch, D.M.; Campbell, B.J. FINDSYM, version 7.0, ISOTROPY Software Suite. 2019. Available online: https://iso.byu.edu/iso/isotropy.php (accessed on 9 December 2020).
- Stokes, H.T.; Hatch, D.M. FINDSYM: Program for identifying the space-group symmetry of a crystal. J. Appl. Crystallogr. 2005, 38, 237–238. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Wollan, E.O.; Koehler, W.C. Neutron Diffraction Study of the Magnetic Properties of the Series of Perovskite-Type Compounds[(1−x)La, xCa]MnO3. Phys. Rev. 1955, 100, 545–563. [Google Scholar] [CrossRef]
- Wang, Z.; Jain, P.; Choi, K.-Y.; Van Tol, J.; Cheetham, A.K.; Kroto, H.W.; Koo, H.-J.; Zhou, H.D.; Hwang, J.; Choi, E.S.; et al. Dimethylammonium copper formate [(CH3)2NH2]Cu(HCOO)3: A metal-organic framework with quasi-one-dimensional antiferromagnetism and magnetostriction. Phys. Rev. B 2013, 87, 224406. [Google Scholar] [CrossRef]
- Hu, K.-L.; Kurmoo, M.; Wang, Z.; Gao, S. Metal-Organic Perovskites: Synthesis, Structures, and Magnetic Properties of [C(NH2)3][MII(HCOO)3] (M = Mn, Fe, Co, Ni, Cu, and Zn; C(NH2)3 = Guanidinium). Chem.-A Eur. J. 2009, 15, 12050–12064. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Benedek, N.A.; Fennie, C.J. Hybrid Improper Ferroelectricity: A Mechanism for Controllable Polarization-Magnetization Coupling. Phys. Rev. Lett. 2011, 106, 107204. [Google Scholar] [CrossRef]
- Baroni, S.; De Gironcoli, S.; Corso, A.D.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).