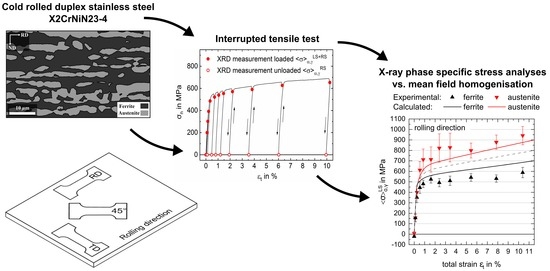
Phase-Specific Strain Hardening and Load Partitioning of Cold Rolled Duplex Stainless Steel X2CrNiN23-4
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
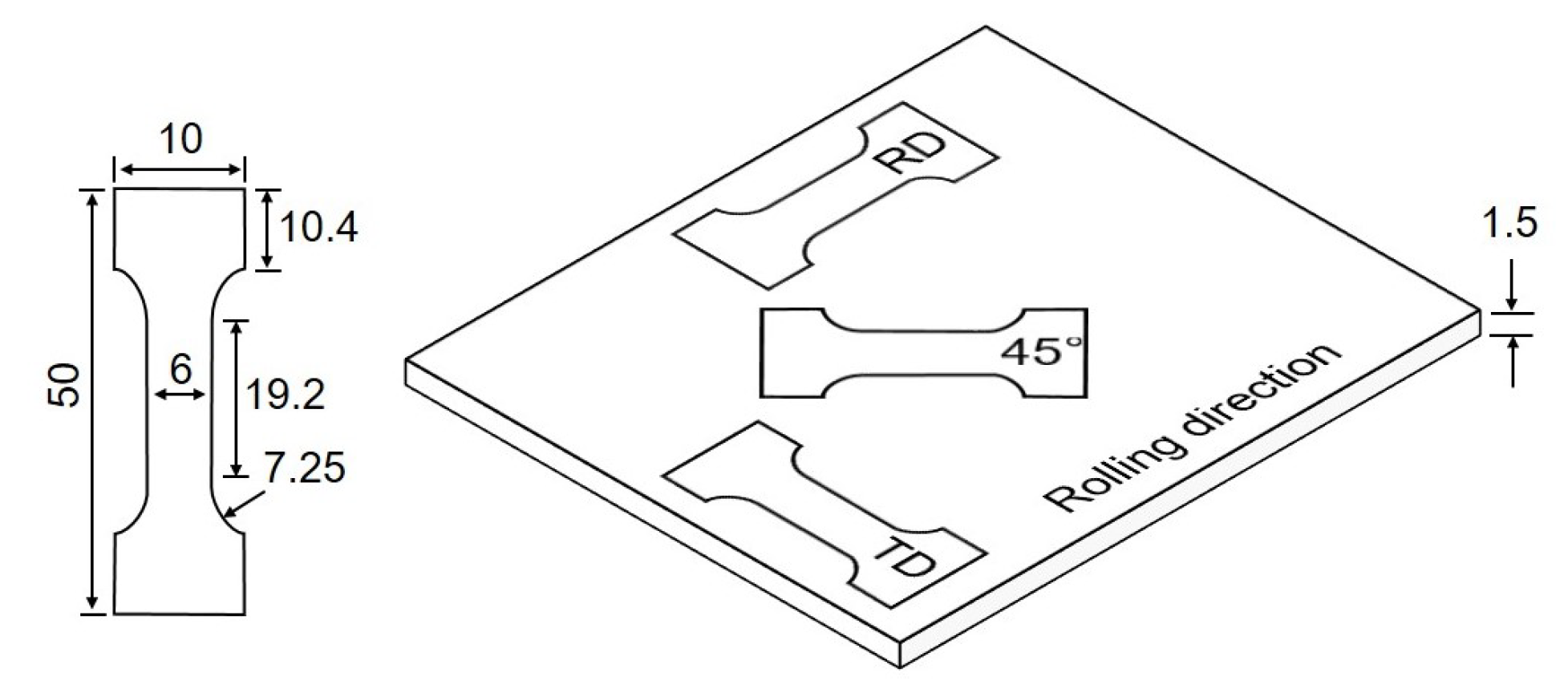
2.2. Experimental Methods
2.3. Numerical Methods
3. Results and Discussion
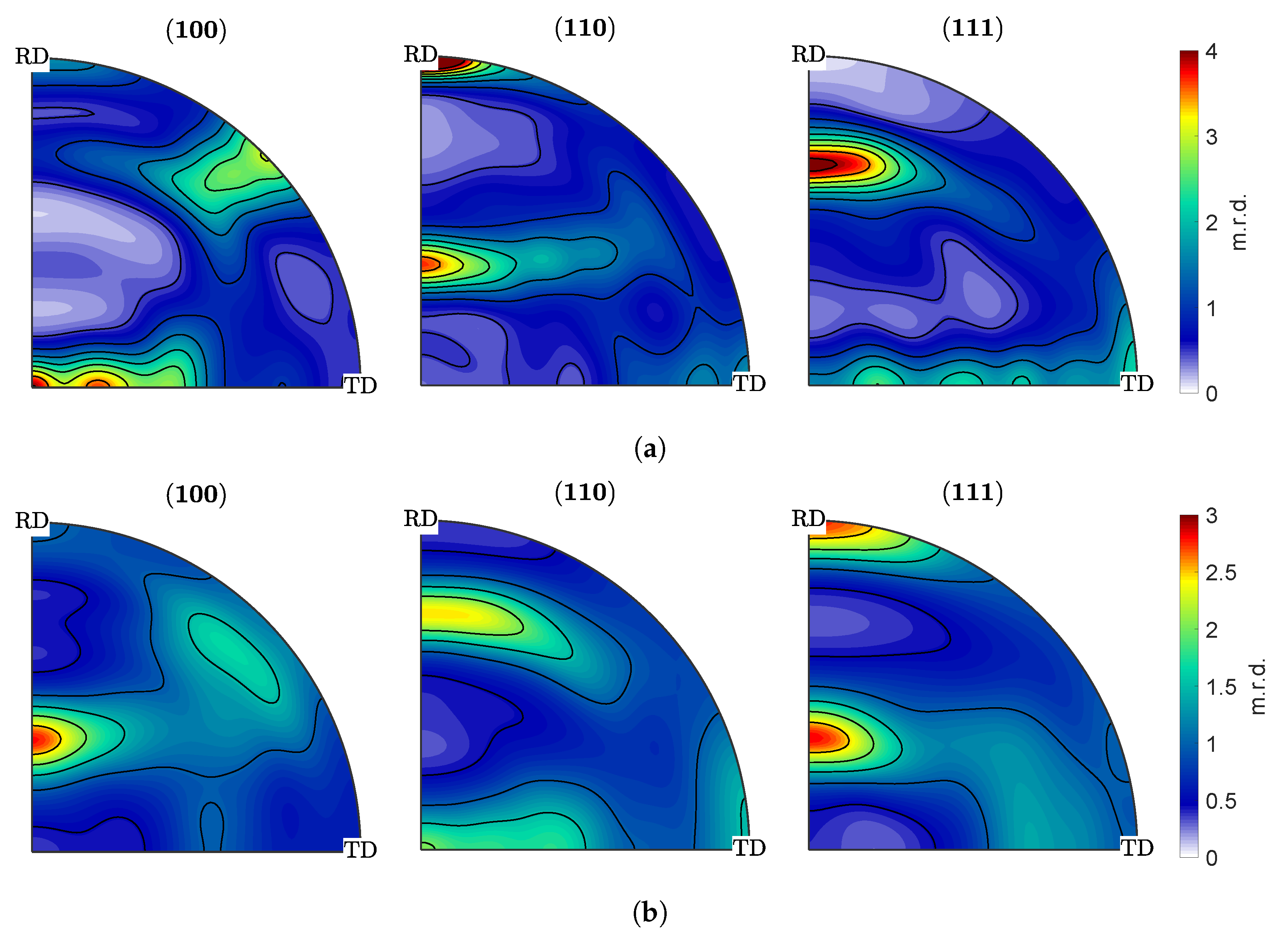
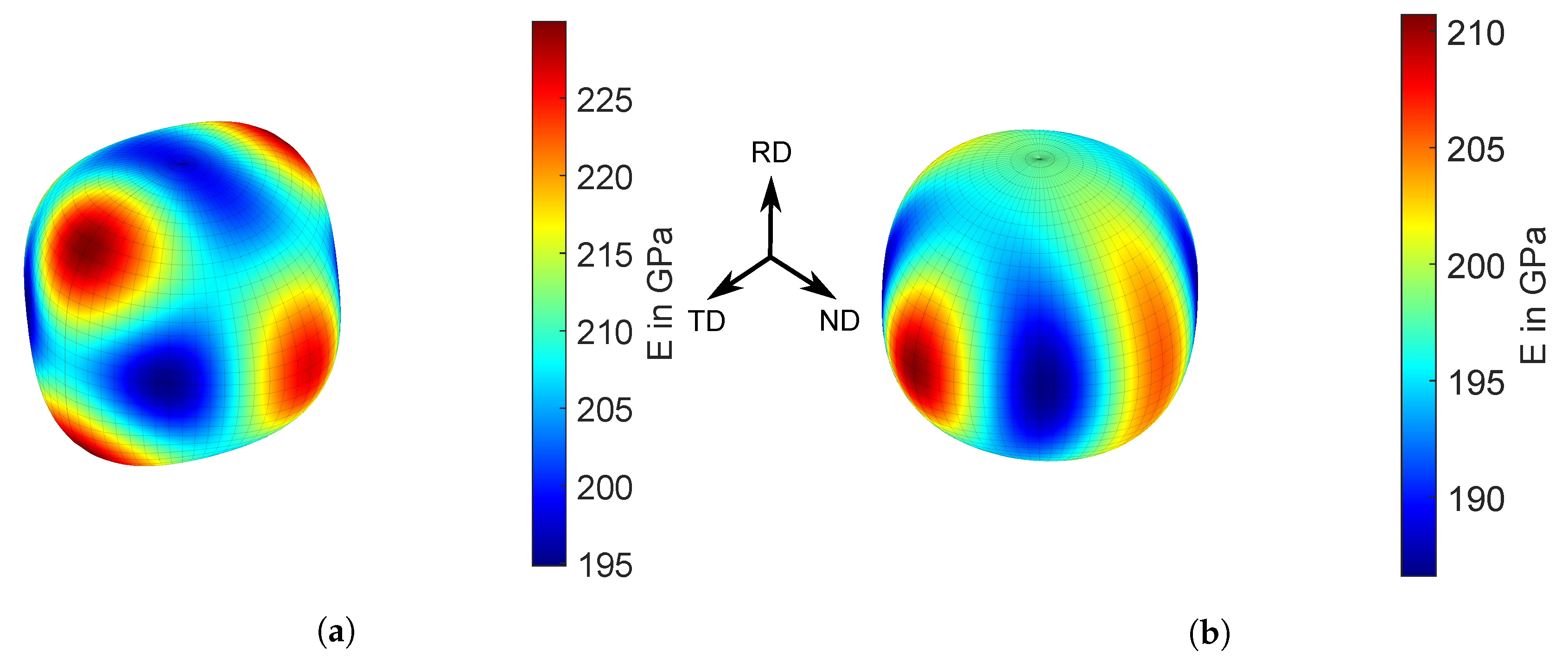
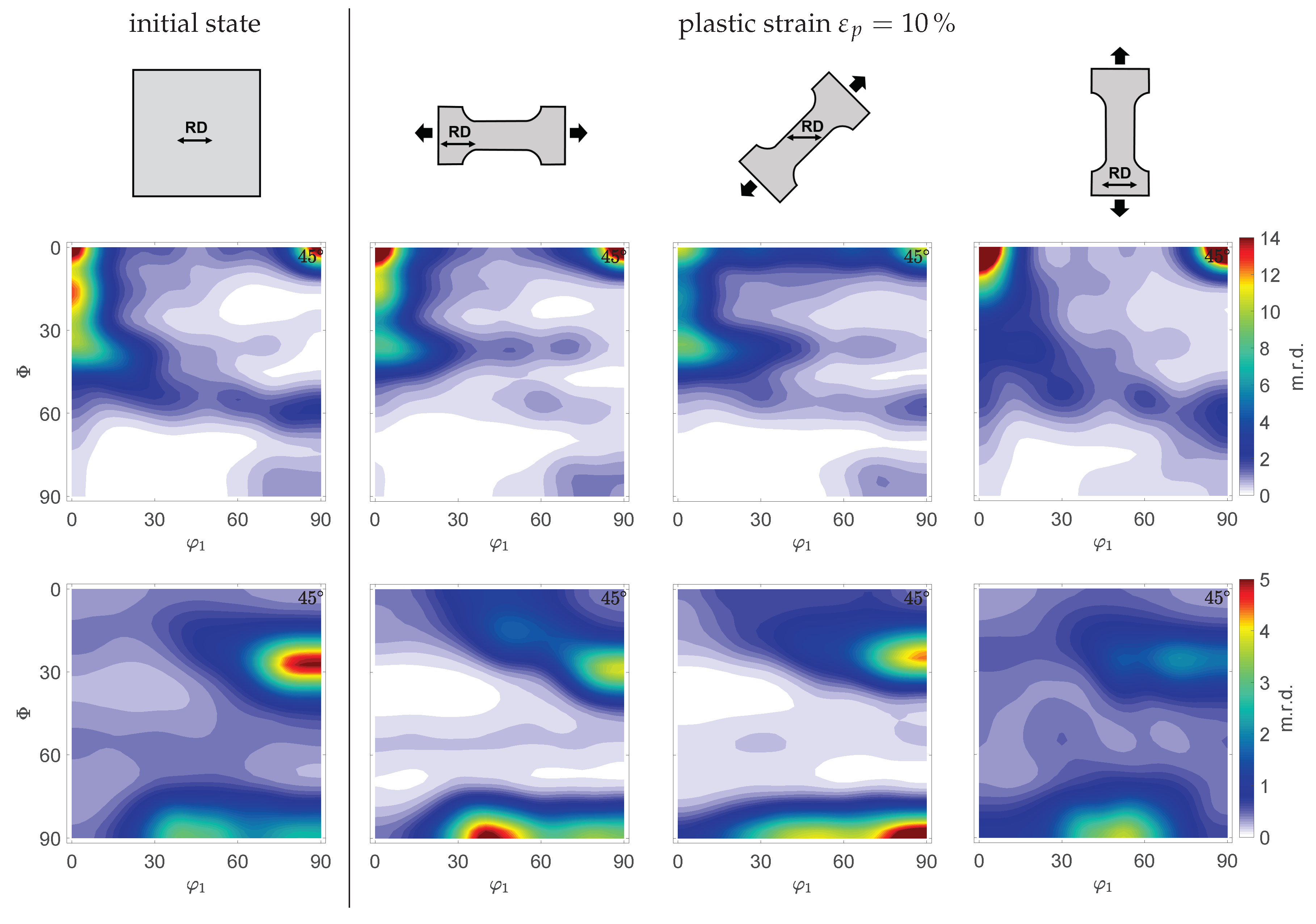
3.1. Development of Crystallographic Texture
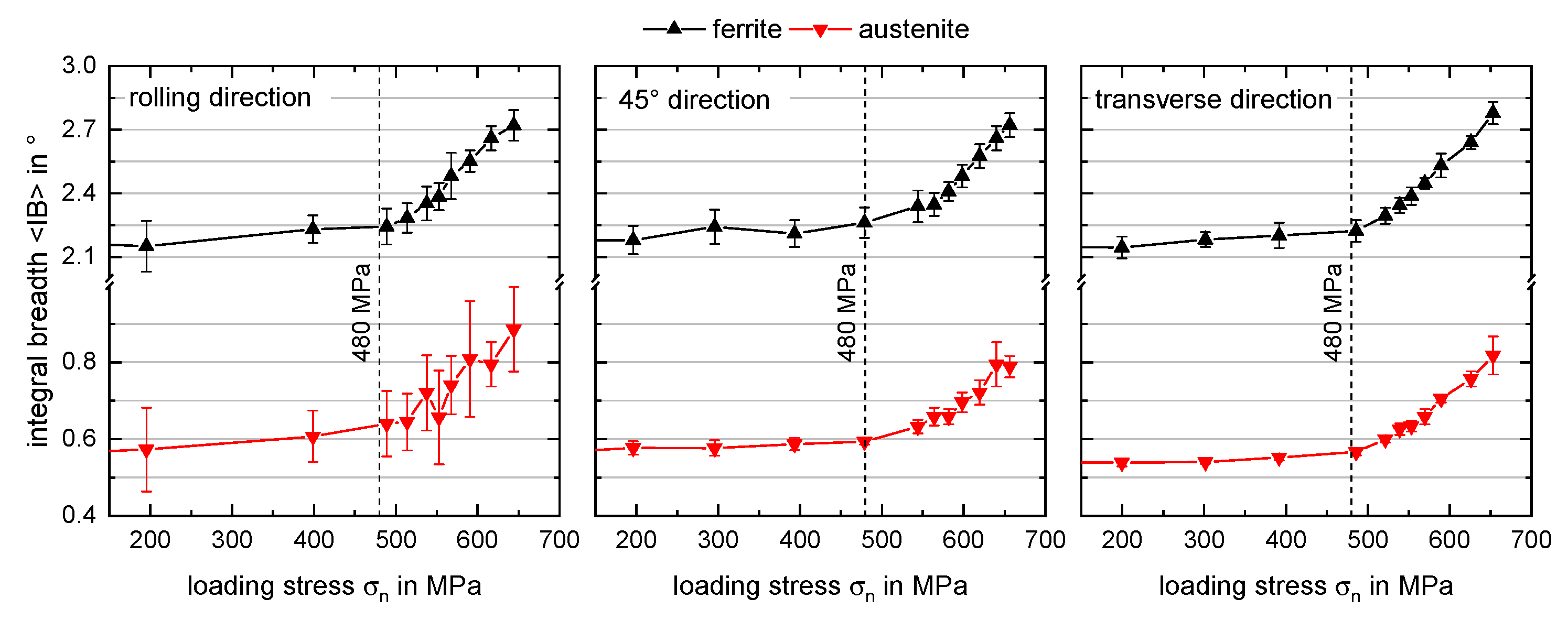
3.2. Evolution of Integral Breadths
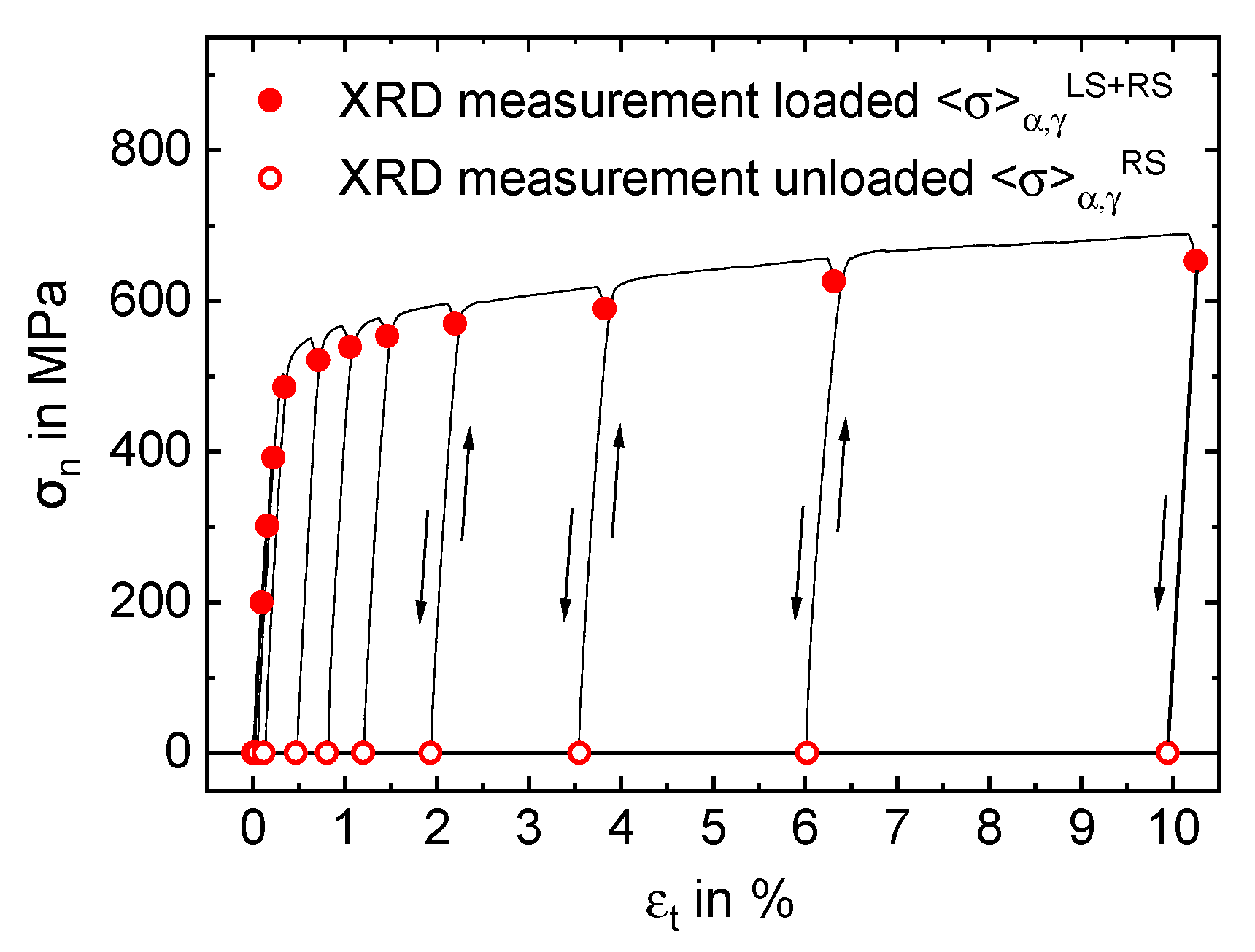
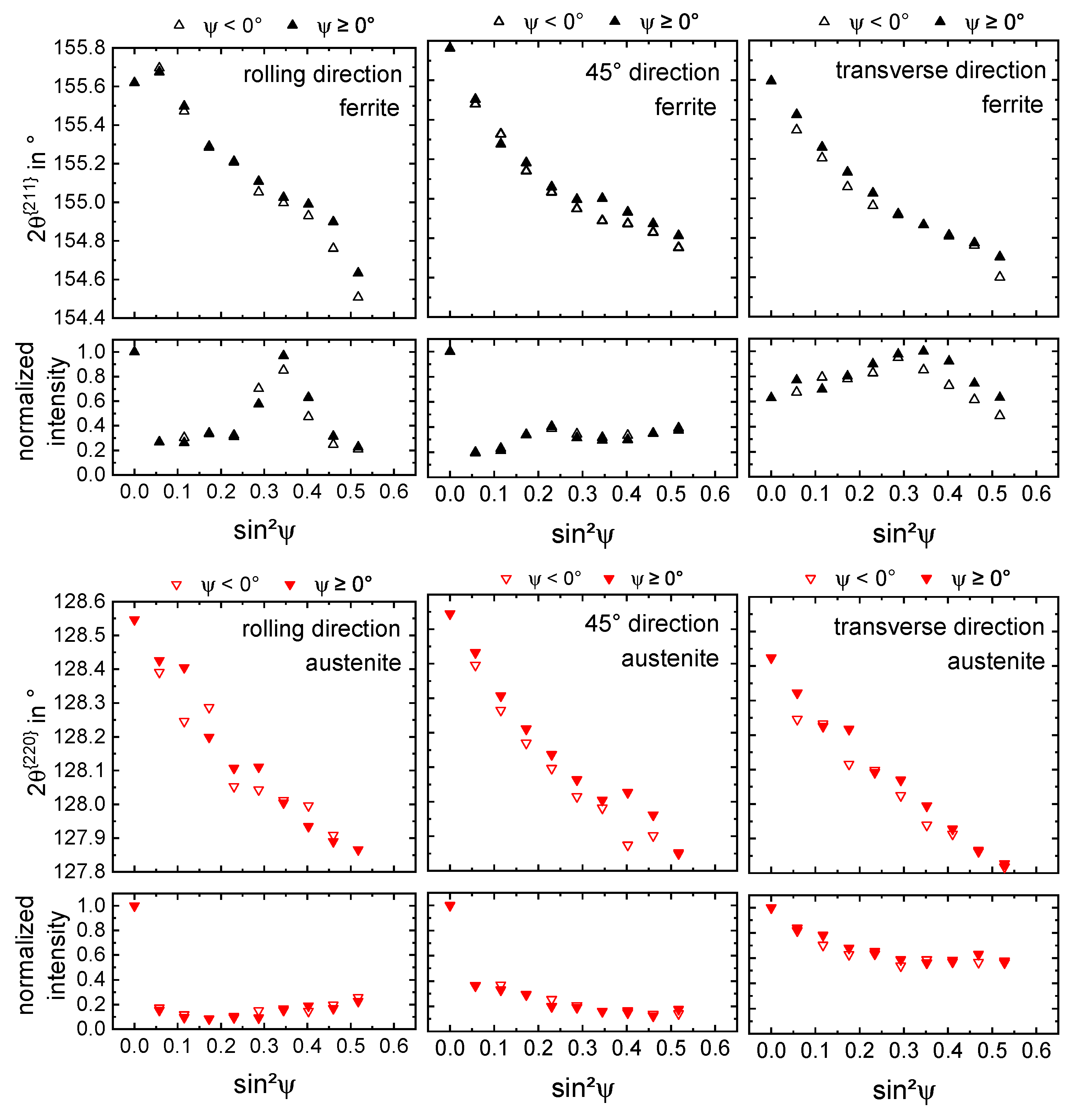
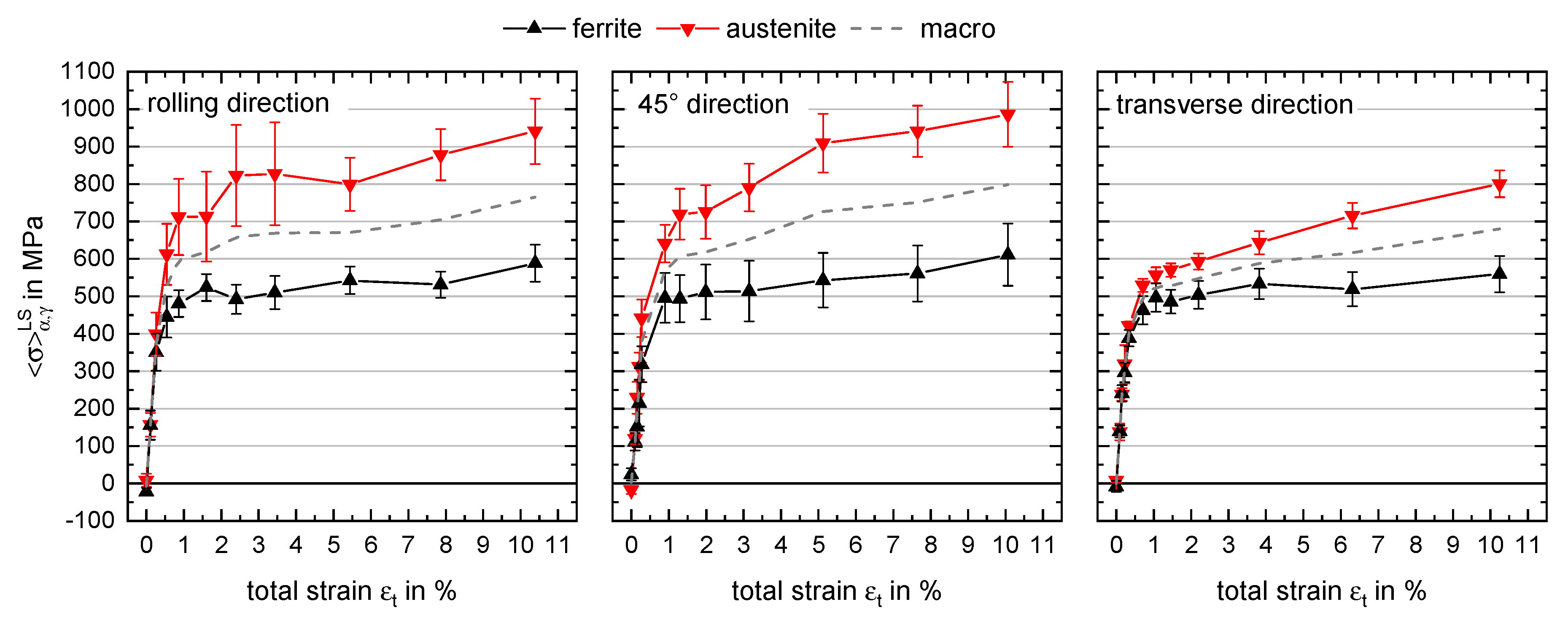
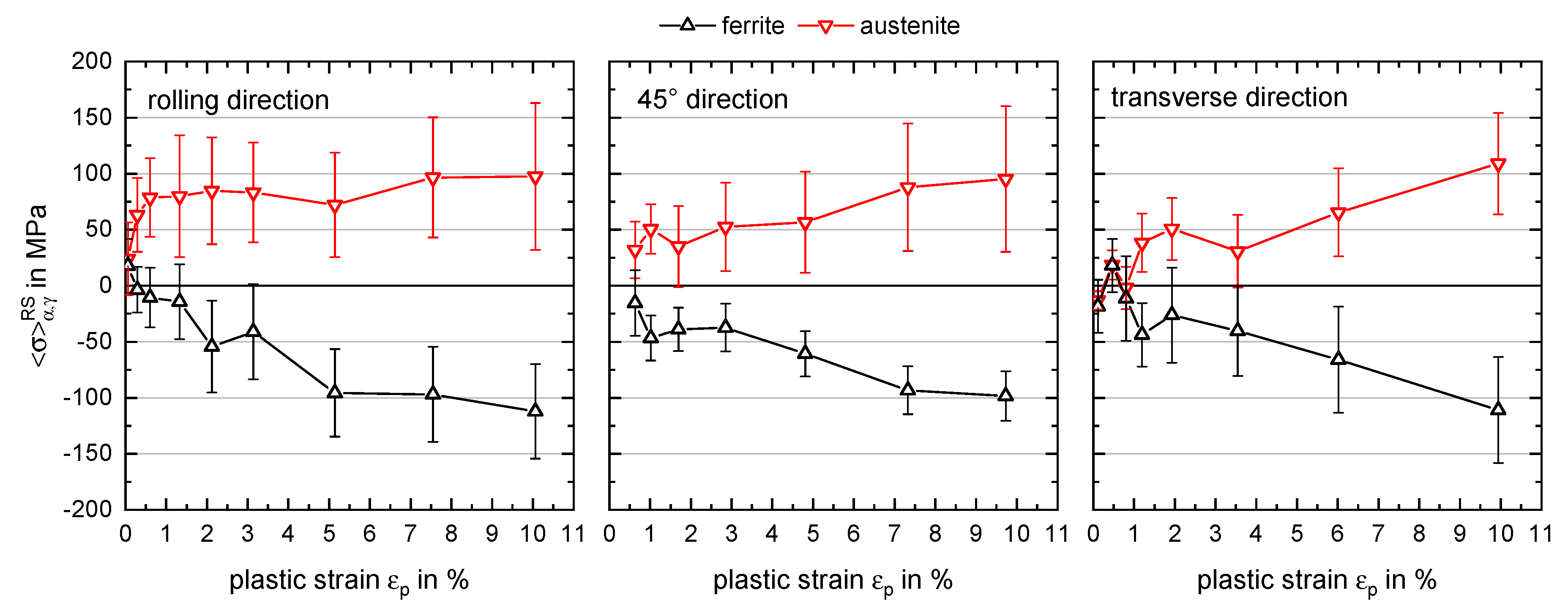
3.3. Load Partitioning Behaviour
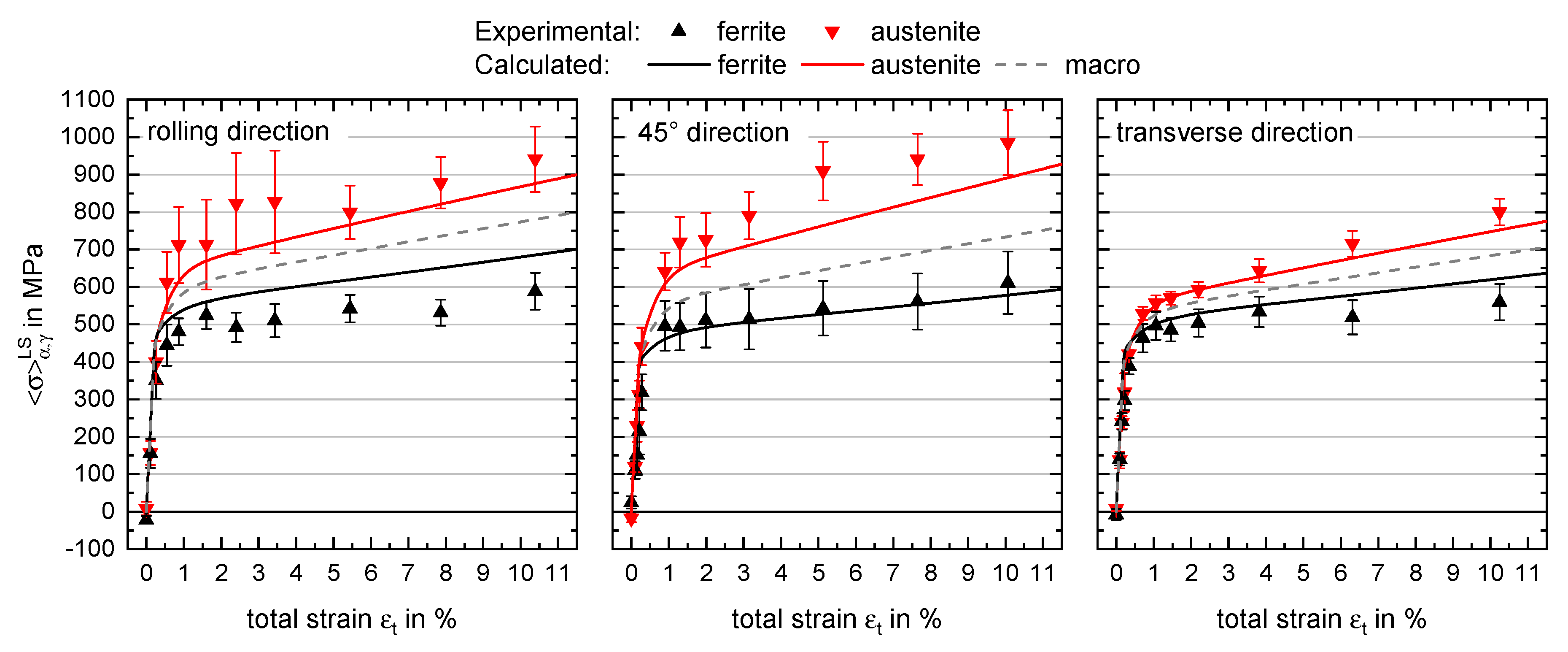
3.4. Numerical Results with Mean-Field Approach
4. Conclusions
- For the material state examined in this work, only minor evolution of crystallographic texture was observed for the given plastic deformations, which justifies neglecting texture development in the simulation.
- From the evolution of integral breadths of ferrite {211}- and austenite {220}-diffraction lines, it is concluded that only negligible differences in the phase-specific yield strengths exist.
- The austenitic phase possesses higher strength compared to the ferritic phase for all investigated directions of load application, resulting in the evolution of phase-specific residual stresses even for homogeneous plastic deformation. This is due to the smaller grain size of austenite and the solid solution strengthening by nitrogen.
- The proposed fast simulation approach based on phase specific strain hardening combined with macroscopic plastic anisotropy enables phase-specific RS simulation of satisfying accordance with experimental results. Deviations are caused in part by inaccuracies in the experimental approach, causing the neglecting of texture effects in the stress evaluation. Additionally, some deviations are due to the simplification of the phase specific plastic anisotropy approximated by the macroscopic Lankford parameters.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| XRD | X-ray diffraction |
| EBSD | Electron backscatter diffraction |
| ODF | Orientation density function |
| XEC | X-ray elastic constants |
| fcc | face-centred cubic |
| bcc | body-centred cubic |
| RS | residual stress |
| LS | loading stress |
| RD/TD/ND | rolling/transverse/normal direction |
References
- Behnken, H.; Hauk, V. On the influence of micro-residual stresses during cyclic loading. In Proceedings of the 3rd European Conference on Residual Stresses, Frankfurt, Germany, 4–6 November 1992; pp. 733–742. [Google Scholar]
- Hofinger, J.; Erdle, H.; Böhlke, T. Prediction of residual stresses of second kind in deep drawing using an incremental two-scale material model. Philos. Mag. 2020, 1–21. [Google Scholar] [CrossRef]
- Johansson, J.; Oden, M.; Zeng, X.H. Evolution of the residual stress state in a duplex stainless steel during loading. Acta Mater. 1999, 47, 2669–2684. [Google Scholar] [CrossRef]
- Inal, K.; Lebrun, J.; Belassel, M. Second-order stresses and strains in heterogeneous steels: Self-consistent modeling and X-ray diffraction analysis. Metall. Mater. Trans. A 2004, 35, 2361–2369. [Google Scholar] [CrossRef]
- Dakhlaoui, R.; Braham, C.; Baczmański, A. Mechanical properties of phases in austeno-ferritic duplex stainless steel—Surface stresses studied by X-ray diffraction. Mater. Sci. Eng. A 2007, 444, 6–17. [Google Scholar] [CrossRef]
- Tseng, C.M.; Liou, H.Y.; Tsai, W.T. The influence of nitrogen content on corrosion fatigue crack growth behavior of duplex stainless steel. Mater. Sci. Eng. A 2003, 344, 190–200. [Google Scholar] [CrossRef]
- Simon, N.; Erdle, H.; Walzer, S.; Gibmeier, J.; Böhlke, T.; Liewald, M. Phase-specific residual stresses induced by deep drawing of lean duplex steel: Measurement vs. simulation. Prod. Eng. 2019, 13, 227–237. [Google Scholar] [CrossRef]
- Matthies, S.; Humbert, M. On the principle of a geometric mean of even-rank symmetric tensors for textured polycrystals. J. Appl. Crystallogr. 1995, 28, 254–266. [Google Scholar] [CrossRef]
- Every, A.; Mccurdy, A. Landolt-Börnstein—Group III Condensed Matter, Second and Higher Order Elastic Constants; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar] [CrossRef]
- Ledbetter, H. Predicted monocrystal elastic constants of 304-type stainless steel. Phys. B+ C 1985, 128, 1–4. [Google Scholar] [CrossRef]
- Wolfstieg, U. Die Symmetrisierung unsymmetrischer Interferenzlinien mit Hilfe von Spezialblenden. HTM 1976, 31, 23. (In German) [Google Scholar]
- Warren, B.; Averbach, B. The effect of cold-work distortion on x-ray patterns: Jour. Appl. Phys. 1950, 21, 595–599. [Google Scholar] [CrossRef]
- Hauk, V.; Macherauch, E. Eigenspannungen und Lastspannungen; Hauk, V., Macherauch, E., Eds.; Carl Hanser Verlag: München, Germany, 1982. (In German) [Google Scholar]
- Kneer, G. Zur Elastizität Vielkristalliner Aggregate Mit und Ohne Textur. Ph.D. Thesis, Bergakademie Clausthal (TH), Clausthal-Zellerfeld, Germany, 1964. (In German). [Google Scholar]
- Kröner, E. Berechnung der elastischen Konstanten des Vielkristalls aus den Konstanten des Einkristalls. Z. Phys. 1958, 151, 504–518. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Hauk, V.; Nikolin, H.J. The evaluation of the distribution of residual stresses of the I. kind (RS I) and of the II. kind (RS II) in textured materials. Textures Microstruct. 1988, 8, 693–716. [Google Scholar] [CrossRef] [Green Version]
- Böhlke, T.; Bertram, A.; Krempl, E. Modeling of deformation induced anisotropy in free-end torsion. Int. J. Plast. 2003, 19, 1867–1884. [Google Scholar] [CrossRef] [Green Version]
- Bertram, A.; Böhlke, T. Simulation of texture induced elastic anisotropy of polycrystalline copper. Comput. Mater. Sci. 1999, 16, 2–9. [Google Scholar] [CrossRef]
- Foct, J.; Akdut, N. Cleavage-like fracture of austenite in duplex stainless steel. Scr. Metall. Mater. 1993, 29, 153. [Google Scholar] [CrossRef]

| C | Cr | Ni | Mn | Co | Si | Mo | N | Fe |
|---|---|---|---|---|---|---|---|---|
| 0.034 | 23.91 | 4.74 | 1.326 | 0.104 | 0.38 | 0.37 | 0.13 | balance |
| Phase | |||
|---|---|---|---|
| Ferrite [9] | 230 GPa | 134 GPa | 117 GPa |
| Austenite [10] | 209 GPa | 133 GPa | 121 GPa |
| Austenite | 420 | 640 | 3490 | 3.0 | |
| Ferrite | 380 | 427 | 21 | −5.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simon, N.; Krause, M.; Heinemann, P.; Erdle, H.; Böhlke, T.; Gibmeier, J. Phase-Specific Strain Hardening and Load Partitioning of Cold Rolled Duplex Stainless Steel X2CrNiN23-4. Crystals 2020, 10, 976. https://doi.org/10.3390/cryst10110976
Simon N, Krause M, Heinemann P, Erdle H, Böhlke T, Gibmeier J. Phase-Specific Strain Hardening and Load Partitioning of Cold Rolled Duplex Stainless Steel X2CrNiN23-4. Crystals. 2020; 10(11):976. https://doi.org/10.3390/cryst10110976
Chicago/Turabian StyleSimon, Nicola, Maximilian Krause, Paul Heinemann, Hannes Erdle, Thomas Böhlke, and Jens Gibmeier. 2020. "Phase-Specific Strain Hardening and Load Partitioning of Cold Rolled Duplex Stainless Steel X2CrNiN23-4" Crystals 10, no. 11: 976. https://doi.org/10.3390/cryst10110976
APA StyleSimon, N., Krause, M., Heinemann, P., Erdle, H., Böhlke, T., & Gibmeier, J. (2020). Phase-Specific Strain Hardening and Load Partitioning of Cold Rolled Duplex Stainless Steel X2CrNiN23-4. Crystals, 10(11), 976. https://doi.org/10.3390/cryst10110976