Lithium Niobate Single Crystals and Powders Reviewed—Part I

Abstract

A review of lithium niobate single crystals and polycrystals in the form of powders has been prepared. Both the classical and recent literature on this topic are revisited. It is composed of two parts with sections. The current part discusses the earliest developments in this field. It treats in detail the basic concepts, the crystal structure, some of the established indirect methods to determine the chemical composition, and the main mechanisms that lead to the manifestation of ferroelectricity. Emphasis has been put on the powdered version of this material: methods of synthesis, the accurate determination of its chemical composition, and its role in new and potential applications are discussed. Historical remarks can be found scattered throughout this contribution. Particularly, an old conception of the crystal structure thought as a derivative structure from one of higher symmetry by generalized distortion is here revived.

1. Introduction

Aside from being an important ferroelectric material, lithium niobate (LiNbO₃, LN) is linked to a gamut of pronounced physical properties. Practically little less than a myriad of technologically significant usages unfold from it in single crystal form. The keenest advocates of applications may easily list its versatility: “acoustic wave transducers, acoustic delay lines, acoustic filters, optical amplitude modulators, optical phase modulators, second-harmonic generation, Q-switches, beam deflectors, phase conjugators, dielectric waveguides, memory elements, holographic data processing devices”, among others (the cornerstone paper by Weis and Gaylord is herein quoted) [1]. Although it is an entirely synthetic material, back in the late 1970s, LN was important for the development of surface acoustic wave (SAW) devices; it took second place only to quartz in the market of single-crystalline piezoelectrics [2]. Today, nearly 70% of the radio-frequency filters based on SAW, are fabricated on LN single crystals [3,4]. As for the future, a glimpse of the role of this material to achieve practical integrated on-chip micro-photonic devices might be grasped as it is already considered the cornerstone in photonics, just as silicon has been for electronics [5,6]. Indeed, for little more than a decade, LN has been dubbed as ‘the silicon of photonics’, a statement which seems to be more precise nowadays given the breathtaking results recently reported by Zhang et al. [7]. Such implications have been confirmed and updated by the same group [8]. It is “the workhorse material in optical communication applications”, it has been elsewhere stated [9]. Hence, credit is here given to Pang et al., having stated that LN is one of the most favorite multifunctional crystals [10]: other important applications (potential and already achieved) are to be succinctly described all over the review.

The main goal of this review is to expose in a convenient and ordered way the primary elements necessary to explicitly state/understand the scientific paradigm shared by the community advocated to investigate LN [11]. In short, and on a first level, it relies upon solid state physics, chemistry, and crystallography: the crystalline state of matter is very stable, ruled simply in terms of electric charge stabilization and bonding considerations, and the ascribed physical properties to a given crystal are deeply related to its chemical composition and crystal structure. Secondly: on regular circumstances of growth, LN is a congruent melt crystal whose chemical composition at room temperature (and for a broad range of higher temperatures) is nothing more than a macrostate of its crystal structure, the latter being characterized by the presence of intrinsic defect clusters composed of Li vacancies and Nb_Li antisites. However, solid solutions can adopt a continuous range of chemical compositions. Upon different mechanisms, a physical instance close enough to the stoichiometric point can be reached, among which, doping with various kinds of elements (filling the voids) is aesthetic.

Some terms and concepts are to be revisited in accomplishing this goal, such as how the crystal structure is introduced in recent literature (Section 3). In this respect, we reintroduce the idea once developed by famous crystallographer Helen Megaw on conceiving the structure of ferroelectrics as variants of the family of distorted perovskites [12,13,14]. To our judgment (and best of our knowledge), the best introduction to the LN crystal structure has been made by Räuber [2], who acknowledged the work by Megaw, so that it builds it up, step by step, starting from a reparameterization trick of the atomic positions introduced by the latter. Also, some of the indirect methods to determine the chemical composition accurately (CC) of LN powders (LNPws) are discussed; important references are highlighted for the case of single crystals (Section 4). On the other hand, ferroelectricity is often associated with LN: it is both historically and practically relevant. In this review, a succinct recount is also given on how the main ideas to explain the mechanisms behind ferroelectricity have changed over time (Section 5). In this 2020, we celebrate that a century ago, Ph. D. student Joseph Valasek gestated the field of ferroelectricity by presenting his results on the Rochelle salt at the American Physical Society meeting [15,16].

Further insight could be obtained by adopting the ideas by Megaw. For example, the slight differences between the stoichiometric (ST) composition and near-ST (nST) compositions could be studied on mathematical grounds (theoretically or by simulation) in terms of a continuous set of distorted structures and local symmetry variations parametrized by a kind-of-ordering parameter of small change. It would hardly be explained in terms of the CC itself: as it is the case of the congruent composition, which is disputed to fall in between 48.38 and 48.60 mol % of the Li content [17], the ST point is probably yet undetermined as well (Section 4). This subject is discussed along with the basic principle of adjusting the stoichiometry by elemental doping. Lately, the mainstream idea of reverting the nominal off-stoichiometry of LN by an effective elimination of site and antisite point defects through doping with metal ions has permeated increasingly. It implies nothing else than the controlled interchange of intrinsic and extrinsic defects, and although it seems quite natural or intuitive, such conception is revisited in Part II of this paper. The potential use of nanocrystalline LN powders (LNPws) in a wide range of applications has been recently highlighted [18,19]. These will be revisited and further extended within the present contribution. Remarkably, the role of LNPws towards effectively reducing the amount of lead in commercial piezoelectrics based on complex ternary and four-component systems is treated, among others (Section 4).

2. Basic Notions and Early Developments

In the words of Volk and Wöhlecke, authors of the most comprehensive monograph written up to date on LN, this type of crystals are “colorless, chemically stable and insoluble in water and organic solvents, and have high melting points” [20]. By colorless, it is meant a high transparency window of the order of <0.1 cm⁻¹ for radiation between 400 and 5000 nm [21]. This, combined with the fact LN crystals are non-centrosymmetric and have a high nonlinear coefficient, makes them suitable materials for the second harmonic generation and optical parametric generation in this range of the electromagnetic spectrum. High melting points along with a high Curie temperature (T_C~1200 °C) translates into the exhibition of a spontaneous polarization (ferroelectricity) in a broad range of temperatures. In its classic text, Räuber states, on the other hand, that LN “is a fairly useless material from a chemical point of view, its only application being as a starting material for crystal growth” [2].

The LiNbO₃ phase was first described by Zhachariasen in 1928 [22], who is considered one of the giants in crystal structure analysis, alongside Pauling and Belov [23]. The first-ever synthesis of LN can be traced back to 1937 [24,25]: small crystals having the shape of small prisms were obtained, although this information could not be corroborated in the present bibliographical survey. Remeika is credited with having grown large-single crystals for the first time a little before 1949 and, in this year, the same and Matthias published the first report on the ferroelectric behavior of such crystals [26,27]. In 1965, Ballman—and Fedulov et al., this is not often mentioned in recent literature—managed to grow larger crystals using the Czochralski method [27,28,29]. Since then, a parallel growth in scientific and engineering activities took place, remarkably at the Bell Laboratories, and ever since this pioneering work (published in 1966, five papers), details on the structure of this material are known to a high precision [30,31,32,33,34]. Particularly, [32,33,34] constitute a paramount contribution to the whole scientific community involved in the study of LN: they form the basis of all further discussions on the LN structure.

Solid solutions (SSs) of LN are characterized by showing a compositional change, parametrized by the ratio R = {Li}/{Nb} (the brackets denoting concentration in mol %). Single crystals have an intrinsic nature to deviate from the stoichiometric (ST) point R = 1. It can be readily seen in Figure 1, showing the binary phase diagram that describes the Li₂O—Nb₂O₅ system. Another important point—or perhaps the most important—is the congruent (CG) one R = 0.944, for which the highest uniformity of properties is attained. This point is so-called CG because, as shown in Figure 1, within the LN phase, an inflection on the liquidus–solidus curve takes place at this point, implying preservation of the CC in the process of passing from the Li₂O:Nb₂O₅ melt to the growing crystal. Said differently, CG means R_melt(liq) = R_crystal(sol) = 0.944. For off-congruent melts, the as-grown crystals are compositionally non-uniform, particularly along the growth axis, due to slight variations in the melt and crystal compositions in the growth process [20]. Different two-component phases delimit the LN phase, homogeneous mixtures of LN, and a SS of a secondary phase: methaniobates Li₃NbO₄ and LiNb₃O₈. Because of the preference of single or pure phase compounds over those with a mixture of phases, added to the fact that sub-CG compositions of LN present poor physical properties, these have been elsewhere referred to as ‘parasitical’ [35]. Interestingly, in the presence of Li₃NbO₄ (LiNb₃O₈), the existent SS of single-phase LN is of fixed ST (most defective) composition: in these cases, the formation of the parasitical phases compensates the excess (deficiency) of Li. Figure 1 is redrawn from the publications by Volk and Wöhlecke [20], and Hatano et al. [36].

In general, under regular growth circumstances, high-quality ST crystals are not obtained even for a R_melt(liq) ≥ 1. In fact, nST crystals were available until 1992, year in which three independent methods for this purpose were reported, entailing a modification to the growth method combined with Li enrichment in the melt (double crucible Czohralski method) [37], lowering the crystallization temperature by use of melts containing 6 wt % K₂O [38], and diffusion of Li from a powder richer in this element than the crystal (this process takes several days and requires high-temperature annealing treatments, c.a. to 1100 °C) [39]. Five years later, the K₂O-based flux method was revisited by Polgár et al. [40], and from a conceptual refinement, it has been after that addressed as high temperature top seeded solution growth (HTTSSG). In the early 2000s, this method became popular; Polgár et al. (2002) demonstrated that the stoichiometry of the crystal could be further improved by using a solution or flux with starting compositions [K₂O]/[LiNbO₃]~0.16–0.195 and R = 1 [41]. Today, the synthesis of LN single-large crystals with ST composition still is a state-of-the-art matter: a piece of an ST crystal costs nearly 12 times more than an equivalent (cut and dimensions) CG one [19]. LN crystals with a strict stoichiometry are important because a perfect lattice translates into a lower density of local field distortions and the lessening of anharmonic crystal interactions (phonon coupling) prerequisites for any kind of resonance with a small linewidth [20]. The unsolved problem of supply and demand of sLN crystals has already been identified, and the development of a growth technique to fabricate them is urgently needed, without being unpractical or expensive [17]. Recently, the HTTSSG method has been reviewed, the earliest developments in this field and its dynamic progress leading to new generation technologies of crystal growth are also discussed [42].

On the other hand, from our paradigm (explicitly stated above, see the Introduction), it follows that the exacerbation/detriment of a physical property attributed to LN can be tuned by proper control of point defects. Considering only intrinsic defects, most of the measured coefficients follow a tendency to favor nST compositions with respect to compositions with a higher population of defects, as shown in

Table 1. Optical and non-optical coefficients for LN single crystals with congruent (CG) and near-stochiometric (nST) compositions—as given by Volk and Wöhlecke in Ref. [20].

Property	CG	nST
OPTICAL
Transparency region (nm)	320–5000	300–5000
Refractive index @ 633 nm (no, ne)	(2.286, 2.203)	(2.288, 2.190)
Electro-optical coefficient @ 633 nm
$r_{33}^T$, $r_{31}^T$, $r_{22}^T$ (pm V−1)	32, 10, 6.8	38, 10.4, ---
$r_{33}^S$, $r_{31}^S$, $r_{22}^S$ (pm V−1)	31, 8.6, 3.4	---, ---, 4.5
Nonlinear optical coefficient @ 1060 nm
d33, d31, d22 (pm V−1)	34, 6, 3	42, 5, 2.5
NON-OPTICAL
Crystal structure	Trigonal
Space and point group (RT, hex)	R3c, 3m
Lattice constant aH (pm)	515.0	514.7
Lattice constant cH (pm)	1386.4	1385.6
Melting point (°C)	1255	<1200
Curie temperature (°C)	1140	1206
Density (g cm−1)	4.647	4.635
Thermal expansion @ 300 K
αa 10−6 (K−1)	14.1	14.1
αc 10−6 (K−1)	4.1	6.0
Specific heat at RT (kJ kg−1 K−1)	0.628	0.651
Thermal conductivity at RT (W m−1 K−1)	3.92	5.97
Spontaneous polarization (µC cm−2)	71	62
Dielectric constant
${\epsilon }_{11}^T$, ${\epsilon }_{33}^T$, ${\epsilon }_{11}^S{\epsilon }_{33}^S$	84, 30, 44, 29	54, 42, 42, 41

; as it is discussed in Part II of this review, sLN crystals are particularly important for applications involving interaction with high energy laser light. In the case of the Curie temperature T_C—the temperature at which the paraelectric-ferroelectric phase transition turns out in most perovskite-type materials—its sensitivity to the CC can be readily seen in the phase diagram (Figure 1), not only for two fixed points but rather continuously on the whole range of the LN single-phase. To determine the CC (or the Li content within the crystal c_Li) using an empirical linear equation having T_C as the independent variable is nowadays a standard method [43].

Because it is a light element, the Li concentration within SSs of LN can be directly estimated only by chemical methods: chromatography [44], atomic absorption analysis [45], and inductively coupled plasma atomic emission spectroscopy (ICP-AES) [46]. Apart from being destructive, these methods also consume large amounts of material and offer low precision (no better than 0.2 mol %) [3,47]. Likewise, the use of calorimetric methods for the determination of T_C has the main drawback of reaching T values very close to the melting point of the material (see Figure 1). In 1993, Schlarb et al. [48] and Malovichko et al. [49] independently revived the practical importance of other indirect methods to describe the CC of single crystals. These are shown in

Table 2. Some indirect optical and non-optical methods for the determination of the chemical composition of LN single crystals.

Method	Measured Parameter	Equation; Accuracy (mol %)	References
OPTICAL
Fundamental UV optical absorption	fundamental absorption edge	nonlinear; 0.02	[51,52]
Polarized Raman spectroscopy	linewidth of Raman modes	linear; 0.05	[47,48,49]
Unpolarized infrared spectroscopy	intensity ratio I3480/I3465 of peaks located at the wavenumbers in subscripts	linear; 0.01	[53,54]
Sellmeier equation	refractive index (extraordinary)	nonlinear; ---	[55]
Dispersion of birefringence	refractive index (ordinary and extraordinary)	linear; <0.01	[47,48,49]
Phase matching T for second harmonic generation (SHG)	phase matching T for SHG	linear; <0.01	[39,56,57,58,59]
spontaneous noncolinear frequency doubling	cone angle	nonlinear; ---	[60]
Holographic scattering (photorefractive effect)	reading and writing angles with respect to the normal of the crystal surface	---; ---	[61]
NON-OPTICAL
Melt composition	Li2O content of the melt	nonlinear; 0.3	[46,47,62]
Differential thermal analysis	Curie temperature	nonlinear/linear; 0.1	[39]/[43]
X-ray and neutron diffraction + structure refinement	cell volume	linear; 0.3	[45,63]
Density measurements	Density	---; ---	[45,64,65,66]
Nuclear magnetic resonance (NMR) and electron paramagnetic resonance (EPR)	linewidth of NMR and EPR signals	linear for Fe doping concentrations smaller than 0.01 mol %; ---	[49,67,68]
Velocity of surface acoustic waves (SAW)	velocity of SAW	---; 0.01	[69,70]

, among others. Notice that [48,49] were published just one year after nST single crystals were available, their novel content can be outlined in three main aspects: (1) introducing a new chemistry, the ternary system K₂O—Li₂O—Nb₂O₅, “responsible for the unexpected growth nST LN single crystals” [49]; (2) characterization covered almost over the whole compositional range; and (3) information on the crystal composition instead of the melt composition. We consider these contributions are nowadays seminal because they reviewed and informed our community about the number of different methods to describe the CC of LN single crystals. Such information was back then scattered throughout several publications. The review was extended—perhaps improved—three years later [47]. Also, it might be more precise to credit Vartanyan (1985) for point 1 above [42,50].

The inexorable tendency of LN to crystallize with the CG composition has been introduced above from a phenomenological point of view. To understand the why and how of the formation of the type of intrinsic defects or lattice imperfections involved, a formal discussion of a proper defect model must be given (Part II). In this respect, the description of the crystalline structure should precede. It will soon be treated in the next section. Not without addressing, however, additional comments of historical relevance.

Nowadays, a broad consensus exists in our community regarding the LN crystal structure as a ‘pseudoilmenite’ [20]. Thus, a side has been taken on the once important debate on whether it could be formally considered ilmenite or if it would better be conceived as a highly distorted perovskite [14]. As already said, in 1928, Zachariasen described it for the first time in history [22]. Reference [22] could not be consulted to write the present manuscript. However, by reading the first report on the ferroelectric behavior of LN (and isostructural LiTaO₃) by Matthias and Remeika (1949), it can be inferred that Zachariasen originally described the crystal structure of LN as being isostructural to that of ilmenite [FeTiO₃]. By putting the original mineral composition inside square brackets, the whole family of ilmenite structures is meant, according to the convention introduced by Muller and Roy [71]. Matthias and Remeika had already pointed out that something did not fit entirely by assuming that LN crystals adopt [FeTiO₃], stating that whereas the latter is a centrosymmetric structure, at the same time, “the existence of a spontaneous polarization […] indicates the absence of a center of symmetry” [26]. If LN manifested ferroelectric behavior, then why would it adopt a centrosymmetric structure?

By 1952, the ilmenite-type picture persisted, a year in which a second article was written by Schweinler [72], anecdotally under the same title as that of Matthias and Remeika: “Ferroelectricity in the Ilmenite Structure” (Schweinler cites the work of the other!). Although the title is invariant to references [26,72], apart from the content, they differ by a trifle: whereas the most recent one indeed labeled LN as LiNbO₃, the one that precedes did it as ‘LiCbO₃’. Historically, niobium (in Greek mythology, the daughter of Tantalus) was originally named ‘columbium’ in honor of America, the continent whence the mineral arose. In 1950 (149 years after its discovery), the International Union of Pure and Applied Chemistry (IUPAC) adopted ‘niobium’ as the official name [73]. In 1954, Megaw put perovskite into the scene, refuting kinship between LN and ilmenite. In her own words: “it is misleading to classify the LiNbO₃ structure as a member of the ilmenite family” [12]. Her explanation was based on the results presented in the doctoral thesis by Bailey [74], which is acknowledged to be the first extensive study on the LN crystal structure (at room T, RT). Bailey was the first to show that the LN crystal structure at RT is not identical to ilmenite due to a different stacking sequence of the cations. Nevertheless, according to Räuber, the ideas by Megaw were widely accepted in the 1970s [2].

3. Crystal Structure

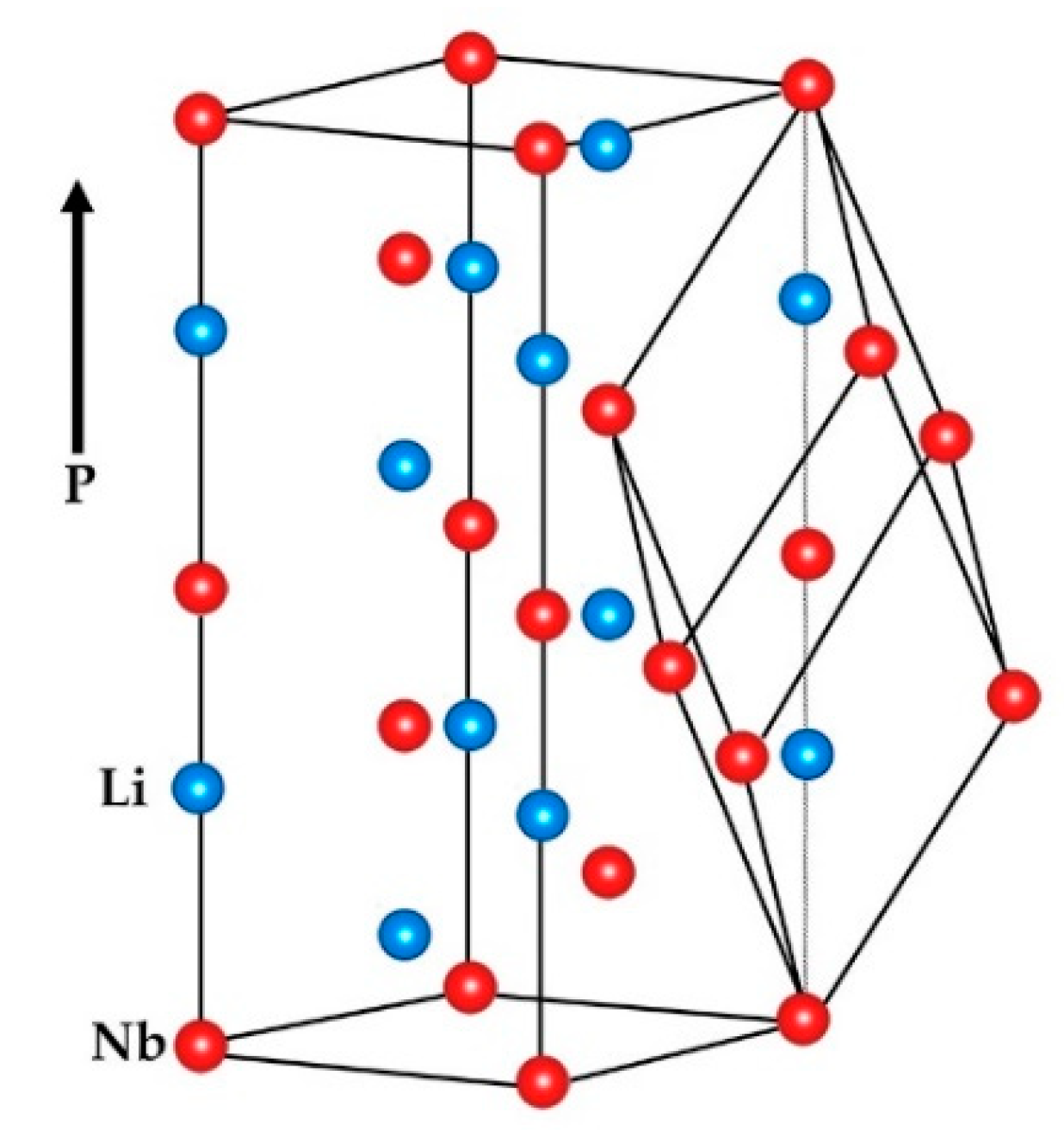
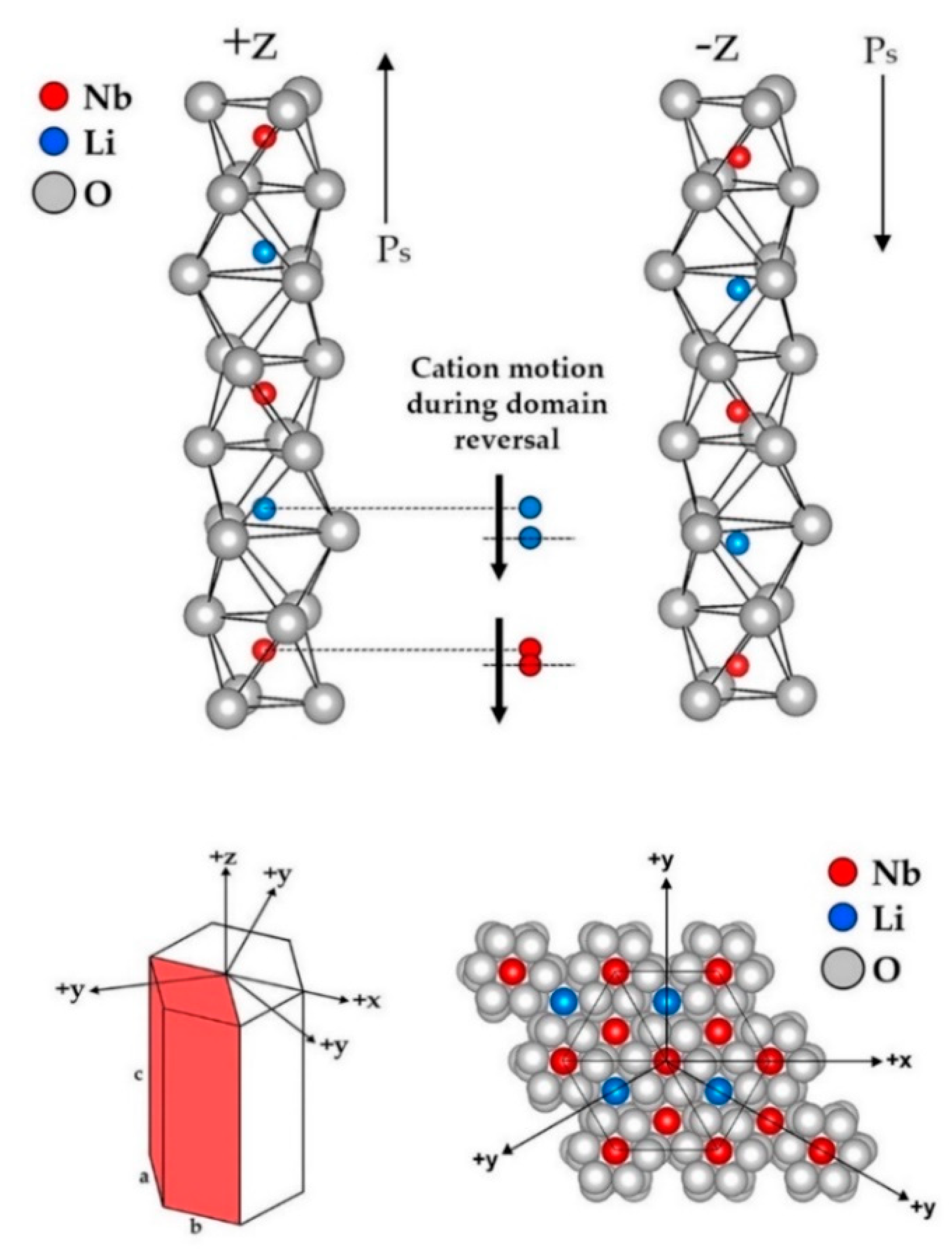
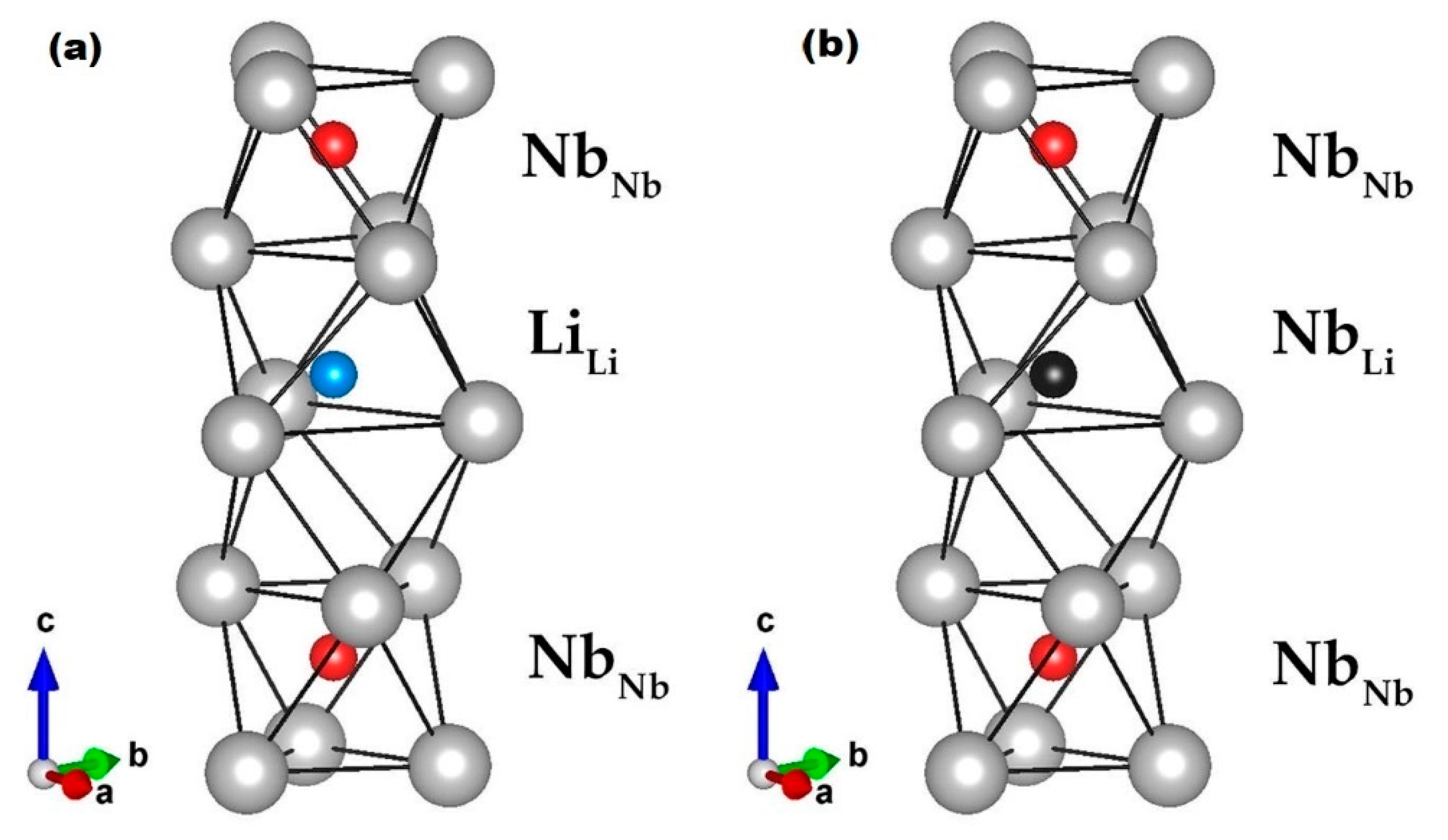
3.1. Modern/Practical Viewpoint

When the crystal structure of lithium niobate (LiNbO₃, LN) is nowadays addressed in a theoretical framework, little or nothing new can be added. This subject has been extensively studied, formulated, and re-formulated over time. All angles and edges have been covered. One thus has no other option than to re-tell the story as close as possible to an original and recent source because, after decades of work and a myriad of written reports, the story can hardly be better told. This being said, the present section thus saves ink and paper by being limited in describing the crystal structure of LN succinctly. The minimum of references needed to acquire comprehensive knowledge on this subject is provided.

We believe that the story of the LN crystal structure has been better told in the classic text by Räuber (1978) because the concept, which is a complex one, is therein built up step by step, details on pertinent symmetry issues are given along with a series of intermediate visual aids that contribute to a better understanding of the actual array of atoms [2]. Conversely, most consulted references limit themselves to treat it very succinctly by a text 1–2 pages long and a lone figure. See, for example, [1,75] which also excel in this subject and, because they are more recent, they may provide more reliable experimental data than [2]: atomic positions, lattice dimensions, phase transition temperatures, and compositional variations. Weis and Gaylord (1985) provide a detailed discussion on the symmetry elements of the point group pertaining to the ferroelectric phase (trigonal, space group R3c, point group 3m), sense of the c-axis, and cleavage plane [1]. They also describe the two most common choices of axes or unit cell abstractions (ferroelectric phase): hexagonal and rhombohedral. These two choices are convenient for crystallographic purposes, the latter being the most popular to describe the LN crystal structure. Both are merged into Figure 2; redrawn from the publication by Sanna and Schmidt [75,76]. For most physical applications, the tensor properties are neither described in terms of the hexagonal system nor the rhombohedral. The cartesian system is rather used, denoted as ‘orthohexagonal’ in [2]. Its conventional definition in terms of the hexagonal system is given in [1]. Hence, while the structure description given by Räuber stands out from the others, perhaps the best approximation to it relies on properly combining and adapting the information found in [1,2,76]. Complementary information or a different way to introduce the concept may be consulted from [17,77]. Besides, Räuber considered the description by Megaw [12,13,14], namely by assuming that the LN crystal structure results from a set of large distortions of the atomic arrangement within a reference structure of higher symmetry, the ideal cubic perovskite. In this case, a fourth unit cell abstraction is introduced, the ‘pseudocubic’ setting [2].

Figure 3 (redrawn from the publication by Gopalan et al. [77]) shows a scheme of the LN crystal structure (stoichiometric composition) stable for T < T_C ~1210 °C (ferroelectric); as before mentioned, the Curie point moves according to the chemical composition, roughly from 1100 to 1200 °C. The basic net is formed from six equidistant plane layers of oxygen per unit distance, stacked in the direction of the polar axis c [2]. The essential feature to be noticed from the low-T structure (non-centrosymmetric, space group R3c, point group 3m) is the partial filling of the octahedral interstitials in c-row: one-third filled by Li ions, one-third by Nb ions, and one-third are empty. This situation can be schematically depicted as –Li—Nb—□—Li—Nb—, where □ denotes a vacant octahedral site, also referred to as the structural vacancy. The Li octahedron is larger than the Nb one. Such a distorted octahedral environment is addressed to a transition from the nonpolar or paraelectric phase (for T > T_C, centrosymmetric, space group $R\overline{3}c$, point group $\overline{3}m$) to the paraelectric phase as T decreases. Small displacements of the Li and Nb cations are involved with respect to the oxygen layers and along the c-axis, measured to be 45 and 25 pm, respectively [34,75]. The displacement of oxygens is neglected in first order (~6 pm), and, thus, the oxygen framework is assumed to be fixed [34]. In the paraelectric phase, the Li cations are localized within the oxygen planes, whereas the Nb cations are in the center of the oxygen octahedra, that is, in between the planes.

It is important to realize, however, that such a scheme is an idealized one. Remind that, under regular circumstances of growth, LN single crystals are off-stoichiometric. Instead, the congruent (CG) composition prevails, characterized by an excess of Nb. It can be understood in terms of crystal chemistry: during crystallization, Li vacancies form in the unit cell with ease, since in the crystal the Li–O bond is significantly weaker than the Nb–O one [17]. Thus, it is natural to reason that Li deficiency implies an Nb surplus, or better said, “a decreasing Li content is accompanied by increasing content of the heavier Nb” [75]. However, how do these tendencies simultaneously conciliate as to have a stable LN solid solution? The occurrence of a stacking fault envisioned as the relatively excess Nb partially occupying Li vacancies, has been proposed and termed Nb antisite (Nb_Li) [64,78]. It is schematically shown in Figure 4, redrawn from the publication by Volk and Wöhlecke [75] The existence of this type of antisite defects has been repeatedly proven by detailed structure studies [45,63,65,79].

3.2. Earlier Thoughts: Relation to Basic Structures of Higher Symmetry

Following the short discussion presented by the end of Section 2, Megaw referred to the structures of ferroelectrics (that of LN per se) as pseudosymmetric structures of polar symmetry that result as a competing effect between isotropic (ionic character) and directed (covalent character) binding. She assumed that the LN crystal structure for the paraelectric phase at high T was the ideal cubic perovskite—back then, the experimental information was only available for temperatures far below from the Curie temperature of LN. Then, she proposed the continuous transition to the ferroelectric phase structure under the hypothesis of a monotonical increment of the covalent character as T decreases, as far as the overall binding characteristics are still mainly ionic [12]. Indeed, 12 years later, Abrahams et al. (1966) concluded (also supported on the results by Peterson [80], cited in Ref. [28]) that LN “is not primarily an ionic crystal, but one in which directed, largely covalent, bonds play a determining role” [32]. Remarkably, the prediction by Megaw (the covalency role in ferroelectrics) reverberates until today because it agrees to the current most widely accepted theoretical framework regarding the innermost cause of ferroelectricity, that is, the stabilization of structural distortion through second-order Jahn Teller effects (see further discussion in Section 5). Moreover, it is interesting to notice that (apparently) back in 1954, Megaw was not aware of the work by Buerger (1947), who in the spirit of explaining the ‘genesis of twin crystals’ and superstructures, developed a formalism to describe some of the relations pertaining to a crystal structure called the basic structure, as contrasted to derivative structures derived from it by (mathematical) generalization [81,82]. The derivative structures would always present lower symmetry with respect to the basic structure. According to Bärnighausen, who refined and further extended the ideas of Buerger into the so-called Bärnighausen trees [83,84], Megaw (1973) herself introduced the terms arystotype and hettotype as synonyms of the basic and derivative structures, respectively [85]. These terms are nowadays widely accepted and used.

The structural family of perovskites is perhaps the best available example of distorted hettotypes. Most perovskite compounds are distorted and do not crystallize in the ideal cubic structure as SrTiO₃, and other few compounds do at RT [84,86,87,88]. It is believed that of all the structures adopting this crystal structure, only about a 10% adopt the ideal cubic one [88,89]. Even the original mineral composition CaTiO₃ is known to be slightly distorted [86,88]. Thus, SrTiO₃ is naturally regarded as the high-symmetry reference, the aristotype prototype within this crystal structure family. It also happens to be the stable phase at a high T (paraelectric) for most ferroelectrics based on perovskite oxides [90]. Before introducing the main aspects of the conceptualization conceived by Megaw, first, the documented quantitative analysis of how the perovskite crystal structure relates to some of its derivative structures by distortion is discussed. An introduction to the details of this crystal structure can be consulted elsewhere [84,86,87,91,92].

Three main types of distortion or framework perturbation in ABO₃ compounds adopting a perovskite crystal structure have been identified: (1) tilting or puckering of the octahedral framework, (2) B-cation displacements within these octahedra, and (3) tilting of the BO₆ octahedra relative to one another as practically rigid corner-linked units [88,92]. An example of how the ilmenite structure can be derived in successive steps from the ideal perovskite structure by octahedral tilting has been described by Johnsson and Lemmens [86]. The distortions may occur separately or in combination, just as one is hardly addressed to a single effect responsible for the distortion, these being mainly: size effects, deviations from the ideal composition, and the Jahn–Teller effect [86]. Focusing on the size effects, these can be quantitatively described in terms of the Goldsmith tolerance factor (GTF), which “reflects the structural distortion, force constants of binding, rotation and tilt of the octahedrons” [87]. Naturally, one may ask: how far from the ideal packing can the framework of BO₆ octahedra be perturbed by substituting cations of different ionic radii, and still being ‘tolerated’ by the perovskite structure? The GTF estimates the degree of distortion, or better said, “the structural frustration of the cubic perovskite structure regarded as an ionic solid” [91]. It is defined as the ratio [84,86,89,91,92] (in the discussion that follows, these references have been indistinctly used)

$$t=\frac{r_{AO}}{\sqrt{2}{r}_{BO}}=\frac{r_A+r_O}{\sqrt{2}\left(r_B+r_O\right)},$$

(1)

where the r terms are bond lengths calculated as sums of ionic radii and $a=\sqrt{2}{r}_{AO}=2r_{BO}$ is the geometrical definition of the a-axis within the ideal cubic cell. In using this equation, the ‘effective’ ionic radii are typically used, after Shannon and Prewitt [93]. Both cations can be accommodated in the ideal cubic perovskite SrTiO₃ if t = 1, thus having the optimal cation-anion bond lengths, in which case $\left(r_A, r_B, r_O\right)=$ (1.44, 0.605, 1.40) $\dot{A}$. Perovskites still could form for deviations from unity, typically in the range t: 0.8–1.1. In such cases, the degree of distortion from cubic symmetry increases, whereas the thermodynamic stability decreases with increments of the absolute value of (1 − t)² [92,94]. A tolerance factor less than unity indicates that the A cation is small compared to the site bounded by the oxygen octahedra. Under these circumstances, the A cation cannot be effectively bond to as many as 12 oxygen atoms, a situation that typically leads to a structural distortion by means of cooperative tilting of the octahedra. It is the most commonly occurring type of distortion. The prototypical cases include the mineral perovskite CaTiO₃ and the compound GdFeO₃; for both t = 0.81, as $\left(r_A, r_B\right)$ = (1.107, 0.78) $\dot{A}$. The arrangement of atoms is still considered to be of cubic symmetry in the range of 0.89 < t < 1. The ilmenite structure is stable for values of t less than 0.8. According to Kubo et al., either ilmenite or corundum are adopted by compounds for which $r_A~r_B\approx$ 0.7 $\dot{A}$. Ilmenite is favored in the cases when the A and B cations are largely different in terms of electric charge and electronegativity [95]. By further lowering the value of t, a strongly distorted structure would be favored down to the extreme of having a very low coordination number of 6 for both cations, as in the LN structure.

A review on phase transitions between these three polymorphs (LN, ilmenite, and perovskite) on titanates and related systems reveals a trend of ilmenites transforming into perovskite [CaTiO₃] at high pressures, which then quench to the LN structure on pressure release [92]. By applying pressure, the LN structure transforms reversibly to the perovskite one. Interestingly, at RT for both phase transitions [FeTiO₃] (ilmenite) → [CaTiO₃] and [LiNbO₃] → [CaTiO₃], the same amount of pressure is needed (around 16 GPa) [92,96,97,98]. Thus, the type and extent of distortion are sensitive to the (T, P) pair, and in the account of the same discussion, the LN phase can only be obtained, in the sense of a hettotype, as a quench product of perovskite at a high P, previously obtained by exerting pressure on an ilmenite structure. The GTF for the initial ilmenite must be restricted to be less than 0.78 in general, or in the case of titanates, the restriction translates into divalent cation radii less than 0.8 $\dot{A}$ [92]. Interestingly, the use of Equation (1) with $r_A$ (Li⁺, 6-fold coordination) = 0.74 $\dot{A},$ $r_B$ (Nb⁵⁺, 6-fold coordination) = 0.64 $\dot{A}$, $r_O$ = 1.40 $\dot{A}$ (after Shannon and Prewitt [93]), gives t = 0.74 for the LN structure. However, it should be acknowledged that the GTF is only a rough estimate given that perovskites are not completely ionic compounds. Still, as expected, it is highly correlated to the electrophysical parameters featured by important perovskites. It has been a useful figure in guiding the synthesis of intelligent materials which “have been the heart and soul of several multibillion-dollar industries”, such as polycrystalline ceramics based on BaTiO₃ [87,99].

The conceptualization conceived by Megaw relied on a profound analysis of the crystallographic data obtained for LN (Bailey, 1952 [74]) and ilmenite (Barth and Posnjak, 1934 [100]). Disregarding details, she concluded that whereas the transition paraelectric-ferroelectric in LN is continuous and reversible, implying however large atomic displacements of the order of 200 pm for Li and 70 pm for oxygen, the ilmenite structure cannot be attained by any distortion of a perovskite structure given that such a transition would involve a serious rearrangement of the structure and is irreversible [12]. Instead of considering a kinship between the LN and ilmenite structures, it was instead proposed that the former be closely related to the rhombohedral variant of BaTiO_3, which possibly “represents the early stages of distortion which LiNbO₃ shows fully developed” [12]. Megaw herself found an “obvious difficulty” in her explanation due to the large magnitude of the displacements involved. In 1957 they changed to 100 pm for Li and 60 pm for O in a book she wrote, where she also acknowledges that such displacements might not be physically possible [13]. These values conflicted with those reported by Abrahams et al. in a series of three papers, which together are considered the most extensive and detailed structural analysis of LN [32,33,34]. Reference [34] is a study of the atomic arrangement in polycrystalline LN as a function of T (RT to 1200 °C). In it, and accounting also for the results in a single crystal at RT by X-ray and neutron diffraction [32,33], it is shown that in this range of temperatures, the atomic arrangement is essentially unchanged: whereas a fixed oxygen framework exists, given the non-significant displacement of 6 pm within the oxygen layers, the Nb and Li cations exhibit small displacements along a common direction of magnitude 25 and 45 pm, respectively [34].

Besides this fact, the model proposed by Megaw was refuted, given the absence of evidence for a change in the crystal system between the ferroelectric and paraelectric phases. The comparison of the diffractograms obtained below and above T_C did not show appreciable changes in the positions of the lines, only did the intensities change in a non-reproducible way [34]. The large discrepancy to the calculated displacements by Megaw relied on the original ambiguity in determining the Nb position relative to those of Li and O, as originally done by Bailey [32,74]. Also, on the large error of about 100 pm existing in the determination by Bailey on the atomic coordinate of Li [34]. Together, these two aspects constitute the main criticism from Abrahams et al. to the work of Megaw (1954). Because of the ambiguity and inaccuracy present in the work of Bailey, Shiozaki, and Mitsui (1963) did neutron diffraction on polycrystalline LN to improve the results [101]. However, these also conflict with those obtained by Abrahams et al. (1966) [33]. Hence, it can be said that this researching group favored kinship of the LN crystal structure to that of ilmenite instead of perovskite, and probably due to it, they erroneously addressed the space group for the nonpolar paraelectric phase as $R\overline{3}$ instead of $R\overline{3}c$ [14,34]. That $R\overline{3}c$ is the proper space group for the paraelectric phase was shown in 1968 by Niizeki et al. [102]. In the case of the ferroelectric phase, the space group assigned by Bailey was confirmed, R3c, with lattice constants a = b = 5.148 $\dot{A}$, c = 13.863 $\dot{A}$, and atomic positions in the hexagonal reference [34]

Nb: (0, 0, 0)
Li: (0, 0, 0.2829) ± (0, 0, 0.0023)
O: (0.0492, 0.3446, 0.0647) ± (0.0003, 0.0005, 0.0004)

In R3c, the z-position of the origin can be arbitrarily chosen. Clearly, in the ferroelectric phase, neither Nb nor Li is aligned to the oxygen lattice. Hence, Abrahams et al. chose the Nb site as the origin since it is the principal X-ray and neutron scatterer [32]. In 1968 Megaw, based on all the results by Abrahams et al. [32,33,34], found an improved argument to relate the LN crystal structure to perovskite by a reparameterization trick [14]. The origin in z was proposed to be reassigned, so that it lies midway between two oxygen layers, in the vicinity of an Nb site. A high-symmetry structural reference is obtained in this way, an idealized structure with hexagonally-closed packed oxygen atoms. Upon successive approximations in terms of small quantities expressing displacement parameters, the actual Nb–O framework, as determined by Abrahams et al. [14], can be obtained. Another set of successive approximations or displacement parameters would lead to the perovskite framework. The reparameterization gives the following coordinates for the actual structure in terms of the ideal [14].

$$\begin{gathered} \mathrm{Nb}: \left(0, 0, w\right) \\ \mathrm{O}: \left(u, \frac{1}{3}+v, \frac{1}{12}\right) \\ \mathrm{Li}: \left(0, 0, \frac{1}{3}+w^{\prime }\right) \end{gathered}$$

With u = 0.0492, v = 0.0113, w = 0.0816, $w^{\prime }$ = −0.01318. The value of the axial ratio is $\frac{c}{a}=2\sqrt{2}\left(1+\frac{1}{2}\beta \right)$, with β = −0.0936. The idealized structure is then described when all the parameters are equal to zero. It can be regarded as the zeroth-order approximation to the actual Nb–O framework, a centrosymmetric structure with axis ratio $\frac{c}{a}=2\sqrt{2}$. In the first-order approximation u ≠ 0 while the rest of the parameters remain equal to zero. A higher symmetry structure is described where the axis ratio tends to decrease from its ideal value. The perovskite framework is described by this first-order approximation when $u=\frac{1}{6}$. Insertion of Li into the octahedral interstices causes symmetry reduction, thus allowing parameters u, v, w to be different from zero, that is, the second-order approximation, describing the actual LN crystal structure. Moreover, regarding the effect of temperature, unexpectedly, as T increases, the actual structure (ferroelectric phase) would not tend towards the idealized structure (the zeroth-order approximation), but rather towards the first-order model with increasing u, while v and w would tend to zero. Again, by stating this, Megaw avoids saying that the ferroelectric LN crystal structure can be derived from the ideal cubic perovskite. In her own words: “it is not suggested that a change of framework configuration from one extreme to the other can take place in any actual material” [14]. That the ferroelectric phase follows from a small distortion of a high symmetry reference phase has demonstrated to be a powerful principle [91]. As already said, the detailed discussion of the LN crystal structure, as presented by Räuber [2], assumes the reparameterization trick herein discussed.

Although this conceptualization might not necessarily be correct, the LN crystal structure might be grasped more naturally by understanding its pros and cons. For a deeper insight, previous knowledge on the corundum, ilmenite, and perovskite structures would be advantageous for a proper comparison: these can be consulted from references [92,96,103], [92,96,100], and [84,86,87,91,92], respectively. The book by Lima-di-Faria provides useful descriptive charts in pages [23]: 99, 100, and 103, respectively.

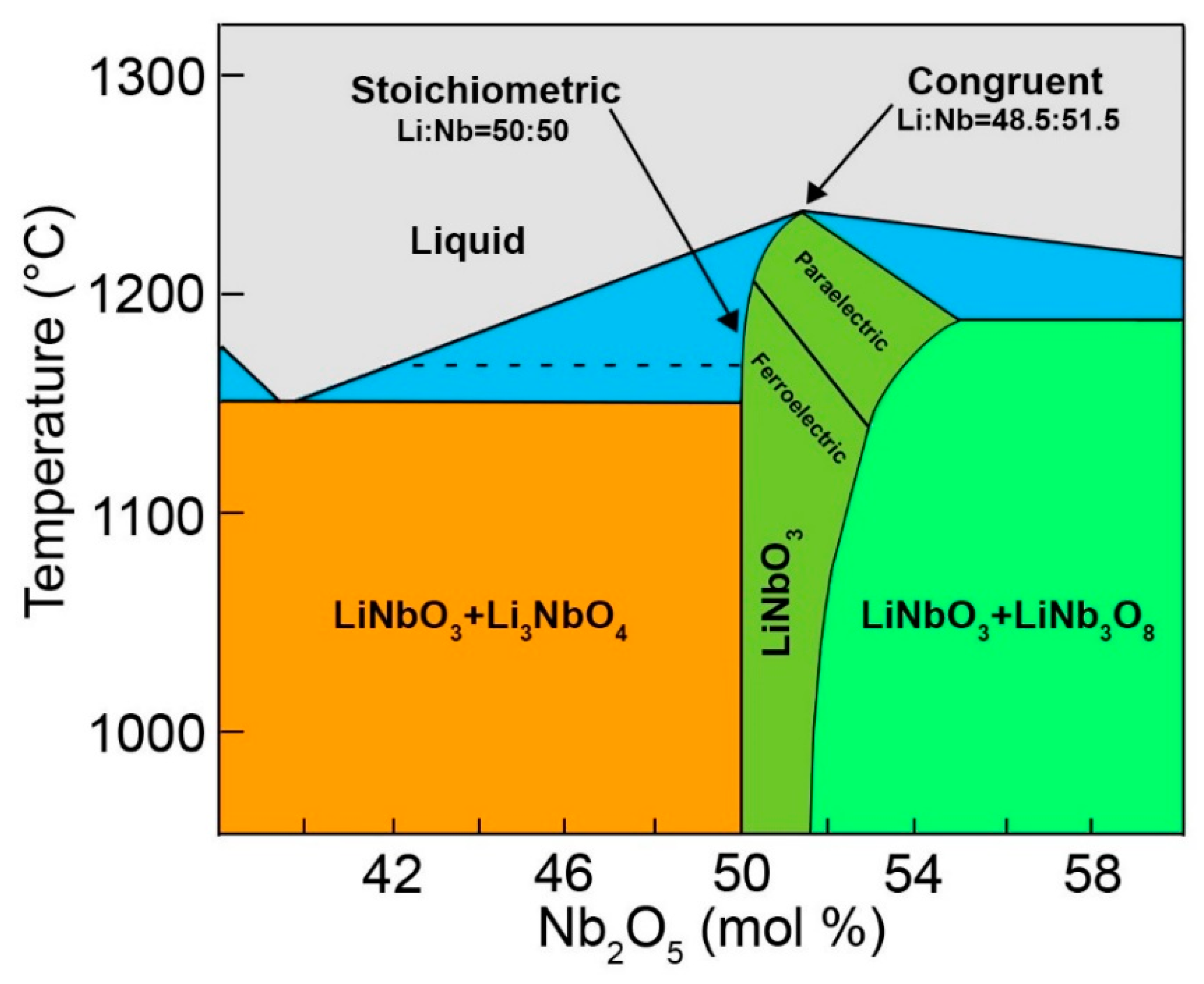
4. Powders

4.1. Accurate Description of the Chemical Composition

Until recently, the lack of an accurate (indirect) method to determine the CC of LN powders (LNPws) was a reality. We demonstrated that none of four conventional indirect characterization techniques could be used for this purpose as they are nominally used for the case of single crystals. These are (for the case of single crystals, further details may be consulted in the given references):

• X-ray diffraction + structure refinement [45,47,63]. Abrahams and Marsh did earlier measurements by use of a Bond diffractometer [65,104]. Some of the available program packages for Rietveld refinement, commercial and public, and an introduction into this subject can be consulted in [104,105,106,107,108,109,110,111,112].
• Polarized raman spectroscopy [47,48,49,113,114]. The group theory elements in this field and the assignment of phonon modes in LN are discussed elsewhere [115,116,117,118,119], having a common root in the seminal paper by Schaufele and Weber (1966) [120]. The scattering geometry in polarized Raman experiments is described after Porto and Krishnan (1967) [121]. The high sensitiveness of the functional form (and intensity) of the recorded Raman spectra in LN to the experimental configuration might be observed from the educational video ‘Convenient Application of Polarized Raman Spectroscopy’, provided by the HORIBA Raman Academy [122]. The resolution of Raman bands or fitting techniques is critical for achieving great accuracy in determining the CC by this method [123,124]. Regarding this method of CC characterization, the works by Scott and Burns (1972) [125] and Balanevskaya et al. (1983) [126], are considered pioneers (both done on LNPws).
• Fundamental absorption edge [47,51,52]. One of the earliest reports on this subject was written by Redfield and Burke (1974) [127]. For practical reasons, a direct transition can be assumed regarding the intrinsic nature of the bandgap (no phonons involved for momentum conservation) [128], in which case the fundamental band gap is proportional to the square of the absorption coefficient α² [129].
• Differential thermal analysis [43,44,45,47]. Measurement of the Curie temperature (T_C) is one of the earliest calibration methods for determining the CC in LN single crystals [62]. Regarding this type of transition, as previously stated, a change in the crystal structure occurs in which the symmetry of the system decreases. The symmetry-breaking relation between the high-symmetry paraelectric structure and the ferroelectric one is consistent with a second-order transition, described by the Landau order-disorder theory [130,131]. A finite discontinuity in the heat capacity of the system having this transition has been addressed as a direct thermodynamic consequence.

Research was conducted in our group, where these characterization techniques were used (modified when needed) to obtain a set of equations that appropriately describe the CC of LNPws. These results have been published in [19]. Within the following lines, we shortly describe the main aspects of such publication. The current necessity for the correct characterization of LNPws in this context is also further discussed. We believe such a missing point in the literature for so long is that, historically, LNPws have been overlooked for research in favor of single crystals and thin films mainly because of their poor performance in most applications. For example, within the context of nonlinear optics, powders have been relegated compared to single crystals due to surface inhomogeneities and strong scattering effects, although they are tacitly considered easier and far less expensive to synthesize. Besides, the urgent demand for large single crystals of high quality to match the microfabrication process requirement in modern applications has already been outlined [17].

Our recent contribution arose from noticing that at least one of the equations given in [47,48,49] describing the CC of LN single crystals by using polarized Raman spectroscopy—is not accurate for the case of powders. Also, contrary to what could be expected, the approach of using an empirical equation formulated for single crystals to describe powders does not even work for T_C measurements (see equations in [43,44,45]). Since temperature is a scalar quantity (light propagates and interacts with matter in a vector-like form), it would be permissible to expect a single description of the CC of LN in terms of T_C, regardless of the solid solution being a single crystal or a powder. However, the differences in surface and grain size/boundary effects between single crystals on polycrystalline powders cannot be neglected. Before our work, the systematic measurement of lower T_C values (about 10 °C) for LNPws compared to equivalent single crystals, had been addressed [47,132]. As for the case of optical absorption, there is no point in using an equation that describes single crystals [52], since the terms ‘refractive index’ and ‘absorption coefficient’ lack sense when related to powders; a powdered sample can be conceived as a material of infinite thickness from the optical point of view. Instead of conventional optical absorption measurements, the UV–vis diffuse reflectance technique is usually employed while relying on the Kubelka–Munk approximation to describe the measured functional form or reemission function, a proxy the actual absorption spectrum [133,134,135]. The experimental details to make this approximation valid can be consulted in [133]. Thus, recently we gave a first step towards the accurate description of the CC of LNPws by developing a facile method based mainly on imposing X-ray diffraction as a seed characterization technique. Raman spectroscopy (non-polarized), UV–vis diffuse reflectance, and DTA enrich the work, representing various alternatives for the independent determination of this fundamental quantity in LNPws. An empirical equation that describes it in terms of a corresponding experimental parameter is given for each of these four characterization techniques (valid for LNPws with crystallite and particle dimensions close to 160 nm and 2.6 µm, respectively) [19]

$$\langle c_{Nb}\rangle =\left(8.6207V_{cell}-2692.5216\right) \mathrm{mol} \% \pm 0.5 \mathrm{mol} \%,$$

(2)

X-ray diffraction (XRD)

$$\langle c_{Nb}\rangle {}_L=\left(256.4103\ast \left(\frac{{\Gamma }_L}{2x_c}\right)+43.5385\right)\mathrm{mol} \% \pm 0.4 \mathrm{mol} \%,$$

(3)

$$\langle c_{Nb}\rangle {}_G=\left(588.2353\ast \left(\frac{{\Gamma }_G}{2x_c}\right)+42.7059\right)\mathrm{mol} \% \pm 0.5 \mathrm{mol} \%,$$

(4)

(non-polarized) Raman spectroscopy (RS)

$$\langle c_{Nb}\rangle =\left(3.9078\ast E_g+34.6229\right) \mathrm{mol} \% \pm 0.4 \mathrm{mol} \%,$$

(5)

UV–vis diffuse reflectance (DR)

$$\langle c_{Nb}\rangle =\left(-0.0515T_C+110.8505\right) \mathrm{mol} \% \pm 0.4 \mathrm{mol} \%,$$

(6)

Differential thermal analysis (DTA)

where the brackets in the Nb concentration stand for an average of this quantity in the sampled crystallites. $V_{cell}=\sqrt{3}{a}^{2}c/2$ stands for the cell volume in (angstrom)³ units, calculated by a standard structure refinement method. In Equations (3) and (4), Γ_i stands for the FWHM in cm⁻¹ of the Raman band around 876 cm⁻¹, resolved by linear fitting either using a Lorentzian (i:=L) or a Gaussian (i:=G) line shape, x_c denotes the center of this Raman band. Normalization of the full Raman spectra precedes the linear fitting and, regardless of the line shape, enlargement around this band is suggested, extending as much as possible (precise determination of the baseline). Application of a single or double-peak fitting, rather than performing a multi-peak fitting of the full Raman spectra, is also convenient. In Equation (5), E_g stands for the fundamental band gap in eV units, being determined by assuming a direct interband transition, that is, the obtained reemission function is elevated to the power of 2. In Equation (6), T_C is the Curie temperature measured in Celsius degrees. Also, notice that in contrast to pioneering works (on single crystals, [47,48,49]), the equations are given in terms of the averaged Nb content in the crystallites $\langle c_{Nb}\rangle$, rather than $\langle c_{Li}\rangle$. By putting these equations in terms of $\langle c_{Li}\rangle$, a more straightforward comparison could have been attained to data available in the literature. However, it was decided to do it in terms of $\langle c_{Nb}\rangle$ because of a simpler interpretation and association with a phase diagram describing LN, like that given in Figure 1. It has been noticed that most of the phase diagrams existent in the literature to describe LN are presented in terms of Nb₂O₅ mol %. Because in the synthesis of the studied powders in [19], Li₂CO₃ was used as the other precursor, and also relative not too high temperatures were used in the calcination process (850 °C), a one-to-one correspondence exists between the Nb and Li contents in Equations (2)–(6). The equivalent relations in terms of $\langle c_{Li}\rangle$ can be consulted in Appendix B in [19]. We now wish to underline the main aspects of the method devised to obtain such equations.

The calibration of the cited methods is based on the quantification of pure and secondary phase percentages by XRD, followed by Rietveld structure refinement. Secondly, relying on the LN phase diagram (Figure 1), the chemical composition of the studied samples is inferred, and thereafter labeled in terms of the Nb content in the crystallites. Lastly, having done this, any of the four mentioned characterization techniques could be used to relate such labeling with their corresponding experimental parameter. In the case of a user who wants to determine the CC of LNPws only, she/he would only need to perform the last step and use any of Equations (2)–(6). On the other hand, in wanting to describe other powders apart from LNPws, the whole method (three main steps described above) might be further applied inasmuch as akin materials are investigated, lithium tantalate (LiTaO₃) powders for example.

The validity of this methodology is proven self-consistently with the determination of the CC of several samples, where the content of Nb and Li is varied in a controlled way. However, the main shortcoming of this investigation is the large uncertainty associated with Equations (2)–(6). Rigorously, they should not be used for a practical composition determination and, instead, it only could be stated with more confidence that, by using these equations, the composition of LN powder would be closer to the stoichiometric or congruent point, or rather in an intermediate one. It will soon be solved, noticing that both the resolution and the associated uncertainties of this methodology can be significantly improved by analyzing larger powder quantities. The major contribution to uncertainty emerges from the determination of the boundaries of the pure ferroelectric LN phase (details given in [19]). The associated uncertainty to Equations (2)–(6) can be significantly reduced if a larger number of samples are synthesized in this range, which can be more easily achieved if larger quantities of powder are prepared. For example, it is expected that by synthesizing approximately 10 g of powder, around 40 points would be available for analysis, assuming an increasing step of 0.1% in the Nb precursor mass. As a result, the overall uncertainties would decrease by about 50–80% (noticing that the linear fitting uncertainty would also be reduced significantly). Conclusively, apart from providing four distinct alternatives to describe the CC of LNPws accurately, the innovative character of our recently published work is the self-consistency character of the whole method. No other direct method is needed to confirm the CC of the powders since the determination of the pure ferroelectric LN phase boundaries by XRD analysis suffices for this purpose. The four involved characterization techniques are standard, accessible nowadays to large scientific communities in developing countries.

4.2. Role in New Potential Applications

Nonlinear optical powders such as LNPws have served in the past as survey materials. In 1968, Kurtz and Perry developed a method to predict the second-order nonlinear susceptibilities of materials unavailable under large single crystals by performing second harmonic generation (SHG) experiments on the powdered version of the material [136]. Thus, SHG experiments on powders are conceived initially as secondary within this method, which is by far the most popular approach to powders in relation to SHG. However, recent experiments have proposed a new paradigm to quantitatively study SHG efficiency with notable implications for pharmaceutical materials [137]. However, another feature that makes the SHG that arises from powders attractive nowadays is the possible tuning of the SHG intensity from LNPws, ascribed to proper control of the CC and grain size of the powders [138]. This feature has already been outlined in our recent publication, among others [19]. Here, we further extend details on such recent developments on LNPws (for which the necessity of a proper CC description of the LNPws is implied). In recent years:

▪

(2020) Strong and weak light scattering effects can be present simultaneously in random media (random in terms of its refractive index), such as powders. Here, accounting for optical nonlinear powders, photons can undergo multiple scattering in the sense that they undergo one SHG scattering event and single or multiple linear scattering events at the fundamental and harmonic frequencies. In contrast, ballistic photons undergo a single SHG scattering event and no linear scattering event. Depth profiling with polarization resolution of the SHG intensity from a powder stack of sLN microparticles/nanocrystals has been done in back-scattering or retro-reflection configuration. The results, supported by modeling, show that competition between multiple scattered and ballistic photons contributions holds during the focus longitudinal translation, which can be disentangled in observing polarization distortions occurring as the beam focus moves from air into powder [139]. The contribution from the multiple scattered photons dominates at all depths, whereas, at the maximum of the intensity depth profiles, the contribution of ballistic photons is at its maximum and enhanced due to collection efficiency. This work paves the way for a close and quantitative investigation of the SHG response from nonlinear optical powders and, combined with the derived conclusions in [138], the experimental configuration might also play a role in the discrimination of information: transmission experiments for the evaluation of averaged properties such as SHG efficiency (micrometer size scale of the powder) and retro-reflection experiments for overall scattering properties and local crystalline properties (nanometer size scale). The latter is a general idea somehow (not explicitly) postulated in a revision of the Kurtz and Perry method done by Aramburu et al. [140].

▪

(2018) Fe-doped LNPws show, after a post-thermal treatment in a controlled reducing atmosphere, a rather strong ferromagnetic response at room temperature for a doping concentration of the order of 1 mol % [141]. This may be considered a first report of the manifestation of ferromagnetism in nanocrystalline LNPws within the regime of very low doping concentrations. Post-thermal treatment in a controlled atmosphere is a key point for inducing this behavior, which could be explained as the recombination of unpaired electrons from the donor sites (Fe impurities) to the acceptor sites (oxygen vacancies) in the surfaces of the material. A statement that needs to be further scrutinized since the opinion on the existence of this type of vacancies has changed over time; lately they are neglected, at least with respect to single crystals and within the volume (see discussion in Part II). Bulk diffusion of oxygen has been exluded from the explanation of the results recently presented by Kocksor et al. [18], where LN nanocrystals were prepared by ball-milling the crucible residues of a Czochralski grown congruent crystal. Anywise, neither the enhanced factor of surface effects nor the depletion of oxygen at the surfaces can be overruled in LNPws prepared by a mechanochemical-calcination route.

▪

(2017) The same method of synthesis has been used to prepare LN micropowders whose SHG intensity is maximal at a certain λ_max, in terms of the fundamental excitation wavelength. Possible tuning of λ_max could be ascribed to the control of the composition and grain size of the powder [138]. Also, there is the possibility of obtaining major technical benefits by exploiting the SHG from disordered materials such as LNPws, given that neither a critical adjustment of the orientation/temperature in the material (phase-matching condition) nor the accurate engineering of a microstructure (quasi-phase matching condition), are substantially needed [142].

▪

(2017) A novel fabrication process based on the powder-in-tube method to realize polarization-maintaining optical fibers has been demonstrated. It relies on the principle of “inducing an anisotropy of the refractive index in the core region by internal stress”, in which the use of powdered material with a thermal expansion coefficient (TEC) higher than that of silica (fiber core) is the key point [143]. Glass complex systems based on SiO₂-Al₂O₃-La₂O₃, with a TEC around 10 times larger (5.32–6.46 × 10⁻⁶ K⁻¹) compared to silica (0.54 × 10⁻⁶ K⁻¹), has been used. Single crystalline LN has a TEC along the c-axis of the same order as the complex systems just mentioned (~5 × 10⁻⁶ K⁻¹) and almost three times higher for either of the other axes (14.1 × 10⁻⁶ K⁻¹); see Table 1. In the case of LNPws, a TEC value between these two is expected, and thus they are, in principle, good candidates for the fabrication of polarization maintaining optical fibers.

▪

(2013) Cementation materials based on LN have been proposed as potential materials for an effective formation of eco-friendly end products through artificial photosynthesis; this is considered important for the global warming reduction problem [144]. Despite its wider band gap (3.8–4.1 eV) compared to that of TiO₂ (3.2 eV), LN is considered a better artificial photocatalyst due to its strong remnant polarization (70 μc(cm)⁻²) [145]. Paraphrasing Nath et al.: “the photocatalyst LiNbO₃ can be used as a construction material to emit oxygen using atmospheric CO₂ and water reliably and inexpensively. The reduction of the global warming problem through the use of this photocatalyst would have a remarkably positive impact on the environment in the near future” [144]. Regarding LNPws, we emphasize that powders would not only be easier to implement than single crystals into cement-based materials but also they would enhance surface effects, perhaps improving this way the lifetime of the carriers (photo-generated electrons and holes) involved in artificial photosynthesis [145]. The importance of LNPws on these crucial matters must not be overlooked.

▪

(2012) LN and LT powders of several particle sizes at the microscale and with averaged crystallite size between 30 and 300 nm, have proved to be antimicrobial agents in aqueous solutions based on cyclical thermal excitation [146]. The powders were directly obtained from the crushing of single crystals by high-energy ball milling and various solution percussion routes. The powders obtained by the latter method show smaller particle and crystallite sizes, showing improved disinfection properties due to the increased direct surface contact with the bacterium.

On the other hand, perhaps an even more fascinating feature of LNPws is their role in the field of lead-free piezoelectric materials. This research field is nowadays vast and very active due to the environmental laws and regulations imposed by the government in 2003, the so-called RoHS directive, which may be considered as “the most disruptive event in the history of electronic manufacturing” [147]. It was approved in 2006 to minimize health and safety risks, dictating that new generation electrical and electronic devices are to be manufactured without any of the following compounds: lead, mercury, cadmium, hexavalent chromium, polybrominated biphenyls, or polybrominated diphenyl ethers [147]. The truth is that neither the RoHS directive has been fully applied nor research on lead-based materials has been stopped so far. This because lead zirconate (Pb(Z_rxTi_1−x)O3), PZT), and lead titanate (PbTiO₃, PT) perovskites by far feature the best performances on these grounds (sensors, actuators, and other electronic components) at reasonably low production costs [148]. The existence of a morphotropic phase boundary (MPB) is acknowledged to be the driving force. It is a region of a structural phase transition, accompanied by extremes of electrophysical parameters, particularly, high dielectric and piezoelectric parameters: the anomalous increase in these properties shown by MPB compositions is the result of the enhanced polarizability that arises from the coupling of two equivalent energy states, that is, the coexistence of two structural phases [149,150]. The MPB is nearly temperature independent, and its existence is attributed to high polymorphism (apart from the high piezoelectric characteristics) in which PZT outstands. Nowadays, piezoelectric PZT-based ceramics dominate a $1 billion market of actuators, sensors, and transducers that merge into the realization of novel applications such as medical ultrasound, high precision accelerometers, sonar systems, fish finders, thermal sensors, and precise positioners, among others (in the future it may also earn a position in the development of the Internet of Things) [151].

Researching interests on lead-free materials is far from dropping, and, today, most experts share the common belief that a possible way to replace lead-based materials is the synthesis of solid solutions of alkali metal niobates (AMN) [148,150,152]. LN belongs to this category of materials: recently, LNPws have been mixed with alike powders in the sense of forming a novel green compact to be sintered into a high-performance ceramic. Complex ternary and four-component systems involving LNPws have been studied: NaNbO₃–LiNbO₃–PbTiO₃ and (1−x)(Na, Li)NbO₃–xPb(Ti, Zr)O₃, respectively. The latter has shown a considerable increase of electrophysical parameters [152]. Although AMN systems are still inferior to systems mainly based on PZT, the four-component transition already features good figures of merit for applications in microwave devices (for a low content of x) and low-frequency electromechanical converters (for 0.70 < x < 0.85) [152]. The influence of the CC of LNPws on the performance of these complex ceramics is evident and, thus, the urgent need to properly characterize it. However, in our first aim to furnish an accurate description (discussed above), we have missed one important point, that of the influence of the quality and macroproperties of the precursors on the product. Reznichenko et al. have pointed out the possible influence of the quality of niobium pentoxide (Nb₂O₅) on the resulted four-component system ceramics [152]. Almost 30 years ago, this question was settled regarding the CC of LN single crystals (see Section 4.4).

4.3. Methods of Synthesis

Conventionally, LNPws are prepared by solid state-reactions between the precursors at a temperature above 1000 °C. Although this method is simple, it may lead to the composition deviation from stoichiometry because of lithium evaporation at higher temperatures [153,154,155]. Concerning the work done so far in our group, the synthesis of the studied powdered materials practically summarizes into the successive combination of the following process: grinding (high-energy ball milling) and thermal annealing or calcination. In short, the precursors lithium carbonate (Li₂CO₃) and niobium pentoxide (Nb₂O₅), are mixed in solid phase (room temperature) and ground, and then subjected to a thermal annealing process (calcination). The precursors are bought with high purity, and the technique used in the grinding process is closely related to that of mechanochemical synthesis.

Strictly speaking, mechanochemical synthesis denotes a grinding process in which chemical reactions are necessarily involved: the simultaneous grinding of more than one precursor (chemically distinct). With the breaking of certain chemical bonds, the formation of new ones is favored. When no chemical reactions are involved, as in the investigations so far being held in our group, the precursors are ground only, and it is convenient to denote this process as merely grinding. The concepts and involved variables are, however, very similar for both processes. Detailed reviews are available after Suryanarayana (2001) and Kong et al. (2008) [156,157]. Recently, the available knowledge regarding this synthesis route connected with LNPws has been extended [18]. On the other hand, to state that no chemical reactions occur in the grinding process might not be accurate to some extent. Apart from contamination issues depending on the chemical and physical characteristics of the used vial and grinding medium [18,158,159], in the preparation of LNPws by high-energy ball milling, the product usually shows a greyish coloration (before calcination), also observed for LN single crystals after chemical reduction (near the surface) [160]. Another common finding is the remaining non-reacted and amorphous milled powder [161,162]. The preparation of pure LNPws by a mechanochemical method assisted by subsequent calcination at relatively high temperatures has been achieved and reported elsewhere [163,164]. The main mechanisms in the high-energy ball milling process are now discussed.

In the process, the particles that constitute the milled powder are exposed to an iterative combination of the following mechanisms: flattening, cold welding, fracture, and recombination. Because there is high mobility regarding the balls, there exist mainly three types of collisions: ball-ball, ball-powder, and ball-walls (the internal walls of the vial). However, ball-powder-ball type collisions also exist; in some instances, a given fraction of the powder is being pressed by two or more balls. Approximately a thousand particles with a total (aggregated) mass of 0.2 mg are confined in this type of collision [156]. At the initial stage, the impact force deforms the particles inelastically. As a result, work hardening and fracture take place at the surface level. New surfaces are formed, allowing the particles to weld. Thus, an effective increment of the averaged size of the particles follows. The size distribution widens in cases for which the new particles can be as three times larger than the original ones [156]. Then, deformation keeps its pace, and the particles harden due to mechanical fatigue or fragmentation of their layers or fragile sheets. The formation of this type of fragments might continue as far as no significant agglomeration forces exist. It translates into the reverse effect: an effective decrease in the average size of the particles. At this stage, the tendency of the particles to fragment dominates their tendency to weld [156]. Because the ball impacts continue, the structure of the particles keeps being refined and refined, no matter the size of the particles remains constant (it repeatedly increases and decreases due to the mechanism competition above described). Consequently, the inter-layer spacing decreases, whereas the number of layers per particle increases.

Now, so far, only the refinement mechanism of the particles has been discussed. The chemical reactions between the precursors have not been considered. Assuming that the precursors are oxides, then the particle refinement (and fragmentation) results in defect formation and an effective reduction of the diffusion distances. The interaction between the precursors is thus enhanced. Moreover, given the formation of new surfaces and interfaces, a substantial increment in the reactivity of the precursors is achieved [157]. This is what is understood by the ‘chemical activation’ of the precursors. If the process keeps going on, the chemical activation will also continue, and, in some instances, the necessary chemical reactions for the formation of a new phase start to appear. If the process still goes on further, it is possible that other processes also occur, such as nucleation, particle growth, and crystalline phase formation. The formation of an amorphous phase can even occur, which is not other than the extreme case of defect formation [157]. The localized heat transfer right at the impact zones (ball-powder-ball collisions) might contribute to this process. This hypothesis is justified by the fact that even when the temperature inside the vial hardly reaches 100 °C, the in situ temperature at each impact event can be large enough to activate the solid state reactions (~>800 °C) [165,166].

A Chinese group has extensively discussed other non-conventional methods to produce LNPws of high quality at the State Key Laboratory of fine Chemicals, Dalian University of Technology. This group has mainly focused on soft-chemistry methods such as sol-gel and hydrothermal processes [132], combustion method with urea as fuel [154], and wet chemical synthesis [155]. Within such references, Liu et al. have provided information on other synthesis methods for this purpose. Some are: sol–gel [167,168,169], Pechini method [170], metal alkoxides [171], hydrothermal process [172], and the peroxide route [168]. The synthesis of other ferroelectric powders by similar methods can also be consulted in the literature: chemical coprecipitation [173,174,175], sol–gel process [176,177,178], hydrothermal process [179,180,181,182], combustion [183], and molten salt [184,185].

Back to LN, the wet chemistry methods are based on the adoption of a kind of an α-carboxylic acid (citric acid) to coordinate with hydrated niobium acid (Nb₂O₅·nH₂O, often called as niobic acid), which is more reactive than the starting precursor based on niobium oxide, as described by Liu et al. [155]. In contrast, the mechanochemical-route is a dry environment method where, as mentioned, the reactivity of the Nb₂O₅ precursor is carried out through the high-energy ball milling process. While wet chemistry-based synthesis methods effectively tend to achieve the product at lower calcination temperatures, by employing high-energy ball milling the use of any kind of acid (organic or inorganic) is avoided. It is advantageous since the use of acids usually implies regulations to the exposure of hazardous or toxic fumes and vapors (ventilation issues), thus following strict security protocols.

4.4. Are the Stoichiometric and Congruent Compositions Univocally Determined?

In 1993 Kuz’minov and Osiko pointed out that the ‘disturbance’ of stoichiometry in LN crystals is primarily due to the lack of oxygen in Nb₂O₅, used as a raw material initial melt (Czochralski method) [186]. Accordingly, depending on its production technology, niobium pentoxide can adopt a wide range of compositions Nb₂O_5−x. Thus, once ST LN single crystals were believed to be only obtained for x = 0 at the synthesis stage. Although this is a severe statement, and even less likely to be correct because LN single crystals are hardly obtained without entailing a modification to the Czochralski method or an assisting process (as described in Section 2), the systematic study of the role of the CC of the precursor on that of the product would give interesting results. Among others, the documented indetermination of the CG point could be solved, since it is nowadays disputed to be in the range 48.38 mol % to 48.60 mol % of Li content [17]. Such an indetermination has been recently exposed for isostructural LiTaO₃ (LT) [187]: different defect concentrations were found on two CG LT single crystals synthesized by the same method but by distinct manufacturers. This type of analysis has not yet been conducted, according to the consulted literature. To answer these questions is a fundamental science problem, research of the kind of normal science concerning our scientific community. In principle, it can be solved without much effort or resources if treated at the level of synthesis and characterization of polycrystalline samples in the form of powders.

Research is here proposed where a mechanochemical-calcination route synthesizes LNPws. Before synthesizing several samples, the Nb₂O₅ precursor is to be processed to the extent of controlling the number of oxygen defects and characterized. The role of high-energy ball-milling is of interest, but no more than the role of annealing treatments under a controlled atmosphere in which at least both extremes must be studied: (1) passivated precursor powder (optimized conditions under an oxidizing treatment) and (2) highly-defective precursor powder (optimized conditions under a reduction treatment). The processed precursors would then be mixed with Li₂CO₃ and high-energy ball-milled for chemical activation; the milling atmosphere may or may not be controlled; an inert atmosphere would prevent oxygen defect formation. Calcination under an inert atmosphere would follow for the obtention of the products. Characterization by standard techniques such as XRD and Raman spectroscopy are recommended at all stages. For the case of the products, research like that described at the beginning of this section (and reported in [19]) could be conducted. However, in this case, the use of a direct method for determining the CC of the resultant LNPws is also suggested. The influence of the quality of the Nb₂O₅ precursor on that of the product should be traceable this way.

5. Ferroelectricity behind the Curtain

The origin of ferroelectric behavior in LN relies on the non-centrosymmetric arrangement of the constituent ions and their corresponding electrons (at low temperature) [188,189]. So far, this accounts only for the so-called ‘spontaneous’ polarization but not for its switching. The first concept stands for the existence of at least “two discrete stable or metastable states of different nonzero electric polarization in zero applied electric field”, whereas switching describes the possibility to switch between these states with an applied electric field $\overrightarrow{E}$, which “changes the relative energy of the states through the coupling of the field to the polarization $-\overrightarrow{E}·\overrightarrow{P}$” [91]. Some non-centrosymmetric polar structures, the wurtzite structure as an example, do not exhibit ferroelectric behavior since its intrinsic polarization cannot be switched at known experimental conditions [188]. Ferroelectricity is sensitive to T, the same as other related properties like piezoelectricity, pyroelectricity, and SHG. With increasing T, most ferroelectrics exhibit a “phase transition from the ferroelectric state, with multiple symmetry-related variants, to a nonpolar paraelectric phase, with a single variant” [91]. The measured Curie temperatures range for a gamut of ferroelectric materials from 1 K to 1000 K; for very high Ts, the probability of the material melting down before the transition occurs increases.

As previously stated, the symmetry-breaking relation between the high-symmetry paraelectric structure and the ferroelectric one is consistent with a second-order transition, described by the Landau order–disorder theory [130,131]. Apart from a finite discontinuity in the heat capacity of the system, this analysis also implies that the dielectric susceptibility diverges at the transition, and this can be linked to the vanishing frequency of a polar phonon. It is the central idea of the ‘soft-mode’ theory of ferroelectrics [189]. According to Rabe et al., during the 1960s and 1970s, the observation of the T-dependence of polar phonons was a “key ingredient in the great progress made in understanding the physics of ferroelectricity” [91]. Phonon spectroscopy is still a benchmark concerning the characterization of this type of transition, both via neutron scattering and optical spectroscopy [190,191]. Despite the success of this theoretical framework, no consensus exists today regarding the origin of ferroelectricity or ionic off-centering in known ferroelectrics [188,189].

Prototypical displacive transitions, characterized by a zone-centre vibrational mode—the soft mode—“with vanishing frequency at the phase transition and an eigenvector similar to the displacements observed in the ferroelectric phases”, were long considered to be behind this type of phase transitions [189,192]. Displacive type transitions might be pictured as the multitudinous physical shifting of either the A or B cations (or both) off-center relative to the oxygen anions and, because of the dipole moment created by this shift, the emerging of a spontaneous polarization [188]. Nevertheless, in this respect, the so-called order-disorder type transitions have become popular lately. The difference between these types of transitions resides on whether a collective displacement of the cation sublattice is involved (displacive) or, instead, several local displacements of individual cations (order-disorder) [189]. In LN and LT, the latter type of displacements are thought to be induced by the second-order Jahn–Teller (SOJT) effect of the NbO₆ and TaO₆ octahedral units, respectively [189].

These ideas can be traced back to 1992 when Cohen made a paramount contribution regarding perovskite oxides [192]: he realized that the “great sensitivity of ferroelectrics to chemistry, defects, electrical boundary conditions, and pressure arises from a delicate balance between long-range Coulomb forces (which favor the ferroelectric state) and short-range repulsions (which favor the nonpolar state).” Most importantly, he concluded that “for ferroelectric perovskites in general, hybridization between the B cation and O is essential to weaken the short-range repulsions and allow the ferroelectric transition. Most ferroelectric oxide perovskites have B cations, whose lowest unoccupied states are d-states (Ti⁴⁺, Nb⁵⁺, Zr⁴⁺, etcetera). It allows for d-hybridization with the O that softens the B–O repulsion and allows the ferroelectricity instability at low pressures” [192]. Hence, generally speaking (not only perovskites), the existence or absence of ferroelectric behavior relies on a balance between these short-range repulsions and additional bonding considerations, which act to stabilize the distortions that enable the transition to the polar state [188]. The ‘additional bonding considerations’ were pointed out by Megaw in 1954 [12]. The discussion in the next paragraph has been mostly adapted/reprinted from the content available in [188].

In terms of coordination chemistry, the stabilization of distorted structures is recognized to have its origin on chemical binding perturbations, denoted as SOJT effects [193,194,195], or sometimes pseudo-Jahn–Teller effects [196]. On the other hand, in plain physical terms, such effects can be seen by writing down a perturbative expansion of the energy of the electronic ground state E(Q), as a function of the coordinate of the distortion Q [197]

$$E\left(Q\right)=E\left(0\right)+\langle 0\left|{\left(\frac{\delta H}{\delta Q}\right)}_0\right|0\rangle Q+\frac{1}{2}\left(\langle 0\left|{\left(\frac{{\delta }^{2}H}{\delta Q^2}\right)}_0\right|0\rangle -2{{\displaystyle \sum }}_n^{\prime }\frac{{\left|\langle 0\left|{\left(\frac{\delta H}{\delta Q}\right)}_0\right|n\rangle \right|}^2}{E_n-E\left(0\right)}\right)Q^2+\cdots ,$$

(7)

where E(0) is the energy of the undistorted ground state, and the E_ns the energies describing the excited states. The term that is linear in Q is the first-order Jahn–Teller contribution, which is zero except for degenerate states. It is responsible for the characteristic tetragonal distortions in d¹ and d⁴ perovskites, for example. Of the second-order terms, the first is always positive, whereas the second is always negative (provided that it is different from zero). If the second term is larger than the first, then distortion will cause an energy reduction. An increase in energy on distortion is described by the first second-order term, under the assumption of the absence of redistribution of electrons. Thus, it is dominated by the Coulomb repulsions between electron clouds and is the smallest for closed-shell ions that lack spatially extended valence electrons. On the other hand, two criteria must be satisfied for the second term to be large: (1) the energy denominator, E_n − E(0), must be small, therefore, there must be excited states available of energy not largely separated from the ground state; and (2) the matrix element $\langle 0\left|{\left(\frac{\delta H}{\delta Q}\right)}_0\right|n\rangle$ must be nonzero; this occurs if the product of the symmetry representations for the ground and excited state and the distortion is totally symmetric. Thus, for a non-centrosymmetric distortion, if the ground state is centrosymmetric, then the lowest excited state must be non-centrosymmetric. Note that this term represents the mixing of the ground state with the excited states as a result of the distortion perturbation, and as such, it is associated with the formation of new chemical bonds in the low-symmetry configuration [198]. A non-centrosymmetric distortion then results if the lowering in energy associated with the mixing of term two is larger than the repulsion opposing the ion shift, described by term one [199].

In short, nowadays, ferroelectricity is often associated with materials having d⁰ transition metal ions (V⁵⁺, Nb⁵⁺, Ta⁵⁺, Ti⁴⁺, Zr⁴⁺) and cations with a lone pair s² electrons (Pb²⁺ and Bi³⁺) [89,200]. In terms of crystal chemistry, these are SOJT active cations and, by breaking the centrosymmetric structure, have the potential of energy gain [89,189]. The d⁰ ions tend towards the more covalent character in their bonding, leading to asymmetric coordination geometries that favor the development of a spontaneous polarization [200]. In LN and LT, the Nb and Ta ions have 5⁺ formal charges with d⁰ configuration, leading to cation displacement along the trigonal c-axis [189].

6. Conclusions

The scientific paradigm concerning lithium niobate (LiNbO3, LN) research has been explicitly stated and partially justified by presenting a conceptual framework with a convenient order. The concepts have been introduced having in mind both kinds of audience, the experienced researcher and the young contributors to this community. The present review is supported by the revision of several specialized references on this topic. We apologize in advance for the non-deliberated omission of any relevant piece of literature. The justification is to be completed with the content presented in Part II.

In the current part, special attention was put on the subject of the crystal structure. In this respect, we add that, rigorously, a correct statement would be that LN belongs to no other family of crystal structures, but it forms its own. Perhaps this may be implicitly stated when referred to as a ‘pseudoilmenite’ in recent literature. In other words, LN belongs to the family of pseudoilmenites, probably acknowledging the fact that LN is not a mineral that naturally forms on the surface of the Earth; it might be just probable that LN, or at least a close relative, may exist deep beneath the sea level (accounting for polymorphism and the extreme conditions in temperature and pressure) [201,202]. Then, the question arises: why not refer to it as the family of ‘pseudoperovskites’, or simply as a member of the larger family of highly distorted perovskites? Would this be somehow of advantage for future investigations?

Besides the exposition of various indirect methods to determine the chemical composition of LN powders (LNPws), the role of this polycrystalline version of the material in complex piezoelectric ceramics related modern electronic components and the innermost cause of ferroelectricity have also been discussed. The reader may have noticed that these two functionalities—the former concerning powders only—have had their corresponding progress out of this field based on the perovskite framework. Perovskites are currently shaping our modern life with computers, smartphones, and medical ultrasound, and seem to keep doing it with the advent of efficient solar cells and the Internet of Things [151,203,204]. Unprecedented profit might be obtained by relaxing our conceptions about our favorite material and exhorting its kinship to perovskites. In this respect, it is interesting that in a contribution in which its fresh ink still can be smelled, LN and isostructural LiTaO₃ are classified as perovskite ferroelectrics [16]. Finally, the possibility of the stoichiometric and congruent compositions yet not being univocally determined, regardless of the solid solution of LN (single crystal or polycrystal), has been signaled. A strategy that would not convey much effort nor expense has been designed to answer this conundrum.