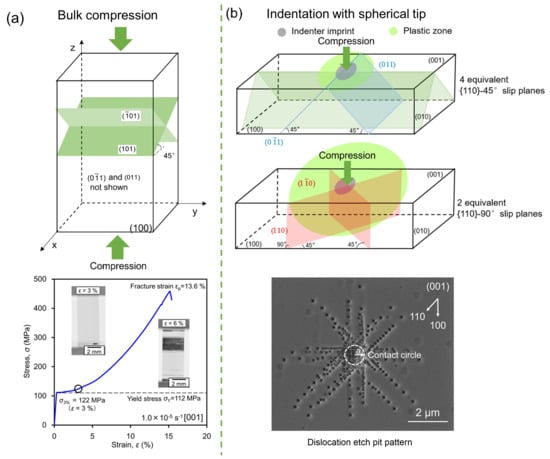
Bridging the Gap between Bulk Compression and Indentation Test on Room-Temperature Plasticity in Oxides: Case Study on SrTiO3
Abstract
:1. Introduction
2. Experimental Method
2.1. Materials
2.2. Mechanical Testing
2.3. Characterization
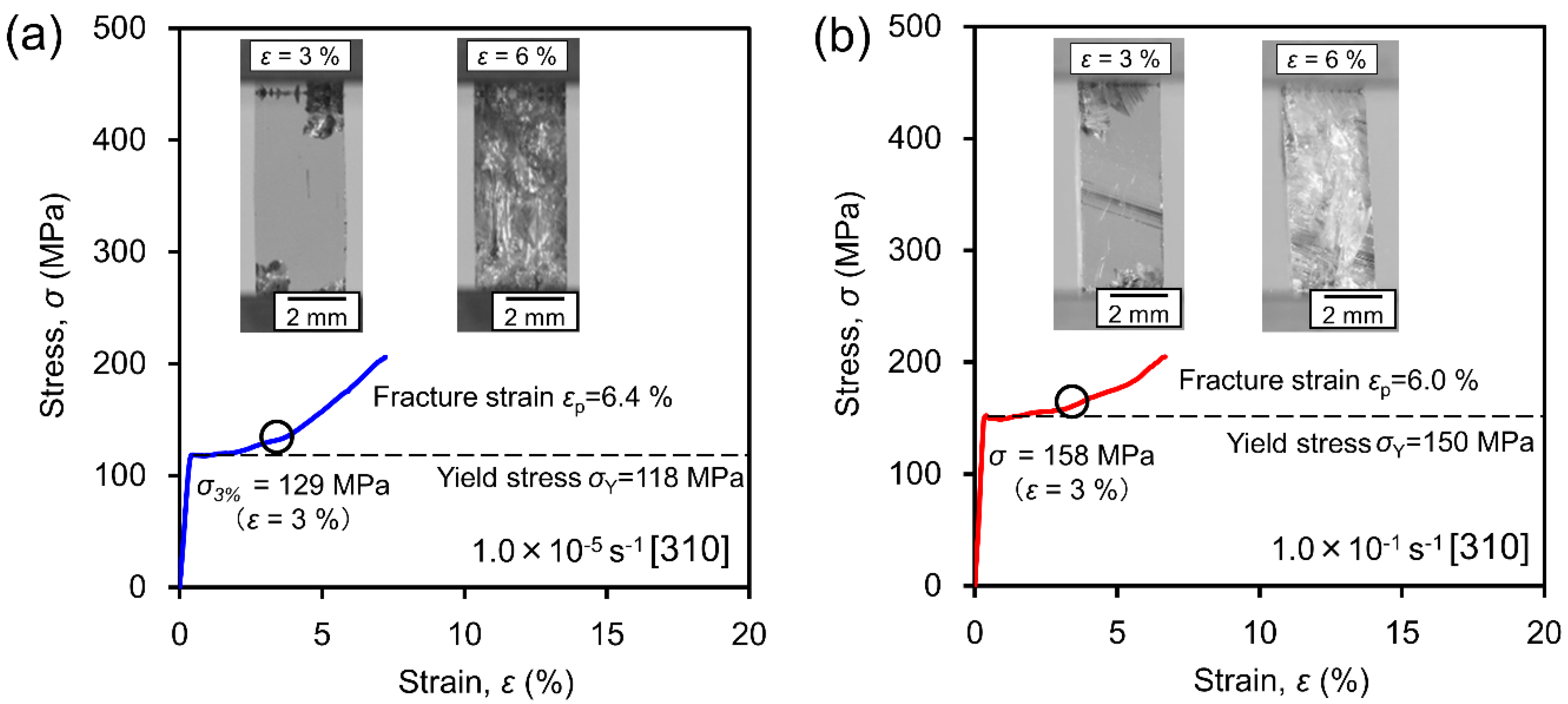
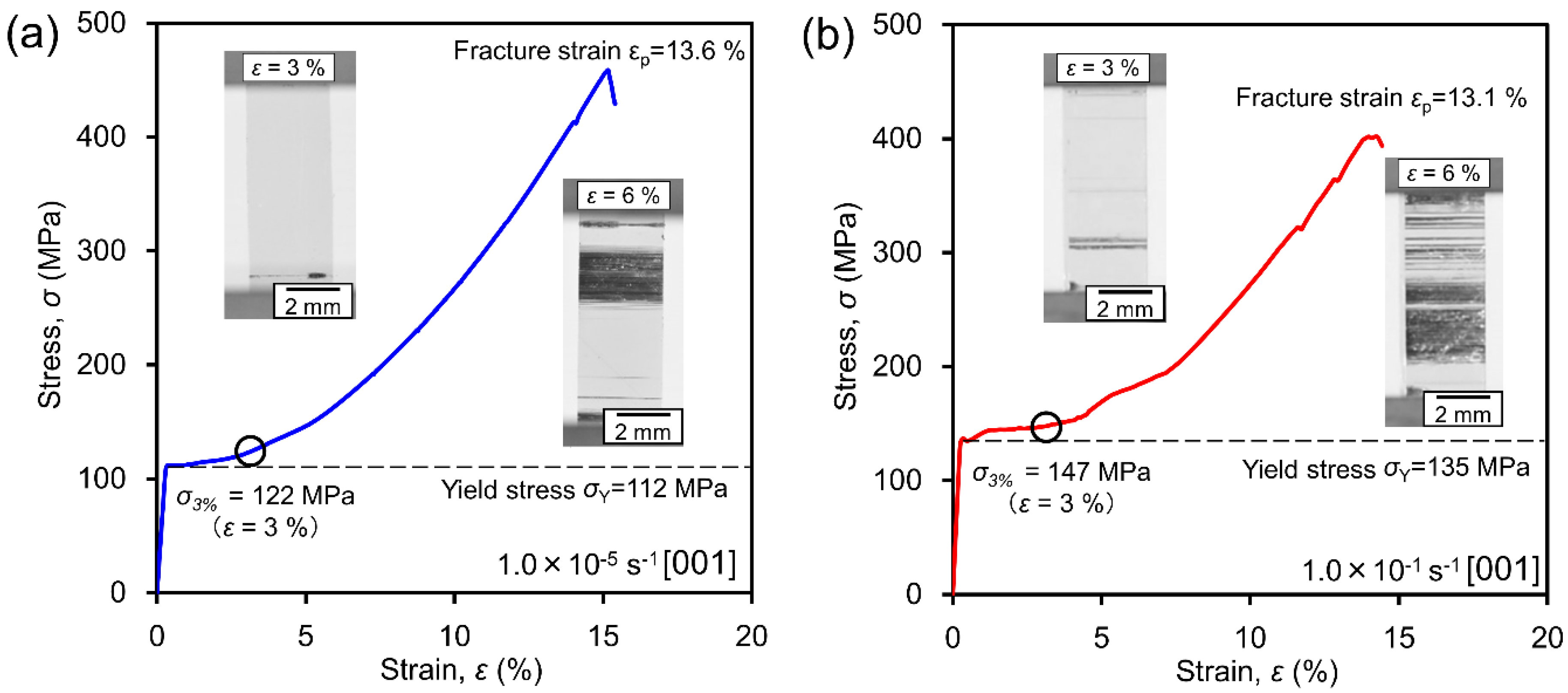
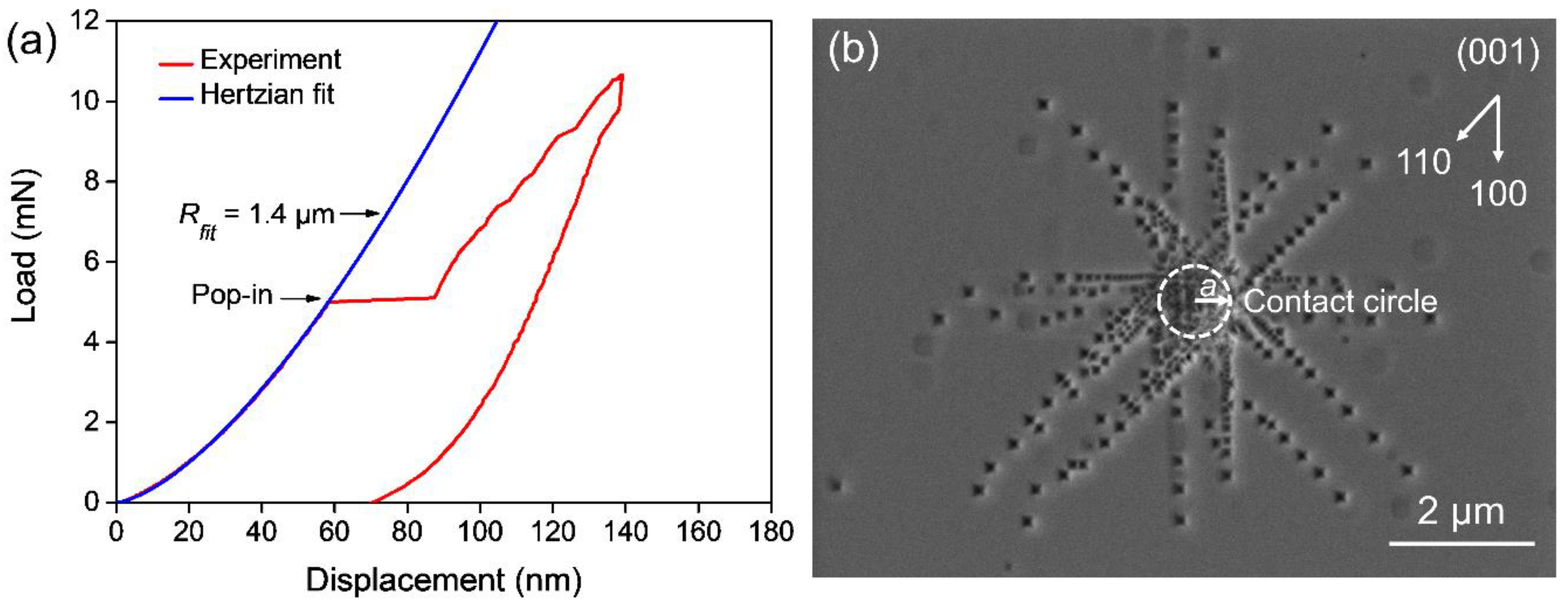
3. Results
3.1. Bulk Deformation
3.2. Indentation Tests
4. Analyses and Discussions
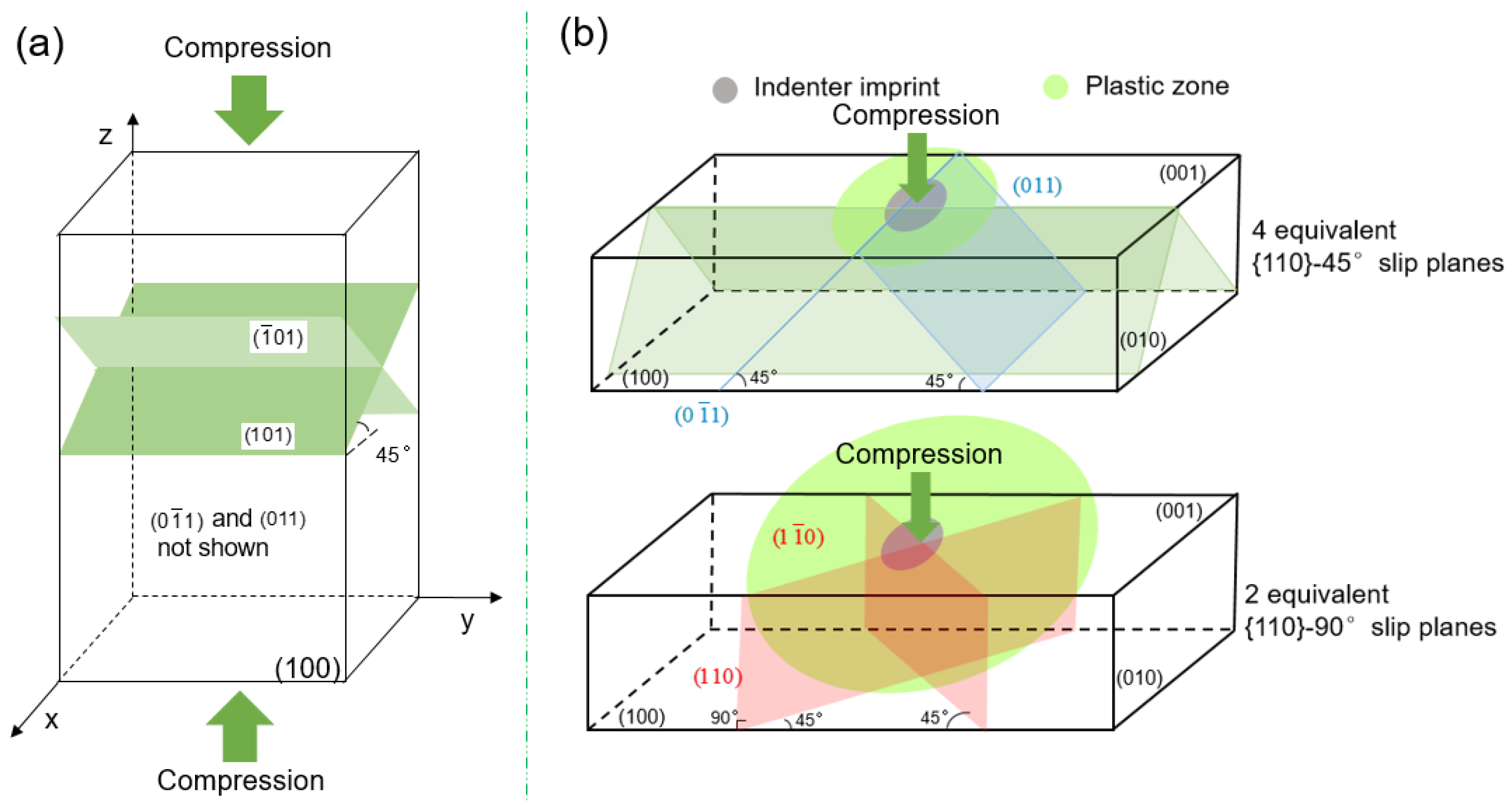
4.1. Stress Comparison and Activation of the Slip Systems
4.2. Strain Comparison
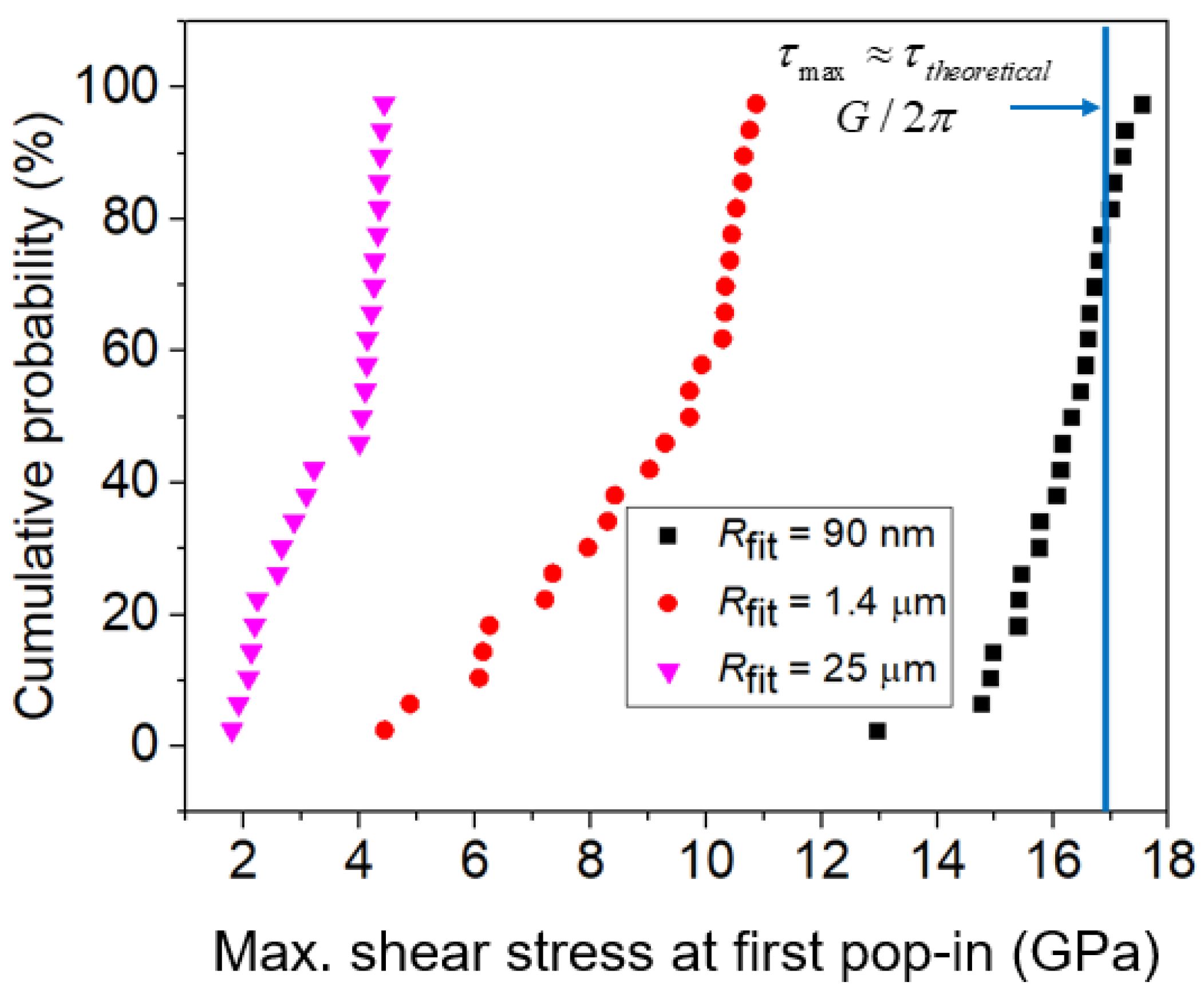
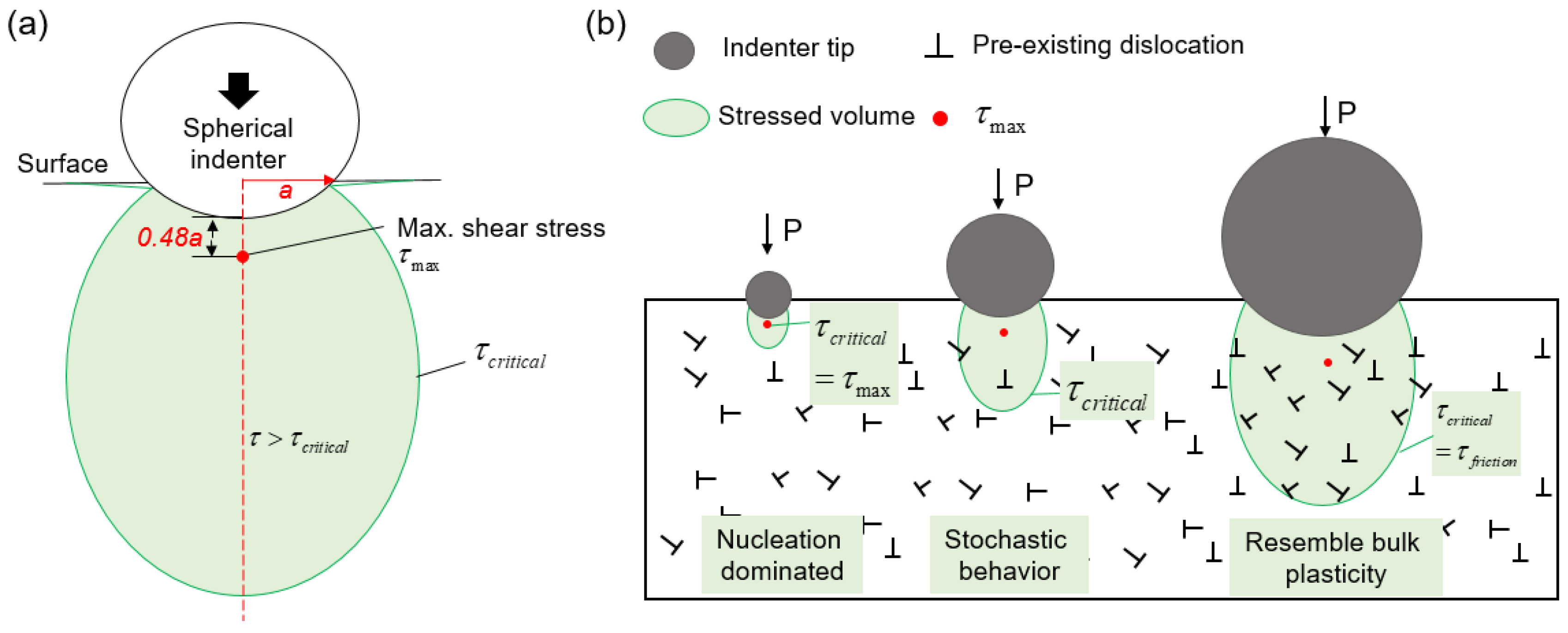
4.3. Indentation Pop-in Related to Defect Population
4.4. Pros & Cons between Bulk and Indentation Tests
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nakamura, A.; Matsunaga, K.; Tohma, J.; Yamamoto, T.; Ikuhara, Y. Conducting nanowires in insulating ceramics. Nat. Mater. 2003, 2, 453–456. [Google Scholar] [CrossRef]
- Ikuhara, Y. Nanowire design by dislocation technology. Prog. Mater. Sci. 2009, 54, 770–791. [Google Scholar] [CrossRef]
- Szot, K.; Speier, W.; Bihlmayer, G.; Waser, R. Switching the electrical resistance of individual dislocations in single-crystalline SrTiO3. Nat. Mater. 2006, 5, 312–320. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Haunschild, G.; Polanco, C.; Ju, J.Z.; Lindsay, L.; Koblmuller, G.; Koh, Y.K. Dislocation-induced thermal transport anisotropy in single-crystal group-III nitride films. Nat. Mater. 2019, 18, 136–140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khafizov, M.; Pakarinen, J.; He, L.; Hurley, D.H. Impact of irradiation induced dislocation loops on thermal conductivity in ceramics. J. Am. Ceram. Soc. 2019, 102, 7533–7542. [Google Scholar] [CrossRef]
- Kim, S.I.; Lee, K.H.; Mun, H.A.; Kim, H.S.; Hwang, S.W.; Roh, J.W.; Yang, D.J.; Shin, W.H.; Li, X.S.; Lee, Y.H.; et al. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 2015, 348, 109–114. [Google Scholar] [CrossRef] [Green Version]
- Ren, P.; Höfling, M.; Koruza, J.; Lauterbach, S.; Jiang, X.; Frömling, T.; Khatua, D.K.; Dietz, C.; Porz, L.; Ranjan, R.; et al. High Temperature Creep-Mediated Functionality in Polycrystalline Barium Titanate. J. Am. Ceram. Soc. 2019. [Google Scholar] [CrossRef] [Green Version]
- Argon, A.S.; Orowan, E. Plastic deformation in mgo single crystals. Philos. Mag. 1964, 9, 1003–1021. [Google Scholar] [CrossRef]
- Gaillard, Y.; Tromas, C.; Woirgard, J. Quantitative analysis of dislocation pile-ups nucleated during nanoindentation in MgO. Acta Mater. 2006, 54, 1409–1417. [Google Scholar] [CrossRef]
- Johnston, W.G.; Gilman, J.J. Dislocation Multiplication in Lithium Fluoride Crystals. J. Appl. Phys. 1960, 31, 632–643. [Google Scholar] [CrossRef]
- Brunner, D.; Taeri-Baghbadrani, S.; Sigle, W.; Rühle, M. Surprising Results of a Study on the Plasticity in Strontium Titanate. J. Am. Ceram. Soc. 2001, 84, 1161–1163. [Google Scholar] [CrossRef]
- Oshima, Y.; Nakamura, A.; Matsunaga, K. Extraordinary plasticity of an inorganic semiconductor in darkness. Science 2018, 360, 772–774. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nakamura, A.; Yasufuku, K.; Furushima, Y.; Toyoura, K.; Lagerlöf, K.; Matsunaga, K. Room-Temperature Plastic Deformation of Strontium Titanate Crystals Grown from Different Chemical Compositions. Crystals 2017, 7, 351. [Google Scholar] [CrossRef] [Green Version]
- Oshima, Y.; Nakamura, A.; Lagerlöf, K.P.D.; Yokoi, T.; Matsunaga, K. Room-temperature creep deformation of cubic ZnS crystals under controlled light conditions. Acta Mater. 2020, 195, 690–697. [Google Scholar] [CrossRef]
- Feng, B.; Ishikawa, R.; Kumamoto, A.; Shibata, N.; Ikuhara, Y. Atomic Scale Origin of Enhanced Ionic Conductivity at Crystal Defects. Nano Lett. 2019, 19, 2162–2168. [Google Scholar] [CrossRef]
- Furushima, Y.; Nakamura, A.; Tochigi, E.; Ikuhara, Y.; Toyoura, K.; Matsunaga, K. Dislocation structures and electrical conduction properties of low angle tilt grain boundaries in LiNbO3. J. Appl. Phys. 2016, 120. [Google Scholar] [CrossRef]
- Lee, H.S.; Mizoguchi, T.; Mistui, J.; Yamamoto, T.; Kang, S.J.L.; Ikuhara, Y. Defect energetics in SrTiO3 symmetric tilt grain boundaries. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
- Ikuhara, Y.; Nishimura, H.; Nakamura, A.; Matsunaga, K.; Yamamoto, T.; Lagerloef, K.P.D. Dislocation Structures of Low-Angle and Near-Sigma 3 Grain Boundaries in Alumina Bicrystals. J. Am. Ceram. Soc. 2003, 86, 595–602. [Google Scholar] [CrossRef]
- Adepalli, K.K.; Kelsch, M.; Merkle, R.; Maier, J. Enhanced ionic conductivity in polycrystalline TiO2 by “one-dimensional doping”. Phys. Chem. Chem. Phys. Pccp 2014, 16, 4942–4951. [Google Scholar] [CrossRef]
- Li, J.; Wang, H.; Zhang, X. Nanoscale stacking fault–assisted room temperature plasticity in flash-sintered TiO2. Sci. Adv. 2019, 5, eaaw5519. [Google Scholar] [CrossRef] [Green Version]
- Johanning, M.; Porz, L.; Dong, J.; Nakamura, A.; Li, J.-F.; Rödel, J. Influence of dislocations on thermal conductivity of strontium titanate. Appl. Phys. Lett. 2020, 117, 021902. [Google Scholar] [CrossRef]
- Nakamura, A.; Lagerlöf, K.P.D.; Matsunaga, K.; Tohma, J.; Yamamoto, T.; Ikuhara, Y. Control of dislocation configuration in sapphire. Acta Mater. 2005, 53, 455–462. [Google Scholar] [CrossRef]
- Gumbsch, P.; Taeri-Baghbadrani, S.; Brunner, D.; Sigle, W.; Ruhle, M. Plasticity and an inverse brittle-to-ductile transition in strontium titanate. Phys. Rev. Lett. 2001, 87, 085505. [Google Scholar] [CrossRef] [PubMed]
- Johnston, W.G.; Gilman, J.J. Dislocation Velocities, Dislocation Densities, and Plastic Flow in Lithium Fluoride Crystals. J. Appl. Phys. 1959, 30, 129–144. [Google Scholar] [CrossRef]
- Gaillard, Y.; Tromas, C.; Woirgard, J. Pop-in phenomenon in MgO and LiF: Observation of dislocation structures. Philos. Mag. Lett. 2010, 83, 553–561. [Google Scholar] [CrossRef]
- Tromas, C.; Gaillard, Y.; Woirgard, J. Nucleation of dislocations during nanoindentation in MgO. Philos. Mag. 2006, 86, 5595–5606. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Ding, K.; Janocha, S.; Minnert, C.; Rheinheimer, W.; Frömling, T.; Durst, K.; Nakamura, A.; Rödel, J. Nanoscale to microscale reversal in room-temperature plasticity in SrTiO3 by tuning defect concentration. Scr. Mater. 2020, 188, 228–232. [Google Scholar] [CrossRef]
- Taeri, S.; Brunner, D.; Sigle, W.; Rühle, M. Deformation behaviour of strontium titanate between room temperature and 1800 K under ambient pressure. Z. Met. 2004, 95, 433–446. [Google Scholar] [CrossRef]
- Patterson, E.A.; Major, M.; Donner, W.; Durst, K.; Webber, K.G.; Rodel, J. Temperature-Dependent Deformation and Dislocation Density in SrTiO3 (001) Single Crystals. J. Am. Ceram. Soc. 2016, 99, 3411–3420. [Google Scholar] [CrossRef]
- Mark, A.F.; Castillo-Rodriguez, M.; Sigle, W. Unexpected plasticity of potassium niobate during compression between room temperature and 900 °C. J. Eur. Ceram. Soc. 2016, 36, 2781–2793. [Google Scholar] [CrossRef]
- Dehm, G.; Jaya, B.N.; Raghavan, R.; Kirchlechner, C. Overview on micro- and nanomechanical testing: New insights in interface plasticity and fracture at small length scales. Acta Mater. 2017, 142, 248–282. [Google Scholar] [CrossRef]
- Pharr, G.M.; Oliver, W.C. Measurement of Thin Film Mechanical Properties Using Nanoindentation. Mrs Bull. 1992, 17, 28–33. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Greer, J.R.; De Hosson, J.T.M. Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect. Prog. Mater. Sci. 2011, 56, 654–724. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge/London, UK, 1985. [Google Scholar]
- Li, W.; Bei, H.; Qu, J.; Gao, Y. Effects of machine stiffness on the loading–displacement curve during spherical nano-indentation. J. Mater. Res. 2013, 28, 1903–1911. [Google Scholar] [CrossRef]
- Javaid, F.; Bruder, E.; Durst, K. Indentation size effect and dislocation structure evolution in (001) oriented SrTiO3 Berkovich indentations: HR-EBSD and etch-pit analysis. Acta Mater. 2017, 139, 1–10. [Google Scholar] [CrossRef]
- Swain, M.V.; Lawn, B.R. A Study of Dislocation Arrays at Spherical Indentations in LiF as a Function of Indentation Stress and Strain. Phys. Stat. Sol. 1969, 35, 909–923. [Google Scholar] [CrossRef]
- Javaid, F.; Stukowski, A.; Durst, K. 3D Dislocation structure evolution in strontium titanate: Spherical indentation experiments and MD simulations. J. Am. Ceram. Soc. 2017, 100, 1134–1145. [Google Scholar] [CrossRef]
- Javaid, F.; Johanns, K.E.; Patterson, E.A.; Durst, K. Temperature dependence of indentation size effect, dislocation pile-ups, and lattice friction in (001) strontium titanate. J. Am. Ceram. Soc. 2018, 101, 356–364. [Google Scholar] [CrossRef] [Green Version]
- Field, J.S.; Swain, M.V. A simple predictive model for spherical indentation. J. Mater. Res. 1993, 8, 297–306. [Google Scholar] [CrossRef]
- Gao, Y.; Bei, H. Strength statistics of single crystals and metallic glasses under small stressed volumes. Prog. Mater. Sci. 2016, 82, 118–150. [Google Scholar] [CrossRef] [Green Version]
- Morris, J.R.; Bei, H.; Pharr, G.M.; George, E.P. Size Effects and Stochastic Behavior of Nanoindentation Pop In. Phys. Rev. Lett. 2011, 106, 165502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, K.; Xia, Y.; Crespillo, M.; Xue, H.; Zhang, Y.; Gao, Y.F.; Bei, H. Quantifying early stage irradiation damage from nanoindentation pop-in tests. Scr. Mater. 2018, 157, 49–53. [Google Scholar] [CrossRef]
- Bei, H.; Xia, Y.Z.; Barabash, R.I.; Gao, Y.F. A tale of two mechanisms: Strain-softening versus strain-hardening in single crystals under small stressed volumes. Scr. Mater. 2016, 110, 48–52. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, J.A.; Kelchner, C.L.; Klein, P.A.; Hamilton, J.C.; Foiles, S.M. Surface step effects on nanoindentation. Phys. Rev. Lett. 2001, 87, 165507. [Google Scholar] [CrossRef]
- Matsunaga, K.; Ii, S.; Iwamoto, C.; Yamamoto, T.; Ikuhara, Y. In situ observation of crack propagation in magnesium oxide ceramics. Nanotechnology 2004, 15, S376–S381. [Google Scholar] [CrossRef]
- Kondo, S.; Shibata, N.; Mitsuma, T.; Tochigi, E.; Ikuhara, Y. Dynamic observations of dislocation behavior in SrTiO3 by in situ nanoindentation in a transmission electron microscope. Appl. Phys. Lett. 2012, 100, 181906. [Google Scholar] [CrossRef]
- Kondo, S.; Mitsuma, T.; Shibata, N.; Ikuhara, Y. Direct observation of individual dislocation interaction processes with grain boundary. Sci. Adv. 2016, 2, e1501926. [Google Scholar] [CrossRef] [Green Version]
- Kondo, S.; Ishihara, A.; Tochigi, E.; Shibata, N.; Ikuhara, Y. Direct observation of atomic-scale fracture path within ceramic grain boundary core. Nat. Commun. 2019, 10, 2112. [Google Scholar] [CrossRef]
- Nie, A.; Bu, Y.; Huang, J.; Shao, Y.; Zhang, Y.; Hu, W.; Liu, J.; Wang, Y.; Xu, B.; Liu, Z.; et al. Direct Observation of Room-Temperature Dislocation Plasticity in Diamond. Matter 2020, 2, 1222–1232. [Google Scholar] [CrossRef] [Green Version]
- Sernicola, G.; Giovannini, T.; Patel, P.; Kermode, J.R.; Balint, D.S.; Britton, T.B.; Giuliani, F. In situ stable crack growth at the micron scale. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Cho, J.; Li, J.; Wang, H.; Li, Q.; Fan, Z.; Mukherjee, A.K.; Rheinheimer, W.; Wang, H.; Zhang, X. Study of deformation mechanisms in flash-sintered yttria-stabilized zirconia by in-situ micromechanical testing at elevated temperatures. Mater. Res. Lett. 2019, 7, 194–202. [Google Scholar] [CrossRef] [Green Version]
- Malyar, N.V.; Micha, J.S.; Dehm, G.; Kirchlechner, C. Size effect in bi-crystalline micropillars with a penetrable high angle grain boundary. Acta Mater. 2017, 129, 312–320. [Google Scholar] [CrossRef]
- Malyar, N.V.; Micha, J.S.; Dehm, G.; Kirchlechner, C. Dislocation-twin boundary interaction in small scale Cu bi-crystals loaded in different crystallographic directions. Acta Mater. 2017, 129, 91–97. [Google Scholar] [CrossRef]
- Gaillard, Y.; Tromas, C.; Woirgard, J. Study of the dislocation structure involved in a nanoindentation test by atomic force microscopy and controlled chemical etching. Acta Mater. 2003, 51, 1059–1065. [Google Scholar] [CrossRef]
- Zaefferer, S.; Elhami, N.-N. Theory and application of electron channelling contrast imaging under controlled diffraction conditions. Acta Mater. 2014, 75, 20–50. [Google Scholar] [CrossRef]
- Otsuka, K.; Kuwabara, A.; Nakamura, A.; Yamamoto, T.; Matsunaga, K.; Ikuhara, Y. Dislocation-enhanced ionic conductivity of yttria-stabilized zirconia. Appl. Phys. Lett. 2003, 82, 877–879. [Google Scholar] [CrossRef]
- Fang, X.; Jia, J.; Feng, X. Three-point bending test at extremely high temperature enhanced by real-time observation and measurement. Measurement 2015, 59, 171–176. [Google Scholar] [CrossRef]
- Luo, H.; Lu, W.; Fang, X.; Ponge, D.; Li, Z.; Raabe, D. Beating hydrogen with its own weapon: Nano-twin gradients enhance embrittlement resistance of a high-entropy alloy. Mater. Today 2018, 21, 1003–1009. [Google Scholar] [CrossRef]
- Wheeler, J.M.; Armstrong, D.E.J.; Heinz, W.; Schwaiger, R. High temperature nanoindentation: The state of the art and future challenges. Curr. Opin. Solid State Mater. Sci. 2015, 19, 354–366. [Google Scholar] [CrossRef] [Green Version]
- Trenkle, J.C.; Packard, C.E.; Schuh, C.A. Hot nanoindentation in inert environments. Rev. Sci. Instrum. 2010, 81, 073901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Fang, X.; Xia, B.; Feng, X. In situ measurement of oxidation evolution at elevated temperature by nanoindentation. Scr. Mater. 2015, 103, 61–64. [Google Scholar] [CrossRef]
- Li, Y.; Fang, X.; Qu, Z.; Lu, S.; Li, H.; Zhu, T.; Yu, Q.; Feng, X. In situ full-field measurement of surface oxidation on Ni-based alloy using high temperature scanning probe microscopy. Sci. Rep. 2018, 8, 6684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Minnert, C.; Oliver, W.C.; Durst, K. Newultra-high temperature nanoindentation system for operating at up to 1100 °C. Mater. Des. 2020, 192, 108727. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
| Bulk Deformation (Larger than mm Size) | (Nano)Indentation (Nano-/Microscale) | |
|---|---|---|
| Pros |
|
|
| Cons |
|
|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Porz, L.; Ding, K.; Nakamura, A. Bridging the Gap between Bulk Compression and Indentation Test on Room-Temperature Plasticity in Oxides: Case Study on SrTiO3. Crystals 2020, 10, 933. https://doi.org/10.3390/cryst10100933
Fang X, Porz L, Ding K, Nakamura A. Bridging the Gap between Bulk Compression and Indentation Test on Room-Temperature Plasticity in Oxides: Case Study on SrTiO3. Crystals. 2020; 10(10):933. https://doi.org/10.3390/cryst10100933
Chicago/Turabian StyleFang, Xufei, Lukas Porz, Kuan Ding, and Atsutomo Nakamura. 2020. "Bridging the Gap between Bulk Compression and Indentation Test on Room-Temperature Plasticity in Oxides: Case Study on SrTiO3" Crystals 10, no. 10: 933. https://doi.org/10.3390/cryst10100933
APA StyleFang, X., Porz, L., Ding, K., & Nakamura, A. (2020). Bridging the Gap between Bulk Compression and Indentation Test on Room-Temperature Plasticity in Oxides: Case Study on SrTiO3. Crystals, 10(10), 933. https://doi.org/10.3390/cryst10100933