Analysis of Concrete Failure on the Descending Branch of the Load-Displacement Curve

Abstract

In this paper, load-displacement and stress-strain diagrams are considered for the uniaxial compression of concrete and under three-point bending. It is known that the destruction of such materials occurs on the descending branch of the load-displacement diagram. The attention of the presented research is focused on the explanation of this phenomenon. Fracture mechanics approaches are used as a research tool. The method for determining effective stresses and modulus of elasticity of concrete based on the results of uniaxial compression tests has been substantiated. The ratios necessary for the calculation were obtained without any assumptions about the reinforcement of concrete and the mechanical properties of its components. However, the effect of these properties is considered indirectly, using the stress and strain peaks determined by standard concrete compression tests. It was found that the effective stresses increase both on the ascending branch and on the descending branch of the load-displacement diagram. This explains the destruction of concrete on the descending branch of the load-displacement diagram. The results of determining the stresses and modulus of elasticity under uniaxial compression are comparable with the results obtained in experiments known in the literature.

1. Introduction

Numerous studies are focused on improving the technical, economic and environmental characteristics of concrete, the continuous flow of which confirms the relevance and complexity of the problems of increasing the competitiveness of this material [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. As a result of research, there are more economical components of concrete, new materials for reinforcement, and improved technologies for the manufacture of concrete as a multicomponent composite material [5,6,7]. Experimental studies are required to ensure sufficient structural reliability, but the cost remains high. Modern methods of mathematical modeling can reduce the cost of studying concrete and other materials [8,9]. The most complete information about concrete behavior is obtained using stress-strain models, reviews of which can be found in the articles [5,10]. For a sufficiently accurate prediction of the behavior of concrete under various influences, a significant number of studies have been carried out to improve the corresponding models, which, however, remain the subject of discussion. When constructing stress-strain models, methods of analytical mechanics, numerical methods and methods of fracture mechanics can be used [11,12], as well as methods of curve fitting to the experimentally obtained data [13,14,15,16]. A typical load–displacement curve is shown in Figure 1.

In this study, the application of the basic concepts of fracture mechanics to the substantiation of the total stress-strain relations for concrete under uniaxial compression is considered. Such relationships have been studied in numerous works, reviews of which can be found in the articles [12,13,14]. However, an analysis of the literature showed that the following questions that determine the purpose of this work remained insufficiently studied: How does one explain that concrete samples under uniaxial compression fail on the descending branch of the stress-strain diagram? Is it necessary to take into account the Poisson effect in the proposed approach?

Purpose of the work: development of a methodology for theoretical analysis of the interdependencies of load and displacement, stresses and strains, deformations and material damage, material damage and effective stresses.

In this work, an analytical model is theoretically substantiated, which coincides with the experimentally substantiated Furamura model [17] known from the literature (an analysis of the Furamura model is also available in [14,18]). In addition to the data known from the literature, the model was analyzed using definitions known in fracture mechanics, such as damage function, effective area, effective stresses, and effective elastic modulus. For the listed definitions, in accordance with their physical meaning, analytical relationships are obtained. Using the obtained relations, the coefficient for determining the effective modulus of elasticity was refined: instead of the experimentally found 2.18 [18], a theoretically substantiated coefficient of 2.72 is proposed. In addition, it is substantiated that the effective stresses, in accordance with Hooke’s law, continuously increase, both on the ascending and descending branches of the stress-strain diagram under the uniaxial compression. This theoretically explains the destruction of concrete samples on the descending branch of the diagram.

2. Materials and Methods

2.1. Mechanical Model: A Brief Description

• Concrete is viewed as a structure composed of interacting mesoscale elements.
• The material of each element obeys Hooke’s law.
• The modulus of elasticity, strength and other physical and mechanical properties of the material of each element do not depend on its size and do not change over time.
• With an increase in the external load, and hence displacement, individual mesoscale elements are destroyed, as a result of which the effective area decreases, and the load is redistributed to the elements that remain intact. As a result, the average statistical value of the effective stresses in the material of the remaining intact mesoscale elements increases.
• The destruction of mesoscale elements and their conglomerates leads to a decrease in the effective area and a decrease in the resistance of the macrostructure to external force, which corresponds to the descending branch of the “load - displacement” diagram. However, effective stresses (i.e., stresses in the material of mesoscale elements) increase. The growth of effective stresses is limited by the ultimate strength of the material of mesoscale elements.
• Stresses determined without taking damage into account can be called apparent stresses [12].
• The Poisson effect can cause some growth in the transverse dimensions and a corresponding change in the cross-sectional area of the sample under uniaxial compression. Thus, two trends should be analyzed: first, a decrease in cross-sectional area due to destruction of mesoscale elements and, second, an increase in area due to the Poisson effect.
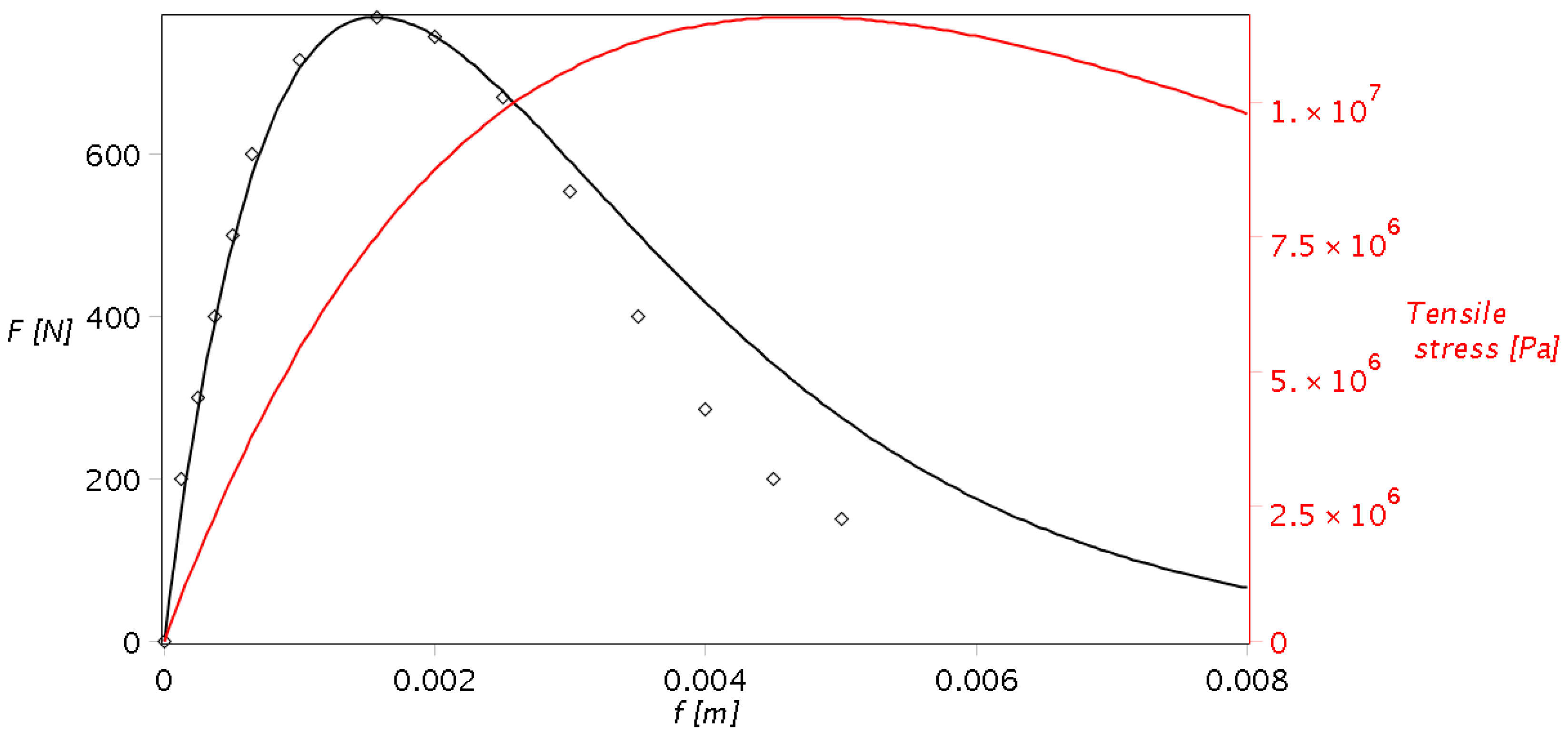
• The primary source of information for the mathematical description of the model and obtaining numerical results is the load-displacement diagram (Figure 1).

2.2. Mathematical Description of the Mechanical Model

Let the initial length and cross-sectional area of the sample be equal to $L_0$ and $A_0$, respectively. Effective cross-sectional area is $0<\tilde{A}\le A_0$.

It follows from the above that a certain displacement value $f$ corresponds to $\tilde{A}=A_0-{\tilde{A}}_D+{\tilde{A}}_{\mu }$. Here, ${\tilde{A}}_D$ and ${\tilde{A}}_{\mu }$ are partial cross-sectional areas depending on the destruction of mesoscale elements and the Poisson effect, respectively.

The value $f+\Delta f$ corresponds to $\tilde{A}=A_0-({\tilde{A}}_D+\Delta {\tilde{A}}_D)+({\tilde{A}}_{\mu }\hspace{0.17em}+\Delta A_{\mu })$.

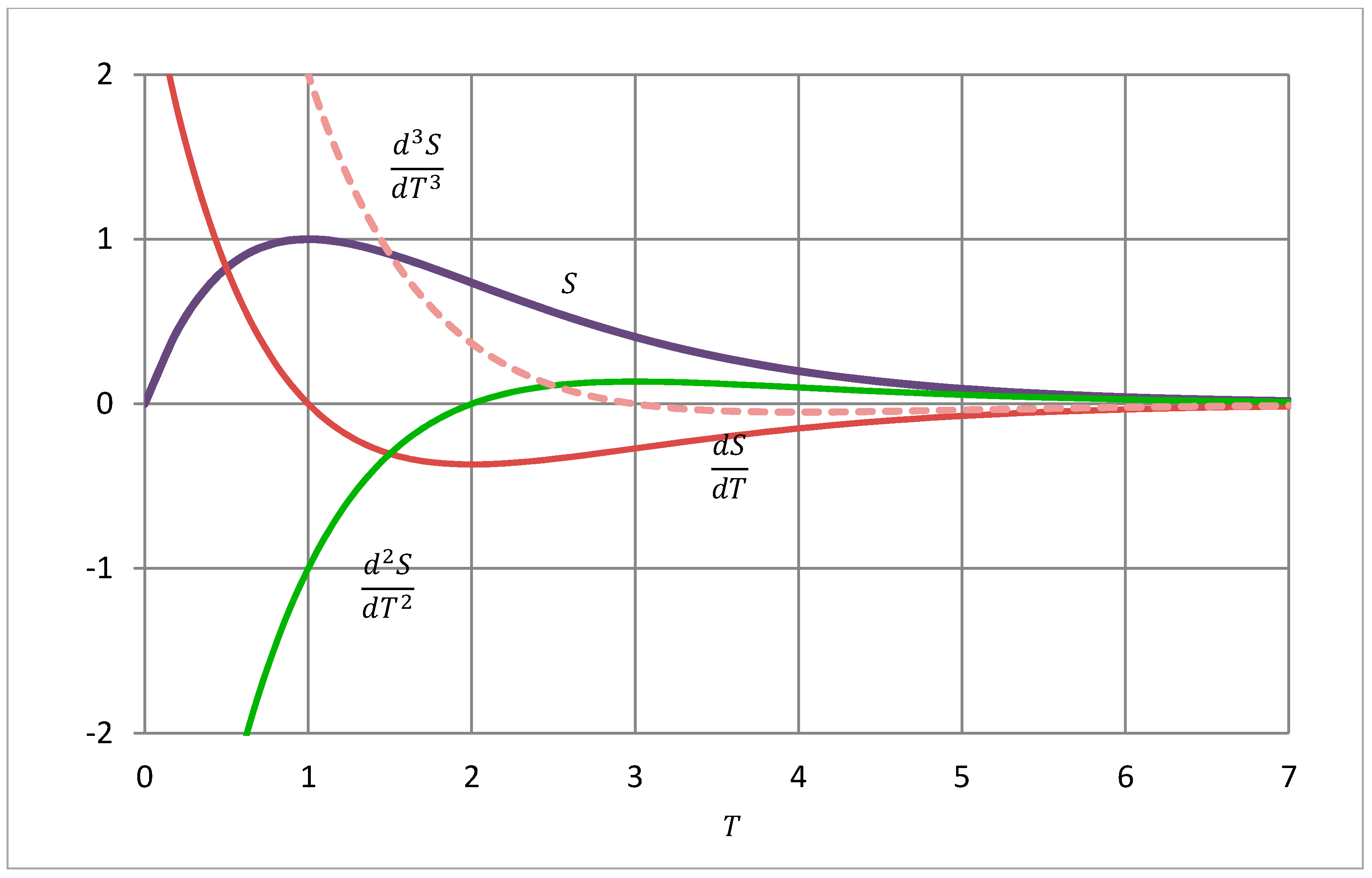
2.2.1. Determination of $\Delta {\tilde{A}}_D$

If $\Delta f$ is a small enough value, then we can assume that

$$\Delta {\tilde{A}}_D=-\frac{\Delta f}{f_{extr}^{test}}\tilde{A}$$

(1)

With an increase in axial strain, mesoscale elements are destroyed, and the effective area $\tilde{A}$ decreases, i.e., the area increment is negative, which is taken into account in (1) by the minus sign. The ratio $\Delta f/f_{extr}^{test}$ is the normalized displacement increment. Axial strain $\epsilon =f/L_0$ and ${\epsilon }_{extr}^{test}=f_{extr}^{test}/L_0$. Then, instead of (1), we write (2):

$$\Delta {\tilde{A}}_D=-\frac{\Delta \epsilon }{{\epsilon }_{extr}^{test}}\tilde{A}.$$

(2)

2.2.2. Determination of $\Delta A_{\mu }$

Let $\tilde{a}$ be the characteristic size of the cross section, such that $\tilde{A}={\tilde{a}}^2$. If displacement increases from $f$ to $f+\Delta f$, then the effective area under uniaxial compression will be equal to $\tilde{A}+\Delta \tilde{A}={(\tilde{a}+\mu \epsilon \tilde{a})}^2\approx \tilde{A}(1+2\mu \epsilon )$, where $\mu$ is the Poisson’s ratio, $\epsilon$ is axial strain. Thus, ${\tilde{A}}_{\mu }=2\mu \epsilon \tilde{A}$ and

$$\Delta {\tilde{A}}_{\mu }=2\mu \Delta \epsilon \tilde{A}.$$

(3)

2.2.3. Determination of $\Delta \tilde{A}$

Using relations (2) and (3), and taking into account that for concrete ${\epsilon }_{extr}^{test}\ll 1$, let’s define $\Delta \tilde{A}=\Delta {\tilde{A}}_D+\Delta {\tilde{A}}_{\mu }$:

$$\Delta \tilde{A}=-\tilde{A}\frac{\Delta \epsilon }{{\epsilon }_{extr}^{test}}(1-2\mu {\epsilon }_{extr}^{test})\approx -\tilde{A}\frac{\Delta \epsilon }{{\epsilon }_{extr}^{test}}.$$

(4)

2.2.4. Effective Area, Damage Function and Effective Modulus of Elasticity

We transform relation (4) to dimensionless form, dividing both parts by $A_0$. We denote $\tilde{A}/A_0=\mathrm{\Theta }$ and $\Delta \tilde{A}/A_0=\Delta \mathrm{\Theta }$. When $\Delta \epsilon \to 0$, instead of Equation (4), we obtain:

$$\frac{d\mathrm{\Theta }}{\mathrm{\Theta }}=-\frac{d\epsilon }{{\epsilon }_{extr}^{test}}.$$

(5)

Taking into account that if ε = 0, then $\tilde{A}=A_0$ and $\mathrm{\Theta }=1$, from Equation (5), we find $\mathrm{\Theta }=e^{-\hspace{0.17em}\frac{\epsilon }{{\epsilon }_{extr}^{test}}}$. Then, the effective area

$$\tilde{A}=A_0{e}^{-\hspace{0.17em}\frac{\epsilon }{{\epsilon }_{extr}^{test}}}.$$

(6)

It follows from relation (6) that the function $\mathrm{\Theta }(\epsilon )$ is a function of damage: $\tilde{A}=A_0\mathrm{\Theta }$. If $\epsilon =0$, then there is no damage, $\tilde{A}=A_0$, $\mathrm{\Theta }=1$. If $\epsilon \gg {\epsilon }_{extr}^{test}$, then $\tilde{A}\approx 0$, $\mathrm{\Theta }=0$.

Let’s substitute relation (6) into the Equation $F=\epsilon \tilde{E}\tilde{A}$, where $\tilde{E}$—effective modulus of elasticity:

$$F=\epsilon \tilde{E}{A}_0{e}^{-\frac{\epsilon }{{\epsilon }_{extr}^{test}}}.$$

(7)

If, then $\epsilon ={\epsilon }_{extr}^{test}$ then ${F_{extr}^{test}/A}_0={\sigma }_{extr}^{test}$ and from Equation (7), we find

$$\tilde{E}=\frac{{\sigma }_{extr}^{test}}{{\epsilon }_{extr}^{test}}e.$$

(8)

Note that Formula (8) in form and physical meaning coincides with the formula for determining the modulus of elasticity from the paper [18] p. 3; only the coefficients differ, namely, $e\approx 2.72$ in Formula (8), and 2.18 in the cited paper [18].

2.2.5. Curve Equation $\sigma (\epsilon )$

Substituting (8) into (7), we obtain the equation of the curve $\sigma =\sigma (\epsilon )$:

$$\sigma ={\sigma }_{extr}^{test}\frac{\epsilon }{{\epsilon }_{extr}^{test}}{e}^{1-\frac{\epsilon }{{\epsilon }_{extr}^{test}}}.$$

(9)

We rewrite (9) in the normalized form (10):

$$\frac{\sigma }{{\sigma }_{extr}^{test}}=\frac{\epsilon }{{\epsilon }_{extr}^{test}}{e}^{1-\frac{\epsilon }{{\epsilon }_{extr}^{test}}}.$$

(10)

Model in the form (10) coincides with the above-mentioned Furamura model, the analysis of which can be found in the paper [18].

The values of ${\sigma }_{extr}^{test}$ and ${\epsilon }_{extr}^{test}$ are determined from the results of standard compression tests.

3. Results and Discussion

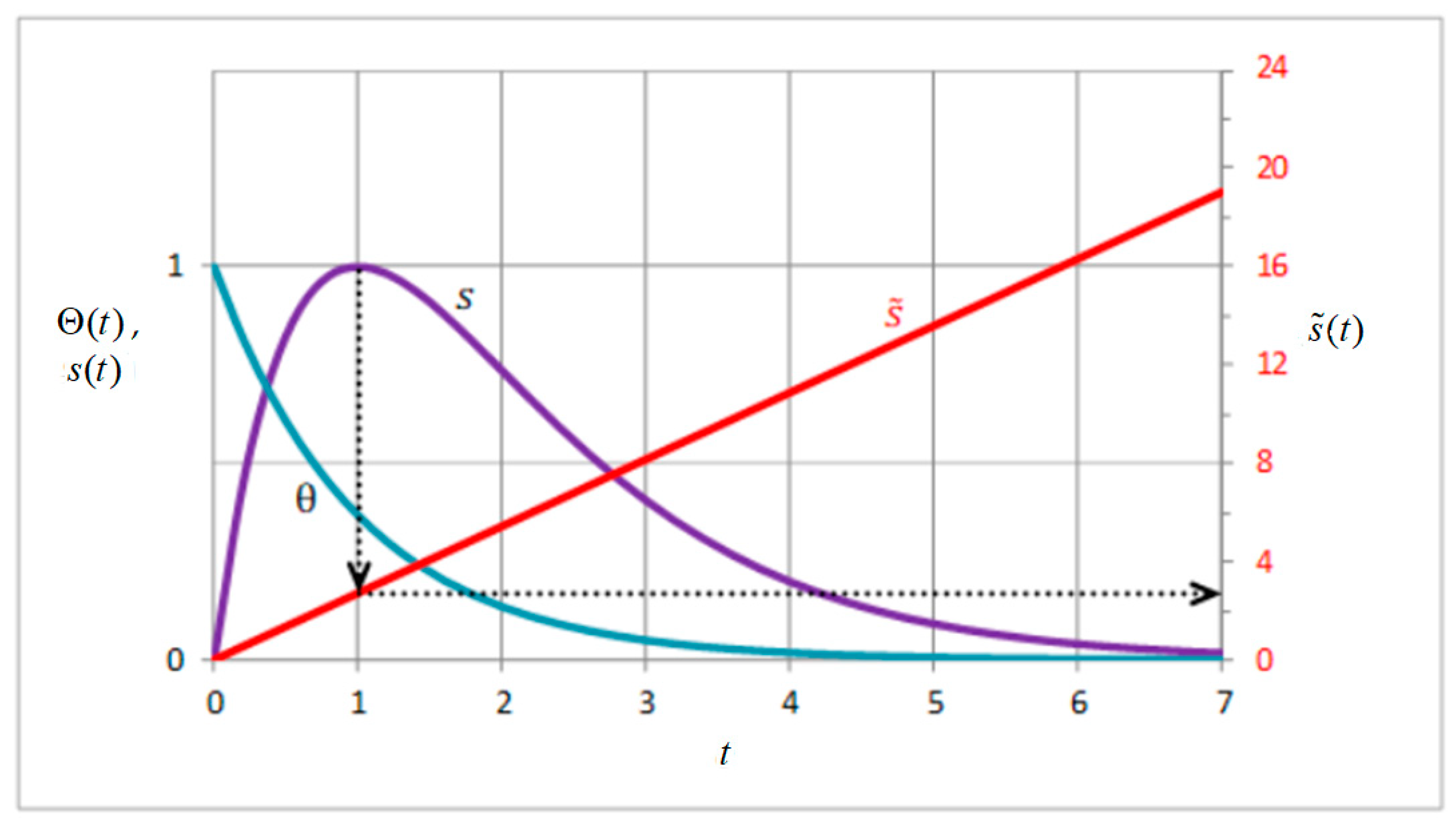
3.1. Some Features of the Model

If the test is carried out at a constant speed of movement of the crosshead of the testing machine $v$ during time $t$, then $\epsilon =f/L_0=vt/L_0$. We denote $S=\sigma /{\sigma }_{extr}^{test}$, $T=t/t_{extr}^{test}$. Then, using (10), we write

$$S=T{e}^{1-T}.$$

(11)

The speed and acceleration of process (11) are determined by the corresponding derivatives $(n=1,\hspace{0.17em}2,\hspace{0.17em}3)$:

$$\frac{d^{n}S}{d{T}^n}={(-1)}^{n-1}{(n-T)}^{1-T}.$$

(12)

If, in Equation (12), $T$ = 1, 2, 3, then $\frac{d^{n}S}{d{T}^n}=0$ (Figure 2).

On the ascending branch of the diagram, the process speed and the absolute value of the acceleration decrease. On the descending branch of the diagram, the speed $dS/dT$ and acceleration $d^{2}S/d{T}^2$ of the process are extreme if $S=2$ and $S=3$, respectively. It can be assumed that destruction is most likely in the vicinity of these points, which is shown, for example, by diagrams known from the literature [16].

It should be noted that relations (9), (10), and (11) determine changes in the apparent stress σ (in the terminology of [12]), i.e., excluding damage (6). Therefore, contradictions are possible when analyzing the physical meaning of the curves in Figure 2.

The actual question is: why does the sample collapse on the descending branch of the diagram? To find the answer, it is necessary to consider the effect of damage (6) and the effective characteristics of the material. Known results in this area are presented, for example, in articles [9,11,12,19,20,21]. Furthermore, in this work, the above relations (1)–(10) are used.

3.2. Effective Stress

Force and displacement are determined experimentally, taking into account (directly or indirectly) all factors that influence the behavior of the sample. Therefore, force and displacement can be attributed to effective characteristics. However, we are interested in predicted characteristics that include effective area $\tilde{A}$ and damage function $\mathrm{\Theta }=\exp (-\epsilon /{\epsilon }_{extr}^{test})$ (6), effective modulus $\tilde{E}$ (8) and effective stress.

Using (8), we calculate the effective stress $\tilde{\sigma }=\epsilon \tilde{E}$:

$$\tilde{\sigma }=\epsilon \frac{{\sigma }_{extr}^{test}}{{\epsilon }_{extr}^{test}}e.$$

(13)

How are apparent and effective stresses interrelated? It follows from relations (9) and (13) that

$$\sigma =\tilde{\sigma }{e}^{-\frac{\epsilon }{{\epsilon }_{extr}^{test}}}.$$

(14)

$$\tilde{\sigma }=\sigma e^{\frac{\epsilon }{{\epsilon }_{extr}^{test}}}.$$

(15)

Let’s denote $\tilde{s}=\tilde{\sigma }/{\sigma }_{extr}^{test}$, $\tilde{e}=\epsilon /{\epsilon }_{extr}^{test}$. Then, using (13), we write $\tilde{e}=\epsilon e$. The behavior of the effective and apparent stresses is modeled by the graphs of the functions $\tilde{s}(t)$ and $s(t)$, respectively (Figure 3).

If the magnitude of the external force during compression tests changes at a constant rate, then the dependences $\mathrm{\Theta }(t)$, $\tilde{s}(t)$ and $s(t)$ are similar to the graphs in Figure 3.

Figure 3, as well as Formula (13), shows that, with an increase in deformation, the effective stresses only increase. This explains the phenomenon of the destruction of concrete on the descending branch of the load-displacement diagram. The growth of effective stresses is limited by the strength of the material.

It is necessary to pay attention to the fact that the above relations (1)–(15) were obtained without direct assumptions about concrete reinforcement, granulometric composition of the aggregate and about other material properties. Obviously, however, these properties are taken into account indirectly by means of $F_{extr}^{test}$ and $f_{extr}^{test}$ (Figure 1) (either ${\sigma }_{extr}^{test}$ and ${\epsilon }_{extr}^{test}$). Consequently, the presented dependences can be used to simulate other brittle materials, the compression curves of which are similar to the curve in Figure 1. To test this assumption, let us compare the simulation results with experimental data known from the literature [22].

3.3. Comparison with Experiments Known in the Literature

In the article [22] (Table 6), stress-strain characteristics for low and high strength concrete (30 and 70 MPa) are presented. In this study, in particular, stress-strain curves are obtained, and peak values of stresses and strains during uniaxial compression of steel-fiber-reinforced concrete are given. The fiber volume fraction varied from 0.00 to 1.25%.

The initial data for calculating the effective modulus of elasticity $\tilde{E}$ and effective stress $\tilde{\sigma }$ are given in

Table 1. Comparison with literature data [18,22].

Number of Samples:	1	2	3	4	5	6	7	8	9
Fiber volume, %	0.00	0.50	0.75	1.00	0.00	0.50	0.75	1.00	1.25
${\sigma }_{extr}^{test}$, MPa [22]	28.19	29.34	29.94	30.87	54.65	54.86	57.94	59.82	56.91
${\epsilon }_{extr}^{test}$, mε; [22] (1 mε = 0.001)	1.950	2.657	2.931	2.954	2.050	3.08	3.000	3.080	3.080
$\tilde{\sigma }$, MPa, (13) (if $\epsilon$ = ${\epsilon }_{extr}^{test}$)	76.63	79.75	81.39	83.91	148.55	149.12	157.50	162.61	154.70
$\tilde{E}$, MPa; (8)	39,297	30,017	27,767	28,407	72,465	48,417	52,499	52,795	50,226
$E$, MPa; [22]	25,260	25,090	25,900	25,990	45,210	46,570	47,160	47,400	46,540
1$E$, MPa; [18]	31,515	24,073	22,269	22,782	58,116	38,829	42,103	42,340	40,280

¹ Calculated by the formula $E=2.18\frac{{\sigma }_{extr}^{test}}{{\epsilon }_{extr}^{test}}$ according to [18].

.

The dependences σ(ε) and $\tilde{\sigma }$(ε) for the initial data presented in Table 1 are shown in Figure 4 and Figure 5, respectively.

Figure 5 clearly shows that reinforcement reduces the effective stresses in concrete and, as a result, hinders cracking.

The results presented in Table 1 and Figure 4 and Figure 5 are comparable with the results obtained in experiments [18,22]. With an increase in the reinforcement from 0.5% to 1.25%, the differences between the experimental and calculated values of the elastic modulus (Table 1) decrease from 16% (sample No. 1) to 4% (sample No. 7). These deviations are permissible for practical use. In this case, the determination of effective stresses and elastic modulus is easy to implement using Formulas (8) and (13). Peak values of stresses and strains are used as the initial data for calculations, which are determined experimentally using standard methods.

3.4. Relationship between Load and Displacement and Bending Stress-Strain

Using the above approach (Section 2.2.4), we investigate the load-displacement and stress-strain relationships during the bending of the beam. The purpose of this part of the work is to substantiate the statement: the extrema of the load-displacement and stress-strain curves do not coincide. Thus, new (but not exhaustive) data will be obtained on the causes of the destruction of concrete and other brittle materials when the load decreases after passing the extremum on the load-displacement curve.

The current section contains a small theoretical framework for the analysis methodology and an example of analysis of a beam from frozen sandy soil. Note that frozen soil can be viewed as an analogue of concrete, in which ice acts as a binder. The material in this section is a development of an earlier study [25]. This section discusses a new version of the model for analyzing effective tensile stresses in a beam during three-point bending.

Let $B$ and $H_0$—respectively, the width and height of the cross-section of the beam, $f$—the vertical displacement of the point of application of the force $F$ (Figure 6).

With increasing load $F$, crack of length h appear and grow, as a result of which, the effective section height $\tilde{H}$ decreases. If the displacement $f$ changes by some value $\Delta f$, then the change in effective height is equal to $\Delta \tilde{H}$. For sufficiently small increments, the dependence of $\Delta \tilde{H}$ on $\Delta f$ can be written as a linear function with a constant proportionality coefficient $K_1$:

$$\Delta \tilde{H}=\frac{\Delta f}{f_{extr}}{K}_1\tilde{H}.$$

(16)

We divide both sides of Equality (16) by $H_0$ and pass to the dimensionless parameters $\mathrm{\Theta }$ and $\Delta \mathrm{\Theta }$:

$$\mathrm{\Theta }=\frac{\tilde{H}}{H_0}. \Delta \mathrm{\Theta }=\frac{\Delta \tilde{H}}{H_0}.$$

(17)

The parameter $\mathrm{\Theta }$ can be considered as a dimensionless characteristic of the effective cross-sectional area of the beam. The values range from 0 to 1; the value $\mathrm{\Theta }=0$ corresponds to complete destruction; the value $\mathrm{\Theta }=1$ corresponds to a condition without damage (no cracks).

If Δθ → 0, then instead of Equality (16), we write:

$$\frac{d\mathrm{\Theta }}{\mathrm{\Theta }}=\frac{df}{f_{extr}}{K}_1.$$

(18)

Integrating both sides of Equality (18), we determine the integration constant from the conditions: if $f=0$, then $\tilde{H}=H_0$, i.e., $\mathrm{\Theta }=1$. We obtain, after transformations:

$$\tilde{H}=H_0{e}^{\frac{f}{f_{extr}}}{K}_1.$$

(19)

Using (19), we determine $\tilde{I}$—the effective moment of inertia of the cross section with an evolving crack and $\tilde{W}$—the effective moment of resistance of the same cross section:

$$\tilde{I}=\frac{B{\tilde{H}}^3}{12}.$$

(20)

$$\tilde{W}=\frac{B{\tilde{H}}^2}{6}.$$

(21)

Experiments have shown that the ratio load $F$—displacement $f$ can be adequately represented as (22):

$$F=\frac{48\tilde{E}\tilde{I}f}{L^3}.$$

(22)

Using (19) and (20), we write (22) as a function $F=F(f)$:

$$F=\frac{48\tilde{E}{I}_{0}f}{L^3}{e}^{\frac{3f{K}_1}{f_{extr}}}.$$

(23)

Here $I=B{H}_0^3/12$.

Let us consider such a case when function (23) has an extremum (Figure 7). We also assume that the $f_{extr}$ and $F_{extr}$ values are determined from the three-point bend test. Then, from the condition $dF/df=0$, we find: $K_1=-1/3$. Knowing $K_1$, using (23), from the condition $F=F_{extr}$ at $f=f_{extr}$, we determine the effective modulus of elasticity $\tilde{E}$:

$$\tilde{E}=\frac{F_{extr}{L}^3}{48I_0{f}_{extr}}e=Ee.$$

(24)

Here, $E$ is the modulus of elasticity, which is usually used in the formula for calculating the deflection of a beam in the middle of the span: $f=(F{L}^3)/(48E{I}_0)$. Thus, Equality (24) establishes the relationship between the effective modulus of elasticity $\tilde{E}$ and the ordinary secant modulus of elasticity $E$.

Using the found values $K_1$, $\tilde{E}$ and taking into account relation (23), after transformations, we explicitly define the dependence $F=F(f)$:

$$F=F_{extr}\frac{f}{f_{extr}}{e}^{1-\frac{f}{f_{extr}}}.$$

(25)

For the beam according to Figure 6 in experiments, it was found: $F_{extr}$= 769 N and $f_{extr}=1.574\hspace{0.17em}\mathrm{mm}$. The test results are shown in Figure 7 with markers. Load-displacement curve (25) in Figure 7 with black line. Tests [26] were performed on a SHIMADZU AGS-300kNX STD.

The effective tensile stresses in the section with a crack (Figure 6), presented in Figure 7 (red line), were calculated using the Formula (26):

$$\tilde{\sigma }=\frac{FL}{4\tilde{W}}.$$

(26)

Here, $\tilde{W}$ is determined by (21), taking into account relation (19).

4. Conclusions

1. The method for determining the effective stresses and modulus of elasticity of concrete based on the results of uniaxial compression tests, taking into account changes in the cross-sectional area, has been substantiated. The ratios necessary for the calculation were obtained without direct assumptions about the reinforcement of concrete, the granulometric composition of the aggregate and about other properties of the material. However, these properties are taken into account indirectly, using stress and strain peaks. Therefore, the presented dependencies can be used to model a certain class of brittle materials.

2. It was found that the effective stresses increase both on the ascending branch and on the descending branch of the load-displacement diagram. This explains the physical meaning of the phenomenon that the destruction of concrete (and other brittle materials) occurs on the descending branch of the load-displacement diagram.

3. The results of determining the stresses and modulus of elasticity under uniaxial compression are comparable with the results obtained in experiments known in the literature. It has been confirmed that, with an increase in reinforcement, the differences between the experimental and calculated values of the elastic modulus decrease from 16% to 4%. These deviations are permissible for practical use. The effective stress plots clearly show that the reinforcement reduces the effective stresses in the concrete and, as a consequence, hinders the formation of cracks.