Revealing the Bonding Nature in an ALnZnTe3-Type Alkaline-Metal (A) Lanthanide (Ln) Zinc Telluride by Means of Experimental and Quantum-Chemical Techniques
Abstract
:1. Introduction
2. Materials and Methods
2.1. Syntheses
2.2. X-ray Diffraction Studies and Crystal Structure Determinations
2.3. Computational Details
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kanatzidis, M.G. Discovery-Synthesis, Design, and Prediction of Chalcogenide Phases. Inorg. Chem. 2017, 56, 3158–3173. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, W.S. Polychalcogenide Anions: Structural Diversity and Ligand Versatility. Z. Anorg. Allg. Chem. 2012, 638, 2401–2424. [Google Scholar] [CrossRef]
- Böttcher, P.; Doert, T. Chalcogene-Rich Chalcogenides: From the First Ideas to a Still Growing Field of Research, Phosphorus, Sulfur, and Silicon and the Related Elements. Phosphorus Sulfur Silicon Relat. Elem. 1998, 136, 255–282. [Google Scholar] [CrossRef]
- Fries, K.S.; Steinberg, S. Fermi-Level Characteristics of Potential Chalcogenide Superconductors. Chem. Mater. 2018, 30, 2251–2261. [Google Scholar] [CrossRef]
- Wuttig, M.; Yamada, N. Phase-change materials for rewriteable data storage. Nat. Mater. 2007, 6, 824–832. [Google Scholar] [CrossRef]
- Wuttig, M.; Raoux, S. The Science and Technology of Phase Change Materials. Z. Anorg. Allg. Chem. 2012, 638, 2455–2465. [Google Scholar] [CrossRef]
- Toberer, E.S.; Snyder, G.J. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef]
- Sootsman, J.R.; Chung, D.Y.; Kanatzidis, M.G. New and Old Concepts in Thermoelectric Materials. Angew. Chem. Int. Ed. 2009, 48, 8616–8639. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological Insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef] [Green Version]
- Miller, G.J. The “Coloring Problem” in Solids: How It Affects Structure, Composition and Properties. Eur. J. Inorg. Chem. 1998, 1998, 523–536. [Google Scholar] [CrossRef]
- Curtarolo, S.; Hart, G.L.W.; Nardelli, M.B.; Mingo, N.; Sanvito, S.; Levy, O. The high-throughput highway to computational materials design. Nat. Mater. 2013, 12, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Wuttig, M.; Deringer, V.L.; Gonze, X.; Bichara, C.; Raty, J.-Y. Incipient Metals: Functional Materials with a Unique Bonding Mechanism. Adv. Mater. 2018, 30, 1803777. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raty, J.-Y.; Schumacher, M.; Golub, P.; Deringer, V.L.; Gatti, C.; Wuttig, M. A Quantum-Mechanical Map for Bonding and Properties in Solids. Adv. Mater. 2019, 31, 1806280. [Google Scholar] [CrossRef] [PubMed]
- Böttcher, P. Tellurium-Rich Tellurides. Angew. Chem. Int. Ed. Engl. 1988, 27, 759–772. [Google Scholar] [CrossRef]
- Papoian, G.A.; Hoffmann, R. Hypervalent Bonding in One, Two, and Three Dimensions: Extending the Zintl-Klemm Concept to Nonclassical Electron-Rich Networks. Angew. Chem. Int. Ed. 2000, 39, 2408–2448. [Google Scholar] [CrossRef]
- Zintl, E. Intermetallische Verbindungen. Angew. Chem. 1939, 52, 1–6. [Google Scholar] [CrossRef]
- Schäfer, H.; Eisenmann, B.; Müller, W. Zintl Phases: Transitions between Metallic and Ionic Bonding. Angew. Chem. Int. Ed. 1973, 12, 694–712. [Google Scholar] [CrossRef]
- Miller, G.J.; Schmidt, M.W.; Wang, F.; You, T.-S. Quantitative Advances in the Zintl-Klemm Formalism. Struct. Bond. 2011, 139, 1–55. [Google Scholar] [CrossRef]
- Meng, C.-Y.; Chen, H.; Wang, P.; Chen, L. Syntheses, Structures, and Magnetic and Thermoelectric Properties of Double-Tunnel Tellurides: AxRE2Cu6-xTe6 (A = K-Cs; RE = La-Nd). Chem. Mater. 2011, 23, 4910–4919. [Google Scholar] [CrossRef]
- Meng, C.-Y.; Chen, H.; Wang, P. Syntheses, Structures, and Physical Properties of CsRE2Ag3Te5 (RE = Pr, Nd, Sm, Gd-Er) and RbRE2Ag3Te5 (RE = Sm, Gd-Dy). Inorg. Chem. 2014, 53, 6893–6903. [Google Scholar] [CrossRef]
- Lin, H.; Chen, H.; Shen, J.-N.; Chen, L.; Wu, L.-M. Chemical Modification and Energetically Favorable Atomic Disorder of a Layered Thermoelectric Material TmCuTe2 Leading to High Performance. Chem. Eur. J. 2014, 20, 15401–15408. [Google Scholar] [CrossRef]
- Gladisch, F.C.; Steinberg, S. Revealing the Nature of Bonding in Rare-Earth Transition-Metal Tellurides by Means of Methodes Based on First Principles. Eur. J. Inorg. Chem. 2017, 2017, 3395–3400. [Google Scholar] [CrossRef]
- Göbgen, K.C.; Fries, K.S.; Gladisch, F.C.; Dronskowski, R.; Steinberg, S. Revealing the Nature of Chemical Bonding in an ALn2Ag3Te5-Type Alkaline-Metal (A) Lanthanide (Ln) Silver Telluride. Inorganics 2019, 7, 70. [Google Scholar] [CrossRef] [Green Version]
- Eickmeier, K.; Fries, K.S.; Gladisch, F.C.; Dronskowski, R.; Steinberg, S. Revisiting the Zintl-Klemm Concept for ALn2Ag3Te5-Type Alkaline-Metal (A) Lanthanide (Ln) Silver Tellurides. Crystals 2020, 10, 184. [Google Scholar] [CrossRef] [Green Version]
- Göbgen, K.C.; Gladisch, F.C.; Steinberg, S. The Mineral Stutzite: A Zintl-Phase or Polar Intermetallic? A Case Study Using Experimental and Quantum-Chemical Techniques. Inorg. Chem. 2018, 57, 412–421. [Google Scholar] [CrossRef] [PubMed]
- Smid, S.; Steinberg, S. Probing the Validity of the Zintl Klemm Concept for Alkaline-Metal Copper Tellurides by Means of Quantum-Chemical Techniques. Materials 2020, 13, 2178. [Google Scholar] [CrossRef] [PubMed]
- Mayasree, O.; Sankar, C.R.; Kleinke, K.M.; Kleinke, H. Cu clusters and chalcogen-chalcogen bonds in various copper polychalcogenides. Coord. Chem. Rev. 2012, 256, 1377–1383. [Google Scholar] [CrossRef]
- Seong, S.; Albright, T.A.; Zhang, X.; Kanatzidis, M. Te-Te Bonding in Copper Tellurides. J. Am. Chem. Soc. 1994, 116, 7287–7293. [Google Scholar] [CrossRef]
- Pyykkö, P. Strong Closed-Shell Interactions in Inorganic Chemistry. Chem. Rev. 1997, 97, 597–636. [Google Scholar] [CrossRef]
- Mitchell, K.; Ibers, J.A. Rare-Earth Transition-Metal Chalcogenides. Chem. Rev. 2002, 102, 1929–1952. [Google Scholar] [CrossRef]
- WinXPow; Version 2.23; STOE & Cie GmbH: Darmstadt, Germany, 2008.
- Match! Version 3.8.0.137; Crystal Impact GbR: Bonn, Germany, 2019.
- Wang, F.F.Y.; Cox, D.E. The coherent neutron scattering amplitude of Rb: A neutron diffraction study of RbCl. Acta Crystallogr. Sect. A Found. Crystallogr. 1970, 26, 377–379. [Google Scholar] [CrossRef]
- Rabadanov, M.K. Anharmonic and “disorder” models of ZnTe structure: High-temperature single-crystal X-ray diffraction studies. Kristallografiya 1995, 40, 505–510. [Google Scholar]
- Nawash, J.M.; Twamley, B.; Lynn, K.G. ZnTe6O13, a new ZnO-TeO2 phase. Acta Crystallogr. Sect. C Struct. Chem. 2007, 63, i66–i68. [Google Scholar] [CrossRef] [PubMed]
- Bruker, A.P.E.X. SAINT+ and SADABS; Bruker AXS Inc.: Madison, WI, USA, 2009. [Google Scholar]
- XPREP; Version 6.03; Bruker AXS Inc.: Madison, WI, USA, 2014.
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Marsman, M.; Furthmüller, J. Vienna Ab-initio Simulation Package VASP: The Guide; Faculty of Physics, Universität Wien: Vienna, Austria, 2014. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Provino, A.; Steinberg, S.; Smetana, V.; Kulkarni, R.; Dhar, S.K.; Manfrinetti, P.; Mudring, A.-V. Gold-rich R3Au7Sn3: Establishing the interdependence between electronic features and physical properties. J. Mater. Chem. C 2015, 3, 8311–8321. [Google Scholar] [CrossRef]
- Smetana, V.; Steinberg, S.; Mudryk, Y.; Pecharsky, V.; Miller, G.J.; Mudring, A.-V. Cation-Poor Complex Metallic Alloys in Ba(Eu)−Au−Al(Ga) Systems: Identifying the Keys that Control Structural Arrangements and Atom Distributions at the Atomic Level. Inorg. Chem. 2015, 54, 10296–10308. [Google Scholar] [CrossRef] [PubMed]
- Bigun, I.; Steinberg, S.; Smetana, V.; Mudryk, Y.; Kalychak, Y.; Havela, L.; Pecharsky, V.; Mudring, A.-V. Magnetocaloric Behavior in Ternary Europium Indides EuT5In: Probing the Design Capability of First-Principles-Based Methods on the Multifaceted Magnetic Materials. Chem. Mater. 2017, 29, 2599–2614. [Google Scholar] [CrossRef] [Green Version]
- Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Crystal Orbital Hamilton Population (COHP) Analysis As Projected from Plane-Wave Basis Sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef]
- Dronskowski, R.; Blöchl, P.E. Crystal Orbital Hamilton Populations (COHP). Energy-Resolved Visualization of Chemical Bonding in Solids Based on Density-Functional Calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Steinberg, S.; Dronskowski, R. The Crystal Orbital Hamilton Population (COHP) Method as a Tool to Visualize and Analyze Chemical Bonding in Intermetallic Compounds. Crystals 2018, 8, 225. [Google Scholar] [CrossRef] [Green Version]
- Maintz, S.; Deringer, V.L.; Tchougréff, A.L.; Dronskowski, R. Analytic Projection from Plane-Wave and PAW Wavefunctions and Application to Chemcial-Bonding Analysis in Solids. J. Comput. Chem. 2013, 34, 2557–2567. [Google Scholar] [CrossRef]
- Maintz, S.; Deringer, V.L.; Tchougréff, A.L.; Dronskowski, R. LOBSTER: A tool to extract chemical bonding from plane-wave based DFT. J. Comput. Chem. 2016, 37, 1030–1035. [Google Scholar] [CrossRef] [Green Version]
- Ertural, C.; Steinberg, S.; Dronskowski, R. Development of a robust tool to extract Mulliken and Löwdin charges from plane waves and its application to solid-state materials. RSC Adv. 2019, 9, 29821–29830. [Google Scholar] [CrossRef] [Green Version]
- Eck, B. wxDragon 2.2.3; RWTH Aachen University: Aachen, Deutschland, 2020. [Google Scholar]
- Mansuetto, M.F.; Keane, P.M.; Ibers, J.A. Synthesis, Structure, and Conductivity of the New Group IV Chalcogenides, KCuZrQ3 (Q = S, Se, Te). J. Solid State Chem. 1992, 101, 257–264. [Google Scholar] [CrossRef]
- Koscielski, L.A.; Ibers, J.A. The Structural Chemistry of Quaternary Chalcogenides of the Type AMM’Q3. Z. Anorg. Allg. Chem. 2012, 638, 2585–2593. [Google Scholar] [CrossRef]
- Yao, J.; Deng, B.; Sherry, L.J.; McFarland, A.D.; Ellis, D.E.; Van Duyne, R.P.; Ibers, J.A. Syntheses, Structure, Some Band Gaps, and Electronic Structures of CsLnZnTe3 (Ln = La, Pr, Nd, Sm, Gd, Tb, Dy, Ho, Er, Tm, Y). Inorg. Chem. 2004, 43, 7735–7740. [Google Scholar] [CrossRef]
- Cordero, B.; Gómez, V.; Platero-Prats, A.E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Covalent radii revisited. Dalton Trans. 2008, 2008, 2832–2838. [Google Scholar] [CrossRef] [PubMed]
- Rustige, C.; Brühmann, M.; Steinberg, S.; Meyer, E.; Daub, K.; Zimmermann, S.; Wolberg, M.; Mudring, A.-V.; Meyer, G. The Prolific {ZR6}X12R and {ZR6}X10 Structure Types with Isolated Endohedrally Stabilized (Z) Rare-Earth Metal (R) Cluster Halide (X) Complexes. Z. Anorg. Allg. Chem. 2012, 638, 1922–1931. [Google Scholar] [CrossRef]
- Provino, A.; Steinberg, S.; Smetana, V.; Paramanik, U.; Manfrinetti, P.; Dhar, S.K.; Mudring, A.-V. Gold in the Layered Structures of R3Au7Sn3: From Relativity to Versatility. Cryst. Growth Des. 2016, 16, 5657–5668. [Google Scholar] [CrossRef]
- Tappe, F.; Pöttgen, R. Rare earth-transition metal-cadmium intermetallics—Crystal chemistry and physical properties. Rev. Inorg. Chem. 2011, 31, 5–25. [Google Scholar] [CrossRef]
- Steinberg, S.; Brgoch, J.; Miller, G.J.; Meyer, G. Identifying a Structural Preference in Reduced Rare-Earth Metal Halides by Combining Experimental and Computational Techniques. Inorg. Chem. 2012, 51, 11356–11364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bell, T.; Steinberg, S.; Meyer, G. Electron Counting Rules and Electronic Structure in Tetrameric Transition-Metal (T)-Centered Rare-Earth (R) Cluster Complex Halides (X). Inorg. Chem. 2015, 54, 1026–1037. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Tabassum, D.; Mar, A. Narrowing the gap: From semiconductor to semimetal in the homologous series of rare-earth zinc arsenides RE2−yZn4As4·n(REAs) and Mn-substituted derivatives RE2−yMnxZn4−xAs4·n(REAs) (RE = La–Nd, Sm, Gd). Dalton Trans. 2015, 44, 20254–20264. [Google Scholar] [CrossRef]
- Kim, S.-J.; Kraus, F.; Fässler, T.F. Na6ZnSn2, Na4.24K1.76(1)ZnSn2, and Na20Zn8Sn11: Three Intermetallic Structures Containing the Linear {Sn-Zn-Sn}6- Unit. J. Am. Chem. Soc. 2009, 131, 1469–1478. [Google Scholar] [CrossRef]
- Simon, A.; Mattausch, H.; Ryazanov, M.; Kremer, R.K. Lanthanides as d Metals. Z. Anorg. Allg. Chem. 2006, 632, 919–929. [Google Scholar] [CrossRef]
- Corbett, J.D. Exploratory Synthesis: The Fascinating and Diverse Chemistry of Polar Intermetallic Phases. Inorg. Chem. 2010, 49, 13–28. [Google Scholar] [CrossRef]
- Gladisch, F.C.; Steinberg, S. Revealing Tendencies in the Electronic Structures of Polar Intermetallic Compounds. Crystals 2018, 8, 80. [Google Scholar] [CrossRef] [Green Version]
- Lin, Q.; Miller, G.J. Electron-Poor Polar Intermetallics: Complex Structures, Novel Clusters, and Intriguing Bonding with Pronounced Electron Delocalization. Acc. Chem. Res. 2018, 51, 49–58. [Google Scholar] [CrossRef] [PubMed]
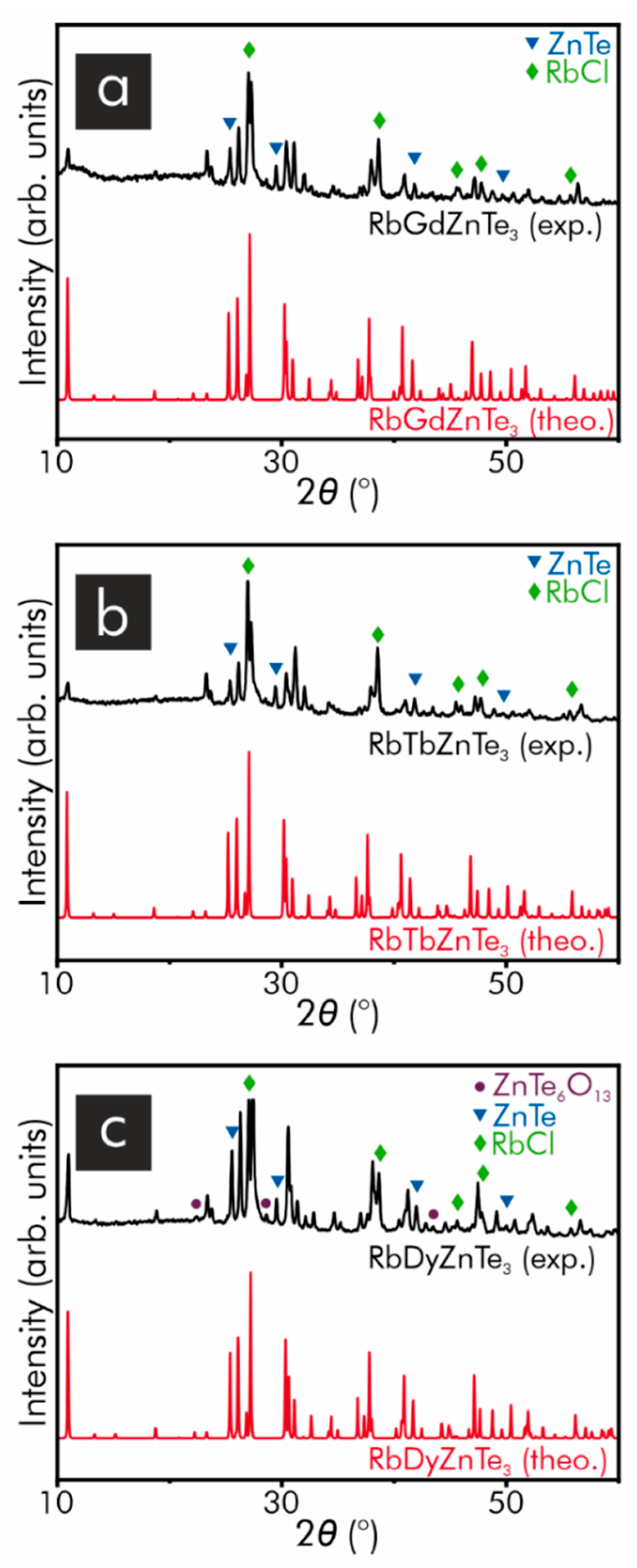
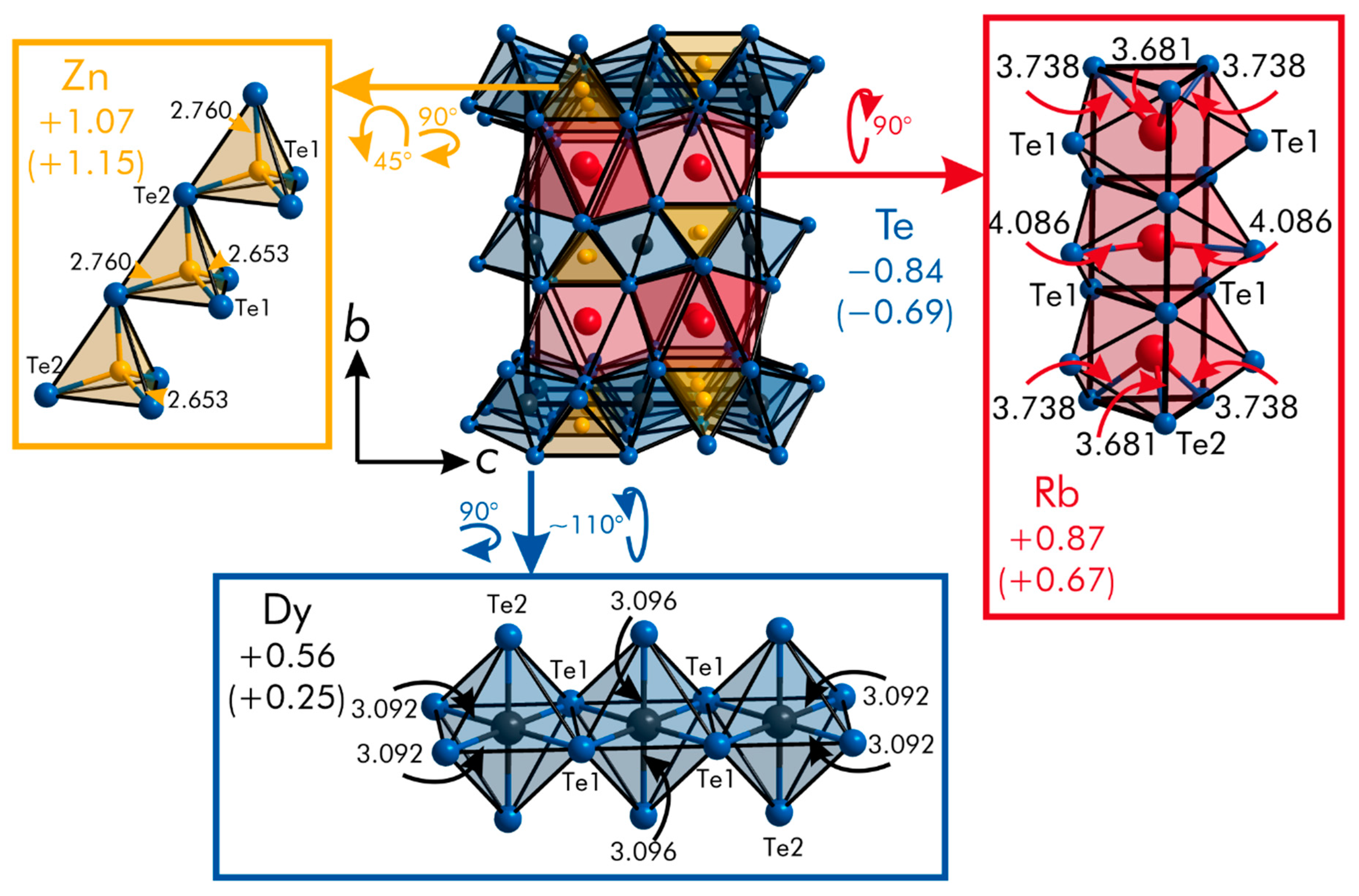
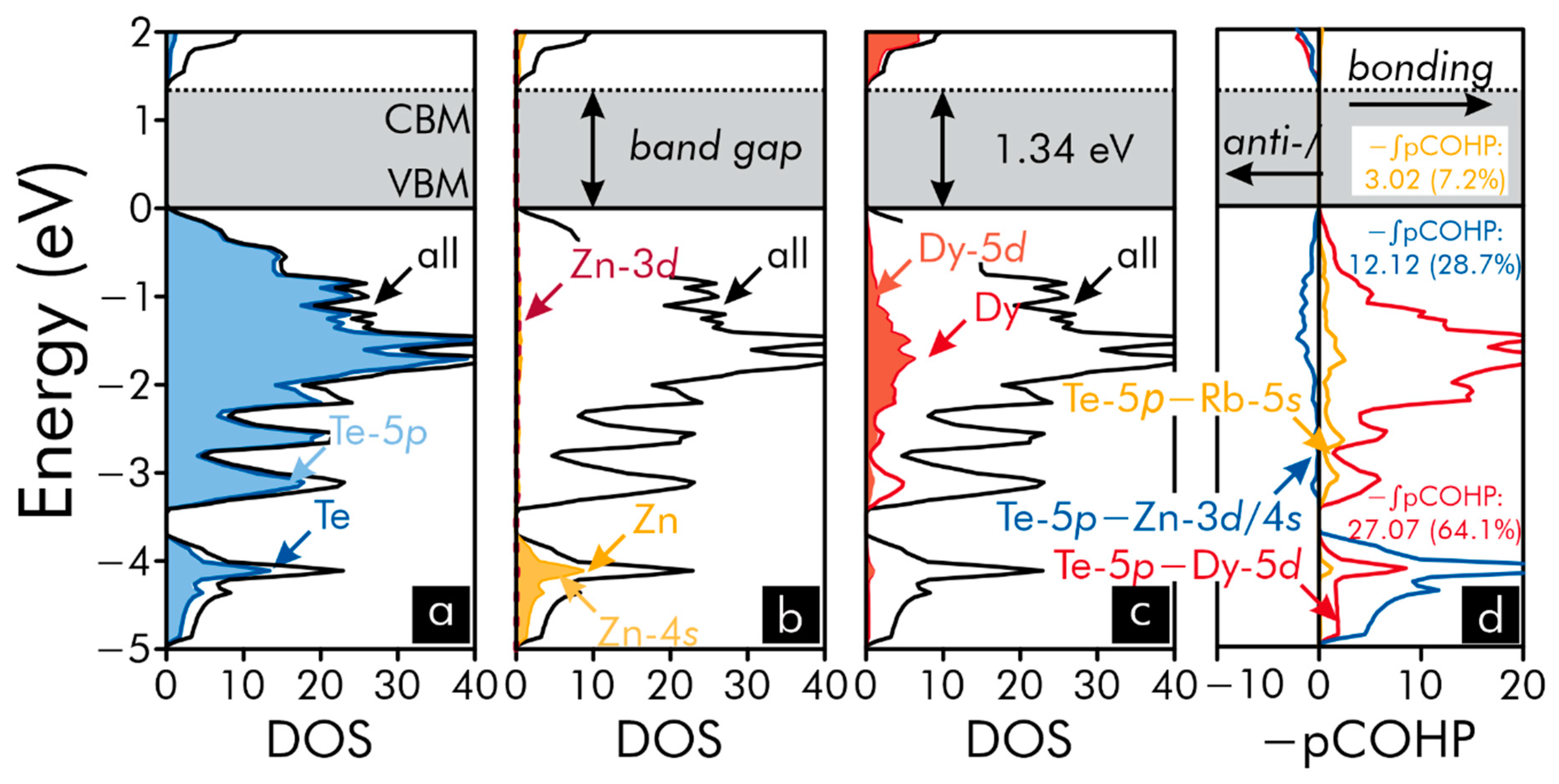
| Formula | RbGdZnTe3 | RbTbZnTe3 | RbDyZnTe3 |
|---|---|---|---|
| form wt. | 690.89 | 692.56 | 696.14 |
| space group | Cmcm | ||
| a (Å) | 4.419(1) | 4.395(1) | 4.410(2) |
| b (Å) | 16.072(5) | 16.058(5) | 16.144(6) |
| c (Å) | 11.716(4) | 11.651(4) | 11.671(4) |
| volume (Å3) | 832.0(4) | 822.3(4) | 831.0(5) |
| Z | 4 | 4 | 4 |
| density (calc.), g/cm3 | 5.515 | 5.594 | 5.564 |
| µ (mm−1) | 26.797 | 27.648 | 27.842 |
| F(000) | 1148 | 1152 | 1156 |
| θ range (°) | 2.53−25.64 | 2.54−25.65 | 2.52−25.62 |
| index range | −5 ≤ h ≤ 5 | −5 ≤ h ≤ 5 | −5 ≤ h ≤ 5 |
| −15 ≤ k ≤ 19 | −19 ≤ k ≤ 16 | −19 ≤ k ≤ 19 | |
| −14 ≤ l ≤ 14 | −14 ≤ l ≤ 13 | −12 ≤ l ≤ 14 | |
| reflections collected | 2031 | 2385 | 2367 |
| independent reflections | 473 | 468 | 473 |
| refinement method | Full matrix least squares on F2 | ||
| data/restraints/parameters | 473/0/23 | 468/0/23 | 473/0/23 |
| goodness-of-fit on F2 | 1.176 | 1.190 | 1.258 |
| final R indices [I > 2σ(I)] | R1 = 0.019; wR2 = 0.043 | R1 = 0.018; wR2 = 0.036 | R1 = 0.032; wR2 = 0.079 |
| R indices (all data) | R1 = 0.020; wR2 = 0.044 | R1 = 0.018; wR2 = 0.036 | R1 = 0.032; wR2 = 0.079 |
| Rint | 0.024 | 0.020 | 0.040 |
| largest diff. peak and hole, e−/Å3 | 1.077 and −0.900 | 0.667 and −0.922 | 2.051 and −2.067 |
| Atom | Position | x | y | z | Ueq, Å2 |
|---|---|---|---|---|---|
| RbGdZnTe3 | |||||
| Gd1 | 4a | 0 | 0 | 0 | 0.0147(2) |
| Te1 | 8f | 0 | 0.37160(3) | 0.06048(4) | 0.0156(2) |
| Te2 | 4c | 0 | 0.06418(4) | ¼ | 0.0135(2) |
| Rb1 | 4c | 0 | 0.74613(7) | ¼ | 0.0304(3) |
| Zn1 | 4c | 0 | 0.46104(8) | ¼ | 0.0184(3) |
| RbTbZnTe3 | |||||
| Tb1 | 4a | 0 | 0 | 0 | 0.0149(1) |
| Te1 | 8f | 0 | 0.37212(2) | 0.05945(3) | 0.0157(1) |
| Te2 | 4c | 0 | 0.06422(3) | ¼ | 0.0138(1) |
| Rb1 | 4c | 0 | 0.74653(5) | ¼ | 0.0301(2) |
| Zn1 | 4c | 0 | 0.46119(6) | ¼ | 0.0186(2) |
| RbDyZnTe3 | |||||
| Dy1 | 4a | 0 | 0 | 0 | 0.0123(3) |
| Te1 | 8f | 0 | 0.37263(4) | 0.05871(6) | 0.0131(3) |
| Te2 | 4c | 0 | 0.06422(6) | ¼ | 0.0114(3) |
| Rb1 | 4c | 0 | 0.74683(10) | ¼ | 0.0279(4) |
| Zn1 | 4c | 0 | 0.46143(11) | ¼ | 0.0161(4) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eickmeier, K.; Steinberg, S. Revealing the Bonding Nature in an ALnZnTe3-Type Alkaline-Metal (A) Lanthanide (Ln) Zinc Telluride by Means of Experimental and Quantum-Chemical Techniques. Crystals 2020, 10, 916. https://doi.org/10.3390/cryst10100916
Eickmeier K, Steinberg S. Revealing the Bonding Nature in an ALnZnTe3-Type Alkaline-Metal (A) Lanthanide (Ln) Zinc Telluride by Means of Experimental and Quantum-Chemical Techniques. Crystals. 2020; 10(10):916. https://doi.org/10.3390/cryst10100916
Chicago/Turabian StyleEickmeier, Katharina, and Simon Steinberg. 2020. "Revealing the Bonding Nature in an ALnZnTe3-Type Alkaline-Metal (A) Lanthanide (Ln) Zinc Telluride by Means of Experimental and Quantum-Chemical Techniques" Crystals 10, no. 10: 916. https://doi.org/10.3390/cryst10100916
APA StyleEickmeier, K., & Steinberg, S. (2020). Revealing the Bonding Nature in an ALnZnTe3-Type Alkaline-Metal (A) Lanthanide (Ln) Zinc Telluride by Means of Experimental and Quantum-Chemical Techniques. Crystals, 10(10), 916. https://doi.org/10.3390/cryst10100916





