While several species of animals can directly see light polarization, the human eye is blind to it, and it took centuries to determine this property of light [
1]. Polarization is a geometrical concept, and hence a property of symmetry; it is thus not unexpected that the history of light polarization is strongly intertwined with the study of other objects that have a clear symmetry-related character: crystals. It was indeed Huygens that, around 1690, noticed that the light beams emerging from a crystal of calcite can be extinguished if a second, rotated, calcite crystal is placed after the first one [
2]. In some sense, the light propagating in calcite turned out to have a property that had not been noticed before. Actually, the very fact that calcite has the property of splitting a single beam of light in two beams (birefringence) was itself a notable behavior, reported by Erasmus Bartholinus a few years before Huygens’ discovery. The behavior of crystals with respect to light propagation hence stimulated further studies about the connections between crystal structure, on one side, and light intrinsic properties, on the other. After Huygens’ discovery, Newton speculated that light has sides; it was, however, not before the late 18th century that the elastic theory of light by Fresnel introduced the concept of optical waves as transverse waves, providing quantitative predictions for the observations held to date, and laying the solid foundations for subsequent developments [
3].
Calcite happens to be birefringent thanks to its anisotropic crystal structure. Its trigonal crystal structure leads to a uniaxial dielectric response with a large birefringence that is still harnessed to manufacture optical components such as polarizers, although large and defect-free calcite crystals are quite rare (the original deposit in Iceland, which gave the name to pure crystalline calcite as
Iceland spar, is currently exhausted) [
4]. Another common birefringent material, α-quartz, exhibits an additional intriguing effect: polarization rotation [
5]. This is allowed for by the lack of a center of inversion in the crystal structure; such a fact, notably, has consequences also on the macroscopic shape of quartz crystals that can appear in “left” and “right” varieties. Quartz is hence a chiral crystal that can operate on the chiral properties of light. In the mid-19th century, it was by studying the polarization rotation of selected chiral crystals, obtained from a solution of a tartaric acid salt, that allowed Pasteur to realize that also molecules can exist in “left” and “right” varieties; he then noticed that several natural processes prefer a specific “handedness” at the molecular level, and that chirality is pervasive in biological processes (e.g., we all have a heart on the left side) [
6].
The use of polarized light in experimental science and in technology experienced a boost after the development of cheap polarizers (Edwin Land, ca. 1930). Cheap polarizers, or polaroids, were fabricated by embedding and aligning in a polymeric matrix fine crystals of herapathite (a fragile crystal first synthesized in 1852 by William B. Herapath), which has the property of absorbing one of the two linear states of light polarization [
1]. Polaroid technology then abandoned the use of herapathite, but it experienced widespread diffusion and is now at the basics of everyday objects such as computers and mobile phone displays. Notably, polymer films can also act as waveplates, which for instance can be used to convert linearly polarized light into circularly polarized, and vice versa.
In the 20th century, material engineering has brought the development of another extremely important class of polarization-handling materials: liquid crystals. Being at first a scientific curiosity, they found—in conjunction with the above-cited polymer laminated polarizers—a multi-billion dollar market.
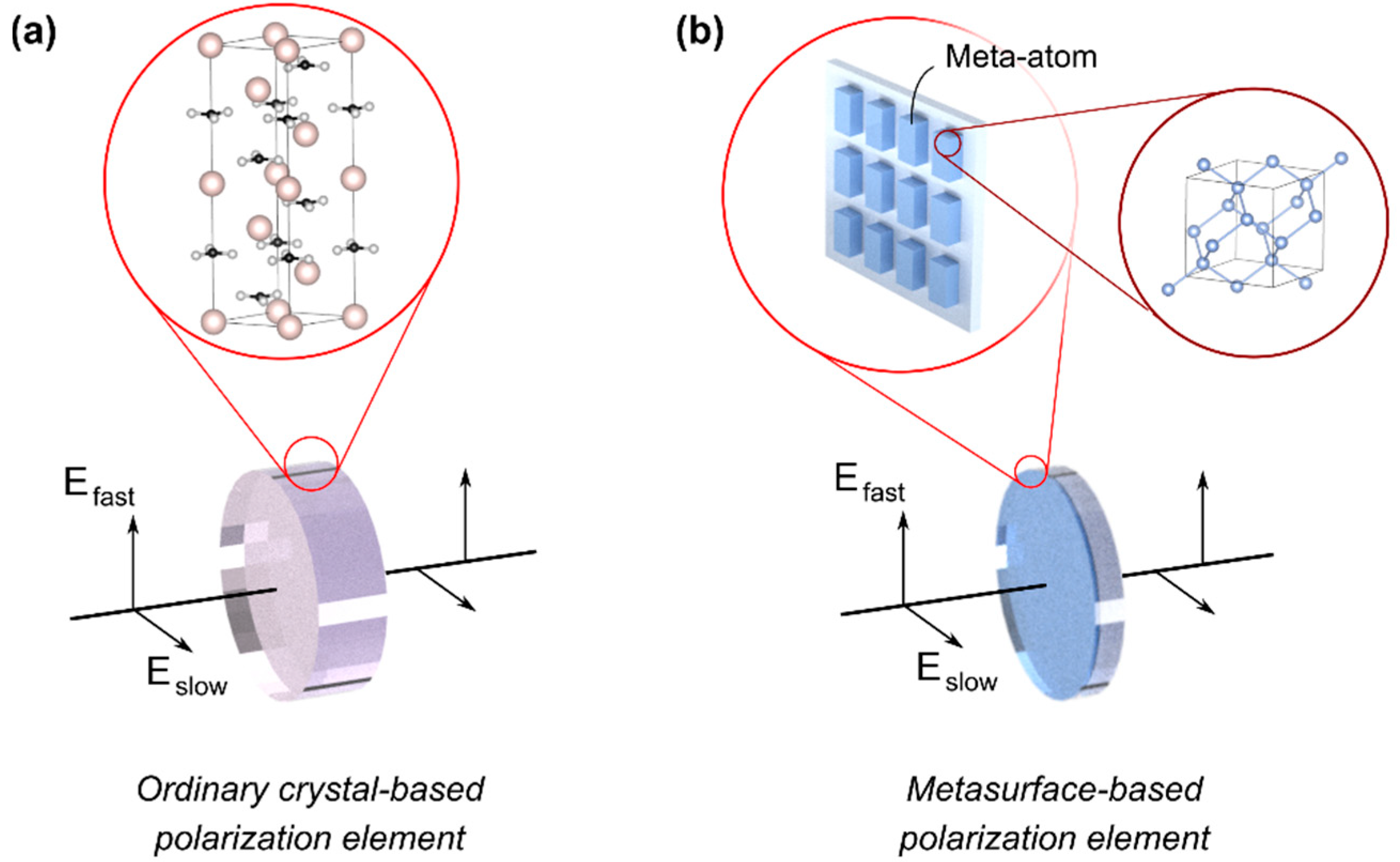
However, polymer-based devices and components generally suffer from a limitation: power handling and stability. Polarizers can heat up and degrade due to light absorption; meanwhile, UV light can damage them. For these reasons, in high-power applications, such as in laser systems, bulky and expensive components based on calcite or quartz are still commonly employed. Researchers have thus attempted to obtain hard and durable, yet inexpensive, objects acting as waveplates and polarizers, only using common solid-state materials, such as dielectrics, metals or semiconductors, either in crystalline, polycrystalline or amorphous forms (
Figure 1). The crucial idea is to work with
metamaterials, where the key concept is to develop objects whose properties are mostly dictated by the structuration rather than by the underlying material(s) employed to fabricate them. The development of metamaterials can be understood as crystal engineering, although at a different scale with respect to ordinary crystals: here, the particles of a certain material (meta-atoms) are arranged, usually but not exclusively in a periodic manner, in such a way that their effective properties meet a certain requirement [
7]. Meta-atoms have dimensions much larger than that of an atom or a molecule; rather, their size is typically a fraction of the wavelength of the radiation that they have to handle. The only ingredients that determine the function of a metasurface are the distribution and shape of the particles (made of the underlying material), and the wave equation (Maxwell equations in our case). For instance, special arrangements of metal patches and loops can be made such that the volume that they occupy propagates waves as if that volume was filled with a homogeneous negative refractive index [
8]. The radiation experiences the metal patches only in an effective way and all the physics can be described, from a macroscopic point of view, as if the metamaterial is a homogeneous region with special properties. Similar observations can be made if the underlying material is arranged in quasi-two dimensional patterns, like a perforated metal screen. When a collimated light beam impinges on such a metasurface, the behavior of its reflection and refraction, in amplitude, phase, polarization and direction, may strongly deviate from what is expected by Fresnel formulas and Snell law [
9].
The concept of metasurface can be traced back to that of
frequency selective surfaces, patterned metal layers typically employed to decrease the radar scattering cross section of airplanes and other targets [
10]. However, it experienced a surge of interest in recent decades, when micro- and nanotechnology techniques allowed to scale down the typical sizes to dimensions of the order of infrared and visible light. It was soon recognized that metasurfaces can act as polarization-handling objects, since a simple asymmetry in the unit cell may lead to different responses for the two linear polarizations of light. This is indeed the operating principle of the wire-grid polarizer, once available only for longer wavelengths (Marconi patented a radio wave version [
11]) and currently also under commerce for the ultraviolet range. However, metasurfaces may perform operations much more complex than that of a linear polarizer, as in principle they can operate on all the elements of the Jones matrix individually. This can be accomplished by employing appropriately complex unit cells, that can embed for instance chiral inclusions such as nano-helices (helices, and other three-dimensional inclusions, are regarded as elements of a metasurface rather than of a metamaterial when their thickness is smaller than the operating wavelength).
From a wave-impedance point of view, polarization-handling metasurfaces are generalized sheet admittance conditions with magnetoelectric coupling. By properly tuning such admittance and magnetoelectric coupling, it is possible, in principle, to devise very general metasurface operation—although constraints such as passivity and reciprocity may hold, depending on the underlying material and on additional considerations such as time invariance [
12,
13]. It can be hence stated that a very active research front consists of the development of metasurfaces that target the most general polarization operations: reciprocal or non-reciprocal, linear, circular, or elliptical retardance, diattenuation, or their combinations. This complex task is increasingly addressed by the means of
inverse design techniques, possibly based on machine learning approaches, that are acquiring a constantly growing role in nanophotonics [
14]. In this regard, there is a wide open front, that concerns the operation bandwidth and angular response. Most often, metasurfaces rely on electromagnetic resonances, that are bandwidth- and angle-limited; this contrasts with most applications, where the broadband and large field-of-view are required. In my opinion, this is one of the most important issues that the metasurface community should address in the future.
A powerful consequence of the fact that a metasurface can be realized by a variety of underlying materials is that certain properties of the material can be chosen at will, leading to operations impossible to achieve from ordinary polarization-handling crystals. For instance, one may include, by design, nonlinearity and tunability, by means of electromechanical, electrochromic, electro-optic, thermomechanical or thermo-optic means. Alternatively, one can join loss and gain sub-elements to induce exotic responses reminiscent of quantum-mechanical non-Hermitian systems [
15].
Finally, and importantly, metasurfaces can be arranged in a space-varying fashion: by distributing different metasurface elements in different regions of space, one can generate the so-called gradient Huygens metasurfaces, that is, metasurfaces capable of creating a forward-directed wavefront that has a well defined shape (the concept is essentially that of a phase hologram) [
16]. At this point, the step towards flat lenses is not large; very intense research is being carried out at present to bring these concepts from proof-of-concept to the large-scale market.
With a market volume estimated to reach 10 billion dollars in the next 10 years [
17], these kinds of artificial crystals called metamaterials and metasurfaces could have a significant impact on our everyday life. However, research is still needed to expand their scope to all the situations where electromagnetic waves, with their key property that is polarization, must be manipulated and detected. These include optical communications, quantum photonics, microscopy, astronomy, biological and chiral molecule sensing, microwave, millimeter-wave (with 5G applications), and terahertz components.