Geometrical Phase Optical Components: Measuring Geometric Phase without Interferometry
Abstract
:1. Introduction
2. Theoretical Aspects
2.1. Closed Path vs. Open Path in the Poincaré Sphere
2.2. A Geometrical Phase Optical Component Based on a General Retarder
2.3. Phase Profiles for the Grating and Lens
3. Experiments
4. Results
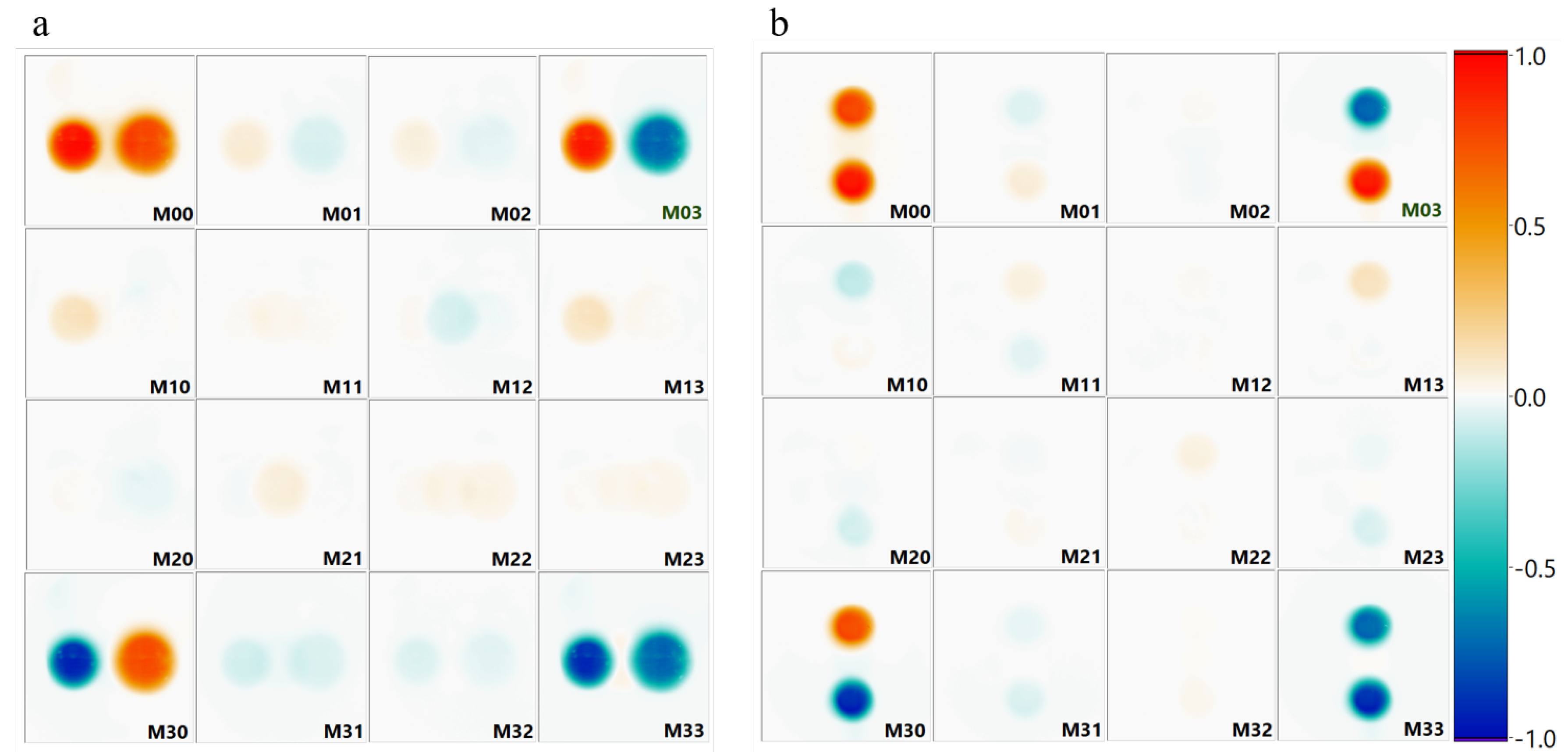
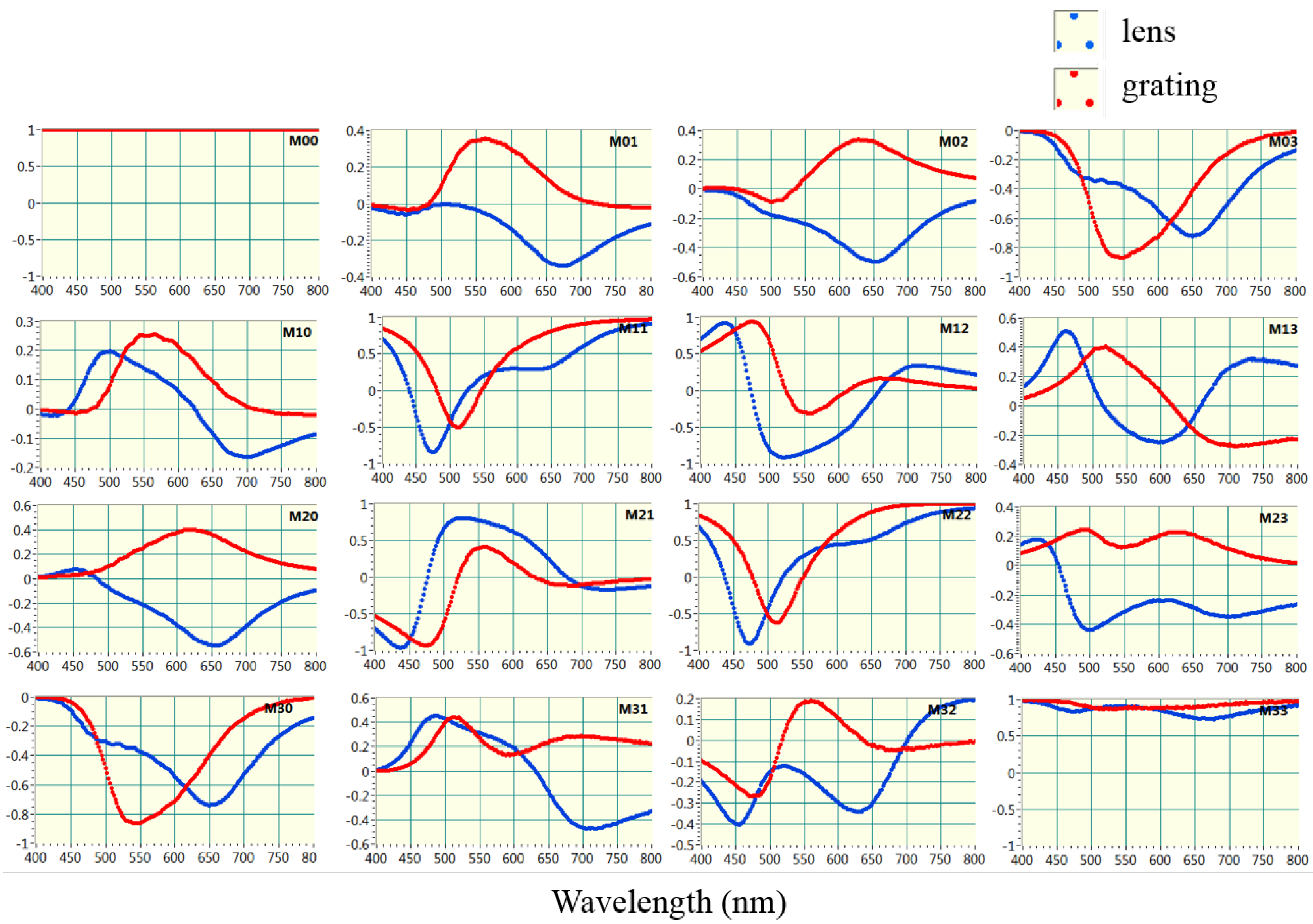
4.1. Phase Profiles
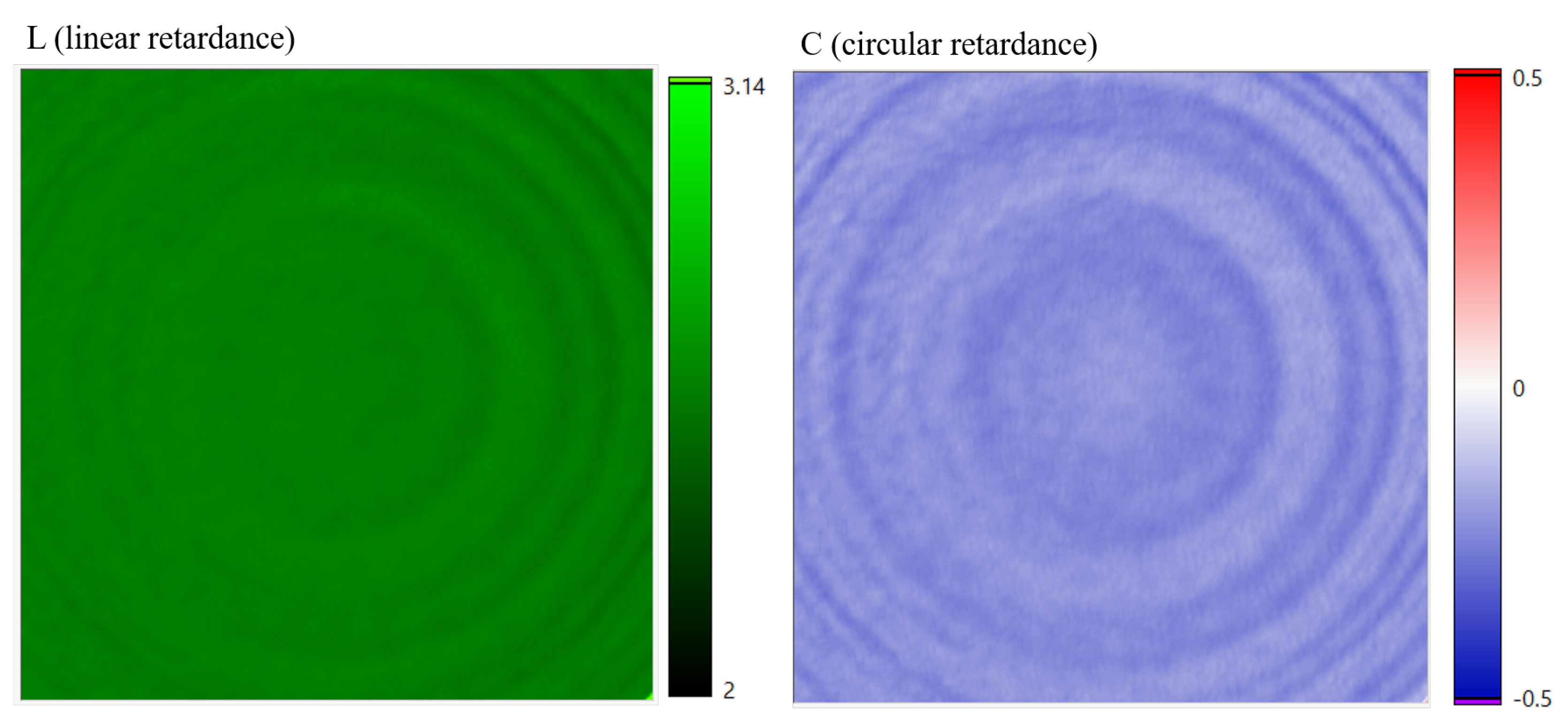
4.2. Linear and Circular Retardances
4.3. Polarization Patterns of the Primary and Conjugate Waves
4.4. Leakage Wave
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Forbes, A. Structured Light: Tailored for Purpose. Opt. Photonics News 2020, 31, 24–31. [Google Scholar] [CrossRef]
- Lee, G.Y.; Sung, J.; Lee, B. Recent advances in metasurface hologram technologies. ETRI J. 2019, 41, 10–22. [Google Scholar] [CrossRef] [Green Version]
- Gerislioglu, B.; Dong, L.; Ahmadivand, A.; Hu, H.; Nordlander, P.; Halas, N.J. Monolithic metal dimer-on-film structure: New plasmonic properties introduced by the underlying metal. Nano Lett. 2020, 20, 2087–2093. [Google Scholar] [CrossRef] [PubMed]
- Gerislioglu, B.; Bakan, G.; Ahuja, R.; Adam, J.; Mishra, Y.K.; Ahmadivand, A. The role of Ge2Sb2Te5 in enhancing the performance of functional plasmonic devices. Mater. Today Phys. 2020, 12, 100178. [Google Scholar] [CrossRef]
- Pancharatnam, S. Generalized theory of interference and its applications. In Proceedings of the Indian Academy of Sciences-Section A; Springer: Berlin/Heidelberg, Germany, 1956; Volume 44, pp. 398–417. [Google Scholar]
- Berry, M. Pancharatnam, virtuoso of the Poincaré sphere: An appreciation. Curr. Sci. 1994, 67, 220–223. [Google Scholar]
- Berry, M.V. The adiabatic phase and Pancharatnam’s phase for polarized light. J. Mod. Opt. 1987, 34, 1401–1407. [Google Scholar] [CrossRef]
- Bhandari, R. Polarization of light and topological phases. Phys. Rep. 1997, 281, 1–64. [Google Scholar] [CrossRef]
- Bomzon, Z.; Biener, G.; Kleiner, V.; Hasman, E. Space-variant Pancharatnam–Berry phase optical elements with computer-generated subwavelength gratings. Opt. Lett. 2002, 27, 1141–1143. [Google Scholar] [CrossRef] [PubMed]
- Roux, F.S. Geometric phase lens. JOSA A 2006, 23, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Marrucci, L.; Manzo, C.; Paparo, D. Pancharatnam-Berry phase optical elements for wave front shaping in the visible domain: Switchable helical mode generation. Appl. Phys. Lett. 2006, 88, 221102. [Google Scholar] [CrossRef] [Green Version]
- Arteaga, O.; Canillas, A. Analytic inversion of the Mueller-Jones polarization matrices for homogeneous media. Opt. Lett. 2009, 35, 559–561. [Google Scholar] [CrossRef]
- Arteaga, O. Mueller Matrix Polarimetry of Anisotropic Chiral Media. Ph.D. Thesis, Universitat de Barcelona, Barcelona, Spain, 2010. [Google Scholar]
- Yu, H.; Zhou, Z.; Qi, Y.; Zhang, X.; Wei, Q.H. Pancharatnam-Berry optical lenses. J. Opt. Soc. Am. B 2019, 36, D107–D111. [Google Scholar] [CrossRef]
- Hasman, E.; Bomzon, Z.; Niv, A.; Biener, G.; Kleiner, V. Polarization beam-splitters and optical switches based on space-variant computer-generated subwavelength quasi-periodic structures. Opt. Commun. 2002, 209, 45–54. [Google Scholar] [CrossRef]
- Kim, J.; Li, Y.; Miskiewicz, M.N.; Oh, C.; Kudenov, M.W.; Escuti, M.J. Fabrication of ideal geometric-phase holograms with arbitrary wavefronts. Optica 2015, 2, 958–964. [Google Scholar] [CrossRef]
- Acher, O.; Richard, S. Easy-to-build Wollaston-like polarization splitter with adjustable beam deviation and tunable chromatic dispersion. Opt. Express 2019, 27, 29232–29240. [Google Scholar] [CrossRef] [PubMed]
- Xiang, X.; Kim, J.; Escuti, M.J. Far-field and fresnel liquid crystal geometric phase holograms via direct-write photo-alignment. Crystals 2017, 7, 383. [Google Scholar] [CrossRef] [Green Version]
- Cui, W.; Chang, C.; Gao, L. Development of an ultra-compact optical combiner for augmented reality using geometric phase lenses. Opt. Lett. 2020, 45, 2808–2811. [Google Scholar] [CrossRef] [PubMed]
- Arteaga, O.; Garcia-Caurel, E.; Ossikovski, R. Stern-Gerlach experiment with light: Separating photons by spin with the method of A. Fresnel. Opt. Express 2019, 27, 4758–4768. [Google Scholar] [CrossRef] [PubMed]
- Komanduri, R.K.; Lawler, K.F.; Escuti, M.J. Multi-twist retarders: Broadband retardation control using self-aligning reactive liquid crystal layers. Opt. Express 2013, 21, 404–420. [Google Scholar] [CrossRef] [Green Version]
- Sakakura, M.; Lei, Y.; Wang, L.; Yu, Y.H.; Kazansky, P.G. Ultralow-loss geometric phase and polarization shaping by ultrafast laser writing in silica glass. Light. Sci. Appl. 2020, 9, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Perez, J.J.G.; Ossikovski, R. Polarized Light and the Mueller Matrix Approach; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Arteaga, O.; Baldrís, M.; Antó, J.; Canillas, A.; Pascual, E.; Bertran, E. Mueller matrix microscope with a dual continuous rotating compensator setup and digital demodulation. Appl. Opt. 2014, 53, 2236–2245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuntman, E.; Arteaga, O.; Antó, J.; Cayuela, D.; Bertran, E. Conversion of a polarization microscope into a Mueller matrix microscope. Application to the measurement of textile fibers. Opt. Pura Apl. 2015, 48, 309–316. [Google Scholar] [CrossRef]
- Arteaga, O.; Nichols, S.M.; Antó, J. Back-focal plane Mueller matrix microscopy: Mueller conoscopy and Mueller diffractrometry. Appl. Surf. Sci. 2017, 421, 702–706. [Google Scholar] [CrossRef]
- Arteaga, O.; Freudenthal, J.; Wang, B.; Kahr, B. Mueller matrix polarimetry with four photoelastic modulators: Theory and calibration. Appl. Opt. 2012, 51, 6805–6817. [Google Scholar] [CrossRef] [PubMed]
- Piccirillo, B.; Picardi, M.F.; Marrucci, L.; Santamato, E. Flat polarization-controlled cylindrical lens based on the Pancharatnam–Berry geometric phase. Eur. J. Phys. 2017, 38, 034007. [Google Scholar] [CrossRef] [Green Version]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arteaga, O.; Bendada, H. Geometrical Phase Optical Components: Measuring Geometric Phase without Interferometry. Crystals 2020, 10, 880. https://doi.org/10.3390/cryst10100880
Arteaga O, Bendada H. Geometrical Phase Optical Components: Measuring Geometric Phase without Interferometry. Crystals. 2020; 10(10):880. https://doi.org/10.3390/cryst10100880
Chicago/Turabian StyleArteaga, Oriol, and Hana Bendada. 2020. "Geometrical Phase Optical Components: Measuring Geometric Phase without Interferometry" Crystals 10, no. 10: 880. https://doi.org/10.3390/cryst10100880
APA StyleArteaga, O., & Bendada, H. (2020). Geometrical Phase Optical Components: Measuring Geometric Phase without Interferometry. Crystals, 10(10), 880. https://doi.org/10.3390/cryst10100880