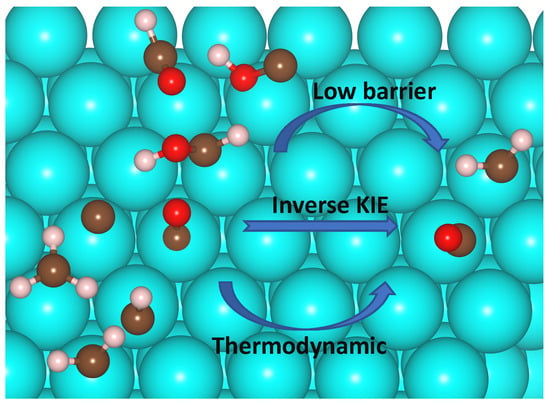
Investigation of C1 + C1 Coupling Reactions in Cobalt-Catalyzed Fischer-Tropsch Synthesis by a Combined DFT and Kinetic Isotope Study
Abstract
:1. Introduction
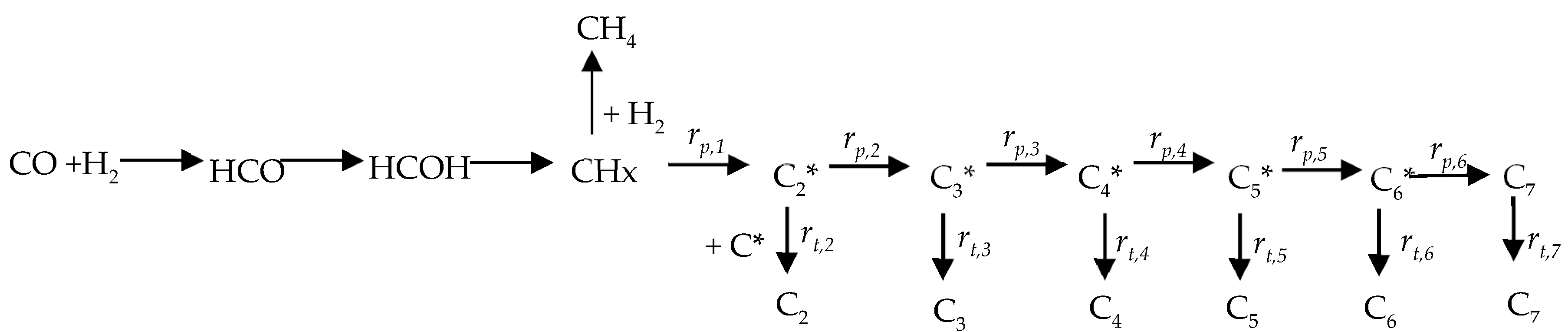
2. Results and Discussion
2.1. Adsorption of C2 Species
2.2. DFT Calculations of C1 + C1 Coupling Reactions
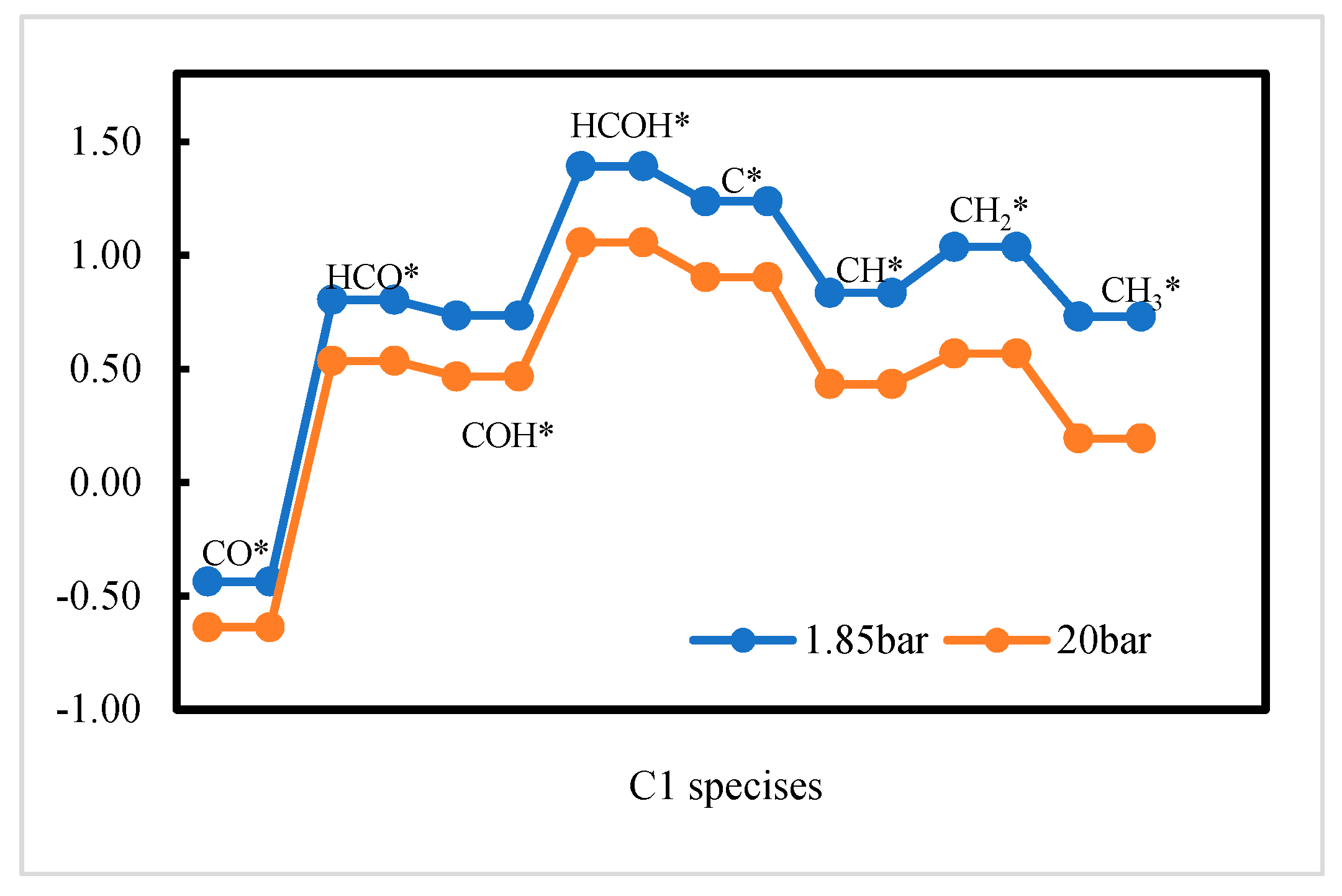
2.3. Thermodynamic Analysis
2.4. Analysis of Kinetic Isotope Effect
3. Method
3.1. Theoretical Method and Model
3.2. Kinetic Isotope Experiment
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ledesma, C.; Yang, J.; Chen, D.; Holmen, A. Recent Approaches in Mechanistic and Kinetic Studies of Catalytic Reactions Using SSITKA Technique. ACS Catal. 2014, 4, 4527–4547. [Google Scholar] [CrossRef]
- Van Santen, R.A.; Markvoort, A.J.; Filot, I.A.W.; Ghouri, M.M.; Hensen, E.J.M. Mechanism and microkinetics of the Fischer-Tropsch reaction. Phys. Chem. Chem. Phys. 2013, 15, 17038–17063. [Google Scholar] [CrossRef] [PubMed]
- Markvoort, A.J.; van Santen, R.A.; Hilbers, P.A.J.; Hensen, E.J.M. Kinetics of the Fischer-Tropsch Reaction. Angew. Chem. Int. Ed. 2012, 51, 9015–9019. [Google Scholar] [CrossRef] [PubMed]
- Dry, M.E. The Fischer-Tropsch process: 1950–2000. Catal. Today 2002, 71, 227–241. [Google Scholar] [CrossRef]
- Yang, J.; Tveten, E.Z.; Chen, D.; Holmen, A. Understanding the Effect of Cobalt Particle Size on Fischer-Tropsch Synthesis: Surface Species and Mechanistic Studies by SSITKA and Kinetic Isotope Effect. Langmuir 2010, 26, 16558–16567. [Google Scholar] [CrossRef]
- Den Breejen, J.P.; Radstake, P.B.; Bezemer, G.L.; Bitter, J.H.; Froseth, V.; Holmen, A.; de Jong, K.P. On the Origin of the Cobalt Particle Size Effects in Fischer-Tropsch Catalysis. J. Am. Chem. Soc. 2009, 131, 7197–7203. [Google Scholar] [CrossRef] [PubMed]
- Bezemer, G.L.; Bitter, J.H.; Kuipers, H.; Oosterbeek, H.; Holewijn, J.E.; Xu, X.D.; Kapteijn, F.; van Dillen, A.J.; de Jong, K.P. Cobalt particle size effects in the Fischer-Tropsch reaction studied with carbon nanofiber supported catalysts. J. Am. Chem. Soc. 2006, 128, 3956–3964. [Google Scholar] [CrossRef] [PubMed]
- Dry, M.E. Practical and theoretical aspects of the catalytic Fischer-Tropsch process. Appl. Catal. A Gen. 1996, 138, 319–344. [Google Scholar] [CrossRef]
- Roferdepoorter, C.K. A comprehensive mechanism for the Fischer-Tropsch synthesis. Chem. Rev. 1981, 81, 447–474. [Google Scholar] [CrossRef]
- Ledesma, C.; Yang, J.; Blekkan, E.A.; Holmen, A.; Chen, D. Carbon Number Dependence of Reaction Mechanism and Kinetics in CO Hydrogenation on a Co-Based Catalyst. ACS Catal. 2016, 10, 6674–6686. [Google Scholar] [CrossRef]
- Zhao, Y.-H.; Sun, K.; Ma, X.; Liu, J.; Sun, D.; Su, H.-Y.; Li, W.-X. Carbon Chain Growth by Formyl Insertion on Rhodium and Cobalt Catalysts in Syngas Conversion. Angew. Chem. Int. Ed. 2011, 50, 5335–5338. [Google Scholar] [CrossRef] [PubMed]
- Zhuo, M.K.; Tan, K.F.; Borgna, A.; Saeys, M. Density Functional Theory Study of the CO Insertion Mechanism for Fischer-Tropsch Synthesis over Co Catalysts. J. Phys. Chem. C 2009, 113, 8357–8365. [Google Scholar] [CrossRef]
- Inderwildi, O.R.; Jenkins, S.J.; King, D.A. Fischer-tropsch mechanism revisited: Alternative pathways for the production of higher hydrocarbons from synthesis gas. J. Phys. Chem. C 2008, 112, 1305–1307. [Google Scholar] [CrossRef]
- Cheng, J.; Hu, P.; Ellis, P.; French, S.; Kelly, G.; Lok, C.M. Chain growth mechanism in Fischer-Tropsch synthesis: A DFT study of C-C coupling over Ru, Fe, Rh, and Re surfaces. J. Phys. Chem. C 2008, 112, 6082–6086. [Google Scholar] [CrossRef]
- Cheng, J.; Hu, P.; Ellis, P.; French, S.; Kelly, G.; Lok, C.M. A DFT study of the chain growth probability in Fischer-Tropsch synthesis. J. Catal. 2008, 257, 221–228. [Google Scholar] [CrossRef]
- Fischer, F.; Tropsch, H. The Synthesis of Petroleum at Atmospheric Pressures from Gasification Products of Coal. Brennstoff Chem. 1926, 7, 97–116. [Google Scholar]
- Brady, R.C.; Pettit, R. On the mechanism of the Fischer-Tropsch reaction-the chain propagation step. J. Am. Chem. Soc. 1981, 103, 1287–1289. [Google Scholar] [CrossRef]
- Brady, R.C.; Pettit, R. Reactions of diazomethane on transition metal surfaces and their relationship to the mechanism of the Fischer-Tropsch reaction. J. Am. Chem. Soc. 1980, 102, 6181–6182. [Google Scholar] [CrossRef]
- Cheng, J.; Gong, X.Q.; Hu, P.; Lok, C.M.; Ellis, P.; French, S. A quantitative determination of reaction mechanisms from density functional theory calculations: Fischer-Tropsch synthesis on flat and stepped cobalt surfaces. J. Catal. 2008, 254, 285–295. [Google Scholar] [CrossRef]
- Zhang, R.; Kang, L.; Liu, H.; He, L.; Wang, B. Insight into the CC chain growth in Fischer-Tropsch synthesis on HCP Co(10-10) surface: The effect of crystal facets on the preferred mechanism. Comput. Mater. Sci. 2018, 145, 263–279. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, R.; Ling, L.; Wang, Q.; Wang, B.; Li, D. Insight into the preferred formation mechanism of long-chain hydrocarbons in Fischer-Tropsch synthesis on Hcp Co(10-11) surfaces from DFT and microkinetic modeling. Catal. Sci. Technol. 2017, 7, 3758–3776. [Google Scholar] [CrossRef]
- Chen, W.; Filot, I.A.W.; Pestman, R.; Hensen, E.J.M. Mechanism of Cobalt-Catalyzed CO Hydrogenation: 2. Fischer-Tropsch Synthesis. ACS Catal. 2017, 7, 8061–8071. [Google Scholar] [CrossRef] [PubMed]
- Zhuo, M.K.; Borgna, A.; Saeys, M. Effect of the CO coverage on the Fischer-Tropsch synthesis mechanism on cobalt catalysts. J. Catal. 2013, 297, 217–226. [Google Scholar] [CrossRef]
- Schweicher, J.; Bundhoo, A.; Kruse, N. Hydrocarbon Chain Lengthening in Catalytic CO Hydrogenation: Evidence for a CO-Insertion Mechanism. J. Am. Chem. Soc. 2012, 134, 16135–16138. [Google Scholar] [CrossRef] [PubMed]
- Su, H.-Y.; Zhao, Y.; Liu, J.-X.; Sun, K.; Li, W.-X. First-principles study of structure sensitivity of chain growth and selectivity in Fischer-Tropsch synthesis using HCP cobalt catalysts. Catal. Sci. Technol. 2017, 7, 2967–2977. [Google Scholar] [CrossRef]
- Yang, J.; Qi, Y.; Zhu, J.; Zhu, Y.-A.; Chen, D.; Holmen, A. Reaction mechanism of CO activation and methane formation on Co Fischer–Tropsch catalyst: A combined DFT, transient, and steady-state kinetic modeling. J. Catal. 2013, 308, 37–49. [Google Scholar] [CrossRef]
- Qi, Y.; Yang, J.; Duan, X.; Zhu, Y.-A.; Chen, D.; Holmen, A. Discrimination of the mechanism of CH4 formation in Fischer-Tropsch synthesis on Co catalysts: A combined approach of DFT, kinetic isotope effects and kinetic analysis. Catal. Sci. Technol. 2014, 4, 3534–3543. [Google Scholar] [CrossRef]
- Lahtinen, J.; Vaari, J.; Kauraala, K.; Soares, E.A.; Van Hove, M.A. LEED investigations on Co(0001): The (3 × 3)R30°-CO overlayer. Surf. Sci. 2000, 448, 269–278. [Google Scholar] [CrossRef]
- Lahtinen, J.; Vaari, J.; Kauraala, K. Adsorption and structure dependent desorption of CO on Co(0001). Surf. Sci. 1998, 418, 502–510. [Google Scholar] [CrossRef]
- Ojeda, M.; Nabar, R.; Nilekar, A.U.; Ishikawa, A.; Mavrikakis, M.; Iglesia, E. CO activation pathways and the mechanism of Fischer-Tropsch synthesis. J. Catal. 2010, 272, 287–297. [Google Scholar] [CrossRef]
- Ojeda, M.; Li, A.W.; Nabar, R.; Nilekar, A.U.; Mavrikakis, M.; Iglesia, E. Kinetically Relevant Steps and H-2/D-2 Isotope Effects in Fischer-Tropsch Synthesis on Fe and Co Catalysts. J. Phys. Chem. C 2010, 114, 19761–19770. [Google Scholar] [CrossRef]
- Gnanamani, M.K.; Jacobs, G.; Shafer, W.D.; Sparks, D.; Davis, B.H. Fischer–Tropsch Synthesis: Deuterium Kinetic Isotope Study for Hydrogenation of Carbon Oxides Over Cobalt and Iron Catalysts. Catal. Lett. 2011, 141, 1420. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Wellendorff, J.; Lundgaard, K.T.; Mogelhoj, A.; Petzold, V.; Landis, D.D.; Norskov, J.K.; Bligaard, T.; Jacobsen, K.W. Density functionals for surface science: Exchange-correlation model development with Bayesian error estimation. Phys. Rev. B 2012, 85, 235149. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Van Hardeveld, R.; Hartog, F. The statistics of surface atoms and surface sites on metal crystals. Surf. Sci. 1969, 15, 189–230. [Google Scholar] [CrossRef]
- Tsakoumis, N.; Dehghan-Niri, R.; Rønning, M.; Walmsley, J.; Borg, Ø.; Rytter, E.; Holmen, A. X-ray absorption, X-ray diffraction and electron microscopy study of spent cobalt based catalyst in semi-commercial scale Fischer-Tropsch synthesis. Appl. Catal. A Gen. 2014, 479, 59–69. [Google Scholar] [CrossRef]
- Jonsson, H.; Mills, G.; Jacobsen, K.W. Nudged elastic band method for finding minimum energy paths of transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; World Scientific: Singapore, 2011; pp. 385–404. [Google Scholar]
- Henkelman, G.; Jonsson, H. A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives. J. Chem. Phys. 1999, 111, 7010–7022. [Google Scholar] [CrossRef]
- Gunasooriya, G.T.K.K.; van Bavel, A.P.; Kuipers, H.P.C.E.; Saeys, M. CO adsorption on cobalt: Prediction of stable surface phases. Surf. Sci. 2015, 642, 6–10. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, B.W.J.; Peng, G.; Mavrikakis, M. Density functional theory study of thermodynamic and kinetic isotope effects of H2/D2 dissociative adsorption on transition metals. Catal. Sci. Technol. 2018, 8, 3321–3335. [Google Scholar] [CrossRef]


| Surface Species | Eads (eV) | dC-C (Å) | dC-O (Å) | dC-H (Å) |
|---|---|---|---|---|
| CC | −6.49 | 1.33 | -- | -- |
| CCH | −4.83 | 1.35 | -- | 1.09 |
| CCH2 | −3.68 | 1.38 | 1.09 | |
| CCH3 | −5.13 | 1.50 | 1.10 | |
| CHCO | −2.82 | 1.39 | 1.25 | 1.09 |
| CH2CO | −0.77 | 1.43 | 1.28 | 1.09 |
| CH3CO | −1.86 | 1.51 | 1.31 | 1.10 |
| CHCH | −2.12 | 1.38 | 1.09 | |
| CHCH2 | −2.46 | 1.41 | 1.09 | |
| CHCH3 | −3.35 | 1.52 | 1.15, 1.09 | |
| CH2CH2 | −0.77 | 1.42 | 1.09 | |
| CH2CH3 | −1.44 | 1.55 | 1.10 | |
| CH3CH3 | −0.35 | 1.53 | 1.09 | |
| C-HCO | −4.67 | 1.42 | 1.28 | 1.10 |
| CHHCO | −3.96 | 1.41 | 1.29 | 1.10 |
| CH2HCO | −2.01 | 1.43 | 1.19 | 1.04 |
| CH3HCO | −0.59 | 1.50 | 1.35 | 1.09 |
| C-COH | −4.79 | 1.39 | 1.34 | -- |
| CHCOH | −2.01 | 1.41 | 1.37 | 1.09 |
| CH2COH | −2.34 | 1.45 | 1.35 | 1.09 |
| CH3COH | −2.36 | 1.50 | 1.34 | 1.09 |
| C-HCOH | −4.43 | 1.38 | 1.34 | 1.09 |
| CHHCOH | −2.77 | 1.39 | 1.35 | 1.11 |
| CH2HCOH | −0.65 | 1.40 | 1.38 | 1.09 |
| CH3HCOH | −1.43 | 1.52 | 1.46 | 1.10 |
| +CO | +HCO | +HCOH | +CH | +CH2 | +CH3 | +C | +COH | |
|---|---|---|---|---|---|---|---|---|
| HCO | -- | -- | -- | 0.34 | 0.05 | 0.80 | -- | -- |
| HCOH | -- | -- | -- | 0.29 | 0.16 | 0.77 | 0.32 | -- |
| CH | 0.90 | 0.34 | 0.29 | 0.57 | 0.49 | 0.75 | 0.71 | 1.40 |
| CH2 | 0.56 | 0.05 | 0.16 | 0.49 | 0.12 | 0.62 | 0.57 | 0.48 |
| CH3 | 1.19 | 0.80 | 0.77 | 0.75 | 0.62 | 1.84 | 0.74 | 1.10 |
| CH3 | HCO | HCOH | CH2 | CH | |
|---|---|---|---|---|---|
| CH3 | 1.84 | 0.80 | 0.77 | 0.62 | 0.75 |
| HCO | 0.80 | -- | -- | 0.05 | 0.34 |
| HCOH | 0.77 | -- | -- | 0.16 | 0.29 |
| CH2 | 0.62 | 0.05 | 0.16 | 0.12 | 0.49 |
| CH | 0.75 | 0.34 | 0.29 | 0.49 | 0.57 |
| Reactants | CO + CH2 | HCO + CH | HCO + CH2 | CH + CH | CH + CH2 | CH2 + CH2 | C + CH2 | CH2 + COH |
|---|---|---|---|---|---|---|---|---|
| G(eV) | 0.60 | 1.64 | 1.84 | 1.67 | 1.87 | 2.07 | 2.28 | 1.77 |
| Reaction Rate [µmol/(gcats)] | rt,H | rt,D | KIE = rt,H/rt,D |
|---|---|---|---|
| rCH4 | 2.349 | 2.383 | 0.99 |
| rC2 | 0.158 | 0.180 | 0.88 |
| rC3 | 0.128 | 0.192 | 0.66 |
| rC4 | 0.076 | 0.152 | 0.50 |
| rC5+ | 0.046 | 0.121 | 0.38 |
| Reaction Rate [mol/(gcats)] | rH | rD | KIE |
|---|---|---|---|
| rp,4 | 0.05 | 0.12 | 0.38 |
| rp,3 | 0.11 | 0.25 | 0.45 |
| rp,2 | 0.21 | 0.38 | 0.56 |
| rp,1 | 0.30 | 0.43 | 0.69 |
| Elementary Step | ZPE Contribution | Entropic Contribution | KIE |
|---|---|---|---|
| CO + CH2→CH2CO | 0.78 | 1.08 | 0.84 |
| HCO + CH→CHHCO | 0.96 | 1.02 | 0.98 |
| CH + CH→CHCH | 0.91 | 1.04 | 0.95 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Y.; Yang, J.; Holmen, A.; Chen, D. Investigation of C1 + C1 Coupling Reactions in Cobalt-Catalyzed Fischer-Tropsch Synthesis by a Combined DFT and Kinetic Isotope Study. Catalysts 2019, 9, 551. https://doi.org/10.3390/catal9060551
Qi Y, Yang J, Holmen A, Chen D. Investigation of C1 + C1 Coupling Reactions in Cobalt-Catalyzed Fischer-Tropsch Synthesis by a Combined DFT and Kinetic Isotope Study. Catalysts. 2019; 9(6):551. https://doi.org/10.3390/catal9060551
Chicago/Turabian StyleQi, Yanying, Jia Yang, Anders Holmen, and De Chen. 2019. "Investigation of C1 + C1 Coupling Reactions in Cobalt-Catalyzed Fischer-Tropsch Synthesis by a Combined DFT and Kinetic Isotope Study" Catalysts 9, no. 6: 551. https://doi.org/10.3390/catal9060551
APA StyleQi, Y., Yang, J., Holmen, A., & Chen, D. (2019). Investigation of C1 + C1 Coupling Reactions in Cobalt-Catalyzed Fischer-Tropsch Synthesis by a Combined DFT and Kinetic Isotope Study. Catalysts, 9(6), 551. https://doi.org/10.3390/catal9060551