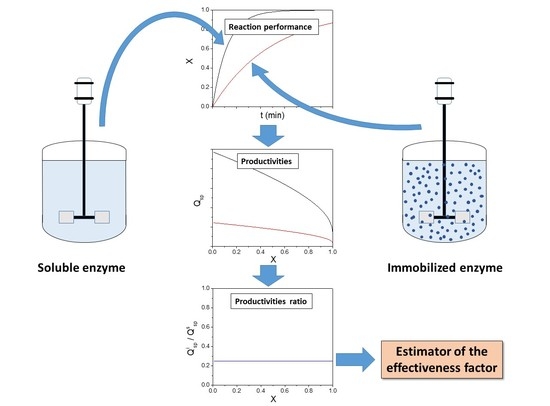
Estimation of the Effectiveness Factor for Immobilized Enzyme Catalysts through a Simple Conversion Assay
Abstract
1. Introduction
- Explicit finite differences schemes [4,10]: These methods have the advantages of easy computational implementation and quick numerical solution in the steady state. However, they are sensitive to stability criteria, require variable changes to replace conditions in the center of the spherical catalytic particles, and fail to represent the behavior of the transient enzyme system.
- Taylor series expansions [11]: This solution method allows us to represent the EF behavior as a function of the competitive and uncompetitive inhibition constants and the Thiele modulus. However, its generalization is not possible, as the different enzymatic mechanisms and catalyst geometries can present singularities where the Taylor series does not converge.
- Runge–Kutta and Runge–Kutta–Gill methods [2,12,13,14,15,16]: These numerical methods have been widely used given their stability and precision in the resolution of PDEs. However, they require a high level of computational solving, which increases with decreasing Thiele modulus and where the boundary conditions involve mass transfer due to convection forces.
- Newton’s iteration techniques [17]: A program to determine the EF was developed in a reaction that presents competitive inhibition by the product and uncompetitive inhibition by the substrate. It includes a model of a nonuniform enzyme distribution with the presence of internal and external mass transfer restrictions. The method replaces the differential equations system for nonlinear algebraic equations such as the Taylor series, which have the same singularity inconveniences discussed before.
- The homotopy perturbation method [18]: This is a modern and promising analytical method to obtain the solutions to nonlinear PDEs. The method consists of expanding the relevant variables and some parameters if needed, as well as power series depending on the homotopy parameter (p). The method has proved to be highly effective, but there are still no studies related to the comparison of experimental data or to its application in multisubstrate reactions.
- Approximated analytical solutions [19,20,21,22,23]: While analytical solutions provide an understanding of the system with a satisfactory precision, they are usually related to one-substrate reactions. They use complex hyperbolic periodic equations, which are tedious to use and diverge from the real EF behavior as the Thiele modulus increases. This happens due to the imposed restrictions and assumptions in the mathematical modelling derivation.
- Modified Adomian decomposition method [24,25]: The method has been widely used as a solution method for nonlinear differential problems, where it cannot always satisfy the boundary conditions imposed (applicability limitations) and also has the added complexity of calculation of the Adomian polynomials, which are usually impractical to apply.
- Orthogonal placement [14,21,22,26,27,28]: This method increases the computational time substantially compared to the Runge–Kutta methods as five or more placement points are implemented in its resolution. Additionally, it presented numerical instabilities in research by Vos et al. [14] for the calculation of mass transfer in thin biofilms.
2. Theory
- The system is exempt from external diffusional restrictions;
- The batch reactor operates isothermally;
- There is a homogeneous distribution of enzyme molecules inside the catalyst particle;
- The enzyme is not (significantly) affected by thermal inactivation during the reaction time;
- There are no pH gradients inside the catalyst;
- The effective diffusion coefficient is independent of the concentration.
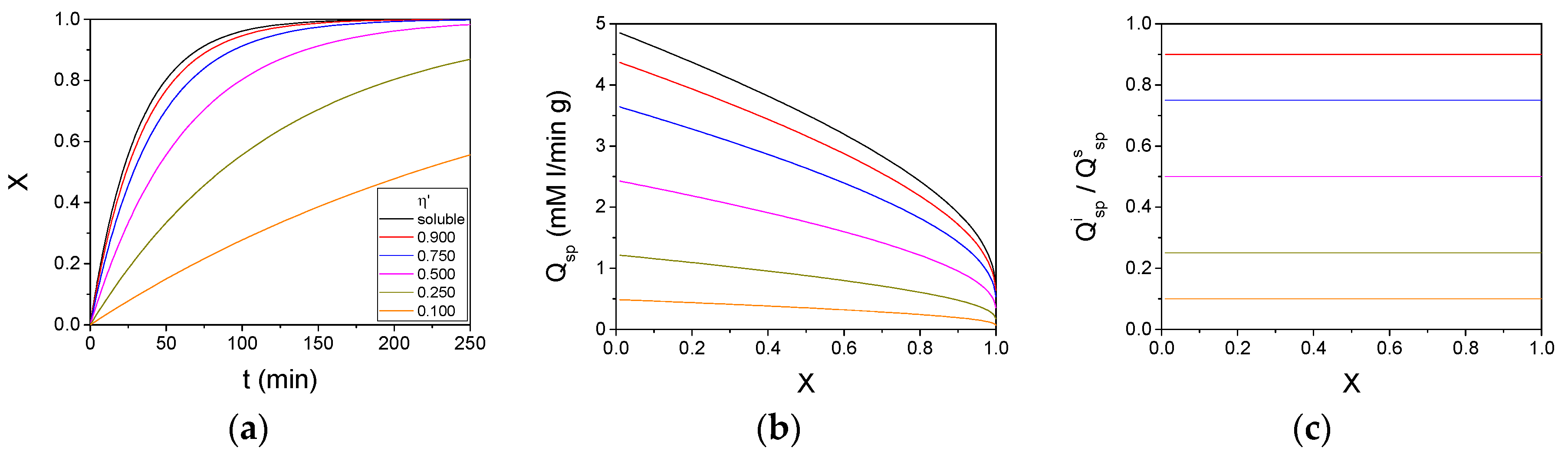
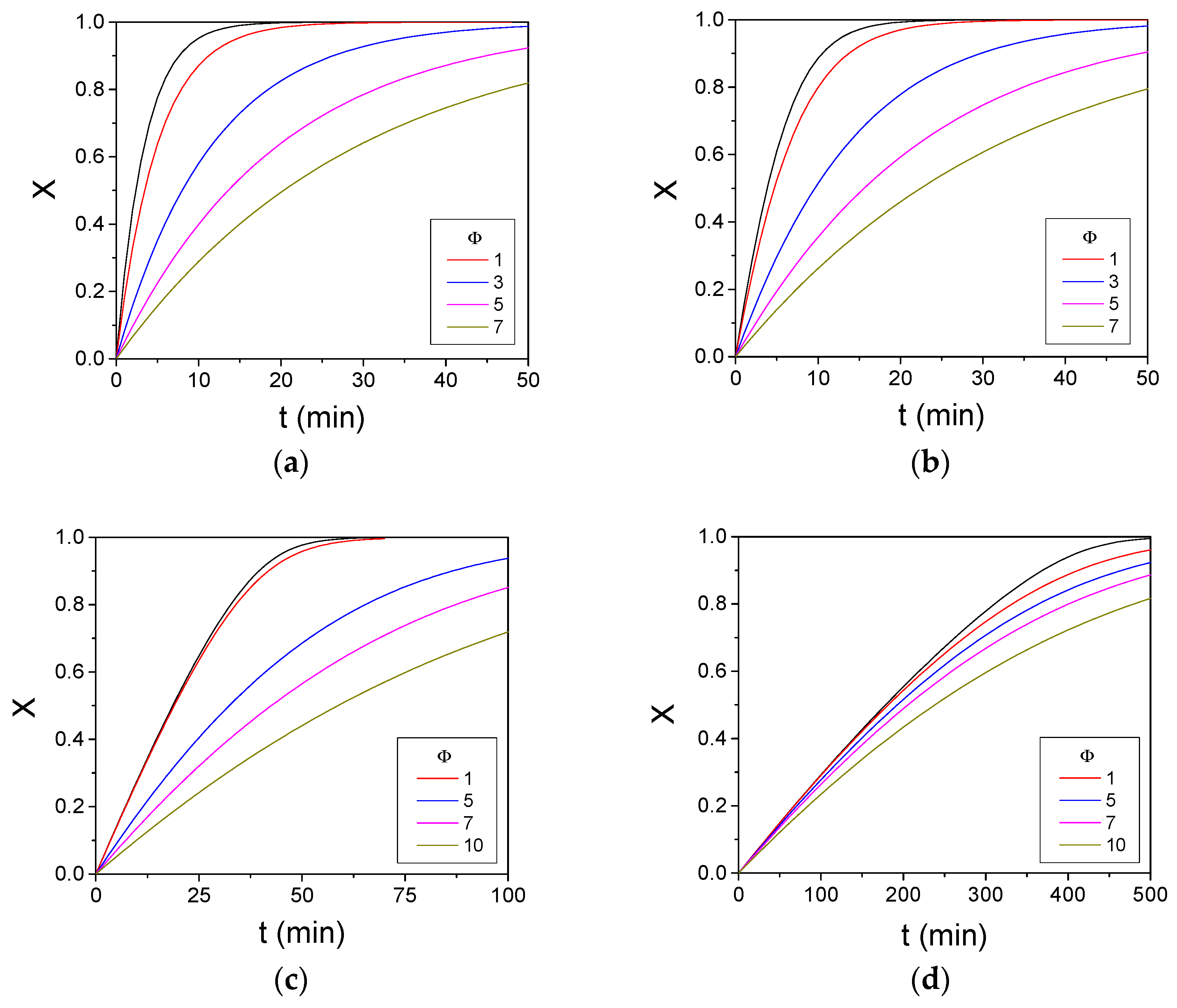
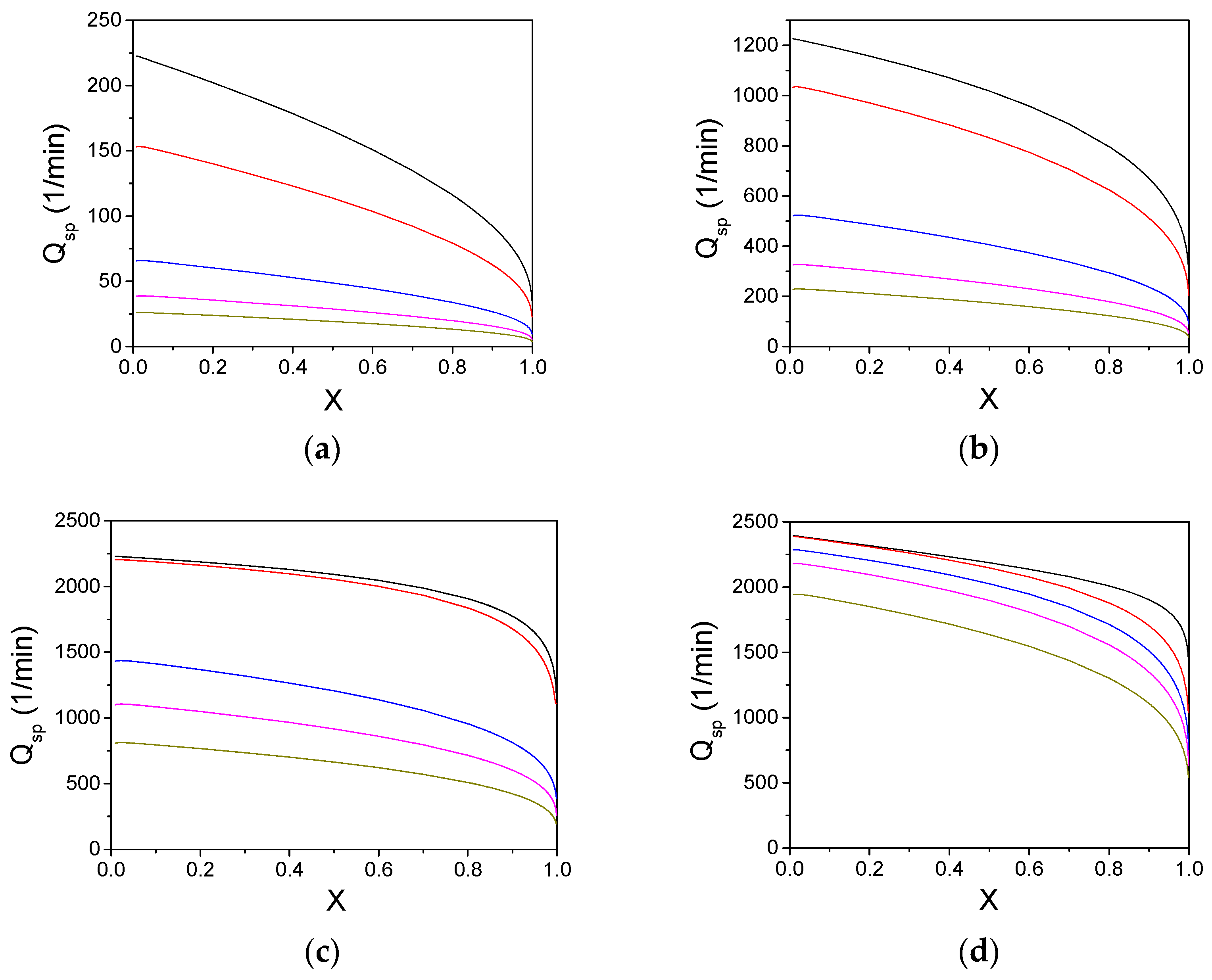
3. Results and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Jesionowski, T.; Zdarta, J.; Krajewska, B. Enzyme immobilization by adsorption: A review. Adsorption 2014, 20, 801–821. [Google Scholar] [CrossRef]
- Oliveira, S.C. Evaluation of effectiveness factor of immobilized enzymes using Runge-Kutta-Gill method: How to solve mathematical undetermination at particle center point? Bioprocess Eng. 1999, 20, 185–187. [Google Scholar] [CrossRef]
- Valencia, P.; Wilson, L.; Aguirre, C.; Illanes, A. Evaluation of the incidence of diffusional restrictions on the enzymatic reactions of hydrolysis of penicillin G and synthesis of cephalexin. Enzym. Microb. Technol. 2010, 47, 268–276. [Google Scholar] [CrossRef]
- Engasser, J.-M.; Horvath, C. Effect of internal diffusion in heterogeneous enzyme systems: Evaluation of true kinetic parameters and substrate diffusivity. J. Theor. Biol. 1973, 42, 137–155. [Google Scholar] [CrossRef]
- Tischer, W.; Wedekind, F. Immobilized Enzymes: Methods and Applications. In Biocatalysis—From Discovery to Application; Fessner, W.-D., Archelas, A., Demirjian, D.C., Furstoss, R., Griengl, H., Jaeger, K.E., Morís-Varas, E., Öhrlein, R., Reetz, M.T., Reymond, J.L., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 95–126. [Google Scholar] [CrossRef]
- Illanes, A.; Miguel Gonzalez, J.; Manuel Gomez, J.; Valencia, P.; Wilson, L. Diffusional restrictions in glyoxyl-agarose immobilized penicillin G acylase of different particle size and protein loading. Electron. J. Biotechnol. 2010, 13. [Google Scholar] [CrossRef]
- Thiele, E.W. Relation between Catalytic Activity and Size of Particle. Ind. Eng. Chem. 1939, 31, 916–920. [Google Scholar] [CrossRef]
- Damkohler, G. Einflusse der stromung, diffusion und des warmeubergangs auf die leistung von reaktionsofen. Z. Elektrochem. Angew. Phys. Chemie 1936, 42, 846–862. [Google Scholar]
- Cohen, D.; Merchuk, J.; Zeiri, Y.; Sadot, O. Catalytic effectiveness of porous particles: A continuum analytic model including internal and external surfaces. Chem. Eng. Sci. 2017, 166, 101–106. [Google Scholar] [CrossRef]
- Carrasco, J.L.G.; Santoyo, A.B.; Gómez, E.G.; Rodríguez, J.B.; Martín, M.F.M.; Gómez, M.G. A short recursive procedure for evaluating effectiveness factors for immobilized enzymes with reversible Michaelis–Menten kinetics. Biochem. Eng. J. 2008, 39, 58–65. [Google Scholar] [CrossRef]
- Alfani, F.; Cantarella, M.; Gallifuoco, A.; Romano, V. On the effectiveness factor of immobilized enzymes with linear mixed-type product inhibition kinetics. Chem. Eng. J. Biochem. Eng. J. 1995, 57, B23–B29. [Google Scholar] [CrossRef]
- Fink, D.J.; Na, T.; Schultz, J.S. Effectiveness factor calculations for immobilized enzyme catalysts. Biotechnol. Bioeng. 1973, 15, 879–888. [Google Scholar] [CrossRef]
- Manjón, A.; Iborra, J.L.; Gómez, J.L.; Gómez, E.; Bastida, J.; Bódalo, A. Evaluation of the effectiveness factor along immobilized enzyme fixed-bed reactors: Design of a reactor with naringinase covalently immobilized into glycophase-coated porous glass. Biotechnol. Bioeng. 1987, 30, 491–497. [Google Scholar] [CrossRef] [PubMed]
- Vos, H.J.; Heederik, P.J.; Potters, J.J.M.; Luyben, K.C.A.M. Effectiveness factor for spherical biofilm catalysts. Bioprocess Eng. 1990, 5, 63–72. [Google Scholar] [CrossRef]
- Bódalo, A.; Gómez, J.L.; Gómez, E.; Bastida, J.; Iborra, J.L.; Manjón, A. Analysis of diffusion effects on immobilized enzymes on porous supports with reversible Michaelis-Menten kinetics. Enzym. Microb. Technol. 1986, 8, 433–438. [Google Scholar] [CrossRef]
- Gómez, J.L.; Bódalo, A.; Gómez, E.; Bastida, J.; Máximo, M.F. Two-parameter model for evaluating effectiveness factor for immobilized enzymes with reversible Michaelis–Menten kinetics. Chem. Eng. Sci. 2003, 58, 4287–4290. [Google Scholar] [CrossRef]
- Gusakov, A.V. A Fortran Program for Evaluation of the Effectiveness Factor of Biocatalysts in the Presence of External and Internal Diffusional Limitations. Biocatalysis 1988, 1, 301–320. [Google Scholar] [CrossRef]
- Rani, J.; Sevukaperumal, S.; Rajendran, L. Analytical expression of effectiveness factor for immobilized enzymes system with reversible Michaelis-Menten kinetics. Asian J. Sci. Appl. Technol. 2015, 4, 10–16. [Google Scholar]
- Moo-Young, M.; Kobayashi, T. Effectiveness factors for immobilized-enzyme reactions. Can. J. Chem. Eng. 1972, 50, 162–167. [Google Scholar] [CrossRef]
- Fang, Y.; Govind, R. A New Thiele’s Modulus for the Monod Biofilm Model. Chin. J. Chem. Eng. 2008, 16, 277–286. [Google Scholar] [CrossRef]
- Gottifredi, J.C.; Gonzo, E.E. On the effectiveness factor calculation for a reaction—Diffusion process in an immobilized biocatalyst pellet. Biochem. Eng. J. 2005, 24, 235–242. [Google Scholar] [CrossRef]
- Xiu, G.-H.; Jiang, L.; Li, P. Mass-Transfer Limitations for Immobilized Enzyme-Catalyzed Kinetic Resolution of Racemate in a Batch Reactor. Ind. Eng. Chem. Res. 2000, 39, 4054–4062. [Google Scholar] [CrossRef]
- Szukiewicz, M.; Petrus, R. Approximate model for diffusion and reaction in a porous pellet and an effectiveness factor. Chem. Eng. Sci. 2004, 59, 479–483. [Google Scholar] [CrossRef]
- Narayanan, K.; Meena, V.; Rajendran, L.; Gao, J.; Subbiah, S. Mathematical analysis of diffusion and kinetics of immobilized enzyme systems that follow the Michaelis-Menten mechanism. Appl. Comput. Math. 2017, 6, 143–160. [Google Scholar] [CrossRef]
- Praveen, T.; Valencia, P.; Rajendran, L. Theoretical analysis of intrinsic reaction kinetics and the behavior of immobilized enzymes system for steady-state conditions. Biochem. Eng. J. 2014, 91, 129–139. [Google Scholar] [CrossRef]
- Al-Muftah, A.E.; Abu-Reesh, I.M. Effects of internal mass transfer and product inhibition on a simulated immobilized enzyme-catalyzed reactor for lactose hydrolysis. Biochem. Eng. J. 2005, 23, 139–153. [Google Scholar] [CrossRef]
- Al-Muftah, A.E.; Abu-Reesh, I.M. Effects of simultaneous internal and external mass transfer and product inhibition on immobilized enzyme-catalyzed reactor. Biochem. Eng. J. 2005, 27, 167–178. [Google Scholar] [CrossRef]
- Ramachandran, P.A. Solution of immobilized enzyme problems by collocation methods. Biotechnol. Bioeng. 1975, 17, 211–226. [Google Scholar] [CrossRef]
- Jurado, E.; Camacho, F.; Luzón, G.; Vicaria, J.M. A new kinetic model proposed for enzymatic hydrolysis of lactose by a β-galactosidase from Kluyveromyces fragilis. Enzym. Microb. Technol. 2002, 31, 300–309. [Google Scholar] [CrossRef]
- Kheirolomoom, A.; Ardjmand, M.; Fazelinia, H.; Zakeri, A. Clarification of penicillin G acylase reaction mechanism. Process Biochem. 2001, 36, 1095–1101. [Google Scholar] [CrossRef]
- Valencia, P.; Flores, S.; Wilson, L.; Illanes, A. Effect of Internal Diffusional Restrictions on the Hydrolysis of Penicillin G: Reactor Performance and Specific Productivity of 6-APA with Immobilized Penicillin Acylase. Appl. Biochem. Biotechnol. 2011, 165, 426–441. [Google Scholar] [CrossRef]
- Van Roon, J.L.; Arntz, M.M.H.D.; Kallenberg, A.I.; Paasman, M.A.; Tramper, J.; Schroën, C.G.P.H.; Beeftink, H.H. A multicomponent reaction–diffusion model of a heterogeneously distributed immobilized enzyme. Appl. Microbiol. Biotechnol. 2006, 72, 263–278. [Google Scholar] [CrossRef] [PubMed]
- Mateo, C.; Palomo, J.M.; Fuentes, M.; Betancor, L.; Grazu, V.; López-Gallego, F.; Pessela, B.C.C.; Hidalgo, A.; Fernández-Lorente, G.; Fernández-Lafuente, R.; et al. Glyoxyl agarose: A fully inert and hydrophilic support for immobilization and high stabilization of proteins. Enzym. Microb. Technol. 2006, 39, 274–280. [Google Scholar] [CrossRef]
| Constant/Parameter | Value | Unit |
|---|---|---|
| kcat | 5.15 | mM⋅L/g⋅min |
| KM | 8.43 | mM |
| ER | 1.00 | g/L |
| S0 | 150 | mM |
| Constant/Parameter | Value | Unit |
|---|---|---|
| E0″ | 16.0 1 | g/L |
| D0 | 3.97 × 10−8 | m2/min |
| De | 2.98 × 10−8 | m2/min |
| ε/τ | 0.75 | - |
| Ccat | 50 | g/L |
| R (µm) | Φ | η′ |
|---|---|---|
| 316 | 0.4 | 0.90 |
| 574 | 0.8 | 0.75 |
| 1132 | 1.6 | 0.50 |
| 2607 | 3.6 | 0.25 |
| 6930 | 9.7 | 0.10 |
| Constant/Parameter | Value | Unit |
|---|---|---|
| KM | 0.13 | mM |
| KS | 821 | mM |
| K1 | 1.82 | mM |
| K2 | 48.0 | mM |
| kcat | 2460 | min−1 |
| E0″ | 4.0 | mM |
| De | 3.18 × 10−8 | m2/min |
| De1 | 4.40 × 10−8 | m2/min |
| De2 | 3.53 × 10−8 | m2/min |
| T | 303 | K |
| Catalyst concentration | 2.5 | g/L |
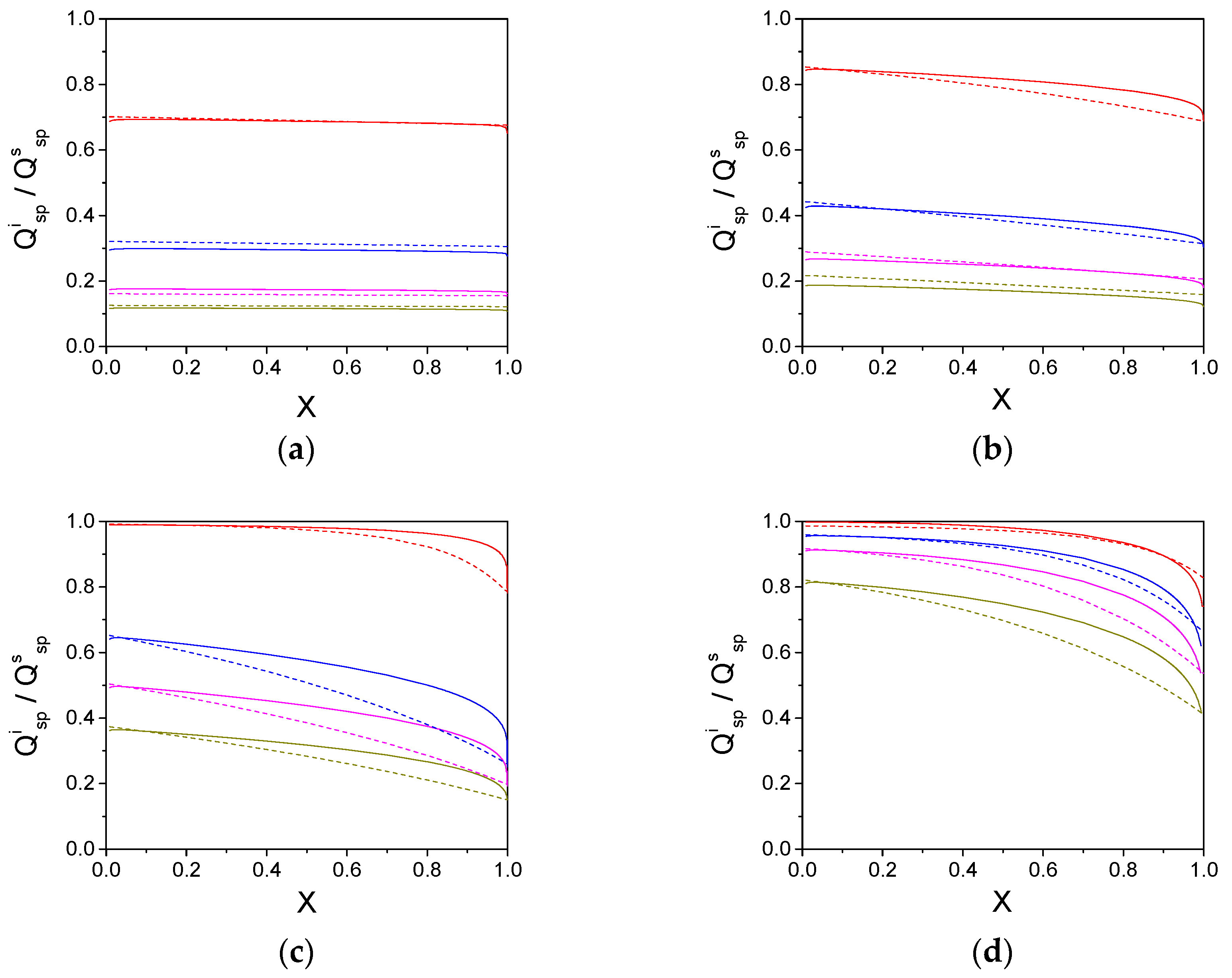
| S0/KM | Thiele Modulus (Φ) | Initial | Final | ||
|---|---|---|---|---|---|
| SPR | MIEF | SPR | MIEF | ||
| 0.1 | 1 | 0.687 | 0.702 | 0.651 | 0.676 |
| 3 | 0.295 | 0.321 | 0.276 | 0.306 | |
| 5 | 0.174 | 0.161 | 0.161 | 0.155 | |
| 7 | 0.116 | 0.126 | 0.108 | 0.122 | |
| 1 | 1 | 0.843 | 0.853 | 0.716 | 0.688 |
| 3 | 0.425 | 0.442 | 0.304 | 0.314 | |
| 5 | 0.265 | 0.289 | 0.180 | 0.207 | |
| 7 | 0.186 | 0.217 | 0.122 | 0.159 | |
| 10 | 1 | 0.989 | 0.992 | 0.782 | 0.787 |
| 5 | 0.641 | 0.652 | 0.251 | 0.261 | |
| 7 | 0.493 | 0.504 | 0.192 | 0.198 | |
| 10 | 0.362 | 0.373 | 0.150 | 0.151 | |
| 100 | 1 | 0.998 | 0.986 | 0.741 | 0.828 |
| 5 | 0.954 | 0.959 | 0.620 | 0.662 | |
| 7 | 0.910 | 0.917 | 0.538 | 0.536 | |
| 10 | 0.811 | 0.821 | 0.416 | 0.411 | |
| S0/KM | Thiele Modulus (Φ) | Estimated Φ | |
|---|---|---|---|
| Initial | Final | ||
| 0.1 | 1 | 0.959 | 1.057 |
| 3 | 3.02 | 3.25 | |
| 5 | 5.39 | 5.86 | |
| 7 | 8.27 | 8.91 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valencia, P.; Ibañez, F. Estimation of the Effectiveness Factor for Immobilized Enzyme Catalysts through a Simple Conversion Assay. Catalysts 2019, 9, 930. https://doi.org/10.3390/catal9110930
Valencia P, Ibañez F. Estimation of the Effectiveness Factor for Immobilized Enzyme Catalysts through a Simple Conversion Assay. Catalysts. 2019; 9(11):930. https://doi.org/10.3390/catal9110930
Chicago/Turabian StyleValencia, Pedro, and Francisco Ibañez. 2019. "Estimation of the Effectiveness Factor for Immobilized Enzyme Catalysts through a Simple Conversion Assay" Catalysts 9, no. 11: 930. https://doi.org/10.3390/catal9110930
APA StyleValencia, P., & Ibañez, F. (2019). Estimation of the Effectiveness Factor for Immobilized Enzyme Catalysts through a Simple Conversion Assay. Catalysts, 9(11), 930. https://doi.org/10.3390/catal9110930