Theoretical Calculations on the Mechanism of Enantioselective Copper(I)-Catalyzed Addition of Enynes to Ketones
Abstract
1. Introduction
2. Results and Discussion
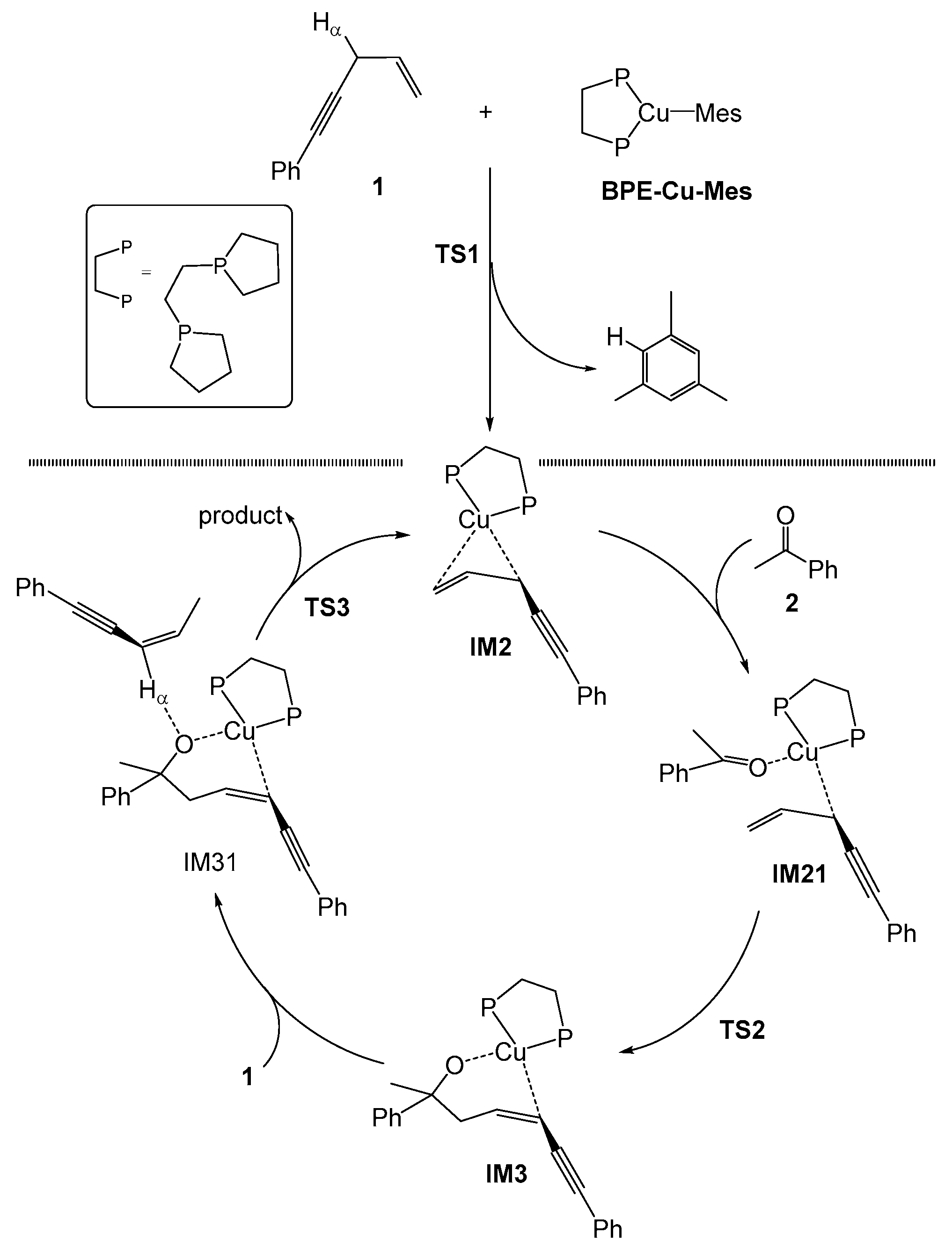
2.1. Mechanism of the BPE–CuMes Model System
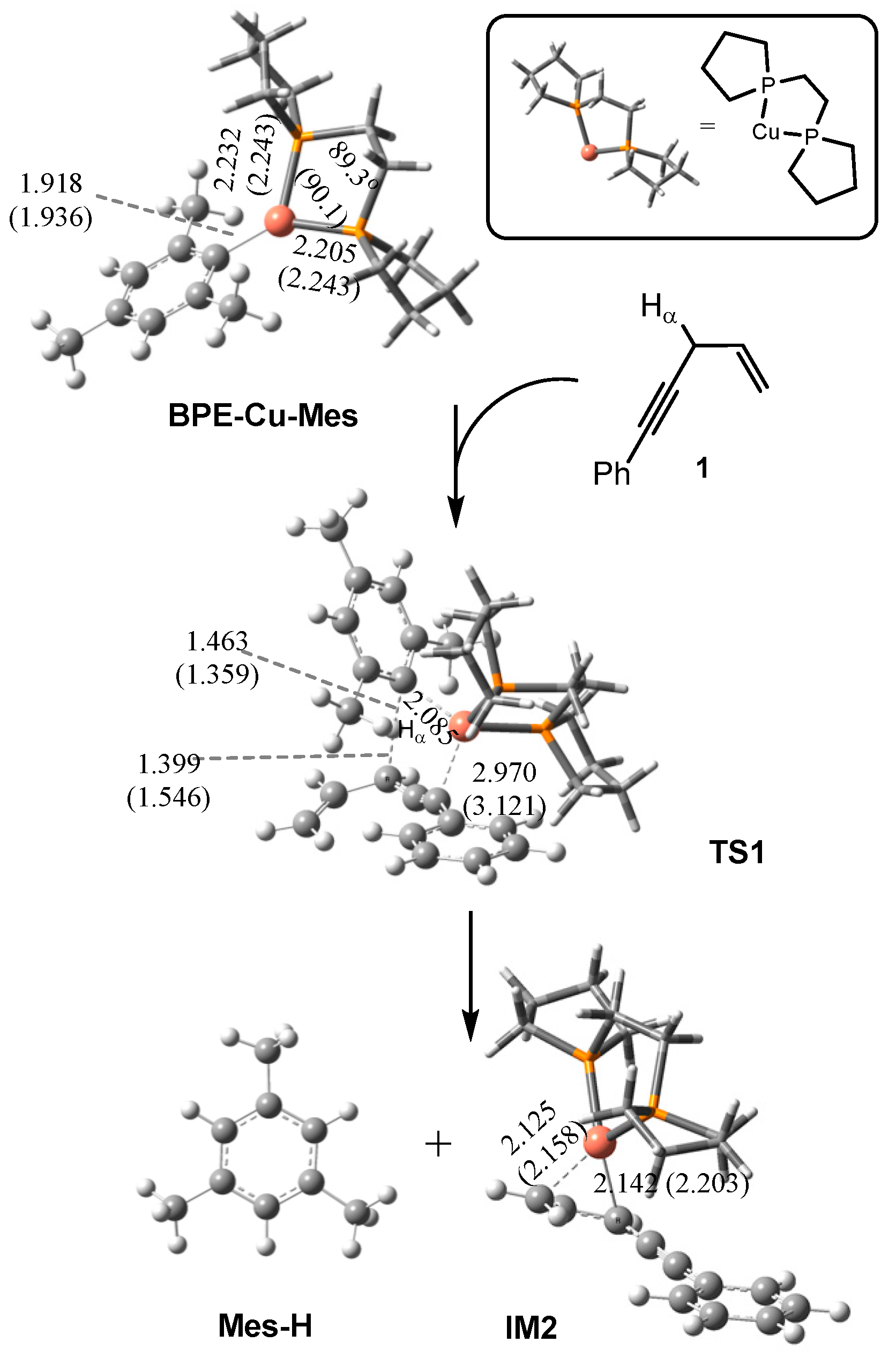
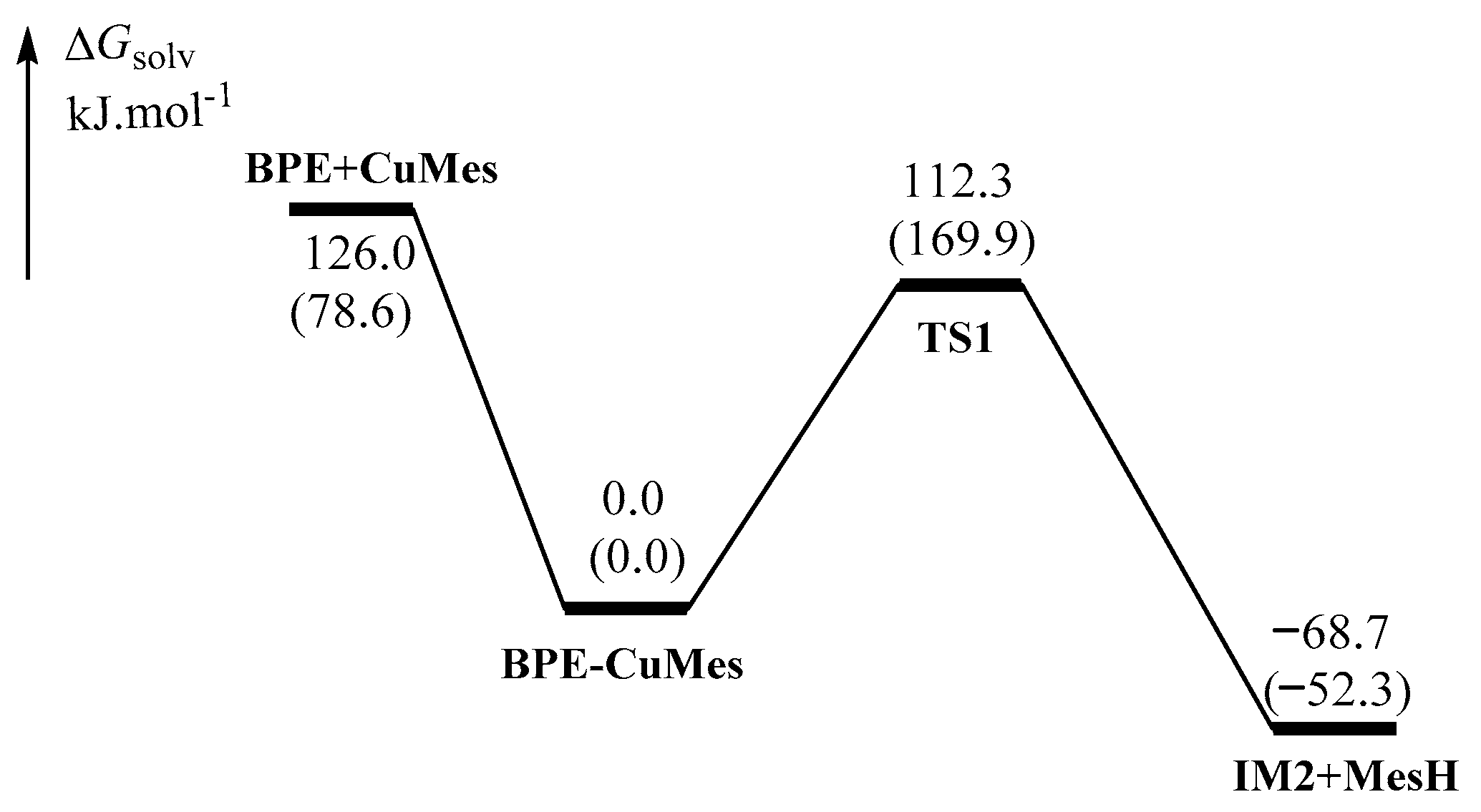
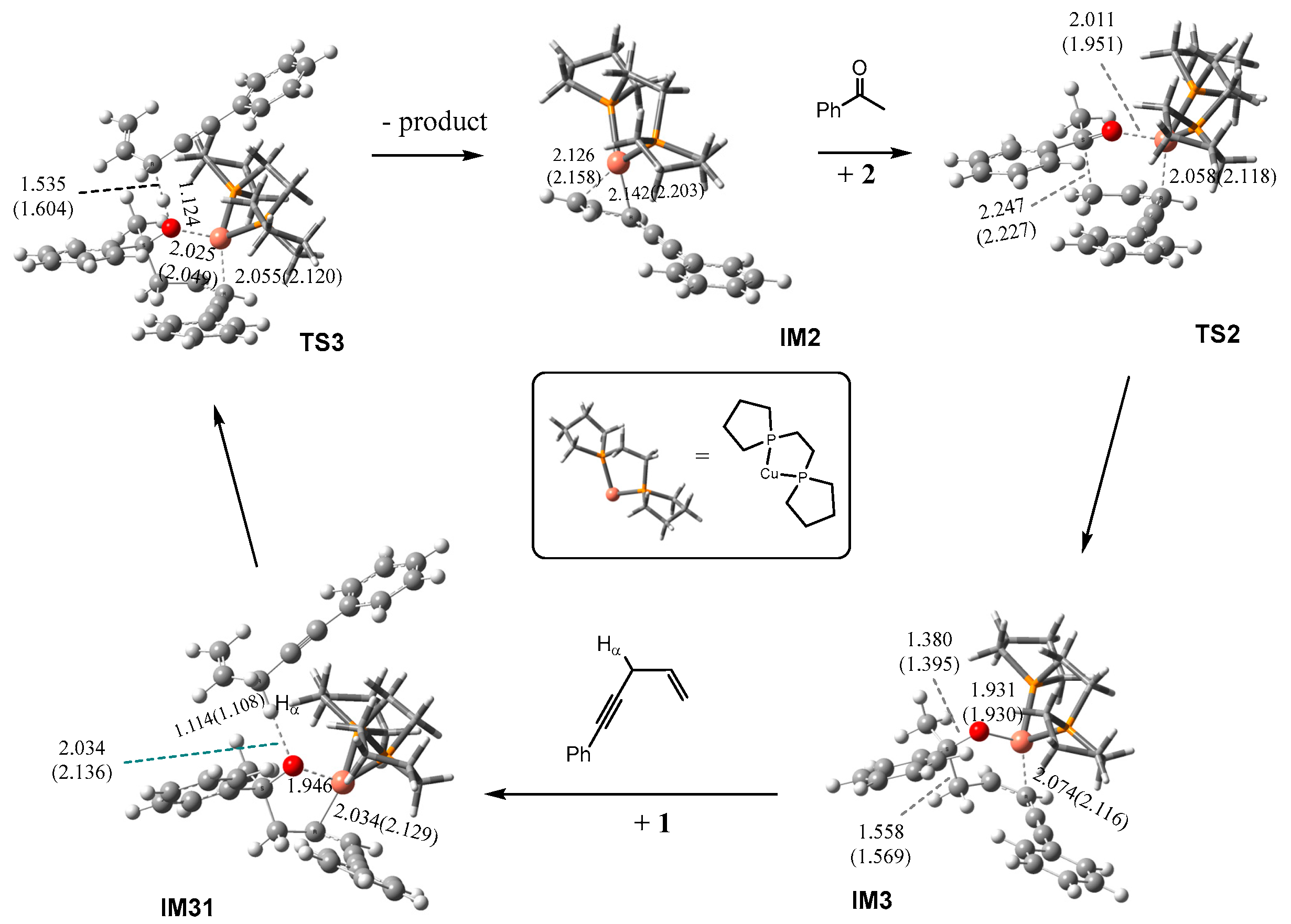
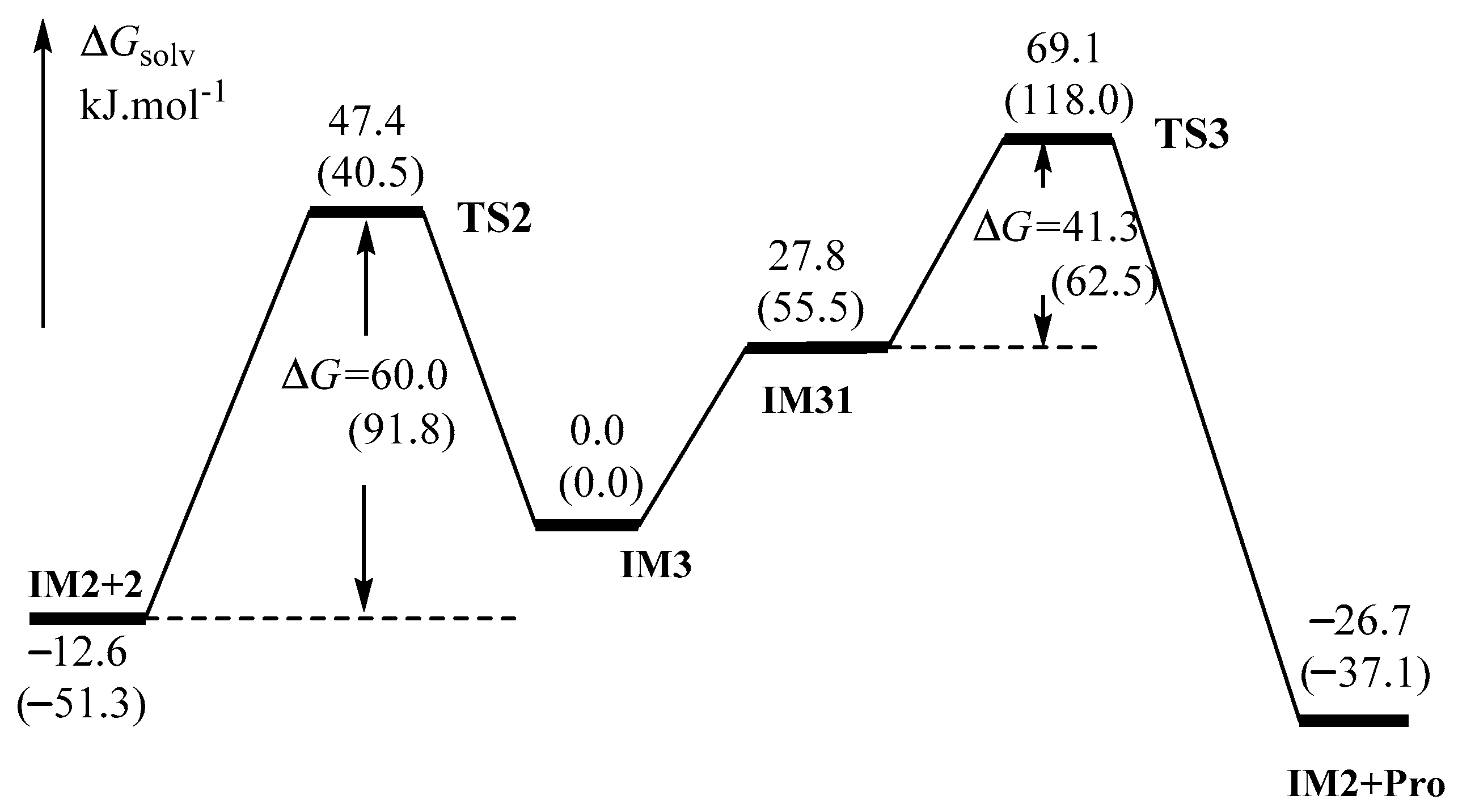
2.1.1. Formation of the Active Intermediate IM2
2.1.2. Catalytic Cycle Over IM2
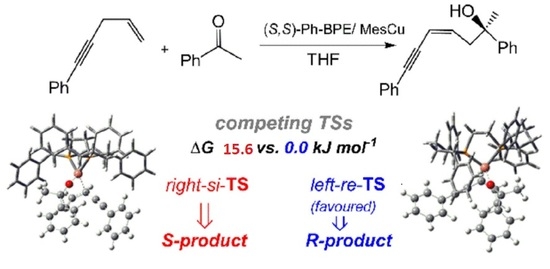
2.2. Stereochemistry of Such Reactions
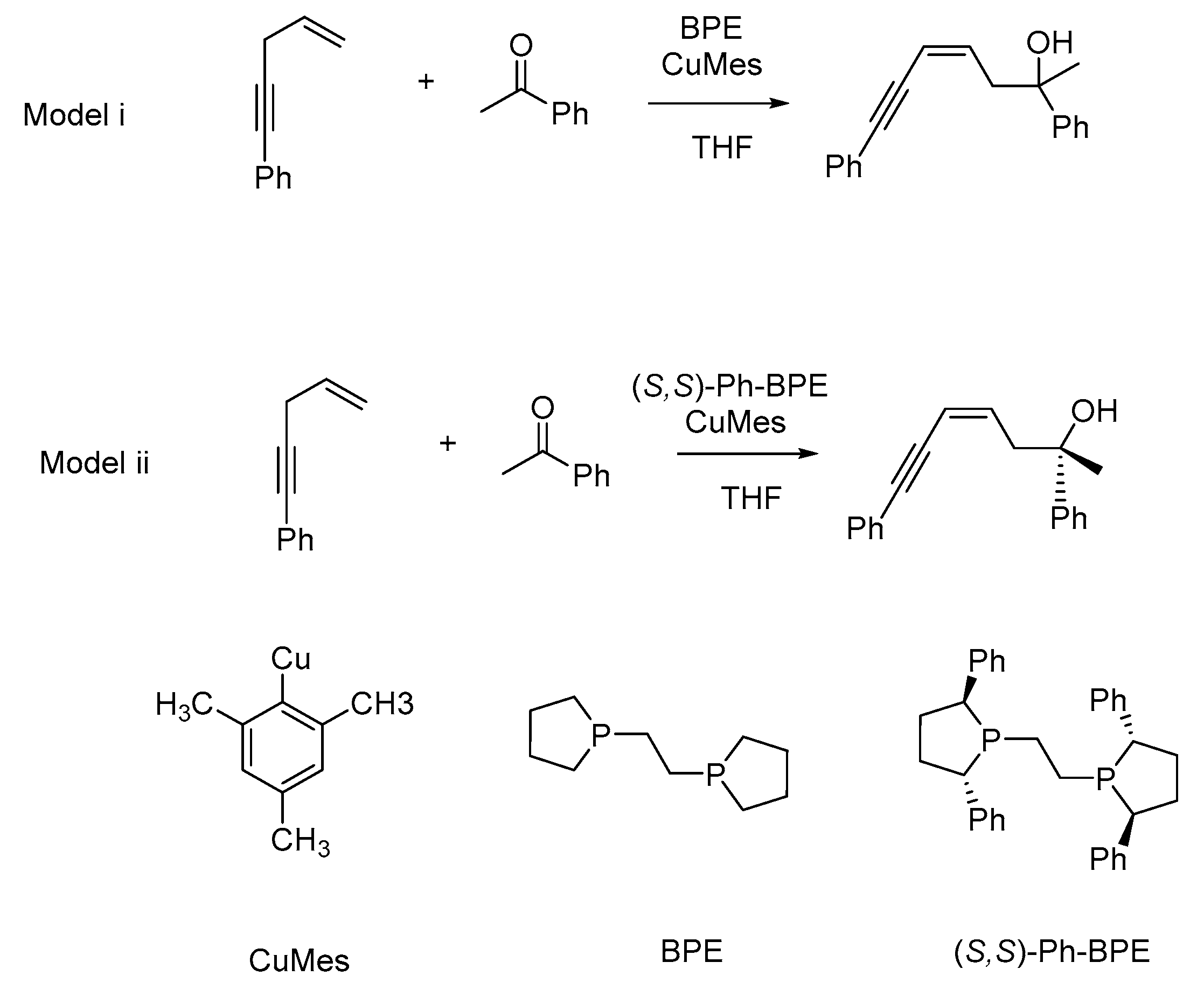
2.2.1. Stereoselectivity of the (S,S)-Ph-BPE System
2.2.2. Origin of Stereoselectivity
3. Models and Computational Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Riant, O.; Hannedouche, J. Asymmetric catalysis for the construction of quaternary carbon centres: Nucleophilic addition on ketones and ketimines. Org. Biomol. Chem. 2007, 5, 873–888. [Google Scholar] [CrossRef] [PubMed]
- Corey, E.J.; Guzman-Perez, A. The Catalytic Enantioselective Construction of Molecules with Quaternary Carbon Stereocenters. Angew. Chem. Int. Ed. 1998, 37, 388–401. [Google Scholar] [CrossRef]
- Fuji, K. Asymmetric Creation of Quaternary Carbon Centers. Chem. Rev. 1993, 93, 2037–2066. [Google Scholar] [CrossRef]
- Douglas, C.J.; Overman, L.E. Catalytic asymmetric synthesis of all-carbon quaternary stereocenters. Proc. Natl. Acad. Sci. USA 2004, 101, 5363–5367. [Google Scholar] [CrossRef] [PubMed]
- Abozeid, M.A.; Sairenji, S.; Takizawa, S.; Fujita, M.; Sasai, H. Enantioselective synthesis of tetrahydrocyclopenta [b]-indole bearing a chiral quaternary carbon center via Pd(II)–SPRIX-catalyzed C–H activation. Chem. Commun. 2017, 53, 6887–6890. [Google Scholar] [CrossRef] [PubMed]
- Ghorai, M.K.; Halder, S.; Das, S. ; Domino Michael-Michael and Aldol-Aldol Reactions: Diastereoselective Synthesis of Functionalized Cyclohexanone Derivatives Containing Quaternary Carbon Center. J. Org. Chem. 2015, 80, 9700–9712. [Google Scholar] [CrossRef] [PubMed]
- Yi, Y.; Lee, H.; Ho Jun, C. Rh(III)-catalyzed C–H activation reactions forming 1H-isoindoles containing a quaternary carbon center from aryl ketones or benzylamines. Chem. Commun. 2016, 52, 10171–10174. [Google Scholar] [CrossRef] [PubMed]
- Franckevičius, V. Palladium-catalyzed construction of quaternary carbon centers with propargylic electrophiles. Tetrahedron Lett. 2016, 57, 3586–3595. [Google Scholar] [CrossRef]
- Dosa, P.I.; Fu, G.C. Catalytic Asymmetric Addition of ZnPh2 to Ketones: Enantioselective Formation of Quaternary Stereocenters. J. Am. Chem. Soc. 1998, 120, 445–446. [Google Scholar] [CrossRef]
- Pályi, G.; Váradi, G.; Vizi-Orosz, A.; Markó, L. Reactivity of μ2-acetylenes coordinated to cobalt. Stereochemistry of the formation of butene-2-olide-4 complexes. J. Organomet. Chem. 1975, 90, 85–91. [Google Scholar] [CrossRef]
- Váradi, G.; Horváth, I.T.; Palágyi, J.; Bak, T.; Pályi, G. On the reactivity of acetylenes coordinated to cobalt IV. The influence of tertiary phosphorous compounds on the catalytic synthesis of bifurandiones. J. Mol. Catal. 1980, 9, 457–460. [Google Scholar] [CrossRef]
- Pályi, G.; Váradi, G.; Horváth, I.T. Activation of carbon monoxide and acetylenes by cobalt carbonyls. J. Mol. Catal. 1981, 13, 61–70. [Google Scholar] [CrossRef]
- Bán, I.M.; Révész, M.; Bálint, I.; Váradi, G.; Palyi, G. A CNDO/2 study of (μ2-actelyene) hexacarbonyl-dicobalt (CoCo) complexes. J. Mol. Struct. THEOCHEM 1982, 88, 357–370. [Google Scholar] [CrossRef]
- Happ, B.; Bartik, T.; Zucchi, C.; Rossi, M.C.; Ghelfi, F.; Palyi, G.; Varadi, G.; Szalontai, G.; Horvath, I.T.; Guastini, C. On the reactivity of acetylenes coordinated to cobalt. 9. Effects of substitution and coordination on the 13C-NMR chemical shifts of the sp Carbons of (μ2-R1C2R2) Co2(CO)6 Complexes. Molecular Structure of (μ2-PhC2SiPh3)Co2(CO)6. Organometallics 1995, 14, 809–819. [Google Scholar] [CrossRef]
- Kong, J.R.; Ngai, M.Y.; Krische, M.J. Highly Enantioselective Direct Reductive Coupling of Conjugated Alkynes and α-Ketoesters via Rhodium-Catalyzed Asymmetric Hydrogenation. J. Am. Chem. Soc. 2006, 128, 718–719. [Google Scholar] [CrossRef] [PubMed]
- Komanduri, V.; Krische, M.J. Enantioselective Reductive Coupling of 1,3-Enynes to Heterocyclic Aromatic Aldehydes and Ketones via Rhodium-Catalyzed Asymmetric Hydrogenation: Mechanistic Insight into the Role of Brønsted Acid Additives. J. Am. Chem. Soc. 2006, 128, 16448–16449. [Google Scholar] [CrossRef] [PubMed]
- Cozzi, P.G. Enantioselective Alkynylation of Ketones Catalyzed by Zn(Salen) Complexes. Angew. Chem. Int. Ed. 2003, 42, 2895–2898. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Chen, Z.; Tang, X. Highly Enantioselective Alkynylation of α-Keto Ester: An Efficient Method for Constructing a Chiral Tertiary Carbon Center. Org. Lett. 2002, 4, 3451–3453. [Google Scholar] [CrossRef] [PubMed]
- Pu, L. Asymmetric alkynylzinc additions to aldehydes and ketones. Tetrahedron 2003, 59, 9873–9886. [Google Scholar] [CrossRef]
- Cozzi, P.G.; Hilgraf, R.; Zimmermann, N. Acetylenes in Catalysis: Enantioselective Additions to Carbonyl Groups and Imines and Applications Beyond. Eur. J. Org. Chem. 2004, 4095–4105. [Google Scholar] [CrossRef]
- Lu, G.; Li, Y.M.; Li, X.S.; Chan, A.S.C. Synthesis and application of new chiral catalysts for asymmetric alkynylation reactions. Chem. Rev. 2005, 249, 1736–1744. [Google Scholar] [CrossRef]
- Langner, M.; Bolm, C. C1-Symmetric Sulfoximines as Ligands in Copper-Catalyzed Asymmetric Mukaiyama-Type Aldol Reactions. Angew. Chem. Int. Ed. 2004, 43, 5984–5987. [Google Scholar] [CrossRef] [PubMed]
- Langner, M.; Rémy, P.; Bolm, C. Highly Modular Synthesis of C1-Symmetric Aminosulfoximines and Their Use as Ligands in Copper-Catalyzed Asymmetric Mukaiyama-Aldol Reactions. Chem. Eur. J. 2005, 11, 6254–6255. [Google Scholar] [CrossRef] [PubMed]
- Oisaki, K.; Suto, Y.; Kanai, M.; Shibasaki, M. A New Method for the Catalytic Aldol Reaction to Ketones. J. Am. Chem. Soc. 2003, 125, 5644–5645. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.S.; Marek, I. Copper mediated carbometalation reactions. Chem. Soc. Rev. 2016, 45, 4552–4556. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Chiba, S. Copper-catalyzed oxidative carbon–heteroatom bond formation: A recent update. Chem. Soc. Rev. 2016, 45, 4504–4523. [Google Scholar] [CrossRef] [PubMed]
- Shibasaki, M.; Kanai, M. Asymmetric Synthesis of Tertiary Alcohols and α-Tertiary Amines via Cu-Catalyzed C-C Bond Formation to Ketones and Ketimines. Chem. Rev. 2008, 108, 2853–2873. [Google Scholar] [CrossRef] [PubMed]
- Thapa, S.; Shrestha, B.; Gurung, S.K.; Giri, R. Copper-catalysed cross-coupling: An untapped potential. Org. Biomol. Chem. 2015, 13, 4816–4827. [Google Scholar] [CrossRef] [PubMed]
- Maaliki, C.; Thiery, E.J. Thibonnet, Emergence of Copper-Mediated Formation of C–C Bonds. Eur. J. Org. Chem. 2017, 209–228. [Google Scholar] [CrossRef]
- Yoshikai, N.; Nakamura, E. Mechanisms of Nucleophilic Organocopper(I) Reactions. Chem. Rev. 2012, 112, 2339–2372. [Google Scholar] [CrossRef] [PubMed]
- Jumde, R.P.; Lanza, F.; Veenstra, M.J.; Harutyunyan, S.R. Catalytic asymmetric addition of Grignard reagents to alkenyl-substituted aromatic N-heterocycles. Science 2016, 352, 433–437. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Perry, I.B.; Buchwald, S.L. Copper-Catalyzed Enantioselective Addition of Styrene-Derived Nucleophiles to Imines Enabled by Ligand-Controlled Chemoselective Hydrocupration. J. Am. Chem. Soc. 2016, 138, 9787–9790. [Google Scholar] [CrossRef] [PubMed]
- Kubota, K.; Watanabe, Y.; Hayama, K.; Ito, H. Enantioselective Synthesis of Chiral Piperidines via the Stepwise Dearomatization/Borylation of Pyridines. J. Am. Chem. Soc. 2016, 138, 4338–4341. [Google Scholar] [CrossRef] [PubMed]
- Hojoh, K.; Ohmiya, H.; Sawamura, M. Synthesis of α-Quaternary Formimides and Aldehydes through Umpolung Asymmetric Copper Catalysis with Isocyanides. J. Am. Chem. Soc. 2017, 139, 2184–2187. [Google Scholar] [CrossRef] [PubMed]
- Wada, R.; Shibuguchi, T.; Makino, S.; Oisaki, K.; Kanai, M.; Shibasaki, M. Catalytic Enantioselective Allylation of Ketoimines. J. Am. Chem. Soc. 2006, 128, 7687–7691. [Google Scholar] [CrossRef] [PubMed]
- Oisaki, K.; Zhao, D.; Kanai, M.; Shibasaki, M. Catalytic Enantioselective Alkylative Aldol Reaction: Efficient Multicomponent Assembly of Dialkylzincs, Allenic Esters, and Ketones toward Highly Functionalized δ-Lactones with Tetrasubstituted Chiral Centers. J. Am. Chem. Soc. 2007, 129, 7439–7443. [Google Scholar] [CrossRef] [PubMed]
- Pulis, A.P.; Yeung, K.; Procter, D.J. Enantioselective copper catalysed, direct functionalisation of allenes via allyl copper intermediates. Chem. Sci. 2017, 8, 5240–5247. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Jang, H.; Jung, B.; Hoveyda, A.H. Cu-catalyzed Chemoselective Preparation of 2-(Pinacolato)boron Substituted Allylcopper Complexes and their In Stitu Site-, Diastereo-, and Enantioselective Additions to Aldehydes and Ketones. Angew. Chem. Int. Ed. 2013, 52, 5046–5051. [Google Scholar] [CrossRef] [PubMed]
- Kawai, J.; Chikkade, P.K.; Shimizu, Y.; Kanai, M. In situ Catalytic Generation of Allylcopper Species for Asymmetric Allylation: Toward 1H-Isochromene Skeletons. Angew. Chem. Int. Ed. 2013, 52, 7177–7180. [Google Scholar] [CrossRef] [PubMed]
- Jang, H.; Jung, B.; Hoveyda, A.H. Catalytic Enantioselective Protoboration of Disubstituted Allenes. Access to Alkenylboron Compounds in High Enantiomeric Purity. Org. Lett. 2014, 16, 4658–4661. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.F.; Xie, X.W.; Shimizu, Y.; Kanai, M. Copper(I)-Catalyzed Enantioselective Addition of Enynes to Ketones. J. Am. Chem. Soc. 2017, 139, 4647–4650. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, H.; Nagasaki, I.; Saito, K. Recent advances in biaryl-type bisphosphine ligands. Tetrahedron 2005, 61, 5405–5432. [Google Scholar] [CrossRef]
- Lipshutz, B.H.; Keith, J.; Papa, P.; Vivian, R. A convenient, efficient method for conjugate reductions using catalytic quantities of Cu(I). Tetrahedron Lett. 1998, 39, 4627–4630. [Google Scholar] [CrossRef]
- Lipshutz, B.H.; Frieman, B.A.; Tomaso, A.E., Jr. Copper-in-Charcoal (Cu/C): Heterogeneous, Copper-Catalyzed Asymmetric Hydrosilylations. Angew. Chem. 2006, 118, 1281–1286. [Google Scholar] [CrossRef]
- Lipshutz, B.H.; Frieman, B.A. CuH in a Bottle: A Convenient Reagent for Asymmetric Hydrosilylation, Angew. Chem. Int. Ed. 2005, 44, 6345–6348. [Google Scholar] [CrossRef] [PubMed]
- Lipshutz, B.H.; Papa, P. Copper-Catalyzed Reductive Alkylations of Enones: A Novel Transmetalation Protocol. Angew. Chem. 2002, 114, 4762–4764. [Google Scholar] [CrossRef]
- Lipshutz, B.H.; Servesko, J.M. CuH-Catalyzed Asymmetric Conjugate Reductions of Acyclic Enones. Angew. Chem. Int. Ed. 2003, 42, 4789–4792. [Google Scholar] [CrossRef] [PubMed]
- Lipshutz, B.H.; Servesko, J.M.; Petersen, T.B.; Papa, P.P.; Lover, A.A. Asymmetric 1,4-Reductions of Hindered â-Substituted Cycloalkenones Using Catalytic SEGPHOS−Ligated CuH. Org. Lett. 2004, 6, 1273–1275. [Google Scholar] [CrossRef] [PubMed]
- Lipshutz, B.H.; Tanaka, N.; Ta, B.R.; Lee, C.T. Chiral Silanes via Asymmetric Hydrosilylation with Catalytic CuH. Org. Lett. 2006, 8, 1963–1966. [Google Scholar] [CrossRef] [PubMed]
- Baker, B.A.; Bošković, Ž.V.; Lipshutz, B.H. (BDP) CuH: A “Hot” Stryker’s Reagent for Use in Achiral Conjugate Reductions. Org. Lett. 2008, 10, 289–292. [Google Scholar] [CrossRef] [PubMed]
- Gallagher, B.D.; Taft, B.R.; Lipshutz, B.H. Asymmetric Conjugate Reductions of Coumarins. A New Route to Tolterodine and Related Coumarin Derivatives. Org. Lett. 2009, 11, 5374–5377. [Google Scholar] [CrossRef] [PubMed]
- Lipshutz, B.H.; Servesko, J.M.; Taft, B.R. Asymmetric 1,4-Hydrosilylations of α,β-Unsaturated Esters. J. Am. Chem. Soc. 2004, 126, 8352–8353. [Google Scholar] [CrossRef] [PubMed]
- Moser, R.; Bošković, Ž.V.; Crowe, C.S.; Lipshutz, B.H. CuH-Catalyzed Enantioselective 1,2-Reductions of α,β-Unsaturated Ketones. J. Am. Chem. Soc. 2010, 132, 7852–7853. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Perry, I.B.; Lu, G.; Liu, P.; Buchwald, S.L. Copper-catalyzed asymmetric addition of olefin-derived nucleophiles to ketones. Science 2016, 353, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Lipshutz, B.H.; Chrisman, W.; Noson, K.; Papa, P.; Sclafani, J.A.; Vivian, R.W.; Keith, J.M. Copper Hydride-Catalyzed Tandem 1,4-Reduction/Alkylation Reactions. Tetrahedron 2000, 56, 2779–2788. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functional. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Zhao, Y.; Truhlar, D. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Bryantsev, V.S.; Diallo, M.S.; Duin, A.C.T.; Goddard, W.A., III. Evaluation of B3LYP, X3LYP, and M06-Class Density Functionals for Predicting the Binding Energies of Neutral, Protonated, and Deprotonated Water Clusters. J. Chem. Theory Comput. 2009, 5, 1016–1026. [Google Scholar] [CrossRef] [PubMed]
- Jacquemin, D.; Perpète, E.A.; Ciofini, I.; Adamo, C.; Valero, R.; Zhao, Y.; Truhlar, D.G. On the Performances of the M06 Family of Density Functionals for Electronic Excitation Energies. J. Chem. Theory Comput. 2010, 6, 2071–2085. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.L.; Xu, L.W.; Oisaki, K.; Kanai, M.; Shibasaki, M. Identification of Modular Chiral Bisphosphines Effective for Cu(I)-Catalyzed Asymmetric Allylation and Propargylation of Ketones. J. Am. Chem. Soc. 2010, 132, 6638–6639. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.Y.; Zhang, W.; He, L.; Luo, M.L.; Qin, S. Computational investigations on the phosphine-ligated CuH-catalyzed conjugate reduction of α-β unsaturated ketones: Regioselectivity and stereoselectivity. RSC Adv. 2014, 4, 5726–5733. [Google Scholar] [CrossRef]
- Zhang, W.; Li, W.Y.; Qin, S. Origins of enantioselectivity in the chiral diphosphine-ligated CuH-catalyzed asymmetric hydrosilylation of ketones. Org. Biomol. Chem. 2012, 10, 597–604. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Huber, S.M.; Gagliardi, L.; Cramer, C.C.; Tolman, W.B. Copper(I)-r-Ketocarboxylate Complexes: Characterization and O2 Reactions That Yield Copper-Oxygen Intermediates Capable of Hydroxylating Arenes. J. Am. Chem. Soc. 2007, 129, 14190–14192. [Google Scholar] [CrossRef] [PubMed]
- Bar-Nahum, I.; Gupta, A.K.; Huber, S.M.; Ertem, M.Z.; Cramer, C.J.; Tolman, W.B. Reduction of Nitrous Oxide to Dinitrogen by a Mixed Valent Tricopper-Disulfido Cluster. J. Am. Chem. Soc. 2009, 131, 2812–2814. [Google Scholar] [CrossRef] [PubMed]
- Cramer, C.J.; Gour, J.R.; Kinal, A.; Wloch, M.; Piecuch, P.; Moughal Shahi, A.R.; Gagliardi, L. Stereoelectronic Effects on Molecular Geometries and State-Energy Splittings of Ligated Monocopper Dioxygen Complexes. J. Phys. Chem. A. 2008, 112, 3754–3767. [Google Scholar] [CrossRef] [PubMed]
- Tabuchi, K.; Ertem, M.Z.; Sugimoto, H.; Kunishita, A.; Tano, T.; Fujieda, N.; Cramer, C.J.; Itoh, S. Reactions of Copper(II)-Phenol Systems with O2: Models for TPQ Biosynthesis in Copper Amine Oxidases. Inorg. Chem. 2011, 50, 1633–1647. [Google Scholar] [CrossRef] [PubMed]
- Kumsapaya, C.; Bobuatong, K.; Khongpracha, P.; Tantirungrotechai, Y.; Limtrakul, J. Mechanistic Investigation on 1,5- to 2,6-Dimethylnaphthalene Isomerization Catalyzed by Acidic β Zeolite: ONIOM Study with an M06-L Functional. J. Phys. Chem. C 2009, 113, 16128–16137. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Saielli, G. Differential Solvation Free Energies of Oxonium and Ammonium Ions: Insights from Quantum Chemical Calculations. J. Phys. Chem. A 2010, 114, 7261–7265. [Google Scholar] [CrossRef] [PubMed]
- Gusev, D.G. Assessing the Accuracy of M06-L Organometallic Thermochemistry. Organometallics 2013, 32, 4239–4243. [Google Scholar] [CrossRef]
- Chen, X.B.; Liu, Z.C.; Lin, X.R.; Huang, R.; Yan, S.J.; Lin, J. Highly Diastereoselective Convergent Synthesis of Polycyclic Pyrroles with Consecutive Quaternary Stereocenters: Cascade Construction of Multiple C–C and C–Hetero Bonds. ACS Sustain. Chem. Eng. 2014, 2, 2391–2398. [Google Scholar] [CrossRef]
- Ribeiro, R.F.; Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Prediction of SAMPL2 aqueous solvation free energies and tautomeric ratios using the SM8, SM8AD, and SMD solvation models. J. Comput. Aided Mater. 2010, 24, 317–333. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Performance of SM6, SM8, and SMD on the SAMPL1 Test Set for the Prediction of Small-Molecule Solvation Free Energies. J. Phys. Chem. B 2009, 113, 4538–4543. [Google Scholar] [CrossRef] [PubMed]
- Halim, M.A.; Shaw, D.M.; Poirier, R.A. Medium effect on the equilibrium geometries, vibrational frequencies and solvation energies of sulphanilamide. J. Mol. Struct. THEOCHEM. 2010, 960, 63–72. [Google Scholar] [CrossRef]
- Tran, A.T.; Liu, P.; Houk, K.N.; Nicholas, K.M. Regioselectivity in the Cu(I)-Catalyzed [4+2]-Cycloaddition of 2-Nitrosopyridine with Unsymmetrical Dienes. J. Org. Chem. 2014, 79, 5617–5626. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09; Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
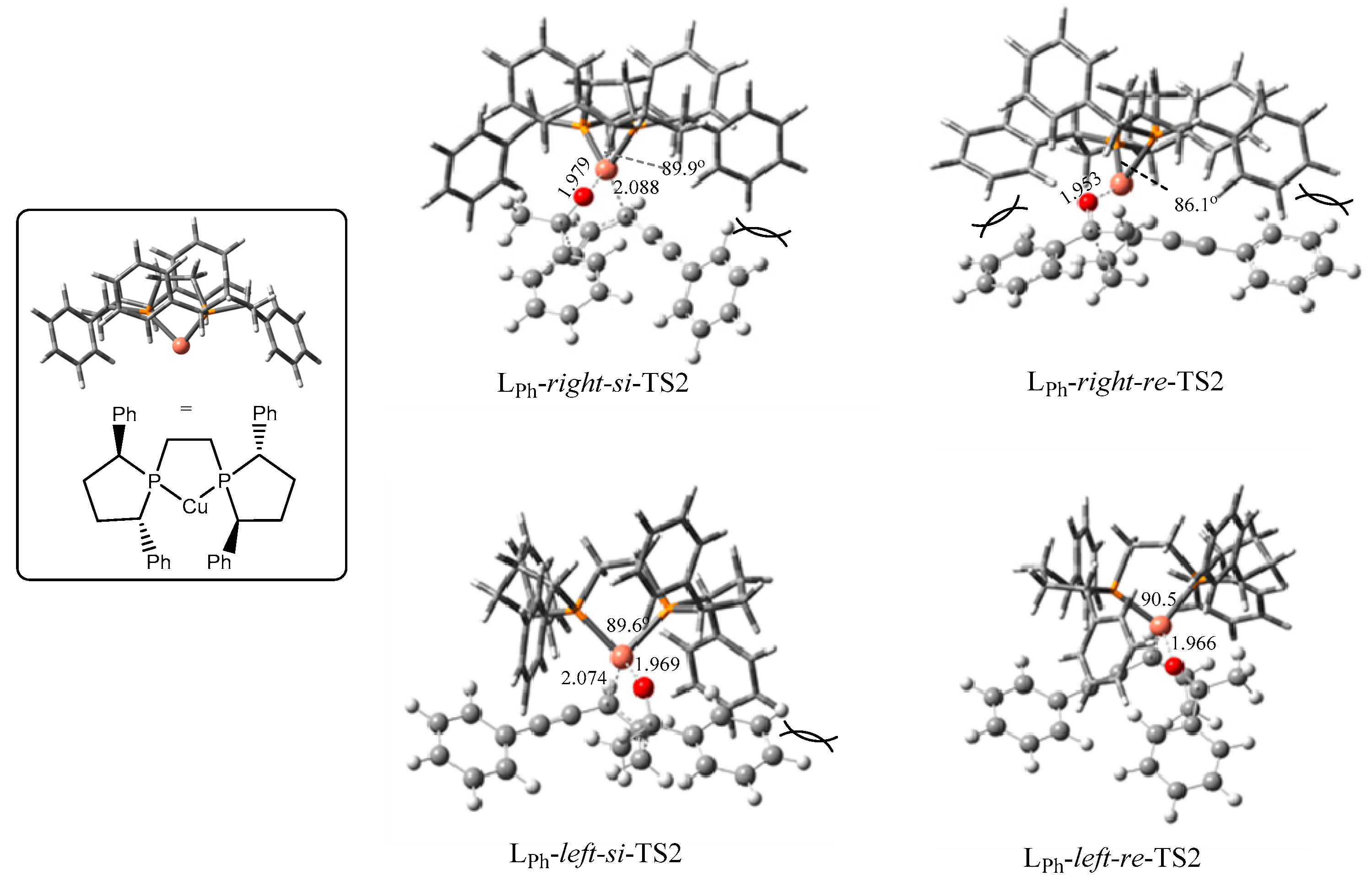
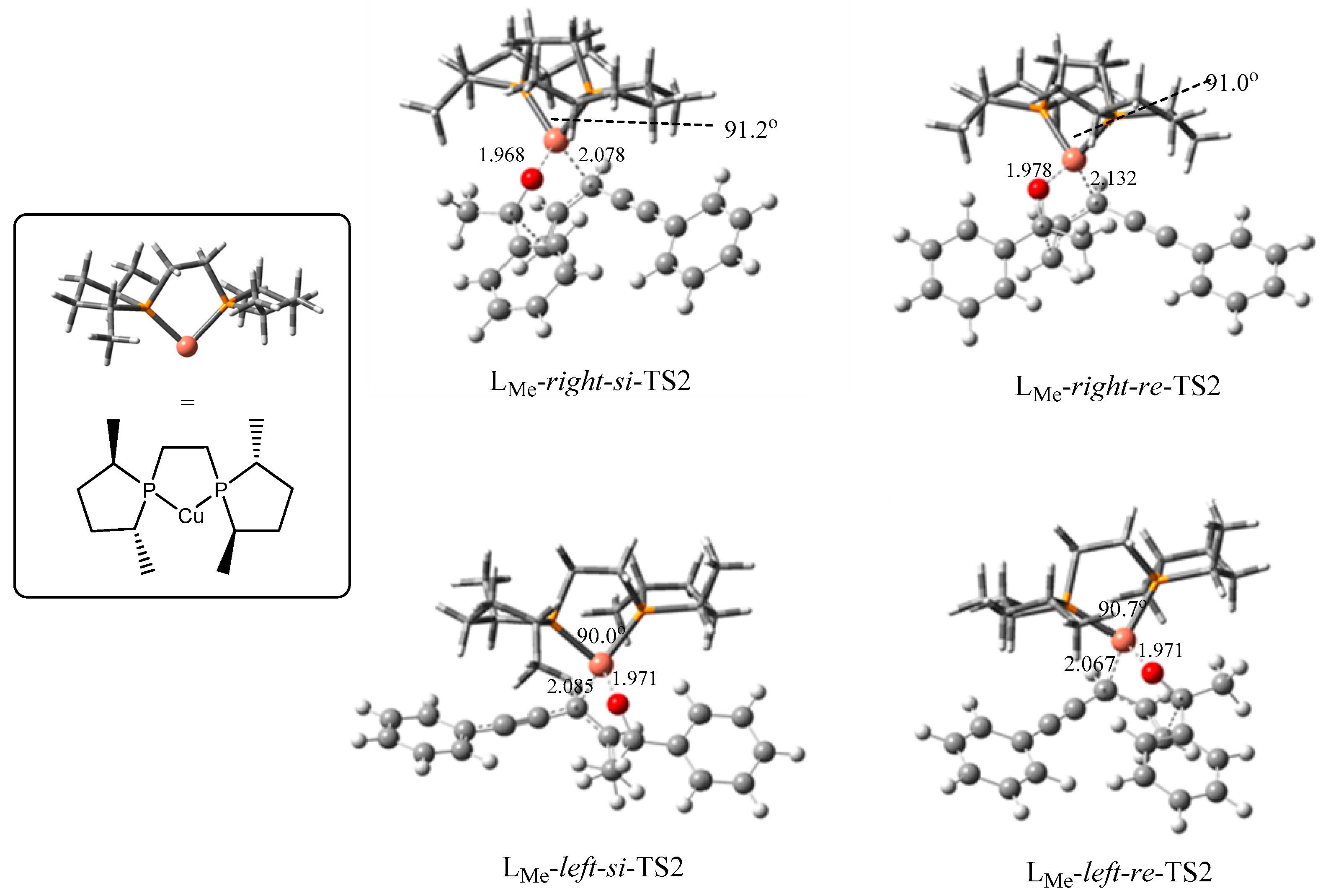
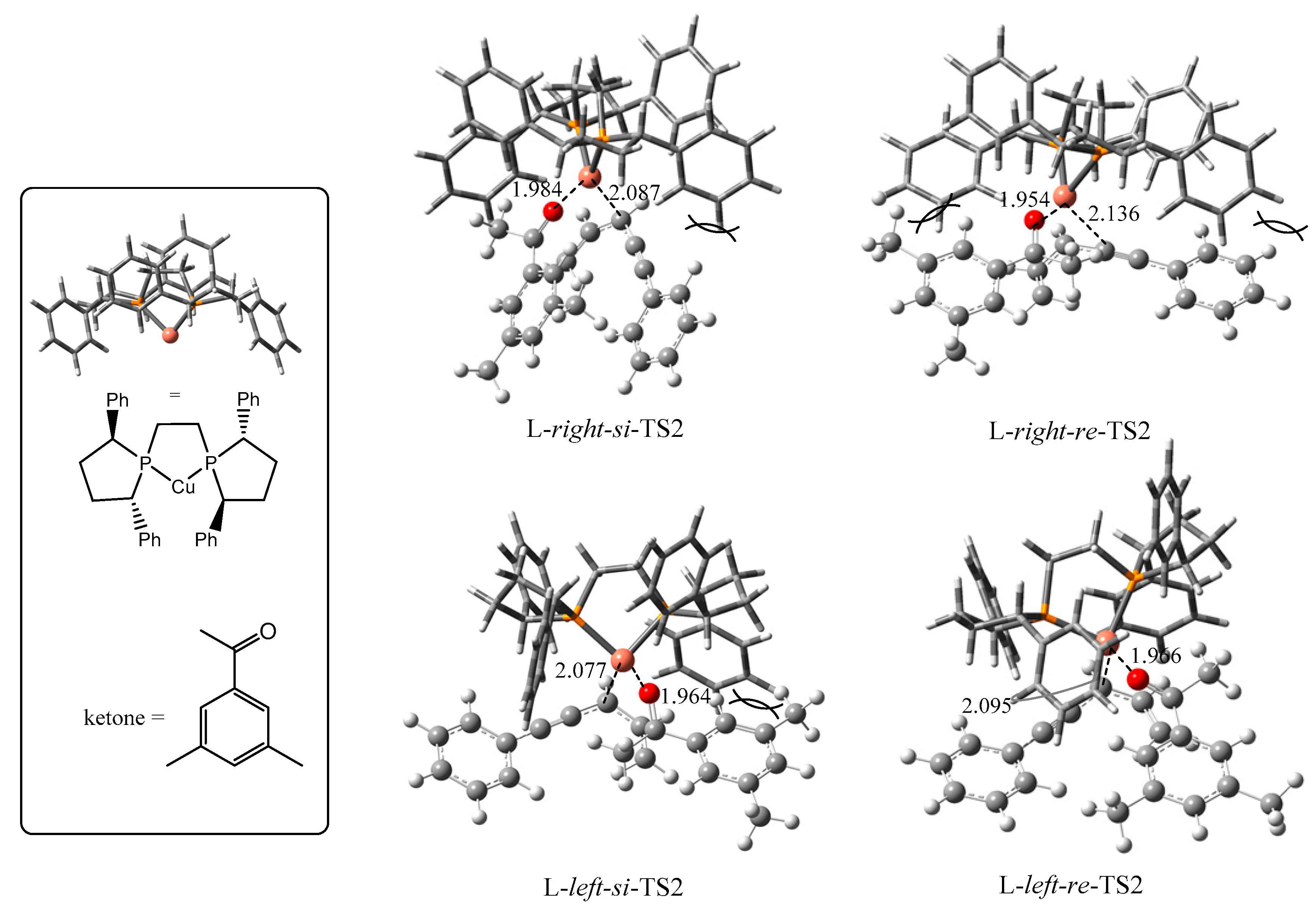
| TS2s | P-cu-p Angle | Configuration of Products | ΔG (kJ/mol) |
|---|---|---|---|
| LPh-right-si | 89.9° | S | 15.6 |
| LPh-right-re | 86.1° | R | 43.5 |
| LPh-left-si | 89.6° | S | 33.4 |
| LPh-left-re | 90.5° | R | 0.0 |
| TS2s | ΔGsolv-M06 | ΔGsolv-B3 | ΔGgas-M06 | ΔGgas-B3 |
|---|---|---|---|---|
| LPh-right-si | 15.6 | 16.3 | 6.2 | 12.0 |
| LPh-right-re | 43.5 | 30.8 | 26.9 | 25.4 |
| LPh-left-si | 33.4 | 23.2 | 19.4 | 21.1 |
| LPh-left-re | 0.0 | 0.0 | 0.0 | 0.0 |
| TS2s | P–Cu–P Angle | Configuration of Products | ΔGsolv (kJ/mol) |
|---|---|---|---|
| LMe-right-si | 91.2° | S | 0.0 |
| LMe-right-re | 91.0° | R | 13.3 |
| LMe-left-si | 90.0° | S | 17.3 |
| LMe-left-re | 90.7° | R | 0.7 |
| TS2s | P-Cu-P Angle | Configuration of Products | ΔGsolv (kJ/mol) |
|---|---|---|---|
| L-right-si | 90.0° | S | 13.8 |
| L-right-re | 84.9° | R | 39.1 |
| L-left-si | 90.1 | S | 32.8 |
| L-left-re | 90.2 | R | 0.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Luo, M.; Tao, G.; Qin, S. Theoretical Calculations on the Mechanism of Enantioselective Copper(I)-Catalyzed Addition of Enynes to Ketones. Catalysts 2018, 8, 359. https://doi.org/10.3390/catal8090359
Li H, Luo M, Tao G, Qin S. Theoretical Calculations on the Mechanism of Enantioselective Copper(I)-Catalyzed Addition of Enynes to Ketones. Catalysts. 2018; 8(9):359. https://doi.org/10.3390/catal8090359
Chicago/Turabian StyleLi, Hanwei, Mingliang Luo, Guohong Tao, and Song Qin. 2018. "Theoretical Calculations on the Mechanism of Enantioselective Copper(I)-Catalyzed Addition of Enynes to Ketones" Catalysts 8, no. 9: 359. https://doi.org/10.3390/catal8090359
APA StyleLi, H., Luo, M., Tao, G., & Qin, S. (2018). Theoretical Calculations on the Mechanism of Enantioselective Copper(I)-Catalyzed Addition of Enynes to Ketones. Catalysts, 8(9), 359. https://doi.org/10.3390/catal8090359