Kinetic Modeling of Catalytic Olefin Cracking and Methanol-to-Olefins (MTO) over Zeolites: A Review
Abstract
| 1 | Introduction | 3 | ||
| 2 | Theoretical Background | 5 | ||
| 2.1 | Thermodynamics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 5 | ||
| 2.2 | Kinetic Modeling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 8 | ||
| 2.3 | Zeolites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 12 | ||
| 2.4 | Reaction Mechanisms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 13 | ||
| 2.4.1 | Olefin Cracking . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 13 | ||
| 2.4.2 | Methanol-to-Olefins . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 14 | ||
| 3 | Kinetic models for Olefin Cracking | 16 | ||
| 3.1 | Studies Focusing on Olefin Interconversion over ZSM-5 . . . . . . . . . . . . . . . . . . . | 19 | ||
| 3.1.1 | Epelde et al.: Eight- and Five-Lump Approach for C Feeds at Elevated Partial Pressures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 19 | ||
| 3.1.2 | Ying et al.: Eight-Lump Model for Arbitrary Olefin Feeds Including Side Product Formation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 22 | ||
| 3.1.3 | Huang et al.: Six-Lump Approach for Arbitrary Olefin Feeds Including LH and HW Types of Mechanism . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 24 | ||
| 3.1.4 | Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 26 | ||
| 3.2 | Studies Focusing on Feed Olefin Consumption over ZSM-5 . . . . . . . . . . . . . . . . . | 27 | ||
| 3.2.1 | Borges et al.: Three-Lump Approach for Oligomerization of C to C Feed Olefins | 27 | ||
| 3.2.2 | Oliveira et al.: 17-Lump Model for C to C Feeds Considering Heterogeneity in Acid Sites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 28 | ||
| 3.2.3 | Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 30 | ||
| 3.3 | Microkinetic Study over ZSM-5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 30 | ||
| 3.3.1 | von Aretin et al.: Model for Arbitrary Olefin Feeds Considering all Interconversion Steps with Maximum Carbon Number of Twelve . . . . . . . . . | 30 | ||
| 3.3.2 | Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 32 | ||
| 3.4 | Study Elucidating the Peculiarities over SAPO-34 . . . . . . . . . . . . . . . . . . . . . . | 32 | ||
| 3.4.1 | Zhou et al.: Eight-Lump Model for C to C Feeds Considering Side Product Formation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 32 | ||
| 3.4.2 | Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 34 | ||
| 3.5 | Other Studies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 34 | ||
| 4 | Kinetic Models for Methanol-to-Olefins without Olefin Co-Feed | 35 | ||
| 4.1 | Studies with Lumped Oxygenates over ZSM-5 . . . . . . . . . . . . . . . . . . . . . . . . | 38 | ||
| 4.1.1 | Menges and Kraushaar-Czarnetzki: Six-Lump Approach Focusing on Lower Olefins Production . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 38 | ||
| 4.1.2 | Jiang et al.: Eight-Lump Model Including Side Product Formation . . . . . . . . | 39 | ||
| 4.1.3 | Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 41 | ||
| 4.2 | Studies with Differentiated Reactivity of Methanol and Dimethyl Ether over ZSM-5 . . | 41 | ||
| 4.2.1 | Gayubo et al.: Four-Lump Approach Analyzing the Inhibiting Effect of Water Adsorption . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 41 | ||
| 4.2.2 | Aguayo et al.: Seven-Lump Model for Significant Side Product Formation and Resulting Interconversion Reactions . . . . . . . . . . . . . . . . . . . . . . . . . . | 43 | ||
| 4.2.3 | Pérez-Uriarte et al.: Eleven-Lump Approach for Dimethyl Ether Feeds . . . . . . | 46 | ||
| 4.2.4 | Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 49 | ||
| 4.3 | Microkinetic Studies over ZSM-5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 49 | ||
| 4.3.1 | Park and Froment: Analysis of First C-C Bond Formation Mechanisms . . . . . . | 49 | ||
| 4.3.2 | Kumar et al.: Implementation of Aromatic Hydrocarbon Pool . . . . . . . . . . . | 51 | ||
| 4.3.3 | Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 52 | ||
| 4.4 | Studies with Significant Deactivation Effects over SAPO-34, SAPO-18 and ZSM-22 . . . | 52 | ||
| 4.4.1 | Gayubo et al.: Six- and Five-Lump Approach with and without Differentiation in Side Products over SAPO-34 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 52 | ||
| 4.4.2 | Ying et al.: Seven-Lump Model with Subsequent Fitting of Deactivation Parameters over SAPO-34 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 55 | ||
| 4.4.3 | Chen et al.: Seven-Lump Model with Simultaneous Fitting of Deactivation Parameters over SAPO-34 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 57 | ||
| 4.4.4 | Alwahabi and Froment: Microkinetic Implementation over SAPO-34 . . . . . . . | 59 | ||
| 4.4.5 | Gayubo et al.: Four- and Five-Lump Approach Including Deactivation Parameters over SAPO-18 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 59 | ||
| 4.4.6 | Kumar et al.: Microkinetic Implementation over ZSM-22 . . . . . . . . . . . . . . | 61 | ||
| 4.4.7 | Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 62 | ||
| 4.5 | Other Studies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 63 | ||
| 5 | Kinetic Models for Methanol-to-Olefins with Olefin Co-Feed | 63 | ||
| 5.1 | Huang et al.: Eight-Lump Approach Extending the Olefin Cracking Model to Methanol-to-Olefins . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 65 | ||
| 5.2 | Wen et al.: Ten-Lump Model Being Valid for ZSM-5 Powder and for ZSM-5 on Stainless Steel Fibers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 67 | ||
| 5.3 | Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 69 | ||
| 5.4 | Other Studies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 70 | ||
| 6 | Concluding Remarks and Outlook | 70 | ||
| References | 75 | |||
1. Introduction
2. Theoretical Background
2.1. Thermodynamics
2.2. Kinetic Modeling
2.3. Zeolites
2.4. Reaction Mechanisms
2.4.1. Olefin Cracking
2.4.2. Methanol-to-Olefins
3. Kinetic models for Olefin Cracking
3.1. Studies Focusing on Olefin Interconversion over ZSM-5
3.1.1. Epelde et al.: Eight- and Five-Lump Approach for C Feeds at Elevated Partial Pressures
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
3.1.2. Ying et al.: Eight-Lump Model for Arbitrary Olefin Feeds Including Side Product Formation
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
3.1.3. Huang et al.: Six-Lump Approach for Arbitrary Olefin Feeds Including LH and HW Types of Mechanism
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
3.1.4. Summary
3.2. Studies Focusing on Feed Olefin Consumption over ZSM-5
3.2.1. Borges et al.: Three-Lump Approach for Oligomerization of C to C Feed Olefins
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
3.2.2. Oliveira et al.: 17-Lump Model for C to C Feeds Considering Heterogeneity in Acid Sites
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
3.2.3. Summary
3.3. Microkinetic Study over ZSM-5
3.3.1. von Aretin et al.: Model for Arbitrary Olefin Feeds Considering all Interconversion Steps with Maximum Carbon Number of Twelve
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
3.3.2. Summary
3.4. Study Elucidating the Peculiarities over SAPO-34
3.4.1. Zhou et al.: Eight-Lump Model for C to C Feeds Considering Side Product Formation
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
3.4.2. Summary
3.5. Other Studies
4. Kinetic Models for Methanol-to-Olefins without Olefin Co-Feed
4.1. Studies with Lumped Oxygenates over ZSM-5
4.1.1. Menges and Kraushaar-Czarnetzki: Six-Lump Approach Focusing on Lower Olefins Production
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.1.2. Jiang et al.: Eight-Lump Model Including Side Product Formation
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.1.3. Summary
4.2. Studies with Differentiated Reactivity of Methanol and Dimethyl Ether over ZSM-5
4.2.1. Gayubo et al.: Four-Lump Approach Analyzing the Inhibiting Effect of Water Adsorption
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.2.2. Aguayo et al.: Seven-Lump Model for Significant Side Product Formation and Resulting Interconversion Reactions
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.2.3. Pérez-Uriarte et al.: Eleven-Lump Approach for Dimethyl Ether Feeds
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.2.4. Summary
4.3. Microkinetic Studies over ZSM-5
4.3.1. Park and Froment: Analysis of First C-C Bond Formation Mechanisms
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.3.2. Kumar et al.: Implementation of Aromatic Hydrocarbon Pool
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.3.3. Summary
4.4. Studies with Significant Deactivation Effects over SAPO-34, SAPO-18 and ZSM-22
4.4.1. Gayubo et al.: Six- and Five-Lump Approach with and without Differentiation in Side Products over SAPO-34
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.4.2. Ying et al.: Seven-Lump Model with Subsequent Fitting of Deactivation Parameters over SAPO-34
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.4.3. Chen et al.: Seven-Lump Model with Simultaneous Fitting of Deactivation Parameters over SAPO-34
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.4.4. Alwahabi and Froment: Microkinetic Implementation over SAPO-34
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.4.5. Gayubo et al.: Four- and Five-Lump Approach Including Deactivation Parameters over SAPO-18
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.4.6. Kumar et al.: Microkinetic Implementation over ZSM-22
Catalyst
Setup and Conditions
Reaction Network
Parameter Estimation
4.4.7. Summary
4.5. Other Studies
5. Kinetic Models for Methanol-to-Olefins with Olefin Co-Feed
5.1. Huang et al.: Eight-Lump Approach Extending the Olefin Cracking Model to Methanol-to-Olefins
5.1.1. Catalyst
5.1.2. Setup and Conditions
5.1.3. Reaction Network
5.1.4. Parameter Estimation
5.2. Wen et al.: Ten-Lump Model Being Valid for ZSM-5 Powder and for ZSM-5 on Stainless Steel Fibers
5.2.1. Catalyst
5.2.2. Setup and Conditions
5.2.3. Reaction Network
5.2.4. Parameter Estimation
5.3. Summary
5.4. Other Studies
6. Concluding Remarks and Outlook
6.1. General
- Reparameterization should be performed. The choice of reference temperature is not of highest importance; nevertheless, an optimum value can improve the model performance.
- Forward and backward reactions should be expressed as such and not be fitted independently. The equilibrium constant of the reaction can be extracted from thermodynamics to have less unknown parameters. However, when lumps consisting of several species are involved, the equilibrium constant should be estimated because the lump might deviate from an equilibrium distribution. Thermodynamic consistency has to be retained.
- Expressing the rate equations via partial pressures is advantageous as the influence of pressure changes is directly included. In contrast, when carbon based values are chosen, this effect might be ignored.
- Inclusion of adsorption effects, especially via the HW type of mechanism, should lead to a comparably robust model. The agreement with experimental data can still be satisfying when adsorption is ignored, especially when high partial pressures are applied. However, one should be aware that such a model tends to extrapolation errors when different feed compositions are chosen.
- Negative activation energies might occur when these apparent values contain adsorption effects. However, also in empirical models, positive adsorption enthalpies should be avoided because these are physically not reasonable and contradictory to thermodynamics. In such a case, other phenomena seem to impair the underlying model.
- When no microkinetic model is applied, interpretation about preferred reaction pathways should be avoided. The estimated parameters describe the reactivity in an empirical way, but the values are influenced by too many factors to allow mechanistic analyses. Nevertheless, effect of conditions on product distributions can be elucidated; for example, negative activation energies show that this pathway is less preferred at higher temperatures.
- Although high agreement can be achieved in any way, the stoichiometry within one reaction step should be retained to have a reasonable characterization of the reactivity. Moreover, when the concept of elementary reactions is chosen, this should be applied consistently. It can cause problems when the same lump appears both as reactant and as product within one step.
6.2. Olefin Cracking and MTO
- For hydrocarbon conversion, a maximum carbon number of seven seems to be sufficient, although the level of detail can be increased by exceeding this value. Nevertheless, some higher intermediates can be included in the network which crack down immediately, thus having no fitting answer. Furthermore, this recommended value also depends on the feed: when pure hexenes are applied, the dimerization to C has to be included.
- Lower olefins should not be summarized to one lump as their formation mechanisms and reactivity are different. The same holds for methanol and DME.
- Concerning ethene reactivity, reasonable results are obtained by assuming ethene both as reversibly and as irreversibly formed. However, the latter approach might be advantageous to reduce the number of estimated parameters.
- The complex interaction between zeolite and water is still not fully understood. Nevertheless, a useful approach is the inclusion of water as diluent and as competing adsorptive.
- Especially for MTO, the underlying chemistry is very complex through many different types of reactions. Consequently, it is difficult to describe the whole reactivity with one model. It is recommended to implement the types of reactions stepwise (e.g., first olefin interconversion, then methanol related reactions, and then side reactions) with individual experimental datasets. This reduces the number of unknown parameters in each fitting step and allows focusing on the respective type of reaction.
- Whenever MTO models for pure methanol feeds are created, one has to be aware that the unresolved initiation phase might influence the performance at low contact times which could impede the model. For such cases, it could be reasonable to simulate the product generation not from zero catalyst mass on. In contrast, this effect can be ignored for industrial MTP conditions where hydrocarbons are available from the beginning.
- For pure methanol feeds, an equilibrated state is reached comparably quickly because of the slow formation of the first C-C bond. However, when hydrocarbons are co-fed, this equilibrium among methanol, DME and water might not be reached.
- For MTO, it depends on the catalyst and the reaction conditions whether an implementation of the aromatic hydrocarbon pool is reasonable or not. If so, the underlying reactions have to be simplified to only some characteristic steps that are representative for the whole catalytic cycle.
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Preexponential factor, variable |
| a | Catalytic activity, - |
| Single-event preexponential factor, variable | |
| Concentration, mol m−3 | |
| Concentration of total Brønsted acid sites, | |
| Concentration of strong Brønsted acid sites, | |
| Heat capacity, K−1 | |
| Degree of freedom, - | |
| Particle diameter, m | |
| Activation energy, J mol−1 | |
| Molar flow rate, mol s−1 | |
| Fugacity, Pa | |
| Gibb’s free energy, J mol−1 | |
| Total Gibb’s free energy, | |
| Enthalpy, mol−1 | |
| h | Planck constant, J s |
| K | Equilibrium constant, variable |
| Single-event equilibrium constant, variable | |
| Boltzmann constant, J K−1 | |
| Rate constant, variable | |
| Single-event rate constant, variable | |
| Molar mass, kg mol−1 | |
| m | Type of reactant intermediate, - |
| Number of atoms of element , - | |
| Number of experiments, - | |
| Number of parameters, - | |
| Number of fitting responses, - | |
| n | Type of product intermediate, - |
| Number of single events, - | |
| Reaction order of water adsorption, - | |
| Number of moles, mol | |
| Deactivation order, - | |
| Deactivation order of water adsorption, - | |
| p | Pressure, Pa |
| R | Gas constant, J mol−1 K−1 |
| Surface methyl group | |
| Net rate of production, mol s−1 | |
| Reaction rate, variable | |
| Sum of squared residuals, - | |
| Entropy, J mol−1 K−1 | |
| T | Temperature, K |
| t | Time, s |
| W | Catalyst mass, |
| Mass fraction, - | |
| X | Conversion, - |
| Mole fraction, - | |
| Modeled mole fraction, - | |
| Greek letters | |
| Parameter for carbon number dependence, - | |
| Composed preexponential factor, variable | |
| Parameter for carbon number dependence, - | |
| Linearization parameter, - | |
| Parameter for carbon number dependence, - | |
| Parameter for carbon number dependence, - | |
| Difference, variable | |
| Parameter for carbon number dependence, - | |
| Linearization parameter, - | |
| Coverage, - | |
| Reaction order, - | |
| Chemical potential, J mol−1 | |
| Stoichiometric coefficient, - | |
| Parameter for carbon number dependence, - | |
| Deactivation parameter, - | |
| Weighting factor, - | |
| Subscripts | |
| ads | Adsorption |
| C | Carbon |
| cat | Catalyst |
| Element | |
| f | Formation |
| g | Gas phase |
| h | Running index for acid sites |
| i | Arbitrary species |
| j | Running index for arbitrary species |
| k | Running index for experiments |
| l | Reaction step |
| MW | Methanol and water |
| max | Maximum value |
| Ol | Olefin |
| Ox | Oxygenates |
| r | Reaction |
| t | Total |
| ‡ | Transition state |
| Superscripts | |
| ads | Adsorption |
| ar | Aromatization |
| chem | Chemisorption |
| co | Composite value |
| cr | Cracking |
| d | Deactivation |
| dim | Dimerization |
| in | Inlet value |
| MF | Metal fiber |
| PO | Powder |
| RDS | Rate-determining step |
| ref | Reference |
| TD | Thermodynamic |
| complex | |
| ∘ | Standard condition ( = 1 × 105 Pa) |
Abbreviations
| Ads. | Adsorption |
| AEI | Framework code of SAPO-18 |
| BAS | Brønsted acid sites |
| BET | Brunauer–Emmett–Teller |
| Paraffin with carbon number i | |
| n-Paraffin with carbon number i | |
| C | Olefin with carbon number i |
| C | Aliphatic compound with carbon number i |
| C | Aromatic compound with carbon number i |
| C | Hydrocarbon with carbon number i |
| C | Side products with carbon number i |
| C | Protonated intermediate |
| CHA | Framework code of chabazite |
| DFT | Density functional theory |
| DME | Dimethyl ether |
| DSC | Differential scanning calorimetry |
| ER | Eley–Rideal |
| FCC | Fluid catalytic cracking |
| FID | Flame ionization detector |
| GA | Genetic algorithm |
| GC | Gas chromatograph |
| GC-FTIR | Gas chromatograph with Fourier transform infrared |
| GC-MS | Gas chromatograph with mass spectrometer |
| HF | Hartree–Fock |
| HW | Hougen–Watson |
| Int | Intermediates |
| IR | Infrared |
| LAS | Lewis acid sites |
| L | Langmuir |
| LH | Langmuir–Hinshelwood |
| Mech. | Mechanistical scheme |
| MFI | Framework code of ZSM-5 |
| MTG | Methanol-to-gasoline |
| MTH | Methanol-to-hydrocarbons |
| MTO | Methanol-to-olefins |
| MTT | Framework code of ZSM-22 |
| OM | Oxonium methylide |
| Ox | Oxygenates (methanol and DME) |
| PCP | Protonated cyclopropane |
| PSSA | Pseudo-steady state approximation |
| SBU | Secondary building unit |
| SBAS | Strong Brønsted acid sites |
| Side prod. | Side products |
| TCD | Thermal conductivity detector |
| TG | Thermogravimetry |
| TOS | Time-on-stream |
| XRD | X-ray diffraction |
References
- Ren, T.; Patel, M.K.; Blok, K. Steam Cracking and Methane to Olefins: Energy Use, CO2 Emissions and Production Costs. Energy 2008, 33, 817–833. [Google Scholar] [CrossRef]
- Plotkin, J.S. The Propylene Gap: How Can It Be Filled? 2015. Available online: https://www.acs.org/content/acs/en/pressroom/cutting-edge-chemistry/the-propylene-gap-how-can-it-be-filled.html (accessed on 29 October 2018).
- Blay, V.; Epelde, E.; Miravalles, R.; Perea, L.A. Converting Olefins to Propene: Ethene to Propene and Olefin Cracking. Catal. Rev. Sci. Eng. 2018, 60, 278–335. [Google Scholar] [CrossRef]
- Ren, T.; Patel, M.K.; Blok, K. Olefins from Conventional and Heavy Feedstocks: Energy Use in Steam Cracking and Alternative Processes. Energy 2006, 31, 425–451. [Google Scholar] [CrossRef]
- Neelis, M.; Patel, M.K.; Blok, K.; Haije, W.; Bach, P. Approximation of Theoretical Energy-Saving Potentials for the Petrochemical Industry using Energy Balances for 68 Key Processes. Energy 2007, 32, 1104–1123. [Google Scholar] [CrossRef]
- Centi, G.; Iaquaniello, G.; Perathoner, S. Can We Afford to Waste Carbon Dioxide? Carbon Dioxide as a Valuable Source of Carbon for the Production of Light Olefins. ChemSusChem 2011, 4, 1265–1273. [Google Scholar] [CrossRef] [PubMed]
- Torres Galvis, H.M.; de Jong, K.P. Catalysts for Production of Lower Olefins from Synthesis Gas: A Review. ACS Catal. 2013, 3, 2130–2149. [Google Scholar] [CrossRef]
- Mokrani, T.; Scurrell, M. Gas Conversion to Liquid Fuels and Chemicals: The Methanol Route–Catalysis and Processes Development. Catal. Rev. Sci. Eng. 2009, 51, 1–145. [Google Scholar] [CrossRef]
- Rahimi, N.; Karimzadeh, R. Catalytic Cracking of Hydrocarbons over Modified ZSM-5 Zeolites to Produce Light Olefins: A Review. Appl. Catal. A 2011, 398, 1–17. [Google Scholar] [CrossRef]
- Nesterenko, N.; Aguilhon, J.; Bodart, P.; Minoux, D.; Dath, J.P. Methanol to Olefins: An Insight into Reaction Pathways and Products Formation. In Zeolites and Zeolite-Like Materials; Sels, B.F., Kustov, L.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 189–263. [Google Scholar] [CrossRef]
- Olsbye, U.; Svelle, S.; Bjørgen, M.; Beato, P.; Janssens, T.V.W.; Joensen, F.; Bordiga, S.; Lillerud, K.P. Conversion of Methanol to Hydrocarbons: How Zeolite Cavity and Pore Size Controls Product Selectivity. Angew. Chem. Int. Ed. 2012, 51, 5810–5831. [Google Scholar] [CrossRef]
- Balcar, H.; Čejka, J. Mesoporous Molecular Sieves as Advanced Supports for Olefin Metathesis Catalysts. Coord. Chem. Rev. 2013, 257, 3107–3124. [Google Scholar] [CrossRef]
- Gholampour, N.; Yusubov, M.; Verpoort, F. Investigation of the Preparation and Catalytic Activity of Supported Mo, W, and Re Oxides as Heterogeneous Catalysts in Olefin Metathesis. Catal. Rev. Sci. Eng. 2016, 58, 113–156. [Google Scholar] [CrossRef]
- Sattler, J.J.H.B.; Ruiz-Martínez, J.; Santillan-Jimenez, E.; Weckhuysen, B.M. Catalytic Dehydrogenation of Light Alkanes on Metals and Metal Oxides. Chem. Rev. 2014, 114, 10613–10653. [Google Scholar] [CrossRef] [PubMed]
- Nawaz, Z. Light Alkane Dehydrogenation to Light Olefin Technologies: A Comprehensive Review. Rev. Chem. Eng. 2015, 31, 413–436. [Google Scholar] [CrossRef]
- Carrero, C.A.; Schlögl, R.; Wachs, I.E.; Schomäcker, R. Critical Literature Review of the Kinetics for the Oxidative Dehydrogenation of Propane over Well-Defined Supported Vanadium Oxide Catalysts. ACS Catal. 2014, 4, 3357–3380. [Google Scholar] [CrossRef]
- Ghashghaee, M. Heterogeneous Catalysts for Gas-Phase Conversion of Ethylene to Higher Olefins. Rev. Chem. Eng. 2018, 34, 595–655. [Google Scholar] [CrossRef]
- Dumesic, J.A.; Rudd, D.F.; Aparicio, L.M.; Rekoske, J.E.; Treviño, A.A. The Microkinetics of Heterogeneous Catalysis; ACS Professional Reference Book; American Chemical Society: Washington, DC, USA, 1993. [Google Scholar]
- Kumar, P.; Thybaut, J.W.; Svelle, S.; Olsbye, U.; Marin, G.B. Single-Event Microkinetics for Methanol to Olefins on H-ZSM-5. Ind. Eng. Chem. Res. 2013, 52, 1491–1507. [Google Scholar] [CrossRef]
- Vynckier, E.; Froment, G.F. Modeling of the Kinetics of Complex Processes based upon Elementary Steps. In Kinetic and Thermodynamic Lumping of Multicomponent Mixtures; Astarita, G., Sandler, S.I., Eds.; Elsevier: Amsterdam, The Netherlands, 1991; pp. 131–161. [Google Scholar]
- Thybaut, J.W.; Marin, G.B. Single-Event MicroKinetics: Catalyst Design for Complex Reaction Networks. J. Catal. 2013, 308, 352–362. [Google Scholar] [CrossRef]
- Khadzhiev, S.N.; Magomedova, M.V.; Peresypkina, E.G. Kinetic Models of Methanol and Dimethyl Ether Conversion to Olefins over Zeolite Catalysts (Review). Pet. Chem. 2015, 55, 503–521. [Google Scholar] [CrossRef]
- Keil, F.J. Methanol-to-Hydrocarbons: Process Technology. Microporous Mesoporous Mater. 1999, 29, 49–66. [Google Scholar] [CrossRef]
- Chen, N.Y.; Reagan, W.J. Evidence of Autocatalysis in Methanol to Hydrocarbon Reactions over Zeolite Catalysts. J. Catal. 1979, 59, 123–129. [Google Scholar] [CrossRef]
- Chang, C.D. A Kinetic Model for Methanol Conversion to Hydrocarbons. Chem. Eng. Sci. 1980, 35, 619–622. [Google Scholar] [CrossRef]
- Ono, Y.; Mori, T. Mechanism of Methanol Conversion into Hydrocarbons over ZSM-5 Zeolite. J. Chem. Soc. Faraday Trans. 1 1981, 77, 2209–2221. [Google Scholar] [CrossRef]
- Mihail, R.; Straja, S.; Maria, G.; Musca, G.; Pop, G. Kinetic Model for Methanol Conversion to Olefins. Ind. Eng. Chem. Process Des. Dev. 1983, 22, 532–538. [Google Scholar] [CrossRef]
- Mihail, R.; Straja, S.; Maria, G.; Musca, G.; Pop, G. A Kinetic Model for Methanol Conversion to Hydrocarbons. Chem. Eng. Sci. 1983, 38, 1581–1591. [Google Scholar] [CrossRef]
- Schipper, P.H.; Krambeck, F.J. A Reactor Design Simulation with Reversible and Irreversible Catalyst Deactivation. Chem. Eng. Sci. 1986, 41, 1013–1019. [Google Scholar] [CrossRef]
- Sedrán, U.A.; Mahay, A.; de Lasa, H.I. Modelling Methanol Conversion to Hydrocarbons: Revision and Testing of a Simple Kinetic Model. Chem. Eng. J. 1990, 45, 1161–1165. [Google Scholar] [CrossRef]
- Sedrán, U.A.; Mahay, A.; de Lasa, H.I. Modelling Methanol Conversion to Hydrocarbons: Alternative Kinetic Models. Chem. Eng. J. 1990, 45, 33–42. [Google Scholar] [CrossRef]
- Schönfelder, H.; Hinderer, J.; Werther, J.; Keil, F.J. Methanol to Olefins-Prediction of the Performance of a Circulating Fluidized-Bed Reactor on the Basis of Kinetic Experiments in a Fixed-Bed Reactor. Chem. Eng. Sci. 1994, 49, 5377–5390. [Google Scholar] [CrossRef]
- Bos, R.; Tromp, P.J.; Akse, H.N. Conversion of Methanol to Lower Olefins. Kinetic Modeling, Reactor Simulation, and Selection. Ind. Eng. Chem. Res. 1995, 34, 3808–3816. [Google Scholar] [CrossRef]
- Gayubo, A.G.; Benito, P.L.; Aguayo, A.T.; Aguirre, I.; Bilbao, J. Analysis of Kinetic Models of the Methanol-to-Gasoline (MTG) Process in an Integral Reactor. Chem. Eng. J. 1996, 63, 45–51. [Google Scholar] [CrossRef]
- Van Speybroeck, V.; Hemelsoet, K.; Joos, L.; Waroquier, M.; Bell, R.G.; Catlow, R.A. Advances in Theory and Their Application within the Field of Zeolite Chemistry. Chem. Soc. Rev. 2015, 44, 7044–7111. [Google Scholar] [CrossRef]
- Van Speybroeck, V.; de Wispelaere, K.; van der Mynsbrugge, J.; Vandichel, M.; Hemelsoet, K.; Waroquier, M. First Principle Chemical Kinetics in Zeolites: The Methanol-to-Olefin Process as a Case Study. Chem. Soc Rev. 2014, 43, 7326–7357. [Google Scholar] [CrossRef]
- Hemelsoet, K.; van der Mynsbrugge, J.; de Wispelaere, K.; Waroquier, M.; van Speybroeck, V. Unraveling the Reaction Mechanisms Governing Methanol-to-Olefins Catalysis by Theory and Experiment. ChemPhysChem 2013, 14, 1526–1545. [Google Scholar] [CrossRef]
- De Wispelaere, K.; Ensing, B.; Ghysels, A.; Meijer, E.J.; van Speybroeck, V. Complex Reaction Environments and Competing Reaction Mechanisms in Zeolite Catalysis: Insights from Advanced Molecular Dynamics. Chem. Eur. J. 2015, 21, 9385–9396. [Google Scholar] [CrossRef]
- De Wispelaere, K.; Wondergem, C.S.; Ensing, B.; Hemelsoet, K.; Meijer, E.J.; Weckhuysen, B.M.; van Speybroeck, V.; Ruiz-Martínez, J. Insight into the Effect of Water on the Methanol-to-Olefins Conversion in H-SAPO-34 from Molecular Simulations and in Situ Microspectroscopy. ACS Catal. 2016, 6, 1991–2002. [Google Scholar] [CrossRef]
- Moors, S.L.; de Wispelaere, K.; van der Mynsbrugge, J.; Waroquier, M.; van Speybroeck, V. Molecular Dynamics Kinetic Study on the Zeolite-Catalyzed Benzene Methylation in ZSM-5. ACS Catal. 2013, 3, 2556–2567. [Google Scholar] [CrossRef]
- Van der Mynsbrugge, J.; de Ridder, J.; Hemelsoet, K.; Waroquier, M.; van Speybroeck, V. Enthalpy and Entropy Barriers Explain the Effects of Topology on the Kinetics of Zeolite-Catalyzed Reactions. Chem. Eur. J. 2013, 19, 11568–11576. [Google Scholar] [CrossRef]
- Van Speybroeck, V.; van der Mynsbrugge, J.; Vandichel, M.; Hemelsoet, K.; Lesthaeghe, D.; Ghysels, A.; Marin, G.B.; Waroquier, M. First Principle Kinetic Studies of Zeolite-Catalyzed Methylation Reactions. J. Am. Chem. Soc. 2011, 133, 888–899. [Google Scholar] [CrossRef]
- Van der Mynsbrugge, J.; Moors, S.L.; de Wispelaere, K.; van Speybroeck, V. Insight into the Formation and Reactivity of Framework-Bound Methoxide Species in H-ZSM-5 from Static and Dynamic Molecular Simulations. ChemCatChem 2014, 6, 1906–1918. [Google Scholar] [CrossRef]
- Lesthaeghe, D.; van der Mynsbrugge, J.; Vandichel, M.; Waroquier, M.; van Speybroeck, V. Full Theoretical Cycle for both Ethene and Propene Formation during Methanol-to-Olefin Conversion in H-ZSM-5. ChemCatChem 2011, 3, 208–212. [Google Scholar] [CrossRef]
- Yarulina, I.; de Wispelaere, K.; Bailleul, S.; Goetze, J.; Radersma, M.; Abou-Hamad, E.; Vollmer, I.; Goesten, M.; Mezari, B.; Hensen, E.J.; et al. Structure-Performance Descriptors and the Role of Lewis Acidity in the Methanol-to-Propylene Process. Nat. Chem. 2018, 10, 804–812. [Google Scholar] [CrossRef]
- Van der Mynsbrugge, J.; Janda, A.; Lin, L.C.; van Speybroeck, V.; Head-Gordon, M.; Bell, A.T. Understanding Brønsted-Acid Catalyzed Monomolecular Reactions of Alkanes in Zeolite Pores by Combining Insights from Experiment and Theory. ChemPhysChem 2018, 19, 341–358. [Google Scholar] [CrossRef]
- Van der Mynsbrugge, J.; Janda, A.; Mallikarjun Sharada, S.; Lin, L.C.; van Speybroeck, V.; Head-Gordon, M.; Bell, A.T. Theoretical Analysis of the Influence of Pore Geometry on Monomolecular Cracking and Dehydrogenation of n-Butane in Brønsted Acidic Zeolites. ACS Catal. 2017, 7, 2685–2697. [Google Scholar] [CrossRef]
- Cnudde, P.; de Wispelaere, K.; Vanduyfhuys, L.; Demuynck, R.; van der Mynsbrugge, J.; Waroquier, M.; van Speybroeck, V. How Chain Length and Branching Influence the Alkene Cracking Reactivity on H-ZSM-5. ACS Catal. 2018, 8, 9579–9595. [Google Scholar] [CrossRef]
- Cnudde, P.; de Wispelaere, K.; van der Mynsbrugge, J.; Waroquier, M.; van Speybroeck, V. Effect of Temperature and Branching on the Nature and Stability of Alkene Cracking Intermediates in H-ZSM-5. J. Catal. 2017, 345, 53–69. [Google Scholar] [CrossRef]
- Hajek, J.; van der Mynsbrugge, J.; de Wispelaere, K.; Cnudde, P.; Vanduyfhuys, L.; Waroquier, M.; van Speybroeck, V. On the Stability and Nature of Adsorbed Pentene in Brønsted Acid Zeolite H-ZSM-5 at 323 K. J. Catal. 2016, 340, 227–235. [Google Scholar] [CrossRef]
- Martens, G.G.; Marin, G.B.; Martens, J.A.; Jacobs, P.A.; Baron, G.V. A Fundamental Kinetic Model for Hydrocracking of C8 to C12 Alkanes on Pt/US-Y Zeolites. J. Catal. 2000, 195, 253–267. [Google Scholar] [CrossRef]
- Martens, G.G.; Marin, G.B. Kinetics for Hydrocracking Based on Structural Classes: Model Development and Applications. AIChE J. 2001, 47, 1607–1622. [Google Scholar] [CrossRef]
- Martens, G.G.; Thybaut, J.W.; Marin, G.B. Single-Event Rate Parameters for the Hydrocracking of Cycloalkanes on Pt/US-Y Zeolites. Ind. Eng. Chem. Res. 2001, 40, 1832–1844. [Google Scholar] [CrossRef]
- Thybaut, J.W.; Marin, G.B.; Baron, G.V.; Jacobs, P.A.; Martens, J.A. Alkene Protonation Enthalpy Determination from Fundamental Kinetic Modeling of Alkane Hydroconversion on Pt/H-(US)Y-Zeolite. J. Catal. 2001, 202, 324–339. [Google Scholar] [CrossRef]
- Narasimhan, C.S.L.; Thybaut, J.W.; Marin, G.B.; Jacobs, P.A.; Martens, J.A.; Denayer, J.F.; Baron, G.V. Kinetic Modeling of Pore Mouth Catalysis in the Hydroconversion of n-Octane on Pt-H-ZSM-22. J. Catal. 2003, 220, 399–413. [Google Scholar] [CrossRef]
- Thybaut, J.W.; Narasimhan, C.S.L.; Denayer, J.F.; Baron, G.V.; Jacobs, P.A.; Martens, J.A.; Marin, G.B. Acid-Metal Balance of a Hydrocracking Catalyst: Ideal versus Nonideal Behavior. Ind. Eng. Chem. Res. 2005, 44, 5159–5169. [Google Scholar] [CrossRef]
- Narasimhan, C.S.L.; Thybaut, J.W.; Martens, J.A.; Jacobs, P.A.; Denayer, J.F.; Marin, G.B. A Unified Single-Event Microkinetic Model for Alkane Hydroconversion in Different Aggregation States on Pt/H-USY-Zeolites. J. Phys. Chem. B 2006, 110, 6750–6758. [Google Scholar] [CrossRef]
- Quintana-Solórzano, R.; Thybaut, J.W.; Marin, G.B. Catalytic Cracking and Coking of (Cyclo)Alkane/1-Octene Mixtures on an Equilibrium Catalyst. Appl. Catal. A 2006, 314, 184–199. [Google Scholar] [CrossRef]
- Thybaut, J.W.; Choudhury, I.R.; Denayer, J.F.; Baron, G.V.; Jacobs, P.A.; Martens, J.A.; Marin, G.B. Design of Optimum Zeolite Pore System for Central Hydrocracking of Long-Chain n-Alkanes based on a Single-Event Microkinetic Model. Top. Catal. 2009, 52, 1251–1260. [Google Scholar] [CrossRef]
- Choudhury, I.R.; Hayasaka, K.; Thybaut, J.W.; Narasimhan, C.S.L.; Denayer, J.F.; Martens, J.A.; Marin, G.B. Pt/H-ZSM-22 Hydroisomerization Catalysts Optimization Guided by Single-Event Microkinetic Modeling. J. Catal. 2012, 290, 165–176. [Google Scholar] [CrossRef]
- Vandegehuchte, B.D.; Choudhury, I.R.; Thybaut, J.W.; Martens, J.A.; Marin, G.B. Integrated Stefan-Maxwell, Mean Field, and Single-Event Microkinetic Methodology for Simultaneous Diffusion and Reaction inside Microporous Materials. J. Phys. Chem. C 2014, 118, 22053–22068. [Google Scholar] [CrossRef]
- Vandegehuchte, B.D.; Thybaut, J.W.; Marin, G.B. Unraveling Diffusion and Other Shape Selectivity Effects in ZSM5 Using n-Hexane Hydroconversion Single-Event Microkinetics. Ind. Eng. Chem. Res. 2014, 53, 15333–15347. [Google Scholar] [CrossRef]
- Toch, K.; Thybaut, J.W.; Marin, G.B. A Systematic Methodology for Kinetic Modeling of Chemical Reactions Applied to n-Hexane Hydroisomerization. AIChE J. 2015, 61, 880–892. [Google Scholar] [CrossRef]
- Thybaut, J.W.; Marin, G.B. Multiscale Aspects in Hydrocracking: From Reaction Mechanism Over Catalysts to Kinetics and Industrial Application. In Advances in Catalysis; Song, C., Ed.; Academic Press: Cambridge, MA, USA, 2016; Volume 59, pp. 109–238. [Google Scholar] [CrossRef]
- Surla, K.; Vleeming, H.; Guillaume, D.; Galtier, P. A Single Events Kinetic Model: n-Butane Isomerization. Chem. Eng. Sci. 2004, 59, 4773–4779. [Google Scholar] [CrossRef]
- Valéry, E.; Guillaume, D.; Surla, K.; Galtier, P.; Verstraete, J.; Schweich, D. Kinetic Modeling of Acid Catalyzed Hydrocracking of Heavy Molecules: Application to Squalane. Ind. Eng. Chem. Res. 2007, 46, 4755–4763. [Google Scholar] [CrossRef]
- Mitsios, M.; Guillaume, D.; Galtier, P.; Schweich, D. Single-Event Microkinetic Model for Long-Chain Paraffin Hydrocracking and Hydroisomerization on an Amorphous Pt/SiO2·Al2O3 Catalyst. Ind. Eng. Chem. Res. 2009, 48, 3284–3292. [Google Scholar] [CrossRef]
- Becker, P.J.; Serrand, N.; Celse, B.; Guillaume, D.; Dulot, H. A Single Events Microkinetic Model for Hydrocracking of Vacuum Gas Oil. Comput. Chem. Eng. 2017, 98, 70–79. [Google Scholar] [CrossRef]
- Pellegrini, L.; Locatelli, S.; Rasella, S.; Bonomi, S.; Calemma, V. Modeling of Fischer–Tropsch Products Hydrocracking. Chem. Eng. Sci. 2004, 59, 4781–4787. [Google Scholar] [CrossRef]
- Becker, P.J.; Celse, B.; Guillaume, D.; Dulot, H.; Becker, P.J. Hydrotreatment Modeling for a Variety of VGO Feedstocks: A Continuous Lumping Approach. Fuel 2015, 139, 133–143. [Google Scholar] [CrossRef]
- Becker, P.J.; Celse, B.; Guillaume, D.; Costa, V.; Bertier, L.; Guillon, E.; Pirngruber, G. A Continuous Lumping Model for Hydrocracking on a Zeolite Catalysts: Model Development and Parameter Identification. Fuel 2016, 164, 73–82. [Google Scholar] [CrossRef]
- Becker, P.J.; Serrand, N.; Celse, B.; Guillaume, D.; Dulot, H. Comparing Hydrocracking Models: Continuous Lumping vs. Single Events. Fuel 2016, 165, 306–315. [Google Scholar] [CrossRef]
- Lopez Abelairas, M.; de Oliveira, L.P.; Verstraete, J.J. Application of Monte Carlo Techniques to LCO Gas Oil Hydrotreating: Molecular Reconstruction and Kinetic Modelling. Catal. Today 2016, 271, 188–198. [Google Scholar] [CrossRef]
- Browning, B.; Afanasiev, P.; Pitault, I.; Couenne, F.; Tayakout-Fayolle, M. Detailed kinetic modelling of vacuum gas oil hydrocracking using bifunctional catalyst: A distribution approach. Chem. Eng. J. 2016, 284, 270–284. [Google Scholar] [CrossRef]
- Shahrouzi, J.R.; Guillaume, D.; Rouchon, P.; Da Costa, P. Stochastic Simulation and Single Events Kinetic Modeling: Application to Olefin Oligomerization. Ind. Eng. Chem. Res. 2008, 47, 4308–4316. [Google Scholar] [CrossRef]
- Walas, S.M. Phase Equilibria in Chemical Engineering; Butterworth: Boston, MA, USA, 1985. [Google Scholar]
- Zhou, H.; Wang, Y.; Wei, F.; Wang, D.; Wang, Z. Kinetics of the Reactions of the Light Alkenes over SAPO-34. Appl. Catal. A 2008, 348, 135–141. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Z.; Liu, H.; Liu, Z.; Liu, G.; Meng, X. Thermodynamic Equilibrium Distribution of Light Olefins in Catalytic Pyrolysis. Appl. Catal. A 2016, 522, 165–171. [Google Scholar] [CrossRef]
- International Union of Pure and Applied Chemistry (Ed.) Compendium of Chemical Terminology: Gold Book, 2nd ed.; IUPAC: Research Triangle Park, NC, USA, 2014. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 87th ed.; Taylor and Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Alberty, R.A. Extrapolation of Standard Chemical Thermodynamic Properties of Alkene Isomer Groups to Higher Carbon Numbers. J. Phys. Chem. 1983, 87, 4999–5002. [Google Scholar] [CrossRef]
- Alberty, R.A. Chemical Thermodynamic Properties of Isomer Groups. Ind. Eng. Chem. Fundam. 1983, 22, 318–321. [Google Scholar] [CrossRef]
- Alberty, R.A.; Oppenheim, I. A Continuous Thermodynamics Approach to Chemical Equilibrium within an Isomer Group. J. Chem. Phys. 1984, 81, 4603–4609. [Google Scholar] [CrossRef]
- Alberty, R.A. Chemical Equilibrium In Complex Organic Systems. J. Phys. Chem. 1985, 89, 880–883. [Google Scholar] [CrossRef]
- Alberty, R.A.; Gehrig, C.A. Standard Chemical Thermodynamic Properties of Alkane Isomer Groups. J. Phys. Chem. Ref. Data 1984, 13, 1173–1197. [Google Scholar] [CrossRef]
- Alberty, R.A. Standard Chemical Thermodynamic Properties of Alkylbenzene Isomer Groups. J. Phys. Chem. Ref. Data 1985, 14, 177–192. [Google Scholar] [CrossRef]
- Alberty, R.A.; Bloomstein, T.M. Standard Chemical Thermodynamic Properties of Alkylnaphthalene Isomer Groups. J. Phys. Chem. Ref. Data 1985, 14, 821–837. [Google Scholar] [CrossRef]
- Alberty, R.A.; Gehrig, C.A. Standard Chemical Thermodynamic Properties of Alkene Isomer Groups. J. Phys. Chem. Ref. Data 1985, 14, 803–820. [Google Scholar] [CrossRef]
- Alberty, R.A.; Ha, Y.S. Standard Chemical Thermodynamic Properties of Alkylcyclopentane Isomer Groups, Alkylcyclohexane Isomer Groups, and Combined Isomer Groups. J. Phys. Chem. Ref. Data 1985, 14, 1107–1132. [Google Scholar] [CrossRef]
- Alberty, R.A.; Burmenko, E. Standard Chemical Thermodynamic Properties of Alkyne Isomer Groups. J. Phys. Chem. Ref. Data 1986, 15, 1339–1349. [Google Scholar] [CrossRef]
- Alberty, R.A.; Chung, M.B.; Flood, T.M. Standard Chemical Thermodynamic Properties of Alkanol Isomer Groups. J. Phys. Chem. Ref. Data 1987, 16, 391–417. [Google Scholar] [CrossRef]
- Alberty, R.A.; Reif, A.K. Standard Chemical Thermodynamic Properties of Polycyclic Aromatic Hydrocarbons and Their Isomer Groups I. Benzene Series. J. Phys. Chem. Ref. Data 1988, 17, 241–253. [Google Scholar] [CrossRef]
- Alberty, R.A.; Reif, A.K. Erratum: Standard Chemical Thermodynamic Properties of Polycyclic Aromatic Hydrocarbons and Their Isomer Groups I. Benzene Series [J. Phys. Chem. Ref. Data 17, 241 (1988)]. J. Phys. Chem. Ref. Data 1989, 18, 551–553. [Google Scholar] [CrossRef]
- Alberty, R.A.; Chung, M.B.; Reif, A.K. Standard Chemical Thermodynamic Properties of Polycyclic Aromatic Hydrocarbons and Their Isomer Groups. II. Pyrene Series, Naphthopyrene Series, and Coronene Series. J. Phys. Chem. Ref. Data 1989, 18, 77–109. [Google Scholar] [CrossRef]
- Alberty, R.A.; Chung, M.B.; Reif, A.K. Standard Chemical Thermodynamic Properties of Polycyclic Aromatic Hydrocarbons and Their Isomer Groups. III. Naphthocoronene Series, Ovalene Series, and First Members of Some Higher Series. J. Phys. Chem. Ref. Data 1990, 19, 349–370. [Google Scholar] [CrossRef]
- Benson, S.W.; Cruickshank, F.R.; Golden, D.M.; Haugen, G.R.; O’Neal, H.E.; Rodgers, A.S.; Shaw, R.; Walsh, R. Additivity Rules for the Estimation of Thermochemical Properties. Chem. Rev. 1969, 69, 279–324. [Google Scholar] [CrossRef]
- Benson, S.W. Thermochemical Kinetics: Methods for the Estimation of Thermochemical Data and Rate Parameters, 2nd ed.; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Cohen, N.; Benson, S.W. Estimation of Heats of Formation of Organic Compounds by Additivity Methods. Chem. Rev. 1993, 93, 2419–2438. [Google Scholar] [CrossRef]
- Cohen, N. Revised Group Additivity Values for Enthalpies of Formation (at 298 K) of Carbon-Hydrogen and Carbon-Hydrogen-Oxygen Compounds. J. Phys. Chem. Ref. Data 1996, 25, 1411–1481. [Google Scholar] [CrossRef]
- Domalski, E.S.; Hearing, E.D. Estimation of the Thermodynamic Properties of Hydrocarbons at 298.15 K. J. Phys. Chem. Ref. Data 1988, 17, 1637–1678. [Google Scholar] [CrossRef]
- Domalski, E.S.; Hearing, E.D. Estimation of the Thermodynamic Properties of C–H–N–O–S–Halogen Compounds at 298.15 K. J. Phys. Chem. Ref. Data 1993, 22, 805–1159. [Google Scholar] [CrossRef]
- Sabbe, M.K.; Saeys, M.; Reyniers, M.F.; Marin, G.B.; van Speybroeck, V.; Waroquier, M. Group Additive Values for the Gas Phase Standard Enthalpy of Formation of Hydrocarbons and Hydrocarbon Radicals. J. Phys. Chem. A 2005, 109, 7466–7480. [Google Scholar] [CrossRef]
- Sabbe, M.K.; de Vleeschouwer, F.; Reyniers, M.F.; Waroquier, M.; Marin, G.B. First Principles Based Group Additive Values for the Gas Phase Standard Entropy and Heat Capacity of Hydrocarbons and Hydrocarbon Radicals. J. Phys. Chem. A 2008, 112, 12235–12251. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Burgess, D.R. Thermochemical Data. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Chao, J.; Hall, K.R.; Marsh, K.N.; Wilhoit, R.C. Thermodynamic Properties of Key Organic Oxygen Compounds in the Carbon Range C1 to C4. Part 2. Ideal Gas Properties. J. Phys. Chem. Ref. Data 1986, 15, 1369–1436. [Google Scholar] [CrossRef]
- Pilcher, G.; Pell, S.; Coleman, D.J. Measurements of Heats of Combustion by Flame Calorimetry. Part 2.—Dimethyl Ether, Methyl Ethyl Ether, Methyl n-Propyl Ether, Methyl isoPropyl Ether. Trans. Faraday Soc. 1964, 60, 499–505. [Google Scholar] [CrossRef]
- Kennedy, R.M.; Sagenkahn, M.; Aston, J.G. The Heat Capacity and Entropy, Heats of Fusion and Vaporization, and the Vapor Pressure of Dimethyl Ether. The Density of Gaseous Dimethyl Ether. J. Am. Chem. Soc. 1941, 63, 2267–2272. [Google Scholar] [CrossRef]
- Aguayo, A.T.; Ereña, J.; Mier, D.; Arandes, J.M.; Olazar, M.; Bilbao, J. Kinetic Modeling of Dimethyl Ether Synthesis in a Single Step on a CuO-ZnO-Al2O3/γ-Al2O3 Catalyst. Ind. Eng. Chem. Res. 2007, 46, 5522–5530. [Google Scholar] [CrossRef]
- Hayashi, H.; Moffat, J.B. The Properties of Heteropoly Acids and the Conversion of Methanol to Hydrocarbons. J. Catal. 1982, 77, 473–484. [Google Scholar] [CrossRef]
- Diep, B.T.; Wainwright, M.S. Thermodynamic Equilibrium Constants for the Methanol-Dimethyl Ether-Water System. J. Chem. Eng. Data 1987, 32, 330–333. [Google Scholar] [CrossRef]
- Given, P.H. Given—Korrelation zu Methanol-Dehydratisierung, 1943. J. Chem. Soc. 1943, 589. [Google Scholar] [CrossRef]
- Tavan, Y.; Hasanvandian, R. Two Practical Equations for Methanol Dehydration Reaction over HZSM-5 Catalyst—Part I: Second Rrder Rate Equation. Fuel 2015, 142, 208–214. [Google Scholar] [CrossRef]
- Gayubo, A.G.; Aguayo, A.T.; Castilla, M.; Morán, A.L.; Bilbao, J. Role of Water in the Kinetic Modeling of Methanol Transformation into Hydrocarbons on HZSM-5 Zeolite. Chem. Eng. Commun. 2004, 191, 944–967. [Google Scholar] [CrossRef]
- Schiffino, R.S.; Merrill, R.P. A Mechanistic Study of the Methanol Dehydration Reaction on γ–Alumina Catalyst. J. Phys. Chem. 1993, 97, 6425–6435. [Google Scholar] [CrossRef]
- Khademi, M.H.; Farsi, M.; Rahimpour, M.R.; Jahanmiri, A. DME Synthesis and Cyclohexane Dehydrogenation Reaction in an Optimized Thermally Coupled Reactor. Chem. Eng. Process. 2011, 50, 113–123. [Google Scholar] [CrossRef]
- Spivey, J.J. Review: Dehydration Catalysts for the Methanol/Dimethyl Ether Reaction. Chem. Eng. Commun. 1991, 110, 123–142. [Google Scholar] [CrossRef]
- Steinfeld, J.I.; Francisco, J.S.; Hase, W.L. Chemical Kinetics and Dynamics; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Davis, M.E.; Davis, R.J. Fundamentals of Chemical Reaction Engineering; Chemical Engineering Series; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Marin, G.B.; Yablonsky, G.S. Kinetics of Chemical Reactions: Decoding Complexity; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Froment, G.F.; Bischoff, K.B.; de Wilde, J. Chemical Reactor Analysis and Design, 3rd ed.; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Dittmeyer, R.; Emig, G. Simultaneous Heat and Mass Transfer and Chemical Reaction. In Handbook of Heterogeneous Catalysis; Ertl, G., Knözinger, H., Schüth, F., Weitkamp, J., Eds.; Wiley-VCH: Weinheim, Germany, 2008; pp. 1727–1784. [Google Scholar]
- Dumesic, J.A.; Huber, G.W.; Boudart, M. Principles of Heterogeneous Catalysis. In Handbook of Heterogeneous Catalysis; Ertl, G., Knözinger, H., Schüth, F., Weitkamp, J., Eds.; Wiley-VCH: Weinheim, Germany, 2008; pp. 1–15. [Google Scholar]
- Lynggaard, H.; Andreasen, A.; Stegelmann, C.; Stoltze, P. Analysis of Simple Kinetic Models in Heterogeneous Catalysis. Prog. Surf. Sci. 2004, 77, 71–137. [Google Scholar] [CrossRef]
- Neimark, A.V.; Sing, K.S.W.; Thommes, M. Surface Area and Porosity. In Handbook of Heterogeneous Catalysis; Ertl, G., Knözinger, H., Schüth, F., Weitkamp, J., Eds.; Wiley-VCH: Weinheim, Germany, 2008; pp. 721–738. [Google Scholar]
- Schwaab, M.; Pinto, J.C. Optimum Reparameterization of Power Function Models. Chem. Eng. Sci. 2008, 63, 4631–4635. [Google Scholar] [CrossRef]
- Kapteijn, F.; Berger, R.J.; Moulijn, J.A. Rate Procurement and Kinetic Modeling. In Handbook of Heterogeneous Catalysis; Ertl, G., Knözinger, H., Schüth, F., Weitkamp, J., Eds.; Wiley-VCH: Weinheim, Germany, 2008; pp. 1693–1714. [Google Scholar]
- Buzzi-Ferraris, G.; Manenti, F. Kinetic Models Analysis. Chem. Eng. Sci. 2009, 64, 1061–1074. [Google Scholar] [CrossRef]
- Eyring, H. The Activated Complex and the Absolute Rate of Chemical Reactions. Chem. Rev. 1935, 17, 65–77. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Studt, F.; Abild-Pedersen, F.; Bligaard, T. Fundamental Concepts in Heterogeneous Catalysis; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Schwaab, M.; Pinto, J.C. Optimum Reference Temperature for Reparameterization of the Arrhenius equation. Part 1: Problems Involving One Kinetic Constant. Chem. Eng. Sci. 2007, 62, 2750–2764. [Google Scholar] [CrossRef]
- Park, T.Y.; Froment, G.F. Kinetic Modeling of the Methanol to Olefins Process. 2. Experimental Results, Model Discrimination, and Parameter Estimation. Ind. Eng. Chem. Res. 2001, 40, 4187–4196. [Google Scholar] [CrossRef]
- Schwaab, M.; Lemos, L.P.; Pinto, J.C. Optimum Reference Temperature for Reparameterization of the Arrhenius Equation. Part 2: Problems Involving Multiple Reparameterizations. Chem. Eng. Sci. 2008, 63, 2895–2906. [Google Scholar] [CrossRef]
- Toch, K.; Thybaut, J.W.; Vandegehuchte, B.D.; Narasimhan, C.S.L.; Domokos, L.; Marin, G.B. A Single-Event Microkinetic Model for “Ethylbenzene Dealkylation/Xylene Isomerization” on Pt/H-ZSM-5 Zeolite Catalyst. Appl. Catal. A 2012, 425–426, 130–144. [Google Scholar] [CrossRef]
- Wright, P.A.; Pearce, G.M. Structural Chemistry of Zeolites. In Zeolites and Catalysis; Čejka, J., Corma, A., Zones, S., Eds.; Wiley-VCH: Weinheim, Germany, 2010; Volume 1, pp. 171–207. [Google Scholar]
- Schmidt, F.; Reichelt, L.; Pätzold, C. Catalysis of Methanol Conversion to Hydrocarbons. In Methanol, Asinger’s Vision Today; Bertau, M., Offermanns, H., Plass, L., Schmidt, F., Wernicke, H.J., Eds.; Springer: Berlin, Germany, 2014; pp. 423–440. [Google Scholar]
- Wright, P.A. Microporous Framework Solids; RSC Materials Monographs; The Royal Society of Chemistry: Cambridge, UK, 2008. [Google Scholar]
- Ong, L.H. Nature and Stability of Aluminum Species in HZSM-5: Changes upon Hydrothermal Treatment and Effect of Binder. Ph.D. Dissertation, Technical University of Munich, Munich, Germany, 2009. [Google Scholar]
- Menges, M.; Kraushaar-Czarnetzki, B. Kinetics of Methanol to Olefins over AlPO4-Bound ZSM-5 Extrudates in a Two-Stage Unit with Dimethyl Ether Pre-Reactor. Microporous Mesoporous Mater. 2012, 164, 172–181. [Google Scholar] [CrossRef]
- McCusker, L.B.; Baerlocher, C. Zeolite Structures. In Introduction to Zeolite Science and Practice; van Bekkum, H., Flanigen, E.M., Jacobs, P.A., Jansen, J.C., Eds.; Studies in Surface Science and Catalysis; Elsevier: Amsterdam, The Netherlands, 2001; pp. 37–67. [Google Scholar]
- Baerlocher, C.; McCusker, L.B. Database of Zeolite Structures. Available online: http://www.iza-structure.org/databases/ (accessed on 18 October 2018).
- Lobo, R.F. Introduction to the Structural Chemistry of Zeolites. In Handbook of Zeolite Science and Technology; Auerbach, S.M., Carrado, K.A., Dutta, P.K., Eds.; Marcel Dekker: New York, NY, USA, 2003; pp. 80–112. [Google Scholar]
- Kokotailo, G.T.; Lawton, S.L.; Olson, D.H.; Meier, W.M. Structure of Synthetic Zeolite ZSM-5. Nature 1978, 272, 437–438. [Google Scholar] [CrossRef]
- Chang, C.D. Hydrocarbons from Methanol. Catal. Rev. Sci. Eng. 1983, 25, 1–118. [Google Scholar] [CrossRef]
- Rohrman, A.C.; LaPierre, R.B.; Schlenker, J.L.; Wood, J.D.; Valyocsik, E.W.; Rubin, M.K.; Higgins, J.B.; Rohrbaugh, W.J. The Framework Topology of ZSM-23: A High Silica Zeolite. Zeolites 1985, 5, 352–354. [Google Scholar] [CrossRef]
- Kumar, P.; Thybaut, J.W.; Teketel, S.; Svelle, S.; Beato, P.; Olsbye, U.; Marin, G.B. Single-Event MicroKinetics (SEMK) for Methanol to Hydrocarbons (MTH) on H-ZSM-23. Catal. Today 2013, 215, 224–232. [Google Scholar] [CrossRef]
- Teketel, S.; Skistad, W.; Benard, S.; Olsbye, U.; Lillerud, K.P.; Beato, P.; Svelle, S. Shape Selectivity in the Conversion of Methanol to Hydrocarbons: The Catalytic Performance of One-Dimensional 10-Ring Zeolites: ZSM-22, ZSM-23, ZSM-48, and EU-1. ACS Catal. 2012, 2, 26–37. [Google Scholar] [CrossRef]
- Lok, B.M.; Messina, C.A.; Patton, L.; Gajek, R.T.; Cannan, T.R.; Flanigen, E.M. Silicoaluminophosphate molecular sieves: another new class of microporous crystalline inorganic solids. J. Am. Chem. Soc. 1984, 106, 6092–6093. [Google Scholar] [CrossRef]
- Epelde, E.; Ibáñez, M.; Valecillos, J.; Aguayo, A.T.; Gayubo, A.G.; Bilbao, J.; Castaño, P. SAPO-18 and SAPO-34 Catalysts for Propylene Production from the Oligomerization-Cracking of Ethylene or 1-Butenes. Appl. Catal. A 2017, 547, 176–182. [Google Scholar] [CrossRef]
- Stöcker, M. Methanol to Olefins (MTO) and Methanol to Gasoline (MTG). In Zeolites and Catalysis; Čejka, J., Corma, A., Zones, S., Eds.; Wiley-VCH: Weinheim, Germany, 2010; Volume 2, pp. 687–711. [Google Scholar]
- Chen, J.; Thomas, J.M.; Wright, P.A.; Townsend, R.P. Silicoaluminophosphate Number Eighteen (SAPO-18): A New Microporous Solid Acid Catalyst. Catal. Lett. 1994, 28, 241–248. [Google Scholar] [CrossRef]
- Chen, J.; Wright, P.A.; Thomas, J.M.; Natarajan, S.; Marchese, L.; Bradley, S.M.; Sankar, G.; Catlow, R.A.; Gai-Boyes, P.; Townsend, R.P.; et al. SAPO-18 Catalysts and Their Brønststed Acid Sites. J. Phys. Chem. 1994, 98, 10216–10224. [Google Scholar] [CrossRef]
- Dessau, R.M.; LaPierre, R.B. On the Mechanism of Methanol Conversion to Hydrocarbons over HZSM-5. J. Catal. 1982, 78, 136–141. [Google Scholar] [CrossRef]
- Weitkamp, J.; Jacobs, P.A.; Martens, J.A. Isomerization and Hydrocracking of C9 through C16 n-Alkanes on Pt/HZSM-5 Zeolite. Appl. Catal. 1983, 8, 123–141. [Google Scholar] [CrossRef]
- Garwood, W.E. Conversion of C2–C10 to Higher Olefins over Synthetic Zeolite ZSM-5. In Intrazeolite Chemistry; ACS Symposium Series; Stucky, G.D., Dwyer, F.G., Eds.; American Chemical Society: Washington, DC, USA, 1983; Volume 218, pp. 383–396. [Google Scholar] [CrossRef]
- Tabak, S.A.; Krambeck, F.J.; Garwood, W.E. Conversion of Propylene and Butylene over ZSM-5 Catalyst. AIChE J. 1986, 32, 1526–1531. [Google Scholar] [CrossRef]
- Quann, R.J.; Green, L.A.; Tabak, S.A.; Krambeck, F.J. Chemistry of Olefin Oligomerization over ZSM-5 Catalyst. Ind. Eng. Chem. Res. 1988, 27, 565–570. [Google Scholar] [CrossRef]
- Buchanan, J.S.; Santiesteban, J.G.; Haag, W.O. Mechanistic Considerations in Acid-Catalyzed Cracking of Olefins. J. Catal. 1996, 158, 279–287. [Google Scholar] [CrossRef]
- Buchanan, J.S. Gasoline Selective ZSM-5 FCC Additives: Model Reactions of C6–C10 Olefins over Steamed 55:1 and 450:1 ZSM-5. Appl. Catal. A 1998, 171, 57–64. [Google Scholar] [CrossRef]
- Arudra, P.; Bhuiyan, T.I.; Akhtar, M.N.; Aitani, A.M.; Al-Khattaf, S.S.; Hattori, H. Silicalite-1 As Efficient Catalyst for Production of Propene from 1-Butene. ACS Catal. 2014, 4, 4205–4214. [Google Scholar] [CrossRef]
- Von Aretin, T.; Standl, S.; Tonigold, M.; Hinrichsen, O. Optimization of the Product Spectrum for 1-Pentene Cracking on ZSM-5 Using Single-Event Mmethodology. Part 2: Recycle Reactor. Chem. Eng. J. 2017, 309, 873–885. [Google Scholar] [CrossRef]
- Sundberg, J.; Standl, S.; von Aretin, T.; Tonigold, M.; Rehfeldt, S.; Hinrichsen, O.; Klein, H. Optimal Process for Catalytic Cracking of Higher Olefins on ZSM-5. Chem. Eng. J. 2018, 348, 84–94. [Google Scholar] [CrossRef]
- Von Aretin, T.; Standl, S.; Tonigold, M.; Hinrichsen, O. Optimization of the Product Spectrum for 1-Pentene Cracking on ZSM-5 Using Single-Event Methodology. Part 1: Two-Zone reactor. Chem. Eng. J. 2017, 309, 886–897. [Google Scholar] [CrossRef]
- Von Aretin, T.; Schallmoser, S.; Standl, S.; Tonigold, M.; Lercher, J.A.; Hinrichsen, O. Single-Event Kinetic Model for 1-Pentene Cracking on ZSM-5. Ind. Eng. Chem. Res. 2015, 54, 11792–11803. [Google Scholar] [CrossRef]
- Borges, P.; Ramos Pinto, R.; Lemos, A.; Lemos, F.; Védrine, J.C.; Derouane, E.G.; Ramôa Ribeiro, F. Light Olefin Transformation over ZSM-5 Zeolites: A Kinetic Model for Olefin Consumption. Appl. Catal. A 2007, 324, 20–29. [Google Scholar] [CrossRef]
- Huang, X.; Aihemaitijiang, D.; Xiao, W.D. Reaction Pathway and Kinetics of C3–C7 Olefin Transformation over High-silicon HZSM-5 Zeolite at 400–490 °C. Chem. Eng. J. 2015, 280, 222–232. [Google Scholar] [CrossRef]
- Nguyen, C.M.; de Moor, B.A.; Reyniers, M.F.; Marin, G.B. Physisorption and Chemisorption of Linear Alkenes in Zeolites: A Combined QM-Pot(MP2//B3LYP:GULP)-Statistical Thermodynamics Study. J. Phys. Chem. C 2011, 115, 23831–23847. [Google Scholar] [CrossRef]
- Kazansky, V.B.; Frash, M.V.; van Santen, R.A. Quantumchemical Study of the Isobutane Cracking on Zeolites. Appl. Catal. A 1996, 146, 225–247. [Google Scholar] [CrossRef]
- Rigby, A.M.; Kramer, G.J.; van Santen, R.A. Mechanisms of Hydrocarbon Conversion in Zeolites: A Quantum Mechanical Study. J. Catal. 1997, 170, 1–10. [Google Scholar] [CrossRef]
- Quintana-Solórzano, R.; Thybaut, J.W.; Marin, G.B.; Lødeng, R.; Holmen, A. Single-Event Microkinetics for Coke Formation in Catalytic Cracking. Catal. Today 2005, 107–108, 619–629. [Google Scholar] [CrossRef]
- Sun, X.; Müller, S.; Liu, Y.; Shi, H.; Haller, G.L.; Sanchez-Sanchez, M.; van Veen, A.C.; Lercher, J.A. On Reaction Pathways in the Conversion of Methanol to Hydrocarbons on HZSM-5. J. Catal. 2014, 317, 185–197. [Google Scholar] [CrossRef]
- Feng, W.; Vynckier, E.; Froment, G.F. Single-Event Kinetics of Catalytic Cracking. Ind. Eng. Chem. Res. 1993, 32, 2997–3005. [Google Scholar] [CrossRef]
- Chang, C.D.; Silvestri, A.J. The Conversion of Methanol and Other O-Compounds to Hydrocarbons over Zeolite Catalysts. J. Catal. 1977, 47, 249–259. [Google Scholar] [CrossRef]
- Stöcker, M. Methanol-to-Hydrocarbons: Catalytic Materials and their Behavior. Microporous Mesoporous Mater. 1999, 29, 3–48. [Google Scholar] [CrossRef]
- Koempel, H.; Liebner, W. Lurgi’s Methanol To Propylene (MTP®) Report on a Successful Commercialisation. In Natural Gas Conversion VIII; Studies in Surface Science and Catalysis; Noronha, F., Schmal, M., Sousa-Aguiar, E.F., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 167, pp. 261–267. [Google Scholar]
- Forester, T.R.; Howe, R.F. In Situ FTIR Studies of Methanol and Dimethyl Ether in ZSM-5. J. Am. Chem. Soc. 1987, 109, 5076–5082. [Google Scholar] [CrossRef]
- Anderson, M.W.; Barrie, P.J.; Klinowski, J. 1H Magic-Angle-Spinning NMR Studies of the Adsorption of Alcohols on Molecular Sieve Catalysts. J. Phys. Chem. 1991, 95, 235–239. [Google Scholar] [CrossRef]
- Martin, K.A.; Zabransky, R.F. Conversion of Methanol to Dimethylether over ZSM-5 by DRIFT Spectroscopy. Appl. Spectrosc. 1991, 45, 68–72. [Google Scholar] [CrossRef]
- Blaszkowski, S.R.; van Santen, R.A. The Mechanism of Dimethyl Ether Formation from Methanol Catalyzed by Zeolitic Protons. J. Am. Chem. Soc. 1996, 118, 5152–5153. [Google Scholar] [CrossRef]
- Blaszkowski, S.R.; van Santen, R.A. Theoretical Study of the Mechanism of Surface Methoxy and Dimethyl Ether Formation from Methanol Catalyzed by Zeolitic Protons. J. Phys. Chem. B 1997, 101, 2292–2305. [Google Scholar] [CrossRef]
- Maihom, T.; Boekfa, B.; Sirijaraensre, J.; Nanok, T.; Probst, M.; Limtrakul, J. Reaction Mechanisms of the Methylation of Ethene with Methanol and Dimethyl Ether over H-ZSM-5: An ONIOM Study. J. Phys. Chem. C 2009, 113, 6654–6662. [Google Scholar] [CrossRef]
- Jones, A.J.; Iglesia, E. Kinetic, Spectroscopic, and Theoretical Assessment of Associative and Dissociative Methanol Dehydration Routes in Zeolites. Angew. Chem. Int. Ed. 2014, 53, 12177–12181. [Google Scholar] [CrossRef]
- Liu, Y.; Müller, S.; Berger, D.; Jelic, J.; Reuter, K.; Tonigold, M.; Sanchez-Sanchez, M.; Lercher, J.A. Formation Mechanism of the First Carbon-Carbon Bond and the First Olefin in the Methanol Conversion into Hydrocarbons. Angew. Chem. Int. Ed. 2016, 55, 5723–5726. [Google Scholar] [CrossRef]
- Dahl, I.M.; Kolboe, S. On the Reaction Mechanism for Propene Formation in the MTO Reaction over SAPO-34. Catal. Lett. 1993, 20, 329–336. [Google Scholar] [CrossRef]
- Dahl, I.M.; Kolboe, S. On the Reaction Mechanism for Hydrocarbon Formation from Methanol over SAPO-34: I. Isotopic Labeling Studies of the Co-Reaction of Ethene and Methanol. J. Catal. 1994, 149, 458–464. [Google Scholar] [CrossRef]
- Dahl, I.M.; Kolboe, S. On the Reaction Mechanism for Hydrocarbon Formation from Methanol over SAPO-34: 2. Isotopic Labeling Studies of the Co-Reaction of Propene and Methanol. J. Catal. 1996, 161, 304–309. [Google Scholar] [CrossRef]
- Bjørgen, M.; Olsbye, U.; Petersen, D.; Kolboe, S. The Methanol-to-Hydrocarbons Reaction: Insight into the Reaction Mechanism from [12C]Benzene and [13C]Methanol Coreactions over Zeolite H-Beta. J. Catal. 2004, 221, 1–10. [Google Scholar] [CrossRef]
- Wang, W.; Jiang, Y.; Hunger, M. Mechanistic Investigations of the Methanol-to-Olefin (MTO) Process on Acidic Zeolite Catalysts by in situ Solid-State NMR Spectroscopy. Catal. Today 2006, 113, 102–114. [Google Scholar] [CrossRef]
- Olsbye, U.; Bjørgen, M.; Svelle, S.; Lillerud, K.P.; Kolboe, S. Mechanistic Insight into the Methanol-to-Hydrocarbons Reaction. Catal. Today 2005, 106, 108–111. [Google Scholar] [CrossRef]
- Olsbye, U.; Svelle, S.; Lillerud, K.P.; Wei, Z.H.; Chen, Y.Y.; Li, J.F.; Wang, J.G.; Fan, W.B. The Formation and Degradation of Active Species during Methanol Conversion over Protonated Zeotype Catalysts. Chem. Soc. Rev. 2015, 44, 7155–7176. [Google Scholar] [CrossRef]
- Tian, P.; Wei, Y.; Ye, M.; Liu, Z. Methanol to Olefins (MTO): From Fundamentals to Commercialization. ACS Catal. 2015, 5, 1922–1938. [Google Scholar] [CrossRef]
- Mole, T.; Whiteside, J.A. Conversion of Methanol to Ethylene over ZSM-5 Zeolite in the Presence of Deuterated Water. J. Catal. 1982, 75, 284–290. [Google Scholar] [CrossRef]
- Sassi, A.; Wildman, M.A.; Ahn, H.J.; Prasad, P.; Nicholas, J.B.; Haw, J.F. Methylbenzene Chemistry on Zeolite HBeta: Multiple Insights into Methanol-to-Olefin Catalysis. J. Phys. Chem. B 2002, 106, 2294–2303. [Google Scholar] [CrossRef]
- Haw, J.F.; Song, W.; Marcus, D.M.; Nicholas, J.B. The Mechanism of Methanol to Hydrocarbon Catalysis. Acc. Chem. Res. 2003, 36, 317–326. [Google Scholar] [CrossRef]
- Arstad, B.; Nicholas, J.B.; Haw, J.F. Theoretical Study of the Methylbenzene Side-Chain Hydrocarbon Pool Mechanism in Methanol to Olefin Catalysis. J. Am. Chem. Soc. 2004, 126, 2991–3001. [Google Scholar] [CrossRef]
- Lesthaeghe, D.; Horré, A.; Waroquier, M.; Marin, G.B.; van Speybroeck, V. Theoretical Insights on Methylbenzene Side-Chain Growth in ZSM-5 Zeolites for Methanol-to-Olefin Conversion. Chem. Eur. J. 2009, 15, 10803–10808. [Google Scholar] [CrossRef]
- Sullivan, R.F.; Egan, C.J.; Langlois, G.E.; Sieg, R.P. A New Reaction That Occurs in the Hydrocracking of Certain Aromatic Hydrocarbons. J. Am. Chem. Soc. 1961, 83, 1156–1160. [Google Scholar] [CrossRef]
- Dessau, R.M. On the H-ZSM-5 Catalyzed Formation of Ethylene from Methanol or Higher Olefins. J. Catal. 1986, 99, 111–116. [Google Scholar] [CrossRef]
- Svelle, S.; Joensen, F.; Nerlov, J.; Olsbye, U.; Lillerud, K.P.; Kolboe, S.; Bjørgen, M. Conversion of Methanol into Hydrocarbons over Zeolite H-ZSM-5: Ethene Formation is Mechanistically Separated from the Formation of Higher Alkenes. J. Am. Chem. Soc. 2006, 128, 14770–14771. [Google Scholar] [CrossRef]
- Bjørgen, M.; Svelle, S.; Joensen, F.; Nerlov, J.; Kolboe, S.; Bonino, F.; Palumbo, L.; Bordiga, S.; Olsbye, U. Conversion of Methanol to Hydrocarbons over Zeolite H-ZSM-5: On the Origin of the Olefinic Species. J. Catal. 2007, 249, 195–207. [Google Scholar] [CrossRef]
- Svelle, S.; Arstad, B.; Kolboe, S.; Swang, O. A Theoretical Investigation of the Methylation of Alkenes with Methanol over Acidic Zeolites. J. Phys. Chem. B 2003, 107, 9281–9289. [Google Scholar] [CrossRef]
- Svelle, S.; Kolboe, S.; Swang, O.; Olsbye, U. Methylation of Alkenes and Methylbenzenes by Dimethyl Ether or Methanol on Acidic Zeolites. J. Phys. Chem. B 2005, 109, 12874–12878. [Google Scholar] [CrossRef]
- Martínez-Espín, J.S.; Mortén, M.; Janssens, T.V.W.; Svelle, S.; Beato, P.; Olsbye, U. New Insights into Catalyst Deactivation and Product Distribution of Zeolites in the Methanol-to-Hydrocarbons (MTH) Reaction with Methanol and Dimethyl Ether Feeds. Catal. Sci. Technol. 2017, 7, 2700–2716. [Google Scholar] [CrossRef]
- Hutchings, G.J.; Hunter, R. Hydrocarbon Formation from Methanol and Dimethyl Ether: A Review of the Experimental Observations Concerning the Mechanism of Formation of the Primary Products. Catal. Today 1990, 6, 279–306. [Google Scholar] [CrossRef]
- Müller, S.; Liu, Y.; Kirchberger, F.M.; Tonigold, M.; Sanchez-Sanchez, M.; Lercher, J.A. Hydrogen Transfer Pathways during Zeolite Catalyzed Methanol Conversion to Hydrocarbons. J. Am. Chem. Soc. 2016, 138, 15994–16003. [Google Scholar] [CrossRef]
- Martínez-Espín, J.S.; de Wispelaere, K.; Janssens, T.V.W.; Svelle, S.; Lillerud, K.P.; Beato, P.; van Speybroeck, V.; Olsbye, U. Hydrogen Transfer versus Methylation: On the Genesis of Aromatics Formation in the Methanol-To-Hydrocarbons Reaction over H-ZSM-5. ACS Catal. 2017, 7, 5773–5780. [Google Scholar] [CrossRef]
- Huang, X.; Li, H.; Li, H.; Xiao, W.D. Modeling and Analysis of the Lurgi-Type Methanol to Propylene Process: Optimization of Olefin Recycle. AIChE J. 2017, 63, 306–313. [Google Scholar] [CrossRef]
- Svelle, S.; Rønning, P.O.; Kolboe, S. Kinetic Studies of Zeolite-Catalyzed Methylation Reactions 1. Coreaction of [12C]Ethene and [13C]Methanol. J. Catal. 2004, 224, 115–123. [Google Scholar] [CrossRef]
- Svelle, S.; Rønning, P.O.; Olsbye, U.; Kolboe, S. Kinetic Studies of Zeolite-Catalyzed Methylation Reactions. Part 2. Co-Reaction of [12C]Propene or [12C]n-Butene and [13C]Methanol. J. Catal. 2005, 234, 385–400. [Google Scholar] [CrossRef]
- Wu, W.; Guo, W.; Xiao, W.D.; Luo, M. Dominant Reaction Pathway for Methanol Conversion to Propene over High Silicon H-ZSM-5. Chem. Eng. Sci. 2011, 66, 4722–4732. [Google Scholar] [CrossRef]
- Ilias, S.; Bhan, A. Tuning the Selectivity of Methanol-to-Hydrocarbons Conversion on H-ZSM-5 by Co-Processing Olefin or Aromatic Compounds. J. Catal. 2012, 290, 186–192. [Google Scholar] [CrossRef]
- Guo, W.; Xiao, W.D.; Luo, M. Comparison among Monolithic and Randomly Packed Reactors for the Methanol-to-Propylene Process. Chem. Eng. J. 2012, 207–208, 734–745. [Google Scholar] [CrossRef]
- Sun, X.; Müller, S.; Shi, H.; Haller, G.L.; Sanchez-Sanchez, M.; van Veen, A.C.; Lercher, J.A. On the Impact of Co-Feeding Aromatics and Olefins for the Methanol-to-Olefins Reaction on HZSM-5. J. Catal. 2014, 314, 21–31. [Google Scholar] [CrossRef]
- Chang, C.D. Methanol Conversion to Light Olefins. Catal. Rev. Sci. Eng. 1984, 26, 323–345. [Google Scholar] [CrossRef]
- Froment, G.F.; Dehertog, W.J.H.; Marchi, A.J. Zeolite Catalysis in the Conversion of Methanol into Olefins. In Catalysis; Spivey, J.J., Ed.; The Royal Society of Chemistry: Cambridge, UK, 1992; Volume 9, pp. 1–64. [Google Scholar]
- Svelle, S.; Visur, M.; Olsbye, U.; Saepurahman.; Bjørgen, M. Mechanistic Aspects of the Zeolite Catalyzed Methylation of Alkenes and Aromatics with Methanol: A Review. Top. Catal. 2011, 54, 897–906. [Google Scholar] [CrossRef]
- Ilias, S.; Bhan, A. Mechanism of the Catalytic Conversion of Methanol to Hydrocarbons. ACS Catal. 2013, 3, 18–31. [Google Scholar] [CrossRef]
- Svelle, S.; Bjørgen, M. Mechanistic Proposal for the Zeolite Catalyzed Methylation of Aromatic Compounds. J. Phys. Chem. A 2010, 114, 12548–12554. [Google Scholar] [CrossRef]
- Hill, I.M.; Ng, Y.S.; Bhan, A. Kinetics of Butene Isomer Methylation with Dimethyl Ether over Zeolite Catalysts. ACS Catal. 2012, 2, 1742–1748. [Google Scholar] [CrossRef]
- Hill, I.M.; Al Hashimi, S.; Bhan, A. Kinetics and Mechanism of Olefin Methylation Reactions on Zeolites. J. Catal. 2012, 285, 115–123. [Google Scholar] [CrossRef]
- Hill, I.; Malek, A.; Bhan, A. Kinetics and Mechanism of Benzene, Toluene, and Xylene Methylation over H-MFI. ACS Catal. 2013, 3, 1992–2001. [Google Scholar] [CrossRef]
- Brogaard, R.Y.; Wang, C.M.; Studt, F. Methanol-Alkene Reactions in Zeotype Acid Catalysts: Insights from a Descriptor-Based Approach and Microkinetic Modeling. ACS Catal. 2014, 4, 4504–4509. [Google Scholar] [CrossRef]
- Brogaard, R.Y.; Henry, R.; Schuurman, Y.; Medford, A.J.; Moses, P.G.; Beato, P.; Svelle, S.; Nørskov, J.K.; Olsbye, U. Methanol-to-Hydrocarbons Conversion: The Alkene Methylation Pathway. J. Catal. 2014, 314, 159–169. [Google Scholar] [CrossRef]
- Martínez-Espín, J.S.; de Wispelaere, K.; Westgård Erichsen, M.; Svelle, S.; Janssens, T.V.W.; van Speybroeck, V.; Beato, P.; Olsbye, U. Benzene Co-Reaction with Methanol and Dimethyl Ether over Zeolite and Zeotype Catalysts: Evidence of Parallel Reaction Paths to Toluene and Diphenylmethane. J. Catal. 2017, 349, 136–148. [Google Scholar] [CrossRef]
- Li, J.; Wei, Y.; Liu, G.; Qi, Y.; Tian, P.; Li, B.; He, Y.; Liu, Z. Comparative Study of MTO Conversion over SAPO-34, H-ZSM-5 and H-ZSM-22: Correlating Catalytic Performance and Reaction Mechanism to Zeolite Topology. Catal. Today 2011, 171, 221–228. [Google Scholar] [CrossRef]
- Almutairi, S.M.T.; Mezari, B.; Pidko, E.A.; Magusin, P.C.M.M.; Hensen, E.J.M. Influence of Steaming on the Acidity and the Methanol Conversion Reaction of HZSM-5 Zeolite. J. Catal. 2013, 307, 194–203. [Google Scholar] [CrossRef]
- Khare, R.; Bhan, A. Mechanistic Studies of Methanol-to-Hydrocarbons Conversion on Diffusion-Free MFI Samples. J. Catal. 2015, 329, 218–228. [Google Scholar] [CrossRef]
- Westgård Erichsen, M.; de Wispelaere, K.; Hemelsoet, K.; Moors, S.L.; Deconinck, T.; Waroquier, M.; Svelle, S.; van Speybroeck, V.; Olsbye, U. How Zeolitic Acid Strength and Composition Alter the Reactivity of Alkenes and Aromatics towards Methanol. J. Catal. 2015, 328, 186–196. [Google Scholar] [CrossRef]
- Wu, W.; Guo, W.; Xiao, W.D.; Luo, M. Methanol Conversion to Olefins (MTO) over H-ZSM-5: Evidence of Product Distribution Governed by Methanol Conversion. Fuel Process. Technol. 2013, 108, 19–24. [Google Scholar] [CrossRef]
- Kaarsholm, M.; Joensen, F.; Nerlov, J.; Cenni, R.; Chaouki, J.; Patience, G.S. Phosphorous Modified ZSM-5: Deactivation and Product Distribution for MTO. Chem. Eng. Sci. 2007, 62, 5527–5532. [Google Scholar] [CrossRef]
- Janssens, T.V.W. A New Approach to the Modeling of Deactivation in the Conversion of Methanol on Zeolite Catalysts. J. Catal. 2009, 264, 130–137. [Google Scholar] [CrossRef]
- Schulz, H. “Coking” of Zeolites during Methanol Conversion: Basic Reactions of the MTO-, MTP- and MTG Processes. Catal. Today 2010, 154, 183–194. [Google Scholar] [CrossRef]
- Bleken, F.L.; Barbera, K.; Bonino, F.; Olsbye, U.; Lillerud, K.P.; Bordiga, S.; Beato, P.; Janssens, T.V.W.; Svelle, S. Catalyst Deactivation by Coke Formation in Microporous and Desilicated Zeolite H-ZSM-5 During the Conversion of Methanol to Hydrocarbons. J. Catal. 2013, 307, 62–73. [Google Scholar] [CrossRef]
- Müller, S.; Liu, Y.; Vishnuvarthan, M.; Sun, X.; van Veen, A.C.; Haller, G.L.; Sanchez-Sanchez, M.; Lercher, J.A. Coke Formation and Deactivation Pathways on H-ZSM-5 in the Conversion of Methanol to Olefins. J. Catal. 2015, 325, 48–59. [Google Scholar] [CrossRef]
- Epelde, E.; Aguayo, A.T.; Olazar, M.; Bilbao, J.; Gayubo, A.G. Kinetic Model for the Transformation of 1-Butene on a K-Modified HZSM-5 Catalyst. Ind. Eng. Chem. Res. 2014, 53, 10599–10607. [Google Scholar] [CrossRef]
- Ying, L.; Zhu, J.; Cheng, Y.; Wang, L.; Li, X. Kinetic Modeling of C2–C7 Olefins Interconversion over ZSM-5 Catalyst. J. Ind. Eng. Chem. 2016, 33, 80–90. [Google Scholar] [CrossRef]
- Oliveira, P.; Borges, P.; Ramos Pinto, R.; Lemos, A.; Lemos, F.; Védrine, J.C.; Ramôa Ribeiro, F. Light Olefin Transformation over ZSM-5 Zeolites with Different Acid Strengths—A Kinetic Model. Appl. Catal. A 2010, 384, 177–185. [Google Scholar] [CrossRef]
- Epelde, E.; Gayubo, A.G.; Olazar, M.; Bilbao, J.; Aguayo, A.T. Modified HZSM-5 Zeolites for Intensifying Propylene Production in the Transformation of 1-Butene. Chem. Eng. J. 2014, 251, 80–91. [Google Scholar] [CrossRef]
- Epelde, E.; Gayubo, A.G.; Olazar, M.; Bilbao, J.; Aguayo, A.T. Intensifying Propylene Production by 1-Butene Transformation on a K Modified HZSM-5 Zeolite-Catalyst. Ind. Eng. Chem. Res. 2014, 53, 4614–4622. [Google Scholar] [CrossRef]
- Huang, X.; Aihemaitijiang, D.; Xiao, W.D. Co-Reaction of Methanol and Olefins on the High Silicon HZSM-5 Catalyst: A Kinetic Study. Chem. Eng. J. 2016, 286, 150–164. [Google Scholar] [CrossRef]
- Borges, P.; Ramos Pinto, R.; Lemos, A.; Lemos, F.; Védrine, J.C.; Derouane, E.G.; Ramôa Ribeiro, F. Activity-acidity Relationship for Alkane Cracking over Zeolites: n-Hexane Cracking over HZSM-5. J. Mol. Catal. A Chem. 2005, 229, 127–135. [Google Scholar] [CrossRef]
- Schallmoser, S. Insight into Catalytic Cracking of Hydrocarbons over MFI type Zeolites. Ph.D. Dissertation, Technical University of Munich, Munich, Germany, 2014. [Google Scholar]
- Nguyen, C.M.; de Moor, B.A.; Reyniers, M.F.; Marin, G.B. Isobutene Protonation in H-FAU, H-MOR, H-ZSM-5, and H-ZSM-22. J. Phys. Chem. C 2012, 116, 18236–18249. [Google Scholar] [CrossRef]
- Standl, S.; Tonigold, M.; Hinrichsen, O. Single-Event Kinetic Modeling of Olefin Cracking on ZSM-5: Proof of Feed Independence. Ind. Eng. Chem. Res. 2017, 56, 13096–13108. [Google Scholar] [CrossRef]
- Baltanas, M.A.; van Raemdonck, K.K.; Froment, G.F.; Mohedas, S.R. Fundamental Kinetic Modeling of Hydroisomerization and Hydrocracking on Noble-Metal-Loaded Faujasites. 1. Rate Parameters for Hydroisomerization. Ind. Eng. Chem. Res. 1989, 28, 899–910. [Google Scholar] [CrossRef]
- Mhadeshwar, A.B.; Wang, H.; Vlachos, D.G. Thermodynamic Consistency in Microkinetic Development of Surface Reaction Mechanisms. J. Phys. Chem. B 2003, 107, 12721–12733. [Google Scholar] [CrossRef]
- Chen, C.J.; Rangarajan, S.; Hill, I.M.; Bhan, A. Kinetics and Thermochemistry of C4–C6 Olefin Cracking on H-ZSM-5. ACS Catal. 2014, 4, 2319–2327. [Google Scholar] [CrossRef]
- Mazar, M.N.; Al-Hashimi, S.; Cococcioni, M.; Bhan, A. β-Scission of Olefins on Acidic Zeolites: A Periodic PBE-D Study in H-ZSM-5. J. Phys. Chem. C 2013, 117, 23609–23620. [Google Scholar] [CrossRef]
- Li, J.; Li, T.; Ma, H.; Sun, Q.; Li, C.; Ying, W.; Fang, D. Kinetics of Coupling Cracking of Butene and Pentene on Modified HZSM-5 Catalyst. Chem. Eng. J. 2018, 346, 397–405. [Google Scholar] [CrossRef]
- Meng, X.; Xu, C.; Li, L.; Gao, J. Kinetic Study of Catalytic Pyrolysis of C4 Hydrocarbons on a Modified ZSM-5 Zeolite Catalyst. Energy Fuels 2010, 24, 6233–6238. [Google Scholar] [CrossRef]
- Jiang, B.; Feng, X.; Yan, L.; Jiang, Y.; Liao, Z.; Wang, J.; Yang, Y. Methanol to Propylene Process in a Moving Bed Reactor with Byproducts Recycling: Kinetic Study and Reactor Simulation. Ind. Eng. Chem. Res. 2014, 53, 4623–4632. [Google Scholar] [CrossRef]
- Aguayo, A.T.; Mier, D.; Gayubo, A.G.; Gamero, M.; Bilbao, J. Kinetics of Methanol Transformation into Hydrocarbons on a HZSM-5 Zeolite Catalyst at High Temperature (400–550 °C). Ind. Eng. Chem. Res. 2010, 49, 12371–12378. [Google Scholar] [CrossRef]
- Pérez-Uriarte, P.; Ateka, A.; Aguayo, A.T.; Gayubo, A.G.; Bilbao, J. Kinetic Model for the Reaction of DME to Olefins over a HZSM-5 Zeolite Catalyst. Chem. Eng. J. 2016, 302, 801–810. [Google Scholar] [CrossRef]
- Park, T.Y.; Froment, G.F. Kinetic Modeling of the Methanol to Olefins Process. 1. Model Formulation. Ind. Eng. Chem. Res. 2001, 40, 4172–4186. [Google Scholar] [CrossRef]
- Gayubo, A.G.; Aguayo, A.T.; Sánchez del Campo, A.E.; Tarrío, A.M.; Bilbao, J. Kinetic Modeling of Methanol Transformation into Olefins on a SAPO-34 Catalyst. Ind. Eng. Chem. Res. 2000, 39, 292–300. [Google Scholar] [CrossRef]
- Ying, L.; Yuan, X.; Ye, M.; Cheng, Y.; Li, X.; Liu, Z. A Seven Lumped Kinetic Model for Industrial Catalyst in DMTO Process. Chem. Eng. Res. Des. 2015, 100, 179–191. [Google Scholar] [CrossRef]
- Chen, D.; Grønvold, A.; Moljord, K.; Holmen, A. Methanol Conversion to Light Olefins over SAPO-34: Reaction Network and Deactivation Kinetics. Ind. Eng. Chem. Res. 2007, 46, 4116–4123. [Google Scholar] [CrossRef]
- Alwahabi, S.M.; Froment, G.F. Single Event Kinetic Modeling of the Methanol-to-Olefins Process on SAPO-34. Ind. Eng. Chem. Res. 2004, 43, 5098–5111. [Google Scholar] [CrossRef]
- Gayubo, A.G.; Aguayo, A.T.; Alonso, A.; Atutxa, A.; Bilbao, J. Reaction Scheme and Kinetic Modelling for the MTO Process over a SAPO-18 Catalyst. Catal. Today 2005, 106, 112–117. [Google Scholar] [CrossRef]
- Gayubo, A.G.; Aguayo, A.T.; Alonso, A.; Bilbao, J. Kinetic Modeling of the Methanol-to-Olefins Process on a Silicoaluminophosphate (SAPO-18) Catalyst by Considering Deactivation and the Formation of Individual Olefins. Ind. Eng. Chem. Res. 2007, 46, 1981–1989. [Google Scholar] [CrossRef]
- Sánchez del Campo, A.E.; Gayubo, A.G.; Aguayo, A.T.; Tarrío, A.; Bilbao, J. Acidity, Surface Species, and Mechanism of Methanol Transformation into Olefins on a SAPO-34. Ind. Eng. Chem. Res. 1998, 37, 2336–2340. [Google Scholar] [CrossRef]
- Menges, M. Untersuchungen zum MTO-Prozess an AlPO4-gebundenen ZSM-5-Extrudaten und Beschreibung der Reaktionskinetik. Ph.D. Dissertation, Karlsruher Institut für Technologie, Karlsruhe, Germany, 2012. [Google Scholar] [CrossRef]
- Chen, D.; Grønvold, A.; Rebo, H.P.; Moljord, K.; Holmen, A. Catalyst Deactivation Studied by Conventional and Oscillating Microbalance Reactors. Appl. Catal. A 1996, 137, L1–L8. [Google Scholar] [CrossRef]
- Freiding, J.; Patcas, F.C.; Kraushaar-Czarnetzki, B. Extrusion of Zeolites: Properties of Catalysts with a Novel Aluminium Phosphate Sintermatrix. Appl. Catal. A 2007, 328, 210–218. [Google Scholar] [CrossRef]
- Freiding, J. Extrusion von technischen ZSM-5-Kontakten und ihre Anwendung im MTO-Prozess. Ph.D. Dissertation, Karlsruher Institut für Technologie, Karlsruhe, Germany, 2009. [Google Scholar] [CrossRef]
- Freiding, J.; Kraushaar-Czarnetzki, B. Novel Extruded Fixed-Bed MTO Catalysts with High Olefin Selectivity and High Resistance against Coke Deactivation. Appl. Catal. A 2011, 391, 254–260. [Google Scholar] [CrossRef]
- Gayubo, A.G.; Aguayo, A.T.; Morán, A.L.; Olazar, M.; Bilbao, J. Role of Water in the Kinetic Modeling of Catalyst Deactivation in the MTG Process. AIChE J. 2002, 48, 1561–1571. [Google Scholar] [CrossRef]
- Gayubo, A.G.; Aguayo, A.T.; Olazar, M.; Vivanco, R.; Bilbao, J. Kinetics of the Irreversible Deactivation of the HZSM-5 Catalyst in the MTO Process. Chem. Eng. Sci. 2003, 58, 5239–5249. [Google Scholar] [CrossRef]
- Gayubo, A.G.; Arandes, J.M.; Aguayo, A.T.; Olazar, M.; Bilbao, J. Calculation of the Kinetics of Deactivation by Coke in an Integral Reactor for a Triangular Scheme Reaction. Chem. Eng. Sci. 1993, 48, 1077–1087. [Google Scholar] [CrossRef]
- Aguayo, A.T.; Gayubo, A.G.; Ortega, J.M.; Olazar, M.; Bilbao, J. Catalyst Deactivation by Coking in the MTG Process in Fixed and Fluidized Bed Reactors. Catal. Today 1997, 37, 239–248. [Google Scholar] [CrossRef]
- Benito, P.L.; Gayubo, A.G.; Aguayo, A.T.; Castilla, M.; Bilbao, J. Concentration-Dependent Kinetic Model for Catalyst Deactivation in the MTG Process. Ind. Eng. Chem. Res. 1996, 35, 81–89. [Google Scholar] [CrossRef]
- Mier, D.; Aguayo, A.T.; Gayubo, A.G.; Olazar, M.; Bilbao, J. Catalyst Discrimination for Olefin Production by Coupled Methanol/n-Butane Cracking. Appl. Catal. A 2010, 383, 202–210. [Google Scholar] [CrossRef]
- Mier, D.; Aguayo, A.T.; Gamero, M.; Gayubo, A.G.; Bilbao, J. Kinetic Modeling of n-Butane Cracking on HZSM-5 Zeolite Catalyst. Ind. Eng. Chem. Res. 2010, 49, 8415–8423. [Google Scholar] [CrossRef]
- Pérez-Uriarte, P.; Ateka, A.; Gamero, M.; Aguayo, A.T.; Bilbao, J. Effect of the Operating Conditions in the Transformation of DME to Olefins over a HZSM-5 Zeolite Catalyst. Ind. Eng. Chem. Res. 2016, 55, 6569–6578. [Google Scholar] [CrossRef]
- Pérez-Uriarte, P.; Gamero, M.; Ateka, A.; Díaz, M.; Aguayo, A.T.; Bilbao, J. Effect of the Acidity of HZSM-5 Zeolite and the Binder in the DME Transformation to Olefins. Ind. Eng. Chem. Res. 2016, 55, 1513–1521. [Google Scholar] [CrossRef]
- Pérez-Uriarte, P.; Ateka, A.; Gayubo, A.G.; Cordero-Lanzac, T.; Aguayo, A.T.; Bilbao, J. Deactivation Kinetics for the Conversion of Dimethyl Ether to Olefins over a HZSM-5 Zeolite Catalyst. Chem. Eng. J. 2017, 311, 367–377. [Google Scholar] [CrossRef]
- Lox, E.; Coenen, F.; Vermeulen, R.; Froment, G.F. A Versatile Bench-Scale Unit for Kinetic Studies of Catalytic Reactions. Ind. Eng. Chem. Res. 1988, 27, 576–580. [Google Scholar] [CrossRef]
- Hutchings, G.J.; Gottschalk, F.; Hall, M.V.M.; Hunter, R. Hydrocarbon Formation from Methylating Agents over the Zeolite Catalyst ZSM-5. J. Chem. Soc. Faraday Trans. 1 1987, 83, 571–583. [Google Scholar] [CrossRef]
- Park, T.Y.; Froment, G.F. A Hybrid Genetic Algorithm for the Estimation of Parameters in Detailed Kinetic Models. Comput. Chem. Eng. 1998, 22, S103–S110. [Google Scholar] [CrossRef]
- Boudart, M.; Mears, D.E.; Vannice, M.A. Kinetics of Heterogeneous Catalytic Reactions. Ind. Chim. Belge 1967, 32, 281–284. [Google Scholar]
- Evans, M.G.; Polanyi, M. Inertia and Driving Force of Chemical Reactions. Trans. Faraday Soc. 1938, 34, 11–24. [Google Scholar] [CrossRef]
- Park, T.Y.; Froment, G.F. Analysis of Fundamental Reaction Rates in the Methanol-to-Olefins Process on ZSM-5 as a Basis for Reactor Design and Operation. Ind. Eng. Chem. Res. 2004, 43, 682–689. [Google Scholar] [CrossRef]
- Denayer, J.F.; Souverijns, W.; Jacobs, P.A.; Martens, J.A.; Baron, G.V. High-Temperature Low-Pressure Adsorption of Branched C5–C8 Alkanes on Zeolite Beta, ZSM-5, ZSM-22, Zeolite Y, and Mordenite. J. Phys. Chem. B 1998, 102, 4588–4597. [Google Scholar] [CrossRef]
- Denayer, J.F.; Baron, G.V.; Martens, J.A.; Jacobs, P.A. Chromatographic Study of Adsorption of n-Alkanes on Zeolites at High Temperatures. J. Phys. Chem. B 1998, 102, 3077–3081. [Google Scholar] [CrossRef]
- Chen, D.; Rebo, H.P.; Grønvold, A.; Moljord, K.; Holmen, A. Methanol Conversion to Light Olefins over SAPO-34: Kinetic Modeling of Coke Formation. Microporous Mesoporous Mater. 2000, 35–36, 121–135. [Google Scholar] [CrossRef]
- Chen, D.; Bjorgum, E.; Christensen, K.O.; Holmen, A.; Lodeng, R. Characterization of Catalysts under Working Conditions with an Oscillating Microbalance Reactor. In Advances in Catalysis; Gates, B.C., Knözinger, H., Eds.; Academic Press: Cambridge, MA, USA, 2007; Volume 51, pp. 351–382. [Google Scholar]
- Alwahabi, S.M. Conversion of Methanol to Light Olefins on SAPO-34: Kinetic Modeling and Reactor Design. Ph.D. Dissertation, Texas A&M University, College Station, TX, USA, 2003. [Google Scholar]
- Gayubo, A.G.; Vivanco, R.; Alonso, A.; Valle, B.; Aguayo, A.T. Kinetic Behavior of the SAPO-18 Catalyst in the Transformation of Methanol into Olefins. Ind. Eng. Chem. Res. 2005, 44, 6605–6614. [Google Scholar] [CrossRef]
- Bleken, F.; Bjørgen, M.; Palumbo, L.; Bordiga, S.; Svelle, S.; Lillerud, K.P.; Olsbye, U. The Effect of Acid Strength on the Conversion of Methanol to Olefins Over Acidic Microporous Catalysts with the CHA Topology. Top. Catal. 2009, 52, 218–228. [Google Scholar] [CrossRef]
- Teketel, S.; Olsbye, U.; Lillerud, K.P.; Beato, P.; Svelle, S. Selectivity Control through Fundamental Mechanistic Insight in the Conversion of Methanol to Hydrocarbons over Zeolites. Microporous Mesoporous Mater. 2010, 136, 33–41. [Google Scholar] [CrossRef]
- Narasimhan, C.S.L.; Thybaut, J.W.; Marin, G.B.; Martens, J.A.; Denayer, J.F.; Baron, G.V. Pore Mouth Physisorption of Alkanes on ZSM-22: Estimation of Physisorption Enthalpies and Entropies by Additivity Method. J. Catal. 2003, 218, 135–147. [Google Scholar] [CrossRef]
- Denayer, J.F.; Ocakoglu, R.A.; Huybrechts, W.; Martens, J.A.; Thybaut, J.W.; Marin, G.B.; Baron, G.V. Pore Mouth versus Intracrystalline Adsorption of Isoalkanes on ZSM-22 and ZSM-23 Zeolites under Vapour and Liquid Phase Conditions. Chem. Commun. 2003, 1880–1881. [Google Scholar] [CrossRef]
- Kaarsholm, M.; Rafii, B.; Joensen, F.; Cenni, R.; Chaouki, J.; Patience, G.S. Kinetic Modeling of Methanol- to-Olefin Reaction over ZSM-5 in Fluid Bed. Ind. Eng. Chem. Res. 2010, 49, 29–38. [Google Scholar] [CrossRef]
- Yuan, X.; Li, H.; Ye, M.; Liu, Z. Kinetic Modeling of Methanol to Olefins Process over SAPO-34 Catalyst Based on the Dual-Cycle Reaction Mechanism. AIChE J. 2018. [Google Scholar] [CrossRef]
- Yuan, X.; Li, H.; Ye, M.; Liu, Z. Comparative Study of MTO Kinetics over SAPO-34 Catalyst in Fixed and Fluidized Bed Reactors. Chem. Eng. J. 2017, 329, 35–44. [Google Scholar] [CrossRef]
- Lu, B.; Zhang, J.; Luo, H.; Wang, W.; Li, H.; Ye, M.; Liu, Z.; Li, J. Numerical Simulation of Scale-Up Effects of Methanol-to-Olefins Fluidized Bed Reactors. Chem. Eng. Sci. 2017, 171, 244–255. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, B.; Chen, F.; Li, H.; Ye, M.; Wang, W. Simulation of a Large Methanol-to-Olefins Fluidized Bed Reactor with Consideration of Coke Distribution. Chem. Eng. Sci. 2018, 189, 212–220. [Google Scholar] [CrossRef]
- Strizhak, P.; Zhokh, A.; Trypolskyi, A. Methanol Conversion to Olefins on H-ZSM-5/Al2O3 Catalysts: Kinetic Modeling. React. Kinet. Mech. Catal. 2018, 123, 247–268. [Google Scholar] [CrossRef]
- Sedighi, M.; Bahrami, H.; Towfighi, J. Kinetic Modeling Formulation of the Methanol to Olefin Process: Parameter estimation. J. Ind. Eng. Chem. 2014, 20, 3108–3114. [Google Scholar] [CrossRef]
- Fatourehchi, N.; Sohrabi, M.; Royaee, S.J.; Mirarefin, S.M. Preparation of SAPO-34 catalyst and presentation of a kinetic model for methanol to olefin process (MTO). Chem. Eng. Res. Des. 2011, 89, 811–816. [Google Scholar] [CrossRef]
- Taheri Najafabadi, A.; Fatemi, S.; Sohrabi, M.; Salmasi, M. Kinetic Modeling and Optimization of the Operating Condition of MTO Process on SAPO-34 Catalyst. J. Ind. Eng. Chem. 2012, 18, 29–37. [Google Scholar] [CrossRef]
- Azarhoosh, M.J.; Halladj, R.; Askari, S. Presenting a New Kinetic Model for Methanol to Light Olefins Reactions over a Hierarchical SAPO-34 Catalyst Using the Langmuir–Hinshelwood-Hougen–Watson Mechanism. J. Phys. Condens. Matter 2017, 29, 425202. [Google Scholar] [CrossRef]
- Wen, M.; Ding, J.; Wang, C.; Li, Y.; Zhao, G.; Liu, Y.; Lu, Y. High-Performance SS-Fiber@HZSM-5 Core–Shell Catalyst for Methanol-to-Propylene: A Kinetic and Modeling Study. Microporous Mesoporous Mater. 2016, 221, 187–196. [Google Scholar] [CrossRef]
- Wen, M.; Wang, X.; Han, L.; Ding, J.; Sun, Y.; Liu, Y.; Lu, Y. Monolithic Metal-Fiber@HZSM-5 Core-Shell Catalysts for Methanol-to-Propylene. Microporous Mesoporous Mater. 2015, 206, 8–16. [Google Scholar] [CrossRef]
- Huang, X.; Li, H.; Xiao, W.D.; Chen, D. Insight into the Side Reactions in Methanol-to-Olefin Process over HZSM-5: A Kinetic Study. Chem. Eng. J. 2016, 299, 263–275. [Google Scholar] [CrossRef]
- Huang, X.; Li, H.; Li, H.; Xiao, W.D. A Computationally Efficient Multi-Scale Simulation of a Multi-Stage Fixed-Bed Reactor for Methanol to Propylene Reactions. Fuel Process. Technol. 2016, 150, 104–116. [Google Scholar] [CrossRef]
- Huang, X.; Li, X.G.; Li, H.; Xiao, W.D. High-Performance HZSM-5/Cordierite Monolithic Catalyst for Methanol to Propylene Reaction: A Combined Experimental and Modelling Study. Fuel Process. Technol. 2017, 159, 168–177. [Google Scholar] [CrossRef]
- Wang, X.; Wen, M.; Wang, C.; Ding, J.; Sun, Y.; Liu, Y.; Lu, Y. Microstructured Fiber@HZSM-5 Core-Shell Catalysts with Dramatic Selectivity and Stability Improvement for the Methanol-to-Propylene Process. Chem. Commun. 2014, 50, 6343–6345. [Google Scholar] [CrossRef]
- Guo, W.; Wu, W.; Luo, M.; Xiao, W.D. Modeling of Diffusion and Reaction in Monolithic Catalysts for the Methanol-to-Propylene Process. Fuel Process. Technol. 2013, 108, 133–138. [Google Scholar] [CrossRef]
- Ortega, C.; Hessel, V.; Kolb, G. Dimethyl Ether to Hydrocarbons over ZSM-5: Kinetic Study in an External Recycle Reactor. Chem. Eng. J. 2018, 354, 21–34. [Google Scholar] [CrossRef]
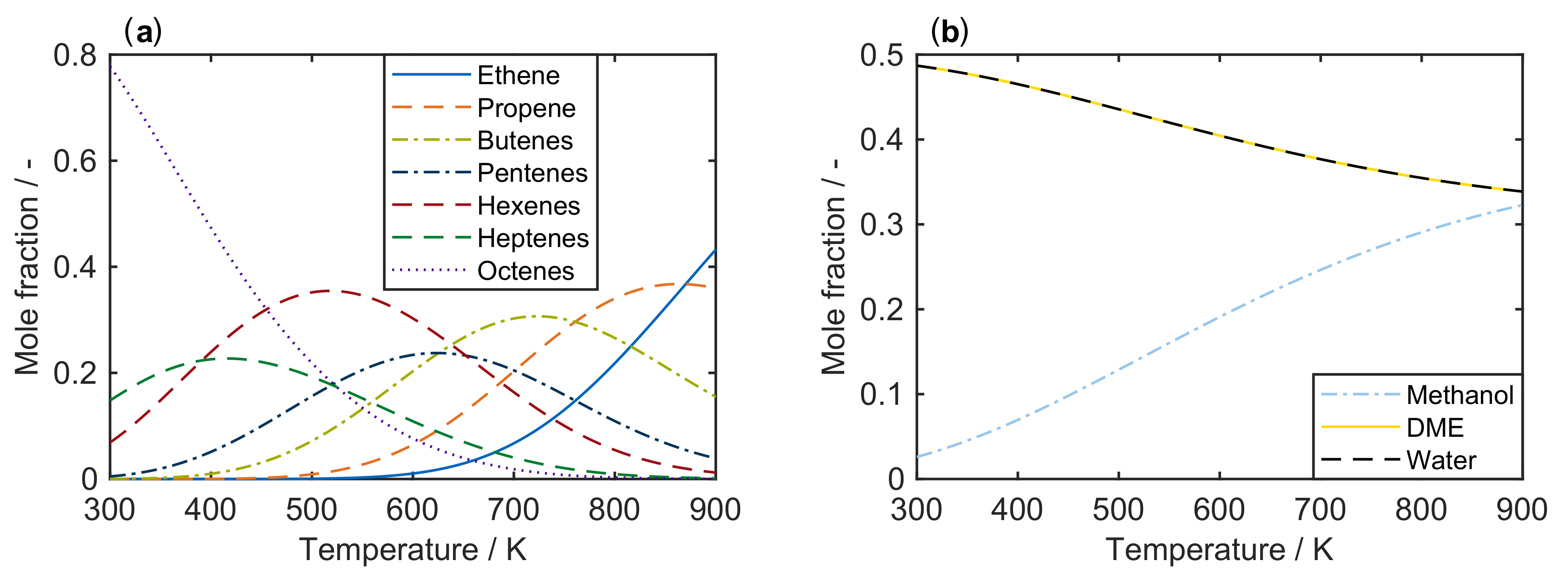
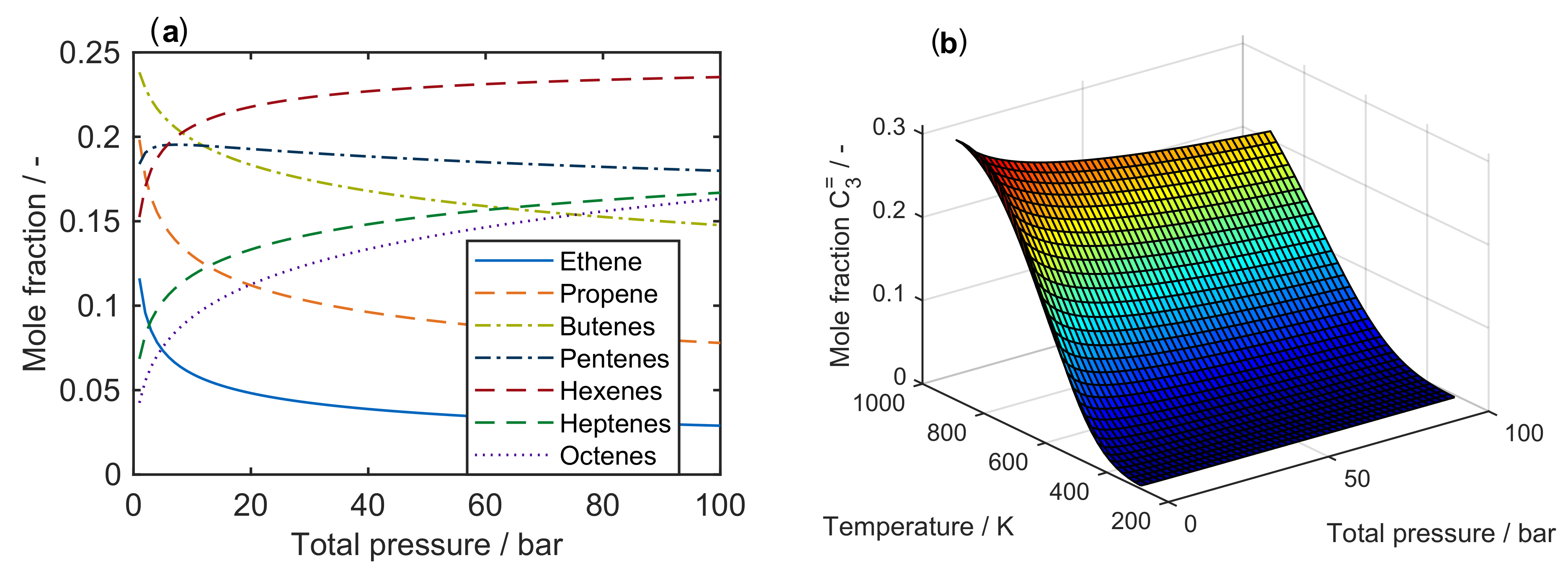
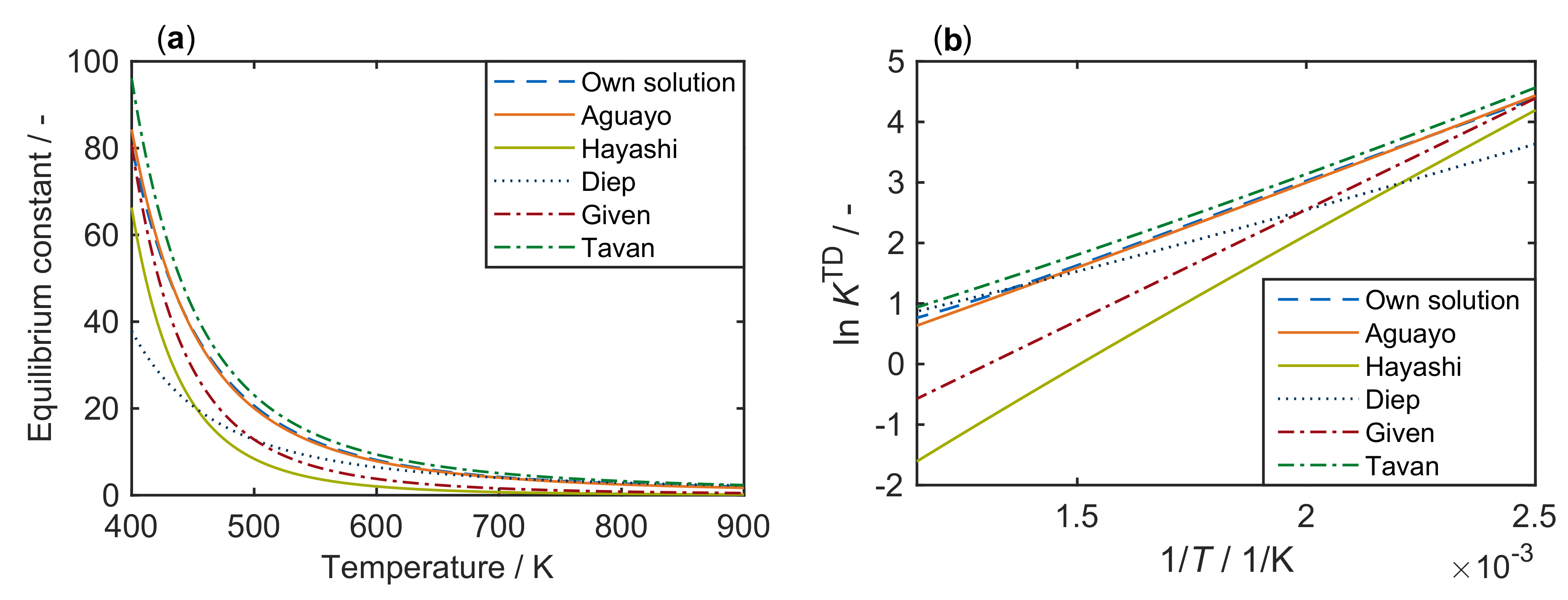
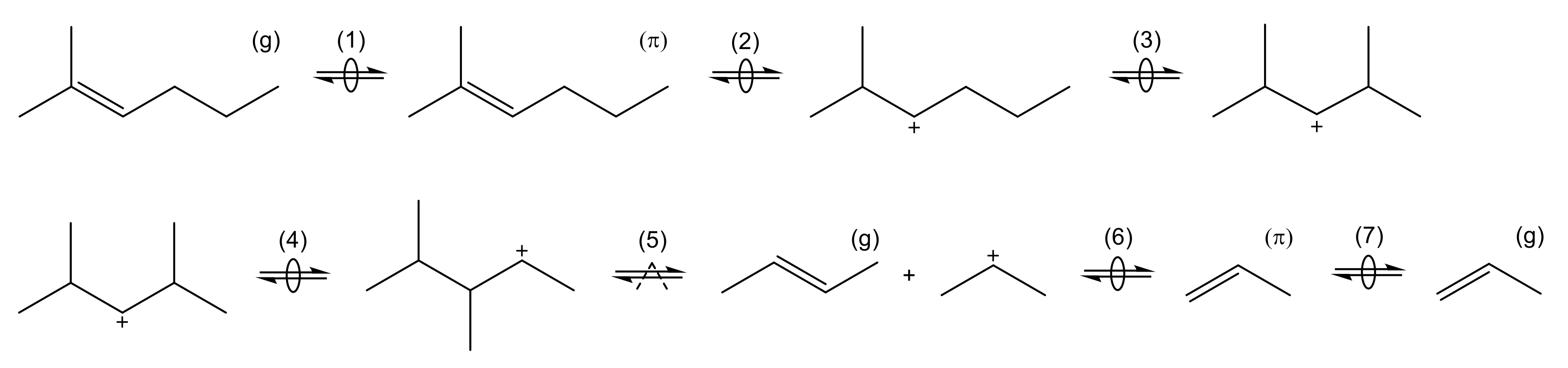
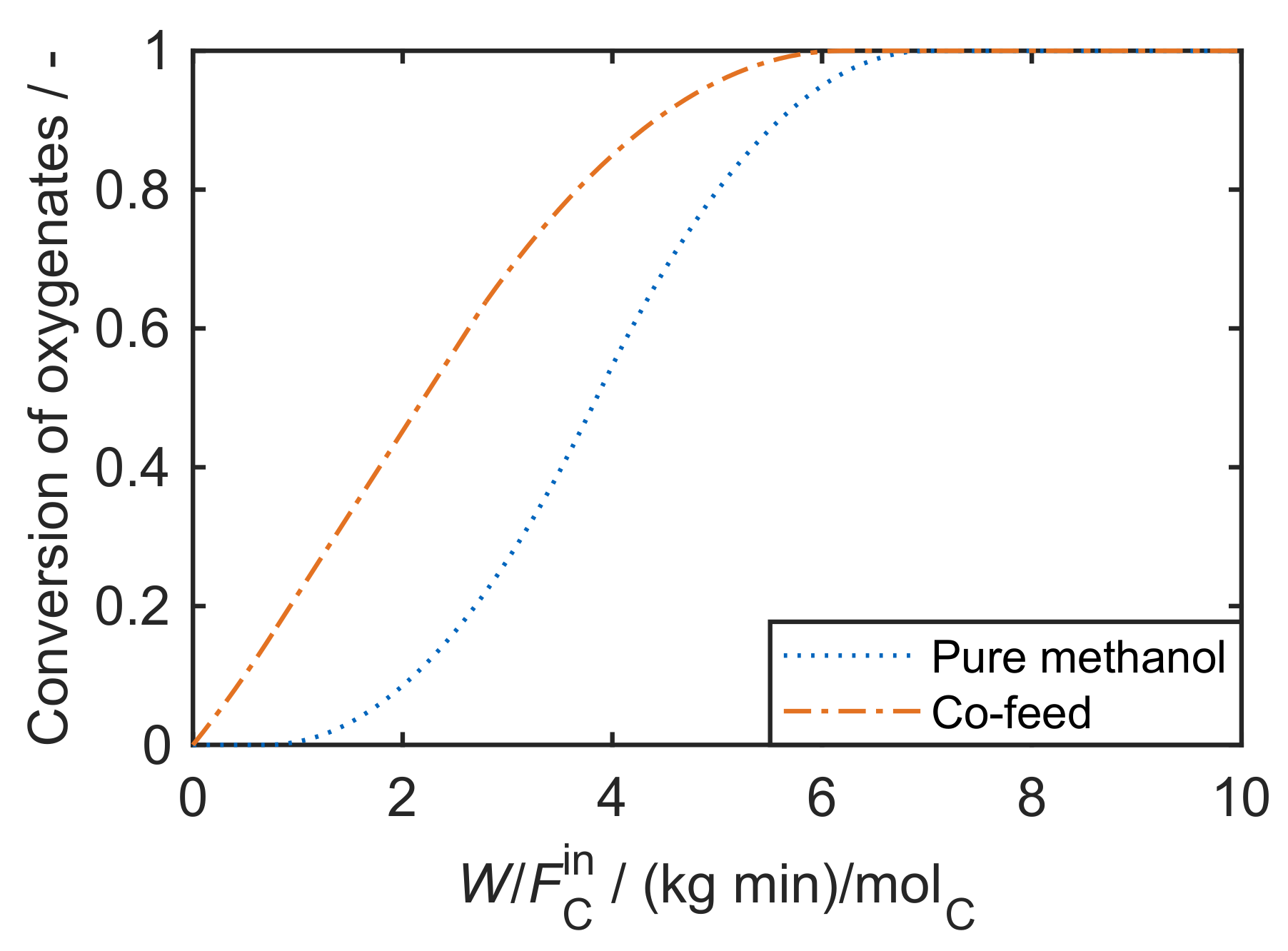
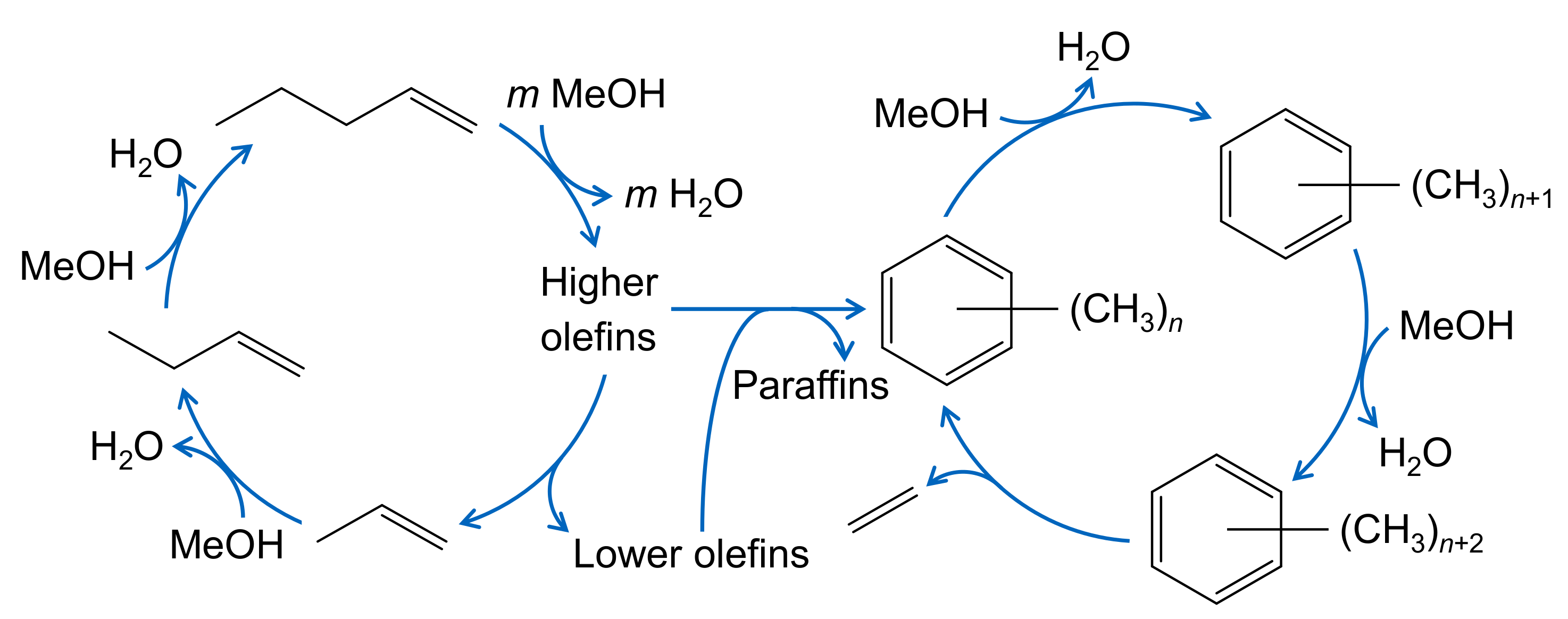

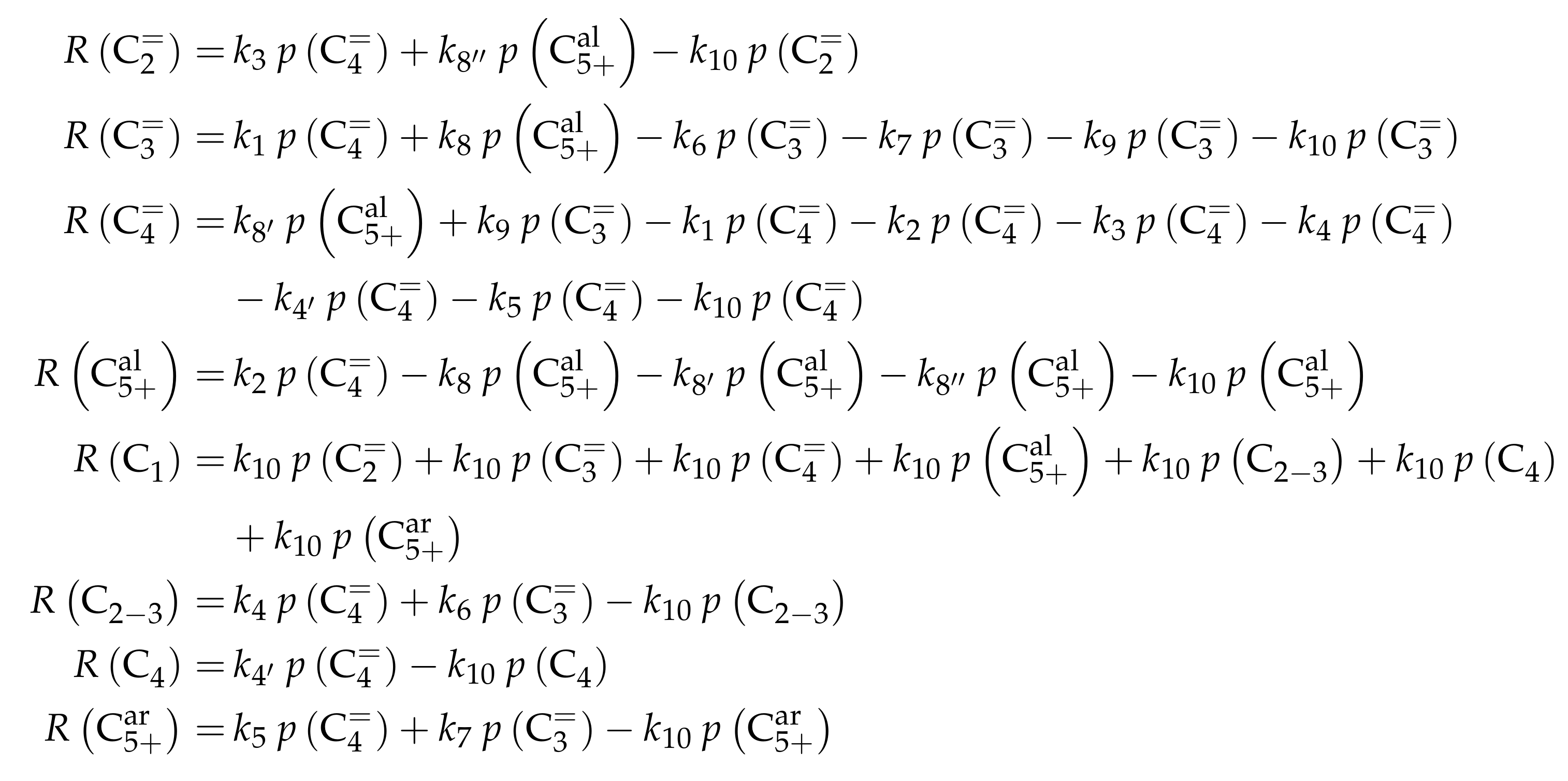

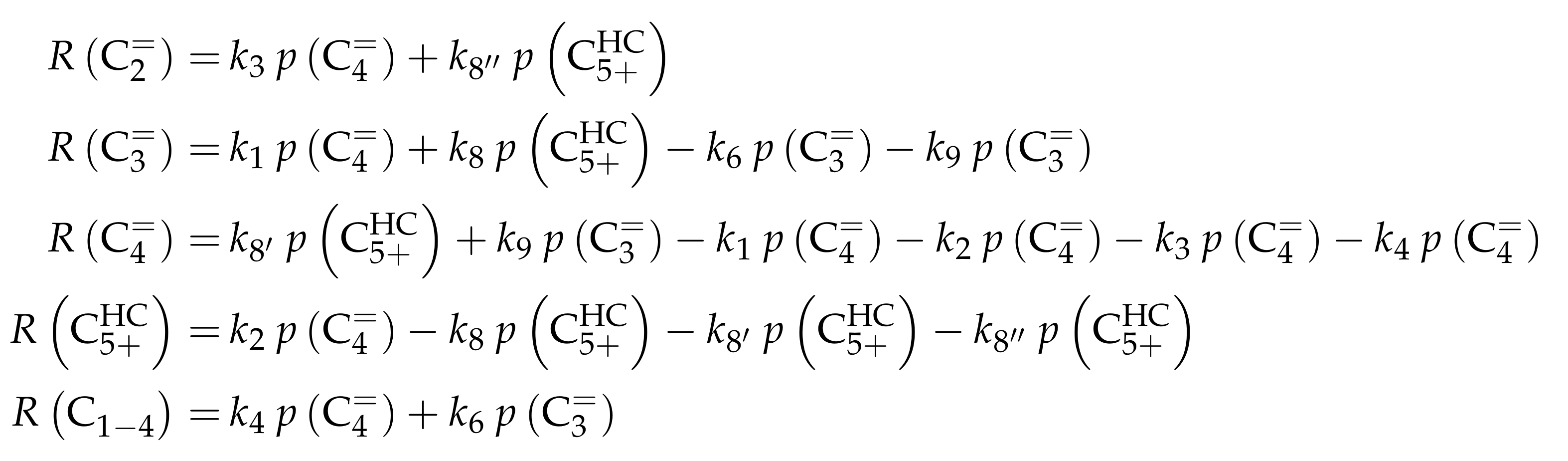
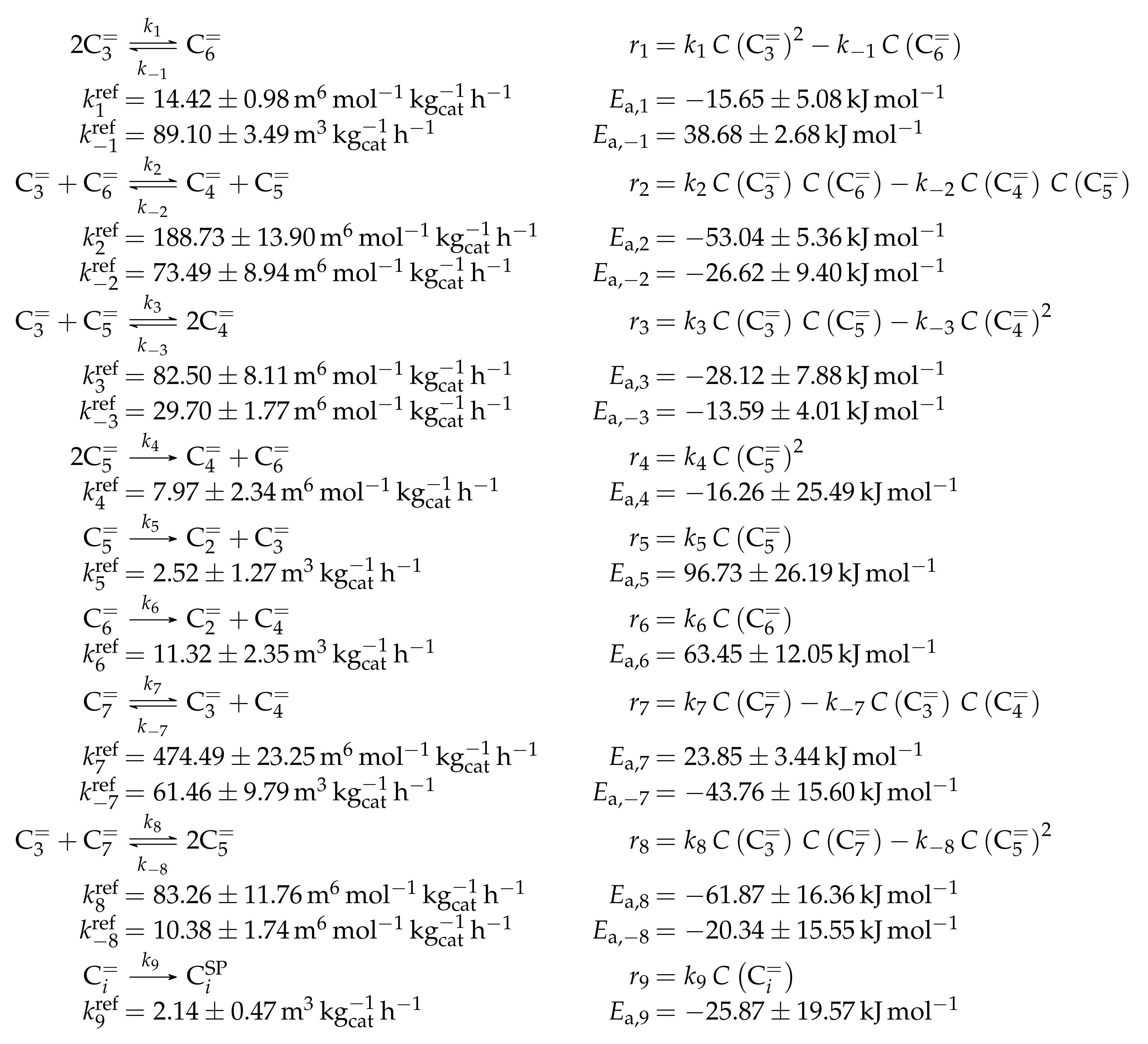
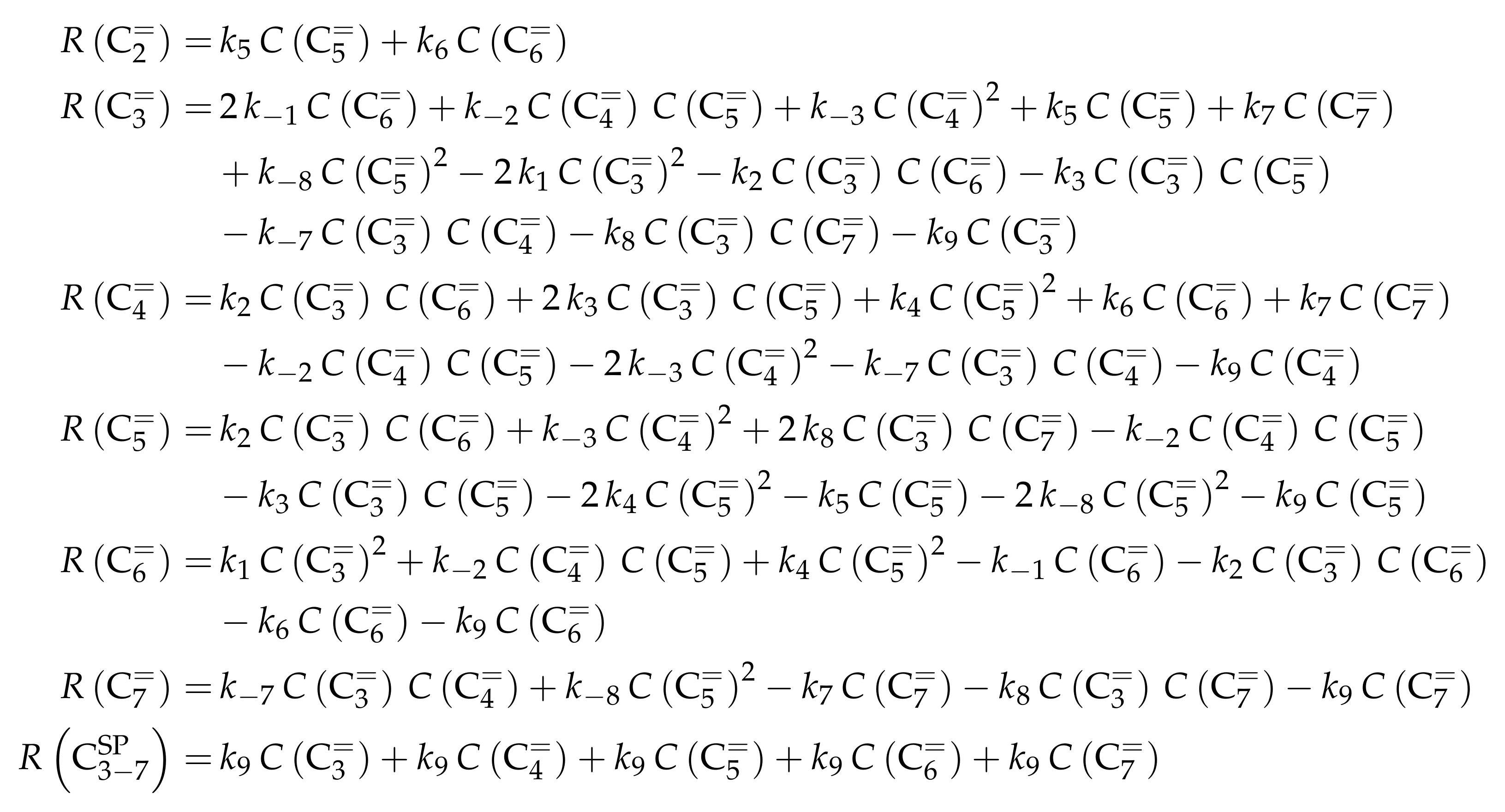

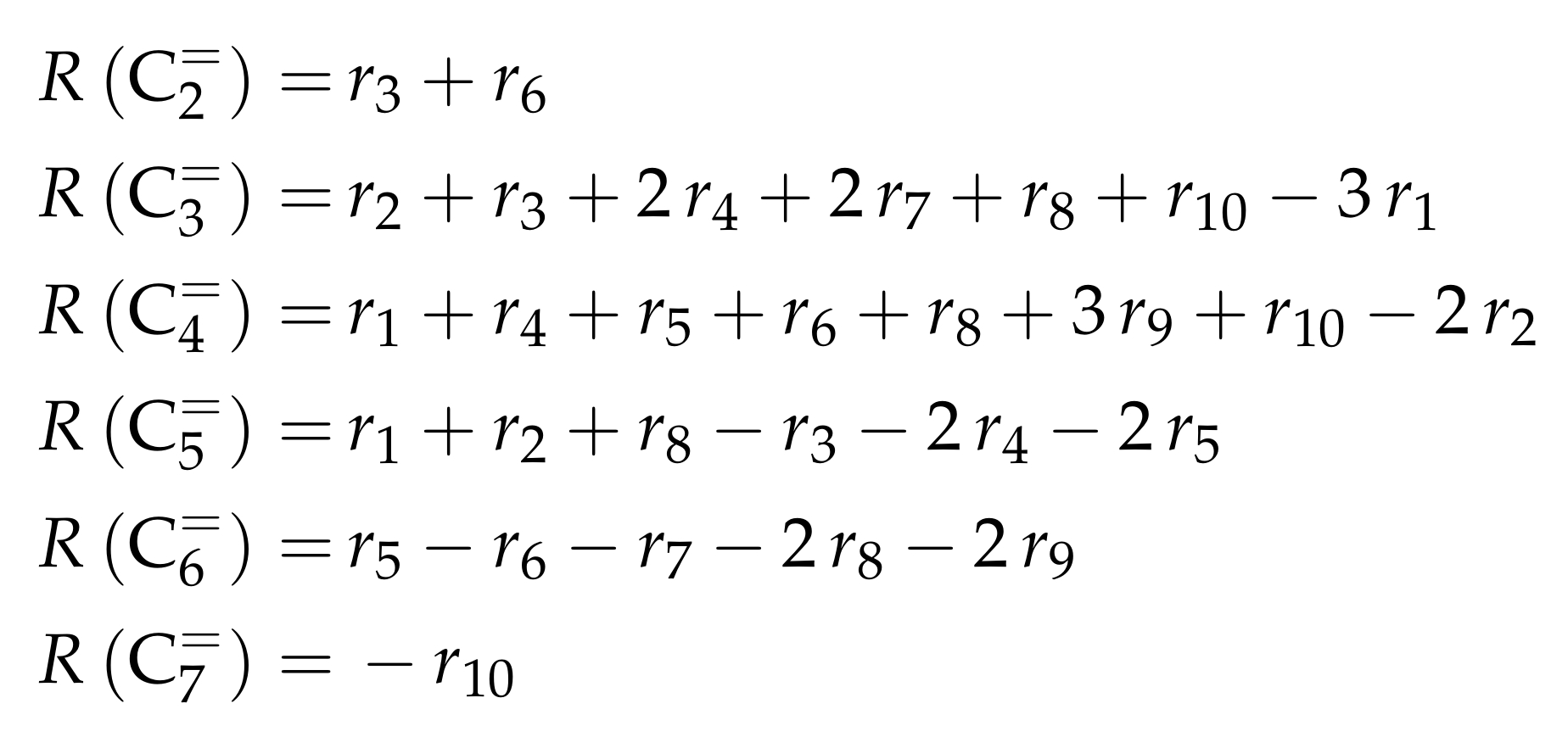
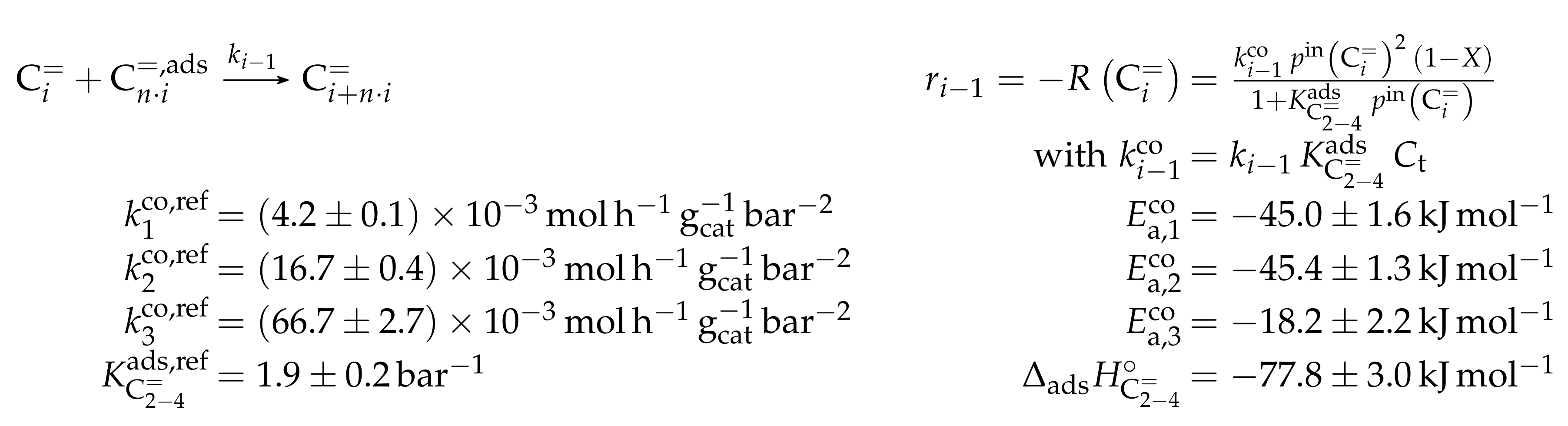

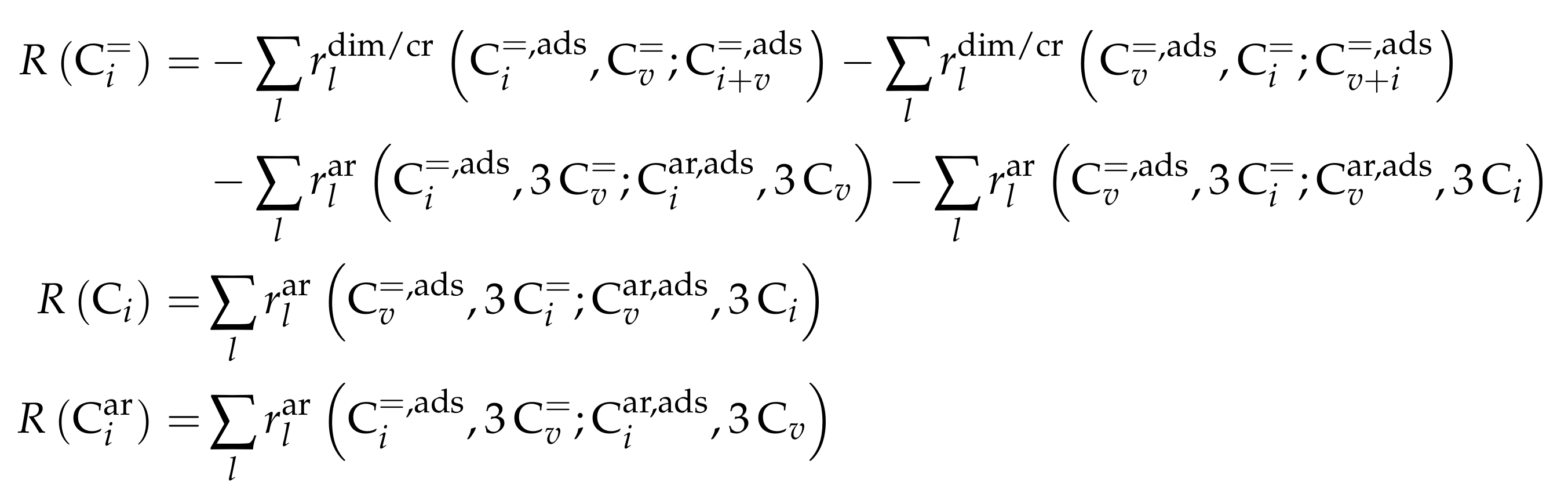
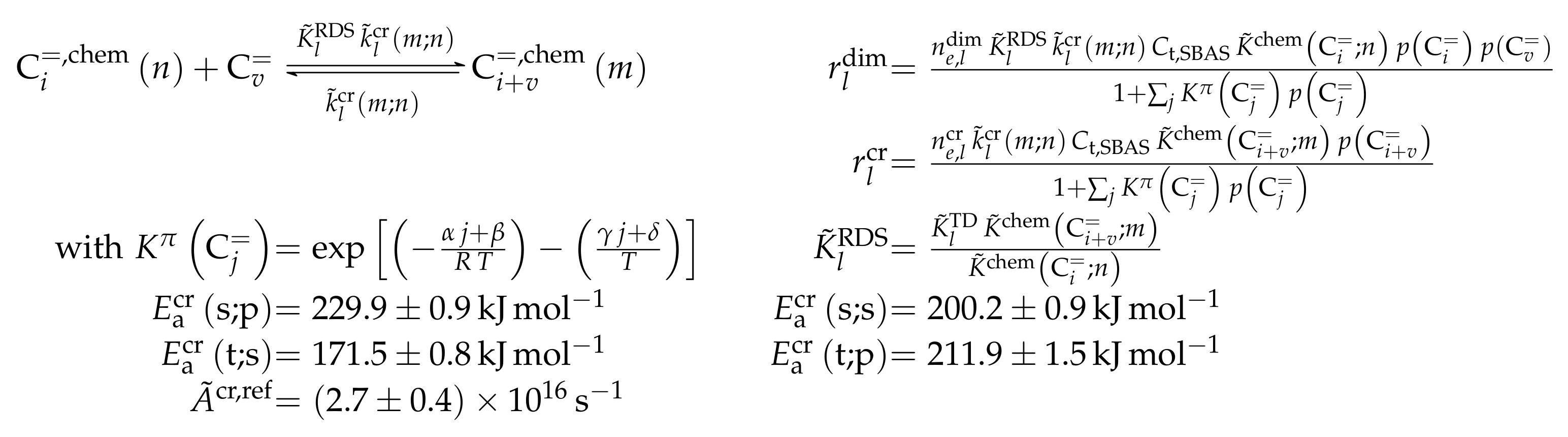
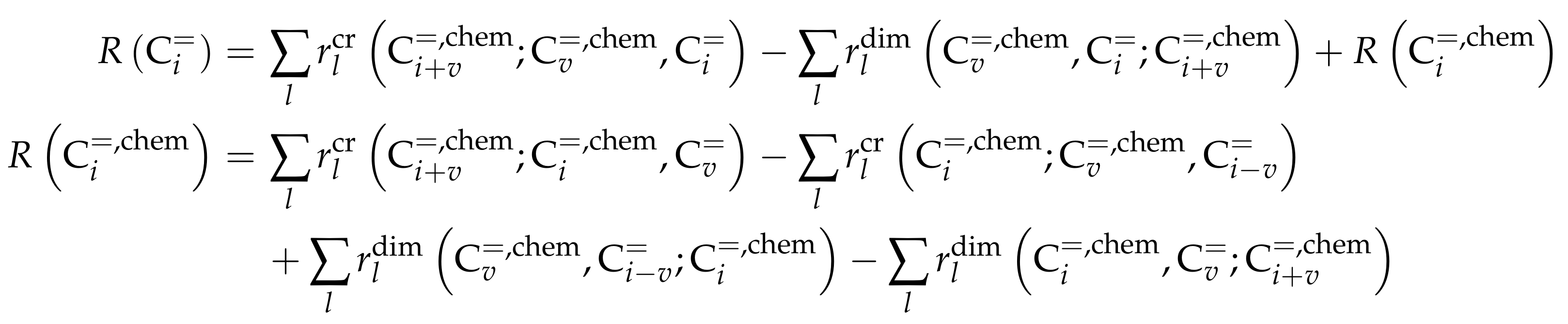
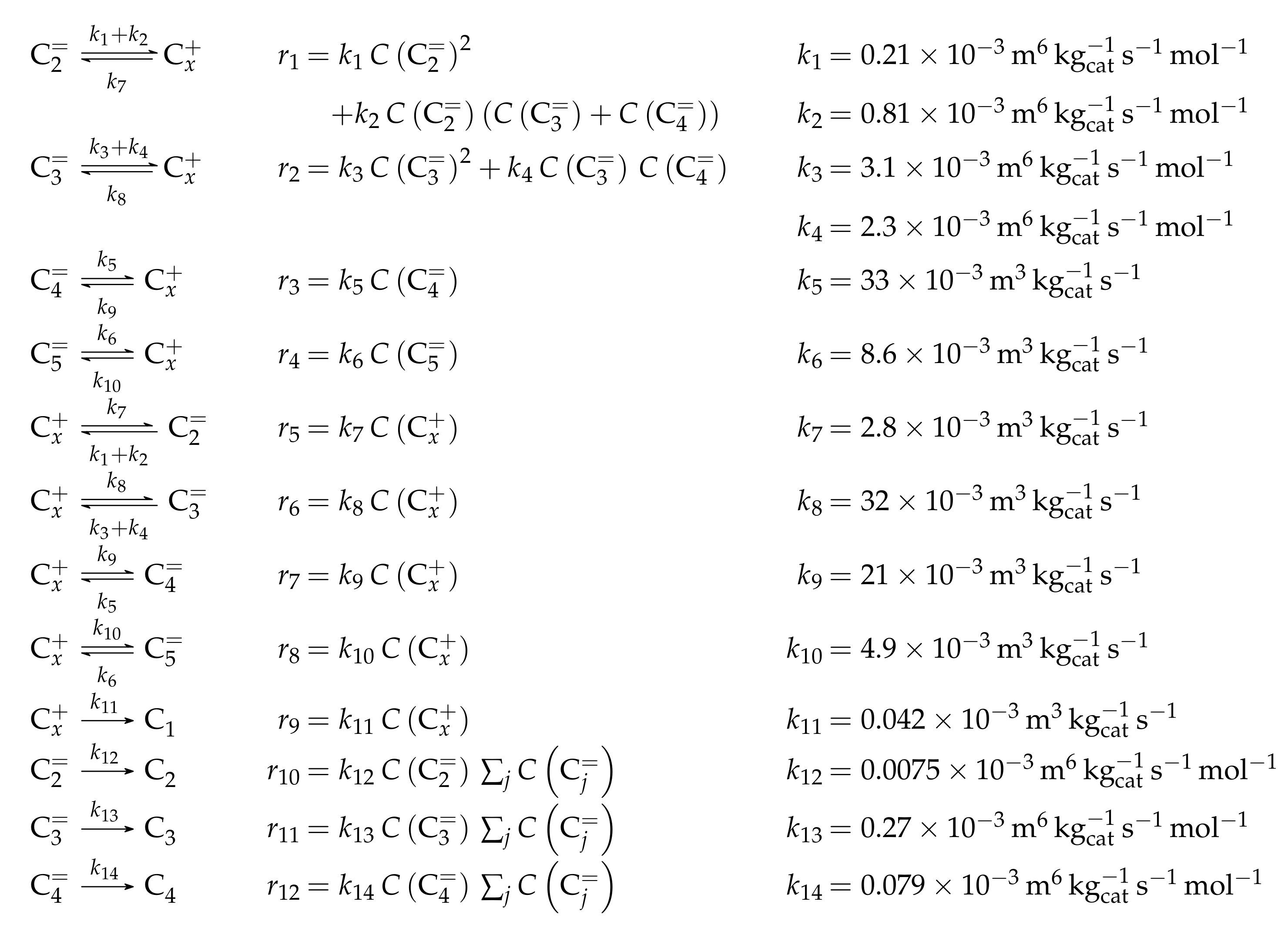
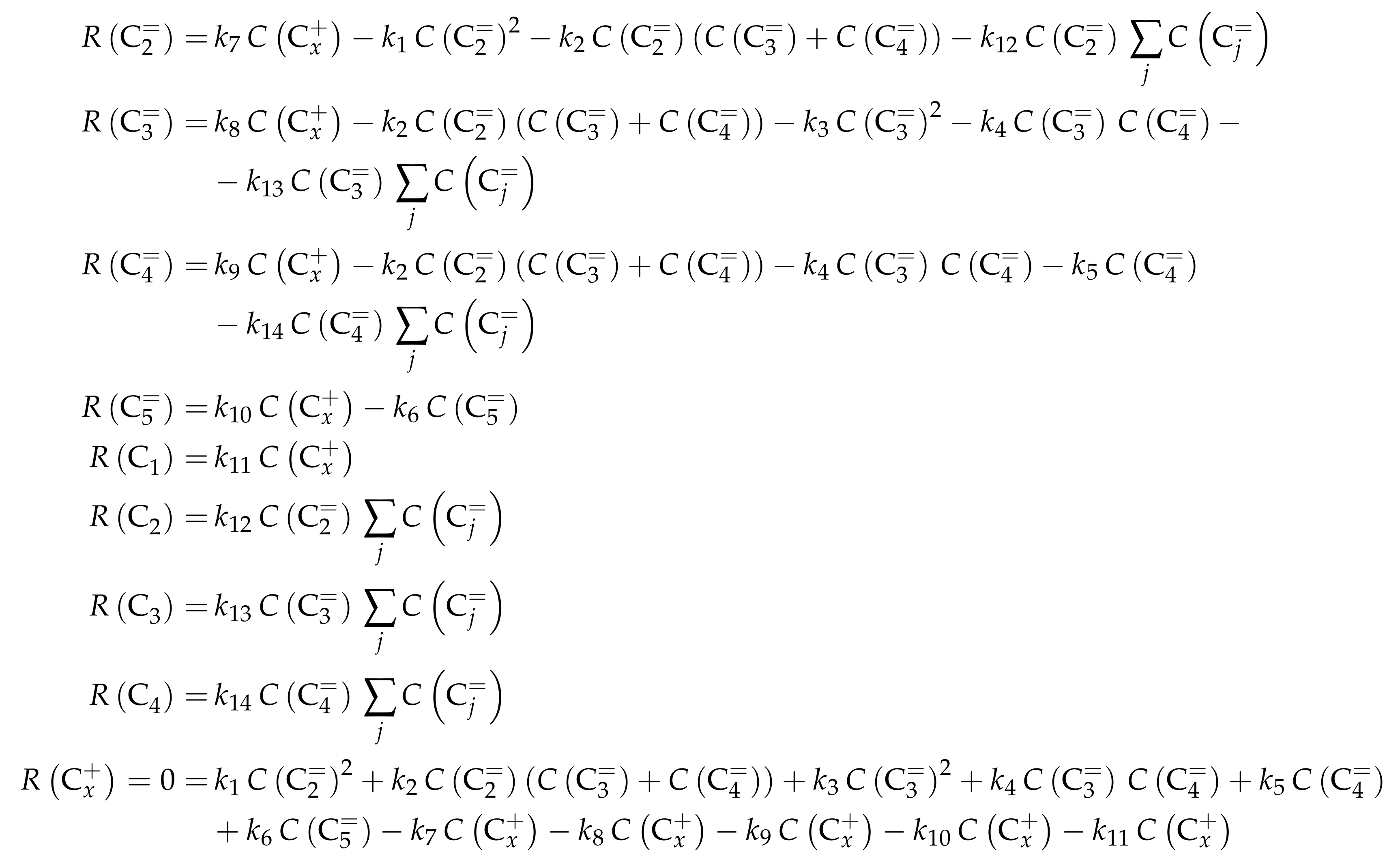

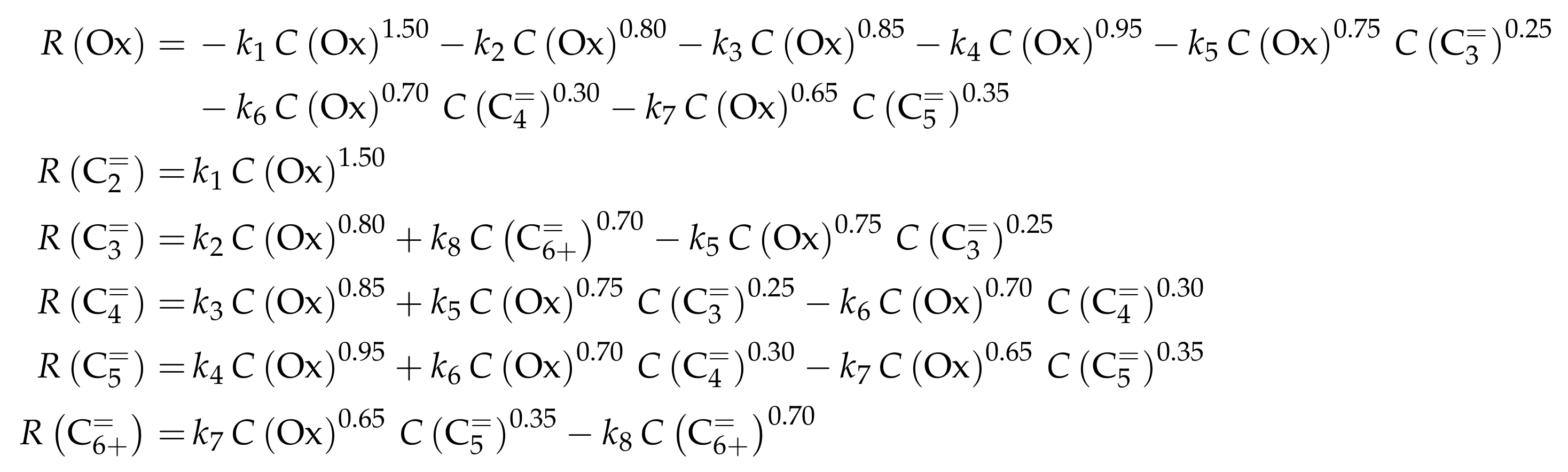

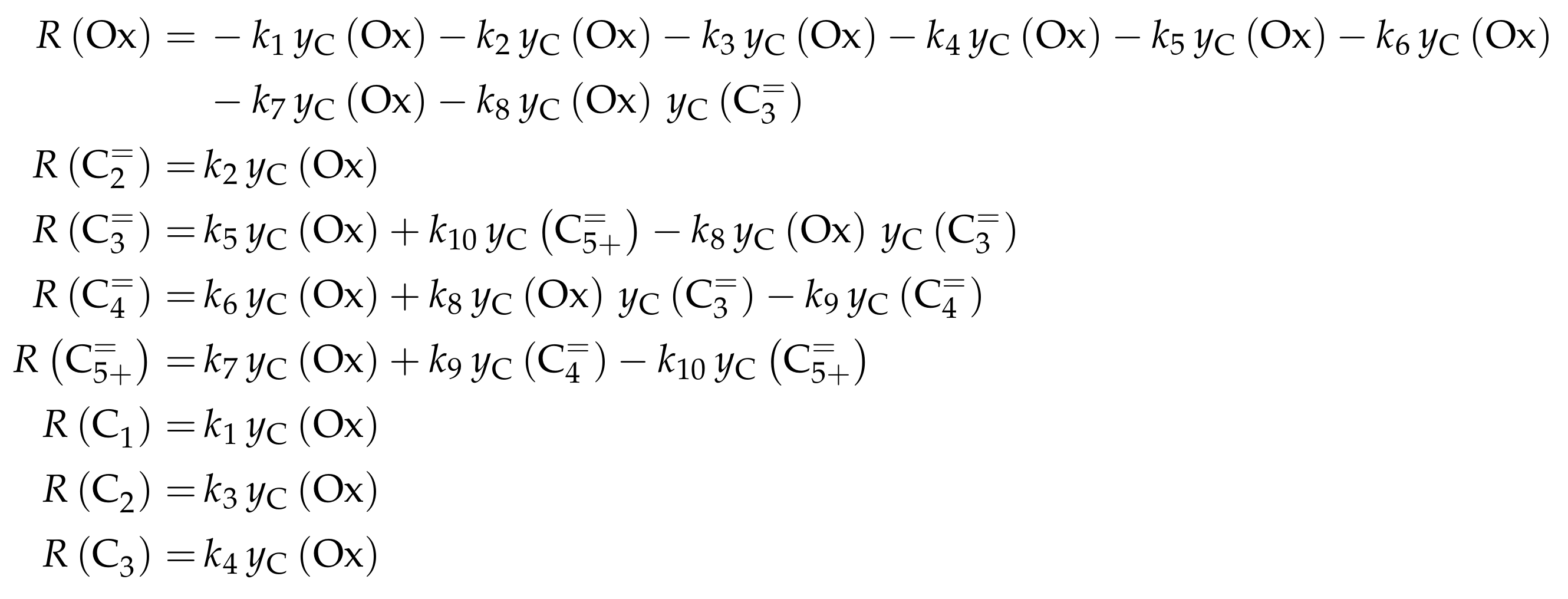



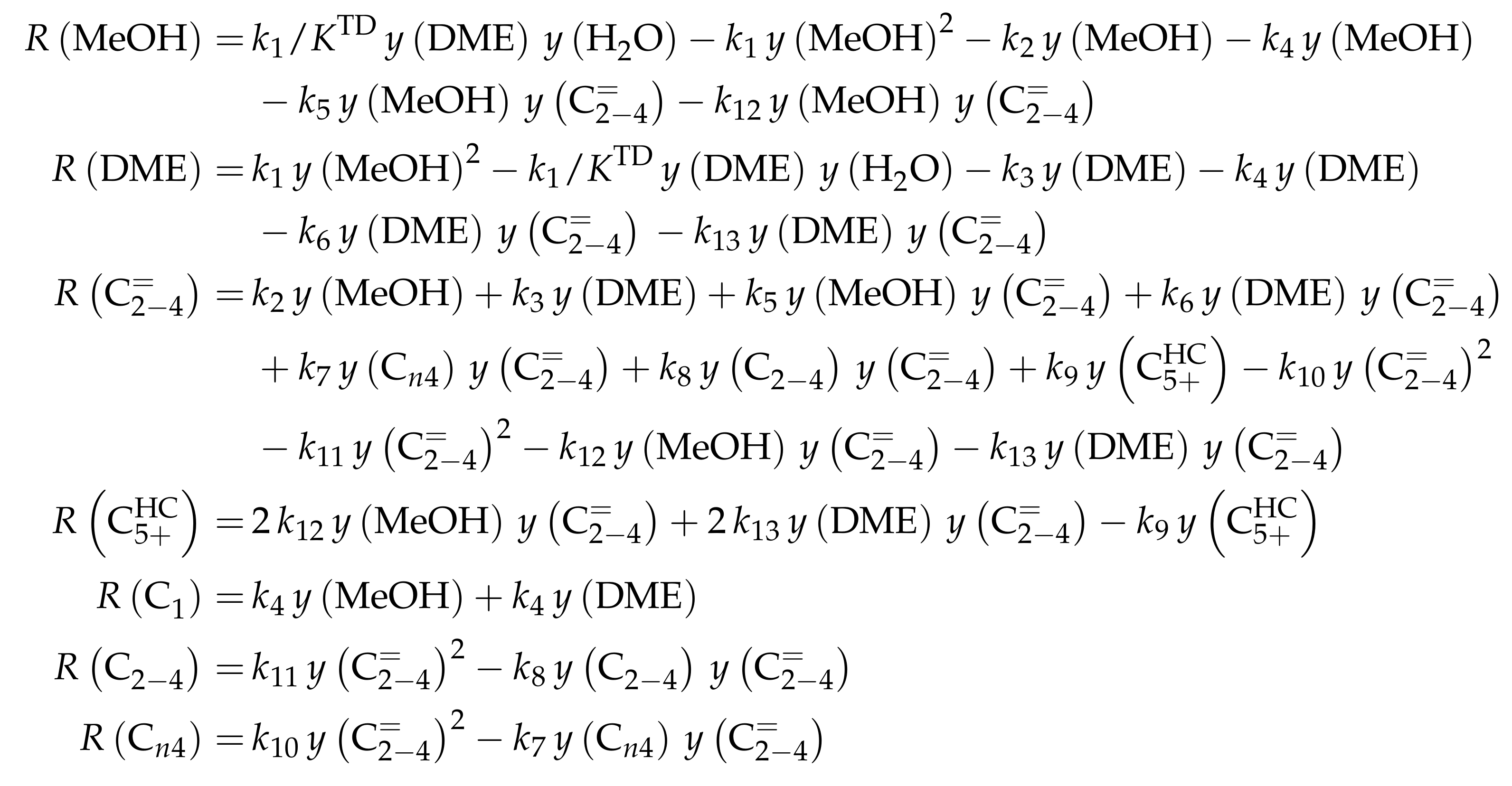



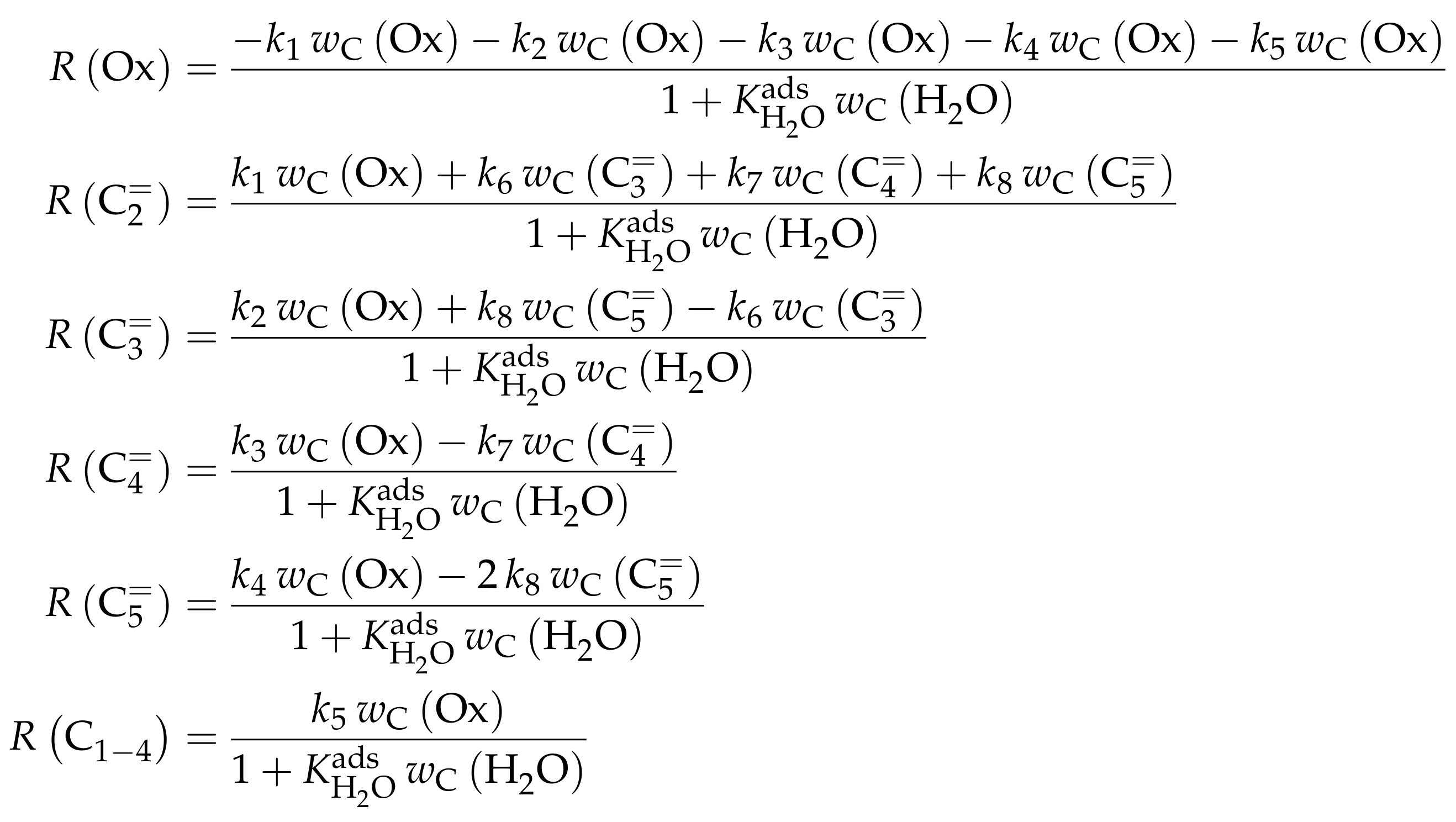
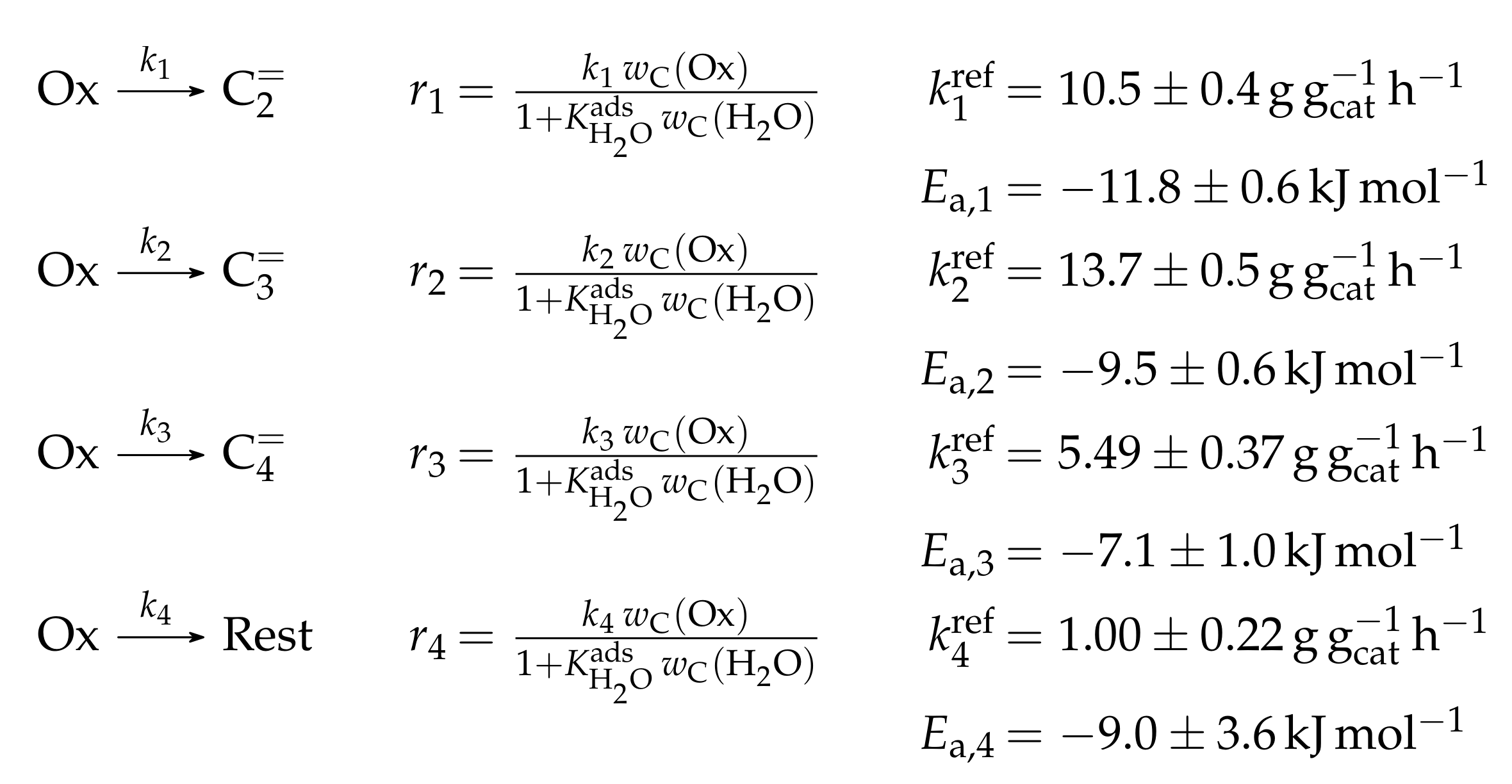
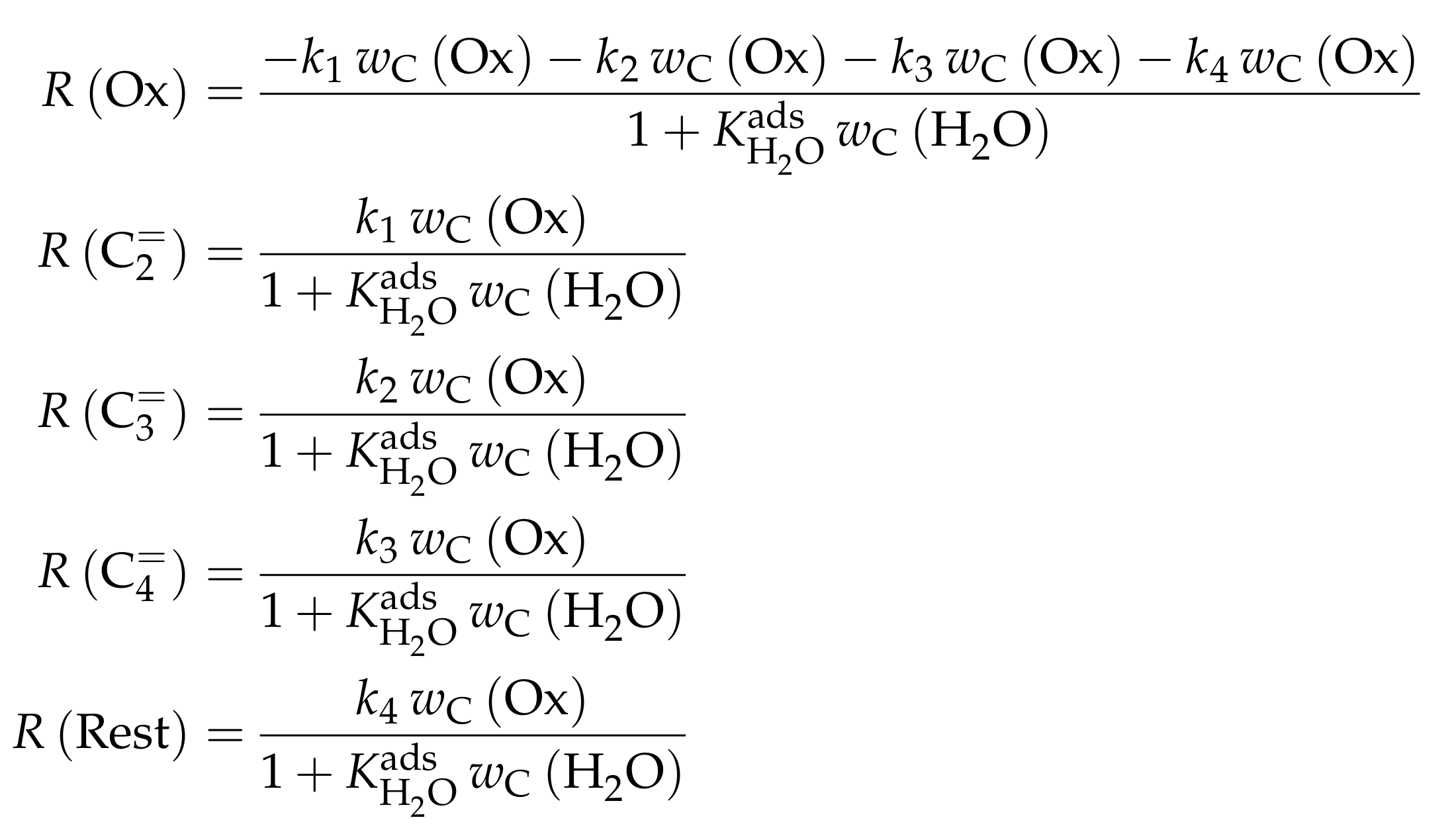


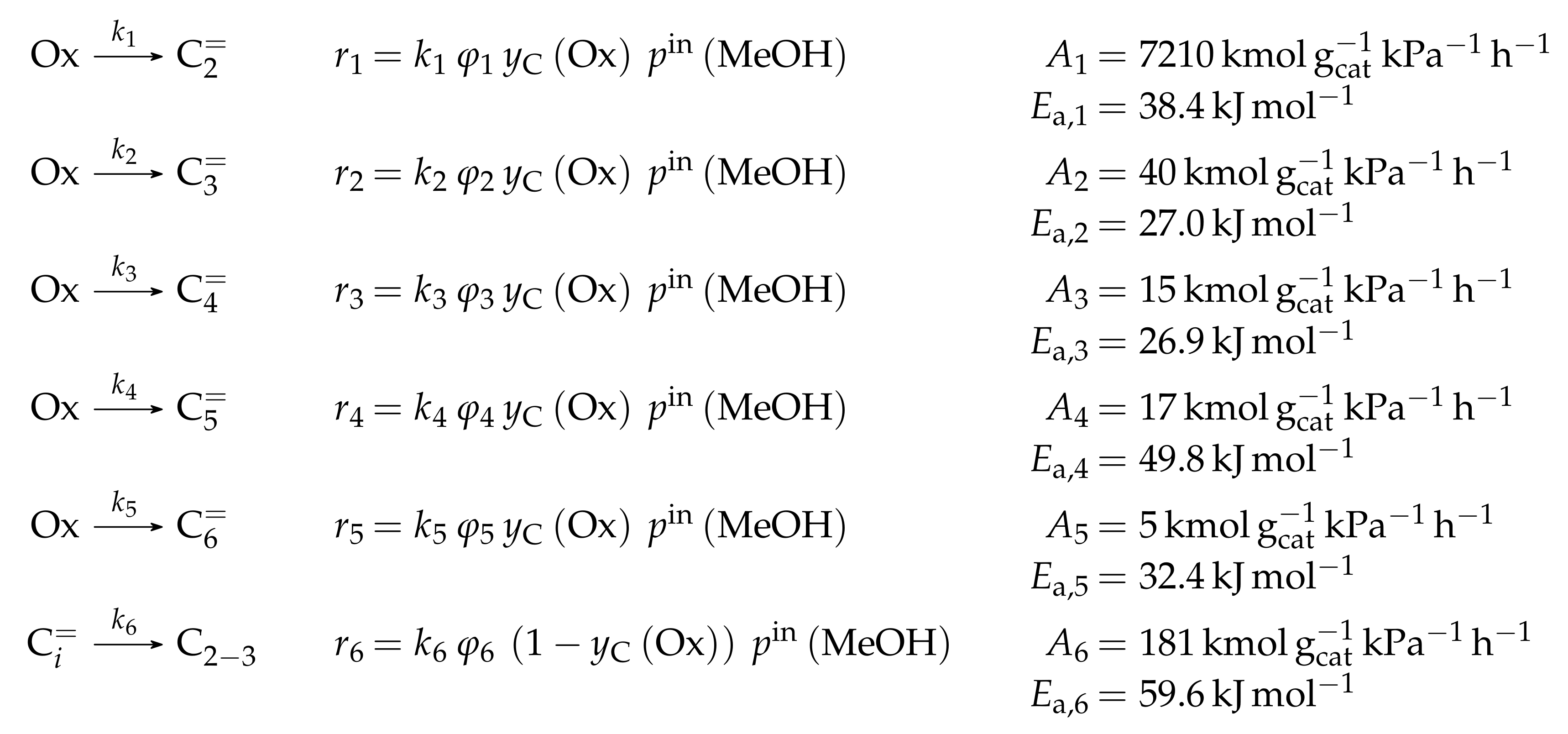
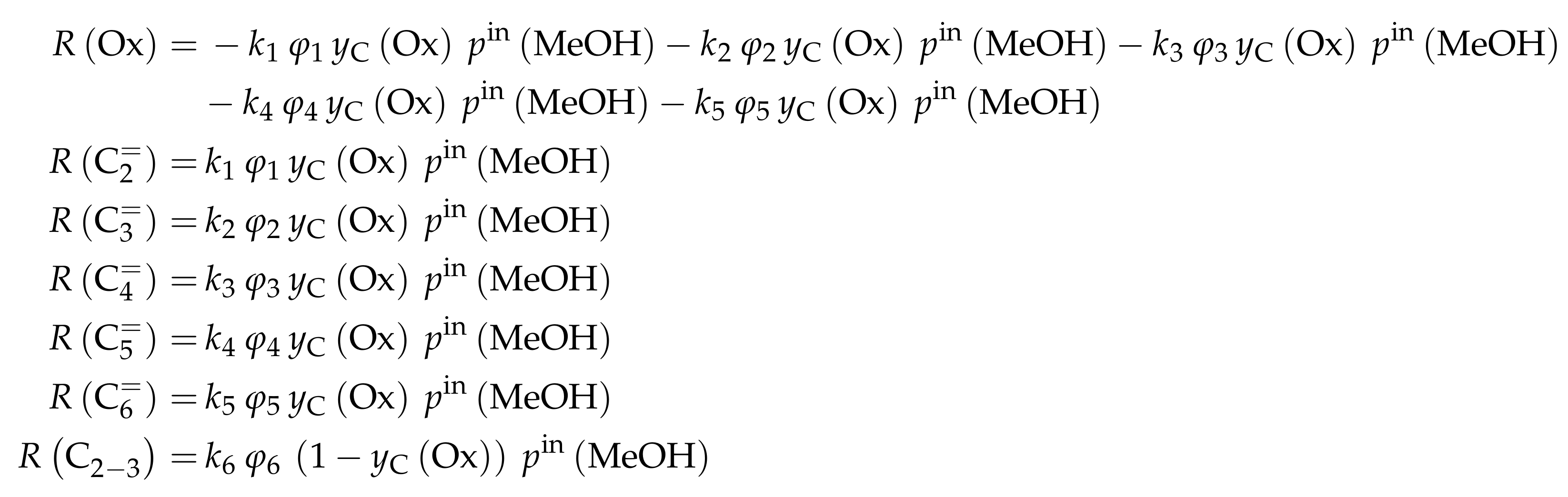

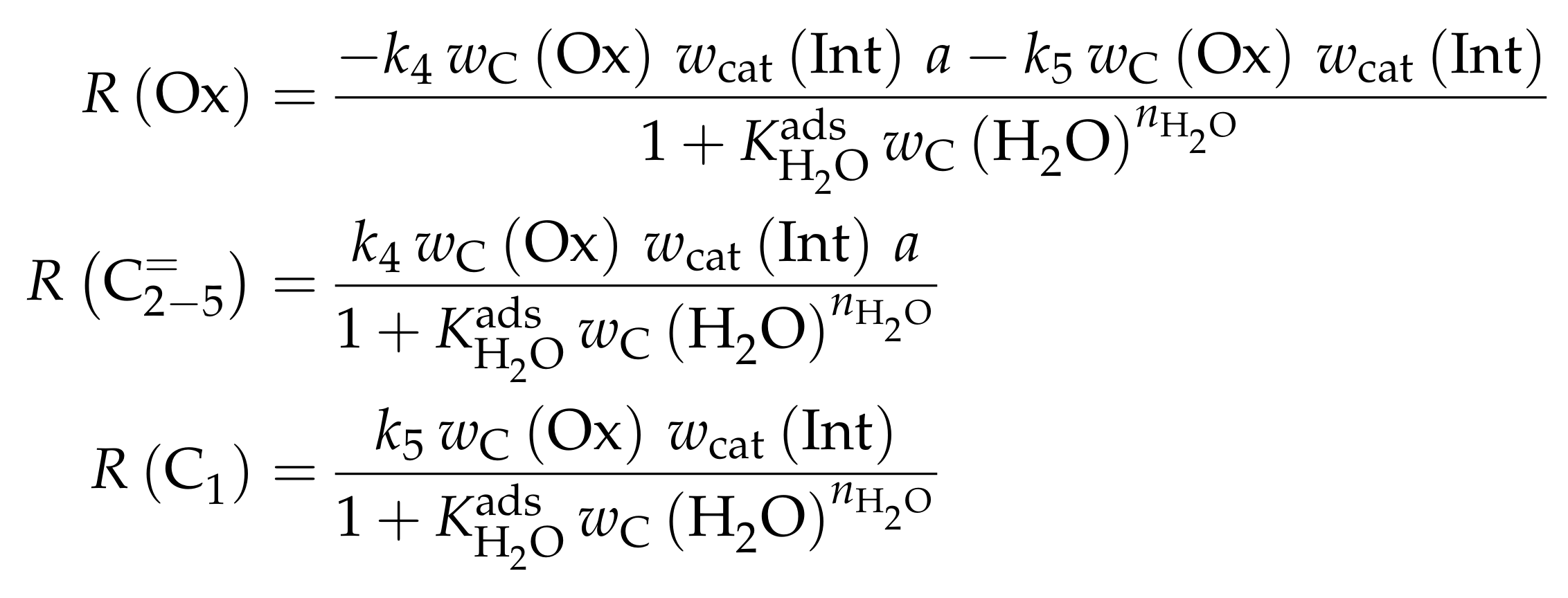


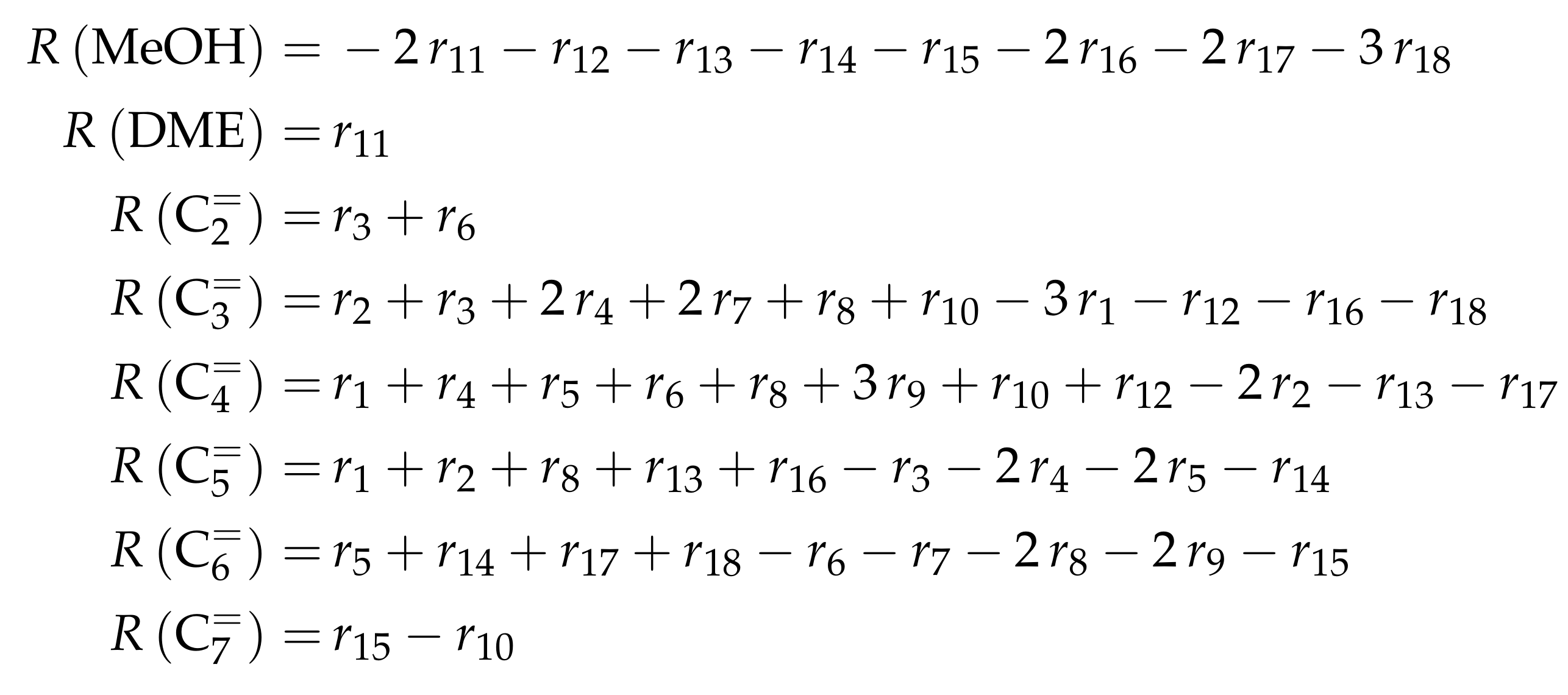

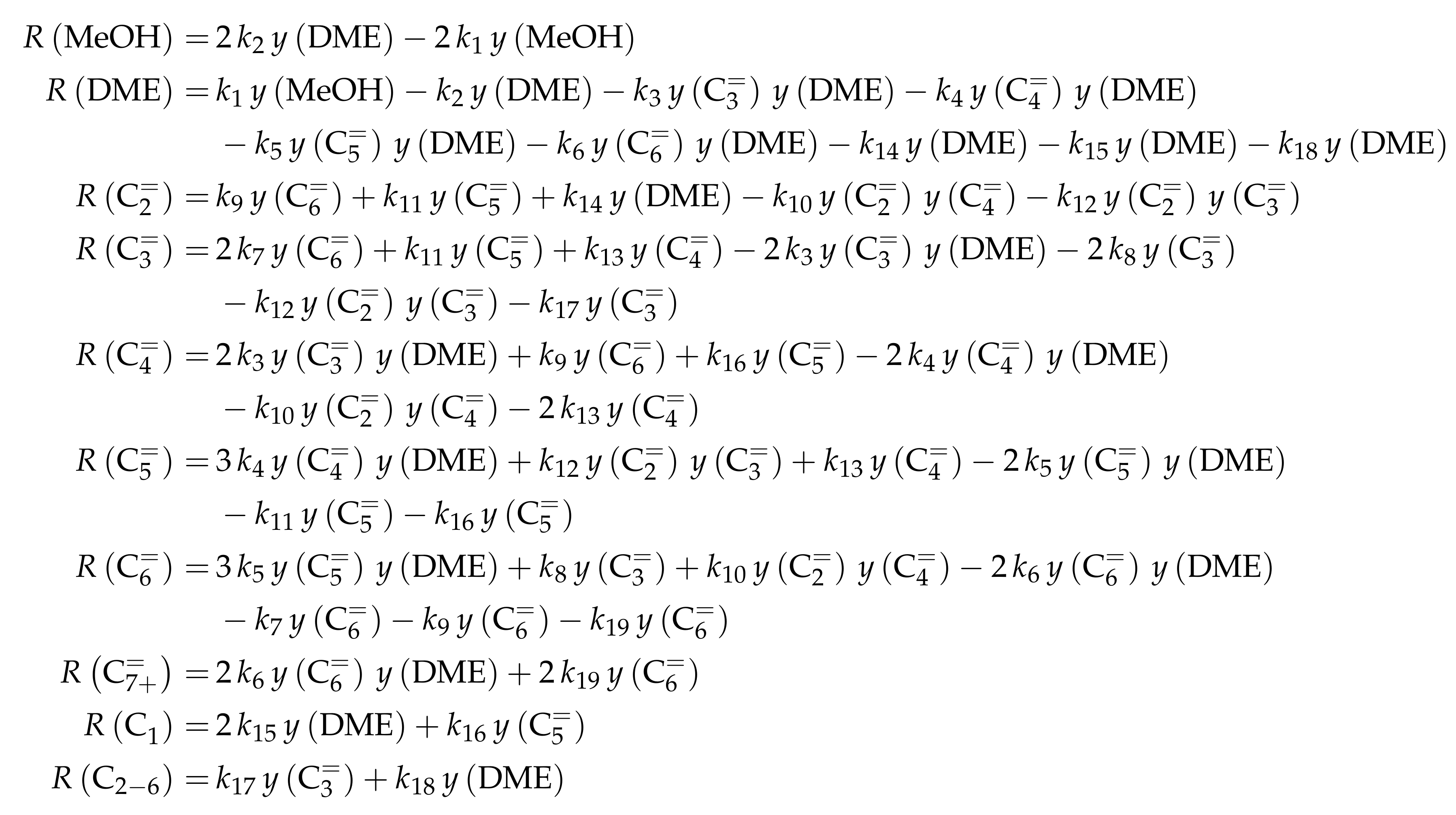
| Model | Zeolite Type | Si/Al | Total Acidity | BAS/LAS | BET | TOS | Extrudate | |
|---|---|---|---|---|---|---|---|---|
| Epelde [235] | ZSM-5 (1 K) | 280 | mmol (t-BA) | - | 194 | 5 | 150–300 μm | 25/30/45 (Zeolite/Bentonite/Alumina) |
| Ying [236] | ZSM-5 | 103 | mmol (NH) | - | 340 | 420–841 μm | Yes | |
| Huang [166] | ZSM-5 | 200 | mmol (NH) | 1.35 at 423 | 0–10 | 125–149 μm | 70/30 (Zeolite/Alumina) | |
| Borges [165] | ZSM-5 | 30 | - | - | 416 | 0– | - | No |
| Oliveira [237] | ZSM-5 (0, 0.52, 0.65 and 0.80 Na) | 30 | - | - | 416 | 0– | - | No |
| von Aretin [164] | ZSM-5 | 90 | mmol (CHN) | 4.27 | 454 | > 6 | 400–500 μm | No |
| Zhou [77] | SAPO-34 | 0.25 | mmol (NH) | - | 550 | μm | No |
| Model | Feed | T | (W/) | Mech. | Ads. | Side prod. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Epelde [235] | , He | 673–873 | 1.5 bar | 0.375–1.35 bar | 0.75 | 8 | 23 | 51 | 385 | No | No | , | |
| 5 | 16 | 51 | 239 | ||||||||||
| Ying [236] | , | 673–763 | bar | bar | 0.67 | 7 | 28 | 115 | 777 | No | No | , | |
| , | 0.16 h (1) | 0.65 | |||||||||||
| , | 0.07 h (1) | 0.57 | |||||||||||
| , | 0.10 h (1) | 0.94 | |||||||||||
| , | 0.04 h (1) | 0.98 | |||||||||||
| Huang [166] | 3 NW (2) | 673–763 | bar | bar | 1.12 kgcat s | 0.33 | 6 | 44 | 104 | 580 | LH, HW | , H2O | No |
| 4 NW (2) | 0.0706 bar | 0.73 kgcat s | 0.40 | ||||||||||
| 5 NW (2) | 0.0601 bar | 0.39 kgcat s | 0.23 | ||||||||||
| 6 NW (2) | 0.0532 bar | 0.20 kgcat s | 0.46 | ||||||||||
| 7 NW (2) | 0.0476 bar | 0.03 kgcat s | 0.46 | ||||||||||
| Borges [165] | , | 473–723 | bar | 0.05– bar | gcat h | - | 3 | 8 | 36 | 100 | ER, HW | No | |
| , | 1.55 gcat h | - | |||||||||||
| , | 0.27 gcat h | - | |||||||||||
| Oliveira [237] | , | 473–723 K | 1.013 bar | 0.05–0.30 bar | 9.33 gcat h | - | 17 | 20 | 61 | 1017 | L, ER, HW | , | |
| , | 1.55 gcat h | - | |||||||||||
| , | 0.27 gcat h | - | |||||||||||
| von Aretin [164] | , | 633–733 | bar | 0.043– bar | 0.55 | 5 | 5 | 141 | 700 | L, ER, HW | No | ||
| Zhou [77] | (3) | 723 K | bar | bar (3) | 0.22 h (4) | 0.78 | 8 | 14 | 16 | 114 | No | No | |
| (3) | 0.12 h (4) | 0.65 | |||||||||||
| (3) | 0.12 h (4) | 0.82 |
| Model | Zeolite Type | Si/Al | Total Acidity | BAS/LAS | BET | TOS | Extrudate | |
|---|---|---|---|---|---|---|---|---|
| Menges [139] | ZSM-5 | 250 | - | - | - | 0–3 | 2 mm | 50/50 |
| (Zeolite/AlPO4) | ||||||||
| Jiang [251] | ZSM-5 | 200 | - | - | - | 2 | 600–900 μm | No |
| Gayubo [114] | ZSM-5 | 24 | mmol (NH) | 2.9 | 124 m2 | 6 h | 150–300 μm | 25/30/45 (Zeolite/Bentonite/Alumina) |
| Aguayo [252] | ZSM-5 | 30 | mmol (NH) | 1.5 at 423 | 220 | 5 h | 150–300 μm | 25/30/45 (Zeolite/Bentonite/Alumina) |
| Pérez [253] | ZSM-5 | 280 | mmol (t-BA) | - | 301 | h | 125–300 μm | 50/30/20 (Zeolite/Boehmite/Alumina) |
| Park [132,254] | ZSM-5 | 200 | - | - | 400 | 0–5 | 500–1000 μm | No |
| Kumar [19] | ZSM-5 | 200 | mmol | - | 400 | 0–5 | 500–1000 μm | No |
| Gayubo [255] | SAPO-34 | 0.16 | mmol (NH) | - | 875 | 1 h | 100–300 μm | 25/30/45 (Zeolite/Bentonite/Alumina) |
| Ying [256] | SAPO-34 | - | - | - | 264 | 0 | 250–400 μm | Yes |
| Chen [257] | SAPO-34 | 0.16 | - | - | - | >0 | 105–290 μm | No |
| Alwahabi [258] | SAPO-34 | - | - | - | - | 0.25 h | 1.1 μm | No |
| Gayubo [259,260] | SAPO-18 | 0.3 | 0.12 mmol (NH) | - | 171 | 0– | 150–250 μm | 25/45/30 (Zeolite/Bentonite/Alumina) |
| Kumar [146] | ZSM-23 | 26 | 0.62 mmol | - | - | 0–7 | 250–420 μm | No |
| Model | Feed | T | (W/) | Mech. | Ads. | Side prod. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Menges [139] | MeOH, N2 | 673–723 K | 1.65 bar | 0.170–0.556 bar | 280 | 1 | 6 | 16 | 78 | 452 | No | No | No |
| Jiang [251] | MeOH | 673–773 | - | - | 384 | - | 8 | 20 | 24 | 172 | No | No | C1–3 |
| Gayubo [114] | MW (3,4) | 573–723 | bar | - | 0.8 | 3 | 15 | - | - | HW | H2O | - | |
| Aguayo [252] | MeOH | 673–823 | bar | bar | 1 | 7 | 26 | 18 | 100 | No | No | C1–4, | |
| Pérez [253] | DME | 598–673 K | 1.10 bar | 1.10 bar | 6 | 1 | 10 | 30 | 39 | 360 | HW | MW | C1–4, |
| DME, He | 648 K | 0.28–1.10 bar | 1 | 0.5 | |||||||||
| DME, H2O | 648 K | 0.99–1.10 bar | 1 | 0.5 | |||||||||
| DME, MeOH | 623–673 K | 1.10 bar | 1 | 0.5 | |||||||||
| Park [132,254] | MNW (4) | 633–753 | 1.04 bar | - | 2 | 0.7 | 9 | 33 | 31 | 246 | LLEH | 28 MD (4) | No |
| Kumar [19] | MNW (4) | 633–753 | 1.04 bar | - | 0.7 | 8 | 29 | - | - | LLEH | 27 MD (4) | No | |
| Gayubo [255] | MW (3,4) | 623–748 | - | - | 0.44 | 1 | 5 | 17 | - | - | HW | H2O | C1–4 |
| 4 | 8 | - | - | HW | H2O | C1–4 | |||||||
| Ying [256] | MW (3,4) | 723–763 | 1.013 bar | 0.203–1.013 bar | 0.03 | 1 | 7 | 13 | 43 | 288 | HW | H2O | C1–6 |
| Chen [257] | HM (4,11) | 673–823 | - | 0.072–0.830 bar | 0.02 h | 0.95 | 7 | 12 (4x) | - | - | No | No | C2–3 |
| Alwahabi [258] | MeOH, H2O | 673–723 | 1.04 bar | 0.208 bar | 2.95 | 0.88 | 6 | 30 | 9 | 24 | LLEH | 25 MD | No |
| Gayubo [259,260] | MW (3,4) | 598–748 | - | - | 0.68 | 0.9 | 4 | 11 | - | - | HW | H2O | C1 |
| 5 | 15 | - | - | HW | H2O | C1–4 | |||||||
| Kumar [146] | MeOH, He | 673 | 1.013 bar | - | 57.7 | 0.95 | 7 | 8 | 12 | 76 | LLEH | 27 MD | No |
| Model | Zeolite Type | Si/Al | Total Acidity | BAS/LAS | BET | TOS | Extrudate | |
|---|---|---|---|---|---|---|---|---|
| Huang [240] | ZSM-5 | 200 | 0.012 mmol (NH) | 1.35 at 423 | 301.1 | 0–10 | 125–149 μm | 70/30 (Zeolite/Alumina) |
| Wen [303] | ZSM-5 on microfibers | 147 | - | - | 93 | - | 16.1 mm | No, but 19/81 (Zeolite/Microfiber) |
| ZSM-5 | 155 | - | - | - | - | 100–300 μm | No |
| Model | Feed | T | (W/) | Mech. | Ads. | Side prod. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Huang [240] | MeOH, , | 673–763 K | 1.013 bar | 0.050 bar | 4.3 | 0.90 | 8 | 20 | 79 | 612 | LH, HW | , H2O, | No |
| N2, H2O (1) | 0.050 bar | ER | MeOH | ||||||||||
| MeOH, , | 2.9 | 0.92 | |||||||||||
| N2, H2O (1) | |||||||||||||
| MeOH, , | 2.5 | 0.92 | |||||||||||
| N2, H2O (1) | |||||||||||||
| MeOH, , | 2.5 | 0.92 | |||||||||||
| Wen [303] | MeOH, N2 (4) | 673–753 | 1.013 bar (5) | 0.304 bar | 32 gcat h | 1 | 10 | 38 | 46 | 422 | No | No | C1–6 |
| Wen [303] | MeOH, N2 (4) | 673–753 | 1.013 bar (5) | 0.304 bar | 32 gcat h | 1 | 10 | 38 | 45 | 412 | No | No | C1–6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Standl, S.; Hinrichsen, O. Kinetic Modeling of Catalytic Olefin Cracking and Methanol-to-Olefins (MTO) over Zeolites: A Review. Catalysts 2018, 8, 626. https://doi.org/10.3390/catal8120626
Standl S, Hinrichsen O. Kinetic Modeling of Catalytic Olefin Cracking and Methanol-to-Olefins (MTO) over Zeolites: A Review. Catalysts. 2018; 8(12):626. https://doi.org/10.3390/catal8120626
Chicago/Turabian StyleStandl, Sebastian, and Olaf Hinrichsen. 2018. "Kinetic Modeling of Catalytic Olefin Cracking and Methanol-to-Olefins (MTO) over Zeolites: A Review" Catalysts 8, no. 12: 626. https://doi.org/10.3390/catal8120626
APA StyleStandl, S., & Hinrichsen, O. (2018). Kinetic Modeling of Catalytic Olefin Cracking and Methanol-to-Olefins (MTO) over Zeolites: A Review. Catalysts, 8(12), 626. https://doi.org/10.3390/catal8120626





