3.1. Differential Form of the TEM
A single-electrode reaction shown as
is a fundamental reaction and is thermodynamically characterized by the Nernst equation. This equation will play an important role in the DPM. The
can be expressed in two ways:
In this paper, usage of the concentration rather than the activity is beneficial due to its easy accessibility to the experimental data. We also know an important kinetic relation between net current density,
i and overpotential,
[
8]:
Arranging the above, another expression of
is obtained. Where,
,
and
. From mathematical point of view,
,
and
are interpreted as weighted functions for
,
, and
, respectively. The term
related to the charge transfer process is independent of the
. It has a constant effect of 1 on the
. The terms
and
, related to the diffusion processes, have noticeable effects at
. The term
emerges in the anodic diffusion transfer process and will have an exponential influence on the
when the
has a positive value. Conversely, the term
shows the opposite effects on the
and negligible value when the
has a positive value.
Considering the current additivity, Equation (4) can be divided into the anodic branch current density,
and the cathodic branch current density,
:
where,
and
.
The
is expressed and arranged below:
Since
is the equilibrium sate, the same sate using the
expression is
, which is equal to
. Therefore, the equilibrium state for Equation (5) is shown as:
Differentiating Equation (4), the following polarization conductance,
, will be obtained:
when being far-cathodically polarized (
), the
will closely approximate to the cathodic branch current density,
:
Then, Equation (9) is simplified to:
Considering the mathematical relation between and the polarization resistance, , the following relations hold true.
Using the above relation, Equation (11) can be arranged to:
when
, the above is simplified to:
Taking logarithms of the above is:
The gradient of the above is:
It is important to know that the relation of Equation (16) is valid for the Tafel equation. The reason is the following: the Tafel equation in the condition of Equation (10) is expressed as:
Differentiating the above, the
h(
i) expression for the Tafel equation is:
Taking the logarithms and the gradient of the above, the same relation of Equation (16) will be obtained. It is important to note that the
E(
i) region that satisfies the Tafel equation (Equation (17)) always satisfies the gradient relation (Equation (16)); the reverse is also true. This is an extremely useful tool when finding the proper Tafel slope region in experimental data. Additionally, Equation (16) is always valid without the need for a knowledge of reaction types such as reversible, irreversible, or quasi-reversible reaction. Visual differences among the reaction types will come to the much understanding. First of all, in order to grasp the graphical characteristics of the reaction types, the
and
h(
i) curves using the feasible data listed in
Table 1 are drawn.
The
curves are shown in
Figure 3.
We can readily distinguish the
of the irreversible reaction from others, but hardly between the reversible and quasi-reversible reaction curves. Another expression (
) of their curves, which is drawn using the same data listed in
Table 1, is shown in
Figure 4.
Figure 4a shows that the Tafel equation (
) is widely satisfied in the irreversible reaction.
Figure 4b shows that the Tafel slope (the
b term) is always valid for all types of reactions, because we can find the geometric evidence of the parallel curve with
in all reactions when making a close observation at
.
Comparing the
Figure 3 or
Figure 4a, the
expression exhibits more clear characteristics than the usual expressions such as
and the
E(
i) expression . Making further careful observations of
Figure 4a,b leads to some geometric commons, which are summarized as follows:
(I): All of the curves show a constant horizontal line at and have the Tafel slope when . Namely, it is acceptable that an .
(II): The reversible reaction (red curve) has a longer horizontal line with smaller h(0).
(III): The irreversible reaction (blue curve) has a shorter horizontal line with larger h(0).
(IV): Especially, there are straight lines with in the irreversible reaction.
(V): The curve for the reversible reaction has asymptotes with vertical lines corresponding to the exact and . ( and ).
(VI): The quasi-reversible reaction (green curve) shows almost the same shape as the reversible reaction, except for the crossing points with near and . ( and ).
When arriving at a decision of the reaction type, the (IV) will be helpful to judge whether
Eexp(
i) belongs to the irreversible reaction or not. To roughly determine the reaction type, let us consider the graphical relationship between the charge transfer rate constant,
, and the diffusion transfer rate constant,
(=
). Since almost all
and
are the order of
in an aqueous solution and practical
and
are
0.01 cm for a stirred solution and
0.05 cm for the stagnant condition, respectively; then, the
is roughly estimated as:
It may be accepted that the
will become less changeable and is regarded as the order of
. The total rate constant,
k, for the whole reaction is introduced [
10] and expressed as:
The relation between
k and
when
is graphically shown in
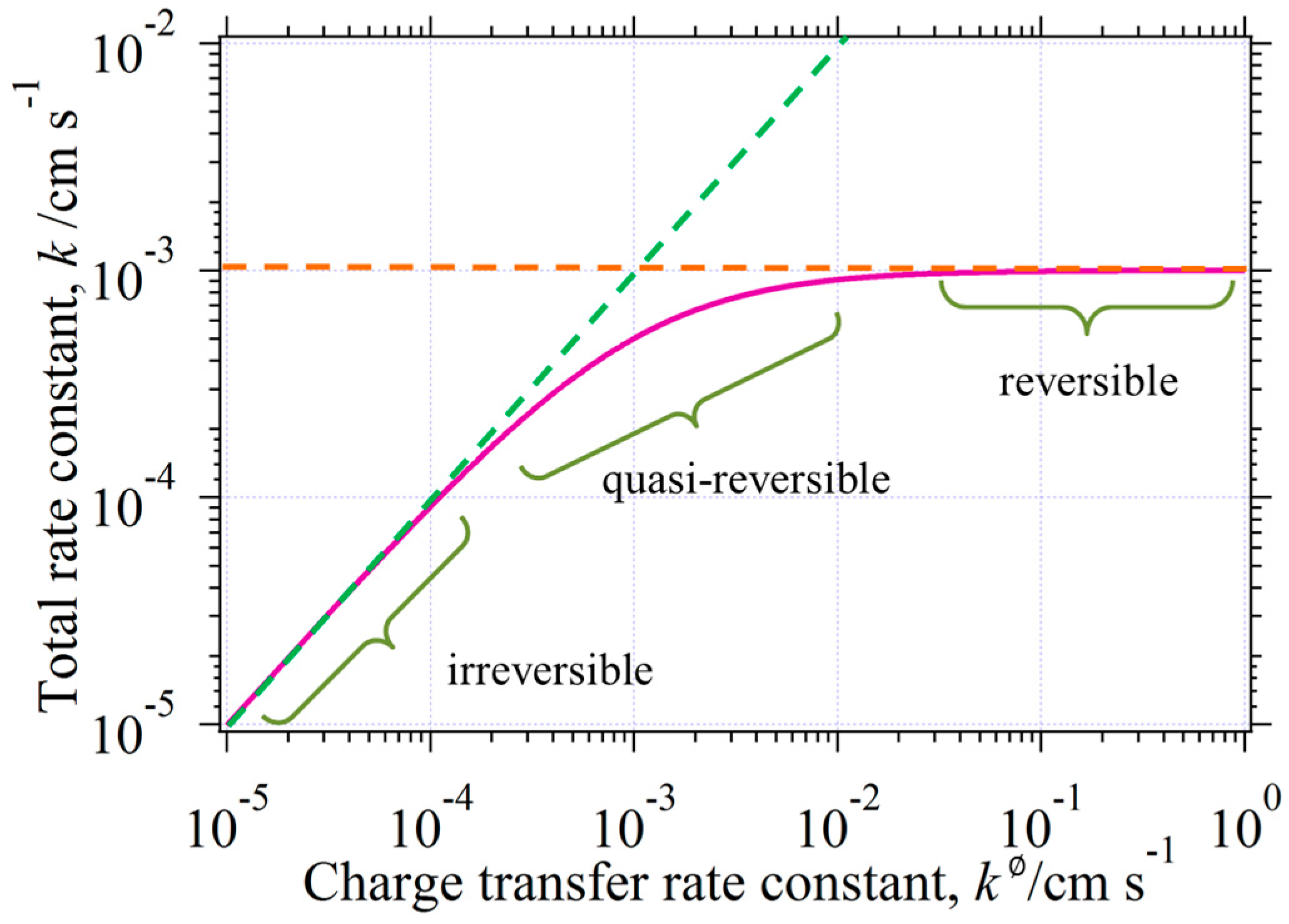
Figure 5.
Figure 5 tells us that the
k is depend on the
: a linear relation (
) is valid for
(the irreversible reaction) and a constant relation (
) is valid for
(the reversible reaction). Roughly speaking, it may be possible to say that the
Eexp(
i) having
is classified to the irreversible reaction and that having
is the reversible reaction.
3.2. Physical Factors Influenced on the h(i) Curve
At the stage of practical treatments of the experimental
Eexp(
i), it is necessary to consider the physical factors such as solution, oxide film, and adsorption gas layer resistances [
11]. Considering the oxide film polarization resistance of the cathodic site (
), the Equation (14) is renewed as:
The
always contains the solution polarization resistance (
):
This
usually includes, to a greater or lesser degree, the adsorption gas layer resistance under cathodic polarization operation. Arranging the Equation (22),
is obtained; where,
. The
is a summation of the two terms:
and
. The first term of
has information about
and the second term of
is on the physical resistances. Because the
is independent of the
i, it will be graphically emerged as the horizontal line when the |
i| becomes large. We can estimate it using the following operation [
8]:
In order to visualize the influence of the
on the
, the log
~log |
i| curves are drawn when
. The results are shown in
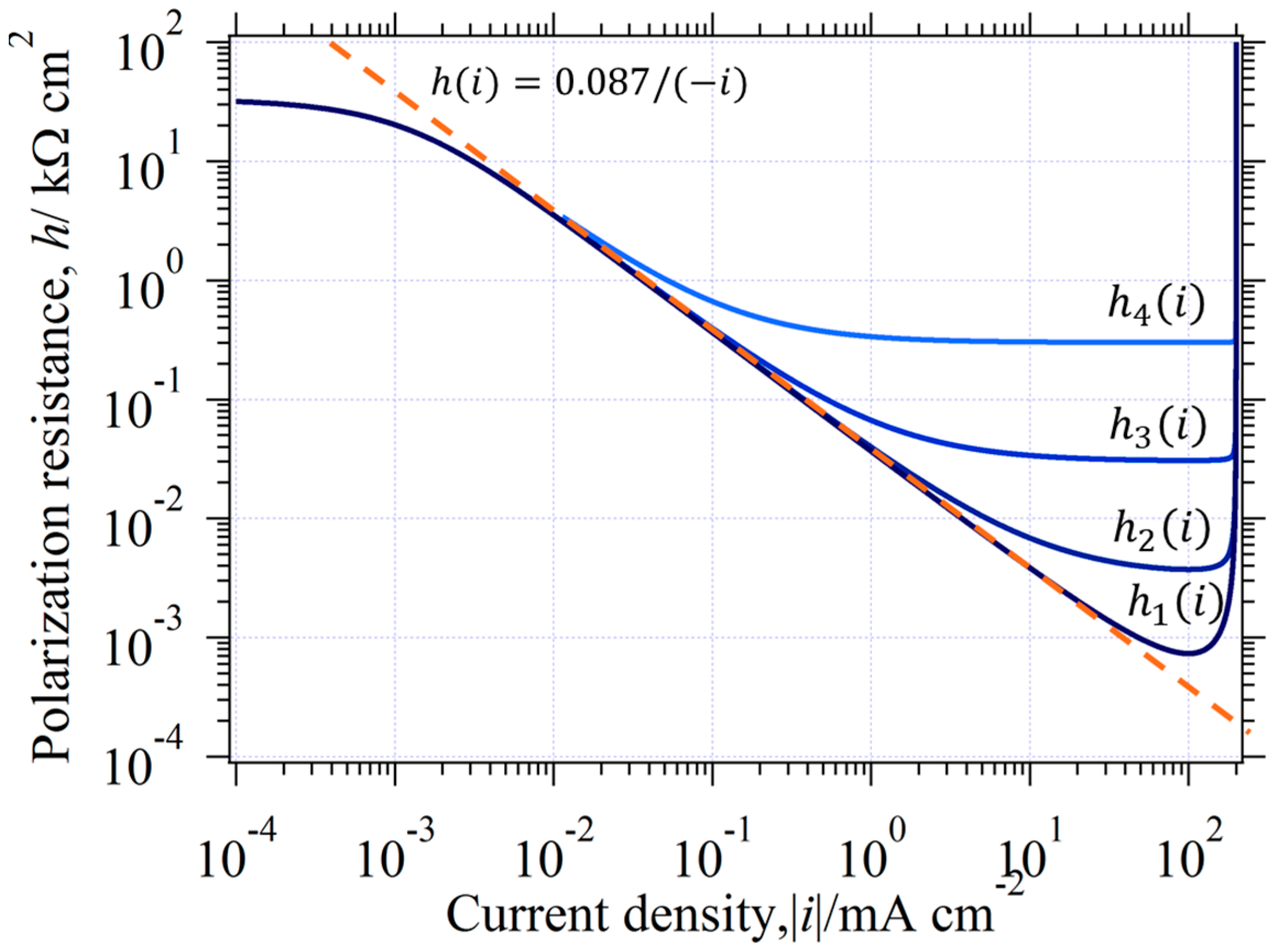
Figure 6.
The orange broken line of , on which the Tafel relation is completely satisfied, is added as a reference. We can see that the has a wide Tafel slope region but the has a very narrow region. Namely, we can hardly catch the Tafel slope region when the h(i) has the larger . Furthermore, we can hardly catch the accurate region when the decreases. In other words, in order to obtain the more accurate Tafel slope region it is necessary to employ a large solution and small environments which can widen the Tafel region.
3.4. Estimation by DPM
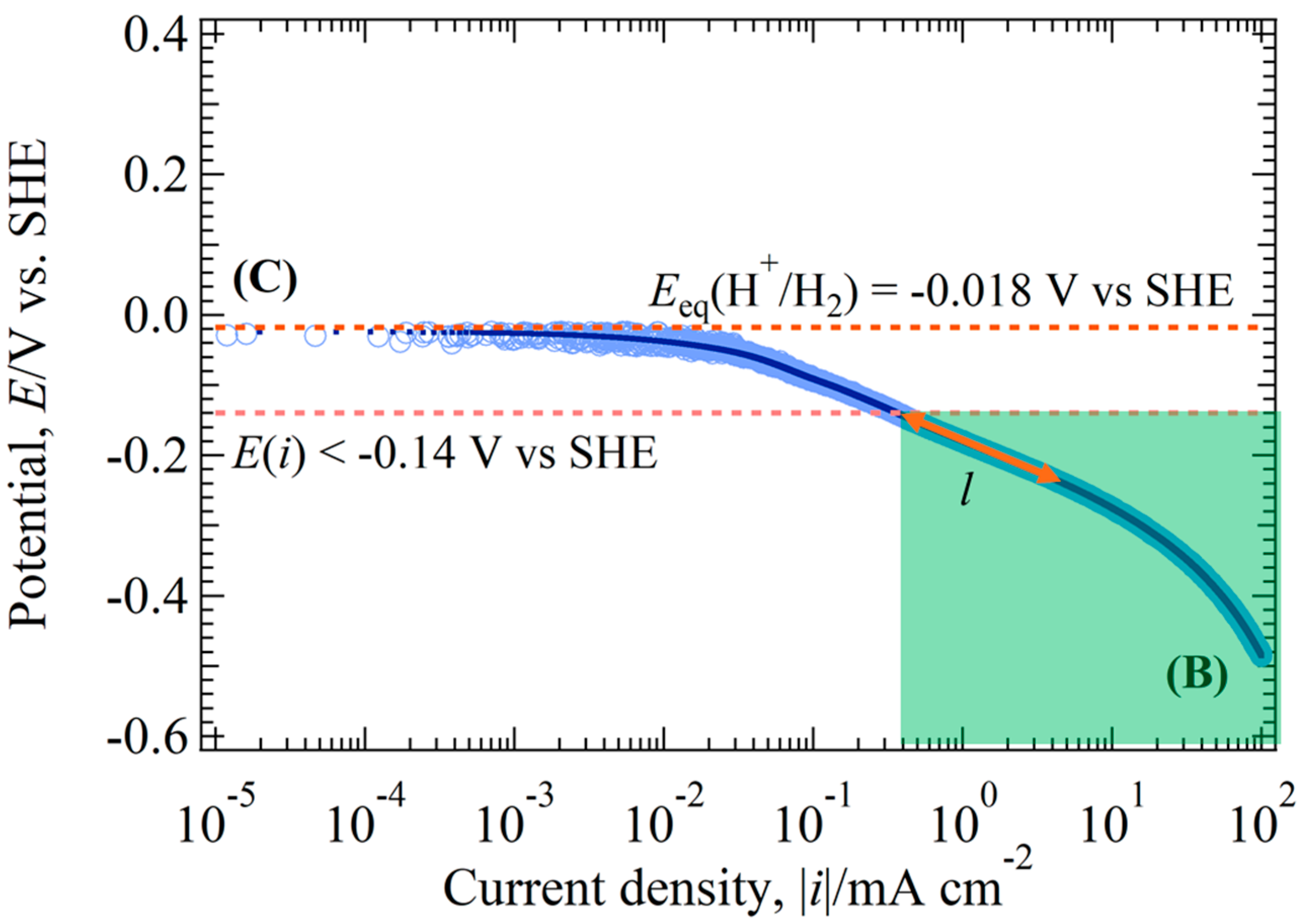
For more accurate estimation, the physical resistances should be compensated. Since
Figure 2 shows no vertical line of
(
), its rough value was calculated using the experimental value of pH = 0.3 shown in 4.2 and
in a book [
12];
(moderately stirring condition), and
z = 1 (see later Equation (31)).
The above large value may be a reason why
Figure 2 has no vertical line of
. The
is graphically estimated using the relation of Equation (24):
The
is selected due to: (1) almost saturated value and (2) making a guess by manual calculation of
h(
i) at
. Then, Equation (23) is specifically expressed as:
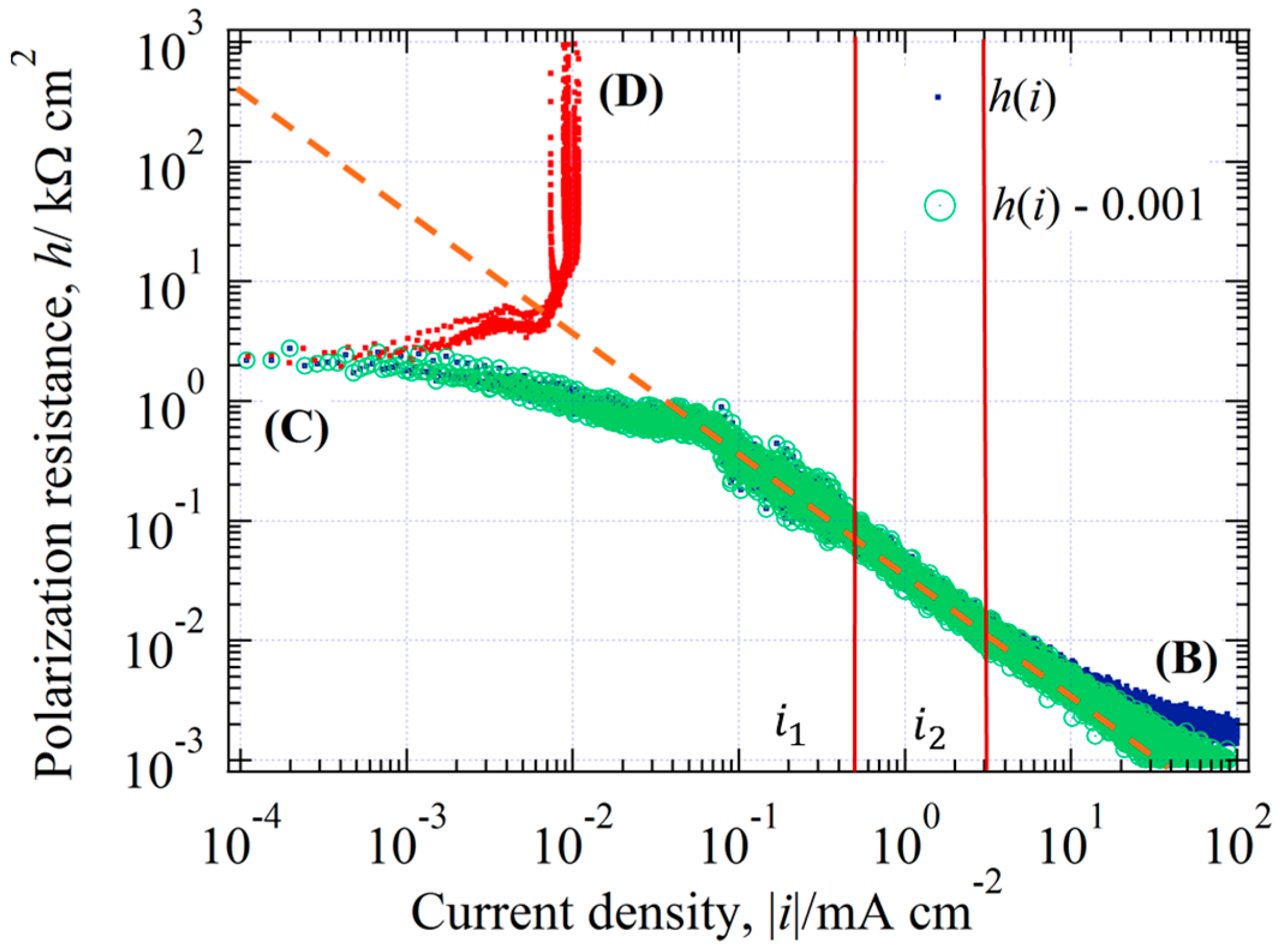
The revised green circles of
against
together with the not-revised
(blue dots) in the cathodic branch, are shown in
Figure 8.
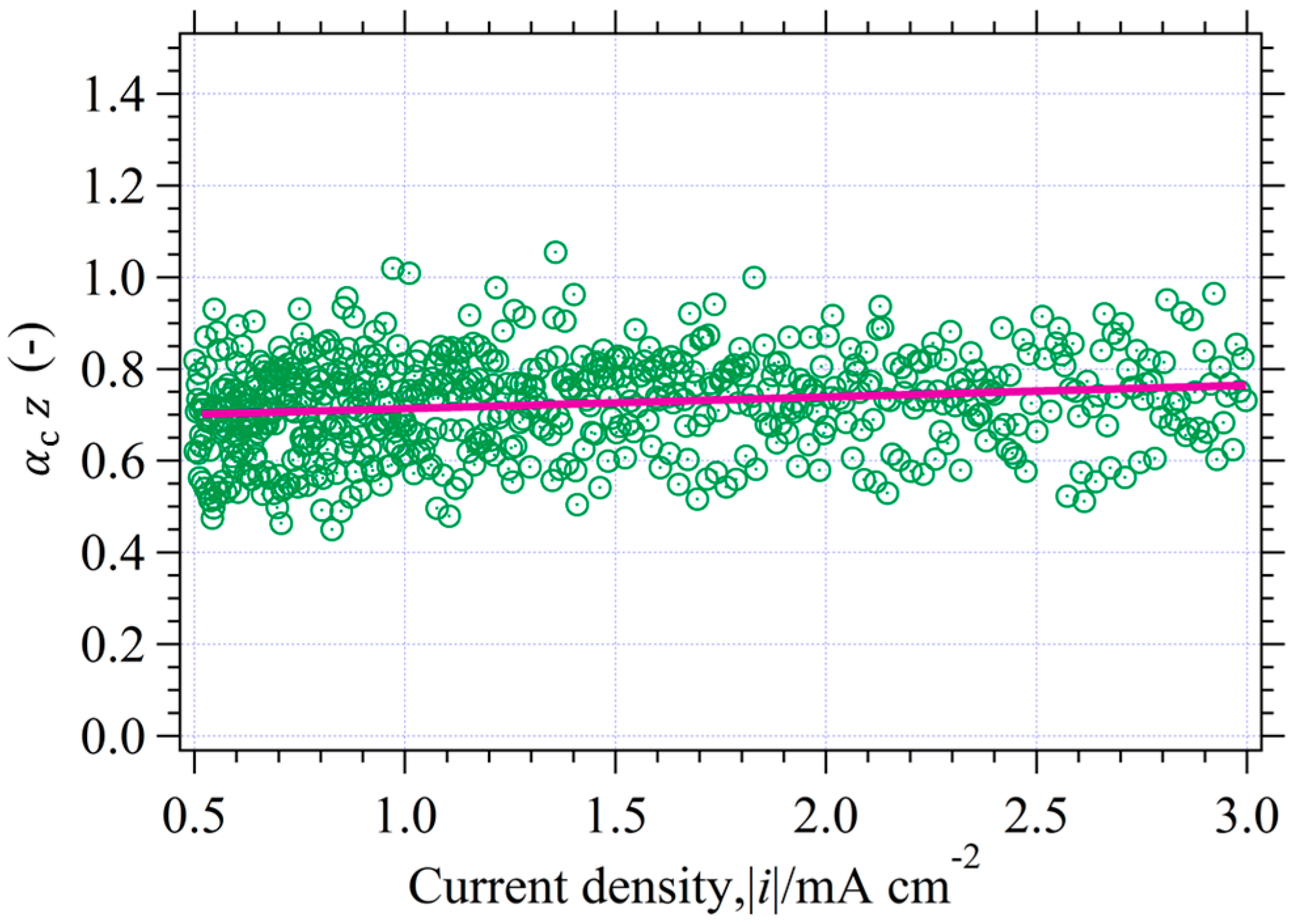
The arrival of green circle plots having a straight line confirms that the physical resistance is practically eliminated due to the disappearance of the horizontal line ( at . In addition, the linear relation of is virtually held in the green plot region. The current data for , which fully satisfies the Tafel slope, were used for the accurate estimation. The value of and were employed as the and , respectively. We can estimate the using the following equation.
The relationship between the calculated
and the employed
is plotted in
Figure 9.
The data were scattered but their dispersion was limited. The value of
was estimated to
using the least-squares approximation method. The
must satisfy two restrictions: (1) the
z must be a positive integer and (2) the
z must be
because the electron number should be up to 2 of the whole reaction (2H
+ + 2e = H
2). Considering them, the most suitable combination is:
The results mean that the reaction is the irreversible and therefore the whole reaction has the rate-determining step (rds). Since this rds reaction was partially revealed to be , the possible rds reaction may be expressed as the well-known reaction in parentheses, if Red = Had .
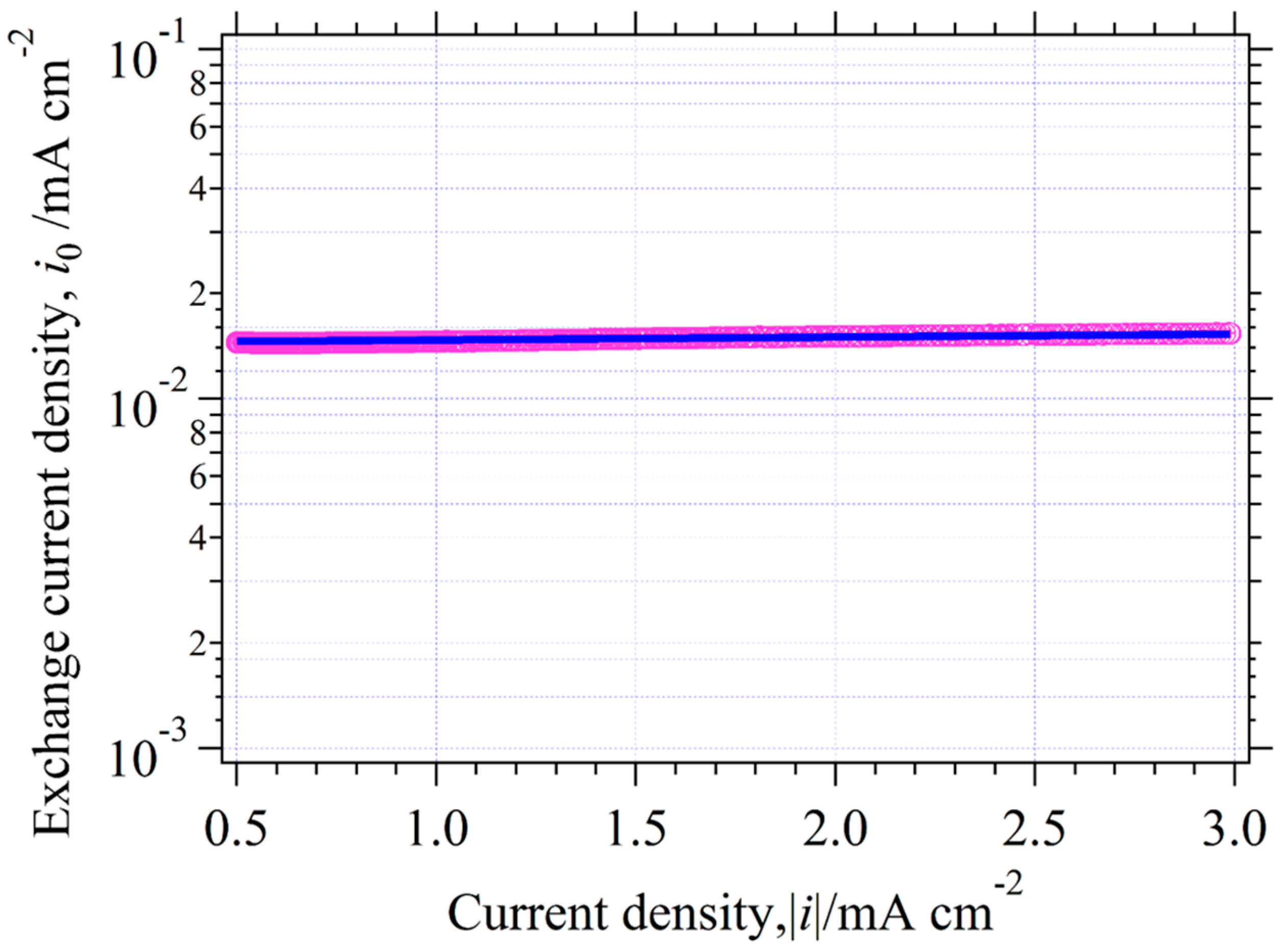
Solving Equation (29) as the first order differential equation under the initial condition of , we can know the .
It will be allowable that
, because the
in reversible reaction is usually very small. Then, the
is simplified and then the relation between the
i0 and the experimental
i is plotted in
Figure 10.
The
was
, which is larger than the results of the papers (
[
4]. We think the difference between them probably had its roots in the finding of the proper Tafel slope region and whether the physical resistances are compensated or not.
The
can be estimated by the experimental reading of
and the experimental pH=0.3 using the
equation [
7,
9]. Their simultaneous relations are shown as:
Solving the above, we can obtain that
. Applying this
value to the curve relation shown in
Figure 5, we can reconfirm that the
her on Ag electrode in the 0.5 mol dm
−3 H
2SO
4 solution belongs to the irreversible reaction.