1. Introduction
The increasing miniaturization of portable electronic devices and engines, such as smart phones, laptop computers, MP3 players, and Global Positioning System (GPS) presents technological challenges in various fronts, namely the manufacture of adequate power sources for such devices. The complexity of this scientific context is aggravated with the present commercial pressure. Predictions for the international trade period of 2013–2019 of the economic market of portable devices and engines estimate revenues more significant than $1 billion dollars [
1]. One of the main factors for attracting the interest of the users of portable electronic devices lies in their mobility, i.e., in the autonomy of its power source, specifically the time independent autonomy of the device regarding the need to recharge its inner battery in an external electrical power source.
A promising alternative to rechargeable batteries are Proton Exchange Membrane Fuel Cells (PEMFCS), especially one type of PEMFC, the direct methanol fuel cell (DMFC), an electrochemical device that uses methanol (or methanol solutions) as fuel, converting chemical energy directly into electrical energy, with working temperature ranges adequate for near room temperature use. DMFCs have also the advantage of presenting other aspects, such as environmentally friendly residues or high energy density [
2,
3]. However, the development of a more commercial viable DMFC is a path not without some problems [
4].
Platinum is the most widely metal used option for DMFC catalyst, within fuel cell context, since as reviewed by Holton and Stevenson, platinum-based catalysts outperform those based on other metals in activity, selectivity and stability [
5]. In fact, catalysts based on this metal have the highest catalytic activities of all the catalysts based on pure metals for methanol oxidation. Unfortunately, one of the products of the decomposition of methanol, carbon monoxide (CO), which blocks the catalyst surface, slows down the kinetics of electro-oxidations through platinum poisoning, curtailing the commercial edge in DMFC [
6].
Ruthenium emerged as a solid promise to surpass the CO poison of the catalyst [
7]. Indeed, alloys of ruthenium–platinum (Ru–Pt) have presented themselves as a feasible industrial solution to avoid the CO poison of platinum catalyst [
8,
9]. As such, it is pertinent to review the data gathered regarding Ru–Pt catalysts in prospective DMFC context. However, experimental data alone are insufficient to thoroughly uncover the likely answers regarding both the microscopic pathways of the methanol reaction and the macroscopic technology in developing ever miniaturized batteries—two fields which are meeting in an increasingly thinner frontier, as the commercial demand for portability is hardening.
Computational data become fundamental to ensure feasible passage of this borderline between micro/macro demands, by positively meeting with the experimental data and simultaneously proposing hypothesis where the latter might be yet incapable of exploring. As far as reaction pathways are concerned, being able to determine chemical parameters of the reacting system or part of it, in nanoscale, is the main goal in computational studies. Though the solving of Schrödinger wave function equation for the reacting system is the cornerstone of quantum methods. Ab initio methods, those based on solving the Schrödinger equation without the inclusion of empirical or semiempirical parameters in the equations, use specific approximations to solve such equation for a many-electron system. Firstly, the adiabatic approximation where electron motion is not correlated with the nuclei motion is used; that is, the nuclei are “frozen” while the electronic part of Schrödinger equation is being solved. Additional approximations are required to solve the many-electron Schrödinger equation as for example the Hartree–Fock approximation; in this approximation each electron is moving under an average potential created by all the others (approximation to independent electrons). Thus, the electronic Coulombic interaction is approximated by a mean field while the electronic exchange interaction is exactly included by the use of a Slater determinant which antisymmetries the wavefunction of the system; the effects in the solutions of this approximation are further corrected with posteriori approximations. Among these secondary approximations are the perturbation theories (PT), the coupled cluster approximation (CC) or the multiconfigurational (MC) method.
An alternative formalism (to those of the wavefunction based methods) to solve the many-electron problem is the Density Functional Theory (DFT) where the electron density is represented by a density functional [
10,
11,
12]; depending on the density functional considered there are a large number of DFT methods. The latter approach, DFT, is also usually considered an ab initio method despite most common density functionals use empirical parameters in their formulation; the combination of the density functional exchange term with that derived from the Hartree–Fock approximation leads to the named “hybrid” density functionals. DFT method has the advantage of better efficiency in many-electron systems treatment, which makes it an interesting choice when dealing with many problems related with technological development.
The “density” referred in the designation of DFT refers to the total electronic charge density. DFT considers the theorems of Hohenberg and Kohn [
13], which state that: (1) the total energy of a system in its ground state is function uniquely of the total electronic charge density which depends only on three spatial coordinates; and (2) the density that minimizes the total energy is the exact ground state electronic density of system. In the Kohn–Sham formulation of DFT [
14] the many-electron system is replaced by a fictitious system of non-interacting electrons (analogous to Hartree–Fock approximation in wavefunction based methods), which gives the same electronic density than real system. Thus, the total energy of the system is expressed as function of the electronic density as a summation of terms representing the kinetic energy of the Kohn–Sam system, the external potential acting on the interacting system which at least include the nuclei-electron interaction, the Coulomb energy for the electrons and an additional term which states the difference between the exact kinetic energy and the kinetic energy of a non-interacting electron gas plus the non-classic electron-electron interaction energy. The last term is the so-called exchange-correlation functional, which allows better energetic accuracy with lesser computational effort [
12,
15,
16]. The exact exchange-correlation functional is unknown which leads to approximations for its description; the first of these approximations is Local Density Approximation (LDA) where it is supposed that the exchange-correlation energy on each point depends only on the local density in that point. This approximation allowed DFT to be used in computer programs [
12,
17,
18]. More precise approximations to the exchange-correlation term were further developed as the Generalized Gradient Approximation (GGA) where it is considered in each point the local density and its gradient [
19,
20,
21]. Following the GGA approximation were developed the most classical exchange-correlation functionals as the Perdew–Burke–Ernzerhof (PBE), Perdew–Wang 91 (PW91), Becke3–Lee–Yang–Parr(B3LYP) or Revised Perdew–Burke–Ernzerhof (RPBE) [
22]. A more flexible type of exchange correlation functionals were obtained by the consideration of the non-interacting kinetic energy density in addition to the local density and the gradient of the local density; these type functionals are known as meta-GGA functionals and the most used are the Tao–Perdew–Staroverov–Scuseria (TPSS) and Minnesota functionals [
22].
As computational studies evolved, both in programming codes and quantum theory approximations, the nature of Ru–Pt alloys as catalysts in the methanol oxidation, namely regarding their application in DMFC, become a subject where computational and experimental data subsided each other in order to fill the gaps when the objective is the establishment of the reaction mechanism.
Though the scope of our present study is ruthenium–platinum catalysts in DMFC context, this review does not intend to be exhaustive in the subject, rather it aims at being surgical in the analysis of the available data. By this, we mean to say the aim of this study lies in analyzing recent and relevant computational and experimental data, which can be related with each in such as way than a coherent narrative of the methanol oxidation is perceivable. One should note that though DMFC technology has been extensively reviewed in recent years, the transversal analysis of theoretical studies and experimental data on Ru–Pt is not a treated theme [
4,
23,
24,
25].
With that in mind, several criteria were followed in the choice of the published sources in this review: (1) Though it is common practice to relate Ru–Pt results with independent Ru and Pt studies, for contrast and comparison,
Section 2 and
Section 3, designated Experimental Data and Indicia and Computational Results and Hypothesis, respectively, will not include explicitly the data resulting from solo platinum studies, as platinum data has been more extensively scrutinized in the last years [
26]. However, platinum experimental and computational data may be referenced through the analysis; (2) Computational studies are selected through proximity with the experimental results in
Section 2, thus aiming to construct both an explanation for the experimental absence of detection of likely intermediate chemical species in a proposed pathway, due to energetic and/or kinetic reasons; (3) Solo ruthenium experimental and computational studies are included when their results add recent and significant data to experimental results and/or enlighten included computational data in the review; (4) The same reasons presented in Criterion (3) are valid when occasional experimental and computational data regarding other metals apart from ruthenium or platinum, and their alloys, apart from Ru–Pt, is included.
Therefore, the aim of this review is to actually present a coherent frame of the recent experimental and computational breakthroughs in an inclusive perspective rather than a broad spectrum of listed data. In each section, summary of experimental or computational data is displayed in tables, which allow transversal analysis, and several subsections carry a more in-depth analysis of the sources and their validation, not only per se, but also through correspondence.
2. Experimental Data and Indicia
Methanol oxidation in DMFCs still presents an elusive mechanism for researchers. However, there are several aspects that gather consensus: (1) hydration of the proton exchange membrane (PEM) leads to proton production in the anode and then begins its transportation through the membrane to the cathode; (2) in the cathode another catalyst is used to combine electrons, protons, and oxygen from the air, resulting in water vapor and carbon dioxide production, while methanol reacts in the anode; and (3) experimental data indicate the methoxy radical (CH
3O) as the first intermediate in the oxidative process [
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39]. Therefore, the discussion presented in this section will have in account these aspects and will especially consider the corroboration of existence of methoxy as intermediate in experimental and computational data as a strong indication of pertinent mechanism.
As stated in the Introduction, in this section, the most recent and/or relevant experimental data and subsequent proposed hypothesis for the mechanisms of the oxidation of methanol on Ru–Pt surfaces are presented and discussed. When appropriate, the data from oxidation of methanol on clean ruthenium surfaces are included in this section, and added to the discussion in order to clarify the indicia.
The summary of relevant and recent experimental data on methanol oxidation in Ru–Pt and clean ruthenium surfaces is displayed in
Table 1 and
Table 2, organized by year of publication and per catalyst surface type. The chronological order is crescent from top line entry to bottom, i.e., it begins with the earlier publications and final entries are the most recent. However, the chronological order is embedded in the organization of entries per catalyst type and has three main sections, according to the substances present in the catalysts: Ru–Pt alloys, clean ruthenium and non-ruthenium alloys.
Table 1 presents four columns: (1) type of catalytic surface; (2) analyzed study; (3) sample description; and (4) experimental methodology.
Table 2 presents the following data per column: (1) type of catalytic surface; (2) study reference; (3) results; and (4) conclusions.
2.1. Experimental Results I: Ru–Pt Catalysts
The published results analyzed in this subsection cover a period of more of a decade of relevant experimental results in Ru–Pt catalysts regarding DMFC or methanol electrooxidation context [
40,
41,
42,
43]. Several aspects of the reaction and DMFC technology are studied, which makes each study adding value to the previous one. One ranges form a study of an in-situ probing of RuPt anode catalyst surfaces, to studying methanol crossover through RuPt/Nafion composite membrane, and investigating the performance decay of anodic RuPt catalyst per DMFC working time, and the effect of different carbon materials supports of Ru/Pt electrocatalysts. Two main aspects can be perceived in influencing the methanol electrooxidation and the DMFC cathodic performance, morphology and composition.
Considering morphology, one can start by emphasizing that not only are the metals involved in the alloys relevant for morphological aspects but also the support, usually being carbon based [
43,
47]. Indeed, the rather extensive proportion of platinum in Ru–Pt electrocatalysts is rather accountable for the alloy cost and to avoid its massive use, they are dispersed in nanoparticle form in a carbon surface which is capable of providing the necessary electronic conductivity for electrode functioning. The carbon support can be porous carbon black (Vulcan XC-72R), mesoporous carbon (CMK-3) and even carbon nanofibers (CNF), nanotubes (CNT) or graphene.
Anodic unsupported Ru–Pt catalysts present an activity dependent on surface area per unit mass of catalyst and a total number of metallic sites close to the number those of a certain composition alloy catalyst, the alloy Ru/Pt = 1:1 [
40]. Nevertheless, it is experimental evidenced that the carbon support will impact the particle size and state of agglomeration of the electrocatalyst, suggesting that these effects of the carbon support may be related either to the porosity or to the chemical nature of the support, and eventually to a combination of these two factors. The likelihood of the carbon support pore effect is obvious if one considers there should be a correlation between pore volume and crystallite size as the electrocatalyst nanoparticles are formed inside the support pores [
43]. Wang et al. also noted, nevertheless, that the dissolution of the carbon support may add to the agglomeration effect in the anodic catalyst, as it seems to desquamate and/or dissolve in the growing catalyst layer, provoking a decrease in the proton conductivity [
42].
In fact, mesoporous carbon guarantees not only the highest level of dispersion of the alloy nanoparticles in the support but also it presents efficiency in crystal growth restrictions. The importance of these characteristics lies in data from cyclic voltammetry and CO striping experiments where a strong correlation between the electrocatalyst size and agglomeration with highest specific electrochemical active area. The better results occurred in the situation of small and well dispersed nanoparticles [
43]. Salgado et al. conducted experiments resulting in the proposition of suitable combination of microstructure and chemical composition, as many modifications which lead to favorable increase of a process might diminish another. An example would be the inclusion of titanium nanoparticles in the electrodes, favoring in a beneficial manner the CO and methanol oxidation activities per se but increasing the agglomeration or the growth of catalyst particles. Thus, a balanced modification should optimize the benefits and minimize the negative impact of the alteration. Salgado et al. suggest this could be achieved through acid treatment of the surface of a mesoporous carbon and combined it with oxides [
43].
Though not analyzed here in detail, one should also remark recent studies aiming to improve Ru–Pt catalysts by consideration of carbon based material as supports [
48,
49,
50,
51,
52] or improving the membrane selectivity [
53]. These carbon-supported catalysts are synthesized through different techniques leading to different nanoparticles sizes and Ru–Pt alloying grades which affects the reactivity [
54,
55].
As above mentioned, proportion in the Ru–Pt electrocatalysts is a factor for their optimum activity but the presence of other chemical species in the cathode also cannot be overlooked in this process. Indeed, these catalysts commonly present in their composition, among others, a measurable level of various oxides, as amorphous types of ruthenium oxide. The ruthenium oxides may be due to the mode of preparation but a likely hypothesis is affinity with oxygen, via either air or water [
40]. Time use may play a role in the appearance of these oxides, as not only the catalyst particle size increased with test time but also operating time implied decrease of the metal amount and increase in platinum and ruthenium oxides in the anodic electrocatalyst layer [
42].
Experimental data point to an inhibiting effect of such chemical species in the alloy catalytic activity, which could be explained by competitively blocking metal alloy sites otherwise employed as active catalytic sites for methanol electrooxidation [
40]. Still, considering adsorption sites, activated water surface species, i.e., OH
ads, is adsorbed directly on a usually identified Ru surface site [
40]. Further, adsorption of species on the metallic surface may provide the necessary catalytic activity of the alloy in anodic carbon monoxide oxidation, even if it is not adsorbed in a Ru surface site, when considering submonolayer coverage layer [
40]. However, the influence of ruthenium dissolution on the performance degradation of DMFC is not without debate, as though representing a minor influence in DMFC performance degradation, still seems to be a factor in the catalyst performance degradation [
42].
Regarding proton conductivity, resulting from the proton production in the anodic catalyst and consequent transportation through the cathodic membrane, it presents dependence with the Ru–Pt loading, as it decreases with the increasing of the catalytic alloying [
41]. This loading is related with the impregnation membrane method. The process is controlled through the concentration ratio of the impregnation solution, with maintenance of the ruthenium and platinum weight and atomic ratios. Experimental data indicate two factors probably responsible for the operating temperature dependence of the composite membrane performance: (1) increase in the methanol oxidation rate, as temperature increases; and (2) decrease of methanol crossover extent as Ru–Pt is impregnated [
41]. The latter might also explain higher current density in one of the studied samples (0.05 wt % RuPt/Nafion
®). In fact, embedded Ru and Pt nanoparticles in pure Nafion membrane might affect methanol crossover both by nanoparticle oxidation of methanol and reducing the path of proton conduction [
41].
Considering two anodic processes, the production of activated water (H
2O → OH
ads + H
+ + e
−) and its eventual reaction with anodic carbon monoxide (CO
ads + OH
ads → CO
2 + H
+ + e
−), experimental data relating CO and methanol electrooxidation activities suggest the stripping of CO at the dispersed Ru–Pt catalysts implies the shift of positive potential, which corresponds the rate of methanol electrooxidation, in a scenario of temperature dependence [
40]. This is particularly interesting as CO stripping current is a measurable tool for the number of exposed surface sites in the catalyst, as carbon monoxide adsorbs only in exposed surface sites. Therefore, it is a reasonable suggestion that desorption of carbon monoxide increases the available catalytic sites for methanol electrooxidation and it is a prerequisite for Ru–Pt catalyzed DMFCs achieving higher anodic activity [
40].
In conclusion, porosity of the carbon support for Ru–Pt catalysts in methanol electrooxidation and high dispersion of adequate small sized Ru–Pt nanoparticles allows a more extensive surface with maximum methanol dissociative chemisorption sites. The surface composition is also a main factor, as the optimized catalytic conditions seem to be favored by a more reduced state of the catalytic surface.
2.2. Experimental Results II: Ru Catalysts
In this subsection, we analyze relevant experimental published results in Ru catalysts regarding DMFC or methanol electrooxidation context [
44,
45]. They explore several aspects of the reaction and catalyst role, in particular those relating with thermal evolution.
Temperature is also a key aspect when producing viable electronic devices, both by considering heat effect in the components and the environmental temperature of daily use, especially in the portable devices where DMFCs are more commercial likely to be used. Barros et al. experiments discriminate temperature effects per surface exposure. At 90 K (considered a low temperature), experimental data indicate a fast dehydrogenation of methanol to methoxide (CH
3O) in the solo low coverage crystal Ru(0001) surface, while at the same temperature and catalyst metal surface, a high coverage presented no evidence of detection of scission of the C–O bond [
44]. Gadzincki et al. found isolated methanol molecules in solo Ru(0001) surfaces, when both temperature (≈80 K) and coverage was low [
45]. Formation of methanol multilayers was also detected and investigated. Though capable of forming at low temperature (below 110 K), they desorb, become after annealing into methanol clusters only at temperatures of 120 K or with increasing surface coverage [
44,
45]. In fact, when the process of surface annealing occurs in small steps, at high temperatures, the formed methoxide decomposes, yielding adsorbed carbon monoxide and adsorbed hydrogen [
44].
Several chemical species were detected. Formaldehyde formation occurs when combining CO and CH
3O in a single large temperature step and two bidentate configurations were identified: bridging [µ
2-η
2 (C,O)-H
2CO] and chelating [µ
1-η
2 (C,O)-H
2CO], as reported by Barros et al. [
44]. Formed formaldehyde through reactivity reduction regarding cleavage of C–H and C–O bonds, partially decomposes to CO
ads above 190 K, and otherwise remaining stable up to 290 K [
44]. In addition, at 190 K, data indicated that methanol reaction with superficial oxygen and subsequent desorption as water followed [
45]. Further, at 220 K, both mentioned processes end and upright methoxy is the dominant surface species. It takes a temperature of 260 K for achieving complete methoxy dissociation, with reaction products H and CO only desorbing at higher temperatures (330–350 K for hydrogen and 470 K for CO), though stabilization of the methoxy species is attainable up to 320–340 K, due to CO co-adsorption, as contribution of a site blocking effect on methoxy dissociation products [
45].
Gadzincki et al. also noted absence of formation and/or desorption in temperature programmed desorption (TPD) for methanol on Ru(0001) of the following species, namely: methane, formaldehyde and carbon dioxide. This absence was verified in co and non-co-adsorbed oxygen conditions. In fact, after methanol adsorption and decomposition through high temperature annealing (600 K), there is a complete lack of methane desorption as well as no detection of oxygen residues [
45]. Interestingly, when imposing methanol adsorption at 190 K, there were no detectable products from this direct methanol adsorption through reflection-absorption infrared system (RAIRS), either for high or low coverage [
44].
Barros et al. found that, at 190 K, there were several aspects which permitted to enlighten parts of methanol electrooxidation pathway in clean ruthenium, Ru(0001), namely scission of O–H, C–H and C–O bonds after methanol adsorption on the surface, though these scissions left no RAIRS detectable species [
44]. In addition, regarding adsorbate orientation, spectra seems compatible with O–H bond appareled with the metallic surface [
56]. Further, the proposed adsorption site for methanol is the face-centered cubic (fcc) three-fold hollow site, while methoxide adsorption site depends on coverage and temperature (for 130 K, the characteristic wavenumber of
nCO mode seems to split, with measures of 1015 cm
−1 for likely hexagonal close packed (hcp) 3-fold hollow site and 1045 cm
−1 for a lesser bonded methoxide in a two-fold tilted bridge site) [
44]. In particular, though a temperature of 220 K is necessary for full conversion of methanol to methoxy, only in a narrow range of 180–220 K, is methoxy stable, being 220 K a more than sufficient temperature for methoxide dissociation without detectable intermediates [
45].
Finally, in clean Ru(0001), it can be established, at 160–180 K, that O–H bond scission is the primary reaction of the methanol decomposition, being the hydroxyl a contributor to the methanol reaction only through its H atom, which is transferred to adsorbed oxygen without adsorbing on Ru(0001), thus, having this reaction step no detectable intermediate [
45]. This first step produces methoxy and surface hydroxyl, though the rate of this step depends of methanol molecular adsorption/empty adsorption sites production, namely for dense layers. In this latter scenario, the step proceeds at slightly higher temperatures [
45].
2.3. Experimental Results III: Non-Ru–Pt Catalysts
In
Section 2.1 above, experimental data emphasized the effect of catalyst nanoparticle size and the porosity of the Ru–Pt alloy support as prime factors in methanol eletrooxidation in DMFC context. As such, for comparison, we include results in non-Ru–Pt catalysts for methanol electrooxidation, which deal with such morphological aspects [
46]. This comparison is also experimentally made in a similar context such as oxygen reduction reaction for non-Pt–Ru catalysts [
57,
58].
The studied non-platinum catalysts for alkaline DMFC, included 20% mass Pd/C, Au/C and PdAu/C. Regarding morphology, solvent dependence was verified and when ethylene glycol acted as solvent, one of the non-platinum catalysts, Pd/C, presents high dispersion of nanoparticles in the carbon support. Further, these nanoparticles were small, spherical shaped and uniform. Moreover, it was observed through transmission electron microscope (TEM) a high dispersion of synthetized nanoparticles in Au/C and PdAu/C as well. Comparing with carbon supported platinum catalysts, Pd/C and PdAu/C had a higher activity at oxygen reduction reaction but a relatively low activity at methanol oxidation reaction. These electrochemical properties were measured by cyclic voltammetry tests. Nevertheless, the Pd/C presented a high performance in membrane electrode assemblies and a relatively high tolerance to methanol crossover.
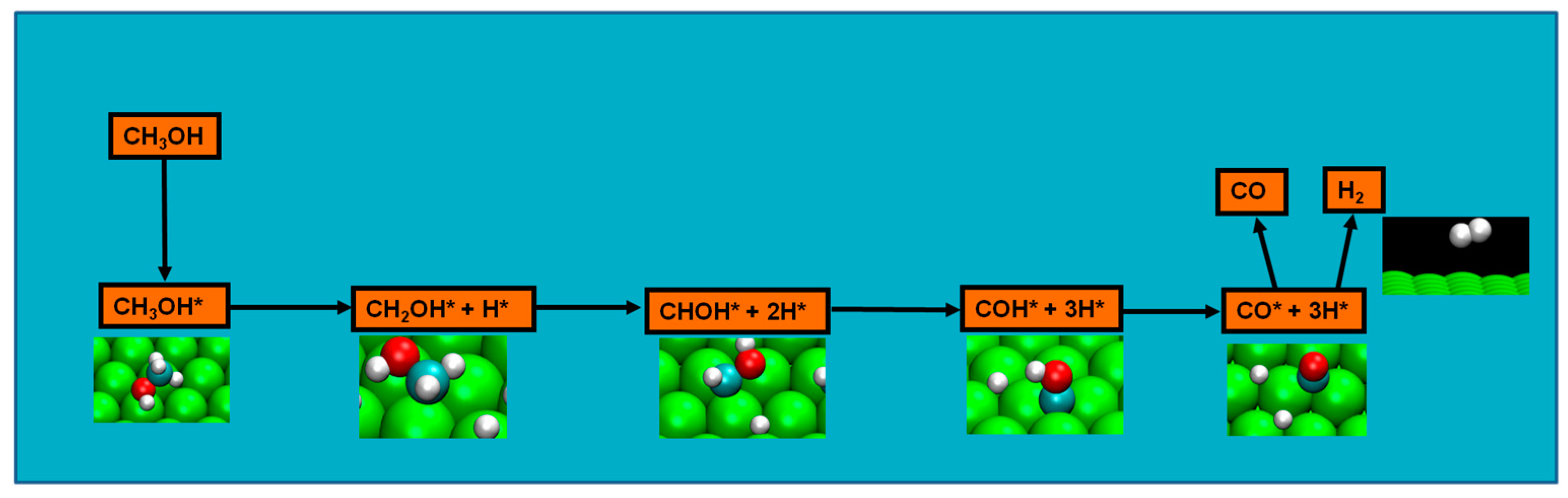
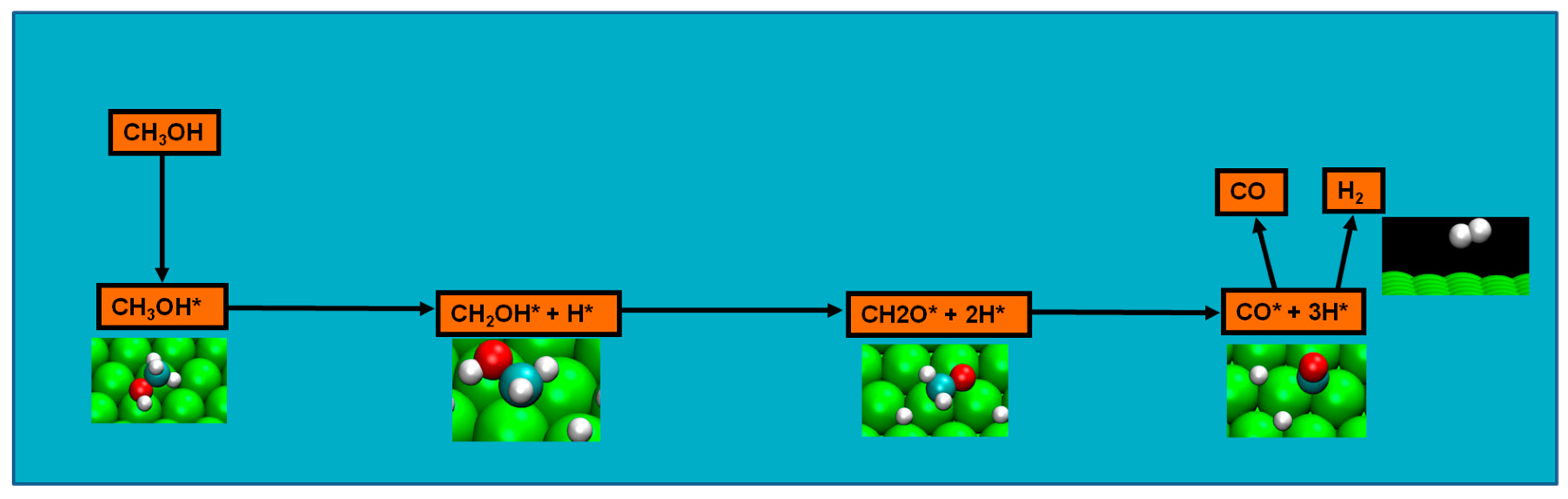
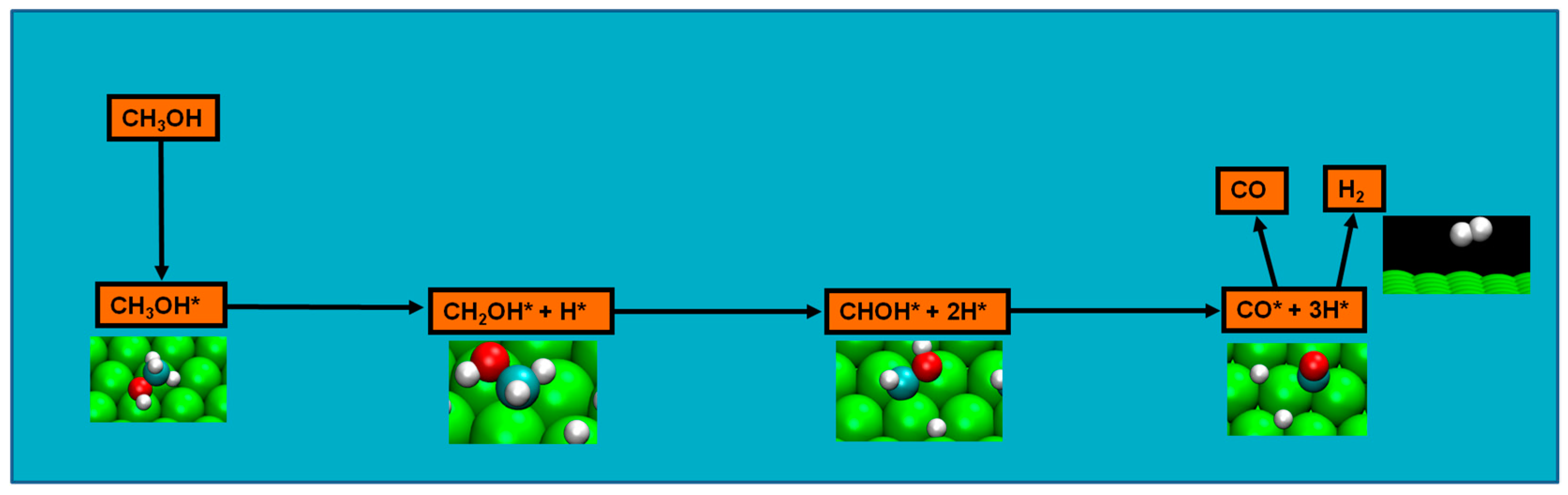
2.4. Possible Pathways for Methanol Electrooxidation in Ru–Pt Catalysts
Methanol decomposition starting by O–H bond scission
Methanol decomposition starting by C−H bond scission
Methanol decomposition via hybrid route (I)
Methanol decomposition via hybrid route (II)
Alternatively, one can envision also the following scenario as methanol adsorbs on the ruthenium surface:
3. Computational Results and Hypothesis
As mentioned, not only does methanol oxidation in DMFCs still presents an elusive mechanism for researchers but there is also experimental limitation at the moment to explore several aspects of the reaction. Computational research can provide data regarding the aspects than can prove technical unfeasible to be studied. The discussion presented in this section takes in account the precious debated experimental data and will also be divided according to studied catalyst.
Again, the review of computational data is not to be extensive, rather precise, either on the corroboration of experimental results or the proposed theoretical models. Thus, the discussion will include not only studies on Ru–Pt catalysts but also on clean Ru and Pt surfaces. As in the previous section, when pertinent, computational data from non-Ru–Pt, Ru or Pt catalysts will be included.
Table 3 and
Table 4 present the summary of computational data from the chosen published studies, organized per catalyst type and in chronological order for each catalyst type. As in
Table 1, the chronological order is crescent from top line entry to bottom, i.e., it begins with the earlier publications and final entries are the most recent for each catalyst, having the above mentioned four main sections, Ru–Pt, Pt, Ru, and non-Ru–Pt surfaces respectively.
Table 3 is organized in five columns: (1) type of catalytic surface; (2) analyzed work; (3) model; (4) software; and (5) methodology.
Table 4 has the following vertical entries: (1) type of catalytic surface; (2) study reference; (3) results; and (4) conclusions.
3.1. Computational Results I: Pt–Ru Catalysts
In this section, there is a call of attention to be made. The published results cover not only Ru–Pt, but also solo Pt and Ru calculations regarding the oxidation of methanol. To avoid repeating the same study in three different entries, the results are all presented in the same entry but indicating separation between the three surface catalysts. However, the results pertaining to Ru–Pt surfaces will be discussed first.
Kua and Goddard define three stages to be considered in their computational research of the oxidation of methanol, stage one, of methanol dehydrogenation, stage two, of water dehydrogenation, and stage three, of second C–O bond formation [
59]. Their data indicated that the most favorable pathway is via reaction of surface adsorbed COH and oxygen, terminating with the dehydrogenation of adsorbed COOH and consequent surface desorption of carbon dioxide. Interestingly, Ishikawa et al. found minor differences between single ruthenium atoms in Ru–Pt and in clean ruthenium when dissociating water, from a reacting energy perspective [
62]. They indicated that the role of ruthenium in Ru–Pt catalysts for methanol oxidation could present two aspects, the promotion of methanol dissociation and of the formation of surface OH, from the adsorbed water [
62]. This is in agreement with Kua and Goddard conclusion for the role each metal plays in methanol oxidation catalysis, i.e., the bifunctional mechanism of Ru–Pt catalyst reveals platinum as the active catalyst responsible for the dehydrogenation of methanol while ruthenium is the active catalyst responsible for the dehydrogenation of water [
59]. In fact, due to ruthenium good performance in activating water to adsorbed OH, or adsorbed O, oxidation can occur before methanol is fully dehydrogenated, and the thermodynamically problematic CO
ads + O
ads state is avoided, due to Ru activity [
59]. Ishikawa et al. propose a “ligand effect”, as Ru atoms seem to significantly reduce the strength of PtRu–CO bond, as this effect would reduce the accumulation of superficial carbon monoxide. Nevertheless, the “ligand effect” is not expected to be significant in the CO oxidation rate [
62]. Moreover, within alloys with Pt–M composition, M being another metal, the platinum site activity regarding the dissociation of methanol should somewhat depends on the M/Pt ratio. However, in the case of M = Ru, the methanol dissociation proceeded with efficiency, unlike the other studied metal. They concluded that a relatively high Ru/Pt ratio metal surface should be beneficial for methanol oxidation [
62].
The role of each metallic species in the alloy catalysis of methanol oxidation can be further explored when contrasting Ru–Pt results with solo platinum and ruthenium results in the same articles. For a platinum catalyst, the methanol oxidation presents a thermodynamic sink with adsorption of CO, though formation of surface carbon monoxide from methanol dissociation is easy and agrees with experimental data [
59,
62,
75]. Further, the calculated thermodynamics of adsorbed carbon monoxide is in agreement with experimental evidence of carbon monoxide poisoning of Pt during methanol catalysis [
59]. Comparing Ru and Pt, solo ruthenium is more active in water dehydrogenation while methanol dehydrogenation is where solo platinum excels, supporting the above-mentioned hypothesis regarding their role in Ru–Pt catalysts [
59,
62]. Nevertheless, both present computational results indicating good performance in methanol dissociation, in agreement with previous experimental data [
62,
75,
76].
Several intermediates were determined in the methanol decomposition in solo Pt and Ru surface and, according to Ishikawa et al. CHO, CHOH and CH
2OH are intermediates, though not all intermediate formations are equally favorable. In fact, OCH
3,s and OCH
2,s formations are much less favorable than the formations of CH
2OH
s and CHOH
s [
62]. In addition, adsorbed COOH is formed via the reaction of adsorbed CO and OH (or eventually, adsorbed water in replace of OH) and is not only likely to be the primary species from second C–O bond formation in Pt but COOH formation would be a rate-determining step in solo ruthenium [
59,
62]. Further, according to Ishikawa et al., the highest energy step in methanol dehydrogenation is CH
2OH
s → CHOH + H and the lowest would be CHO
s (or COH
s) → CO + H. The dissociation of water to form hydrogen is rate determining and endothermic [
62]. According to Kua and Goddard, the dehydrogenation of methanol on platinum proceeds via stripping the hydrogens from the carbon end, i.e., they consider an initial bond scission C–H [
59]. Finally, ruthenium atoms may be blocked with strong water and hydroxyl adsorptions and if so, this could explain why methanol does not undergo oxidation on low voltage ruthenium electrodes [
62].
3.2. Computational Results II: Pt and Ru Catalysts
Computational studies of clean metal surface also contribute to form a clearer picture of methanol decomposition pathway in Ru–Pt catalysts, as the above section demonstrated. Through the years and with the evolution of models as well as scientific trend, these studies brought new clues to the surface reactions and, as integration of experimental data, happened, become the means for coherent proposals.
In 1993, Delbecq et al. proposed Pt–Pt bonds weaken through adsorption and indicated a scenario of competition between a stabilizing influence of two-electron interactions, coming from oxygen, and a destabilizing influence of four-electron interactions, whose magnitude increased quicker than stabilization interactions, and provoked a less inclination for multiple adsorption sites and consequent loss of bonding with the surface [
66]. Delbecq et al. explore methanol decomposition aspects in another study, exploring hydrogen selectivity in unsaturated aldehydes. Though hydrogen adsorption by the C=C bond was found favorable, adding substituents on these bond would destabilize its interaction with the platinum surface. In fact, combining substituents effects with higher molecular coverage was not seen as feasible, in computational data, as specific oxygen geometry, namely vertical atop, would lead to a preferred C=O hydrogenation [
67]. Geometry does seem to play a part as flat form is favored at low coverage (be it for C=C or C=O) and Delbecq et al., considered to be a possible first route in C=O bond hydrogenation. However, the surface and its modification during the reaction pathways needs to be taken into account, as not only the computational data found coadsorption of hydrogen an important factor in selectivity but the platinum surface nature could indeed be altered due to side reactions fragment interactions [
67].
Probing further in the nature of methanol decomposition, as computational methodology rapidly evolved, new data permitted analyzing the energetics of chemical species involved in the reactions. For platinum clean surfaces, energetics favored initial C–H bond breaking possibly due to: (a) intrinsic C–H bond nature is weaker than that of O–H bond; and (b) the product of O–H bond activation, the methoxide intermediate, presented a lesser strength in bonding with the Pt surface than the intermediate resulting from the C–H bond [
70]. In fact, the activation barrier for the formation of the latter intermediate was 50 kJ/mol lower that the one of the methoxide, and concurring with this were the results of Greeley et al., where a microkinetic model indicated the likely methanol decomposition pathway to begin with initial methanol C–H scission followed by a second C–H scission and a quasi simultaneous O–H/C–H scission to CO [
71]. The results of Greeley et al. also concurred with experimental data [
37,
70]. Further, computational data found that: (a) the studied C–H bond-breaking reactions were exothermic (and the C–H bond-activation reactions were found to be increasingly more exothermic for each subsequent elementary step); and (b) O–H bond-breaking reactions were endothermic, and though the research was conducted in vacuum conditions, it seem plausible that the eventual methanol decomposition in non vacuum conditions (as in DMFC context) will imply more easy activation of the C–H bond than of the O–H bond (which leads to the formation of the hydroxymethyl and hydrogen intermediates) [
70].
However, methoxide was experimentally detected as intermediate in the ruthenium Ru(0001) surface [
45]. Therefore, though not disregarding previous results, the new evidence had to be taken in the setup of a viable reaction mechanism. Moura et al. studied four possible pathways from three initial bond scissions (either an initial C–H, C–O, or an O–H bond scission) in the clean ruthenium surface, and initial O–H scission was considered as likely as the methanol decomposition pathway since: (a) it included the experimentally detected methoxy; (b) apart from the initial step of O–H bond scission, the pathway steps consistently presents the most energetically favorable route; (c) the energetics of the route explain both methoxy experimental detection and formaldehyde absence of detection; and, finally, (d) it is the most kinetically favorable pathway, namely, for temperatures of 220 and 340 K [
73]. Nevertheless, in a certain temperature range, another pathway, with initial C–H bond breaking, might also be active as a minority pathway, and energetics of after H
2 formation from methanol decomposition indicates that this formation is likely possible as well [
73]. Computational results also indicate a weak initial methanol adsorption, either in platinum or ruthenium surface, which could compromise effective methanol decomposition [
69,
72].
3.3. Computational Results III: Non Ru–Pt, Pt and Ru Catalysts
We feel it is pertinent to mention a computational study of methanol steam reforming on Co(0001) and Co(111) surfaces by Luo et al. to end the analysis of this section regarding computational breakthroughs in methanol decomposition [
74]. Takewaza et al. proposed that group VIII metals, such as Ni, Rh, Pd, or Pt, might favor methanol decomposition into CO against steam reforming into CO
2, and though not included in the mentioned study, cobalt is a group VIII metal [
77]. Luo et al. found that coadsorbed O and OH can promote O–H bond breaking or forming reactions and with the participation of O and OH, reaction barriers of all O–H bond breaking or forming can be reduced by 25%–90%. Further, conversion of CO to CO
2 on conversion of CO into COOH or CO
2 before desorption into CO(g) is competitive, and therefore the water gas shift may play also an important role [
74].
4. Conclusions: From Experimental Data to Computational Breakthrough, the Construction of a Pathway
This review intends to be surgical rather than extensive, i.e., without overlooking fundamental experimental and computational data, the aim was analytical integration, rather than exhaustive synthesis. Therefore, there was a pre-analysis of published material on the subject, in order to select the relevant breakthroughs presenting a vis-à-vis character between experimental and computational data. The discriminating parameters were also indicated in the Introduction of this work. Therefore, we have attempted to not only highlight relevant contributions from experimental and theoretical research regarding Pt–Ru catalysts in DMFC context but also integrate those contributions in a scientific yet straightforward narrative, with each contribution enhancing and probing several aspects of the issue. We began by introducing the DMFC context and the general concepts of computational research and proceeded with the analysis of data, in two sections, one only dedicated to the experimental data and the other to the computational evidence. Nevertheless, the subsequent section grows and adjusts to the previous, integrating the experimental data, and providing a fluid and likely explanation for the mechanism of methanol decomposition.
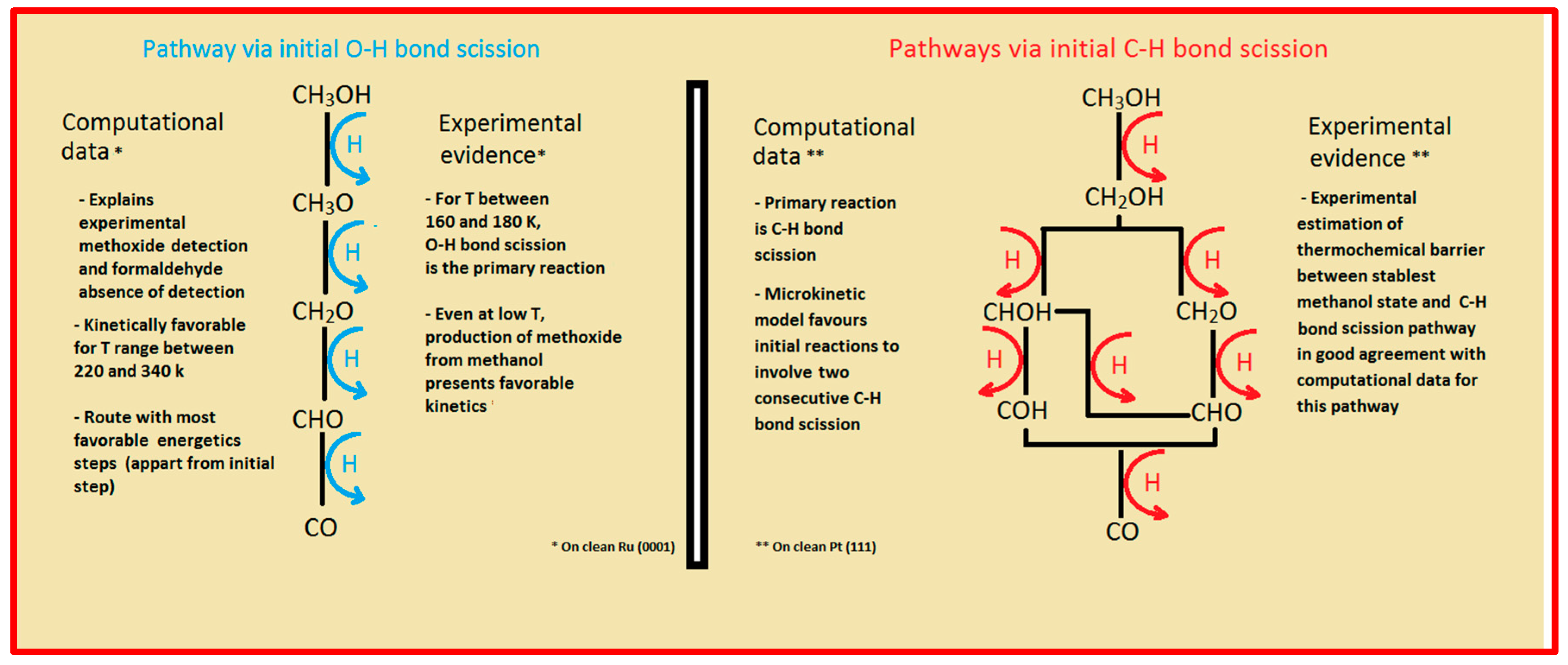
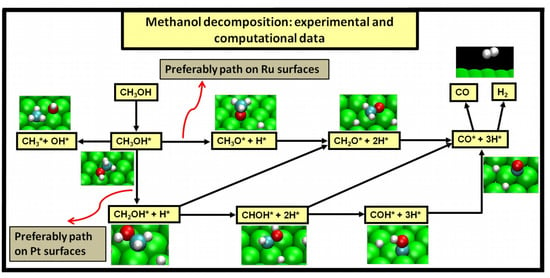
Two major and mutually exclusive possibilities seem to adjust to several computational and experimental data, a pathway with initial O–H bond scission and three likely others, all from an initial C–H bond scission. The summary of these possibilities is depicted in
Figure 5. Mainly from studies on clean Ru(0001), a methanol electrooxidation with an initial O–H bond scission step is supported by experimental data of such, for temperatures between 160 and 180 K, while the computational data not only indicate it to be the most kinetically favorable route, but also can account for experimentally detected intermediates, such as methoxide, as well as the absence of detection of other predicted intermediates, such as formaldehyde. The other possibility, a pathway that starts with an initial C–H bond scission, after methanol adsorption, seems to be more in agreement with computational and experimental data from clean Pt(111) surfaces. Thermochemically, experimental and computational data are in good agreement with specific transitions, namely the initial C–H bond scission. In addition, a microkinetic model favors two initial C–H bond scissions, when the surface is platinum. If, as analyzed in
Section 2 and
Section 3, the mechanism of Pt–Ru is bifunctional, then further studies must be made to determine which pathway prevails when both surfaces are present.
Finally, we conclude by stating our hope this review can promote a more significant collaboration between purely experimental means and theoretical research, as we firmly believe that to be the avenue of scientific investigation in this subject.