Aqueous and Surface Chemistries of Photocatalytic Fe-Doped CeO2 Nanoparticles
Abstract
:1. Introduction
- □ = oxygen vacancy ()
- = Fe3+ substituting on the Ce4+ site (single net negative charge)
- = Oxygen on the oxygen site (no charge)
- = Oxygen vacancy (double net positive charge)
- = Electron hole (single net positive charge)
- Thermodynamic stability diagrams
- Speciation diagrams
- Pourbaix diagrams
2. Experimental Procedure and Results
2.1. Water Absorption
- = Ce4+ on the Ce4+ site (no charge)
- = Ce3+ on the Ce4+ site (single net negative charge)
- = Oxygen on the oxygen site (no charge)
- = Oxygen vacancy (double net positive charge)
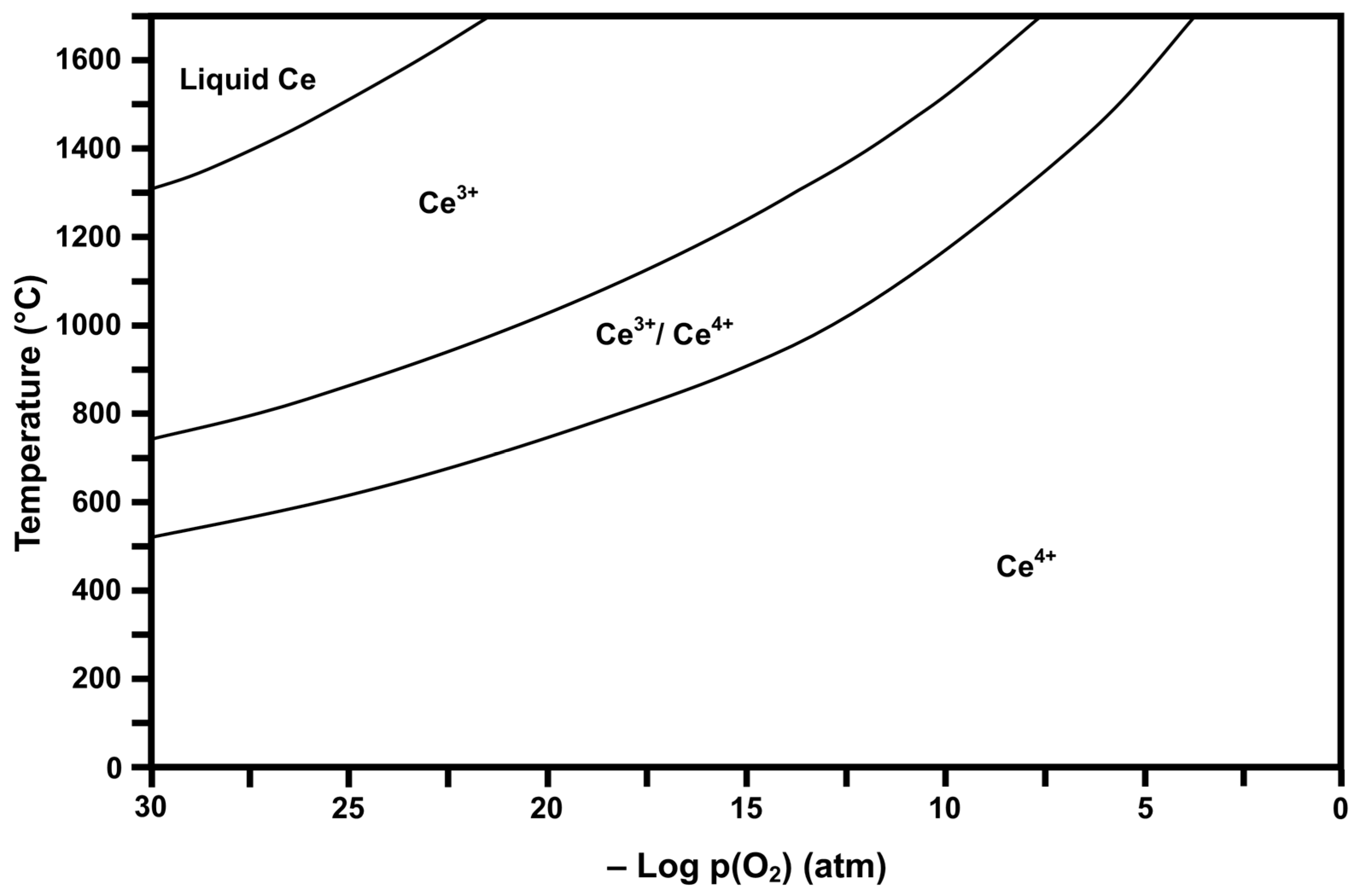
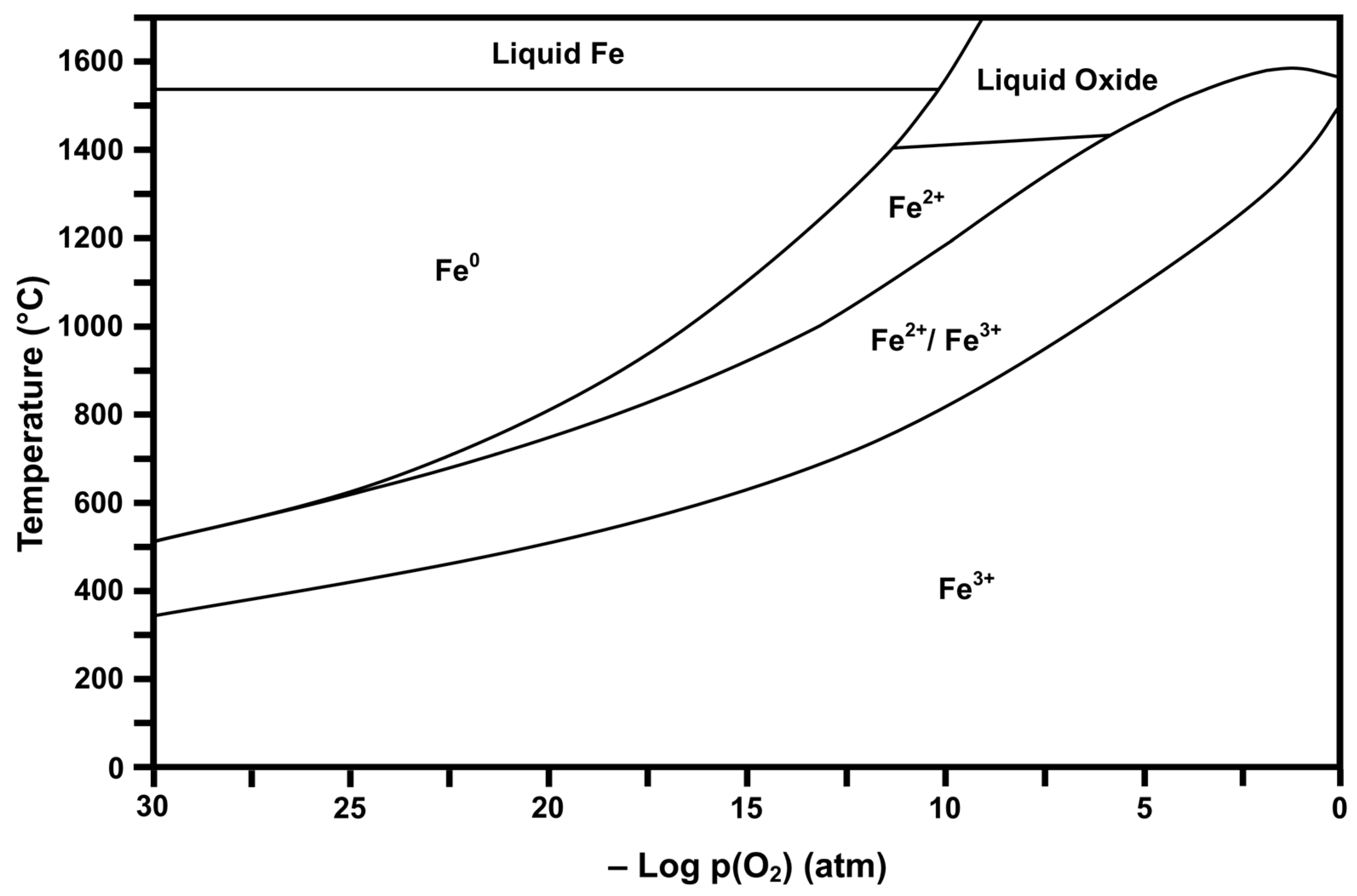
2.2. Thermodynamic Stability Diagrams
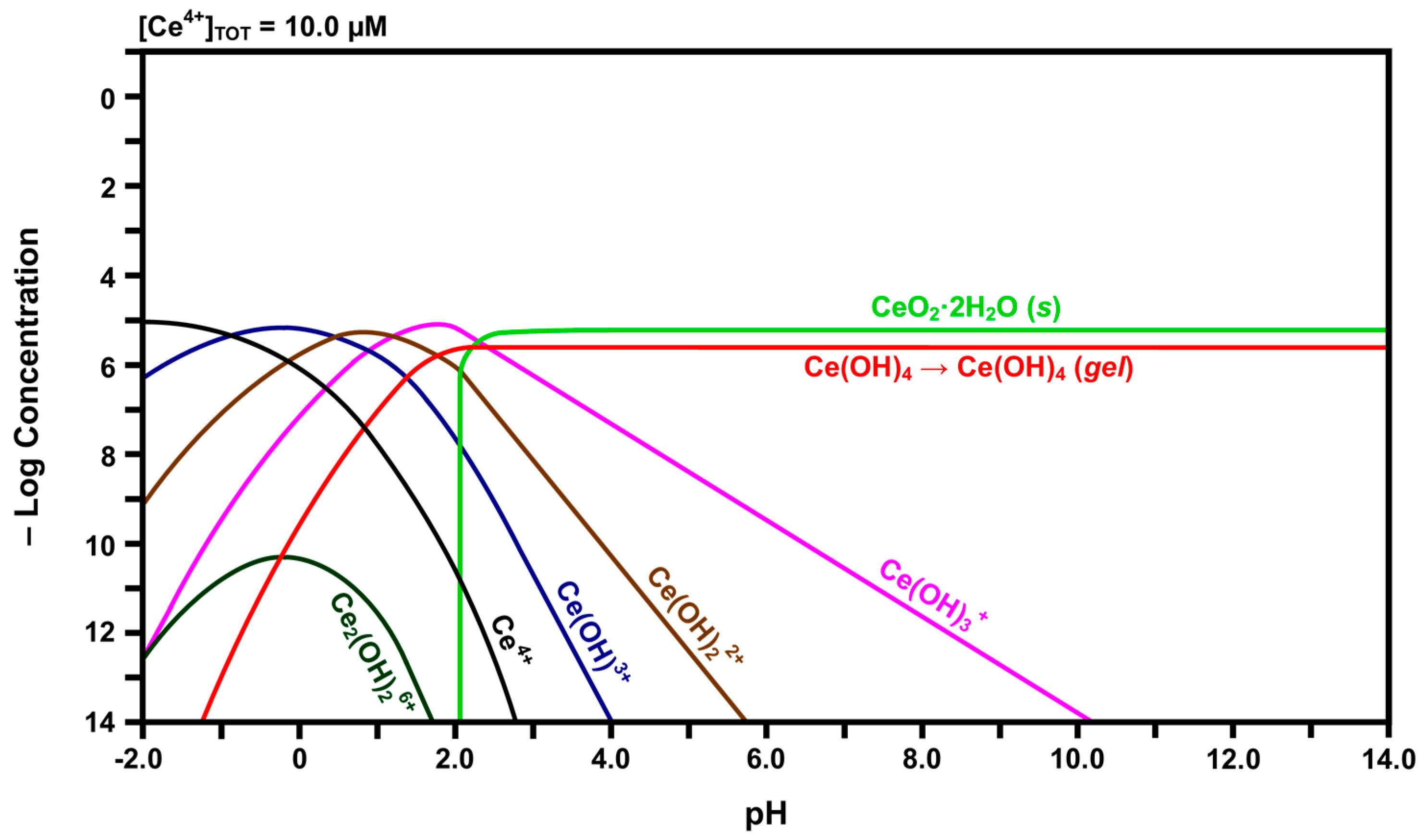
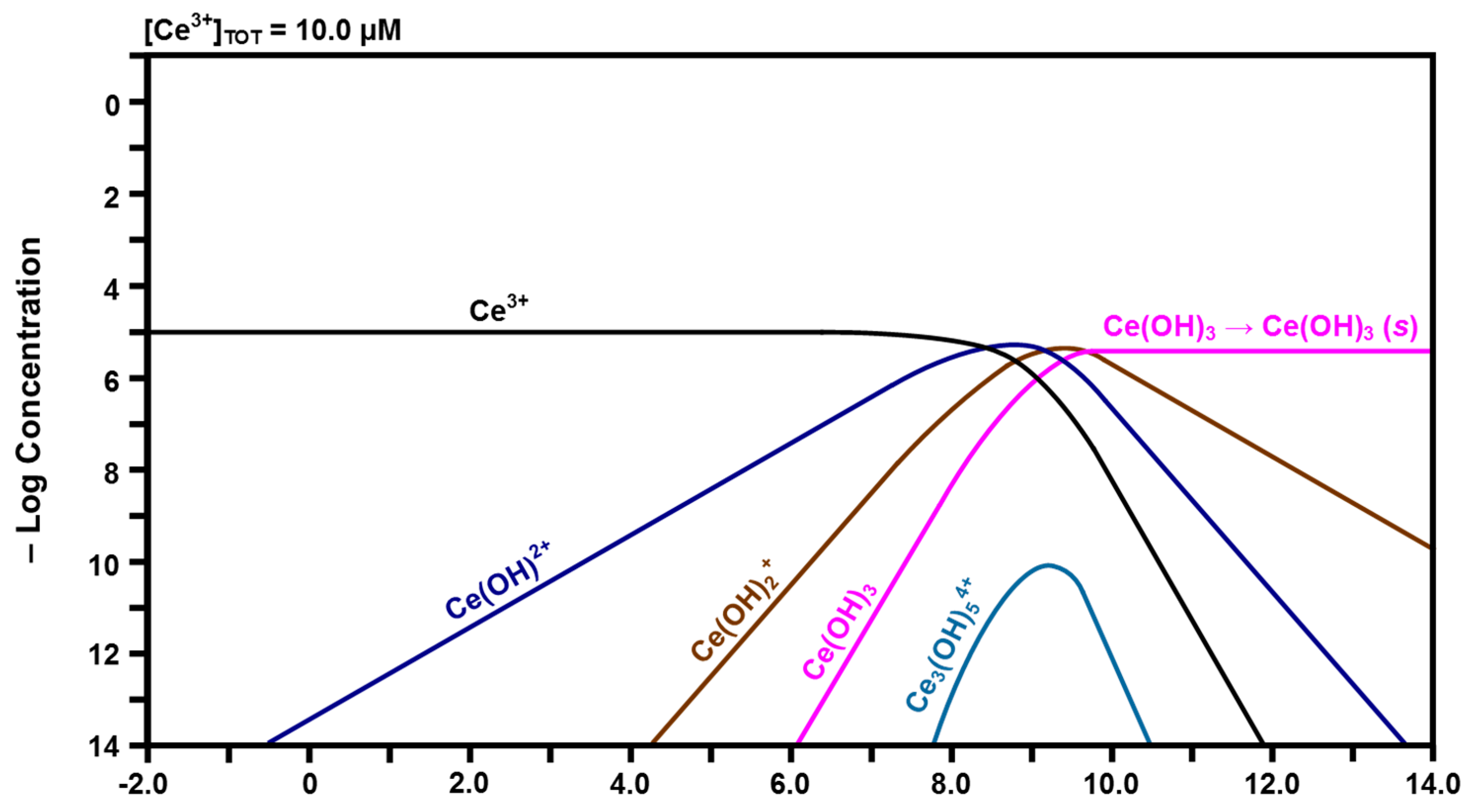
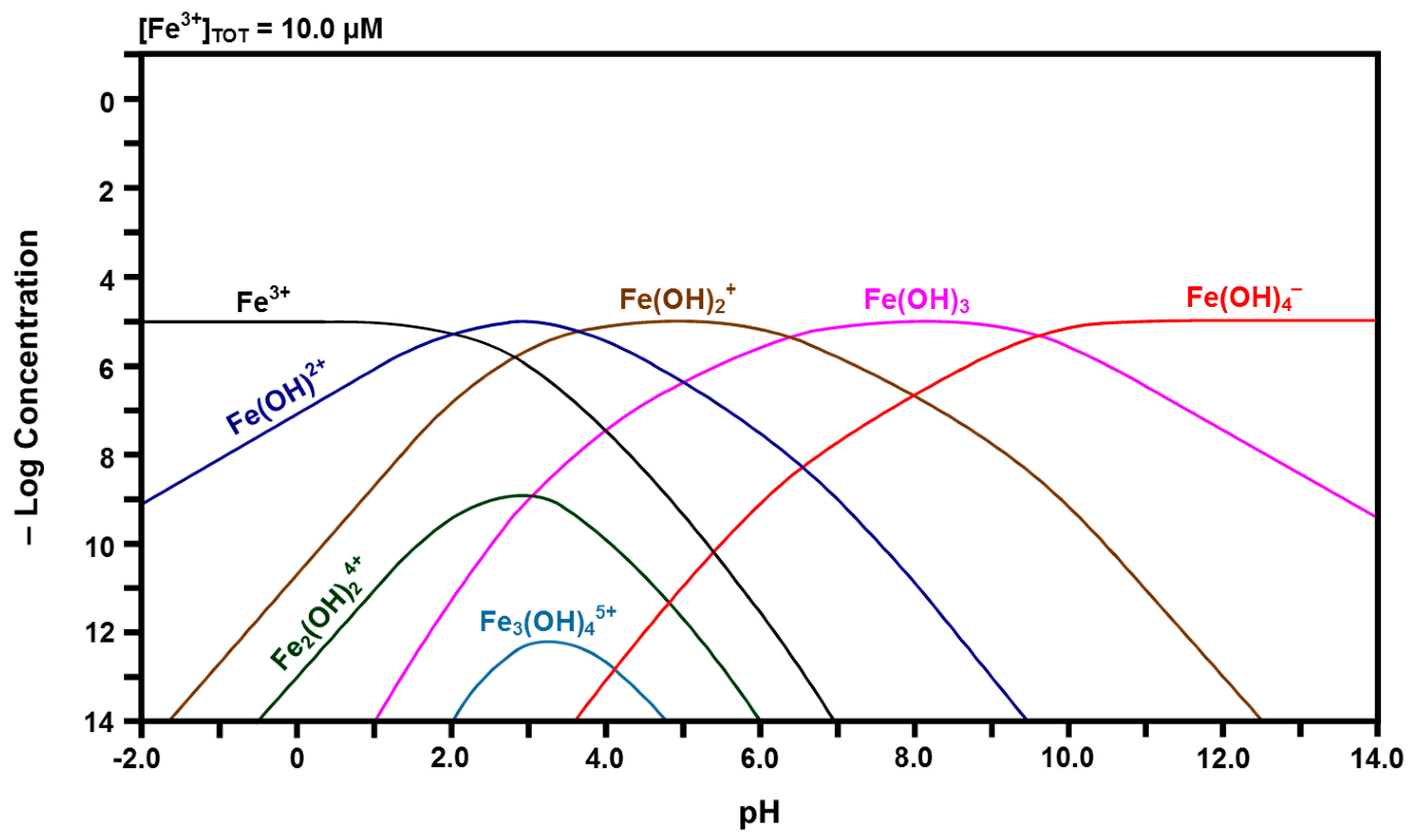
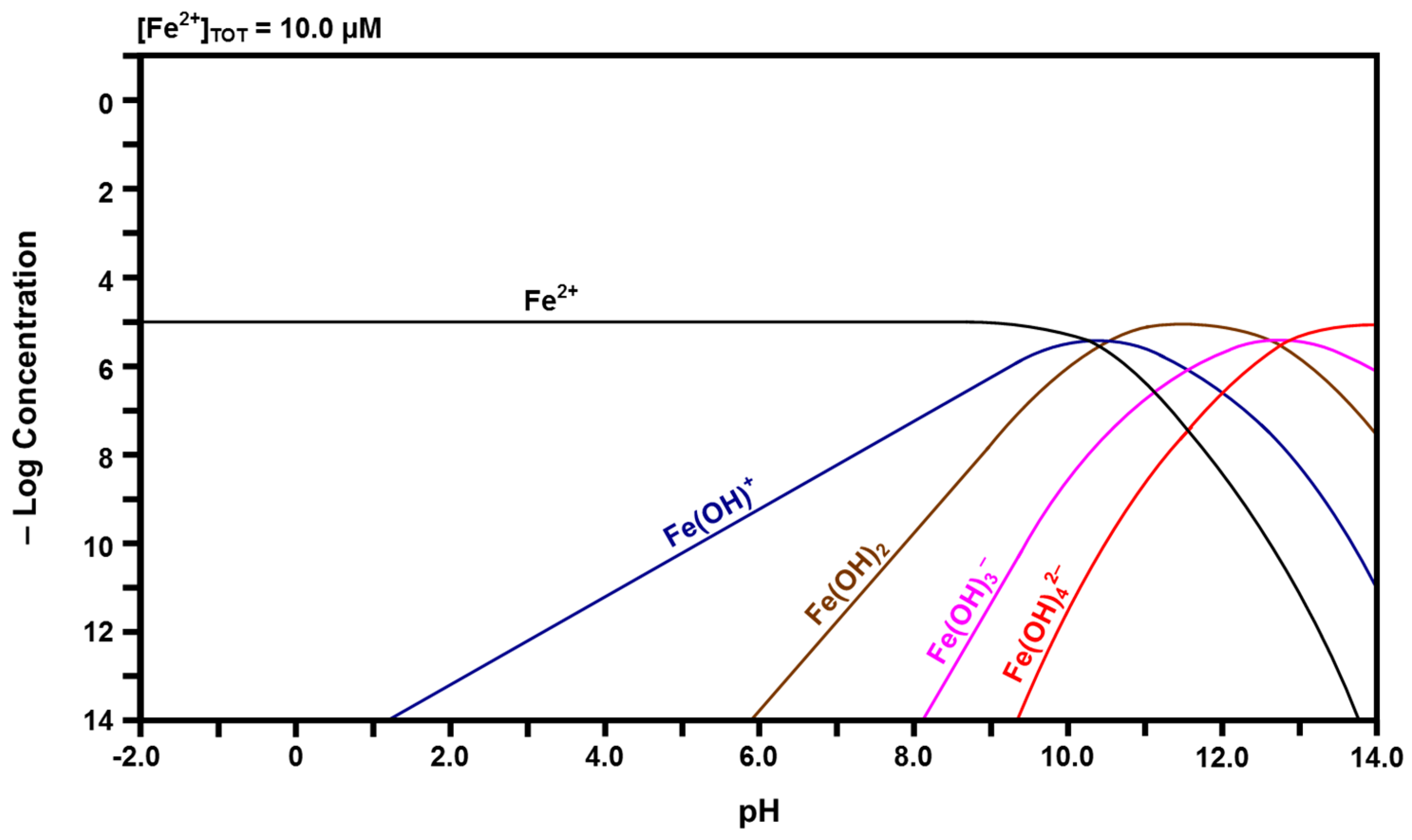
2.3. Speciation Diagrams
- = Gibbs standard free energy of reaction (J/mol)
- = Gas constant (8.314 J/K·mol)
- = Absolute temperature (K)
- = Hydrolysis constant
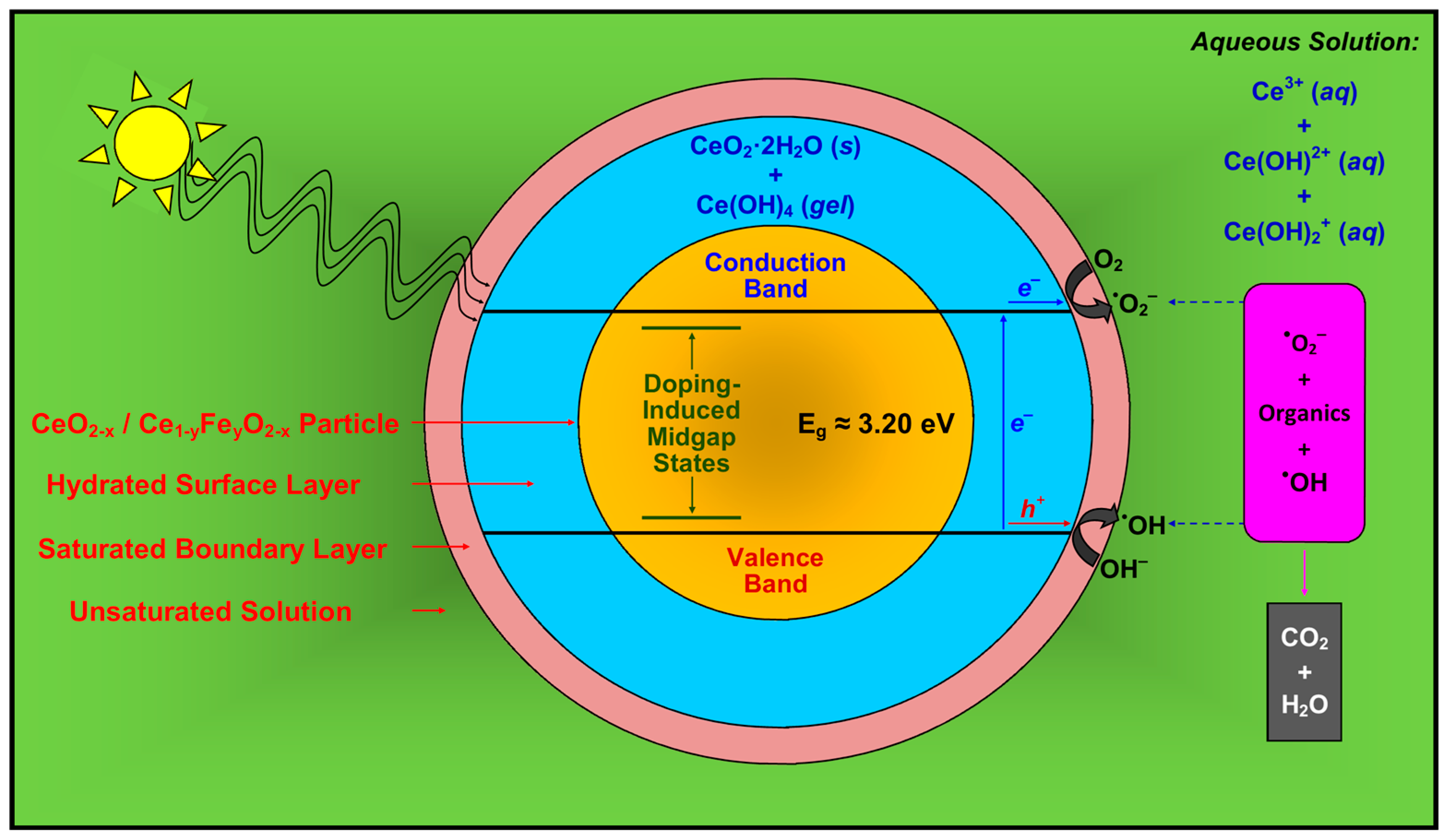
- The solubility of CeO2 in basic solutions (pH 7.00–12.00) was independent of the pH. The authors speculated that this suggested that Ce(OH)4 is the predominant solute under these conditions. However, in light of the speciation diagram of Figure 4, this speculation cannot be supported because the dense passivating layer is established rapidly at a pH slightly greater than 2.00, after which no Ce4+ or Ce3+ species can be dissolved from the underlying CeO2 and only a small amount from the surface CeO2·2H2O.
- No Ce4+-based species were generated at a pH in the range 2.00–7.00. Although this was attributed to reductive solubility, these data are consistent with (a) completion of the hydrolysis sequence by a pH of ~2.60, as shown in Figure 4, and (b) commencement of the establishment of the coherent passivating layer from the formation of solid CeO2·2H2O at a pH slightly greater than 2.00 and gelled Ce(OH)4 at a pH greater than ~2.60, also as shown in Figure 4.
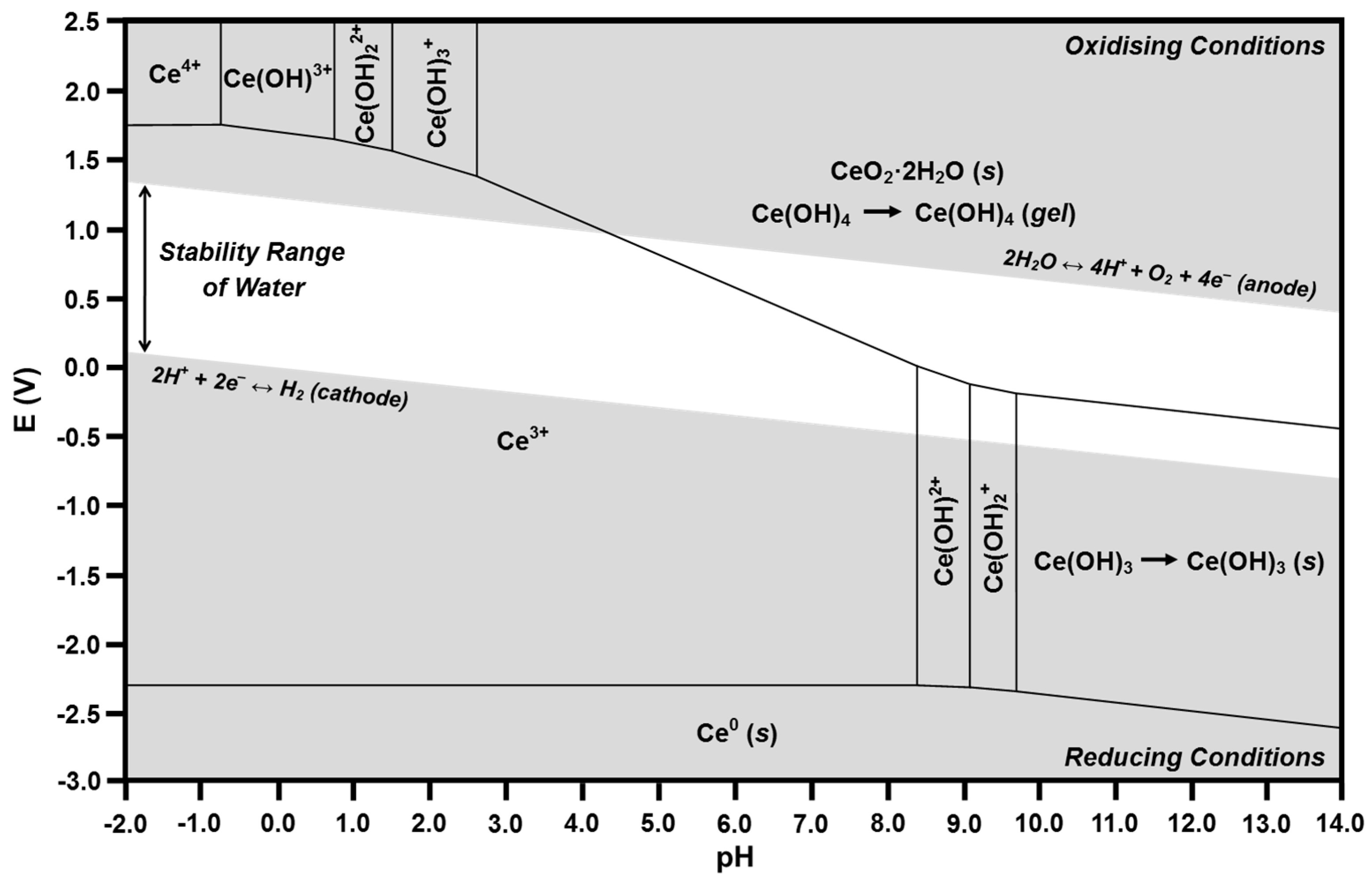
2.4. Pourbaix Diagrams
- (1)
- Vertical lines showing chemical reactions in which no electron transfer occurs; these lines, which bound two predominance regions, correspond to the pH at which both species are of equal concentration (i.e., where the speciation diagram curves intersect).
- (2)
- Horizontal lines showing electrochemical reactions in which no proton transfer occurs; these lines, which also bound two predominance regions, correspond to the standard reduction potentials for the two species.
- (3)
- Diagonal lines showing reactions in which both electron transfer and proton transfer occur; the slopes are inversely proportional to the stoichiometric number of electrons transferred and are directly proportional to the stoichiometric number of protons transferred.
- = Gibbs standard free energy of reaction (J/mol)
- = Stoichiometric number of electrons transferred (valence change)
- = Standard reduction potential (V)
- = Faraday constant (96,485 J/V·mol)
- = Electrochemical potential (V)
- = Standard reduction potential (V)
- = Stoichiometric number of protons transferred
- = Stoichiometric number of electrons transferred (valence change)
- = Activity of reductant (concentration calculated from the Kh)
- = Activity of oxidant (concentration calculated from the Kh)
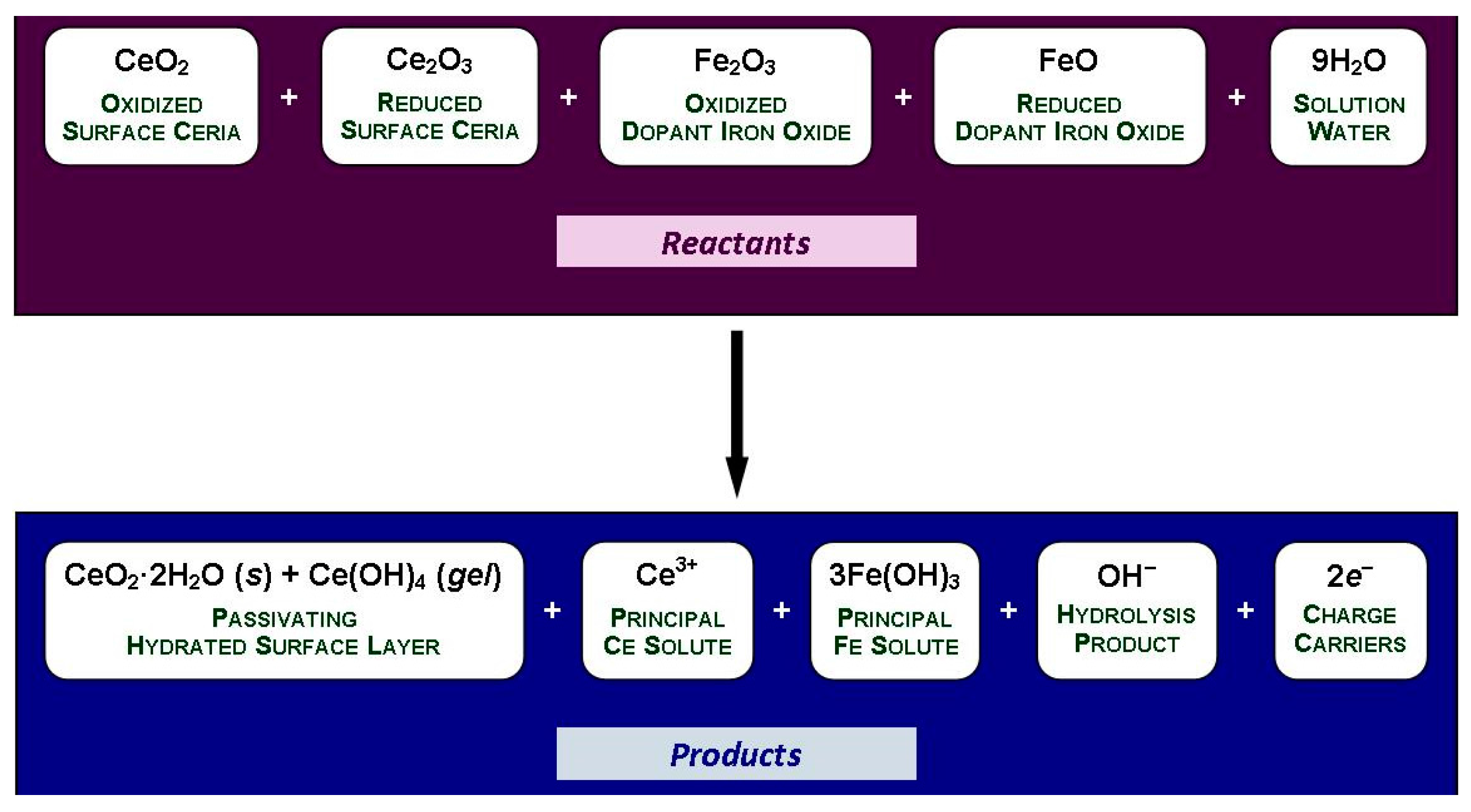
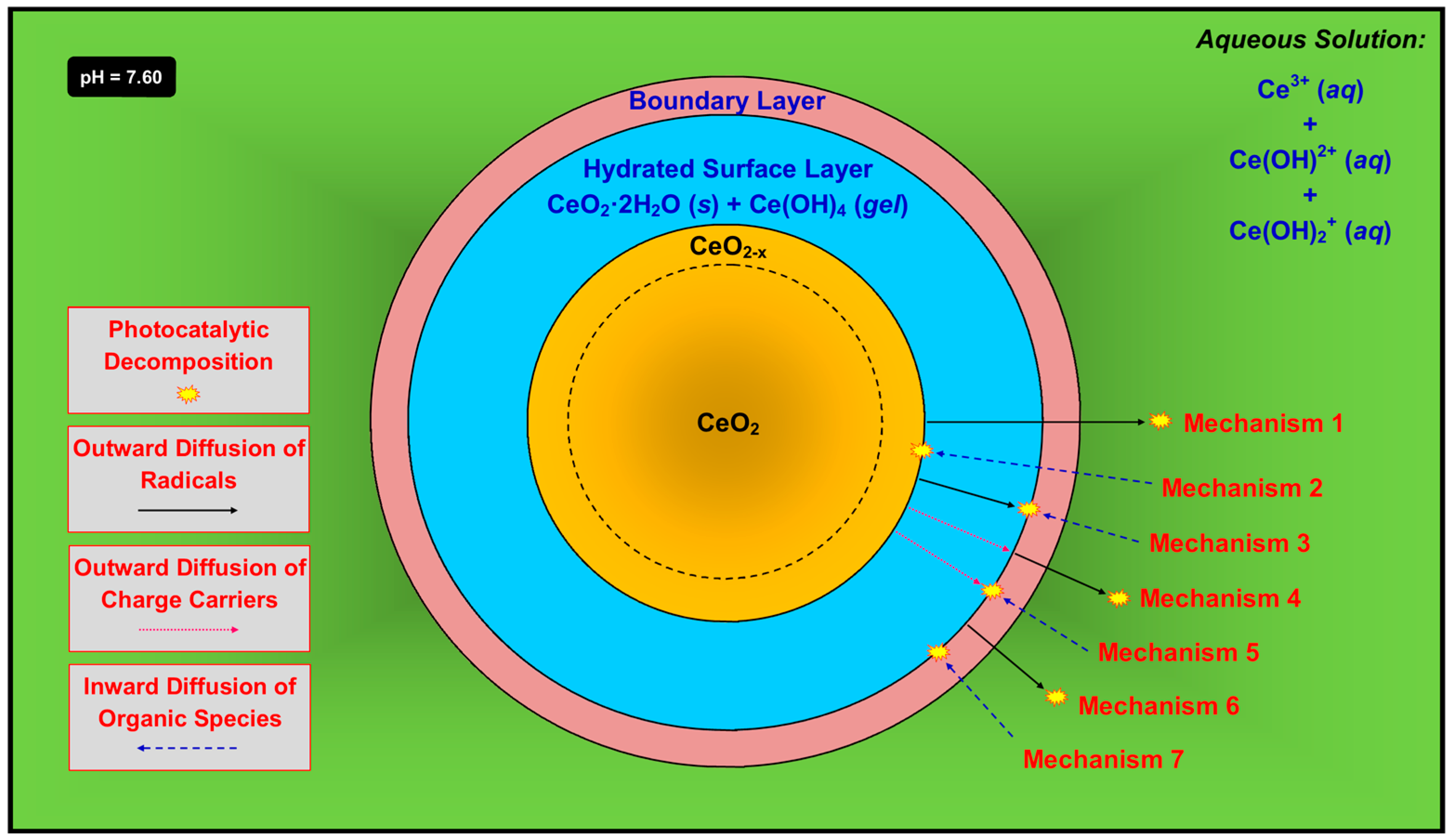
3. Discussion
- (1)
- Mechanism 1—The radicals form at the outer surface of the unhydrated solid, followed by outward diffusion through the hydrated surface layer and boundary layer and into the solution, at which point they decompose the organic species. This is possible but its probability is mitigated by two key factors. First, the radicals, both of which contain an unpaired electron, would have to diffuse through the Ce(OH)4 gel, which is likely to be highly ionic. Second, the radicals also would have to diffuse through the boundary layer, which is comprised largely of positively charged ions in solution. The superoxide radical also would tend to be neutralized by the positive ions. However, the concentrations of these species in the boundary layer can be assumed to be quite low, so they may have a minimal effect on the combination of radical and solute.
- (2)
- Mechanism 2—The radicals form at the outer surface of the unhydrated solid and, simultaneously, the organic species undergo inward diffusion through the boundary layer and the hydrated surface layer, followed by reactions to decompose the organic species. This is very unlikely owing to the difficulty of diffusion of what typically are large organic ions not through liquid but the hydrated surface layer, which consists of solid CeO2·2H2O plus gelled Ce(OH)4 [43].
- (3)
- Mechanism 3—The radicals form at the outer surface of the unhydrated solid, followed by outward diffusion through the hydrated surface layer. In the opposite direction, the organic species undergo inward diffusion through the boundary layer, followed by reactions to decompose the organic species. This is unlikely since each radical, which contains an unpaired electron, would have to diffuse through the highly ionic Ce(OH)4 gel.
- (4)
- Mechanism 4—The charge carriers, which form at the outer surface of the unhydrated solid and/or in the bulk, undergo outward diffusion through the hydrated surface layer, at which point the radicals form. These diffuse through the boundary layer and then into the solution, followed by reactions to decompose the organic species. This is unlikely since the charge carriers would have to diffuse through the highly ionic Ce(OH)4 gel. Furthermore, this is unlikely for electrons because this would require them to diffuse through the boundary layer, which contains positively charged ions in solution. It also is unlikely for holes because this would require them to diffuse through a positively charged environment, which contradicts Le Chatelier’s principle [75].
- (5)
- Mechanism 5—The charge carriers, which form at the outer surface of the unhydrated solid and/or in the bulk, undergo outward diffusion through the hydrated surface layer. In the opposite direction, the organic species undergo inward diffusion through the boundary layer, followed by reactions to decompose the organic species. This is unlikely since the charge carriers would have to diffuse through the highly ionic Ce(OH)4 gel.
- (6)
- Mechanism 6—The charge carriers form at the outer surface of the hydrated surface layer or, less likely, in its bulk. The radicals thus form at the outer surface of the hydrated surface layer, followed by their outward diffusion through the boundary layer and into the solution, at which point they decompose the organic species. This is unlikely because the radicals, each of which contains an unpaired electron, must diffuse through the boundary layer, which is comprised largely of positively charged ions in solution, and the superoxide radical would tend to be neutralized.
- (7)
- Mechanism 7—The charge carriers form at the outer surface of the hydrated surface layer or, less likely, in its bulk, followed by radical formation. The organic species undergo inward diffusion through the boundary layer, followed by reactions to decompose the organic species. This is possible as this mechanism does not include any of the conceptual shortcomings described previously.
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Channei, D.; Nakaruk, A.; Phanichphant, S.; Koshy, P.; Sorrell, C.C. Cerium Dioxide Thin Films Using Spin Coating. J. Chem. 2012, 2013. [Google Scholar] [CrossRef]
- Siriwong, C.; Wetchakun, N.; Inceesungvorn, B.; Channei, D.; Samerjai, T.; Phanichphant, S. Doped-Metal Oxide Nanoparticles for Use as Photocatalysts. Prog. Cryst. Growth Charact. Mater. 2012, 58, 145–163. [Google Scholar] [CrossRef]
- Channei, D.; Inceesungvorn, B.; Wetchakun, N.; Phanichphant, S. Kinetics Study of Photocatalytic Activity of Flame-Made Unloaded and Fe-Loaded CeO2 Nanoparticles. Int. J. Photoenergy 2013, 2013. [Google Scholar] [CrossRef]
- Lin, C.Y.W.; Channei, D.; Koshy, P.; Nakaruk, A.; Sorrell, C.C. Effect of Fe Doping on TiO2 Films Prepared by Spin Coating. Ceram. Int. 2012, 38, 3943–3946. [Google Scholar] [CrossRef]
- Leea, J.H.; Euna, J.H.; Parka, S.Y.; Kimb, S.G.; Kima, H.Y. Hydration of RF Magnetron Sputtered MgO Thin Films for a Protective Layer in AC Plasma Display Panel. Thin Solid Films 2003, 435, 95–101. [Google Scholar] [CrossRef]
- Engkvist, O.; Stone, A.J. Adsorption of Water on the MgO (001) Surface. Surf. Sci. 1999, 437, 239–248. [Google Scholar] [CrossRef]
- Zhao, Y. Design of Higher-k and More Stable Rare Earth Oxides as Gate Dielectrics for Advanced CMOS Devices. Materials 2012, 5, 1413–1438. [Google Scholar] [CrossRef]
- Channei, D.; Inceesungvorn, B.; Wetchakun, N.; Phanichphant, S.; Nakaruk, A.; Koshy, P.; Sorrell, C.C. Photocatalytic Activity under Visible Light of Fe-doped CeO2 Nanoparticles Synthesized by Flame Spray Pyrolysis. Ceram. Int. 2013, 39, 3129–3134. [Google Scholar] [CrossRef]
- Okamoto, J. Ce-O (Cerium-Oxygen). J. Phase Equilib. Diffus. 2008, 29, 545–547. [Google Scholar] [CrossRef]
- Tuller, H.L.; Nowick, A.S. Defect Structure and Electrical Properties of Nonstoichiometric CeO2 Single Crystals. J. Electrochem. Soc. 1979, 126, 209–217. [Google Scholar] [CrossRef]
- Li, L.; Wang, H.; Zou, L.; Wang, X. Controllable Synthesis, Photocatalytic and Electrocatalytic Properties of CeO2 Nanocrystals. RSC Adv. 2015, 5, 41506–41512. [Google Scholar] [CrossRef]
- Muduli, S.K.; Wang, S.; Chen, S.; Ng, C.F.; Huan, C.H.A.; Sum, T.C.; Soo, H.S. Mesoporous Cerium Oxide Nanospheres for the Visible-Light Driven Photocatalytic Degradation of Dyes. Beilstein J. Nanotechnol. 2014, 5, 517–523. [Google Scholar] [CrossRef] [PubMed]
- Farahani, H.; Wagiran, R.; Hamidon, M.N. Humidity Sensors Principle, Mechanism, and Fabrication Technologies: A Comprehensive Review. Sensors 2014, 14, 7881–7939. [Google Scholar] [CrossRef] [PubMed]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. J. Phys. Chem. Solids 1958, 5, 307–435. [Google Scholar] [CrossRef]
- Trovarelli, A. Catalytic Properties of Ceria and CeO2-Containing Materials. Catal. Rev. 2006, 38, 439–520. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Hume-Rothery, W.; Smallman, R.E.; Haworth, C.W. The Structure of Metals and Alloys, 5th ed.; Belgrave Square Publications: London, UK, 1969; pp. 349–407. [Google Scholar]
- Liao, X.H.; Zhu, J.M.; Zhu, J.J.; Xu, J.Z.; Chen, H.Y. Preparation of Monodispersed Nanocrystalline CeO2 Powders by Microwave Irradiation. Chem. Commun. 2001, 10, 937–938. [Google Scholar] [CrossRef]
- Patterson, A.L. The Scherrer Formula for X-Ray Particle Size Determination. Phys. Rev. 1939, 56, 978–982. [Google Scholar] [CrossRef]
- Fan, L.-S.; Zhu, C. Principles of Gas-Solid Flows; Cambridge University Press: Cambridge, UK, 1998; pp. 3–16. [Google Scholar]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multi-Molecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Haynes, W.M. Physical Constants of Inorganic Compounds. In CRC Handbook of Chemistry and Physics, 97th ed.; Lide, D.R., Bruno, T.J., Eds.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Beaudoux, X.; Virot, M.; Chave, T.; Leturcq, G.; Jouan, G.; Venault, L.; Moisy, P.; Nikitenko, S.I. Ultrasound-Assisted Reduction Dissolution of CeO2 and PuO2 in the Presence of Ti Particles. Dalton Trans. 2016, 45, 8802–8815. [Google Scholar] [CrossRef] [PubMed]
- Schwabe, F.; Schulin, R.; Rupper, P.; Rotzetter, A.; Stark, W.; Nowack, B. Dissolution and Transformation of Cerium Oxide Nanoparticles in Plant Growth Media. J. Nanopart. Res. 2014, 16. [Google Scholar] [CrossRef]
- Schwabe, F.; Tanner, S.; Schulin, R.; Rotzetter, A.; Stark, W.; von Quadt, A.; Nowack, B. Dissolved Cerium Contributes to Uptake of Ce in the Presence of Differently Sized CeO2-Nanoparticles by Three Crop Plants. Metallomics 2015, 7, 466–477. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Michaelides, A.; King, D.A.; Jenkins, S.J. Anchoring Sites for Initial Au Nucleation on CeO2 {111}: O Vacancy Versus Ce Vacancy. J. Phys. Chem. C 2009, 113, 6411–6417. [Google Scholar] [CrossRef]
- Gritschneder, S.; Reichling, M. Structural Elements of CeO2 (111) Surfaces. Nanotechnology 2007, 18, 1–6. [Google Scholar] [CrossRef]
- Fronzi, M.; Piccinin, S.; Delley, B.; Traversa, E.; Stampfla, C. Water Adsorption on the Stoichiometric and Reduced CeO2 (111) Surface: A First-Principles Investigation. Phys. Chem. Chem. Phys. 2009, 11, 9188–9199. [Google Scholar] [CrossRef] [PubMed]
- Namai, Y.; Fukui, K.; Iwasawa, Y. The Dynamic Behavior of CH3OH and NO2 Adsorbed on CeO2 (111) Studied by Noncontact Atomic Force Microscopy. Nanotechnology 2004, 15, 49–54. [Google Scholar] [CrossRef]
- Fukui, K.; Namai, Y.; Iwasawa, Y. Imaging of Surface Oxygen Atoms and their Defect Structures on CeO2 (111) by Noncontact Atomic Force Microscopy. Appl. Surf. Sci. 2002, 188, 252–256. [Google Scholar] [CrossRef]
- Gritschneder, S.; Namai, Y.; Iwasawa, Y.; Reichling, M. Structural Features of CeO2 (111) Revealed by Dynamic SFM. Nanotechnology 2005, 16, 41–48. [Google Scholar] [CrossRef]
- Sanchez, M.G.; Gazquez, J.L. Oxygen Vacancy Model in Strong Metal-Support Interaction. J. Catal. 1987, 104, 120–135. [Google Scholar] [CrossRef]
- Pojanavaraphana, C.; Luengnaruemitchaia, A.; Gularic, E. Effect of Support Composition and Metal Loading on Au Catalyst Activity in Steam Reforming of Methanol. Int. J. Hydrog. Energy 2012, 37, 14072–14084. [Google Scholar] [CrossRef]
- Tabakova, T.; Avgouropoulos, G.; Papavasiliou, J.; Manzoli, M.; Boccuzzi, F.; Tenchev, K. CO-Free Hydrogen Production over Au/CeO2–Fe2O3 Catalysts: Part 1. Impact of the Support Composition on the Performance for the Preferential CO Oxidation Reaction. Appl. Catal. B Environ. 2011, 101, 256–265. [Google Scholar] [CrossRef]
- Bale, C.W.; Chartrand, P.; Degterov, S.A.; Eriksson, G.; Hack, K.; Ben Mahfoud, R.; Melançon, J.; Pelton, A.D.; Petersen, S. FactSage Thermochemical Software and Databases. Calphad 2002, 26, 189–228. [Google Scholar] [CrossRef]
- Birks, N.; Meier, G.H.; Pettit, F.S. Introduction to the High Temperature Oxidation of Metals, 2nd ed.; Cambridge University Press: Cambridge, UK, 2006; pp. 83–87. [Google Scholar]
- Bingham, P.A.; Connelly, A.J.; Hyatt, N.C.; Hand, R.J. Corrosion of Glass Contact Refractories for the Vitrification of Radioactive Wastes: A Review. Int. Mater. Rev. 2013, 56, 226–242. [Google Scholar] [CrossRef]
- Latreche, H.; Doublet, S.; Schütze, M. Development of Corrosion Assessment Diagrams for High Temperature Chlorine Corrosion. Part I: State of the Art and Development of the Basis for a New Extended Approach. Oxid. Met. 2009, 72, 1–30. [Google Scholar] [CrossRef]
- vanLoon, G.W.; Duffy, S.J. Environmental Chemistry: A Global Perspective, 3rd ed.; Oxford University Press: New York, NY, USA, 2011; pp. 227–250. [Google Scholar]
- Wilkin, R.T.; Wallschläger, D.; Ford, R.G. Speciation of Arsenic in Sulfidic Waters. Geochem. Trans. 2003, 4, 1–7. [Google Scholar] [CrossRef]
- Doris, K.; Kenneth, E. Chemical Principles Revisited: The Chemistry of Glass. J. Chem. Educ. 1979, 56, 604–608. [Google Scholar]
- KTH/CHE/MEDUSA Downloads. School of Chemical Science and Engineering, KTH Royal Institute of Technology. Available online: https://www.kth.se/en/che/medusa/downloads-1.386254 (accessed on 1 October 2016).
- Hayes, S.A.; Yu, P.; O’Keefe, T.J.; O’Keefe, M.J.; Stoffer, J.O. The Phase Stability of Cerium Species in Aqueous Systems I. E-pH Diagram for the Ce-HClO4-H2O System. J. Electrochem. Soc. 2002, 149, C623–C630. [Google Scholar] [CrossRef]
- Kragten, J.; Dencop-Weever, L.G. Hydroxide Complexes of Cerium (III). Talanta 1978, 25, 147–150. [Google Scholar] [CrossRef]
- Baes, C.F., Jr.; Mesmer, R.E. The Hydrolysis of Cations; John Wiley & Sons Ltd.: New York, NY, USA, 1976; pp. 130–146 and pp. 226–237. [Google Scholar]
- López, J.M.; Gilbank, A.L.; García, T.; Solsona, B.; Agouram, S.; Torrente-Murciano, L. The Prevalence of Surface Oxygen Vacancies over the Mobility of Bulk Oxygen in Nanostructured Ceria for the Total Toluene Oxidation. Appl. Catal. B 2015, 174–175, 403–412. [Google Scholar] [CrossRef]
- Dahle, J.T.; Arai, Y. Environmental Geochemistry of Cerium: Applications and Toxicology of Cerium Oxide Nanoparticles. Int. J. Environ. Res. Public Health 2015, 12, 1253–1278. [Google Scholar] [CrossRef] [PubMed]
- Plakhova, T.V.; Romanchuk, A.Y.; Yakunin, S.N.; Dumas, T.; Demir, S.; Wang, S.; Minasian, S.G.; Shuh, D.K.; Tyliszczak, T.; Shiryaev, A.A.; et al. Solubility of Nanocrystalline Cerium Dioxide: Experimental Data and Thermodynamic Modeling. J. Phys. Chem. C 2016, 120, 22615–22626. [Google Scholar] [CrossRef]
- Haynes, W.M. Solubility Product Constants. In CRC Handbook of Chemistry and Physics, 97th ed.; Lide, D.R., Bruno, T.J., Eds.; CRC Press: Boca Raton, FL, USA, 2017; pp. 5-177–5-178. [Google Scholar]
- Brown, P.L.; Ekberg, C. Hydrolysis of Metal Ions; Wiley-VCH Verlag: Weinheim, Germany, 2016; pp. 601–618. [Google Scholar]
- Crichton, R. Inorganic Biochemistry of Iron Metabolism: From Molecular Mechanisms to Clinical Consequences, 2nd ed.; Boelaert, J.R., Braun, V., Hantke, K., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2001; pp. 4–7. [Google Scholar]
- Ahrens, L.H. The Use of Ionization Potentials Part 2. Anion Affinity and Geochemistry. Geochim. Cosmochim. Acta 1953, 3, 1–29. [Google Scholar] [CrossRef]
- Lewis, G.N.; Randall, M. The Activity Coefficient of Strong Electrolytes. J. Am. Chem. Soc. 1921, 43, 1112–1154. [Google Scholar] [CrossRef]
- Beverskog, B.; Puigdomenech, I. Revised Pourbaix Diagrams for Iron at 25–300 °C. Corros. Sci. 1996, 38, 2121–2135. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, K.; Wang, L.; Wang, B.; Li, Y. Oxygen Vacancy Clusters Promoting Reducibility and Activity of Ceria Nanorods. J. Am. Chem. Soc. 2009, 131, 3140–3141. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Zhang, H.; Cui, L.; Ouyang, C.; Shi, S.; Tang, W.; Li, H.; Chen, L. Electronic States of Metal (Cu, Ag, Au) Atom on CeO2 (111) Surface: The Role of Local Structural Distortion. J. Power Sources 2012, 197, 28–37. [Google Scholar] [CrossRef]
- Chen, W.F.; Koshy, P.; Huang, Y.; Adabifiroozjaei, E.; Yao, Y.; Sorrell, C.C. Effects of Precipitation, Liquid Formation, and Intervalence Charge Transfer on the Properties and Photocatalytic Performance of Cobalt- or Vanadium-Doped TiO2 Thin Films. Int. J. Hydrog. Energy 2016, 41, 19025–19056. [Google Scholar] [CrossRef]
- Ren, H.; Koshy, P.; Cao, F.; Sorrell, C.C. Multivalence Charge Transfer in Doped and Co-Doped Photocatalytic TiO2. Inorg. Chem. 2016, 55, 8071–8081. [Google Scholar] [CrossRef] [PubMed]
- Verink, E.D., Jr. Procedure for Constructing Pourbaix Diagrams. J. Educ. Modul. Mater. Sci. Eng. 1979, 1, 535–560. [Google Scholar]
- Verink, E.D., Jr. Simplified Procedure for Constructing Pourbaix Diagrams. In Uhlig’s Corrosion Handbook, 3rd ed.; Revie, R.W., Ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2011; pp. 93–102. [Google Scholar]
- Serguei, N.L. Introduction to Electrochemical Science and Engineering; Taylor and Francis Group: Boca Raton, FL, USA, 2015; pp. 100–102. [Google Scholar]
- Bilal, B.A.; Müller, E. Thermodynamic Study of Ce4+/Ce3+ Redox Reaction in Aqueous Solutions at Elevated Temperatures. Z. Naturforsch. A 1992, 47a, 974–984. [Google Scholar]
- Brookins, D.G. Eh-pH Diagrams for the Rare Earth Elements at 25 °C and one Bar Pressure. Geochem. J. 1983, 17, 223–229. [Google Scholar] [CrossRef]
- Chirkst, D.E.; Lobacheva, O.L.; Berlinskii, I.V. Gibbs Energies of Formation of Hydroxides of Lanthanides and Yttrium. Russ. J. Phys. Chem. A 2010, 84, 2047–2050. [Google Scholar] [CrossRef]
- Yu, P.; Hayes, S.A.; O’Keefe, T.J.; O’Keefe, M.J.; Stoffer, J.O. The Phase Stability of Cerium Species in Aqueous Systems. J. Electrochem. Soc. 2006, 153, C74–C79. [Google Scholar] [CrossRef]
- Ayala-Luis, K.B.; Koch, C.B.; Hansen, H.C.B. The Standard Gibbs Energy of Formation of Fe(II)Fe(III) Hydroxide Sulfate Green Rust. Clays Clay Miner. 2008, 56, 633–644. [Google Scholar] [CrossRef]
- Lemire, R.J.; Berner, U.; Musikas, C.; Palmer, D.A.; Taylor, P.; Tochiyama, O. Chemical Thermodynamics of Iron, Part 1; OECD Publications: Paris, France, 2013; pp. 44–50. [Google Scholar]
- Hemingway, B.S.; Seal, R.R., II; Chou, I.M. Thermodynamic Data for Modelling Acid Mine Drainage Problems: Compilation and Estimation of Data for Selected Soluble Iron-Sulfate Minerals; Open-File Report 02–161; United States Geological Survey: Reston, VA, USA, 2002. [Google Scholar]
- Robie, R.A.; Hemingway, B.S.; Fisher, J.R. Thermodynamic Properties of Minerals and Related Substances at 298.15 K and 1 Bar (105 Pascals) Pressure and at Higher Temperatures; U.S. Geological Survey Bulletin 1452; U.S. Government Printing Office: Washington, DC, USA, 1978; pp. 12–13.
- Hem, J.D.; Cropper, W.H. Survey of Ferrous-Ferric Chemical Equilibria and Redox Potentials; U.S. Geological Survey Water-Supply Paper 1459-A; U.S. Government Printing Office: Washington, DC, USA, 1962; pp. 3–10.
- Suter, D.; Banwart, S.; Stumm, W. Dissolution of Hydrous Iron (III) Oxides by Reductive Mechanisms. Langmuir 1991, 7, 809–813. [Google Scholar] [CrossRef]
- Petrunic, B.M.; MacQuarrie, K.T.B.; Al, T.A. Reductive Dissolution of Mn Oxides in River-Recharged Aquifers: A Laboratory Column Study. J. Hydrol. 2005, 301, 163–181. [Google Scholar] [CrossRef]
- Wulfsberg, G. Inorganic Chemistry; University Science Books: Mill Valley, CA, USA, 2000; pp. 288–290. [Google Scholar]
- Channei, D.; Inceesungvorn, B.; Wetchakun, N.; Ukritnukun, S.; Nattestad, A.; Chen, J.; Phanichphant, S. Photocatalytic Degradation of Methyl Orange by CeO2 and Fe-Doped CeO2 Films under Visible Light Irradiation. Sci. Rep. 2015, 4, 5757. [Google Scholar] [CrossRef] [PubMed]
- Myers, R. The Basics of Chemistry; Greenwood Press: Westport, CT, USA, 2003; pp. 149–151. [Google Scholar]
- Anpo, M.; Shima, T.; Kodama, S.; Kubokawa, Y. Photocatalytic Hydrogenation of Propyne with Water on Small-Particle Titania: Size Quantization Effects and Reaction Intermediates. J. Phys. Chem. 1987, 91, 4305–4310. [Google Scholar] [CrossRef]
- Jain, P.; Arun, P. Influence of Grain Size on the Band-Gap of Annealed SnS Thin Films. Thin Solid Films 2013, 548, 241–246. [Google Scholar] [CrossRef]
- Khare, A.; Wills, A.W.; Ammerman, L.M.; Norris, D.J.; Aydil, E.S. Size Control and Quantum Confinement in Cu2ZnSnS4 Nanocrystals. Chem. Commun. 2011, 47, 11721–11723. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Koshy, P.; Chen, W.F.; Qi, S.; Sorrell, C.C. Photocatalytic Materials and Technologies for Air Purification. J. Hazard. Mater. 2017, 325, 340–366. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Koshy, P.; Wang, J.; Sorrell, C.C. Pure and Mixed Quantum Size Effects in Doped and Co-doped Photocatalytic TiO2. J. Mater. Sci. 2017. in submission. [Google Scholar]
- Wang, C.-C.; Zhang, Z.; Ying, J.Y. Photocatalytic Decomposition of Halogenated Organics over Nanocrystalline Titania. Nanostruct. Mater. 1997, 9, 583–586. [Google Scholar] [CrossRef]
- Cho, C.H.; Han, M.H.; Kim, D.H.; Kim, D.K. Morphology Evolution of Anatase TiO2 Nanocrystals under a Hydrothermal Condition (pH = 9.5) and their Ultra-High Photo-Catalytic Activity. Mater. Chem. Phys. 2005, 92, 104–111. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.-C.; Zakaria, R.; Ying, J.Y. Role of Particle Size in Nanocrystalline TiO2-Based Photocatalysts. J. Phys. Chem. B 1998, 102, 10871–10878. [Google Scholar] [CrossRef]
- Träubel, H. New Materials Permeable to Water Vapor; Springer: Berlin, Germany, 1999; pp. 133–152. [Google Scholar]
- Rahaman, M.N. Ceramic Processing and Sintering, 2nd ed.; Marcel Dekker: New York, NY, USA, 2003; pp. 243–323. [Google Scholar]
- Thomas, J.J.; Chen, J.J.; Jennings, H.M.; Neumann, D.A. Ca-OH Bonding in the C-S-H Gel Phase of Tricalcium Silicate and White Portland Cement Pastes Measured by Inelastic Neutron Scattering. Chem. Mater. 2003, 15, 3813–3817. [Google Scholar] [CrossRef]
- Provis, J.L.; Bernal, S.A. Geopolymers and Related Alkali-Activated Materials. Ann. Rev. Mater. Sci. 2014, 44, 299–327. [Google Scholar] [CrossRef]
- Kubaschewski, O.; Hopkins, B.E. Oxidation of Metals and Alloys, 2nd ed.; Butterworths: London, UK, 1962; pp. 70–142. [Google Scholar]


| Parameter | Unit | Fe Dopant Concentration (mol % Metal Basis) * | Reference | |||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.36 | 0.96 | 1.38 | 1.73 | ||||
| Absorbed Water | wt % | 28.6 | 30.6 | 31.3 | 32.3 | 34.1 | Present Work | |
| d(111) Spacing | Before Heating | nm | 0.3150 | 0.3138 | 0.3131 | 0.3124 | 0.3122 | |
| After Heating | nm | 0.3141 | 0.3137 | 0.3129 | 0.3126 | 0.3115 | ||
| Crystallite Size | nm | 7.15 | 6.65 | 6.41 | 6.31 | 6.22 | [8] | |
| Particle Size | nm | 6.40 | 6.16 | 6.03 | 5.98 | 5.94 | ||
| Specific Surface Area | m2/g | 130 | 135 | 138 | 139 | 140 | ||
| Parent Ion | Cerium and Iron Species | Relative Concentration (mol %) |
|---|---|---|
| Ce4+ | CeO2·2H2O (s) | 69 |
| Ce(OH)4 (gel) | 30 | |
| Ce(OH)3+ | <10−4 | |
| Ce3+ | Ce3+ | 86 |
| Ce(OH)2+ | 13 | |
| Ce(OH)2+ | 0.3 | |
| Ce(OH)3 | <10−3 | |
| Fe3+ | Fe(OH)3 | 91.5 |
| Fe(OH)2+ | 7.5 | |
| Fe(OH)4− | <1.0 | |
| Fe(OH)2+ | <10−3 | |
| Fe2+ | Fe2+ | 99.7 |
| Fe(OH)+ | <0.1 | |
| Fe(OH)2 | <10−4 |
| No. | Redox Couple Reaction | pH Range | E Range |
|---|---|---|---|
| Reactions between Ce0 and Ce (III) | |||
| 1 | Ce3+ + 3e− → Ce0 | −2.0–8.4 | 2.32 (pH independent) |
| 2 | Ce(OH)2+ + H+ + 3e− → Ce0 + H2O | 8.4–9.1 | −2.15–0.02 pH |
| 3 | Ce(OH)2+ + 2H+ + 3e− → Ce0 + 2H2O | 9.1–9.7 | −1.97–0.04 pH |
| 4 | Ce(OH)3 + 3H+ + 3e− → Ce0 + 3H2O | 9.7–14 | −1.78–0.06 pH |
| Reactions between Ce3+ and Ce (IV) | |||
| 5 | Ce4+ + e− → Ce3+ | −2.0–−0.76 | 1.74 (pH independent) |
| 6 | Ce(OH)3+ + H+ + e− → Ce3+ + H2O | −0.76–0.72 | 1.69–0.06 pH |
| 7 | Ce(OH)22+ + 2H+ + e− → Ce3+ + 2H2O | 0.72–1.5 | 1.74–0.12 pH |
| 8 | Ce(OH)3+ + 3H+ + e− → Ce3+ + 3H2O | 1.5–2.6 | 1.83–0.18 pH |
| 9 | Ce(OH)4 + 4H+ + e− → Ce3+ + 4H2O | 2.6–8.4 | 1.98–0.24 pH |
| Reactions between Ce (III) and Ce (IV) | |||
| 10 | Ce(OH)4 + 3H+ + e− → Ce(OH)2+ + 3H2O | 8.4–9.1 | 1.48–0.18 pH |
| 11 | Ce(OH)4 + 2H+ + e− → Ce(OH)2+ + 2H2O | 9.1–9.7 | 0.94–0.12 pH |
| 12 | Ce(OH)4 + H+ + e− → Ce(OH)3 + H2O | 9.7–14 | 0.37–0.06 pH |
| No. | Redox Couple Reaction | pH Range | E Range |
|---|---|---|---|
| Reactions between Fe0 and Fe (II) | |||
| 1 | Fe2+ + 2e− → Fe0 | 0–10.1 | −0.47 (pH independent) |
| 2 | Fe(OH)+ + H+ + 2e− → Fe0 + H2O | 10.1–10.6 | −0.17–0.03 pH |
| 3 | Fe(OH)2 + 2H+ + 2e− → Fe0 + 2H2O | 10.6–12.6 | 0.09–0.06 pH |
| 4 | Fe(OH)3− + 3H+ + 2e− → Fe0 + 3H2O | 12.6–13.0 | 0.50–0.09 pH |
| 5 | Fe(OH)42− + 4H+ + 2e− → Fe0 + 4H2O | 13.0–14.0 | 0.89–0.12 pH |
| Reactions between Fe2+ and Fe (III) | |||
| 6 | Fe3+ + e− → Fe2+ | 0–2.12 | 0.77 (pH independent) |
| 7 | Fe(OH)2+ + H+ + e− → Fe2+ + H2O | 2.12–3.48 | 0.90–0.06 pH |
| 8 | Fe(OH)2+ + 2H+ + e− → Fe2+ + 2H2O | 3.48–6.30 | 1.10–0.12 pH |
| 9 | Fe(OH)3 + 3H+ + e− → Fe2+ + 3H2O | 6.30–9.50 | 1.47–0.18 pH |
| 10 | Fe(OH)4− + 4H+ + e− → Fe2+ + 4H2O | 9.50–10.1 | 2.05–0.24 pH |
| Reactions between Fe (II) and Fe (III) | |||
| 10 | Fe(OH)4− + 3H+ + e− → Fe(OH)+ + 3H2O | 10.1–10.6 | 1.46–0.18 pH |
| 11 | Fe(OH)4− + 2H+ + e− → Fe(OH)2 + 2H2O | 10.6–12.6 | 0.93–0.12 pH |
| 12 | Fe(OH)4− + H+ + e− → Fe(OH)3− + H2O | 12.6–13.0 | 0.08–0.06 pH |
| 13 | Fe(OH)4− + e− → Fe(OH)42− | 13.0–14.0 | −0.68 (pH independent) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Channei, D.; Phanichphant, S.; Nakaruk, A.; Mofarah, S.S.; Koshy, P.; Sorrell, C.C. Aqueous and Surface Chemistries of Photocatalytic Fe-Doped CeO2 Nanoparticles. Catalysts 2017, 7, 45. https://doi.org/10.3390/catal7020045
Channei D, Phanichphant S, Nakaruk A, Mofarah SS, Koshy P, Sorrell CC. Aqueous and Surface Chemistries of Photocatalytic Fe-Doped CeO2 Nanoparticles. Catalysts. 2017; 7(2):45. https://doi.org/10.3390/catal7020045
Chicago/Turabian StyleChannei, Duangdao, Sukon Phanichphant, Auppatham Nakaruk, Sajjad S. Mofarah, Pramod Koshy, and Charles C. Sorrell. 2017. "Aqueous and Surface Chemistries of Photocatalytic Fe-Doped CeO2 Nanoparticles" Catalysts 7, no. 2: 45. https://doi.org/10.3390/catal7020045
APA StyleChannei, D., Phanichphant, S., Nakaruk, A., Mofarah, S. S., Koshy, P., & Sorrell, C. C. (2017). Aqueous and Surface Chemistries of Photocatalytic Fe-Doped CeO2 Nanoparticles. Catalysts, 7(2), 45. https://doi.org/10.3390/catal7020045






