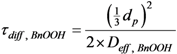2.1. Catalyst Deactivation in Base-Free Conditions
Figure 2 displays the concentration profiles for two subsequent experiments performed under the same conditions and in the absence of a base. It should be noted that for all experimental data points, the mass balance of the 4 main components (BnOH, BnO, BnOOH and BnOOBn) closes to 100% within measurement errors, with rare exceptions where discrepancies up to 4% are present. Therefore, disproportionation and dehydration reactions, as reported by Alhumaimess
et al. [
5], can be neglected. In the first experiment, the initial
TOF is 0.7 s
−1 and conversion levels off at around 55–60% after about 120 min. The selectivity to BnO is 93%, as reported in
Table 1. In view of the large discrepancies in
TOF reported in literature [
1], comparison of our data to previously published ones is not straightforward. It is satisfactory that the values of 0.6 to 0.8 s
−1 reported in the present study are in the order of magnitude of those of 0.04 to 0.22 s
−1 reported in the recent review by Davis
et al. [
1] for nanoparticulate gold and of 2.8 to 4.4 s
−1 for a gold foil reported in the same review [
1]. As indicated by Davis
et al., the values span 2 orders of magnitude. The reason for this is most likely the wide range of reaction conditions used in different studies.
Figure 2.
Catalyst performance in base-free conditions. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for (
a) first run using fresh AUROlite
™ and (
b) second run using spent AUROlite
™. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1 in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Figure 2.
Catalyst performance in base-free conditions. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for (
a) first run using fresh AUROlite
™ and (
b) second run using spent AUROlite
™. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1 in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Table 1.
Benzyl alcohol conversion rate, turn over frequency (TOF), conversion at 240 min and selectivity to benzaldehyde at 60% conversion for AUROlite™ catalyst in different test conditions.
Table 1.
Benzyl alcohol conversion rate, turn over frequency (TOF), conversion at 240 min and selectivity to benzaldehyde at 60% conversion for AUROlite™ catalyst in different test conditions.
| Catalytic system | Figure | BnOH conversion rate a
/mmol·min−1 | TOF b /s−1 | X at 240 min c /% | Sel to BnO d /% |
|---|
| Base-free | 2a | 0.37 ± 0.02 | 0.7 ± 0.1 | 63 ± 3 | 93 ± 1 |
| Base-free re-test | 2b | 0.06 ± 0.04 | 0.1 ± 0.1 | 1 ± 5 | / |
| Base-free–BnO | 3 | 0.09 ± 0.04 | 0.2 ± 0.1 | 20 ± 10 | / |
| Base-free–BnOOH | 4 | 0 | 0 | 2 ± 7 | / |
| K2CO3 | 6a | 0.5 ± 0.1 | 0.9 ± 0.4 | 78 ± 1 | 91 ± 1 |
| K2CO3 re-test | 6b | 0.20 ± 0.02 | 0.4 ± 0.1 | 72 ± 1 | 85 ± 1 |
| KF | 7a | 0.3 ± 0.1 | 0.6 ± 0.3 | 81 ± 1 | 91 ± 1 |
| KF re-test | 7b | 0.5 ± 0.2 | 1.0 ± 0.5 | 95 ± 1 | 83 ± 1 |
| K2CO3–BnOOH | 10 | 0.10 ± 0.03 | 0.2 ± 0.1 | 61 ± 7 | 92 ± 1 |
| K2CO3–H2O | 11 | 0.43 ± 0.03 | 0.8 ± 0.2 | 97 ± 1 | 86 ± 1 |
| Base-free re-test–H2O | 12 | 0.03 ± 0.05 | 0.1 ± 0.1 | 1 ± 4 | / |
In the second experiment, which is identical to the first one but with re-use of the same catalyst sample after washing with toluene, virtually no conversion is observed, indicating that the catalyst was completely deactivated. Since no other reactants than toluene and benzyl alcohol were present in the reaction mixture, the deactivation must be caused either by catalyst deterioration or by an inhibitor formed during the first experiment.
The potential presence of sulfur-containing impurities was investigated by analyzing the toluene and benzyl alcohol by gas chromatography (GC). No sulfur-containing compounds could be detected, implying that their concentration was below 50 ppb (the pulsed flame photometric detector (PFPD) detection limit). Accounting for the quantities of these chemicals introduced in the reaction mixture, this corresponds to 0.4 nmol of sulfur components at maximum in the reactor. That is five orders of magnitude lower than the total amount of gold present. Since similar concentration profiles as shown in
Figure 2 were obtained when using reagents that were pre-treated with activated carbon to remove any strongly adsorbing impurities, we conclude that feed contaminants, including sulfur compounds, are not responsible for the observed deactivation. As a consequence, activated carbon cleaning was deemed not to be necessary and was omitted for the experiments reported here.
These results thus suggest that products or intermediates formed cause the observed deactivation. In order to investigate whether product inhibition is indeed taking place, an experiment was performed with fresh catalyst, where BnO was added to the reactor 20 min prior to the actual start of the catalytic reaction under the same reaction conditions,
i.e., before the introduction of BnOH. The 20 min exposure time was selected based on the results of
Figure 1a where it can be seen that BnOOBn was already formed at that reaction time, thereby ensuring that all potentially inhibiting products were present. The results in
Figure 3 show a very low conversion of 20%, confirming strong product inhibition. It is striking that despite the appreciable amount of BnO introduced at
t < 0, neither BnOOBn nor BnOOH could be detected until the BnOH was introduced at
t = 0. Clearly the sites for the sequential reactions of BnO (
Figure 1a,b) are fully blocked without the presence of alcohol. It should be noted that for
t < 0 the BnO concentration shows a slight decrease, indicating that a small amount of BnO is consumed without producing a detectable amount of BnOOH in the liquid phase. We conclude that some product is formed which remains on the catalyst and inhibits further turnovers. Carboxylic acid moieties are well known to interact strongly with gold nanoparticle surfaces, even allowing the stabilization of small gold clusters in colloidal systems [
21]. BnOOH is therefore suspected to be the inhibitor, since it is the logical product of BnOH oxidation, although its concentration in the solution stayed below the GC detection limit of 0.20 µmol·g
−1.
Figure 3.
Catalyst performance after pre-addition of benzaldehyde. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™. Benzaldehyde was introduced 20 min before benzyl alcohol was added. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1,
CBnO, t<0 = 1.7 × 10
−4 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Figure 3.
Catalyst performance after pre-addition of benzaldehyde. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™. Benzaldehyde was introduced 20 min before benzyl alcohol was added. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1,
CBnO, t<0 = 1.7 × 10
−4 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
In order to evaluate the effect of BnOOH, a similar experiment was performed in which BnOOH was added 20 min prior to the actual start of the test. The concentration profiles are shown in
Figure 4. In this experiment, approximately 40 times less acid was introduced compared to the amount of aldehyde introduced for the experiment in
Figure 3. Nevertheless, an even more dramatic inhibiting effect was observed: hardly any conversion of BnOH occurred. The concentration of BnOOH measured by GC at
t < 0 is 1 µmol·g
−1, which is about 25% of what was added, suggesting a strong interaction of BnOOH with the catalyst. The slight increase in concentration of BnOOH upon addition of BnOH at
t = 0 is attributed to competitive adsorption between the alcohol and the acid. No ester was present at the beginning of the reaction, nor was it detected during the course of the reaction. This suggests that the inhibiting product is either BnOOH or a compound formed from BnOOH. Therefore, product inhibition particularly occurs on catalysts on which BnO can react further to BnOOH. This interpretation is confirmed by a nanostructured gold-based catalyst synthesized in our lab exhibiting 100% selectivity to BnO not showing deactivation for 4 consecutive runs [
22].
Figure 4.
Catalyst performance after pre-addition of benzoic acid. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™. Benzoic acid was introduced 20 min prior to the beginning of the reaction. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1,
CBnOOH, t<0 = 4.1 × 10
−6 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Figure 4.
Catalyst performance after pre-addition of benzoic acid. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™. Benzoic acid was introduced 20 min prior to the beginning of the reaction. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1,
CBnOOH, t<0 = 4.1 × 10
−6 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
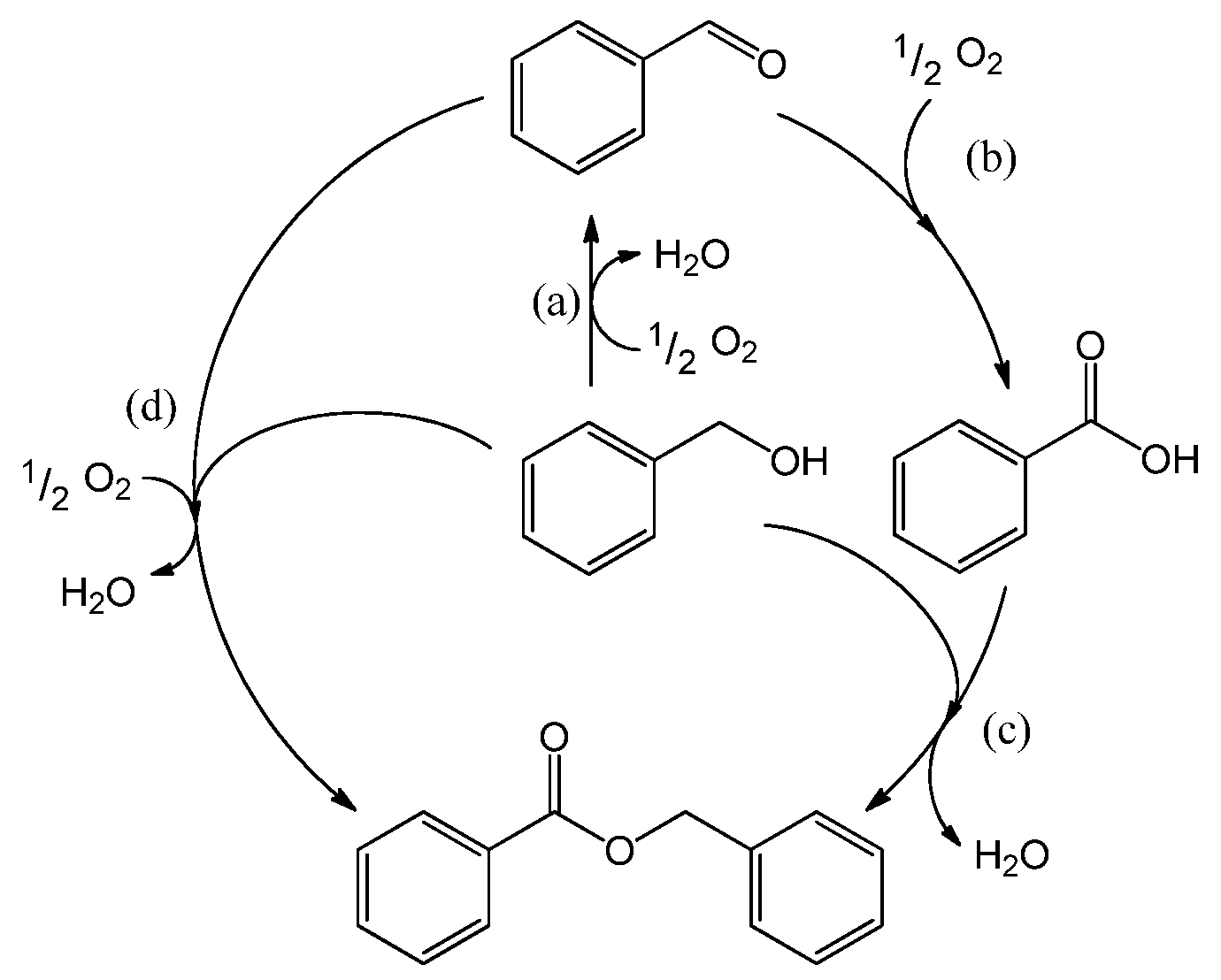
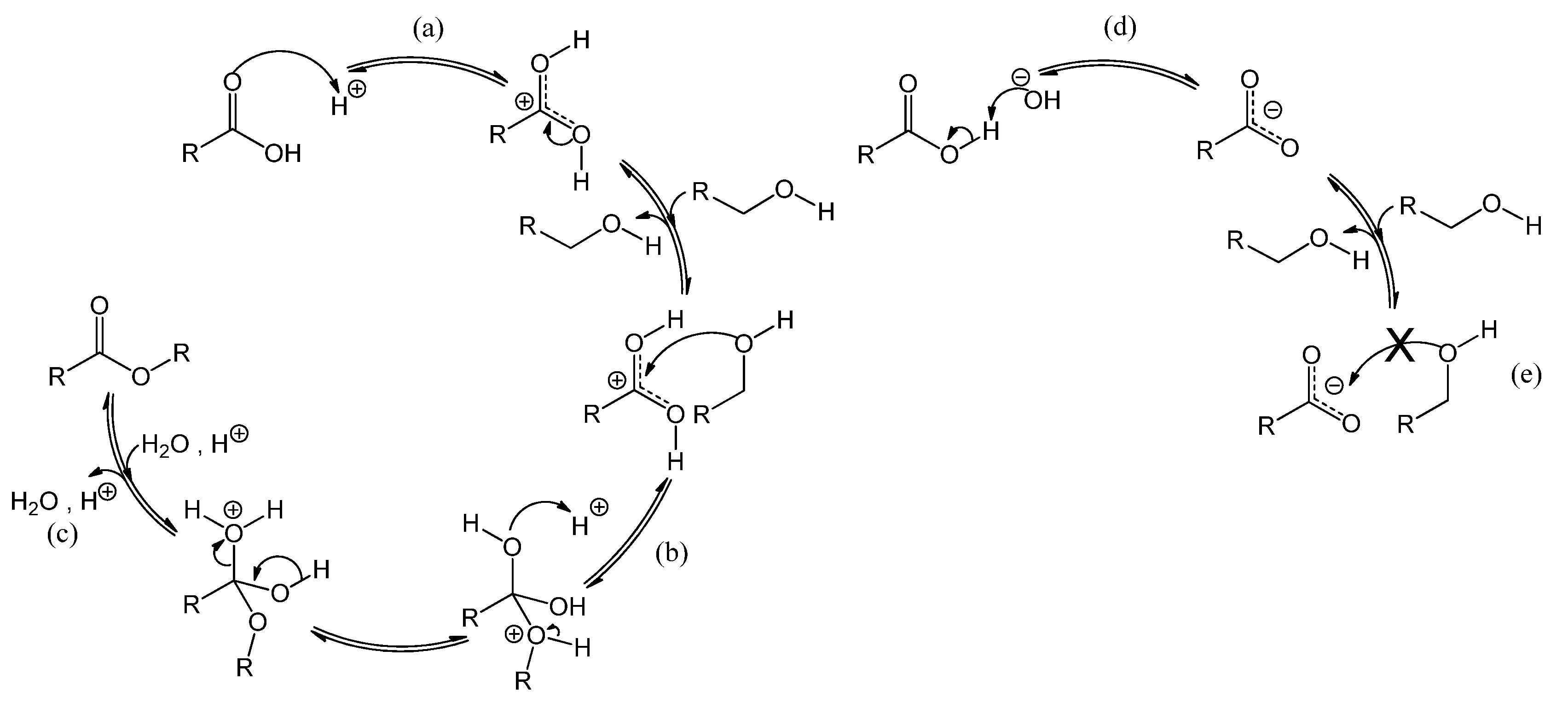
2.2. Influence of a Base on Catalyst Deactivation
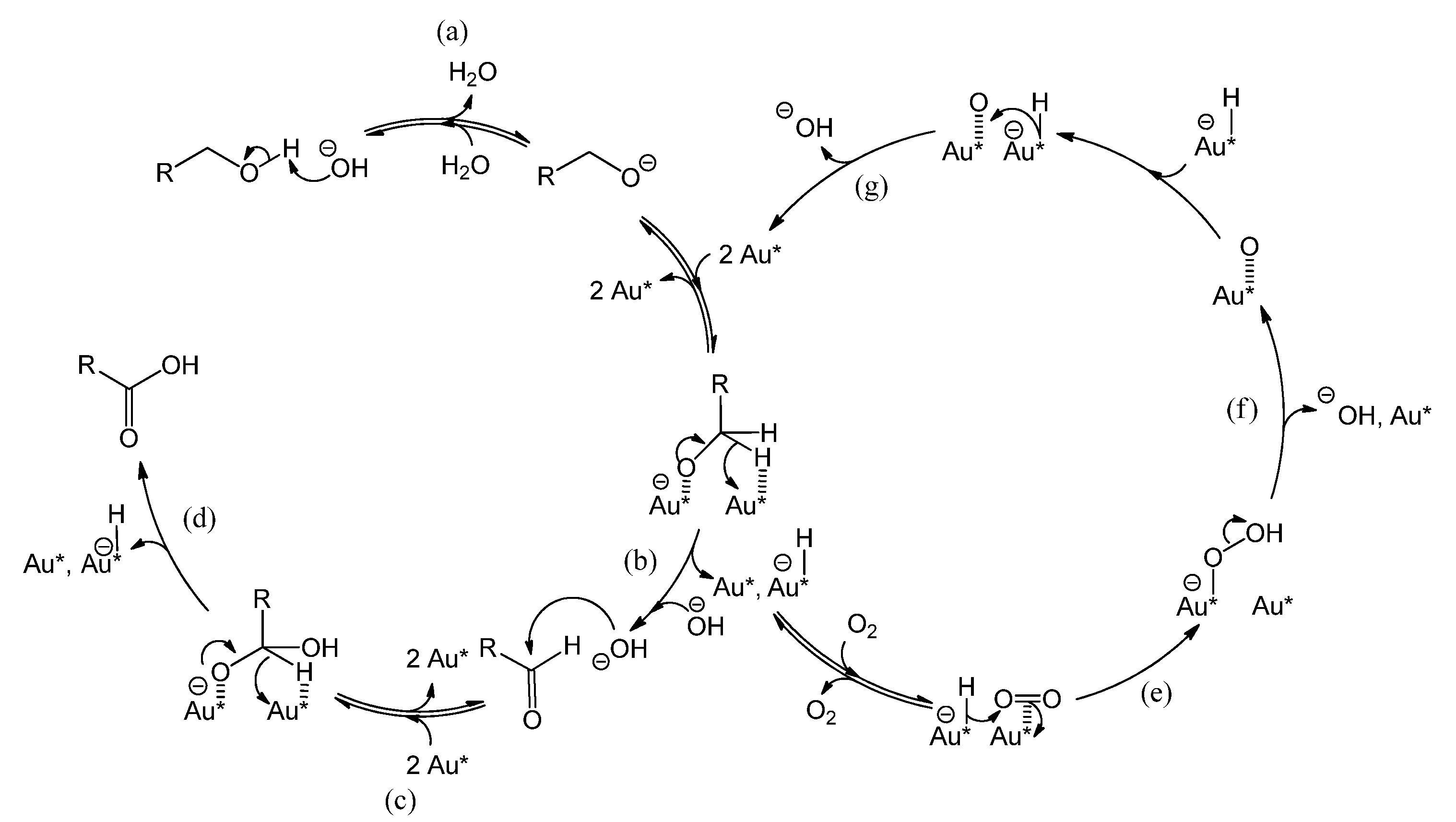
Figure 5 shows the reaction mechanism, in basic conditions, of the oxidation of alcohol to aldehyde and the sequential oxidation to carboxylic acid [
1,
15,
23,
24,
25]. Au* indicates an active site on the gold surface. A dashed line represents a chemical interaction of a species with an adsorption site on the gold surface. Electron transfers corresponding to bond cleavage or formation are indicated by curved arrows. As indicated in
Figure 5, reaction step a, the role of the base is to deprotonate the alcohol, thereby ensuring that the rate limiting step is the reaction on the gold surface, presumably the β-hydride elimination forming the aldehyde (step b yielding R-CH=O) or the carboxylic acid (step d yielding R-COOH) [
1,
15,
23,
24,
25]. However, basic conditions have also been reported to enhance the selectivity towards carboxylic acid, by favoring the conversion of aldehyde to the corresponding geminal diol [
1,
15] as depicted by reaction step c (The diol is shown as R-CH(OH)O
−, partially deprotonated and adsorbed on Au
*). In parallel, the gold site that carries the hydride (Au*-H
−) is regenerated by adsorbed molecular oxygen (Au*||||O
2) via a peroxyl intermediate (step e yielding Au*-O-OH) [
1,
15], or via dissociated oxygen from the catalyst support [
25]. This also regenerates an OH
− (steps f and g) [
15] and closes the catalytic cycle as shown on the right-hand side of
Figure 5. For stoichiometric reasons, it is clear that two hydrides species must react per O
2 molecule. However, it is unclear whether the second hydride reacts after the O-O bond dissociation (step f), or if the O-O bond dissociation is assisted by the second hydride (in the latter case, step f and g would be simultaneous). The question arises if the presence of a base has an influence on the catalyst stability.
Figure 5.
Reaction mechanism of benzyl alcohol oxidation to benzaldehyde and sequential oxidation to benzoic acid over a gold catalyst, co-catalyzed by the base HO
− [
1,
15,
23,
24,
25].
Figure 5.
Reaction mechanism of benzyl alcohol oxidation to benzaldehyde and sequential oxidation to benzoic acid over a gold catalyst, co-catalyzed by the base HO
− [
1,
15,
23,
24,
25].
The catalytic reaction was carried out in the presence of two different bases: potassium carbonate (
pKb1 = 3.68) and potassium fluoride (
pKb = 10.8). Although the
pKb values (defined in aqueous environment) are not directly transferable to the aprotic solvent (toluene), and these bases hardly dissolve in toluene, the
pKb values still indicate the relative basicity of both bases used. The spent catalysts were also re-used. A significant loss of KF was observed during the recovery of the catalyst after the first test, which was compensated for by the addition of another 2.1 g of KF to the spent catalyst, resulting in an estimated total amount of KF present during the second experiment with the spent catalyst of about 3 g. The concentration profiles of these experiments are presented in
Figure 6 and
Figure 7, respectively.
The results of the first run are similar to those for the base-free experiments, although a slight increase in the initial
TOF, from 0.7 to 0.9 s
−1, is observed (
Table 1). Increased activity upon addition of a base has already been reported [
1] and is probably due to the enhanced deprotonation of BnOH. The conversion at 240 min is also higher: 78% compared with 63% in base-free conditions. The selectivity to BnO does not change significantly (93% when no base is present
vs. 91% in the presence of potassium carbonate). However, it should be noted that more ester is formed in the presence of K
2CO
3 (at 240 min: 16 µmol·g
−1 compared to 8 µmol·g
−1 in base free conditions), and the amount of BnOOH remains below detection limit. The most striking difference, when compared to base-free conditions, is the largely maintained activity when re-using the spent catalyst. The initial
TOF is lower than that of the fresh catalyst (0.4 s
−1 compared with 0.9 s
−1), but the conversion at 240 min is comparable (72% compared with 78%). This shows that the addition of a base to the reaction medium largely remediates the strong product inhibition observed under base-free conditions.
Figure 6.
Catalyst performance in the presence of K
2CO
3. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™ in the presence of K
2CO
3. (a) First run using fresh AUROlite
™ (b) second run using spent AUROlite
™. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™, 3.04 g K
2CO
3,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Figure 6.
Catalyst performance in the presence of K
2CO
3. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™ in the presence of K
2CO
3. (a) First run using fresh AUROlite
™ (b) second run using spent AUROlite
™. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™, 3.04 g K
2CO
3,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Figure 7.
Catalyst performance in the presence of KF. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™ in the presence of KF. (a) First run using fresh AUROlite
™ and 2.1 g KF (b) second run using spent AUROlite
™ and ~3 g KF. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Figure 7.
Catalyst performance in the presence of KF. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™ in the presence of KF. (a) First run using fresh AUROlite
™ and 2.1 g KF (b) second run using spent AUROlite
™ and ~3 g KF. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
When K
2CO
3 is replaced by an equimolar amount of KF, the results are similar.
TOF is slightly lower (0.6 s
−1) although the difference is within the measurement error. The conversion is 81% after 240 min when KF is used, and 78% when K
2CO
3 is used (
Table 1). Apparently, the strength of the base does not affect the activity of the fresh catalyst. Upon re-using the spent catalyst however, a higher initial reaction rate is observed (1.0 s
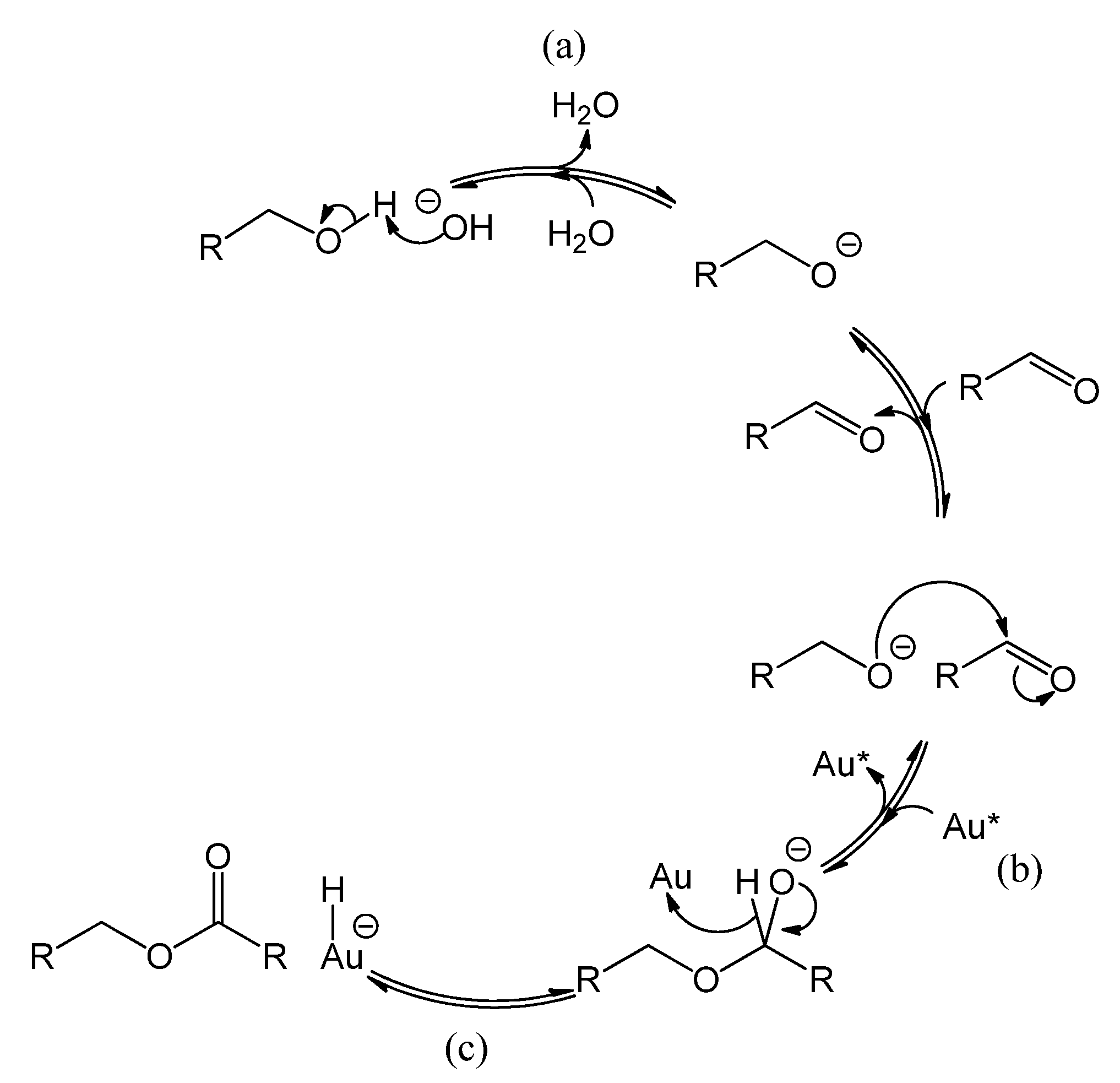
−1) and the final conversion even reaches 95%. This increase is attributed to the additional potassium fluoride added. The preserved catalytic activity proves that no other deactivation mechanism than product inhibition (e.g., sintering or poisoning) is taking place. It is clear that the bases largely neutralize the acid responsible for product inhibition. As this alleviation of the inhibition is always accompanied by an increase of selectivity towards BnOOBn, apparently ester formation is faster in the presence of a base. However, direct esterification of the carboxylic acid with the alcohol catalyzed by a base is mechanistically not likely. After deprotonation of the BnOOH by a base, nucleophilic attack of the alcohol (R-CH
2-OH) on the functional carbon of carboxylate anion (R-COO
−) is highly unlikely as this would imply that a nucleophile (also seen as a Lewis base) would have to react with an electron rich species. This is illustrated in
Figure 8 (steps d and e). The classic acid-catalyzed esterification between carboxylic acid and alcohol is depicted on the left hand-side of
Figure 8 for comparison. It shows that under acidic conditions, the functional carbon becomes positively charged (
Figure 8 step a, yielding R-C(OH)
2+) and thus more prone to nucleophilic attack. Another pathway involving base-catalyzed ester formation from an alcohol and an aldehyde has been suggested by Rodríguez-Reyes
et al. [
19]. This pathway is illustrated in
Figure 9, and can explain why in our system a higher ester production is observed under basic conditions.
Figure 8.
Reaction mechanism of acid catalyzed esterification of carboxylic acid and alcohol. (a) protonation of carbonyl oxygen yielding an electrophilic carbocation; (b) nucleophilic attack of the alcohol and (c) dehydration yielding the corresponding ester. (d) deprotonation of the carboxylic acid by a base yielding a carboxylate anion; (e) the nucleophilic attack of the alcohol is then greatly disfavored.
Figure 8.
Reaction mechanism of acid catalyzed esterification of carboxylic acid and alcohol. (a) protonation of carbonyl oxygen yielding an electrophilic carbocation; (b) nucleophilic attack of the alcohol and (c) dehydration yielding the corresponding ester. (d) deprotonation of the carboxylic acid by a base yielding a carboxylate anion; (e) the nucleophilic attack of the alcohol is then greatly disfavored.
Figure 9.
Reaction mechanism of base-catalyzed ester formation from alcohol and aldehyde, adapted from [
19]. (
a) alcohol deprotonation, (
b) nucleophilic attack of alcoholate on carbonyl, followed by (
c) β-hydride elimination yields the corresponding ester. The rest of the catalytic cycle consists of the oxidation of the hydride left on the gold surface by molecular oxygen, which also regenerates the base as depicted in
Figure 5 (steps f and g).
Figure 9.
Reaction mechanism of base-catalyzed ester formation from alcohol and aldehyde, adapted from [
19]. (
a) alcohol deprotonation, (
b) nucleophilic attack of alcoholate on carbonyl, followed by (
c) β-hydride elimination yields the corresponding ester. The rest of the catalytic cycle consists of the oxidation of the hydride left on the gold surface by molecular oxygen, which also regenerates the base as depicted in
Figure 5 (steps f and g).
To further elucidate the role of the base on product inhibition, an experiment was performed with potassium carbonate and pre-addition of BnOOH. The concentration profiles are shown in
Figure 10 and are directly comparable with the ones shown in
Figure 6a where K
2CO
3 was present but no inhibitor was pre-added, and with
Figure 4 where no base was present but BnOOH was pre-added.
In comparison with
Figure 6a where no BnOOH was added, the initial
TOF is lower: 0.2 s
−1 (
Table 1). The conversion after 240 min is 61% and the selectivity to BnO is 92%. When compared with the results in
Figure 4 (no carbonate added), we can conclude that even though inhibition is still observed, the presence of potassium carbonate greatly reduces it.
Based on our interpretation, the presence of a base results in (partial) neutralization of the BnOOH, thereby alleviating inhibition. In parallel, basic conditions also enhance the subsequent ester formation depicted in
Figure 9, leading to more ester production and decreasing aldehyde selectivity. An effect of the amount of potassium on the inhibition is also suspected based on
Figure 7a,b, but this has not been further quantified.
Figure 10.
Catalyst performance in the presence of K
2CO
3 after pre-addition of benzoic acid. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™ where benzoic acid was introduced prior to the beginning of the reaction. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™, 3.04 g K
2CO
3,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1,
CBnOOH, t<0 = 4.1 × 10
−6 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Figure 10.
Catalyst performance in the presence of K
2CO
3 after pre-addition of benzoic acid. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™ where benzoic acid was introduced prior to the beginning of the reaction. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™, 3.04 g K
2CO
3,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1,
CBnOOH, t<0 = 4.1 × 10
−6 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
2.3. Influence of Water on Catalyst Deactivation
Water was already recognized to be crucial for Au-catalyzed gas phase CO oxidation by Daté
et al. [
26], who demonstrated its great beneficial role. The mechanism was later proposed by Daniells
et al. [
27]. In many of the reaction mechanisms discussed above, water plays a role. It is produced in an amount equimolar to BnO (see
Figure 1a and
Figure 5a). The mechanism of the oxidation of aldehyde to carboxylic acid involves a base-catalyzed hydration of aldehyde to geminal diol. Water is also a byproduct of the equilibrium-limited esterification. Yang
et al. [
28] studied the influence of different water contents on the kinetics of oxidation and determined that water has a promoting effect. They observed higher conversions of BnOH and higher selectivities to BnO when an optimal amount of water was used. More recently, Chang and coworkers [
29] conducted a computational study to better understand this effect on methanol dehydrogenation/oxidation. They concluded that the promoting effect originates from a facilitated peroxyl formation from O
2 by transfer of hydrogen from the water itself or from the alcohol via the water, where hydrogen bonds are reported to play a key role in this mechanism. Therefore, water could play a role in the deactivation of the catalyst in the present study. With this in mind, the reaction was carried out in the presence of the small amount of water that adheres to the catalyst after immersion in water and filtration. The mass difference before and after this treatment indicates about 0.5 g of water per gram of catalyst, which corresponds to around 550 mol of water per mol of gold. The results of this experiment are presented in
Figure 11.
Figure 11.
Catalyst performance in the presence of K
2CO
3 and a small amount of water. Concentration profiles of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™ in the presence of water. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™, 3.04 g K
2CO
3, ~0.4 g H
2O,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Figure 11.
Catalyst performance in the presence of K
2CO
3 and a small amount of water. Concentration profiles of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction over fresh AUROlite
™ in the presence of water. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™, 3.04 g K
2CO
3, ~0.4 g H
2O,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Compared with the dry conditions of
Figure 6a the initial
TOFs are equal within the experimental error, being 0.8 s
−1 in moist conditions and 0.9 s
−1 in dry conditions. We do not observe the kinetic effect of water found by Yang
et al., but in the presence of water our catalyst does not deactivate and the final conversion is close to 100%. The water thus positively influences the catalyst stability. A possible explanation could be that water interacts with the inhibiting product, thereby diminishing its interaction with the catalyst. However, since potassium carbonate was also present in the reactor, a synergistic effect of base and water cannot be excluded. To address this question, the deactivated catalyst obtained after the experiment of
Figure 2b (where no base was present) was tested again in the presence of water and without the addition of any base. Concentration profiles of this experiment are displayed in
Figure 12.
Clearly, catalytic activity could not be recovered by this treatment. Thus, water alone does not remove the species responsible for deactivation, and the beneficial influence of water observed in
Figure 11 is due to a synergistic effect with the potassium carbonate, e.g., by an enhanced dissolution of the inorganic base. It should also be noted that adding more water than used in these experiments provoked phase separation in which the catalyst agglomerated in the water phase, thereby eliminating the dispersion of the catalyst powder in the organic phase and causing the reaction to proceed in a mass-transport limited regime.
Figure 12.
Catalyst performance of the water-washed spent catalyst in base-free conditions from
Figure 2 in the presence of water. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction spent AUROlite
™ in the presence of water. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™, ~1 g H
2O,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
Figure 12.
Catalyst performance of the water-washed spent catalyst in base-free conditions from
Figure 2 in the presence of water. Concentration of (
![Catalysts 04 00089 i048]()
) benzyl alcohol, (
![Catalysts 04 00089 i049]()
) benzaldehyde, (
![Catalysts 04 00089 i050]()
) benzoic acid and (
![Catalysts 04 00089 i051]()
) benzyl benzoate
vs. reaction time for catalytic reaction spent AUROlite
™ in the presence of water. Reaction conditions:
T = 80 °C, 0.8 g AUROlite
™, ~1 g H
2O,
CBnOH, t=0 = 3.0 × 10
−4 mol·g
−1, in 80 mL of toluene, 200 mL·min
−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g
−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
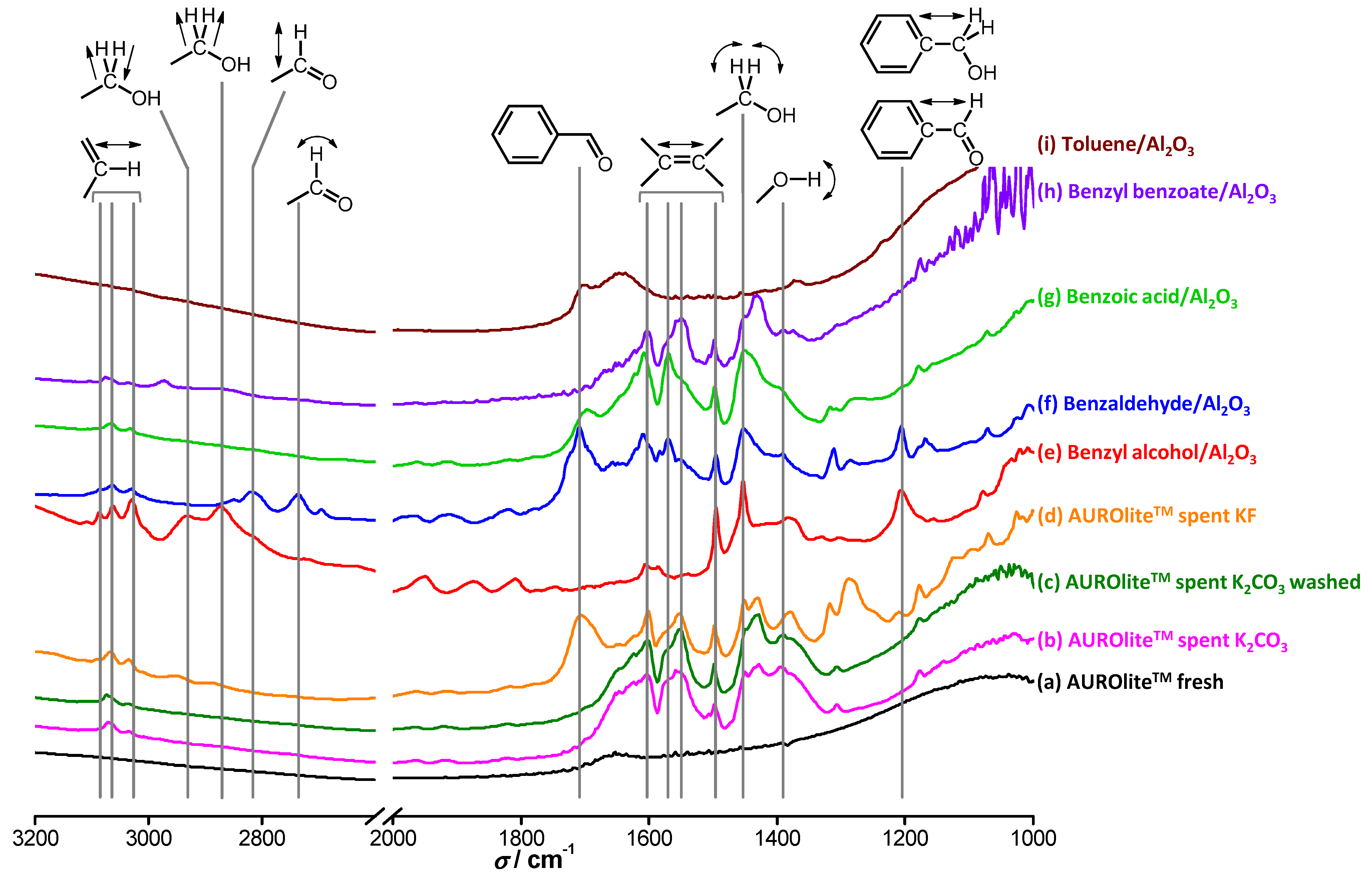
In order to further assess which hypothesis holds, the spent catalyst was analyzed by DRIFTS before and after washing in boiling water for 12 h (
Figure 13). The fresh catalyst barely shows any features. In contrast, both the spent catalyst and the spent catalyst after boiling in water show clear absorption features. The catalyst tested in the presence of KF, which did not deactivate after two runs, exhibited different features. Identification of the species on the surface of the catalysts was based on reference spectra recorded of the compounds present in the reactor adsorbed on alumina. The band at 1200 cm
‑1 is attributed to C
arom–CHO or C
arom–CH
2OH stretching vibrations [
30] and originates only from BnOH and BnO. Interestingly, this band is only present for the catalyst tested with KF. A small absorption band at 1390 cm
‑1 is seen in practically all cases and corresponds to the bending vibration of O–H bonds; thus, it cannot be used to differentiate the components of interest. The sharp absorption at 1450 cm
‑1 is due to in-plane bending vibrations of protons at a primary alcohol carbon and is specific to BnOH. Unfortunately, this band is often masked by a broader one due to other O–H vibrations at the same wavenumber. Absorptions between 1500 and 1600 cm
‑1 are attributed to C
sp2=C
sp2 stretching vibrations present in all the compounds of interest. The broad band at 1710 cm
‑1 is specific to benzaldehydes and is due to π-conjugation of bonds throughout the entire molecule. Again, this characteristic feature is only present for the catalyst tested with KF. A smaller feature is also observed for BnOOH for the same reasons, but the carboxyl moiety seems to alter it drastically. The bending mode of water, which should appear at around 1600–1800 cm
−1, is hardly visible due to the pre-treatment of the samples at 473 K. Some features are also observed at higher wavenumbers. The small bands centered at around 2740 cm
‑1 and 2820 cm
‑1 arise from wagging and stretching vibrations respectively of the BnO carbonyl proton, but these bands are not detected on any of the spent catalysts. The symmetric and anti-symmetric stretching vibrations of primary alcohol methylene group protons give rise to absorptions at 2870 and 2930 cm
‑1, respectively. The three bands between 3030 and 3090 cm
‑1 are assigned to C
sp2–H vibrations, which stem from any aromatic compound in the reaction medium.
Figure 13.
DRIFT spectra of (a) fresh AUROlite™ catalyst; (b) used with K2CO3; (c) used with K2CO3 and washed in boiling water; (d) used with KF, (e)–(i) reference compounds adsorbed on alumina. Catalyst samples were pretreated under He at 473 K before recording.
Figure 13.
DRIFT spectra of (a) fresh AUROlite™ catalyst; (b) used with K2CO3; (c) used with K2CO3 and washed in boiling water; (d) used with KF, (e)–(i) reference compounds adsorbed on alumina. Catalyst samples were pretreated under He at 473 K before recording.
Figure 13 clearly demonstrates that water does not visibly wash off the species involved in the reaction from the catalyst surface. Even after 12 h in boiling water, the intensities of the absorption bands corresponding to aromatic species and oxygenated aromatic species do not show any sign of decrease. Therefore, combined with the results of
Figure 12, the hypothesis that water remediates the product inhibition by enhancing desorption of the inhibiting product is refuted. The absorption features on the catalyst tested in the presence of K
2CO
3 are very similar to those of BnOOH and BnOOBn, although the observed bands are not specific to these compounds. In contrast, the catalyst tested in the presence of KF shows absorption features similar to those of BnO, in particular the characteristic band at 1710 cm
−1. Since this catalyst did not deactivate whereas the catalyst tested with K
2CO
3 showed some deactivation, the attribution of the inhibitor being BnOOH or one of its products is supported. However, in view of the low degree of deactivation shown by the catalyst tested in the presence of K
2CO
3, a signal corresponding to BnO would be expected. It remains unclear why BnO seems to be absent from this catalyst surface despite the fact that KF and K
2CO
3 have similar beneficial effects.
2.4. Kinetic Modeling
Since our experiments show that the BnOOH concentration in solution is very low at all times and that the ester formation increases in the presence of a base, it is assumed that the esterification runs entirely through the reaction of BnO with BnOH by H abstraction. The reactions involved in the model are:
The reaction model is accordingly assumed to consist of the set of surface reactions shown in the following set of equations, in which * stands for a catalytic oxidation site:
It is assumed that all three surface oxidation reactions are irreversible. These reactions require two adjacent sites, one for the adsorbed species originating from the BnOH or BnO and one empty site that was regenerated by the oxygen or, for the esterification, adjacently adsorbed BnOH or BnO. It is also assumed that the hydride species, H*, and the peroxy species. HO
2*, are quickly removed in the excess of oxygen present, leading to the assumption that the occupancy of both species is always very low. Adsorption of water and oxygen is assumed not to inhibit the reaction. The surface reactions are described by the surface species reaction rates shown in the following equations:
Where: ri = reaction rate (mol·gcat−1·s−1)
ki = reaction rate constant (unit according to equations)
Ci = concentration (mol·g−1)
θi = occupancy of the surface sites (-)
NT = total number of surface oxidation sites per unit catalyst mass (gcat−1)
s = number of adjacent sites per site (-)
The hydration of BnO followed by the sequential oxidation of the diol species has been lumped here into a single step (17), as the equilibrium constant of the reversible hydration will be highly correlated with the rate constant of the oxidation step.
In general, adsorption reactions are at
quasi-equilibrium, while the surface reactions are rate-limiting steps. This allows expression of the surface coverages as functions of the concentrations and the adsorption constants:
Where: Ki = adsorption constant of compound i on a gold active site (g·mol−1)
After substitution of all the surface coverage expressions in the site balance:
The kinetic parameter estimation based on the full model showed that not all adsorption constants could be estimated properly due to a too weak sensitivity. It appeared that only the adsorption term of the most polar species present, BnOOH, was significant allowing the estimation of its adsorption constant and neglecting the adsorption terms of the BnOH, the BnO and the BnOOBn. Since it was experimentally observed that the presence of a base, i.e., K2CO3 or KF, results in significant ester formation, it was assumed that this reaction is base-catalyzed. Since hardly any ester is formed in absence of base, it is concluded that the condensation reaction of BnOOH and BnOH does not occur to any significant extent.
By elimination of the coverages of the surface species, the following reaction rate expressions are obtained:
Where: ri = reaction rate (mol·kgcat−1·s−1)
ki = lumped rate constant (unit according to equations)
Ci = concentration (mol·g−1)
Sbase = base strength (K2CO3 or KF) (-)
In the two catalytic experiments in which BnOOH was added prior to the BnOH (
Figure 4 and
Figure 10), it was observed that the catalyst support Al
2O
3 adsorbs BnOOH more strongly than BnOH. In the first experiment (
Figure 4), it was observed that the molar quantity of BnOOH in the liquid was much lower (16 µmol) than that originally added (780 µmol). The amount of BnOOH in solution increased only slightly (to 74 µmol) after subsequent addition of the 22 mmol of BnOH, demonstrating that BnOOH is adsorbed more strongly than BnOH. In the second experiment (
Figure 10), it was observed that despite the addition of a similar amount of BnOOH (712 µmol yielding a theoretical concentration of 10.3 µmol·g
−1), the concentration in solution remained below detection limit (0.20 µmol·g
−1) for the entire reaction. Since the total amount of gold present in the reactor is in all cases 41 µmol, we conclude that adsorption on the catalyst support is responsible for the missing quantities of BnOOH. The adsorption on the support is captured by site coverages assuming to follow Langmuir behavior:
Where:
![Catalysts 04 00089 i032]()
= occupancy of the surface sites (-)
![Catalysts 04 00089 i033]()
= adsorption constant of compound
i on the support (g·mol
−1)
From these experimental data the adsorption constants
![Catalysts 04 00089 i034]()
and
![Catalysts 04 00089 i035]()
were estimated to be 18.1 g·mol
−1 and 2.47 × 10
4 g·mol
−1, respectively, and the total adsorption site density was found to be 1.12 mmol·g
cat−1. With a specific surface area of 230 m
2·g
−1 and using Avogadro’s number, the corresponding site density on the support is equivalent to 2.92 sites per nm
2, which is in good agreement with Matulewicz
et al. [
31] who report a value of 2 sites/nm
2 for their γ-alumina.
This yields a relation between the overall acid concentration in the vessel,
CBnOOH, tot, and the actual acid concentration in the liquid phase,
CBnOOH:
Where: CBnOOH, tot = BnOOH concentration if no adsorption would take place (mol·g−1)
σOH, Al2O3 = adsorption site concentration on the catalyst (mol·gcat−1)
wcat = amount of catalyst in the reactor (gcat)
wliq = amount of liquid in the reactor (g)
Since the amount of BnOH in the liquid phase is about three orders of magnitude larger than the amount of surface adsorption sites, the influence of BnOH adsorption on the concentration in the liquid phase is neglected. The actual acid concentration in the liquid phase can therefore be calculated directly from this quadratic equation with respect to
CBnOOH:
Where:
![Catalysts 04 00089 i038]()
The strong adsorption of BnOOH could be the main cause of the very low activity of catalysts reused for the same experiment after a test in absence of a base, since it was observed that this acid remains on the catalyst during rinsing with toluene and also during boiling in water (
Figure 13). The amount of BnOOH that remains on the catalyst in these ‘second runs’ (
Figure 2b,
Figure 6b,
Figure 7b and
Figure 12) is not known but an estimate can be made. Assuming that the BnOOH concentration in the liquid equals its detection limit of 0.20 µmol·g
−1, a coverage of 0.88 is found from our simulations. Thus, it is tentatively concluded that although the amounts of acid formed in the previous runs is very low (often below the detection limit), the coverage is close to 1. Since the inhibition with a reused catalyst was very small or negligible in the presence of K
2CO
3 or KF, it was assumed for simplicity that in these cases all acid was removed, which seems acceptable in view of the time (approximately half an hour, the time needed for heating plus temperature stabilization) that the catalyst particles were in the close vicinity of the K
2CO
3 or KF crystals at reaction conditions (80 °C and well mixed) before the BnOH was added.
The model also accounts for the time allowed between adding the BnO or the BnOOH to the reactor and adding the main reactant BnOH, in all cases about 20 min at reaction conditions (additionally from the heating time). In the case of BnO this causes the formation of significant amounts of BnOOH, inhibiting the reaction (
Figure 3).
Besides the three rate constants
k1,
k2,
k3, and the three adsorption equilibrium constants,
KBnOOH,
![Catalysts 04 00089 i034]()
and
![Catalysts 04 00089 i035]()
, there are several other unknown parameters, which are related to the effect of the base present. The experimental results show that the main effects of either K
2CO
3 or KF are (i) a decrease of the inhibition and (ii) an increase in formation of the BnOOBn ester.
In order to account for effect (i), it is assumed that the bases react to potassium benzoate with the BnOOH formed. Although acid-base reactions are typically instantaneous reactions, a finite rate is assumed to account for the transport from the catalyst pores to the insoluble crystals of K
2CO
3 or KF. The reaction rate is assumed to be first-order with respect to the acid and independent of the catalyst concentration:
Effect (ii) is accounted for by defining parameters to describe the strength of either K
2CO
3 or KF in the catalysis of the esterification of BnO with BnOH:
SK2CO3 is defined as the base strength of K2CO3 and SKF/K2CO3 as the relative base strength of KF compared to K2CO3.
Since the experiments were performed in batch operation in a vessel that is assumed to be ideally stirred, the reactor model used to describe the process is the batch reactor model:
Where: Ci, L = concentration of component i in the liquid phase (mmol·g−1)
t = time (s)
Ccat = catalyst concentration (mg·g−1)
νi, j = stoichiometric coefficient of component i in reaction j (-)
rj = reaction rate of reaction j (mmol·mgcat−1·s−1)
The complete experimental dataset used for the parameter estimation contains 140 experimental data points obtained in 14 batch experiments at various conditions. The parameter estimation was carried out using the software package Athena Visual Studio [
32], applying Bayesian estimation for multiresponse experiments using the full covariance matrix [
33]. The concentrations (expressed in mol·g
−1) of the four measured liquid components were used as the input for the objective function to be minimized. Since the concentrations of the BnOOH and the ester were typically up to two orders of magnitude smaller than those of the BnOH and BnO, the weight of BnOOBn was set at 10 and that of BnOOH at 100. For experiments with a very low conversion rate of BnOH, the weight of BnO was increased to 10 as well.
With the exception of the experiment of
Figure 4, BnOOH concentrations were mostly below the detection limit of 0.20 μmol·g
−1. Since the model predictions are very sensitive to the acid concentration, it was necessary to estimate acid concentrations for experiments where these were not detectable. In those cases, acid concentrations were arbitrarily assumed to be half of the detection limit.
These data lead to fits of the seven kinetic parameters to the experimental dataset and the results are shown in
Table 2.
Table 2.
Optimal estimates of the kinetic parameters using all experimental data.
Table 2.
Optimal estimates of the kinetic parameters using all experimental data.
| Parameter | Unit | Estimate | 95% confidence range |
|---|
| Value | Relative/% |
|---|
| k1 | /g·mgcat−1·s−1 | 2.69 × 10−3 | ± 5.0 × 10−4 | ± 19 |
| k2 | /g·mgcat−1·s−1 | 2.37 × 10−4 | ± 5.9 × 10−5 | ± 25 |
| k3 | /g2·mmol−1·mgcat−1·s−1 | 6.6 × 10−4 | ± 3.5 × 10−4 | ± 54 |
| kAcBase | /s−1 | 0.71 | ± 0.15 | ± 21 |
| KBnOOH | /g·mmol−1 | 1.23 × 104 | ± 1.5 × 103 | ± 12 |
![Catalysts 04 00089 i044]() | /g·mmol−1 | 18.1 | fixed | |
![Catalysts 04 00089 i045]() | /g·mmol−1 | 2.47 × 104 | fixed | |
| SK2CO3 | /- | 1.39 | ± 0.81 | ± 58 |
| SKF/K2CO3 | /- | 1.37 | ± 0.39 | ± 29 |
| SSR* | /- | 0.414 | - | - |
While relatively good fits of predicted concentrations of BnOH, benzaldehyde and BnOOBn with time are evident in
Figure 2a and
Figure 6a for first batch runs with and without K
2CO
3, relatively poor fits of benzaldehyde concentration are observed for second-time runs (
Figure 2b and
Figure 6b) and the first run with KF (
Figure 7a). The poorer fit of the second runs in the presence of K
2CO
3 is understandable since it was assumed in the model that all BnOOH was removed by the base in between the experiments, which is probably not completely justified, indicating that some acid or another inhibiting species remains on the catalyst. In all other experiments, approximate fits of concentrations of one or both products or of all three species (alcohol, aldehyde and ester) are observed (see
Figure 3,
Figure 4,
Figure 7b,
Figure 10,
Figure 11 and
Figure 12). Thus, variations in how well the fit follows the data are a logical consequence of attempting to simulate in a single model a wide range of concentrations with and without base and in the absence and presence of strongly inhibiting aldehyde and acid product species. Moreover, the model did not include effects of water and was limited to the three most important reactions and four most important species. The 54% and 58% relative confidence intervals for
k3 and
SK2CO3 originate from the strong correlation between these two parameters, which is discussed later in this section. The approximate nature of the model can be attributed to:
(1) Assumptions that are only approximately valid, e.g., (a) arbitrary estimates of benzoic acid concentration, and (b) the assumption that benzoic acid is completely removed from the catalyst by interaction with insoluble K2CO3 or KF crystals.
(2) By practical necessity, the limited scope of the mechanistic scheme, e.g., (a) neglecting effects of adsorption or inhibition of some species such as coverages of BnOH of BnOOBn and (b) neglecting the positive effect of water.
Nevertheless, the model provides (1) accurate predictions of initial reaction rate for oxidation of BnOH to BnO on a gold/alumina catalyst and (2) approximate predictions of the effects of BnOOH inhibition and the neutralizing effect of potassium salts to alleviate this inhibition.
The value of the rate constant for the reaction of the BnOOH with the base to potassium benzoate,
kAcBase, represents the characteristic time for the transport of BnOOH from a catalytic site to the K
2CO
3 or KF crystals. The order of magnitude can be compared with an estimate of the characteristic time for diffusion [
34] of BnOOH through the catalyst pores to the liquid bulk, obtained from a typical diffusion distance (one third of the catalyst particle size 50 μm, estimated from the sieve mesh size) and an effective diffusivity of 4.8 × 10
−10 m
2·s
−1 (estimated using Wilke and Chang’s relationship [
35], using porosity-tortuosity ratio of 0.14, based on data of similar aluminas and catalysts):
Where: τdiff,BnOOH = diffusion time (s)
dp = catalyst particle diameter (m)
Deff, BnOOH = effective diffusivity (m2·s−1)
This yields a typical diffusion time of 0.3 s, which is about 4.8 times smaller than the typical time (kAcBase)−1 = 1.41 s. The latter seems a plausible value in view of the additional transport resistance that might be caused by the transfer from the external catalyst surface towards the K2CO3 or KF crystals.
The correlation matrix for the estimated parameters, shown in
Table 3, shows that the strongest correlation occurs between
k3 and
SK2CO3 with a correlation coefficient of −0.97, which is in line with our conclusion that the ester formation in our system is base-catalyzed. All correlations between the parameters justify maintaining all parameters in the model since these do not exceed the value of 0.99, which is accepted as the limit for a proper parameter estimation [
36].
Table 3.
Correlation matrix between all the parameters estimated using the optimized kinetic model.
Table 3.
Correlation matrix between all the parameters estimated using the optimized kinetic model.
| Parameter | k1 | k2 | k3 | kAcBase | KBnOOH | SK2CO3 | SKF/K2CO3 |
|---|
| k1 | 1 | | | | | | |
| k2 | 0.52 | 1 | | | | | |
| k3 | 0.06 | −0.13 | 1 | | | | |
| kAcBase | 0.12 | −0.17 | −0.02 | 1 | | | |
| KBnOOH | 0.51 | −0.30 | 0.09 | 0.64 | 1 | | |
| SK2CO3 | 0.02 | 0.12 | −0.97 | 0.06 | −0.01 | 1 | |
| SKF/K2CO3 | −0.01 | −0.02 | 0.33 | −0.05 | −0.01 | −0.45 | 1 |
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for (a) first run using fresh AUROlite™ and (b) second run using spent AUROlite™. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1 in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for (a) first run using fresh AUROlite™ and (b) second run using spent AUROlite™. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1 in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for (a) first run using fresh AUROlite™ and (b) second run using spent AUROlite™. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1 in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for (a) first run using fresh AUROlite™ and (b) second run using spent AUROlite™. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1 in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.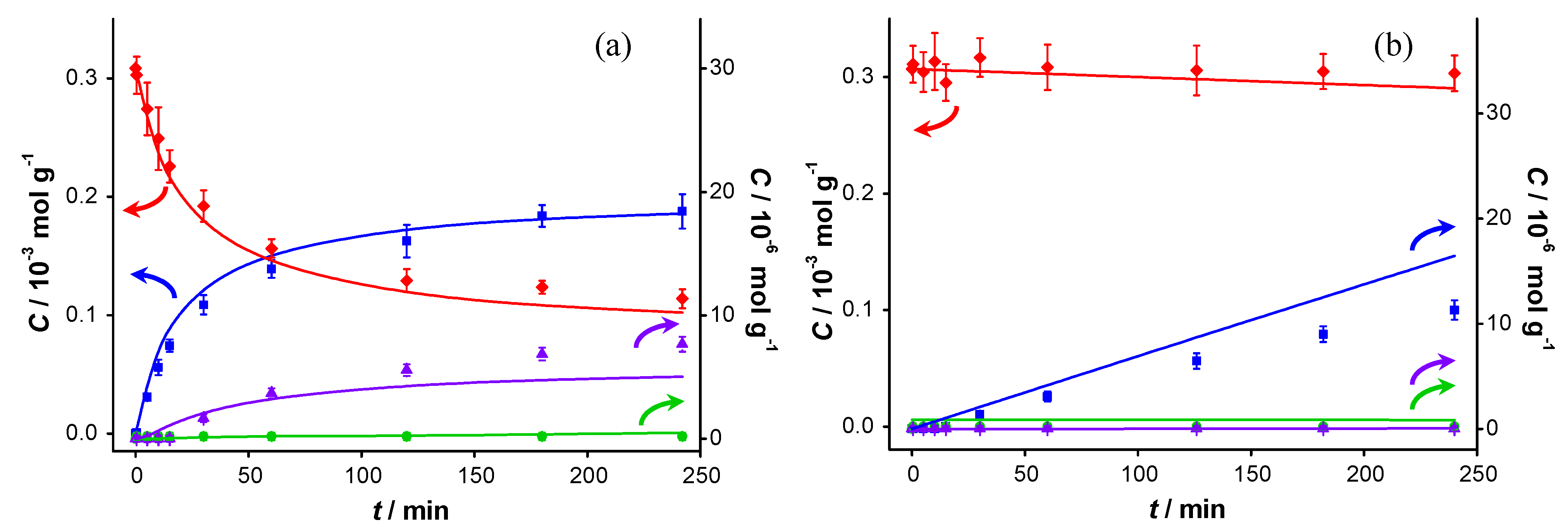
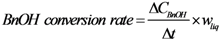 , where
, where 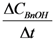 is the conversion rate of benzyl alcohol (mmol·g−1·min−1), calculated by linear regression of the concentration values between 0 and 15 min and wliq is the total mass of liquid (g); b
is the conversion rate of benzyl alcohol (mmol·g−1·min−1), calculated by linear regression of the concentration values between 0 and 15 min and wliq is the total mass of liquid (g); b 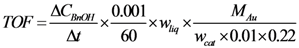 , where
, where 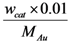 is the total amount of gold in the reactor (mol) and 0.22 is the amount of edge + corner atoms per amount of gold for 2.5 nm gold nanoparticles [20] (mol·mol−1); c
is the total amount of gold in the reactor (mol) and 0.22 is the amount of edge + corner atoms per amount of gold for 2.5 nm gold nanoparticles [20] (mol·mol−1); c 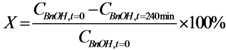 ; d
; d 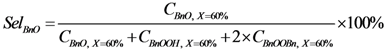 In parallel and series reaction networks, selectivities have to be compared at the same conversion levels. 60% is chosen here, as it is the level in the base free experiment after 240 min.
In parallel and series reaction networks, selectivities have to be compared at the same conversion levels. 60% is chosen here, as it is the level in the base free experiment after 240 min. ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™. Benzaldehyde was introduced 20 min before benzyl alcohol was added. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnO, t<0 = 1.7 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™. Benzaldehyde was introduced 20 min before benzyl alcohol was added. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnO, t<0 = 1.7 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™. Benzaldehyde was introduced 20 min before benzyl alcohol was added. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnO, t<0 = 1.7 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™. Benzaldehyde was introduced 20 min before benzyl alcohol was added. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnO, t<0 = 1.7 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™. Benzoic acid was introduced 20 min prior to the beginning of the reaction. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnOOH, t<0 = 4.1 × 10−6 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™. Benzoic acid was introduced 20 min prior to the beginning of the reaction. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnOOH, t<0 = 4.1 × 10−6 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™. Benzoic acid was introduced 20 min prior to the beginning of the reaction. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnOOH, t<0 = 4.1 × 10−6 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™. Benzoic acid was introduced 20 min prior to the beginning of the reaction. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnOOH, t<0 = 4.1 × 10−6 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.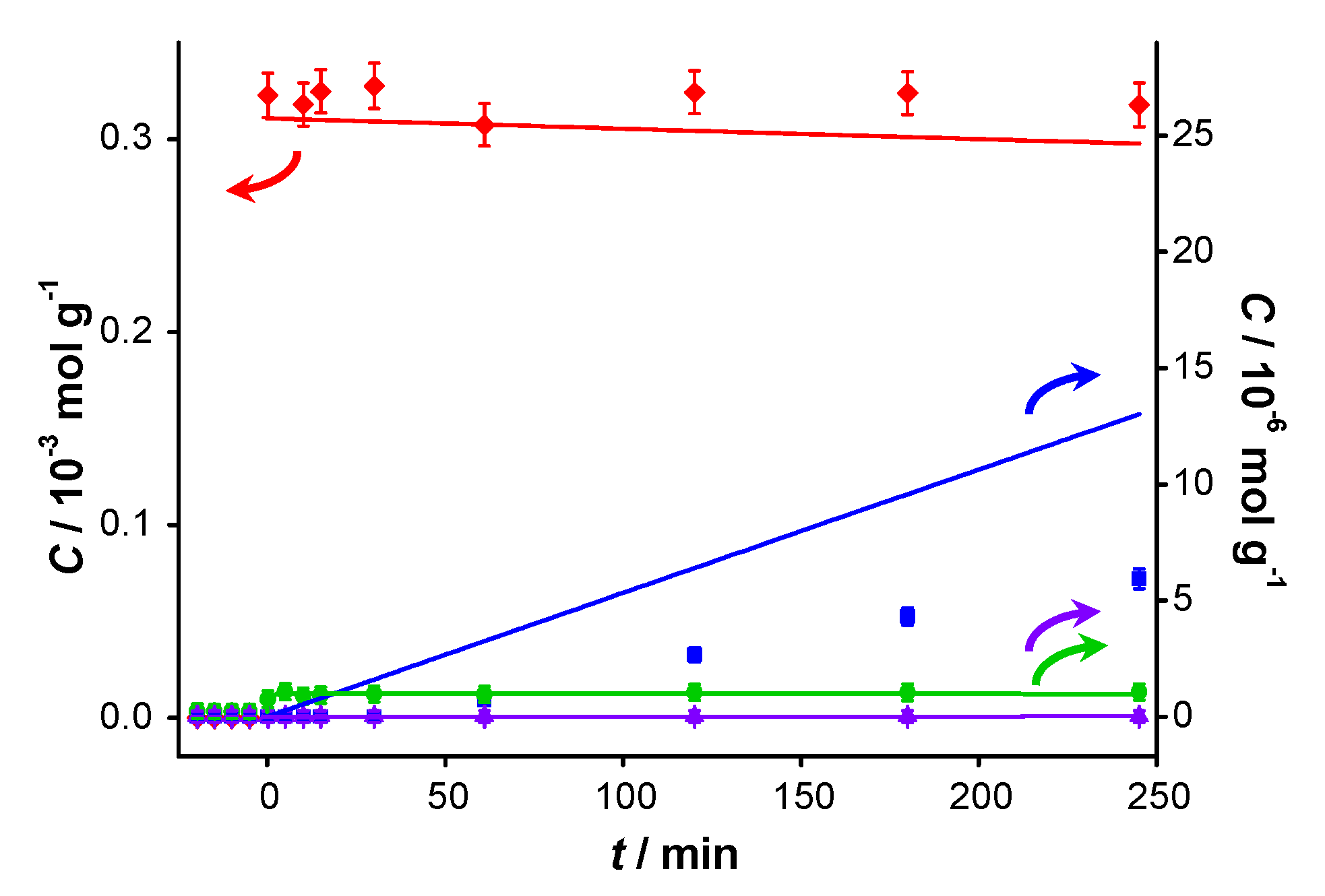
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of K2CO3. (a) First run using fresh AUROlite™ (b) second run using spent AUROlite™. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of K2CO3. (a) First run using fresh AUROlite™ (b) second run using spent AUROlite™. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of K2CO3. (a) First run using fresh AUROlite™ (b) second run using spent AUROlite™. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of K2CO3. (a) First run using fresh AUROlite™ (b) second run using spent AUROlite™. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.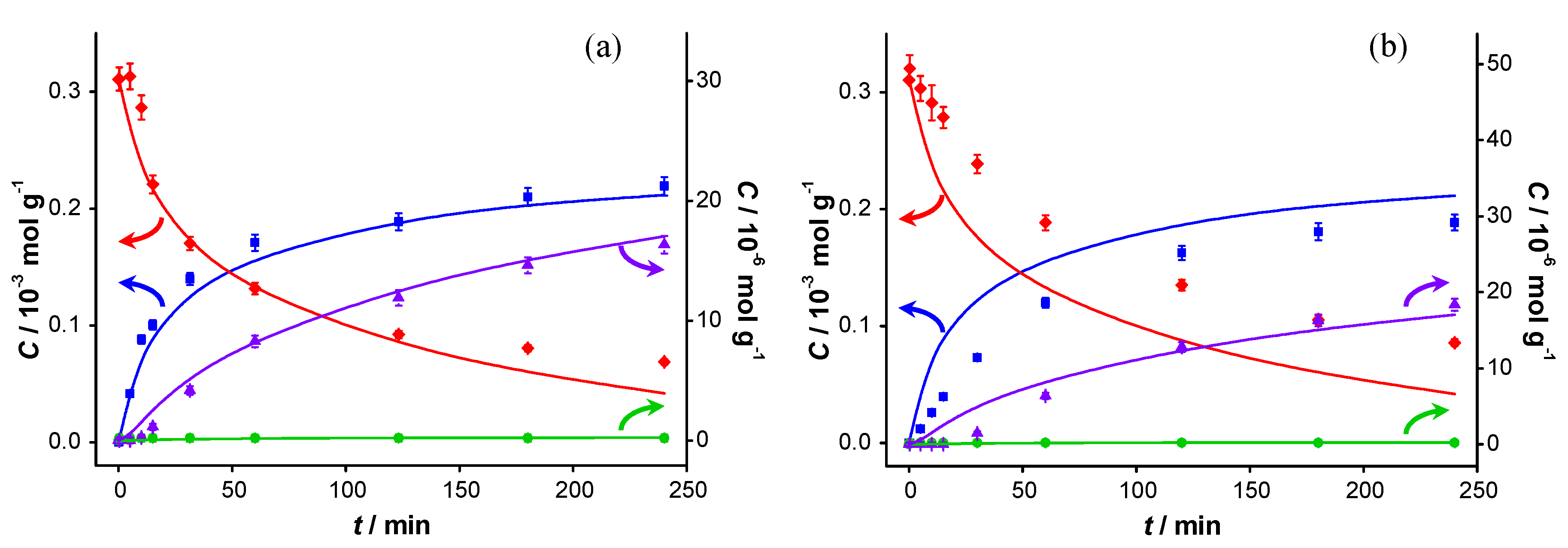
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of KF. (a) First run using fresh AUROlite™ and 2.1 g KF (b) second run using spent AUROlite™ and ~3 g KF. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of KF. (a) First run using fresh AUROlite™ and 2.1 g KF (b) second run using spent AUROlite™ and ~3 g KF. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of KF. (a) First run using fresh AUROlite™ and 2.1 g KF (b) second run using spent AUROlite™ and ~3 g KF. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of KF. (a) First run using fresh AUROlite™ and 2.1 g KF (b) second run using spent AUROlite™ and ~3 g KF. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.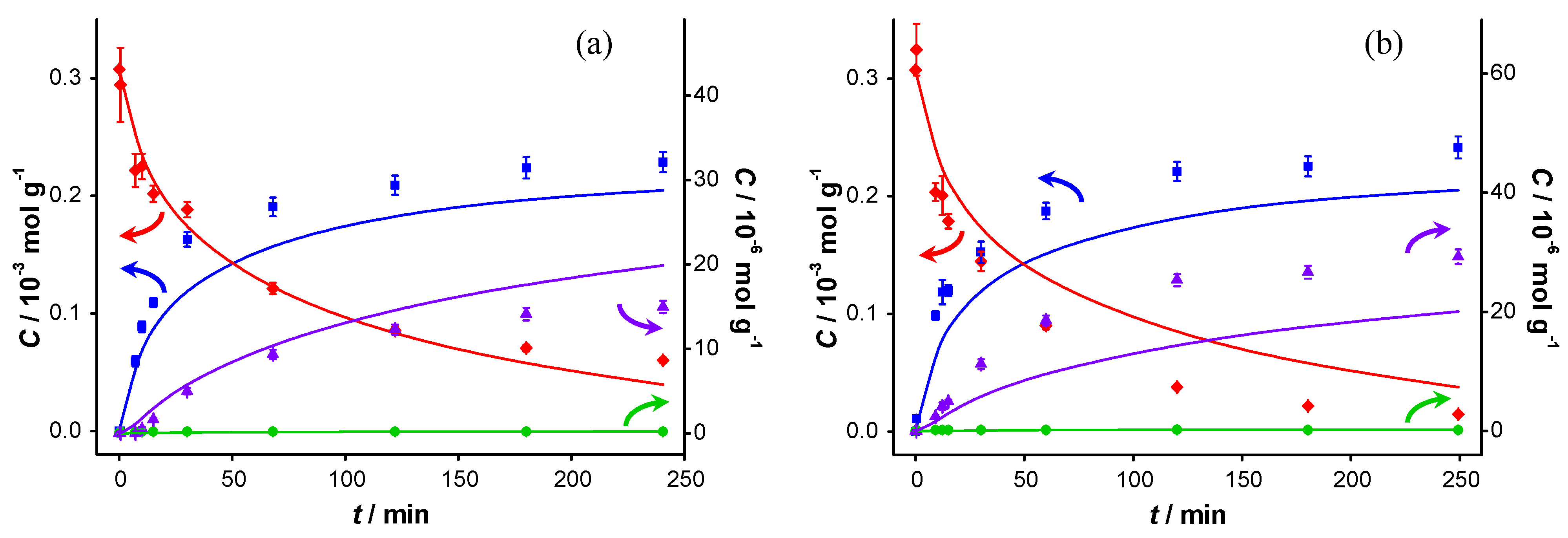
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ where benzoic acid was introduced prior to the beginning of the reaction. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnOOH, t<0 = 4.1 × 10−6 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ where benzoic acid was introduced prior to the beginning of the reaction. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnOOH, t<0 = 4.1 × 10−6 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ where benzoic acid was introduced prior to the beginning of the reaction. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnOOH, t<0 = 4.1 × 10−6 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ where benzoic acid was introduced prior to the beginning of the reaction. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, CBnOOH, t<0 = 4.1 × 10−6 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.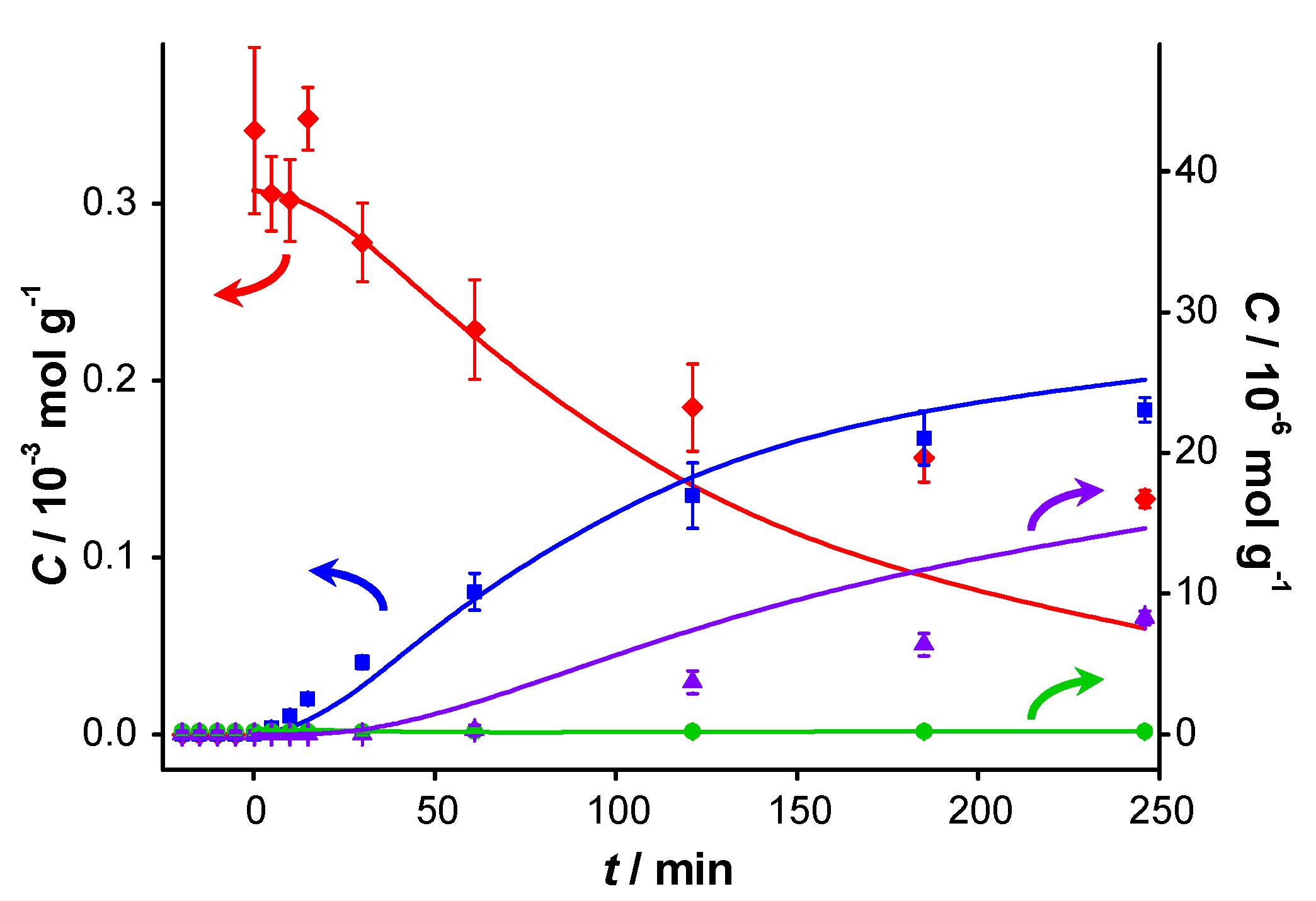
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of water. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, ~0.4 g H2O, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of water. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, ~0.4 g H2O, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of water. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, ~0.4 g H2O, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction over fresh AUROlite™ in the presence of water. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, 3.04 g K2CO3, ~0.4 g H2O, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.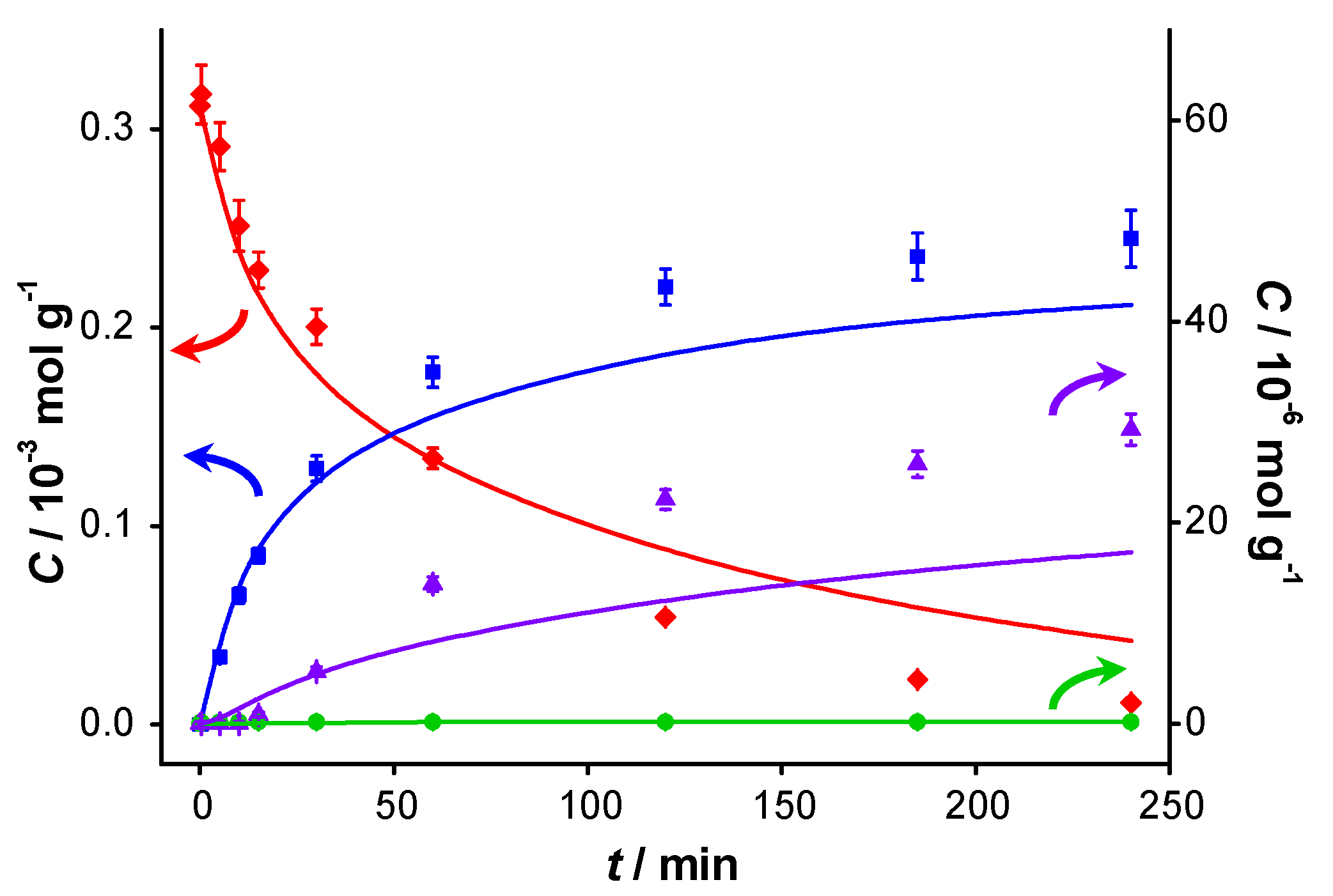
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction spent AUROlite™ in the presence of water. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, ~1 g H2O, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction spent AUROlite™ in the presence of water. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, ~1 g H2O, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
 ) benzyl alcohol, (
) benzyl alcohol, (  ) benzaldehyde, (
) benzaldehyde, (  ) benzoic acid and (
) benzoic acid and (  ) benzyl benzoate vs. reaction time for catalytic reaction spent AUROlite™ in the presence of water. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, ~1 g H2O, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.
) benzyl benzoate vs. reaction time for catalytic reaction spent AUROlite™ in the presence of water. Reaction conditions: T = 80 °C, 0.8 g AUROlite™, ~1 g H2O, CBnOH, t=0 = 3.0 × 10−4 mol·g−1, in 80 mL of toluene, 200 mL·min−1 air flow. Concentrations are expressed in moles per unit mass of liquid in the reactor (mol·g−1). The symbols with error bars are the experimental results and the lines represent the kinetic model.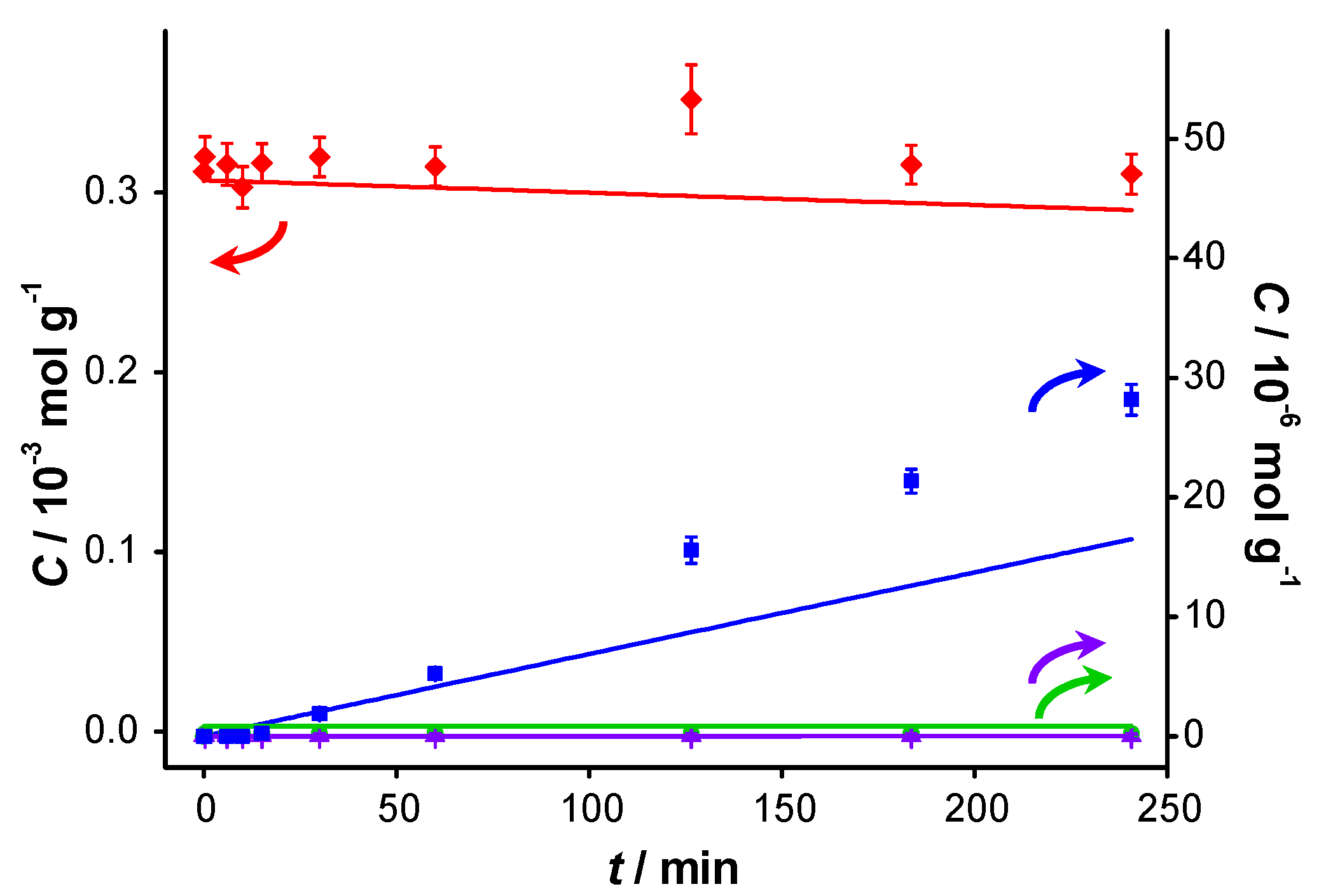

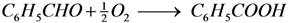
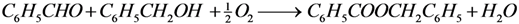
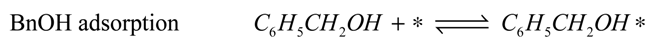
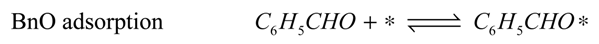
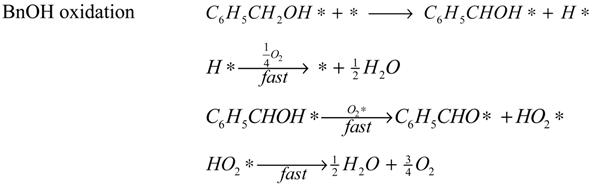

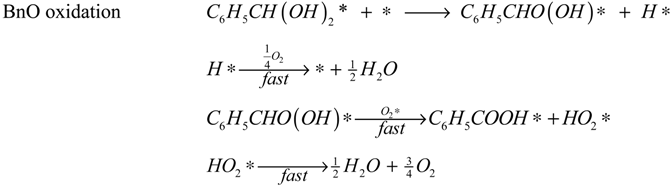
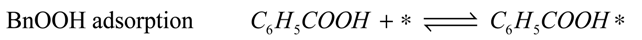
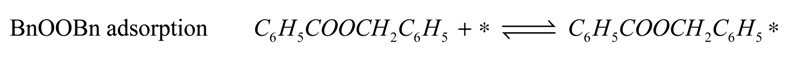




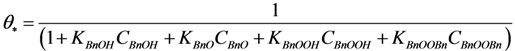
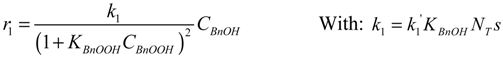
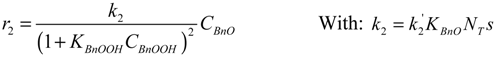
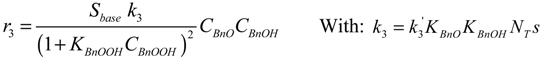
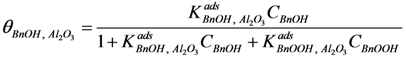
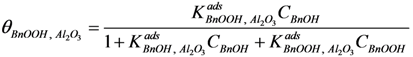
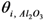 = occupancy of the surface sites (-)
= occupancy of the surface sites (-)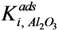 = adsorption constant of compound i on the support (g·mol−1)
= adsorption constant of compound i on the support (g·mol−1)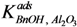 and
and 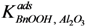 were estimated to be 18.1 g·mol−1 and 2.47 × 104 g·mol−1, respectively, and the total adsorption site density was found to be 1.12 mmol·gcat−1. With a specific surface area of 230 m2·g−1 and using Avogadro’s number, the corresponding site density on the support is equivalent to 2.92 sites per nm2, which is in good agreement with Matulewicz et al. [31] who report a value of 2 sites/nm2 for their γ-alumina.
were estimated to be 18.1 g·mol−1 and 2.47 × 104 g·mol−1, respectively, and the total adsorption site density was found to be 1.12 mmol·gcat−1. With a specific surface area of 230 m2·g−1 and using Avogadro’s number, the corresponding site density on the support is equivalent to 2.92 sites per nm2, which is in good agreement with Matulewicz et al. [31] who report a value of 2 sites/nm2 for their γ-alumina. 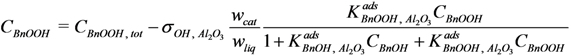
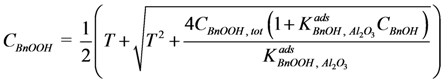

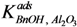 and
and 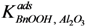 , there are several other unknown parameters, which are related to the effect of the base present. The experimental results show that the main effects of either K2CO3 or KF are (i) a decrease of the inhibition and (ii) an increase in formation of the BnOOBn ester.
, there are several other unknown parameters, which are related to the effect of the base present. The experimental results show that the main effects of either K2CO3 or KF are (i) a decrease of the inhibition and (ii) an increase in formation of the BnOOBn ester.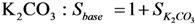
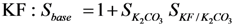
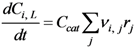
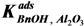
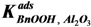
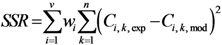 (sum of the squared residuals) (wi = weight factor for response i, v = number of responses, Ci, k, exp = experimental response of component i in experiment k, Ci, k, mod = model response of component i in experiment k, n = number of experiments (samples).
(sum of the squared residuals) (wi = weight factor for response i, v = number of responses, Ci, k, exp = experimental response of component i in experiment k, Ci, k, mod = model response of component i in experiment k, n = number of experiments (samples).