1. Introduction
Although the present author has worked mainly in the field of heterogeneous photocatalysis for more than 30 years since starting research work for a Ph.D. degree in 1981 in Kyoto University and has published more than 200 original and review papers on photocatalysis, there is still frustration at not being able to clarify intrinsic matters closely related to “activity” of photocatalysts, which is the most important topic in both fundamental and application studies on heterogeneous photocatalysis. What is the ghost giving him frustration?
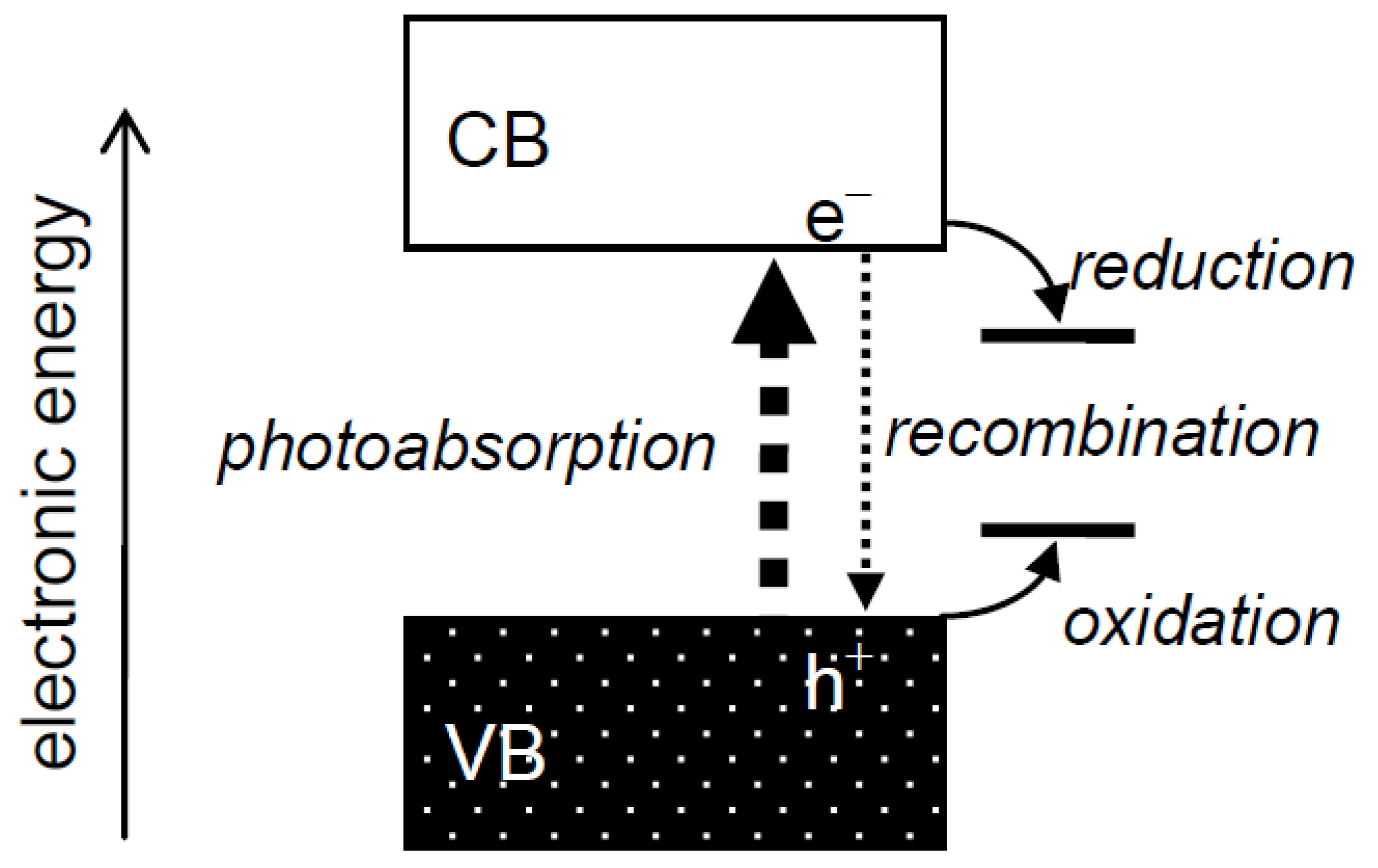
Heterogeneous photocatalysis has always been interpreted using a band structure of electronic energy in photocatalysts (
Figure 1), as described, e.g., in the author's recent reviews [
1,
2]. An electron in a filled valence band (VB) is excited into a vacant conduction band (CB) by a photon of energy greater than the energy of a gap between the VB and CB, a band gap, to give a photoexcited electron (e
−) and a hole (h
+) in the CB and VB, respectively. These species,
i.e., charge carriers, in the CB and VB reduce and oxidize substrates adsorbed on the photocatalyst surface, respectively, or they recombine with each other and disappear without leading to any chemical reaction. Although it is reasonable to attribute the change of photocatalytic reaction rate,
i.e., photocatalytic activity, to the extent of e
−–h
+ recombination, there seemed to have been discussion on photocatalytic activity using the term “recombination” without considering its mechanism. For example, when the activity of a given photocatalyst is lower than expected, the lower activity is attributed to enhanced recombination at unknown “recombination sites”, and when the activity is higher than expected, the higher activity is attributed to suppressed recombination of e
− and h
+, though no evidence for enhanced or suppressed recombination in a photocatalyst has been shown,
i.e., the term “recombination” has been used as a convenient term for explanation of photocatalytic activity or rate. Thus, “recombination” has been used as an “almighty” card, but at the same time “ghost”, for interpretation of photocatalytic activities without leading to progress in an understanding of photocatalysis and/or photocatalysts, since discussion with the term recombination is just an alternative description of experimental results.
Figure 1.
Electronic structure of semiconductor photocatalysts and processes in photocatalytic reactions.
Figure 1.
Electronic structure of semiconductor photocatalysts and processes in photocatalytic reactions.
In this short review, the author discusses recombination, the most elusive phenomenon, in heterogeneous photocatalysis.
2. Direct Observation of Electron–Hole Recombination
As far as the author knows, no in-situ direct observation of recombination in heterogeneous photocatalysis has been reported, because recombination generally proceeds with liberation of heat, and detection of heat is not easy. Although one of our photoacoustic spectroscopic studies on photocatalysis showed liberation of heat during photocatalytic reaction on titanium(IV) oxide (titania) particles [
3], the detected heat was attributable to heat of exothermic chemical reaction, not heat liberated by e
−–h
+ recombination. Of course, photoemission by recombination may occur for photocatalysts of direct-transition semiconductors, though such photoemission is not always observed, and, even if it is observed, recombination with undetectable non-radiative deactivation may occur in parallel.
An alternative way for detecting e
−–h
+ recombination is pump–probe spectroscopy using ultrafast laser pulses. Bowman and coworkers first reported pump–probe diffuse-reflectance spectroscopic measurements of heterogeneous photocatalytic reactions [
4,
5,
6,
7]. Decay kinetics of electrons trapped in levels located below the CB bottom (electron trap = ET) or electrons in the CB after photoexcitation by femtosecond ultraviolet pump pulses was observed in the picosecond time region and analyzed. Since addition of sacrificial electron acceptors or donors, which may trap e
− and h
+ respectively, did not show appreciable influence on the decay, they concluded that the decay reflects e
−–h
+ recombination and proposed second-order kinetics for the recombination. This seems reasonable considering the high density of photons in a femtosecond pump pulse to produce multiple pairs of e
− and h
+, not a single e
−–h
+ pair, to undergo recombination with second-order kinetics. Later, collaboration work with the author's laboratory showed correlations of the second-order recombination-rate constants with physical and structural properties of various titania photocatalysts [
8]. However, there is no guarantee that similar recombination also occurs in practical photocatalytic reaction systems, where the light intensity is markedly lower than that of femtosecond laser pulses to result in creation of only one or a few e
−–h
+ pairs in one photocatalyst particle. It has been suggested that the rate obeys first-order kinetics, not a second-order one, for such mutual recombination induced by low-intensity laser pulses, as reported by e.g., Kato
et al. [
9], and such low-intensity laser measurements may reproduce the practical photocatalytic reaction system under irradiation with continuous light sources such as light from a mercury or xenon arc lamp. However, the low-intensity laser measurements were performed in transmission mode using transparent thin films of a photocatalyst, not diffuse-reflection mode using powder or a suspension of a photocatalyst,
i.e., only nanometer-sized particles could be used as a sample, and decay kinetics of the recombination in submicrometer-sized particles could not be examined. Thus, the dilemma in excitation-light intensity in direct measurement of recombination kinetics remains.
3. Donor Levels in an n-Type Semiconductor
It had been believed that lattice defects in crystalline photocatalyst particles are responsible for e−–h+ recombination when the author started working in this field in the 1980’s; the defects work as a recombination center, though no direct observation of the recombination had been performed, as described in the preceding section. This might be because it is convenient to attribute lower and higher activities of photocatalysts to enhanced and inhibited e−–h+ recombination, respectively, and to attribute the recombination to ambiguous but plausible recombination centers. However, one of the most significant problems might be the misconception that the recombination center must be “crystal lattice defects”.
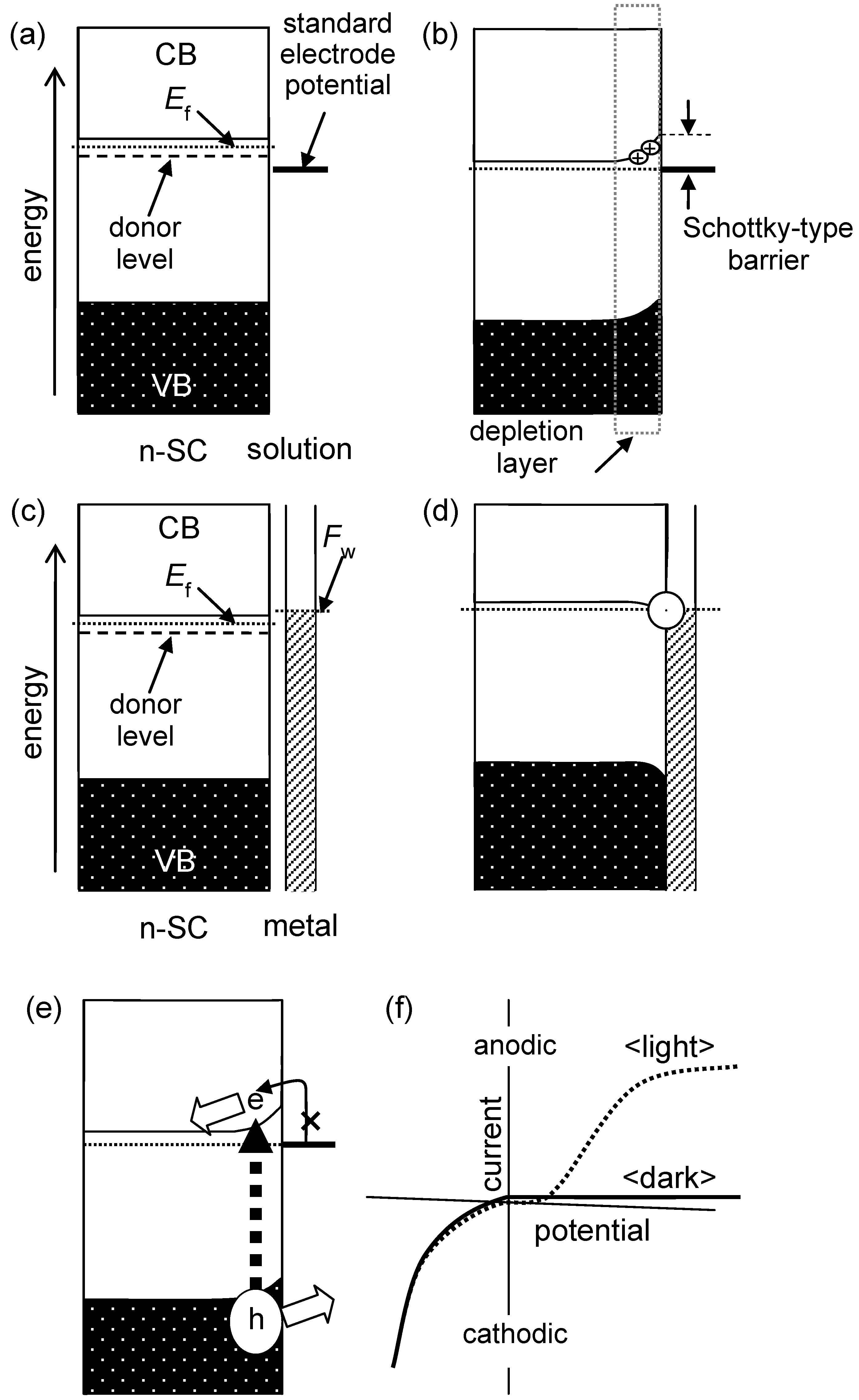
Most photocatalysts, e.g., titania or tungsten (VI) oxide, are categorized as an n-type semiconductors. It is known that metal oxides tend to release oxygen, leaving electrons in the lattice, and this may be an origin of the n-type semiconductor property of metal oxides. Actually, titania in the form of powder or a single crystal turns black or blue-black when heated under reduced atmosphere due to the release of oxygen (O
2) and resulting formation of reduced titanium species,
i.e., trivalent titanium cation (Ti
3+). In an electrochemical sense, this phenomenon corresponds to the formation of electron-filled donor levels located below the CB to give an n-type semiconducting property; Fermi level is located between the CB bottom and those donor levels. When such an n-type semiconductor is immersed, or in contact in an electrolyte solution, electrons in the donor levels go out to the electrolyte since the donor level in an
n-type semiconductor may be more cathodic than the electrode potential of electrolyte solutions. This flow of electrons in the donor level to an electrolyte results in the formation of a so-called Schottky-type barrier [
10] at the interface to prohibit electron flow from an electrolyte to an electrode,
i.e., potential slope due to an electron-deficient so-called depletion layer is built in a semiconductor.
Figure 2.
(a) N-type semiconductor (n-SC) and solution and (b) Schottky-type junction with a depletion layer where electrons in donor levels flow out into the solution to lower the Fermi level (EF); (c) n-SC and metal with work function (Fw) and (d) ohmic contact between them; (e) n-SC–electrolyte interface under photoirradiation and (f) ideal potential–current plots in the dark and under photoirradiation.
Figure 2.
(a) N-type semiconductor (n-SC) and solution and (b) Schottky-type junction with a depletion layer where electrons in donor levels flow out into the solution to lower the Fermi level (EF); (c) n-SC and metal with work function (Fw) and (d) ohmic contact between them; (e) n-SC–electrolyte interface under photoirradiation and (f) ideal potential–current plots in the dark and under photoirradiation.
In the first stage of studies on photocatalysis in the 1980’s, photocatalysts such as platinum-loaded titania particles were often called a miniaturized photoelectrochemical cell composed of a titania photoanode short-circuited with a platinum cathode (The connection between titania and platinum is believed to be ohmic, and no barrier is expected between them, as shown in
Figure 2(c),(d)) [
11], in which e
− migrates to platinum deposits to reduce protons (or water) on their surface and holes oxidize substrates adsorbed on the titania surface. Such so-called charge separation could be expected since in an n-type semiconductor in contact with an electrolyte solution, an e
−–h
+ pair is created upon photoabsorption within the potential slope in the above-mentioned depletion layer. Thus, even in the absence of electrical or chemical bias between titania and platinum as is the case of particulate photocatalyst particles, the potential slope in the depletion layer had been believed to be effective for separation of e
−–h
+ pairs. However, in the 1990’s after the first boom of photocatalysis, it seemed that negligible number of papers claimed such charge separation in photocatalyst particles by the depletion layer, presumably due to the conjecture that donor density of particulate photocatalysts is low and thereby the slope should be negligible,
i.e., the presence of donor levels and the meaning of an
n-type semiconductor for metal oxide photocatalysts has been rarely discussed. (As far as the author knows, there has been no report showing that the donor density in particulate photocatalysts is negligibly small. This seems reasonable considering that the donor density is estimated with samples in the form of a conductive electrode but not in the form of powder, and titania particles with no pretreatment cannot be conductive in the electrode form.) If the donor level is neglected, metal oxide photocatalysts such as titania can be an insulator but not a semiconductor in the sense of electronic structure as depicted in
Figure 1; a fully electron filled VB and a vacant CB separated by the band gap can also be adopted for insulators without any donor (or acceptor) levels.
4. Electron Traps (ETs) in Photocatalyst Particles
Even though the density of donor levels in metal-oxide photocatalyst particles is low, they may exist appreciably, and electrons in those levels may flow out to the electrolyte being in contact with a particle to result in the formation of electron-deficient (vacant) levels below the CB,
i.e., ETs. It is plausible that those ETs accept photoexcited electrons. If the depth,
i.e., the distance of energy level between the CB bottom and ETs, is smaller than the thermal energy of electrons [
12], electrons in these shallow traps can be thermally excited to the CB and be trapped again in another trap,
i.e., electrons migrate through the CB and shallow traps which may be faster than electron hopping between the traps [
13]. On the other hand, if the depth is large, electrons trapped by these deep traps cannot be excited thermally to the CB and recombine with h
+. Thus, as a working hypothesis, it can be assumed that shallow and deep traps enhance and reduce photocatalytic activity of particles by migration of e
− through CB–traps and recombination of an e
−–h
+ pair, respectively. If this is correct, development of photocatalysts with a high level of activity requires precise control of the structural properties of the photocatalyst: maximized density of shallow traps and minimized density of deep traps. Before starting discussion on the strategy to realize this development, results of qualitative and quantitative analyses of ETs are interpreted.
Historically, it is well known that titania in the form of powder or an electrode turns blue or blue-gray upon heating under a reducing atmosphere, as described in the preceding section, or upon photoirradiation in the absence of oxygen and in the presence of electron donors such as methanol or triethanolamine. This is attributed to the accumulation of electrons in titania accompanied by, presumably, insertion of protons into its crystalline lattice to compensate the negative charge of electrons. Sometimes this phenomenon is called “trivalent titanium ion (Ti
3+) formation”. A group of the author has developed a method to measure the density of Ti
3+ by a photochemical reaction [
14].
Briefly describing, a titania sample is suspended in a deaerated aqueous solution of methanol or triethanolamine and irradiated by a mercury arc to result in change of color of the suspension from white to gray or blue-gray. This is attributable to the accumulation of electrons in titania samples. Upon injection of a deaerated aqueous methyl viologen (MV
2+) solution, an intense blue color of methyl viologen cation radical (MV·
+) appears, indicating electron transfer, and the molar amount of accumulated electrons is estimated on the basis of spectroscopic measurement of MV·
+ concentration. Since each titania sample shows a different saturation limit of electron accumulation, by prolonged photoirradiation, depending on the kind of titania sample but not depending on the kind of electron donor, the saturation limit is assumed to be total density of ETs in titania particles. It is reasonable to find that the MV·
+ yield depends on pH of the reaction mixture when an MV
2+ solution is injected, since the standard electrode potential of an MV
2+/MV·
+ redox couple is independent of pH, while the CB bottom and VB top positions as well as the potential of ETs shift more cathodic with increase in pH with a slope of
ca. 60 mV by one pH unit; electron transfer from electron-accumulated titania to MV
2+ is not observed at low pH, and the MV·
+ concentration increases with increase in pH of the reaction mixture to reach its saturation at higher pH. Since pH of the reaction mixture is related to the level of electronic energy of ETs and the CB bottom positions of anatase and rutile titania have been reported [
15], it is possible to obtain the energy-resolved distribution (ERD) of ETs in titania. As an example, it was shown that ETs are located 0.1–0.2 V below the CB bottom for both anatase and rutile titania samples. As far as the author knows, only this paper showed ERD in photocatalyst particles and no other methods for estimating ERD have been developed. One problem is that this ERD measurement requires a long time (one week or more including the time for electron-accumulation saturation and operation in a glove box) and tedious procedures to avoid reaction of accumulated electrons and MV·
+ with oxygen.
The ERD for anatase and rutile samples seemed reasonable, but the distance of electron trapping levels from the CB bottom, 0.1–0.2 V, might be larger than the thermal energy of electrons (
ca. 0.026 eV at 300 K [
12]). Therefore, ETs work as sites of both electron migration and recombination of e
−–h
+ pairs, suggesting that precise ERD analysis of ETs is needed for a correct understanding of the role of ETs and for the development of photocatalysts with a high level of activity.
Thus, there seem several experimental results showing the presence of ETs in titania particles. It is also expected that holes may be trapped by certain trapping sites, and experimental results [
16,
17,
18] and theoretical considerations [
19,
20] of this hole trapping in titania particles has been reported. However, there may be a difference between the nature of traps for electrons and holes due to possible higher reactivity of the holes. For electrons in titania, their transfer to substrates (or water/surface hydroxyl) adsorbed on the surface of titania is too slow to be detected easily.
5. Quantum Efficiency as a Measure for Extent of Recombination
Since recombination of e
−–h
+ pairs generally produces heat only as described in the preceding section, the extent of recombination can be estimated simply by subtraction, 1 –
ϕ (quantum efficiency). Quantum efficiency is defined, as the author's understanding [
1], as efficiency of e
−–h
+-pair utilization,
i.e., number proportion of e
−–h
+-pairs escaping from recombination. There seem to be at least two problems in quantum efficiency measurements. One is that quantum efficiency is calculated as the number ratio of e
−–h
+-pairs producing a product(s) to photons absorbed by a photocatalyst. In a heterogeneous system including solid photocatalysts, determination of the extent of photoabsorption of a photocatalyst is difficult in a strict scientific sense due to scattering of light by a photocatalyst. The other problem is that the number of e
−–h
+-pairs producing a product(s) can be estimated only when the number of e
− or h
+ required for the liberation of a product(s) is determined. To avoid uncertainty due to the latter problem, a formal number of e
−–h
+-pairs required for a given photocatalytic reaction is assumed for quantum efficiency calculation. For example, for the photocatalytic degradation of acetaldehyde in air, the following stoichiometry is assumed.
On the basis of the assumption that reduction of molecular oxygen into water requires 4 electrons per oxygen molecule,
n can be 10 or 5 when acetaldehyde consumption or carbon dioxide production, respectively, is used for calculation of quantum efficiency from reaction rate. This is convenient when photocatalytic reaction systems are compared with each other. However, at the same time, this hides the discussion on intrinsic quantum efficiency,
i.e., efficiency of e
−–h
+-pair utilization, especially for photocatalytic reaction systems including oxygen as an oxidant. In those systems, oxygen may work both as an electron acceptor and as a radical scavenger to produce peroxy radical (RO
2·) working as a chain carrier in the so-called radical-chain mechanism as shown below:
where radical species (R·) are produced by direct oxidation with a hole (h
+) or hydrogen abstraction by hydroxyl radical (HO·) liberated via reaction 3 followed by addition of O
2 to give peroxy radical (RO
2·) as a chain carrier. This relatively long-lived peroxy radical abstracts hydrogen in a substrate RH to produce another R· and then RO· (chain propagation), and a resultant hydroperoxide (RO
2H) is decomposed spontaneously to give the final products, water and carbon dioxide. On the other hand, dimerization of chain carriers (reaction 7) terminates the chain reaction. Chain length, number of RO
2· liberated by initial R·, is regulated by the rate ratio of reactions 6 and 7,
i.e., ratio of propagation and termination. It is expected that the higher is the concentration of ROO· by higher intensity photoiradiation, the faster is the termination to result in a shorter chain length, though the light-intensity dependence has rarely been discussed on the basis of the possible radical-chain mechanism.
Through this radical-chain mechanism, efficiency of product liberation is enhanced, and overall efficiency is a product of intrinsic quantum efficiency and chain length. Therefore, intrinsic quantum efficiency can be estimated only when the chain length is determined, though there seem to be no experimental methods to measure chain length. Assuming that the photocatalytic decomposition of an organic compound proceeds according to the mechanism including primary steps of reactions 2, 5, 6 and 7, dependence of apparent quantum efficiency (Ф
app), molar ratio of product(s) to incident (not “absorbed”) photons, on the light intensity is expressed as
where
ϕ, φ,
k6,
k7,
C and
I are intrinsic quantum efficiency, photoabsorption efficiency, rate constants for reactions 6 and 7, surface concentration of a substrate on a photocatalyst and light intensity, respectively. The plot of Ф
app against
I −1/2 may be a straight line with a
y-intersect as a product of
ϕ and
φ. However, actual plots for photocatalytic decomposition of acetic acid by anatase titania photocatalysts [
21] gave an almost negligible
y-intersect [
22], suggesting that the intrinsic quantum efficiency,
i.e., efficiency of utilization of e
−–h
+ pairs, is very low and that appreciable overall apparent quantum efficiency is obtained by enhancement through the radical-chain mechanism. Thus, even if the apparent rate of a photocatalytic reaction is high, the rate does not guarantee higher intrinsic quantum efficiency of e
−–h
+ utilization.
6. Honda-Fujishima Effect: A Bias Problem
One of the most frequently cited papers in the field of photocatalysis is a paper by Fujishima and Honda published in 1972 in
Nature [
23], which has been often cited as “an origin of titania photocatalysis (though there was no description related to photocatalysis, such as “photocatalysis”, “photocatalyst”, or “photocatalytic” and no description on photocatalysis by titania in this paper). This paper, which is only about one page, showed two examples of probable water splitting by photoelectrochemical systems with a single-crystalline titania electrode. One was oxygen evolution at an irradiated titania electrode (photoanode) when potential of the electrode was controlled to be more anodic than
ca. −0.5 V
versus SCE (Although there was no description of pH of an electrolyte solution, similar electrochemical systems with an electrolyte solution containing potassium chloride at pH 4.7 buffered by acetate buffer were described in a previous paper [
24].). The other example was an electrochemical cell short-circuiting a titania photoanode and a platinum electrode immersed in basic (high pH) and acidic (low pH) electrolyte solutions, respectively [
11]. This implies that bias potential had been applied chemically, though no electrochemical potential bias was applied using an outer circuit; difference in pH by one pH unit corresponds to
ca. 60 mV. Thus, two examples of water photolysis had been suggested in the paper, but both of those seemed to require electrochemical or chemical “bias” for the system including a titania photoanode and a platinum cathode. In other words, it was suggested that titania has sufficient potential for photocatalytic redox reactions, but application of bias is necessary to drive the reaction efficiently. Thus, recombination of e
−–h
+ pairs predominantly occurs without bias application as in the case of photocatalysis by titania particles.
7. Rate-Determining Step in Photocatalysis and Steady-State Approximation
The rate of an ordinary chemical reaction is generally proportional to the concentration of a substrate, and the proportional constant, a rate constant, is a function of activation energy, ∆
Ea, barrier height in a path of the rate-determining step. Since photocatalytic reactions, as well as the other photoreactions, are not governed by ∆
G as is easily predicted by the fact that positive−∆
G photocatalytic reactions such as water splitting proceed, the rate of photocatalytic reactions may not be controlled by ∆
Ea. In fact, ∆
Ea values for a variety of photocatalytic reactions were estimated to be
ca. 10–20 kJ mol
−1 using Arrhenius plots, logarithm of a rate constant
versus reciprocal temperature, much smaller than those for ordinary chemical reactions [
1]. In this sense, there is no rate-determining step in photocatalysis in a strict scientific sense. Rates of photocatalytic reactions are practically governed by recombination of e
−–h
+ pairs.
How is photocatalytic reaction kinetics described? The original idea for photocatalytic reaction kinetics was reported in 1972, the same year in which the above-discussed paper by Fujishima and Honda was published, by Fleischauer and coworkers [
25]. As far as the author knows, this paper showed for the first time the effect of Langmuirian adsorption of a substrate on the rate (or quantum efficiency) of photocatalytic reaction by TiO
2. The rate of photoinduced silver metal deposition was analyzed using a Stern–Volmer plot, a popular method in the field of photochemistry; almost linear double-reciprocal plots of the (apparent) quantum efficiency for the deposition (
Ф) as a function of concentration of silver ion (Ag
+) in solutions (
CAg) were obtained for both TiO
2 and ZnO crystals, as
where
Фlim, and
CL are constants. In the first approximation for interpretation of the meaning of Equation 9, the authors assumed a reaction mechanism in which electrons photoexcited by the efficiency
ϕ react with surface-adsorbed Ag
+ (with the surface concentration
NAg) to give deposits with a rate constant
k3, otherwise e
− is deactivated with a rate constant
k4, as
This equation can be derived by “steady-state (stationary-state) approximation”, which is often employed for reactions induced by short-lived active species such as the photoexcited state of a given material (e
− and h
+ in a photocatalyst), based on the assumption of a constant concentration of e
− that is produced by photoabsorption of a photocatalyst and consumed by (a) surface reaction and (b) recombination with holes. Thus, the rate of photocatalytic reaction is governed by the rate of recombination (
k4), though analysis of actual data using Equation 10 gives only the ratio of rate constants,
k3/
k4.
8. Conclusions
Despite extensive studies having been carried out for at least 40 years since the first-generation boom following the publication of a paper by Fujishima and Honda [
23], we have not yet unraveled the fundamentals of photocatalysis. The most important but unknown point is the e
−–h
+ recombination. The only thing we know about the recombination is that it occurs to result in quantum efficiency smaller than 100% and that so-called photocatalytic activity is governed predominantly by the rate of recombination as discussed in this article, but we do not know where, when and how the recombination occurs. Therefore, the author thinks it necessary to focus on studying the recombination in photocatalysis.
In the early stage of photocatalysis studies, in the 1970’s and 1980’s, there might have been no laboratories in which only photocatalysis was studied; photocatalysis had been studied as one of the topics in laboratories of catalysis, electrochemistry, photochemistry, radiation chemistry, material chemistry, analytical chemistry, surface science, inorganic chemistry or organic chemistry. Recently, photocatalysis has been studied in laboratories, including the author’s laboratory, in which photocatalysis is studied predominantly. Is this beneficial to unravel fundamentals of photocatalysis? The author has to say that the answer is no since people tend to recognize problems such as recombination to be “common sense”. The only possible way to solve these problems is to carry out collaboration work with researchers in fields completely different from photocatalysis.