Comparison of Quadratic vs. Langmuir–Hinshelwood Kinetics for Formic Acid Mineralization in a Photocatalytic Film
Abstract
1. Introduction
2. Results and Discussion
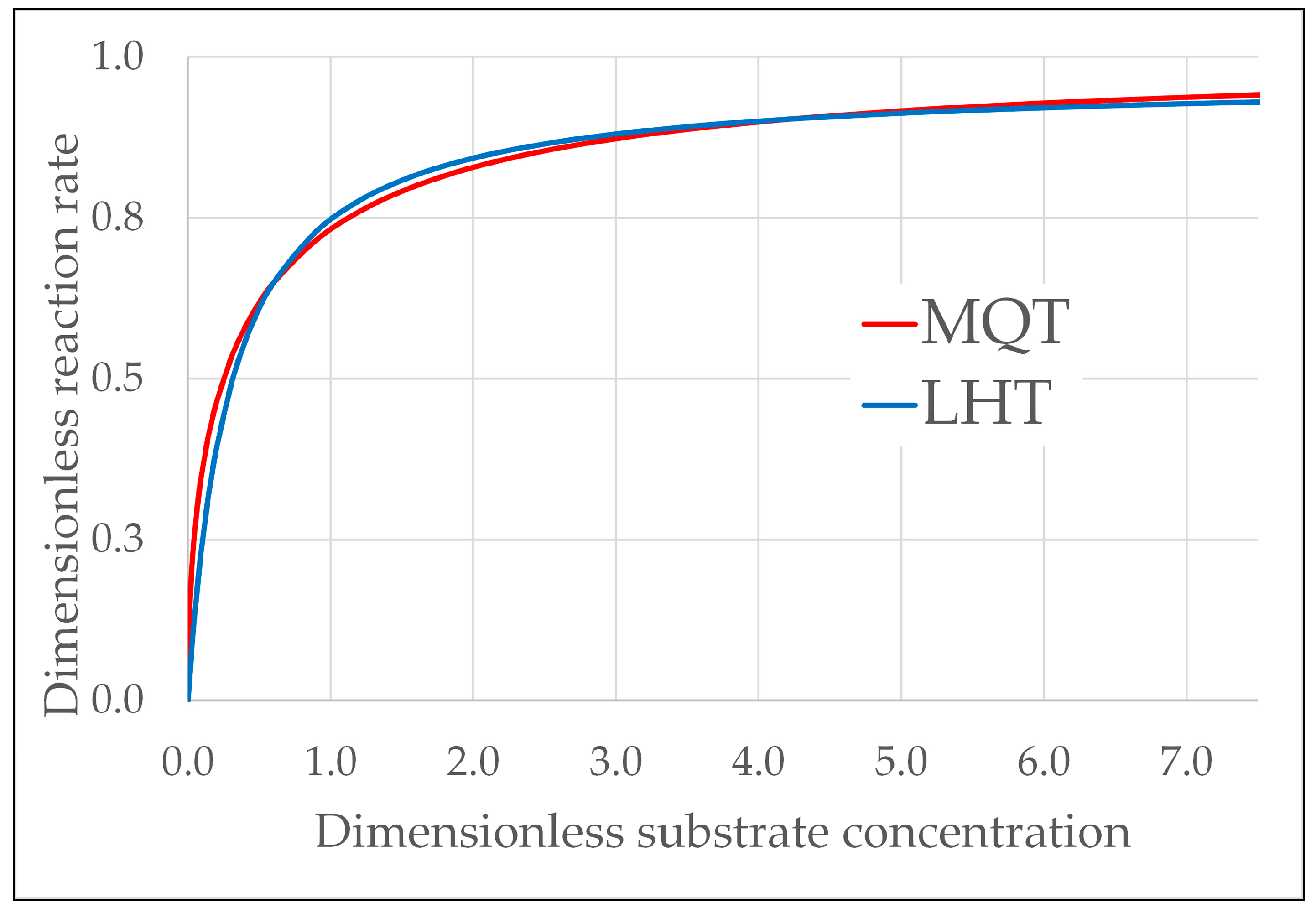
2.1. Kinetic Models
2.2. Analysis of the Possible Limitations Due to External Mass Transfer
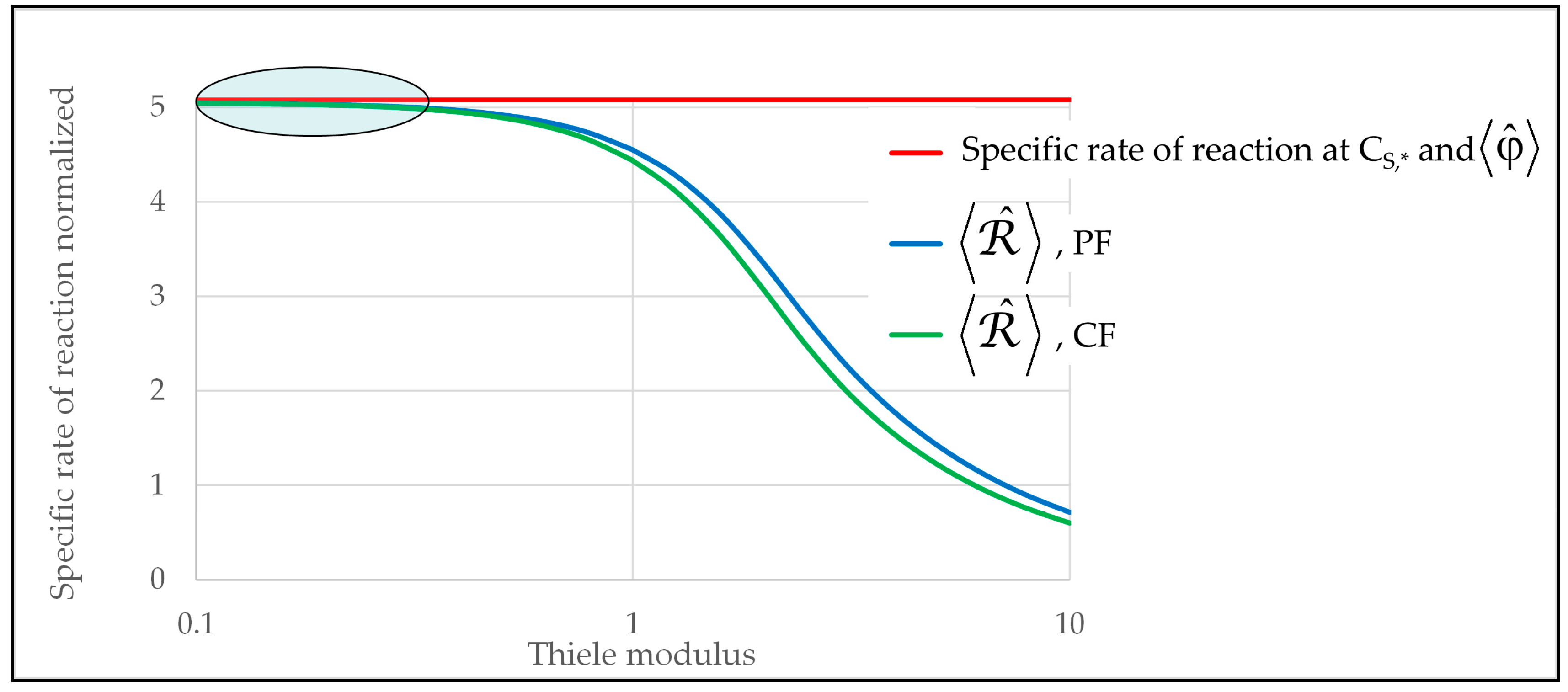
2.3. Analysis of the Possible Limitations Due to Internal Mass Transfer and Due to Transport of the Photons in the Film
- The optical thickness, , defined as , where is the absorption coefficient of the radiation and is the geometrical thickness of the film. The optical thickness represents the ratio of the geometrical thickness to the mean depth of penetration of the photons into the film. Therefore, at relatively low values of , it is expected that the transport of photons is not limiting.
- The Thiele modulus, , defined as , where is the volumetric rate of reaction, is the substrate concentration at the film–solution interface, is the specific rate of photon absorption at the film–solution interface, and is the effective diffusion coefficient of the substrate inside the film. The Thiele modulus represents the square root of the ratio of the characteristic rate of reaction to the characteristic rate of diffusion, or, analogously to the optical thickness, it represents the ratio of the geometrical thickness to the mean depth of penetration of the substrate into the film (see Section S5 of the Supplementary Material and [23]). Therefore, at relatively low values of , it is expected that the internal transport of the substrate is not limiting.
- The dimensionless parameter, , defined as . As previously observed, measures the level of illumination (it represents also the reciprocal of the characteristic quantum yield).
2.4. Application of the Integral Method of Kinetic Analysis
2.4.1. Integral Method for MQT Kinetics
2.4.2. Integral Method for LHT Kinetics
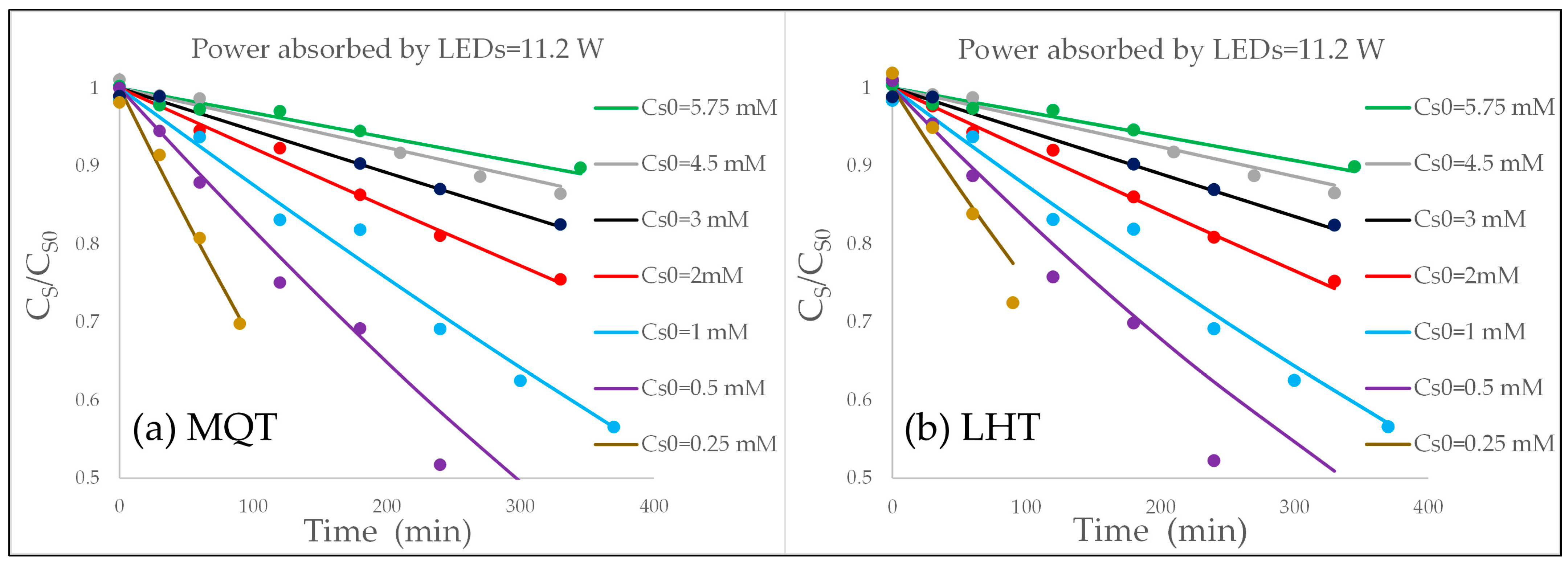
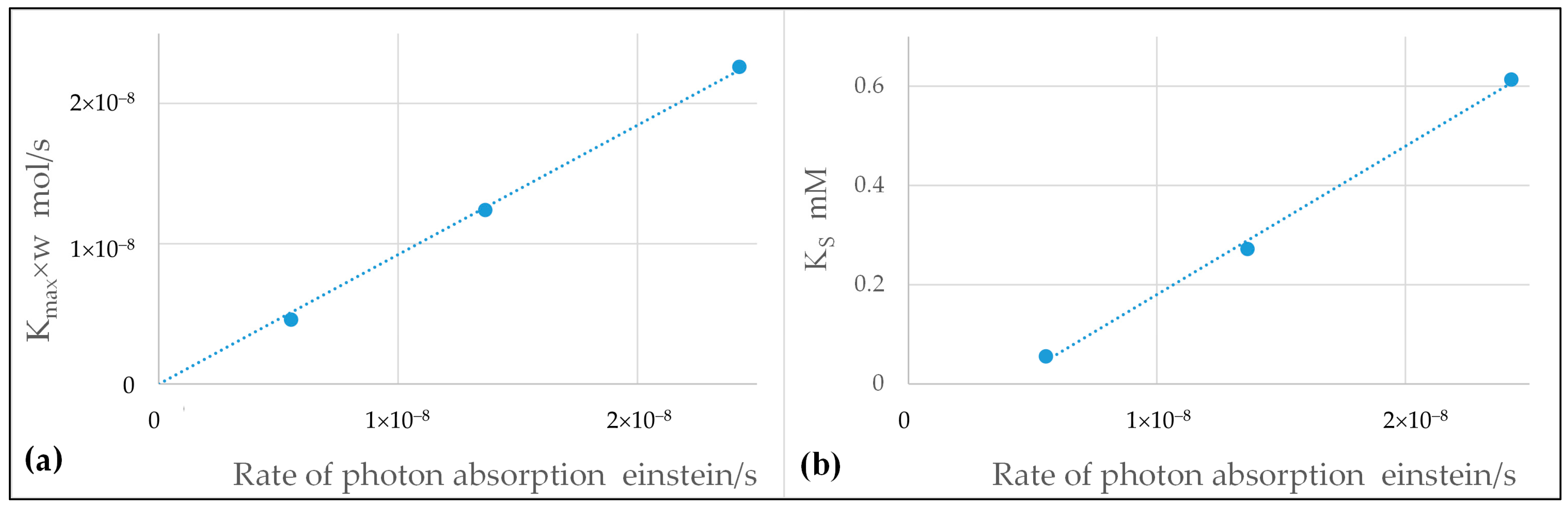
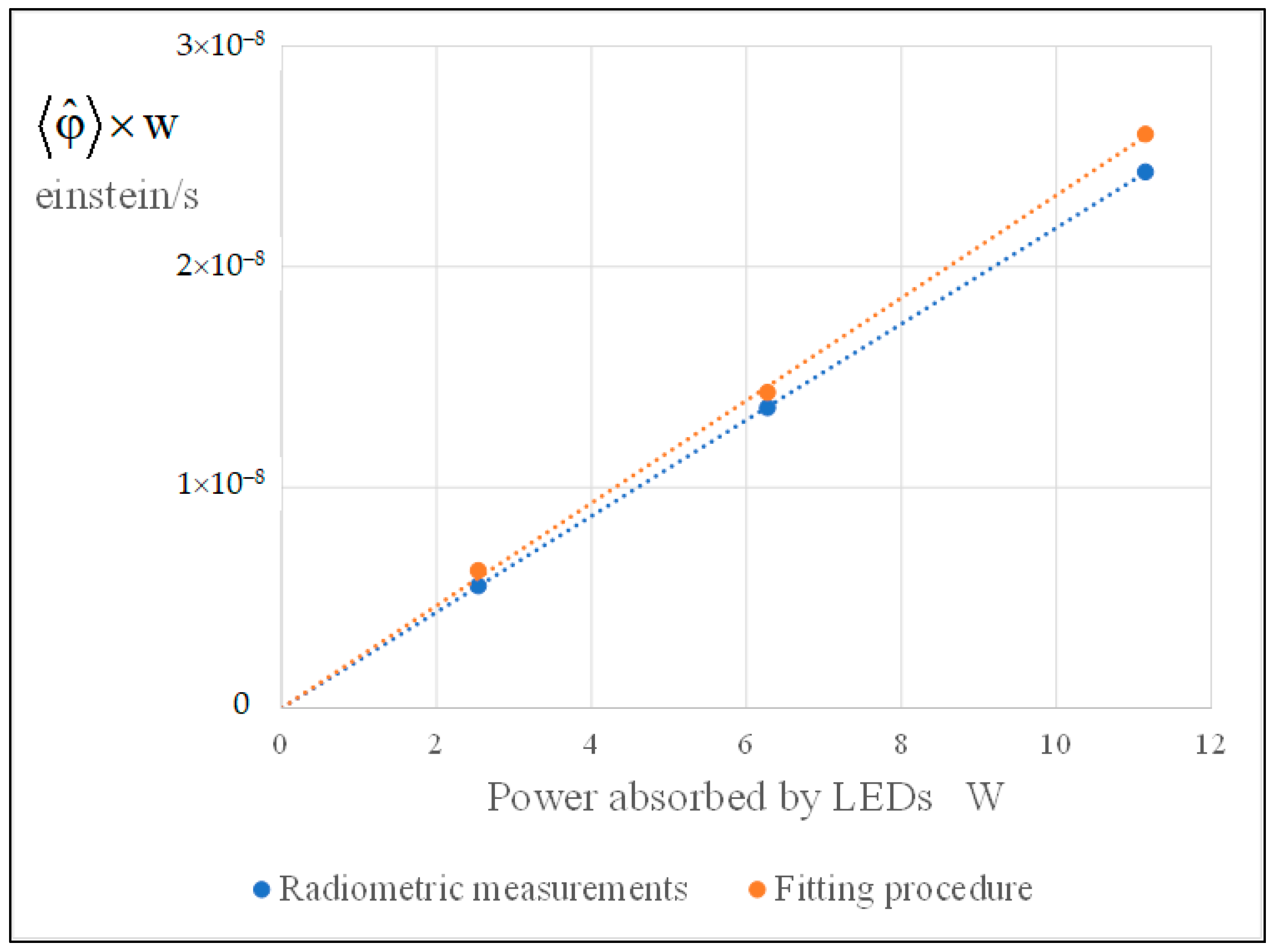
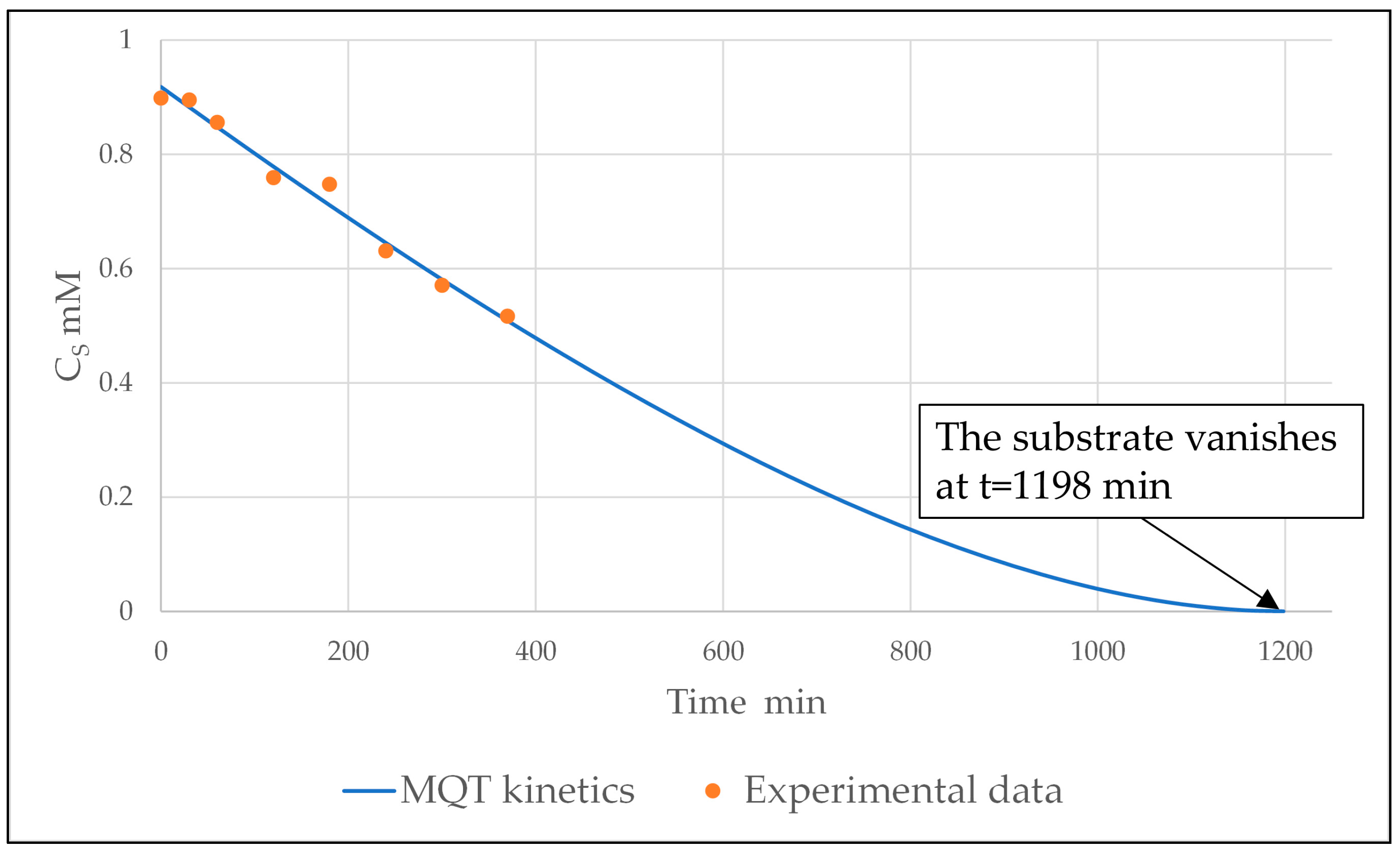
2.5. Best Fitting, Assessment of the Kinetic Parameters, and Discussion
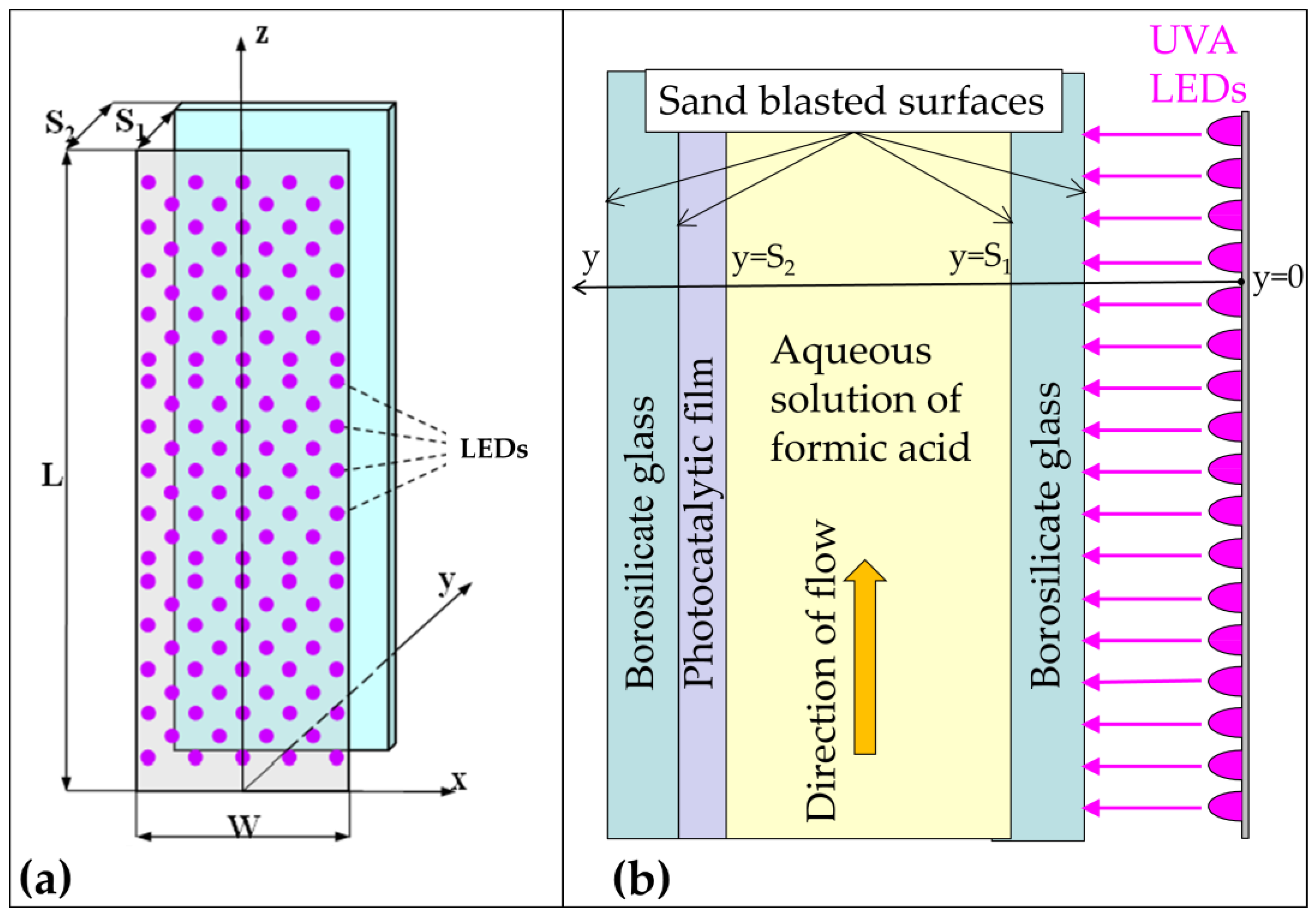
3. Materials and Methods
Chemicals and Experimental Methodology
4. Conclusions
- The goodness of fit was very satisfactory and almost identical with both kinetic models, but the MQT model achieves this result with just one fitting parameter compared to six fitting parameters of the LHT model. So, even if in practice both models are able to predict the vs. time behavior, nonetheless, in terms of simplicity and robustness, the much lower number of fitting parameters is a plus for MQT model.
- In regard to the dependence on the rate of photon absorption, the following conclusions were drawn. With the MQT model, the type of dependence is explicitly formulated in the model and was shown to be very apt to reproduce the experimental data at the different levels of illumination. It was shown that the MQT model with FA as substrate might even be used to measure the rate of photon absorption in a sort of photocatalytic actinometry. With the LHT model, the kinetics parameters and linearly increase with the rate of photon absorption to ensure the best fit of the experimental data. Other types of dependencies would not give the same goodness of fit. However, this linear increase implies that at high levels of illumination, the reaction is of zero order with respect to the rate of photon absorption, and this outcome is not consistent with the 0.5th order of reaction experimentally and commonly observed. Again, the MQT looks to be preferable.
- The order of reaction, , with respect to the substrate concentration varies continuously with , for both the models, but with different limits. The two models have the same limiting order (0) at a high concentration, but when the concentration tends to 0, the limit is 1 for LHT and 0.5 for MQT. If the order of reaction remains below the first order when the concentration diminishes, at some point, a deviation from the experimental evidence occurs. This is what happens with MQT, which works fine except at very low concentrations. This a problem of MQT that, however, only arises at concentrations so low as to be of little practical interest. With the LHT, the limit of the order of reaction is 1, so no inconvenience of this type occurs.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| superficial area of the interface between the film and the solution | |
| oxygen concentration | |
| substrate concentration | |
| substrate concentration at the film-solution interface | |
| substrate concentration in the bulk of the solution | |
| initial substrate concentration | |
| dimensionless substrate concentration | |
| Da | Damköhler number, |
| effective diffusivity of the substrate in the film | |
| diffusivity of the FA in the solution | |
| L | length of the illuminated photocatalytic film |
| kinetic constant of the MQT kinetic equation | |
| kinetic constant of the MQT kinetic equation | |
| , | kinetic constants in the Gerisher equation |
| , , | kinetic constants of the LHT kinetic equations |
| value of the kinetic constant at RPA = | |
| value of the kinetic constant at RPA = | |
| mass transfer coefficient of FA | |
| (N + 1) | total number of the withdrawn samples |
| number of moles of the substrate in the recirculating solution | |
| molar flux of FA at the solution fil interface | |
| the molar rate of disappearance of FA due to the photocatalytic reaction | |
| rate of generation of the substrate (it is negative for the disappearing substrate) | |
| photon flux entering into the film | |
| photon flux transmitted through the film | |
| volumetric rate of reaction | |
| specific rate of reaction | |
| asymptotic value of the reaction rate for MQT model as approaches infinity | |
| dimensionless parameter | |
| t | time |
| time of sampling number i + 2 | |
| time at which the system is filled with the solution and of the first sampling | |
| time at which the LEDs are turned on and of the second sampling | |
| volume of the film | |
| volume of the solution in the time interval | |
| volume of the FA aqueous solution | |
| volumetric flow rate | |
| volume of each withdrawn sample | |
| w | mass of the photocatalyst in the film |
| W | width of the illuminated photocatalytic film |
| W0(x) | principal branch of the Lambert W function |
| Greek symbols | |
| apparent order of reaction with respect to for the LHT model | |
| apparent order of reaction with respect to for the MQT model | |
| apparent order of reaction with respect to for the LHT model | |
| apparent order of reaction with respect to for the MQT model | |
| geometrical thickness of the film | |
| porosity of the film | |
| Thiele modulus, | |
| specific rate of photon absorption, SRPA | |
| specific rate of photon absorption at the film-solution interface | |
| dimensionless rate of photon absorption, | |
| absorption coefficient of the radiation in the film | |
| optical thickness, | |
| tortuosity of the pores | |
Abbreviations
| CF | Counter Flow: the photons and the substrate are transported in opposite directions inside the film. |
| FA | Formic Acid |
| LHT | Langmuir–Hinshelwood Type |
| MQT | Minero Quadratic Type |
| PF | Parallel Flow: the photons and the substrate are transported in the same direction inside the film. |
| RPA | Rate of Photon Absorption |
| SRPA | Specific Rate of Photon Absorption |
| Brackets | |
| denotes the volumetric average in the photocatalytic film | |
References
- Alfano, O.M.; Cabrera, M.I.; Cassano, A.E. Photocatalytic reactions involving hydroxyl radical attack. J. Catal. 1997, 172, 370–379. [Google Scholar] [CrossRef]
- Visan, A.; Rafieian, D.; Ogieglo, W.; Lammertink, R.G.H. Modeling intrinsic kinetics in immobilized photocatalytic microreactors. Appl. Catal. B Environ. 2014, 150–151, 93–100. [Google Scholar] [CrossRef]
- Ollis, D.F. Kinetics of photocatalyzed reactions: Five lessons learned. Front. Chem. 2018, 6, 378. [Google Scholar] [CrossRef] [PubMed]
- Visan, A.; van Ommen, J.R.; Kreutzer, M.T.; Lammertink, R.G.H. Photocatalytic reactor design: Guidelines for kinetic investigation. Ind. Eng. Chem. Res. 2019, 58, 5349–5357. [Google Scholar] [CrossRef]
- Mills, A.; O’Rourke, C.; Moore, K. Powder semiconductor photocatalysis in aqueous solution: An overview of kinetics-based reaction mechanisms. J. Photochem. Photobiol. A Chem. 2015, 310, 66–105. [Google Scholar] [CrossRef]
- Tran, H.D.; Nguyen, D.Q.; Do, P.T.; Tran, U.N.P. Kinetics of photocatalytic degradation of organic compounds: A mini-review and new approach. RSC Adv. 2023, 13, 16915–16925. [Google Scholar] [CrossRef]
- Zhang, L.; Mohamed, H.H.; Dillert, R.; Bahnemann, D. Kinetics mechanisms of charge transfer processes in photocatalytic systems: A review. J. Photochem. Photobiol. C Photochem. Rev. 2012, 13, 263–276. [Google Scholar] [CrossRef]
- Loddo, V.; Camera Roda, G.; Parrino, F. Chapter 7—Kinetic aspects of heterogeneous catalytic versus photocatalytic reactions. In Heterogeneous Photocatalysis; Marcì, G., Palmisano, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 215–233. [Google Scholar]
- Muñoz-Batista, M.J.; Ballari, M.M.; Kubacka, A.; Alfano, O.M.; Fernández-García, M. Braiding kinetics and spectroscopy in photo-catalysis: The spectro-kinetic approach. Chem. Soc. Rev. 2019, 48, 637–682. [Google Scholar] [CrossRef]
- Bloh, J.Z. A holistic approach to model the kinetics of photocatalytic reactions. Front. Chem. 2019, 7, 128. [Google Scholar] [CrossRef]
- Rancaño, L.; Rivero, M.J.; Mueses, M.Á.; Ortiz, I. Comprehensive kinetics of the photocatalytic degradation of emerging pollutants in a LED-assisted photoreactor. S-Metolachlor as Case Study. Catalysts 2021, 11, 48. [Google Scholar] [CrossRef]
- Minero, C.; Vione, D. A quantitative evaluation of the photocatalytic performance of TiO2 slurries. Appl. Catal. B Environ. 2006, 67, 257–269. [Google Scholar] [CrossRef]
- Calza, P.; Minella, M.; Demarchis, L.; Sordello, F.; Minero, C. Photocatalytic rate dependence on light absorption properties of different TiO2 specimens. Catal. Today 2020, 340, 12–18. [Google Scholar] [CrossRef]
- Albini, A. Some remarks on the first law of photochemistry. Photochem. Photobiol. Sci. 2016, 15, 319–323. [Google Scholar] [CrossRef] [PubMed]
- Gerisher, H. Photocatalysis in aqueous solution with small TiO2 particles and the dependence of the quantum yield on particle size and light intensity. Electrochim. Acta 1995, 40, 1277–1281. [Google Scholar] [CrossRef]
- Camera-Roda, G.; Santarelli, F.; Martin, C.A. Design of photocatalytic reactors made easy by considering the photons as immaterial reactants. Sol. Energy 2005, 79, 343–352. [Google Scholar] [CrossRef]
- Balzani, V.; Bergamini, G.; Ceroni, P. Light: A very peculiar reactant and product. Angew. Chem. Int. Ed. 2015, 54, 11320–11337. [Google Scholar] [CrossRef]
- Chapman, B.; Loiselle, D. Perspective–life and death of a photon: An intuitive non-equilibrium thermodynamic distinction between photochemistry and thermochemistry. Photochem. Photobiol. Sci. 2020, 19, 1623–1629. [Google Scholar] [CrossRef]
- Egerton, T.A. UV-Absorption—The primary process in photocatalysis and some practical consequences. Molecules 2014, 19, 18192–18214. [Google Scholar] [CrossRef]
- Wex, B.; Neckers, D.C. The quantum yield: An historical perspective. Spectrum 2005, 18, 10–15. [Google Scholar]
- Camera-Roda, G.; Augugliaro, V.; Cardillo, A.G.; Loddo, V.; Palmisano, L.; Parrino, F.; Santarelli, F. A reaction engineering approach to kinetic analysis of photocatalyticreactions in slurry systems. Catal. Today 2015, 259, 87–96. [Google Scholar] [CrossRef]
- Camera-Roda, G.; Loddo, V.; Palmisano, L.; Parrino, F. Guidelines for the assessment of the rate law of slurry photocatalytic reactions. Catal. Today 2017, 281, 221–230. [Google Scholar] [CrossRef]
- Camera-Roda, G.; Loddo, V.; Palmisano, L.; Parrino, F. Chapter 6—Special needs and characteristic features of (photo)catalytic reactors with a review of the proposed solutions. In Heterogeneous Photocatalysis; Marcì, G., Palmisano, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 177–213. [Google Scholar]
- Camera-Roda, G.; Santarelli, F. Optimization of the thickness of a photocatalytic film on the basis of the effectiveness factor. Catal. Today 2007, 129, 161–168. [Google Scholar] [CrossRef]
- Vezzoli, M.; Martens, W.N.; Bell, J.M. Investigation of phenol degradation: True reaction kinetics on fixed film titanium dioxide photocatalyst. Appl. Catal. A Gen. 2011, 404, 155–163. [Google Scholar] [CrossRef]
- Vezzoli, M.; Farrell, T.; Baker, A.; Psaltis, S.; Martens, W.N.; Bell, J.M. Optimal catalyst thickness in titanium dioxide fixed film reactors: Mathematical modelling experimental validation. Chem. Eng. J. 2013, 234, 57–65. [Google Scholar] [CrossRef]
- Dijkstra, M.F.J.; Panneman, H.J.; Winkelman, J.G.M.; Kelly, J.J.; Beenackers, A.A.C.M. Modeling the photocatalytic degradation of formic acid in a reactor with immobilized catalyst. Chem. Eng. Sci. 2002, 57, 4895–4907. [Google Scholar] [CrossRef]
- Turchi, C.S.; Ollis, D.F. Photocatalytic degradation of organic water contaminants: Mechanisms involving hydroxyl radical attack. J. Catal. 1990, 122, 178–192. [Google Scholar] [CrossRef]
- Smith, J.M. Chemical Reaction Engineering, 3rd ed.; McGraw-Hill Inc.: Columbus, OH, USA, 1981. [Google Scholar]
- Mills, A.; O’Rourke, C. Revised disrupted Langmuir-adsorption model of photocatalysis. J. Phys. Chem. C 2015, 119, 19941–19946. [Google Scholar] [CrossRef][Green Version]
- Nosaka, Y.; Nosaka, A. Langmuir-Hinshelwood light-intensity dependence analyses of photocatalytic oxidation rates by two-dimensional-ladder kinetic simulation. J. Phys. Chem. C 2018, 122, 28748–28756. [Google Scholar] [CrossRef]
- Emeline, A.V.; Ryabchuk, V.K.; Serpone, N. Factors affecting the efficiency of a photocatalyzed process in aqueous metal-oxide dispersions Prospect of distinguishing between two kinetic models. J. Photochem. Photobiol. A Chem. 2000, 133, 89–97. [Google Scholar] [CrossRef]
- Arts, A.; de Groot, M.T.; der Schaaf, J. Separating kinetics mass transfer in formic acid formate oxidation on boron doped diamond electrodes. J. Electroanal. Chem. 2020, 876, 114721. [Google Scholar] [CrossRef]
- Goličnik, M. On the Lambert Wfunction its utility in biochemical kinetics. Biochem. Eng. J. 2012, 63, 116–123. [Google Scholar] [CrossRef]
- Veberič, D. Lambert W function for applications in physics. Comput. Phys. Commun. 2012, 183, 2622–2628. [Google Scholar] [CrossRef]
- Mainardi, F.; Masina, E.; González-Santander, J.L. A Note on the Lambert W Function: Bernstein and Stieltjes Properties for a Creep Model in Linear Viscoelasticity. Symmetry 2023, 15, 1654. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Schnell, S.; Mendoza, C. Closed form solution for time-dependent enzyme kinetics. J. Theor. Biol. 1997, 187, 207–212. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Fox, R.L.; Ratner, M.W. Nonlinear optimization using the generalized reduced gradient method. RAIRO-Oper. Res. 1974, 3, 73–103. [Google Scholar] [CrossRef]
- Hawkins, D.M. The problem of overfitting. J. Chem. Inf. Comput. Sci. 2004, 44, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Langford, C.H. Variation of Langmuir adsorption constant determined for TiO2-photocatalyzed degradation of aceto-phenone under different light intensity. J. Photochem. Photobiol. A Chem. 2000, 133, 67–71. [Google Scholar] [CrossRef]
- Emeline, A.V.; Ryabchuk, V.K.; Serpone, N. Dogmas misconceptions in heterogeneous photocatalysis Some enlightened reflections. J. Phys. Chem. B 2005, 109, 18515–18521. [Google Scholar] [CrossRef]
- Mrowetz, M.; Selli, E. H2O2 evolution during the photocatalytic degradation of organic molecules on fluorinated TiO2. New J. Chem. 2006, 30, 108–114. [Google Scholar] [CrossRef]
- Montoya, J.F.; Velásquez, J.A.; Salvador, P. The direct–indirect kinetic model in photocatalysis: A reanalysis of phenol and formic acid degradation rate dependence on photon flow and concentration in TiO2 aqueous dispersions. Appl. Catal. B Environ. 2009, 88, 50–58. [Google Scholar] [CrossRef]
- Camera-Roda, G.; Loddo, V.; Palmisano, L.; Parrino, F. Photocatalytic ozonation for a sustainable aquaculture: A long-term test in a seawater aquarium. Appl. Catal. B Environ. 2019, 253, 69–76. [Google Scholar] [CrossRef]
- Irandoust, S.; Andersson, B. Concentration–dependent diffusivity of benzoic acid in water and its influence on the liquid–solid mass transfer. Canad. J. Chem.l Eng. 1986, 64, 954–959. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow, 1st ed.; Taylor & Francis: London, UK, 1980. [Google Scholar]
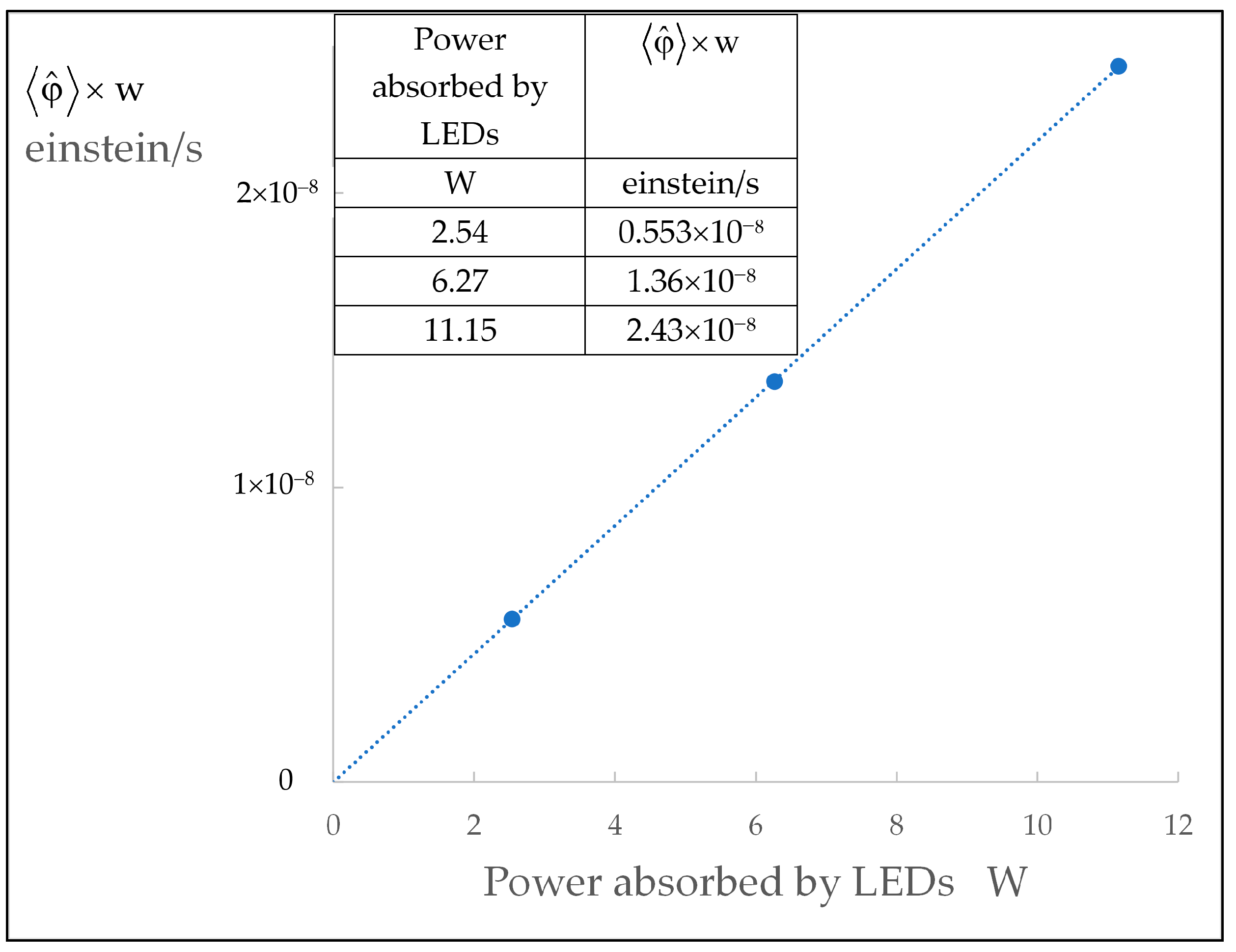


| MQT | LHT | ||
|---|---|---|---|
| from radiometric measurements | |||
| m3/s | einstein/s | mol/s | M |
| 9.54 × 10−9 | 0.553 × 10−8 | 4.58 × 10−9 | 0.056 × 10−3 |
| 1.36 × 10−8 | 12.4 × 10−9 | 0.272 × 10−3 | |
| 2.43 × 10−8 | 22.6 × 10−9 | 0.614 × 10−3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camera-Roda, G.; Papallo, M.; Parrino, F.; Loddo, V.; Palmisano, L. Comparison of Quadratic vs. Langmuir–Hinshelwood Kinetics for Formic Acid Mineralization in a Photocatalytic Film. Catalysts 2025, 15, 887. https://doi.org/10.3390/catal15090887
Camera-Roda G, Papallo M, Parrino F, Loddo V, Palmisano L. Comparison of Quadratic vs. Langmuir–Hinshelwood Kinetics for Formic Acid Mineralization in a Photocatalytic Film. Catalysts. 2025; 15(9):887. https://doi.org/10.3390/catal15090887
Chicago/Turabian StyleCamera-Roda, Giovanni, Maria Papallo, Francesco Parrino, Vittorio Loddo, and Leonardo Palmisano. 2025. "Comparison of Quadratic vs. Langmuir–Hinshelwood Kinetics for Formic Acid Mineralization in a Photocatalytic Film" Catalysts 15, no. 9: 887. https://doi.org/10.3390/catal15090887
APA StyleCamera-Roda, G., Papallo, M., Parrino, F., Loddo, V., & Palmisano, L. (2025). Comparison of Quadratic vs. Langmuir–Hinshelwood Kinetics for Formic Acid Mineralization in a Photocatalytic Film. Catalysts, 15(9), 887. https://doi.org/10.3390/catal15090887








