Evaluation of Vacuum Residue Decomposition Kinetics with a Catalyst by Thermogravimetric Analysis
Abstract
1. Introduction
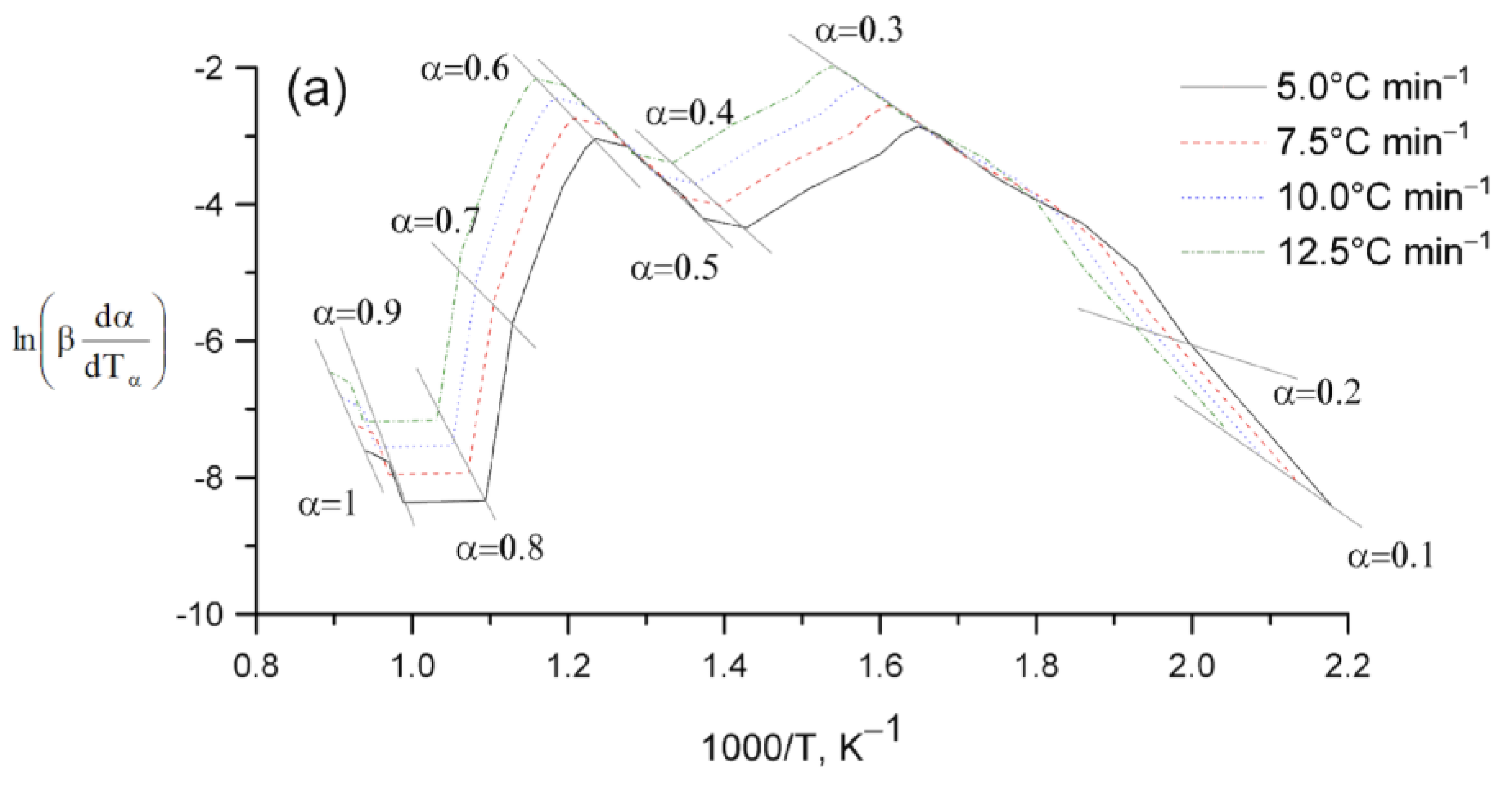
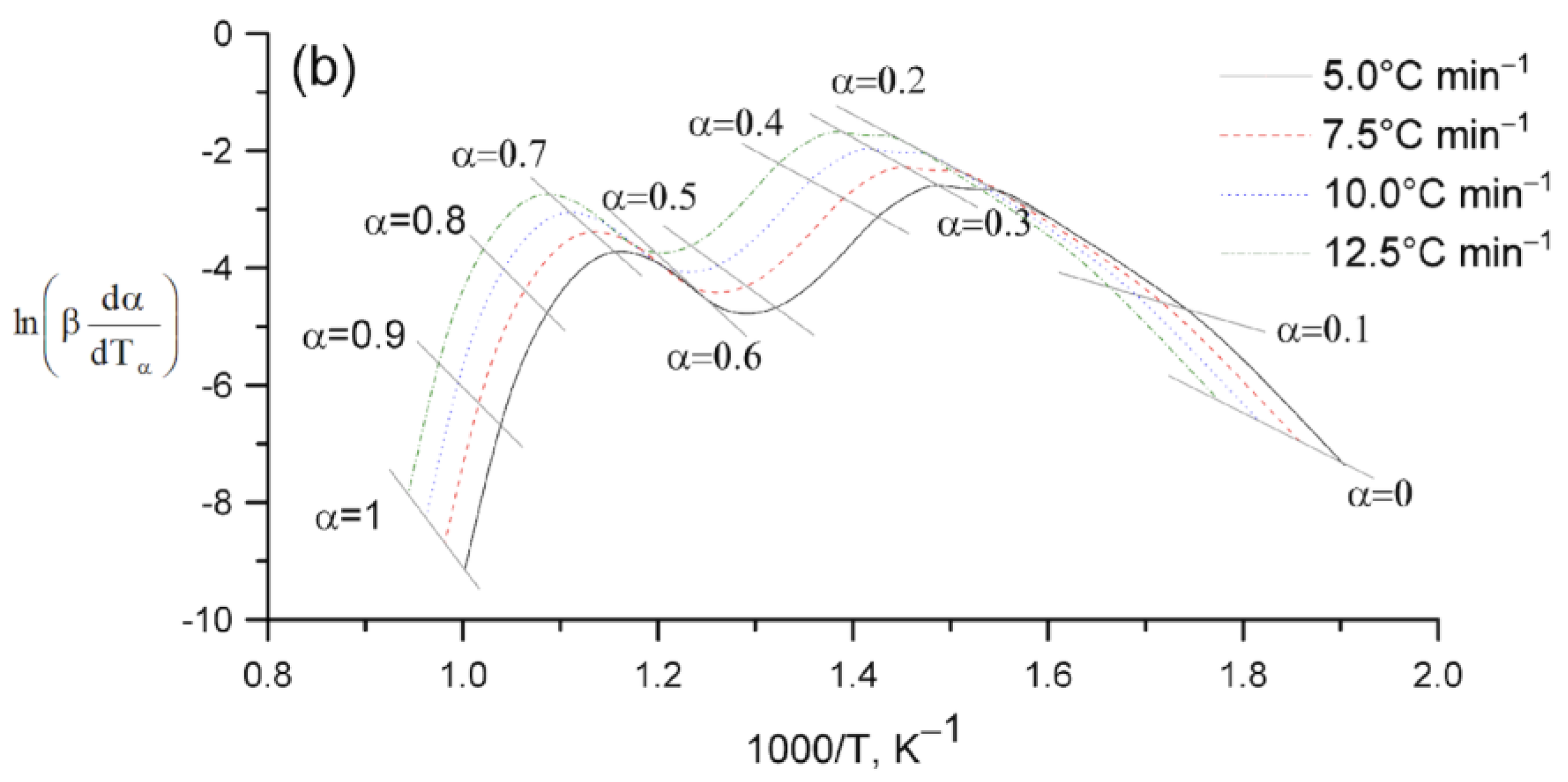
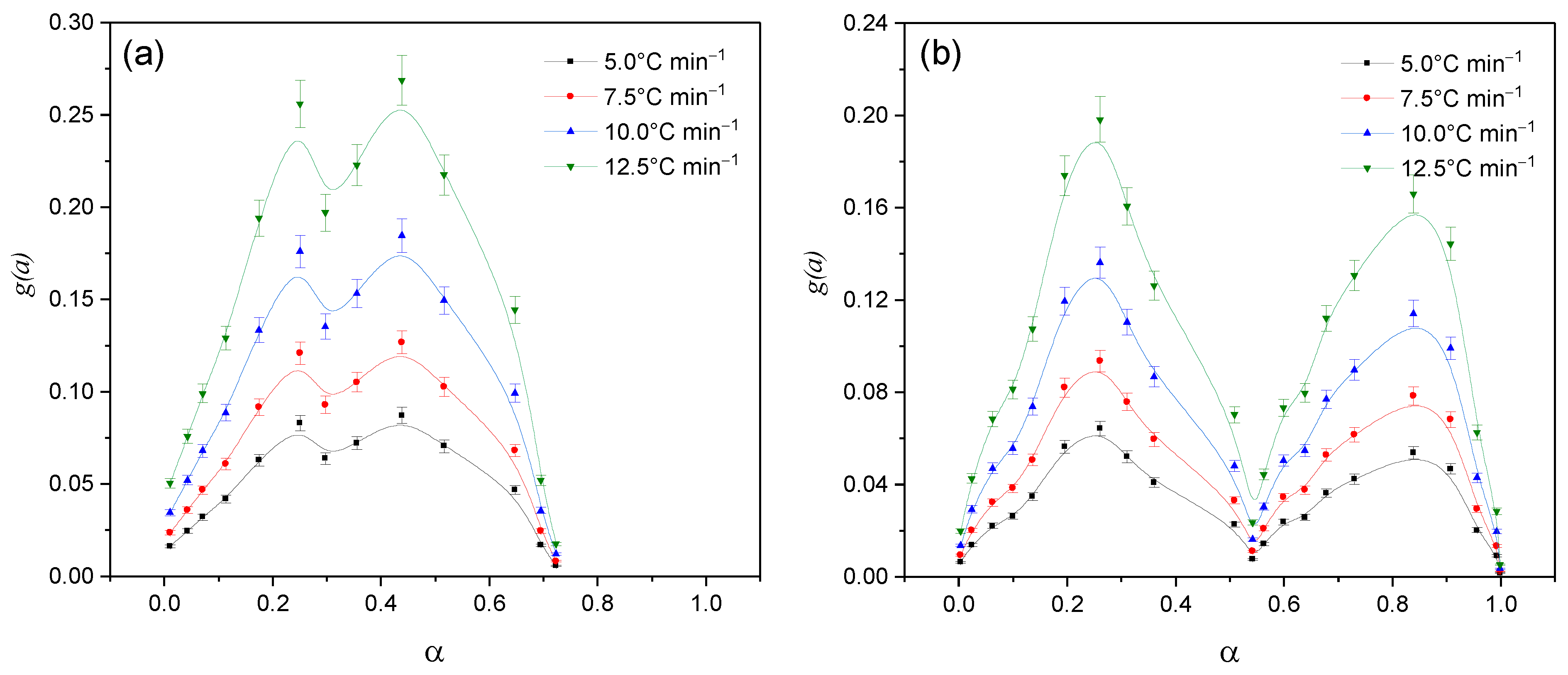
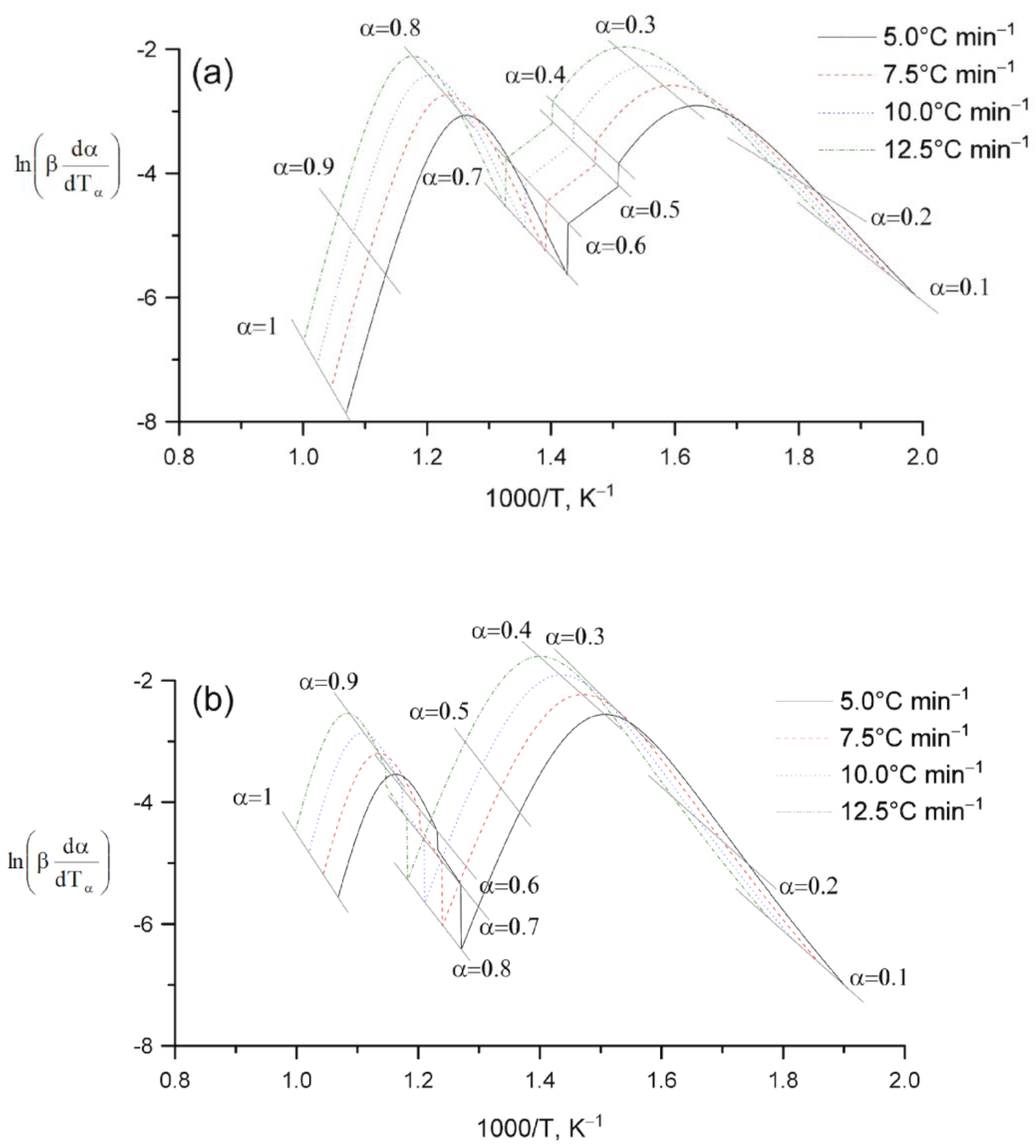
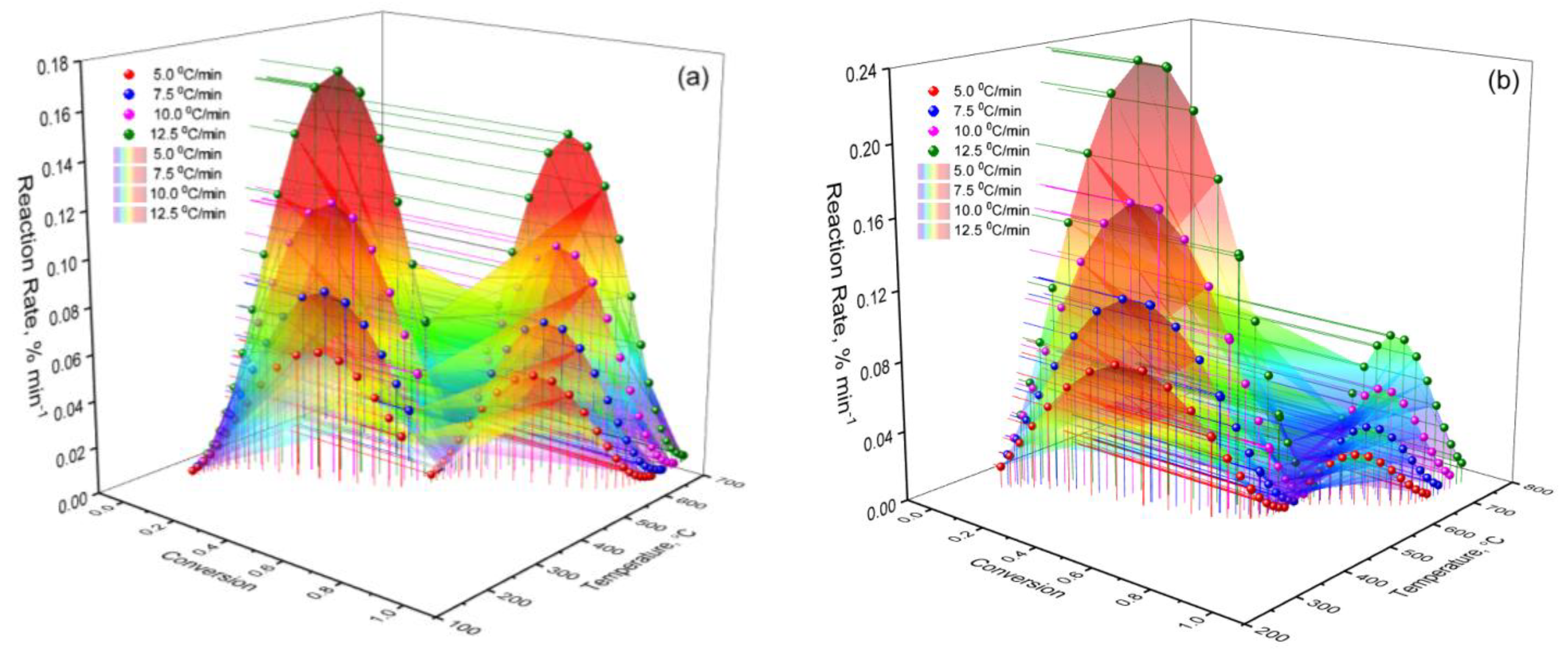
2. Results and Discussion
Kinetic Analysis
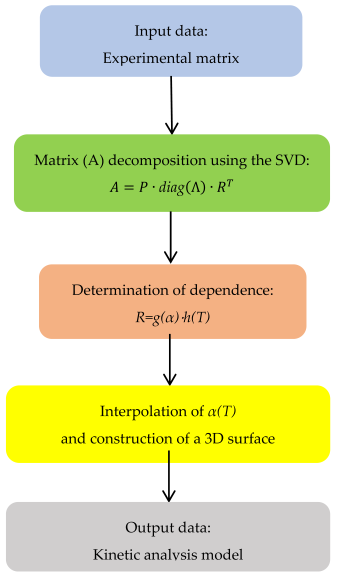
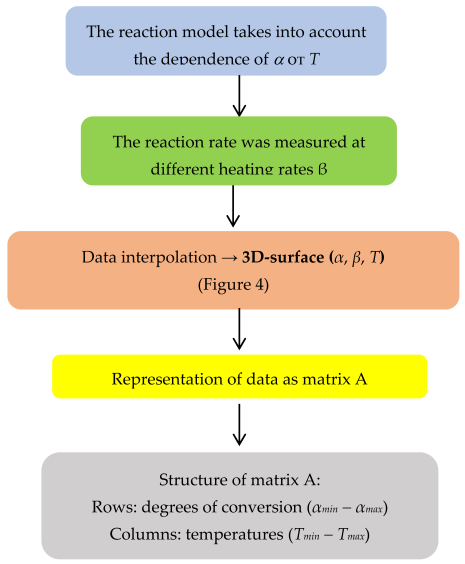
3. Materials and Methods
3.1. Chemical Analysis of the Vacuum Residue
3.2. Determination of Kinematic Viscosity and Vacuum Residue Density
3.3. Synthesis of Fe3O4 Nanocatalyst
3.4. Thermogravimetric Analysis of the Vacuum Residue
- m0—the initial sample weight,
- mt—mass at time t,
- mf—the final mass after degradation.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jenifer, A.C.; Sharon, P.; Prakash, A.; Sande, P.C. A review of the unconventional methods used for the demetallization of petroleum fractions over the past decade. Energy Fuels 2015, 29, 7743–7752. [Google Scholar] [CrossRef]
- Speight, J.G. Heavy and Extra-Heavy Oil Upgrading Technologies; GPP: Houston, TX, USA, 2013. [Google Scholar]
- Liu, H.; Wang, Z.; Guo, A.; Lin, C.; Chen, K. The Distribution of Ni and V in Resin and Asphaltene Subfractions and Its Variation During Thermal Processes. Pet. Sci. Technol. 2014, 33, 203–210. [Google Scholar] [CrossRef]
- Liu, T.; Lu, J.; Zhao, X.; Zhou, Y.; Wei, Q.; Zhang, Y.; Shi, Q. Distribution of Vanadium Compounds in Petroleum Vacuum Residuum and Their Transformations in Hydrodemetallization. Energy Fuels 2015, 29, 2089–2209. [Google Scholar] [CrossRef]
- Ancheyta, J. Modeling of Processes and Reactors for Upgrading of Heavy Petroleum; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2013. [Google Scholar]
- Shin, S.; Ikem, S.; Nho, N.; Bong Lee, K. Kinetic analysis using thermogravimetric analysis for nonisothermal pyrolysis of vacuum residue. J. Therm. Anal. Calorim. 2016, 126, 933–941. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Y.; Wang, Y.; Zhang, G.; Chen, L. Thermogravimetric study of the kinetics and characteristics of the pyrolysis of lignite. React. Kinet. Mech. Catal. 2013, 110, 225–235. [Google Scholar] [CrossRef]
- Baikenov, M.I.; Izbastenova, D.; Sarsenbekova, A.Z.; Balpanova, N.Z.; Tusipkhan, A. Determination of the Kinetic Parameters of Thermal Degradation and Hydrodemetallization of a Mixture of the Heavy Fraction of Low-Temperature Coal Tar and Coal Shale. Energies 2024, 17, 1766. [Google Scholar] [CrossRef]
- Koga, N.; Vyazovkin, S.; Burnham, A.; Favergeon, L.; Muravyev, N.; Pérez-Maqueda, L.; Saggese, C.; Sánchez-Jiménez, P. ICTAC Kinetics Committee recommendations for analysis of thermal decomposition kinetics. Thermochim. Acta 2023, 719, 179384. [Google Scholar] [CrossRef]
- DaCosta, H.; Fan, M. Rate Constant Calculation for Thermal Reactions: Methods and Applications; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Vyazovkin, S.; Chrissafis, K.; Di Lorenzo, M.L.; Koga, N.; Pijolat, M.; Roduit, B.; Sbirrazzuoli, N.; Suñol, J.J. ICTAC Kinetics Committee Recommendations for Collecting Experimental Thermal Analysis Data for Kinetic Computations. Thermochim. Acta 2014, 590, 1–23. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Pérez-Maqueda, L.A.; Sbirrazzuoli, N. ICTAC Kinetics Committee Recommendations for Analysis of Multi-Step Kinetics. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]
- Burkeev, M.Z.; Bolatbay, A.N.; Sarsenbekova, A.Z. Integral Ways of Calculating the Destruction of Copolymers of Polyethylene Glycol Fumarate with Acrylic Acid. Russ. J. Phys. Chem. 2021, 95, 2009–2013. [Google Scholar] [CrossRef]
- Li, Y.; Ma, F.; Su, X.; Sun, C.; Liu, J.; Sun, Z.; Hou, Y. Synthesis and catalysis of oleic acid-coated Fe3O4 nanocrystals for direct coal liquefaction. Catal. Commun. 2012, 26, 231–234. [Google Scholar] [CrossRef]
- Bajus, M. Pyrolysis technologies for biomass and waste treatment to fuels and chemical production. Pet. Coal 2010, 52, 1–10. [Google Scholar]
- Ekejiuba, A.I.B. Natural Petroleum Chemistry and Valuable Products Fractions. Inter-World J. Sci. Technol. 2021, 4, 300–337. [Google Scholar]
- Gautam, R.; Bhaskar, T.; Singh, R. On the products from the pyrolysis of heavy fuel and vacuum residue oil. J. Anal. Appl. Pyrolysis 2023, 171, 106060. [Google Scholar] [CrossRef]
- Gary, J.H.; Handwerk, G.E.; Kaiser, M.J. Petroleum Refining: Technology and Economics, 5th ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Friedman, H.L. Kinetics of Thermal Degradation of Char-Forming Plastics from Thermogravimetry. Application to a Phenolic Plastic. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Flynn, J.H.; Wall, L.A. A Quick, Direct Method for the Determination of Activation Energy from Thermogravimetric Data. J. Polym. Sci. Part B Polym. Lett. 1966, 4, 323–328. [Google Scholar] [CrossRef]
- Ozawa, T. A New Method of Analyzing Thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Balpanova, N.; Baikenov, M. Thermal Degradation Kinetics of Vacuum Residues in the Presence of Chrysotile Supported Ni-Ti Catalyst. Catalysts 2023, 13, 1361. [Google Scholar] [CrossRef]
- Li, Y.; Yang, C.; Ge, J.; Sun, C.; Wang, J.; Su, X. A general microwave-assisted two-phase strategy for nanocrystals synthesis. J. Colloid Interface Sci. 2013, 407, 296–301. [Google Scholar] [CrossRef]
- Serra, R.; Sempere, J.; Nomen, R. A new method for the kinetic study of thermoanalytical data: The non-parametric kinetics method. Thermochim. Acta 1998, 316, 37–45. [Google Scholar] [CrossRef]
- Serra, R.; Nomen, R.; Sempere, J. The Non-Parametric Kinetics A New Method for the Kinetic Study of Thermoanalytical Data. J. Therm. Anal. Calorim. 1998, 52, 933–943. [Google Scholar] [CrossRef]
- Wall, M.E.; Rechtsteiner, A.; Rocha, L.M. Singular Value Decomposition and Principal Component Analysis. In A Practical Approach to Microarray Data Analysis; Berrar, D.P., Dubitzky, W., Granzow, M., Eds.; Springer: Boston, MA, USA, 2003. [Google Scholar]
- ISO 29541:2025; Coal and Coke—Determination of Total Carbon, Hydrogen and Nitrogen—Instrumental Method. ISO: Geneva, Switzerland, 2025.
- GOST 6382-91; Mineral Solid Fuel. Determination of Volatile Matter. GOST: Moscow, Russia, 2023.
- GOST 1461-2023; Petroleum and Petroleum Products. Method of Ash Test. GOST: Moscow, Russia, 2023.
- GOST 33-2016; Petroleum and Petroleum Products. Transparent and Opaque Liquids. Determination of Kinematic and Dynamic Viscosity. GOST: Moscow, Russia, 2016.
- GOST 3900-2022; Petroleum and Petroleum Products. Methods for Determination of Density. GOST: Moscow, Russia, 2022.
- Tyanakh, S.; Baikenov, M.; Yun, M.F.; Khamitova, T.; Balpanova, N.; Tulebayeva, B.; Kyzkenova, A.; Karimova, A.; Rakhimzhanova, N.; Kochegina, E. Kinetic of Oil Sludge Thermolysis Process in Presence of Nickel, Cobalt and Iron-Supported Microsilicate. Pol. J. Chem. Technol. 2023, 25, 101–109. [Google Scholar] [CrossRef]
- Balpanova, N.Z.; Baikenov, M.I.; Gyulmaliev, A.M.; Absat, Z.B.; Batkhan, Z.; Ma, F.; Su, K.; Kim, S.V.; Baikenova, G.G.; Aitbekova, D.E.; et al. Thermokinetic parameters of the primary coal tars destruction in the presence of catalysts and polymeric materials. Bull. Univ. Karaganda—Chem. 2021, 102, 86–95. [Google Scholar] [CrossRef]
- Sarsenbekova, A.Z.; Zhumanazarova, G.M.; Tazhbayev, Y.M.; Kudaibergen, G.K.; Kabieva, S.K.; Issina, Z.A.; Kaldybayeva, A.K.; Mukabylova, A.O.; Kilybay, M.A. Research the Thermal Decomposition Processes of Copolymers Based on Polypropyleneglycolfumaratephthalate with Acrylic Acid. Polymers 2023, 15, 1725. [Google Scholar] [CrossRef] [PubMed]
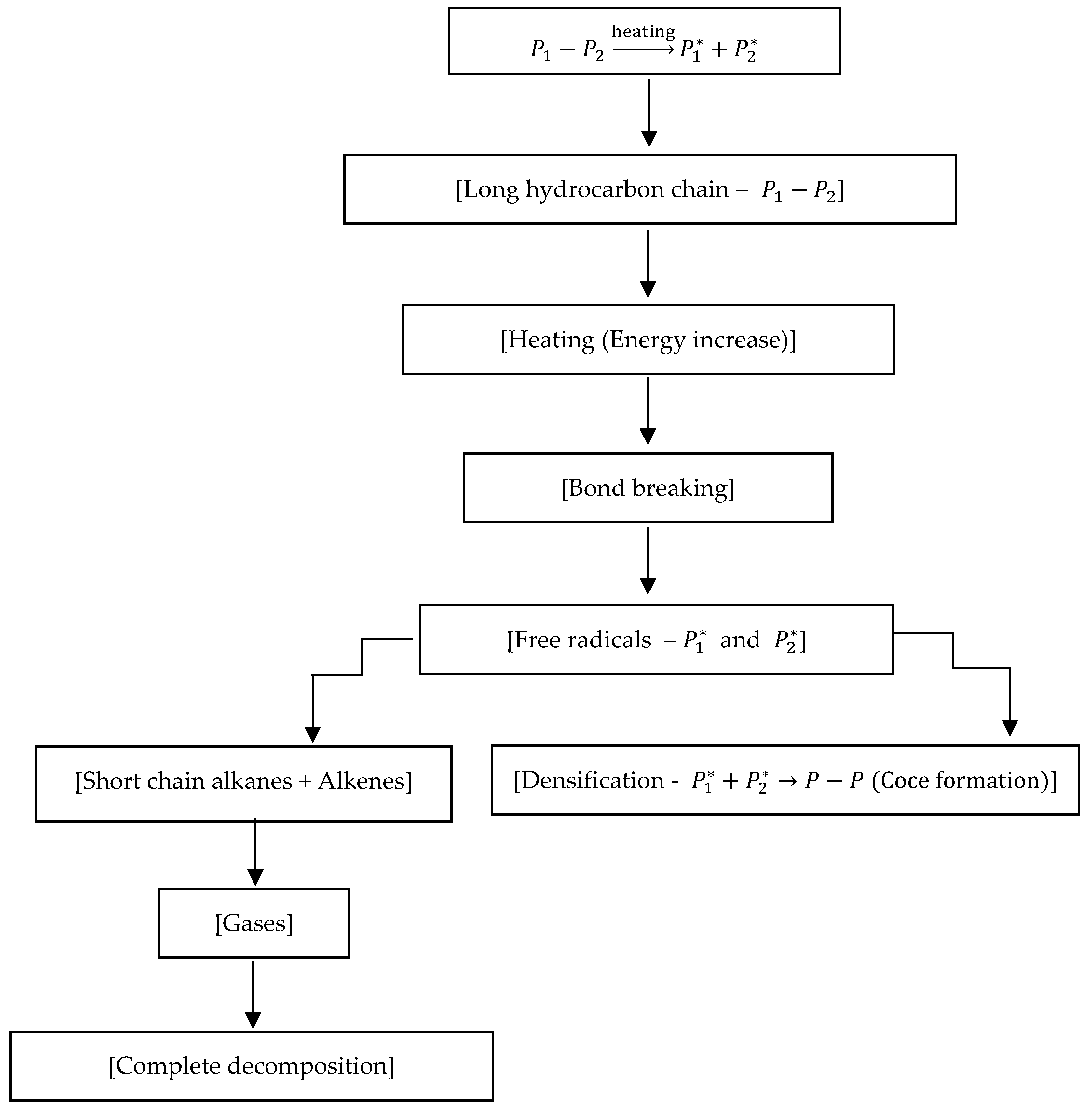
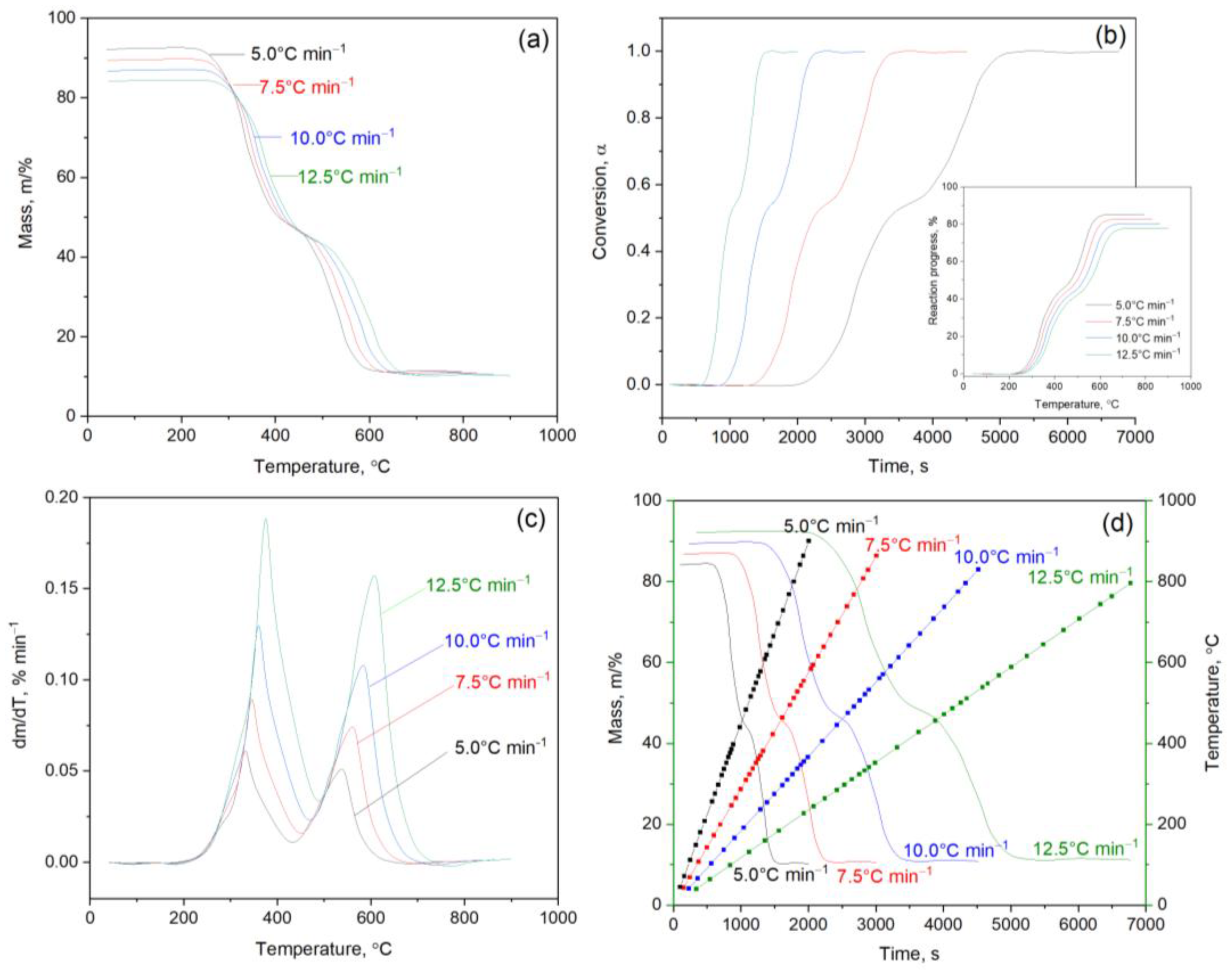



| Sample | , kJ mol−1 ±SD | ·103, s−1 ±SD | Šesták–Berggren | , kJ mol−1 ±SD | · 104, s−1 ±SD | , kJ mol−1 ±SD | · 103, s−1 ±SD | |
|---|---|---|---|---|---|---|---|---|
| αm(1 − α)n | ||||||||
| m | n | |||||||
| Experimental data | ||||||||
| Vacuum residue | 91.54 ±0.18 | 4.83 ±0.12 | 0.75 | 2.36 | 94.23 ±0.56 | 1.49 ±0.05 | 91.54 ±0.26 | 4.80 ±0.05 |
| Vacuum residue with a catalyst | 89.68 ±0.36 | 9.86 ±0.10 | 0.74 | 2.09 | 92.52 ±0.13 | 2.08 ±0.18 | 89.68 ±0.36 | 9.95 ±0.05 |
| Theoretical data | ||||||||
| Vacuum residue | 91.35 ±0.50 | 4.83 ±0.05 | 0.75 | 2.37 | 94.13 ±0.50 | 1.48 ±0.09 | 91.43 ±0.35 | 3.33 ±0.10 |
| Vacuum residue with a catalyst | 90.87 ±0.50 | 7.98 ±0.15 | 0.74 | 2.10 | 91.52 ±0.50 | 2.15 ±0.18 | 90.87 ±0.50 | 8.01 ±0.10 |
| Element | Content (wt%) | Error (±wt. %) | Methodology |
|---|---|---|---|
| Carbon (C) | 82.4 | ±0.20 | Vario MICRO Cube/ISO 29541 |
| Hydrogen (H) | 11.8 | ±0.20 | Vario MICRO Cube/ISO 29541 |
| Nitrogen (N) | 0.9 | ±0.20 | Vario MICRO Cube/ISO 29541 |
| Sulfur (S) | 2.6 | ±0.20 | Vario MICRO Cube/ISO 29541 |
| Oxygen (O) | 2.3 | Estimated value | By elemental difference |
| Indicator | Value (wt%) | Error (±wt. %) | Methodology/Standard |
|---|---|---|---|
| Moisture | 0.21 | ±0.05 | GOST 6382-91 |
| Ash | 1.64 | ±0.02 | GOST 1461-2023 |
| Volatiles | 53.15 | ±0.10 | GOST 6382-91 |
| Fixed carbon | 44.99 | — | By difference |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makenov, D.; Tusipkhan, A.; Sarsenbekova, A.Z.; Baikenov, M.; Balpanova, N.; Aitbekova, D.; Tateeva, A.; Izbastenova, D.; Kokzhalova, B.; Ma, F. Evaluation of Vacuum Residue Decomposition Kinetics with a Catalyst by Thermogravimetric Analysis. Catalysts 2025, 15, 493. https://doi.org/10.3390/catal15050493
Makenov D, Tusipkhan A, Sarsenbekova AZ, Baikenov M, Balpanova N, Aitbekova D, Tateeva A, Izbastenova D, Kokzhalova B, Ma F. Evaluation of Vacuum Residue Decomposition Kinetics with a Catalyst by Thermogravimetric Analysis. Catalysts. 2025; 15(5):493. https://doi.org/10.3390/catal15050493
Chicago/Turabian StyleMakenov, Daulet, Almas Tusipkhan, Akmaral Zh. Sarsenbekova, Murzabek Baikenov, Nazerke Balpanova, Darzhan Aitbekova, Alma Tateeva, Dariya Izbastenova, Bibimariyam Kokzhalova, and Fengyun Ma. 2025. "Evaluation of Vacuum Residue Decomposition Kinetics with a Catalyst by Thermogravimetric Analysis" Catalysts 15, no. 5: 493. https://doi.org/10.3390/catal15050493
APA StyleMakenov, D., Tusipkhan, A., Sarsenbekova, A. Z., Baikenov, M., Balpanova, N., Aitbekova, D., Tateeva, A., Izbastenova, D., Kokzhalova, B., & Ma, F. (2025). Evaluation of Vacuum Residue Decomposition Kinetics with a Catalyst by Thermogravimetric Analysis. Catalysts, 15(5), 493. https://doi.org/10.3390/catal15050493







