Evaluating Theoretical Approaches to Nitrogen-Doped Carbon Supports
Abstract
1. Introduction and Overview of Carbon Materials
2. Computational Methods for Studying Carbon Materials
2.1. Density Function Theory
2.2. Theoretical Metrics
2.2.1. Support Structure
2.2.2. Catalyst–Support Interactions
- Adsorption energy
- 2.
- Ripening energy
- 3.
- Migration energy
2.2.3. Electrocatalytic Energies
3. Role and Computational Representations of Nitrogen-Doped Carbon Materials with Design Challenges
3.1. Defects
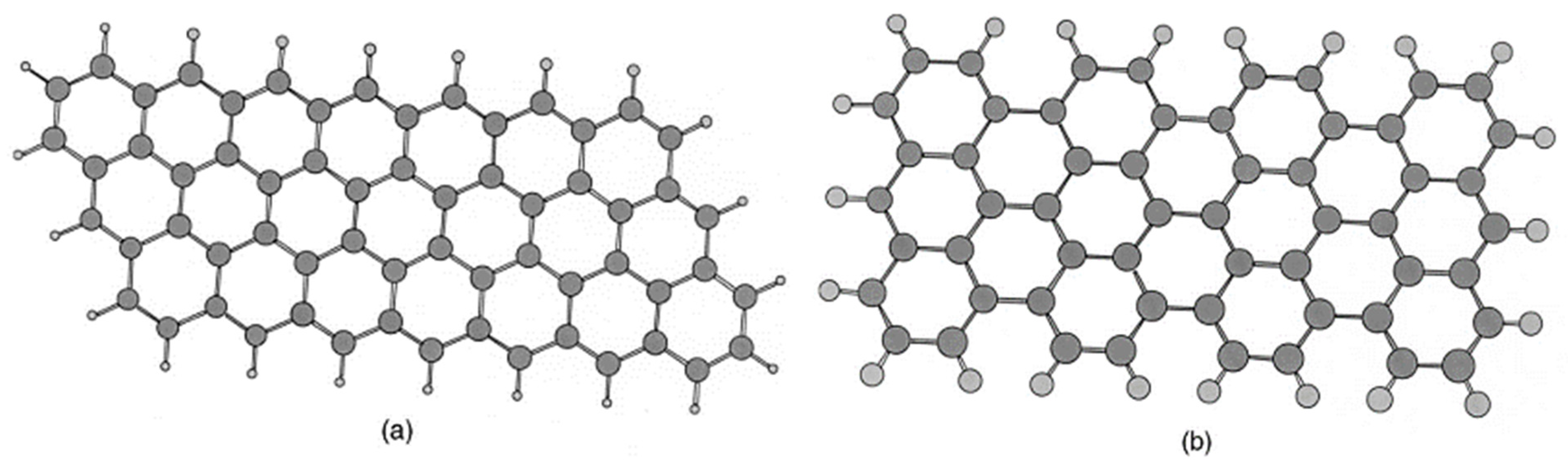
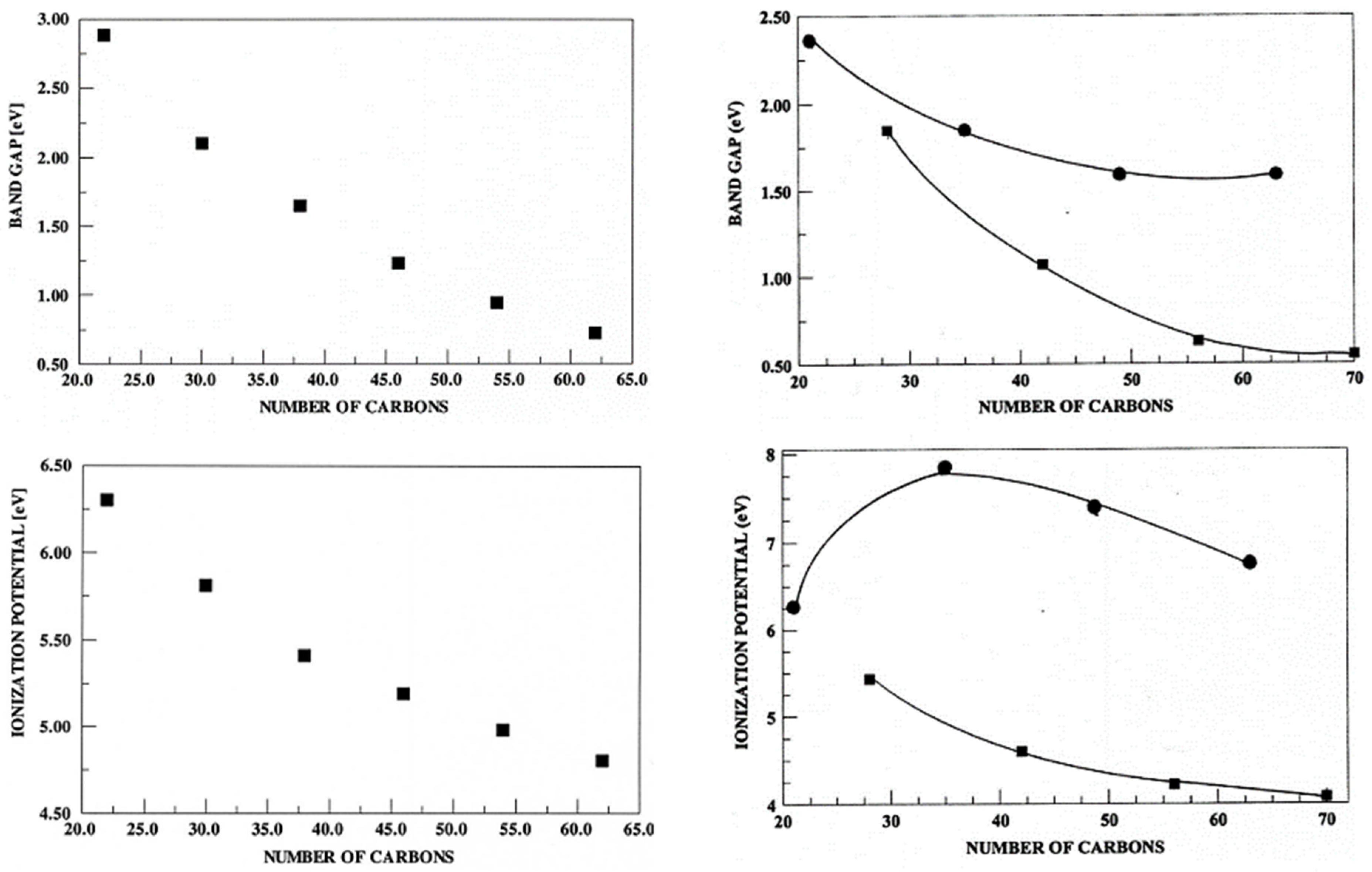
3.2. Truncated Models
3.3. PBC Models
3.3.1. Graphene
3.3.2. Nanoribbons
3.3.3. Other Carbon Structures
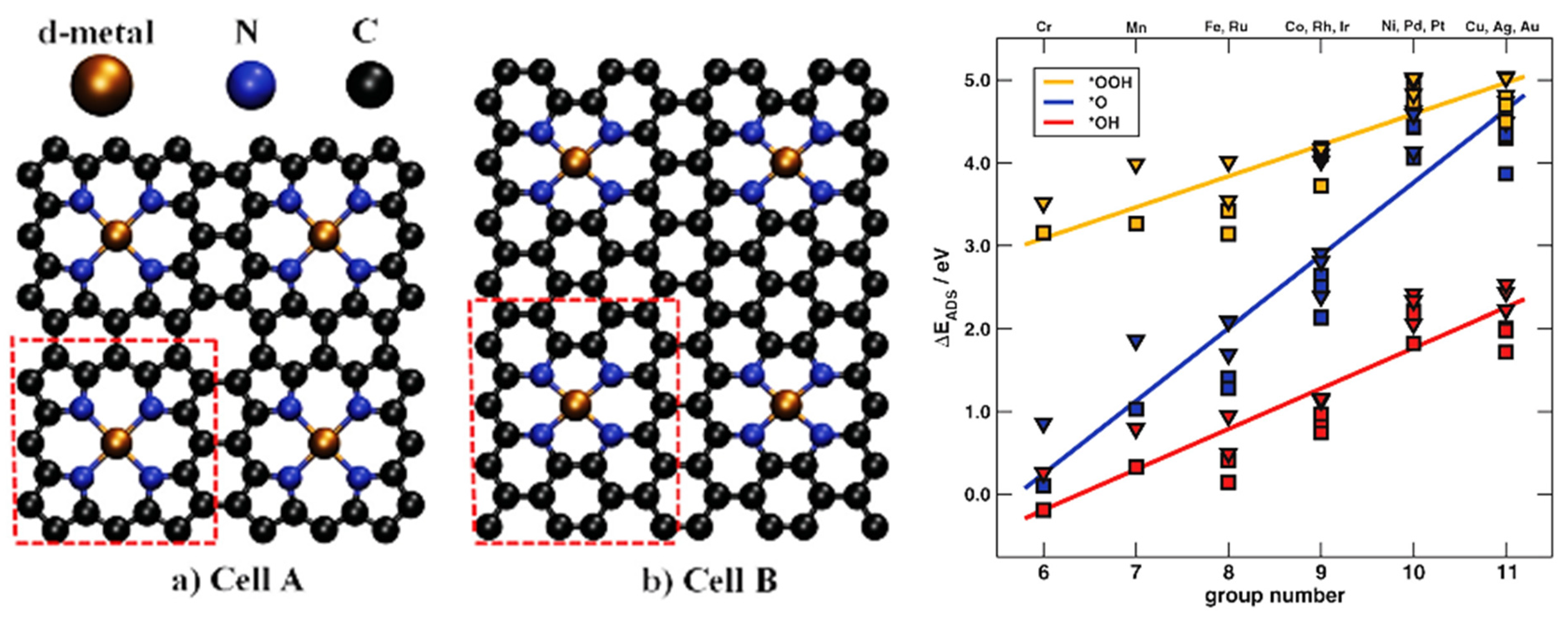
4. Metal–Support Interactions for Describing Catalysis
4.1. Stability
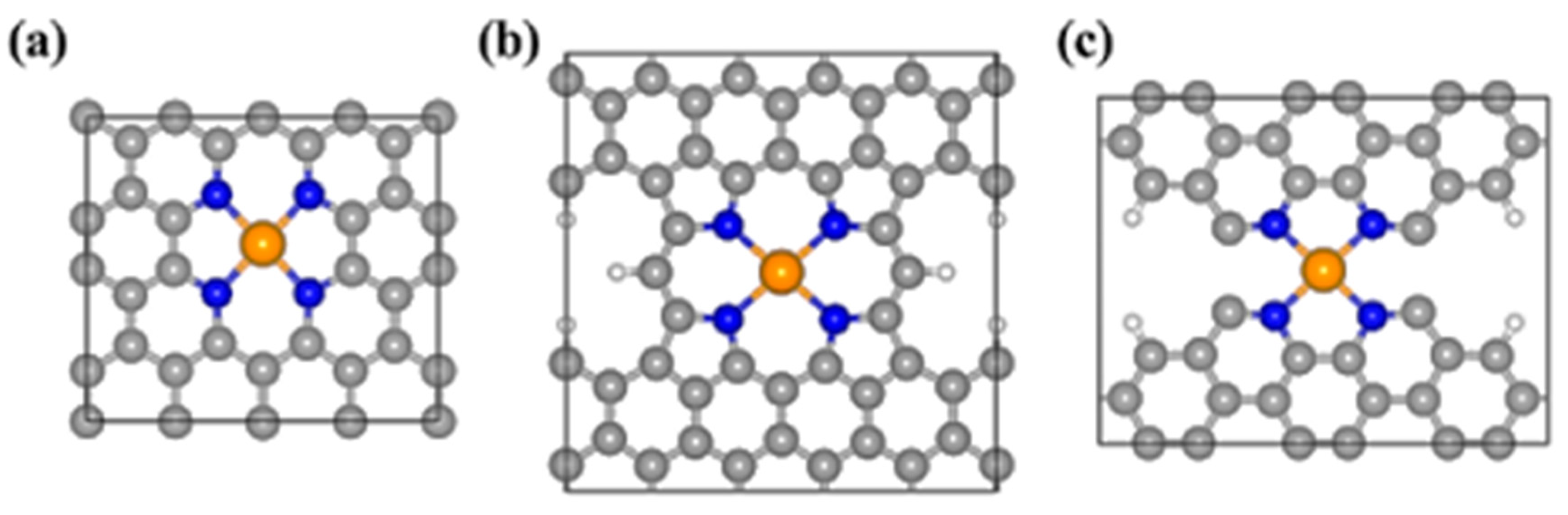
4.2. Single-Atom Catalysts (SACs)
4.3. Nanoclusters
5. Concluding Remarks and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Zhang, J.; Terrones, M.; Park, C.R.; Mukherjee, R.; Monthioux, M.; Koratkar, N.; Kim, Y.S.; Hurt, R.; Frackowiak, E.; Enoki, T.; et al. Carbon science in 2016: Status, challenges and perspectives. Carbon 2016, 98, 708–732. [Google Scholar] [CrossRef]
- Dai, L.; Xue, Y.; Qu, L.; Choi, H.J.; Baek, J.B. Metal-Free Catalysts for Oxygen Reduction Reaction. Chem. Rev. 2015, 115, 4823–4892. [Google Scholar] [CrossRef]
- Chen, D.; Tang, L.; Li, J. Graphene-based materials in electrochemistry. Chem. Soc. Rev. 2010, 39, 3157–3180. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Blaikie, A.; Miller, D.; Alemán, B.J. A fast and sensitive room-temperature graphene nanomechanical bolometer. Nat. Commun. 2019, 10, 4276. [Google Scholar] [CrossRef] [PubMed]
- Bakharev, P.V.; Huang, M.; Saxena, M.; Lee, S.W.; Joo, S.H.; Park, S.O.; Dong, J.; Camacho-Mojica, D.C.; Jin, S.; Kwon, Y.; et al. Chemically induced transformation of chemical vapour deposition grown bilayer graphene into fluorinated single-layer diamond. Nat. Nanotechnol. 2019, 15, 59–66. [Google Scholar] [CrossRef]
- Gao, Y.; Cao, T.; Cellini, F.; Berger, C.; De Heer, W.A.; Tosatti, E.; Riedo, E.; Bongiorno, A. Ultrahard carbon film from epitaxial two-layer graphene. Nat. Nanotechnol. 2018, 13, 133–138. [Google Scholar] [CrossRef]
- Yang, Z.; Nie, H.; Chen, X.; Chen, X.; Huang, S. Recent progress in doped carbon nanomaterials as effective cathode catalysts for fuel cell oxygen reduction reaction. J. Power Sources 2013, 236, 238–249. [Google Scholar] [CrossRef]
- Antolini, E. Graphene as a new carbon support for low-temperature fuel cell catalysts. Appl. Catal. B Environ. 2012, 123–124, 52–68. [Google Scholar] [CrossRef]
- Wang, Y.; Song, W.; Li, M.; Wu, Z. Oxygen reduction reaction mechanisms on heteroatom-doped single-walled carbon nanotube catalysts: Insights from a theoretical study. J. Electrochem. Soc. 2019, 166, F670–F678. [Google Scholar] [CrossRef]
- Antolini, E.; Salgado, J.R.C.; Gonzalez, E.R. The stability of Pt-M (M = first row transition metal) alloy catalysts and its effect on the activity in low temperature fuel cells. A literature review and tests on a Pt-Co catalyst. J. Power Sources 2006, 160, 957–968. [Google Scholar] [CrossRef]
- Muhich, C.L.; Westcott, J.Y.; Morris, T.C.; Weimer, A.W.; Musgrave, C.B. The effect of N and B doping on graphene and the adsorption and migration behavior of Pt atoms. J. Phys. Chem. C 2013, 117, 10523–10535. [Google Scholar] [CrossRef]
- Wu, H.; Wexler, D.; Liu, H. Pt-Ni/C catalysts using different carbon supports for the cathode of the proton exchange membrane fuel cell (PEMFC). Mater. Chem. Phys. 2012, 136, 845–849. [Google Scholar] [CrossRef]
- Hsieh, S.H.; Hsu, M.C.; Liu, W.L.; Chen, W.J. Study of Pt catalyst on graphene and its application to fuel cell. Appl. Surf. Sci. 2013, 277, 223–230. [Google Scholar] [CrossRef]
- Shao, Y.; Yin, G.; Gao, Y. Understanding and approaches for the durability issues of Pt-based catalysts for PEM fuel cell. J. Power Sources 2007, 171, 558–566. [Google Scholar] [CrossRef]
- Holby, E.F.; Sheng, W.; Shao-Horn, Y.; Morgan, D. Pt nanoparticle stability in PEM fuel cells: Influence of particle size distribution and crossover hydrogen. Energy Environ. Sci. 2009, 2, 865–871. [Google Scholar] [CrossRef]
- Speder, J.; Zana, A.; Spanos, I.; Kirkensgaard, J.J.K.; Mortensen, K.; Hanzlik, M.; Arenz, M. Comparative degradation study of carbon supported proton exchange membrane fuel cell electrocatalysts—The influence of the platinum to carbon ratio on the degradation rate. J. Power Sources 2014, 261, 14–22. [Google Scholar] [CrossRef]
- Zhou, Z.M.; Shao, Z.G.; Qin, X.P.; Chen, X.G.; Wei, Z.D.; Yi, B.L. Durability study of Pt-Pd/C as PEMFC cathode catalyst. Int. J. Hydrogen Energy 2010, 35, 1719–1726. [Google Scholar] [CrossRef]
- Dubau, L.; Castanheira, L.; Chatenet, M.; Maillard, F.; Dillet, J.; Maranzana, G.; Abbou, S.; Lottin, O.; De Moor, G.; El Kaddouri, A.; et al. Carbon corrosion induced by membrane failure: The weak link of PEMFC long-term performance. Int. J. Hydrogen Energy 2014, 39, 21902–21914. [Google Scholar] [CrossRef]
- Shao, Y.; Zhang, S.; Wang, C.; Nie, Z.; Liu, J.; Wang, Y.; Lin, Y. Highly durable graphene nanoplatelets supported Pt nanocatalysts for oxygen reduction. J. Power Sources 2010, 195, 4600–4605. [Google Scholar] [CrossRef]
- Pylypenko, S.; Borisevich, A.; More, K.L.; Corpuz, A.R.; Holme, T.; Dameron, A.A.; Olson, T.S.; Dinh, H.N.; Gennett, T.; O’Hayre, R. Nitrogen: Unraveling the secret to stable carbon-supported Pt-alloy electrocatalysts. Energy Environ. Sci. 2013, 6, 2957–2964. [Google Scholar] [CrossRef]
- Wood, K.N.; O’Hayre, R.; Pylypenko, S. Recent progress on nitrogen/carbon structures designed for use in energy and sustainability applications. Energy Environ. Sci. 2014, 7, 1212–1249. [Google Scholar] [CrossRef]
- Paraknowitsch, J.P.; Thomas, A. Doping carbons beyond nitrogen: An overview of advanced heteroatom doped carbons with boron, sulphur and phosphorus for energy applications. Energy Environ. Sci. 2013, 6, 2839–2855. [Google Scholar] [CrossRef]
- Sinthika, S.; Waghmare, U.V.; Thapa, R. Structural and Electronic Descriptors of Catalytic Activity of Graphene-Based Materials: First-Principles Theoretical Analysis. Small 2018, 14, 1703609. [Google Scholar] [CrossRef]
- Deng, D.; Pan, X.; Yu, L.; Cui, Y.; Jiang, Y.; Qi, J.; Li, W.X.; Fu, Q.; Ma, X.; Xue, Q.; et al. Toward N-doped graphene via solvothermal synthesis. Chem. Mater. 2011, 23, 1188–1193. [Google Scholar] [CrossRef]
- Jin, H.; Guo, C.; Liu, X.; Liu, J.; Vasileff, A.; Jiao, Y.; Zheng, Y.; Qiao, S.Z. Emerging Two-Dimensional Nanomaterials for Electrocatalysis. Chem. Rev. 2018, 118, 6337–6408. [Google Scholar] [CrossRef] [PubMed]
- Campisi, S.; Chan-Thaw, C.E.; Villa, A. Understanding heteroatom-mediated metal-support interactions in functionalized carbons: A perspective review. Appl. Sci. 2018, 8, 1159. [Google Scholar] [CrossRef]
- Singh, S.K.; Takeyasu, K.; Nakamura, J. Active Sites and Mechanism of Oxygen Reduction Reaction Electrocatalysis on Nitrogen-Doped Carbon Materials. Adv. Mater. 2019, 31, e1804297. [Google Scholar] [CrossRef]
- Corpuz, A.R.; Olson, T.S.; Joghee, P.; Pylypenko, S.; Dameron, A.A.; Dinh, H.N.; O’Neill, K.J.; Hurst, K.E.; Bender, G.; Gennett, T.; et al. Effect of a nitrogen-doped PtRu/carbon anode catalyst on the durability of a direct methanol fuel cell. J. Power Sources 2012, 217, 142–151. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, L.; Luo, Q.; Hu, Z.; Zhang, W.; Smith, S.; Yang, J. Single Mo1(Cr1) Atom on Nitrogen-Doped Graphene Enables Highly Selective Electroreduction of Nitrogen into Ammonia. ACS Catal. 2019, 9, 3419–3425. [Google Scholar] [CrossRef]
- Hossain, M.D.; Liu, Z.; Zhuang, M.; Yan, X.; Xu, G.L.; Gadre, C.A.; Tyagi, A.; Abidi, I.H.; Sun, C.J.; Wong, H.; et al. Rational Design of Graphene-Supported Single Atom Catalysts for Hydrogen Evolution Reaction. Adv. Energy Mater. 2019, 9, 1803689. [Google Scholar] [CrossRef]
- Wang, L.; Sofer, Z.; Pumera, M. Will Any Crap We Put into Graphene Increase Its Electrocatalytic Effect? ACS Nano 2020, 14, 21–25. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Y.; Zheng, Y.; Davey, K.; Qiao, S.Z. Activity origin and catalyst design principles for electrocatalytic hydrogen evolution on heteroatom-doped graphene. Nat. Energy 2016, 1, 16130. [Google Scholar] [CrossRef]
- Zhao, Z.; Xia, Z. Design Principles for Dual-Element-Doped Carbon Nanomaterials as Efficient Bifunctional Catalysts for Oxygen Reduction and Evolution Reactions. ACS Catal. 2016, 6, 1553–1558. [Google Scholar] [CrossRef]
- Ortiz-Medina, J.; Wang, Z.; Cruz-Silva, R.; Morelos-Gomez, A.; Wang, F.; Yao, X.; Terrones, M.; Endo, M. Defect Engineering and Surface Functionalization of Nanocarbons for Metal-Free Catalysis. Adv. Mater. 2019, 31, e1805717. [Google Scholar] [CrossRef]
- Primbs, M.; Sun, Y.; Roy, A.; Malko, D.; Mehmood, A.; Sougrati, M.T.; Blanchard, P.Y.; Granozzi, G.; Kosmala, T.; Daniel, G.; et al. Establishing reactivity descriptors for platinum group metal (PGM)-free Fe-N-C catalysts for PEM fuel cells. Energy Environ. Sci. 2020, 13, 2480–2500. [Google Scholar] [CrossRef]
- Axet, M.R.; Durand, J.; Gouygou, M.; Serp, P. Surface coordination chemistry on graphene and two-dimensional carbon materials for well-defined single atom supported catalysts. In Advances in Organometallic Chemistry; Academic Press Inc.: Cambridge, MA, USA, 2019; Volume 71, pp. 53–174. [Google Scholar] [CrossRef]
- Gao, Z.; Li, A.; Liu, X.; Ma, C.; Li, X.; Yang, W.; Ding, X. Density functional study of the adsorption of NO on Ni n (n = 1, 2, 3 and 4) clusters doped functionalized graphene support. Appl. Surf. Sci. 2019, 481, 940–950. [Google Scholar] [CrossRef]
- Krishnan, R.; Wu, S.Y.; Chen, H.T. Catalytic CO oxidation on B-doped and BN co-doped penta-graphene: A computational study. Phys. Chem. Chem. Phys. 2018, 20, 26414–26421. [Google Scholar] [CrossRef]
- Workman, M.J.; Dzara, M.; Ngo, C.; Pylypenko, S.; Serov, A.; McKinney, S.; Gordon, J.; Atanassov, P.; Artyushkova, K. Platinum group metal-free electrocatalysts: Effects of synthesis on structure and performance in proton-exchange membrane fuel cell cathodes. J. Power Sources 2017, 348, 30–39. [Google Scholar] [CrossRef]
- Holby, E.F.; Zelenay, P. Linking structure to function: The search for active sites in non-platinum group metal oxygen reduction reaction catalysts. Nano Energy 2016, 29, 54–64. [Google Scholar] [CrossRef]
- Saha, D.; Kienbaum, M.J. Role of oxygen, nitrogen and sulfur functionalities on the surface of nanoporous carbons in CO2 adsorption: A critical review. Microporous Mesoporous Mater. 2019, 287, 29–55. [Google Scholar] [CrossRef]
- Artyushkova, K.; Matanovic, I.; Halevi, B.; Atanassov, P. Oxygen Binding to Active Sites of Fe-N-C ORR Electrocatalysts Observed by Ambient-Pressure XPS. J. Phys. Chem. C 2017, 121, 2836–2843. [Google Scholar] [CrossRef]
- Artyushkova, K.; Kiefer, B.; Halevi, B.; Knop-Gericke, A.; Schlogl, R.; Atanassov, P. Density functional theory calculations of XPS binding energy shift for nitrogen-containing graphene-like structures. Chem. Commun. 2013, 49, 2539–2541. [Google Scholar] [CrossRef] [PubMed]
- Matanovic, I.; Artyushkova, K.; Strand, M.B.; Dzara, M.J.; Pylypenko, S.; Atanassov, P. Core Level Shifts of Hydrogenated Pyridinic and Pyrrolic Nitrogen in the Nitrogen-Containing Graphene-Based Electrocatalysts: In-Plane vs Edge Defects. J. Phys. Chem. C 2016, 120, 29225–29232. [Google Scholar] [CrossRef]
- Ye, R.; Dong, J.; Wang, L.; Mendoza-Cruz, R.; Li, Y.; An, P.F.; Yacamán, M.J.; Yakobson, B.I.; Chen, D.; Tour, J.M. Manganese deception on graphene and implications in catalysis. Carbon 2018, 132, 623–631. [Google Scholar] [CrossRef]
- Wang, T.; Chen, Z.X.; Chen, Y.G.; Yang, L.J.; Yang, X.D.; Ye, J.Y.; Xia, H.P.; Zhou, Z.Y.; Sun, S.G. Identifying the Active Site of N-Doped Graphene for Oxygen Reduction by Selective Chemical Modification. ACS Energy Lett. 2018, 3, 986–991. [Google Scholar] [CrossRef]
- Zhou, Y.; Neyerlin, K.; Olson, T.S.; Pylypenko, S.; Bult, J.; Dinh, H.N.; Gennett, T.; Shao, Z.; O’Hayre, R. Enhancement of Pt and Pt-alloy fuel cell catalyst activity and durability via nitrogen-modified carbon supports. Energy Environ. Sci. 2010, 3, 1437–1446. [Google Scholar] [CrossRef]
- Chaban, V.V.; Prezhdo, O. V Nitrogen–Nitrogen Bonds Undermine Stability of N-Doped Graphene. J. Am. Chem. Soc 2015, 137, 11688–11694. [Google Scholar] [CrossRef]
- Holme, T.; Zhou, Y.; Pasquarelli, R.; O’Hayre, R. First principles study of doped carbon supports for enhanced platinum catalysts. Phys. Chem. Chem. Phys. 2010, 12, 9461–9468. [Google Scholar] [CrossRef]
- Kwak, D.; Khetan, A.; Noh, S.; Pitsch, H.; Han, B. First principles study of morphology, doping level, and water solvation effects on the catalytic mechanism of nitrogen-doped graphene in the oxygen reduction reaction. ChemCatChem 2014, 6, 2662–2670. [Google Scholar] [CrossRef]
- Herath, D.; Dinadayalane, T. Computational investigation of double nitrogen doping on graphene. J. Mol. Model. 2018, 24, 26. [Google Scholar] [CrossRef] [PubMed]
- Jeon, I.Y.; Choi, H.J.; Ju, M.J.; Choi, I.T.; Lim, K.; Ko, J.; Kim, H.K.; Kim, J.C.; Lee, J.J.; Shin, D.; et al. Direct nitrogen fixation at the edges of graphene nanoplatelets as efficient electrocatalysts for energy conversion. Sci. Rep. 2013, 3, srep02260. [Google Scholar] [CrossRef] [PubMed]
- Schiros, T.; Nordlund, D.; Pálová, L.; Prezzi, D.; Zhao, L.; Kim, K.S.; Wurstbauer, U.; Gutiérrez, C.; Delongchamp, D.; Jaye, C.; et al. Connecting dopant bond type with electronic structure in n-doped graphene. Nano Lett. 2012, 12, 4025–4031. [Google Scholar] [CrossRef]
- Matsuyama, H.; Akaishi, A.; Nakamura, J. Effect of water on the manifestation of the reaction selectivity of nitrogen-doped graphene nanoclusters toward oxygen reduction reaction. ACS Omega 2019, 4, 3832–3838. [Google Scholar] [CrossRef] [PubMed]
- Gadipelli, S.; Guo, Z.X. Graphene-based materials: Synthesis and gas sorption, storage and separation. Prog. Mater. Sci. 2015, 69, 1–60. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, W.; Li, C.; Li, W.; Dai, X. Geometric stability, electronic structure, and intercalation mechanism of Co adatom anchors on graphene sheets. J. Phys. Condens. Matter 2015, 27, 255009. [Google Scholar] [CrossRef]
- Vinayan, B.P. Heteroatom-Doped Graphene-Based Hybrid Materials for Hydrogen Energy Conversion. In Recent Advances in Graphene Research; InTech: London, UK, 2016; pp. 177–194. ISBN 978-953-307-695-9. [Google Scholar]
- Dong, Y.; Gahl, M.T.; Zhang, C.; Lin, J. Computational study of precision nitrogen doping on graphene nanoribbon edges. Nanotechnology 2017, 28, 505602. [Google Scholar] [CrossRef]
- Peraça, C.S.T.; Nagurniak, G.R.; Orenha, R.P.; Parreira, R.L.T.; Piotrowski, M.J. A theoretical indicator of transition-metal nanoclusters applied in the carbon nanotube nucleation process: A DFT study. Dalt. Trans. 2020, 49, 492–503. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Shen, P.; Chen, Z. Spin gapless semiconductor-metal-half-metal properties in nitrogen-doped zigzag graphene nanoribbons. ACS Nano 2009, 3, 1952–1958. [Google Scholar] [CrossRef]
- Guo, J.; Huo, J.; Liu, Y.; Wu, W.; Wang, Y.; Wu, M.; Liu, H.; Wang, G. Nitrogen-Doped Porous Carbon Supported Nonprecious Metal Single-Atom Electrocatalysts: From Synthesis to Application. Small Methods 2019, 3, 1900159. [Google Scholar] [CrossRef]
- He, L.; Weniger, F.; Neumann, H.; Beller, M. Synthesis, Characterization, and Application of Metal Nanoparticles Supported on Nitrogen-Doped Carbon: Catalysis beyond Electrochemistry. Angew. Chemie Int. Ed. 2016, 55, 12582–12594. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Mao, S.; Li, M.; Chen, Y.; Wang, Y. Metal/Porous Carbon Composites for Heterogeneous Catalysis: Old Catalysts with Improved Performance Promoted by N-Doping. ACS Catal. 2017, 7, 8090–8112. [Google Scholar] [CrossRef]
- Salinas-Torres, D.; Navlani-García, M.; Mori, K.; Kuwahara, Y.; Yamashita, H. Nitrogen-doped carbon materials as a promising platform toward the efficient catalysis for hydrogen generation. Appl. Catal. A Gen. 2019, 571, 25–41. [Google Scholar] [CrossRef]
- Ma, R.; Lin, G.; Zhou, Y.; Liu, Q.; Zhang, T.; Shan, G.; Yang, M.; Wang, J. A review of oxygen reduction mechanisms for metal-free carbon-based electrocatalysts. Npj Comput. Mater. 2019, 5, 78. [Google Scholar] [CrossRef]
- Wang, H.; Maiyalagan, T.; Wang, X. Review on recent progress in nitrogen-doped graphene: Synthesis, characterization, and its potential applications. ACS Catal. 2012, 2, 781–794. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Bligaard, T.; Rossmeisl, J.; Christensen, C.H. Towards the computational design of solid catalysts. Nat. Chem. 2009, 1, 37–46. [Google Scholar] [CrossRef]
- Kratzer, P.; Neugebauer, J. The basics of electronic structure theory for periodic systems. Front. Chem. 2019, 7, 106. [Google Scholar] [CrossRef]
- BASIUK, V.A. Electron Smearing in DFT Calculations: A Case Study of Doxorubicin Interaction with Single-Walled Carbon Nanotubes. Int. J. Quantum Chem. 2011, 111, 4020–4029. [Google Scholar] [CrossRef]
- Reda, M.; Hansen, H.A.; Vegge, T. DFT study of stabilization effects on N-doped graphene for ORR catalysis. Catal. Today 2018, 312, 118–125. [Google Scholar] [CrossRef]
- Sui, S.; Wang, X.; Zhou, X.; Su, Y.; Riffat, S.; Liu, C. jun A comprehensive review of Pt electrocatalysts for the oxygen reduction reaction: Nanostructure, activity, mechanism and carbon support in PEM fuel cells. J. Mater. Chem. A 2017, 5, 1808–1825. [Google Scholar] [CrossRef]
- Xu, C.; Yang, W.; Ma, G.; Che, S.; Li, Y.; Jia, Y.; Chen, N.; Huang, G.; Li, Y. Edge-Nitrogen Enriched Porous Carbon Nanosheets Anodes with Enlarged Interlayer Distance for Fast harging Sodium-Ion Batteries. Small 2022, 18, 2204375. [Google Scholar] [CrossRef]
- Nakada, K.; Ishii, A. Migration of adatom adsorption on graphene using DFT calculation. Solid State Commun. 2011, 151, 13–16. [Google Scholar] [CrossRef]
- Li, X.F.; Li, Q.K.; Cheng, J.; Liu, L.; Yan, Q.; Wu, Y.; Zhang, X.H.; Wang, Z.Y.; Qiu, Q.; Luo, Y. Conversion of Dinitrogen to Ammonia by FeN3-Embedded Graphene. J. Am. Chem. Soc. 2016, 138, 8706–8709. [Google Scholar] [CrossRef] [PubMed]
- Artyushkova, K.; Serov, A.; Rojas-Carbonell, S.; Atanassov, P. Chemistry of Multitudinous Active Sites for Oxygen Reduction Reaction in Transition Metal-Nitrogen-Carbon Electrocatalysts. J. Phys. Chem. C 2015, 119, 25917–25928. [Google Scholar] [CrossRef]
- She, Y.; Chen, J.; Zhang, C.; Lu, Z.; Ni, M.; Sit, P.H.L.; Leung, M.K.H. Nitrogen-doped graphene derived from ionic liquid as metal-free catalyst for oxygen reduction reaction and its mechanisms. Appl. Energy 2018, 225, 513–521. [Google Scholar] [CrossRef]
- Yang, M.; Wang, L.; Li, M.; Hou, T.; Li, Y. Structural stability and O2 dissociation on nitrogen-doped graphene with transition metal atoms embedded: A first-principles study. AIP Adv. 2015, 5, 067136. [Google Scholar] [CrossRef]
- Lai, L.; Potts, J.R.; Zhan, D.; Wang, L.; Poh, C.K.; Tang, C.; Gong, H.; Shen, Z.; Lin, J.; Ruoff, R.S. Exploration of the active center structure of nitrogen-doped graphene-based catalysts for oxygen reduction reaction. Energy Environ. Sci. 2012, 5, 7936–7942. [Google Scholar] [CrossRef]
- Tai, S.H.; Chang, B.K. Effect of nitrogen-doping configuration in graphene on the oxygen reduction reaction. RSC Adv. 2019, 9, 6035–6041. [Google Scholar] [CrossRef]
- Li, K.; Li, N.; Yan, N.; Wang, T.; Zhang, Y.; Song, Q.; Li, H. Adsorption of small hydrocarbons on pristine, N-doped and vacancy graphene by DFT study. Appl. Surf. Sci. 2020, 515, 146028. [Google Scholar] [CrossRef]
- Wei, Q.; Tong, X.; Zhang, G.; Qiao, J.; Gong, Q.; Sun, S. Nitrogen-doped carbon nanotube and graphene materials for oxygen reduction reactions. Catalysts 2015, 5, 1574–1602. [Google Scholar] [CrossRef]
- Yan, P.; Liu, J.; Yuan, S.; Liu, Y.; Cen, W.; Chen, Y. The promotion effects of graphitic and pyridinic N combinational doping on graphene for ORR. Appl. Surf. Sci. 2018, 445, 398–403. [Google Scholar] [CrossRef]
- Groves, M.N.; Chan, A.S.W.; Malardier-Jugroot, C.; Jugroot, M. Improving platinum catalyst binding energy to graphene through nitrogen doping. Chem. Phys. Lett. 2009, 481, 214–219. [Google Scholar] [CrossRef]
- Inagaki, M.; Toyoda, M.; Soneda, Y.; Morishita, T. Nitrogen-doped carbon materials. Carbon 2018, 132, 104–140. [Google Scholar] [CrossRef]
- Arrigo, R.; Schuster, M.E.; Xie, Z.; Yi, Y.; Wowsnick, G.; Sun, L.L.; Hermann, K.E.; Friedrich, M.; Kast, P.; Hävecker, M.; et al. Nature of the N-Pd interaction in nitrogen-doped carbon nanotube catalysts. ACS Catal. 2015, 5, 2740–2753. [Google Scholar] [CrossRef]
- Noffke, B.W.; Li, Q.; Raghavachari, K.; Li, L.S. A Model for the pH-Dependent Selectivity of the Oxygen Reduction Reaction Electrocatalyzed by N-Doped Graphitic Carbon. J. Am. Chem. Soc. 2016, 138, 13923–13929. [Google Scholar] [CrossRef]
- Zhang, L.; Niu, J.; Dai, L.; Xia, Z. Effect of microstructure of nitrogen-doped graphene on oxygen reduction activity in fuel cells. Langmuir 2012, 28, 7542–7550. [Google Scholar] [CrossRef]
- Matanovic, I.; Artyushkova, K.; Atanassov, P. Understanding PGM-free catalysts by linking density functional theory calculations and structural analysis: Perspectives and challenges. Curr. Opin. Electrochem. 2018, 9, 137–144. [Google Scholar] [CrossRef]
- Owens, F.J. Electronic and magnetic properties of armchair and zigzag graphene nanoribbons. J. Chem. Phys. 2008, 128, 194701. [Google Scholar] [CrossRef]
- Sidik, R.A.; Anderson, A.B.; Subramanian, N.P.; Kumaraguru, S.P.; Popov, B.N. O2 reduction on graphite and nitrogen-doped graphite: Experiment and theory. J. Phys. Chem. B 2006, 110, 1787–1793. [Google Scholar] [CrossRef]
- Jiao, Y.; Zheng, Y.; Jaroniec, M.; Qiao, S.Z. Origin of the electrocatalytic oxygen reduction activity of graphene-based catalysts: A roadmap to achieve the best performance. J. Am. Chem. Soc. 2014, 136, 4394–4403. [Google Scholar] [CrossRef]
- Kim, J.; Lee, N.; Min, Y.H.; Noh, S.; Kim, N.K.; Jung, S.; Joo, M.; Yamada, Y. Distinguishing Zigzag and Armchair Edges on Graphene Nanoribbons by X-ray Photoelectron and Raman Spectroscopies. ACS Omega 2018, 3, 17789–17796. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Da Chai, J.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Garza, A.J.; Scuseria, G.E. Predicting Band Gaps with Hybrid Density Functionals. J. Phys. Chem. Lett. 2016, 7, 4165–4170. [Google Scholar] [CrossRef]
- Calle-Vallejo, F.; Martínez, J.I.; Rossmeisl, J. Density functional studies of functionalized graphitic materials with late transition metals for oxygen reduction reactions. Phys. Chem. Chem. Phys. 2011, 13, 15639–15643. [Google Scholar] [CrossRef]
- Yu, L.; Pan, X.; Cao, X.; Hu, P.; Bao, X. Oxygen reduction reaction mechanism on nitrogen-doped graphene: A density functional theory study. J. Catal. 2011, 282, 183–190. [Google Scholar] [CrossRef]
- Glukhova, O.; Slepchenkov, M. Influence of the curvature of deformed graphene nanoribbons on their electronic and adsorptive properties: Theoretical investigation based on the analysis of the local stress field for an atomic grid. Nanoscale 2012, 4, 3335–3344. [Google Scholar] [CrossRef]
- Ly, Q.; Merinov, B.V.; Xiao, H.; Goddard, W.A.; Yu, T.H. The oxygen reduction reaction on graphene from quantum mechanics: Comparing armchair and zigzag carbon edges. J. Phys. Chem. C 2017, 121, 24408–24417. [Google Scholar] [CrossRef]
- Orlof, A.; Ruseckas, J.; Zozoulenko, I.V. Effect of zigzag and armchair edges on the electronic transport in single-layer and bilayer graphene nanoribbons with defects. Phys. Rev. B-Condens. Matter Mater. Phys. 2013, 88, 125409. [Google Scholar] [CrossRef]
- Lv, Q.; Si, W.; He, J.; Sun, L.; Zhang, C.; Wang, N.; Yang, Z.; Li, X.; Wang, X.; Deng, W.; et al. Selectively nitrogen-doped carbon materials as superior metal-free catalysts for oxygen reduction. Nat. Commun. 2018, 9, 3376. [Google Scholar] [CrossRef] [PubMed]
- Ni, S.; Li, Z.; Yang, J. Oxygen molecule dissociation on carbon nanostructures with different types of nitrogen doping. Nanoscale 2012, 4, 1184–1189. [Google Scholar] [CrossRef] [PubMed]
- An, W.; Turner, C.H. Chemisorption of transition-metal atoms on boron- And nitrogen-doped carbon nanotubes: Energetics and geometric and electronic structures. J. Phys. Chem. C 2009, 113, 7069–7078. [Google Scholar] [CrossRef]
- Xie, X.; He, C.; Li, B.; He, Y.; Cullen, D.A.; Wegener, E.C.; Kropf, A.J.; Martinez, U.; Cheng, Y.; Engelhard, M.H.; et al. Performance enhancement and degradation mechanism identification of a single-atom Co–N–C catalyst for proton exchange membrane fuel cells. Nat. Catal. 2020, 3, 1044–1054. [Google Scholar] [CrossRef]
- Chen, M.; Li, X.; Yang, F.; Li, B.; Stracensky, T.; Karakalos, S.; Mukerjee, S.; Jia, Q.; Su, D.; Wang, G.; et al. Atomically Dispersed MnN4Catalysts via Environmentally Benign Aqueous Synthesis for Oxygen Reduction: Mechanistic Understanding of Activity and Stability Improvements. ACS Catal. 2020, 10, 10523–10534. [Google Scholar] [CrossRef]
- Holby, E.F.; Wang, G.; Zelenay, P. Acid stability and demetalation of PGM-free ORR electrocatalyst structures from density functional theory: A model for “single-atom catalyst” dissolution. ACS Catal. 2020, 10, 14527–14539. [Google Scholar] [CrossRef]
- Holby, E.F.; Wu, G.; Zelenay, P.; Taylor, C.D. Structure of Fe-Nx-C defects in oxygen reduction reaction catalysts from first-principles modeling. J. Phys. Chem. C 2014, 118, 14388–14393. [Google Scholar] [CrossRef]
- Martinez, U.; Komini Babu, S.; Holby, E.F.; Zelenay, P. Durability challenges and perspective in the development of PGM-free electrocatalysts for the oxygen reduction reaction. Curr. Opin. Electrochem. 2018, 9, 224–232. [Google Scholar] [CrossRef]
- Yang, X.F.; Wang, A.; Qiao, B.; Li, J.; Liu, J.; Zhang, T. Single-atom catalysts: A new frontier in heterogeneous catalysis. Acc. Chem. Res. 2013, 46, 1740–1748. [Google Scholar] [CrossRef]
- Zhang, C.; Sha, J.; Fei, H.; Liu, M.; Yazdi, S.; Zhang, J.; Zhong, Q.; Zou, X.; Zhao, N.; Yu, H.; et al. Single-Atomic Ruthenium Catalytic Sites on Nitrogen-Doped Graphene for Oxygen Reduction Reaction in Acidic Medium. ACS Nano 2017, 11, 6930–6941. [Google Scholar] [CrossRef]
- Yang, W.; Gao, Z.; Liu, X.; Ma, C.; Ding, X.; Yan, W. Directly catalytic reduction of NO without NH3 by single atom iron catalyst: A DFT calculation. Fuel 2019, 243, 262–270. [Google Scholar] [CrossRef]
- Jung, E.; Shin, H.; Lee, B.H.; Efremov, V.; Lee, S.; Lee, H.S.; Kim, J.; Hooch Antink, W.; Park, S.; Lee, K.S.; et al. Atomic-level tuning of Co–N–C catalyst for high-performance electrochemical H2O2 production. Nat. Mater. 2020, 19, 436–442. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Cheng, D.; Cao, D.; Zeng, X.C. A universal principle for a rational design of single-atom electrocatalysts. Nat. Catal. 2018, 1, 339–348. [Google Scholar] [CrossRef]
- Sun, X.; Li, K.; Yin, C.; Wang, Y.; Jiao, M.; He, F.; Bai, X.; Tang, H.; Wu, Z. Dual-site oxygen reduction reaction mechanism on CoN4 and CoN2 embedded graphene: Theoretical insights. Carbon 2016, 108, 541–550. [Google Scholar] [CrossRef]
- Liu, K.; Qiao, Z.; Hwang, S.; Liu, Z.; Zhang, H.; Su, D.; Xu, H.; Wu, G.; Wang, G. Mn- and N- doped carbon as promising catalysts for oxygen reduction reaction: Theoretical prediction and experimental validation. Appl. Catal. B Environ. 2019, 243, 195–203. [Google Scholar] [CrossRef]
- Zhu, X.; Yan, J.; Gu, M.; Liu, T.; Dai, Y.; Gu, Y.; Li, Y. Activity Origin and Design Principles for Oxygen Reduction on Dual-Metal-Site Catalysts: A Combined Density Functional Theory and Machine Learning Study. J. Phys. Chem. Lett. 2019, 10, 7760–7766. [Google Scholar] [CrossRef]
- Liu, K.; Wu, G.; Wang, G. Role of Local Carbon Structure Surrounding FeN4 Sites in Boosting the Catalytic Activity for Oxygen Reduction. J. Phys. Chem. C 2017, 121, 11319–11324. [Google Scholar] [CrossRef]
- Bulushev, D.A.; Zacharska, M.; Shlyakhova, E.V.; Chuvilin, A.L.; Guo, Y.; Beloshapkin, S.; Okotrub, A.V.; Bulusheva, L.G. Single Isolated Pd2+ Cations Supported on N-Doped Carbon as Active Sites for Hydrogen Production from Formic Acid Decomposition. ACS Catal. 2016, 6, 681–691. [Google Scholar] [CrossRef]
- Acharya, C.K.; Sullivan, D.I.; Turner, C.H. Characterizing the interaction of Pt and PtRu clusters with boron-doped, nitrogen-doped, and activated carbon: Density functional theory calculations and parameterization. J. Phys. Chem. C 2008, 112, 13607–13622. [Google Scholar] [CrossRef]
- Kim, G.; Jhi, S.H. Carbon monoxide-tolerant platinum nanoparticle catalysts on defect-engineered graphene. ACS Nano 2011, 5, 805–810. [Google Scholar] [CrossRef]
- Rao, R.G.; Blume, R.; Hansen, T.W.; Fuentes, E.; Dreyer, K.; Moldovan, S.; Ersen, O.; Hibbitts, D.D.; Chabal, Y.J.; Schlögl, R.; et al. Interfacial charge distributions in carbon-supported palladium catalysts. Nat. Commun. 2017, 8, 340. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Yang, W.; Jiang, B.; Wang, C.; Zhang, C.; Wu, N.; Zhang, C.; Du, S.; Li, S.; Bai, H.; et al. Engineering of the Core-Shell Boron Nitride@Nitrogen-Doped Carbon Heterogeneous Interface for Efficient Heat Dissipation and Electromagnetic Wave Absorption. ACS Appl. Mater. Interfaces 2023, 15, 7578–7591. [Google Scholar] [CrossRef] [PubMed]
- Kronberg, R.; Lappalainen, H.; Laasonen, K. Hydrogen Adsorption on Defective Nitrogen-Doped Carbon Nanotubes Explained via Machine Learning Augmented DFT Calculations and Game-Theoretic Feature Attributions. J. Phys. Chem. C 2021, 125, 15918–15933. [Google Scholar] [CrossRef]
- Baghban, A.; Habibzadeh, S.; Zokaee Ashtiani, F. On the evaluation of hydrogen evolution reaction performance of metal-nitrogen-doped carbon electrocatalysts using machine learning technique. Sci. Rep. 2021, 11, 21911. [Google Scholar] [CrossRef]
- Nguyen, V.T. Theoretical Probing into the Stabilizing Interplay Between Metal Catalysts and Nitrogen-Doped Carbon Supports. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2022. [Google Scholar]

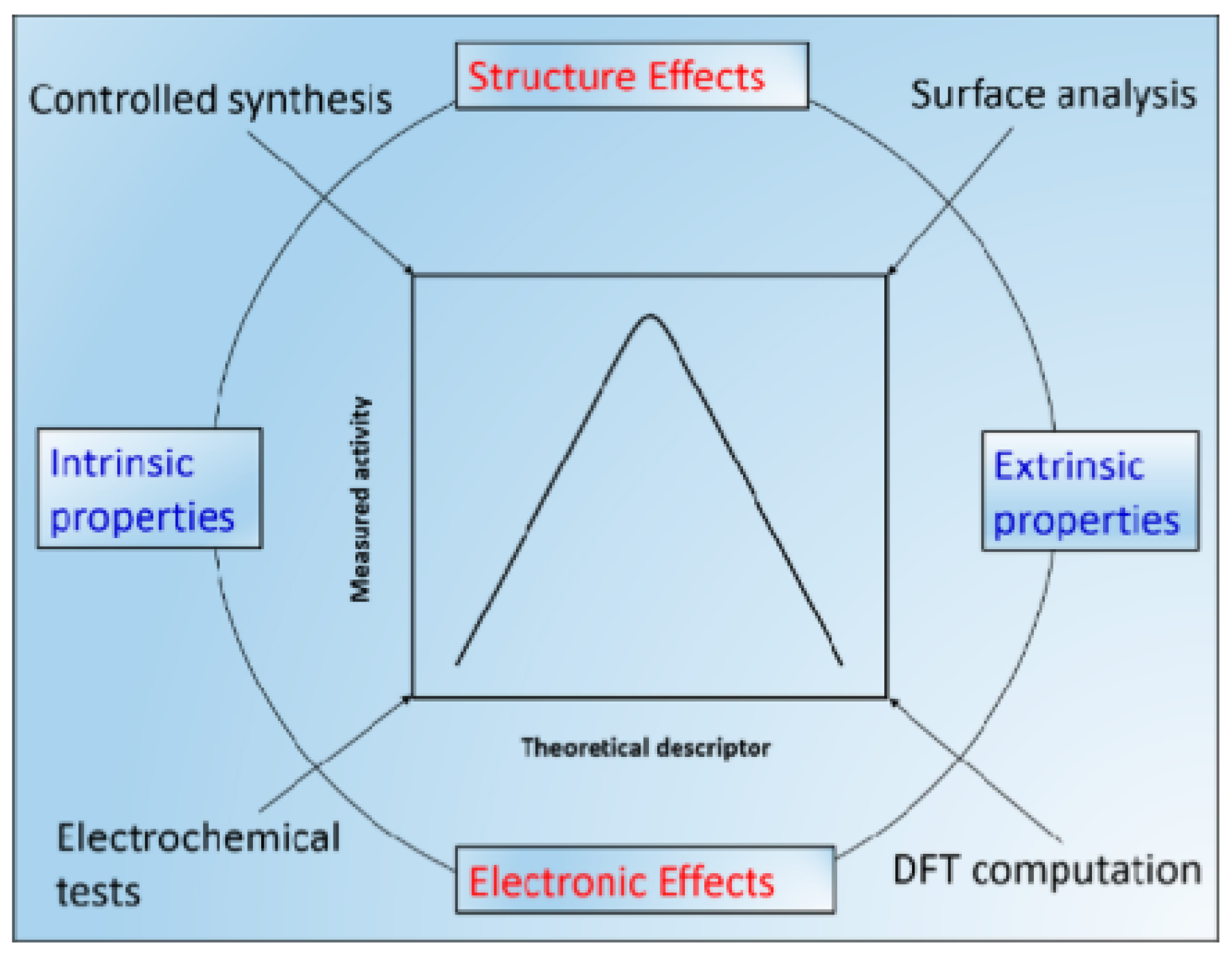
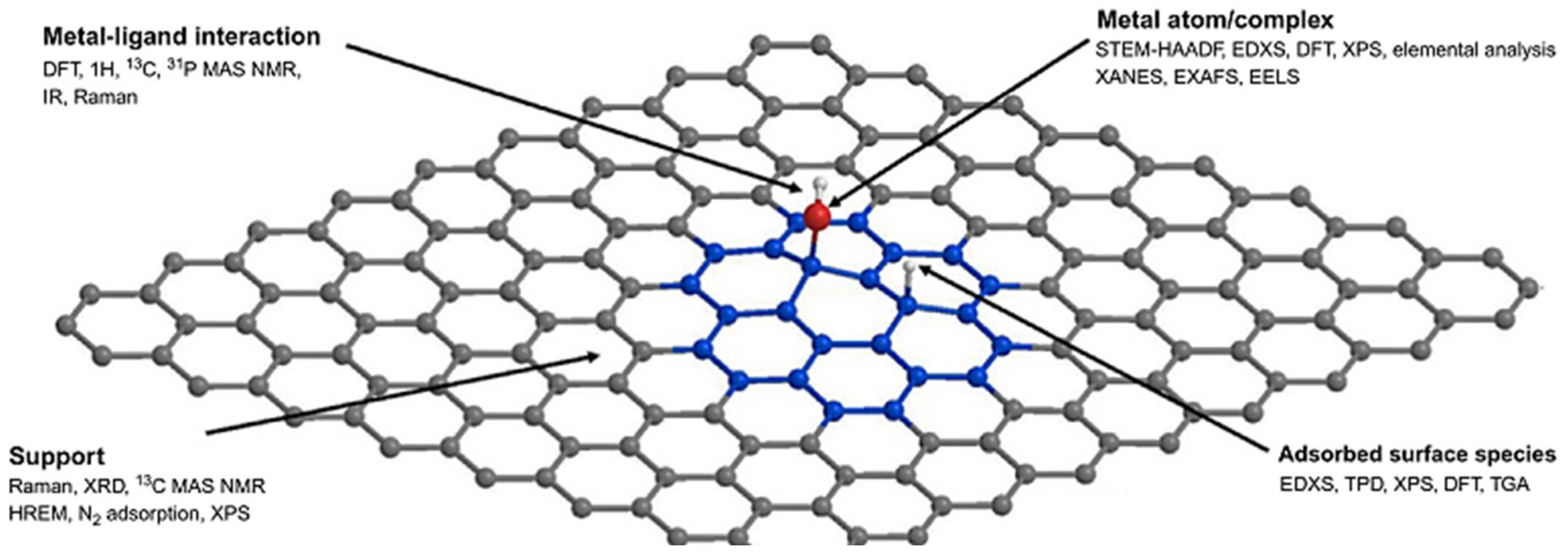


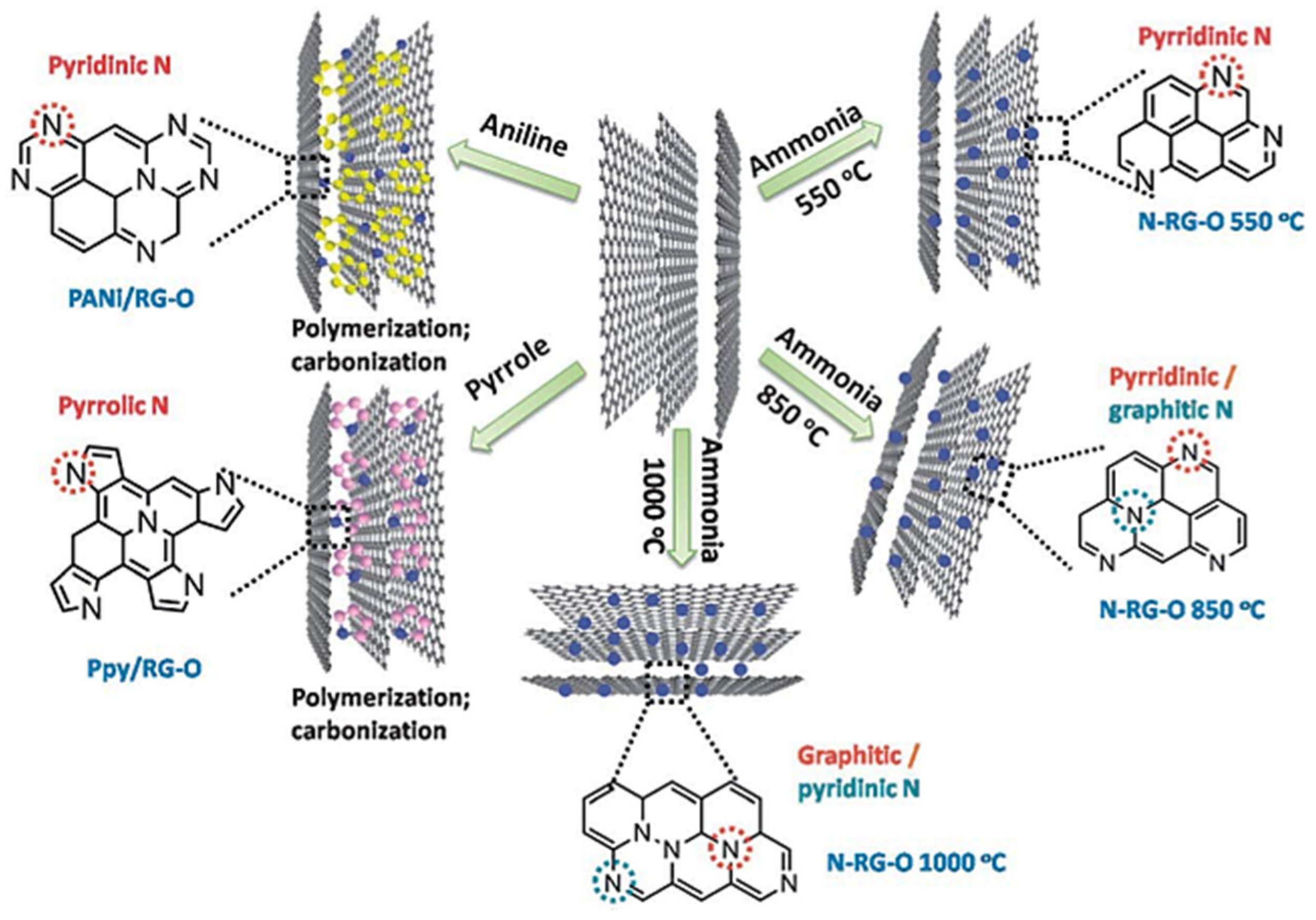
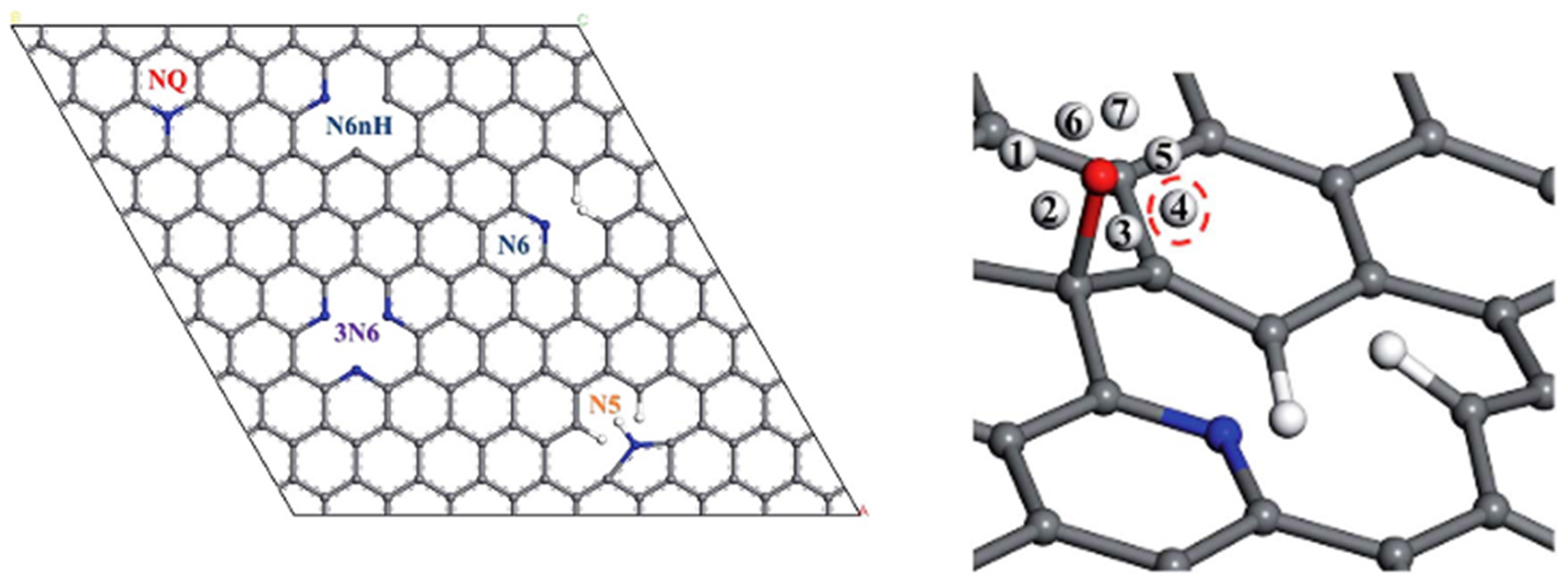




| Theoretical Metrics | Formulation | Physical Relevance |
|---|---|---|
| Adsorption Energy | The difference in free energy between the support and catalyst and the support–catalyst complex; orbital overlap can also be used to gauge the nature of the interaction | Strength of initial durability |
| Ripening Energy | The difference in free energy between various sizes and conformations of catalysts on top of the support | Catalyst growth & dispersion |
| Migration Energy | The energy required to overcome the potential energy barriers of the catalyst moving over the support surface | Catalyst aggregation & dissolution |
| Electrochemistry | The energetic pathways of the proceeding chemical reactions that are directed by the support–catalyst complex | Reactivity |
| Models | Advantages | Limitations |
|---|---|---|
| Truncated |
|
|
| PBC |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, V.; Vyas, S. Evaluating Theoretical Approaches to Nitrogen-Doped Carbon Supports. Catalysts 2025, 15, 473. https://doi.org/10.3390/catal15050473
Nguyen V, Vyas S. Evaluating Theoretical Approaches to Nitrogen-Doped Carbon Supports. Catalysts. 2025; 15(5):473. https://doi.org/10.3390/catal15050473
Chicago/Turabian StyleNguyen, Vu, and Shubham Vyas. 2025. "Evaluating Theoretical Approaches to Nitrogen-Doped Carbon Supports" Catalysts 15, no. 5: 473. https://doi.org/10.3390/catal15050473
APA StyleNguyen, V., & Vyas, S. (2025). Evaluating Theoretical Approaches to Nitrogen-Doped Carbon Supports. Catalysts, 15(5), 473. https://doi.org/10.3390/catal15050473







