Protein Engineering for Industrial Biocatalysis: Principles, Approaches, and Lessons from Engineered PETases
Abstract
1. Introduction
2. Fundamental Principles for Engineering Protein Activity, Specificity, and Stability
2.1. Dependence on Temperature
2.1.1. Optimum Temperature ()
2.1.2. Melting Temperature ()
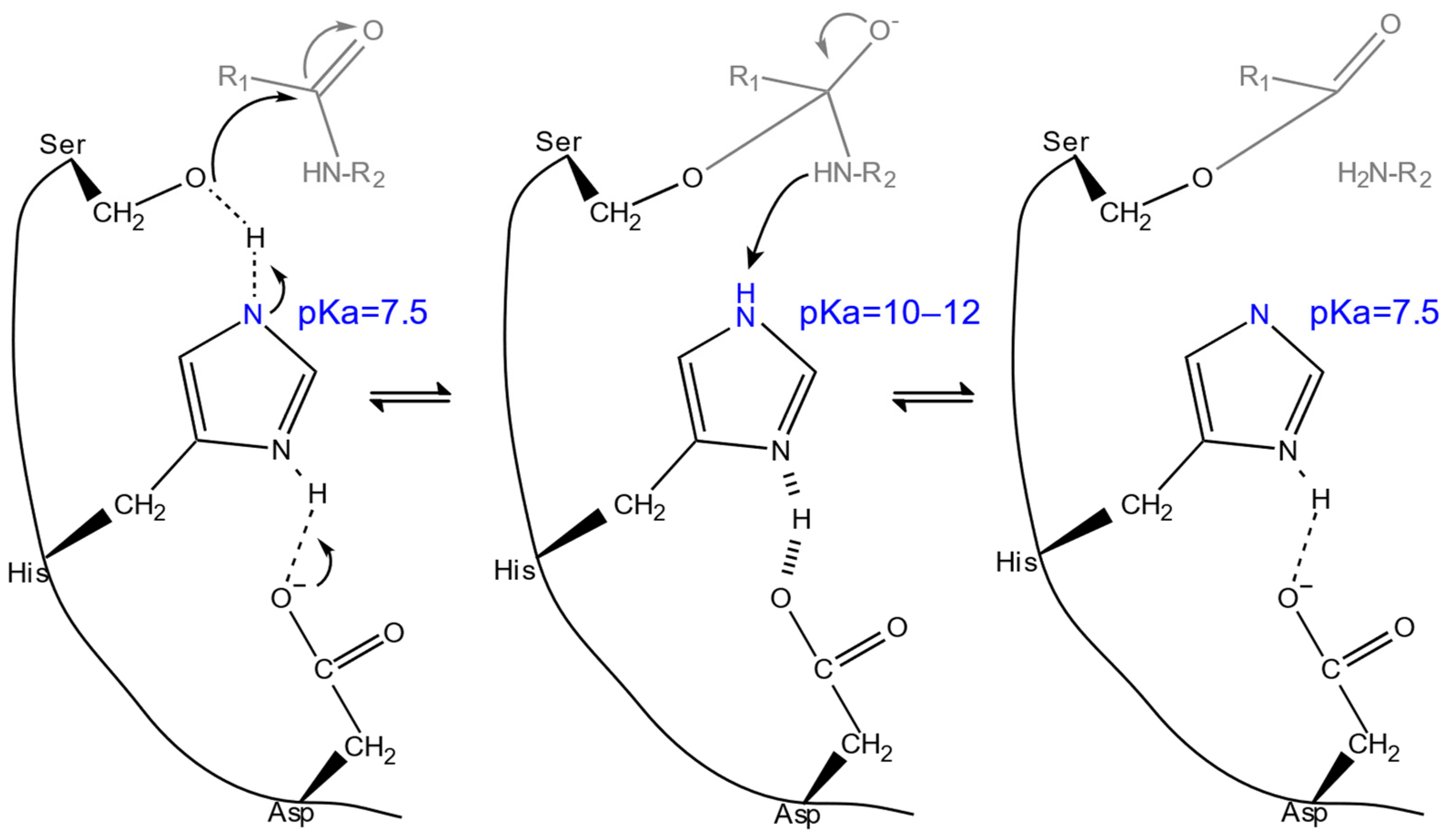
2.2. Dependence on pH
2.2.1. Optimum pH ()
2.2.2. pH Stability
2.3. Structure-Function Relationships
2.3.1. Substrate Affinity and Specificity
2.3.2. Stabilizing Mutations
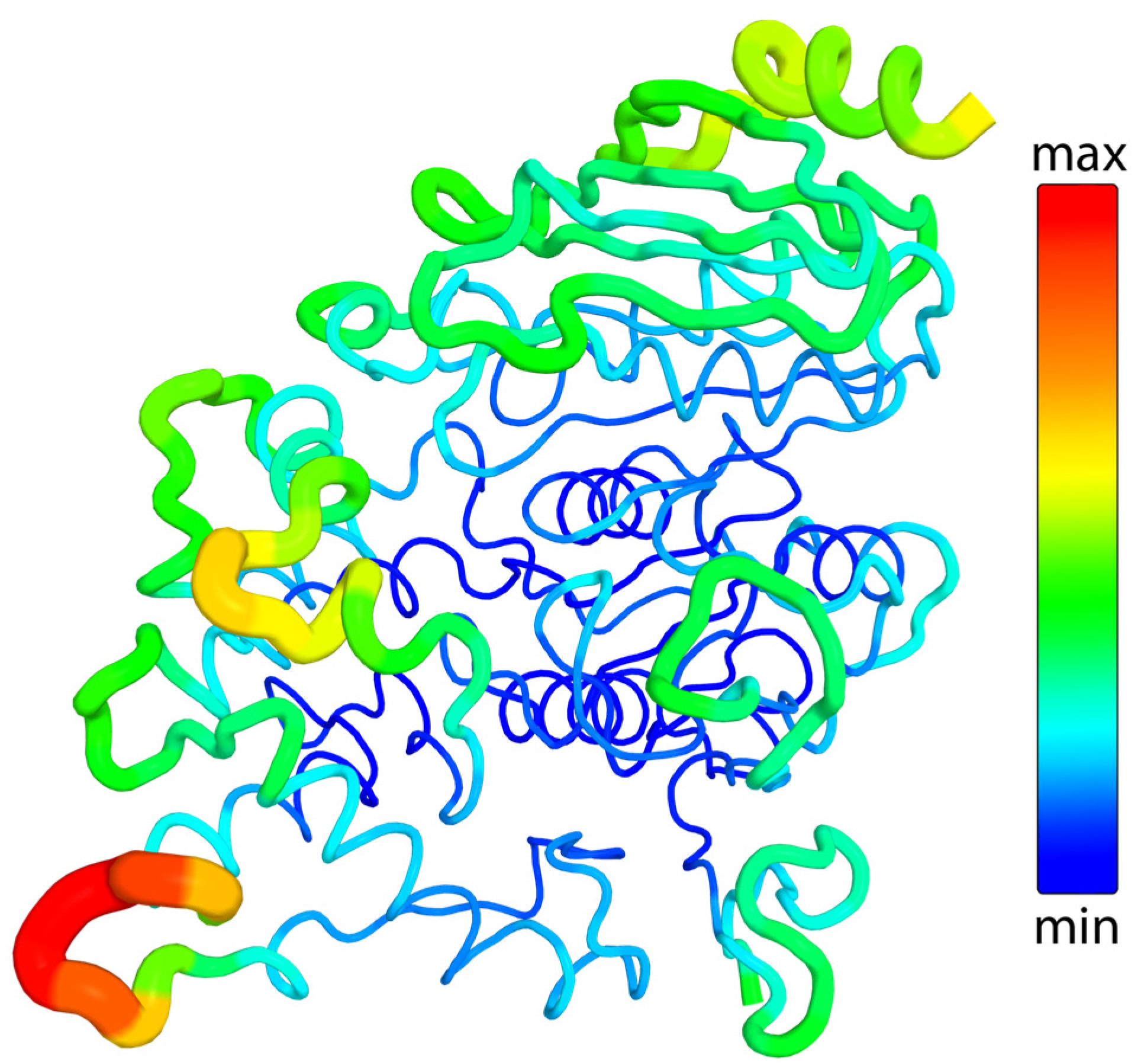
2.3.3. Flexibility
2.3.4. Activity-Stability Trade-Off
2.3.5. Structure-Function Engineering Insights
| Modification | Mechanism | Primary Effects | Engineering Approach | Refs. |
|---|---|---|---|---|
| Single-point mutations | Selective single point mutations with energetically favorable residues (minimizing ), residues important for substrate binding (surface electrostatics/hydrophobicity) or enhancing activity. | activity ↑↓** affinity ↑↓ stability ↑↓ | RD, SRD, DE, ML * | [4,12,21,106,111] |
| Disulfide bridges | Covalent linkage of cysteine residues to rigidify the protein backbone and constrain conformational freedom. | stability ↑ activity ↓ (typically) | RD, ML | [4,12,21,112] |
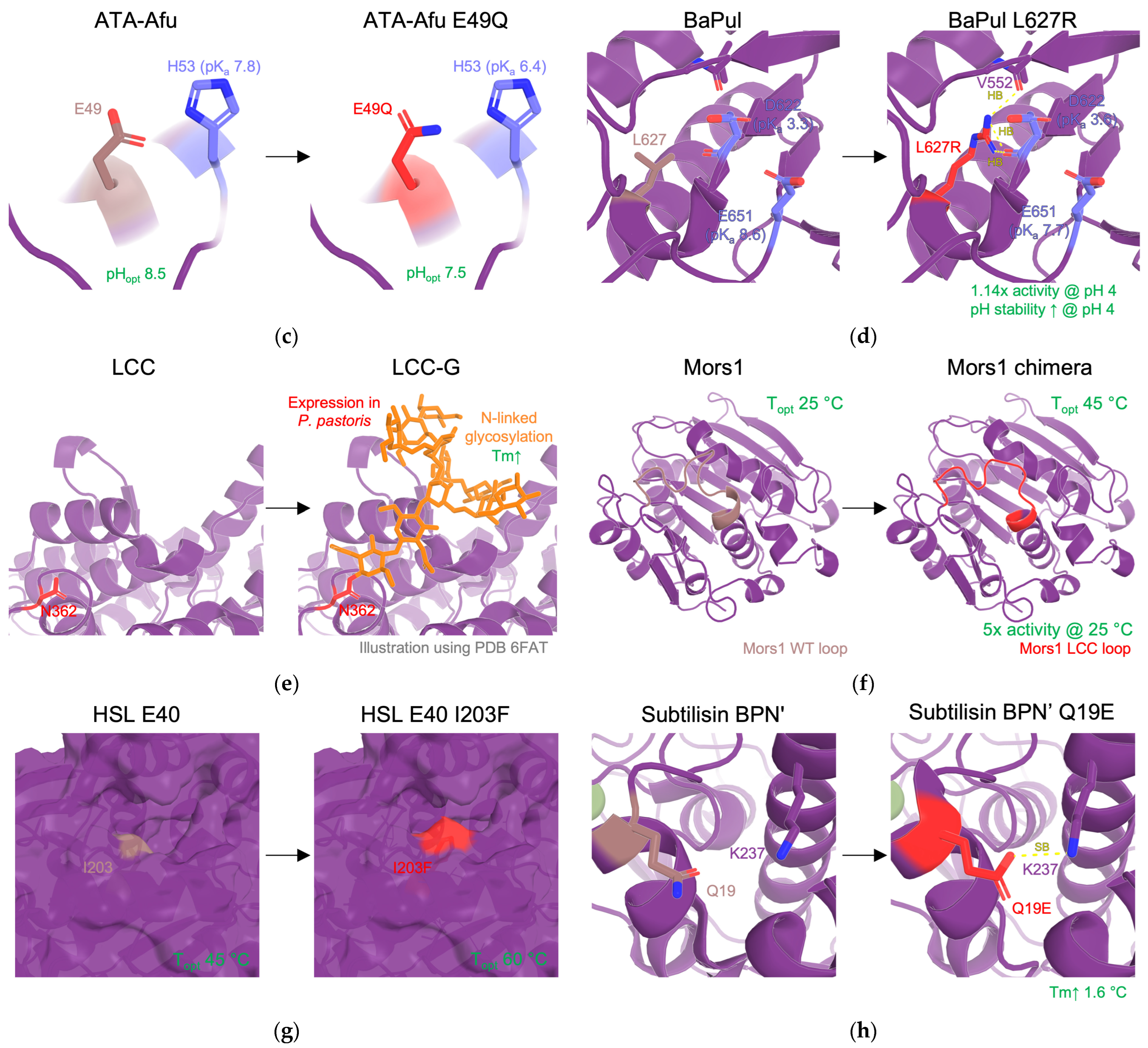
| values | Modifying electrostatic microenvironment with single-point mutations to fine-tune the s of catalytic residues. | activity ↑ (in different pH) | RD, DE | [11,58,59,113] |
| Hydrogen bond network optimization | Modification of hydrogen-bonding network to reinforce affinity with substrate and active site stability. | activity ↑ affinity ↑ | RD | [114] |
| Salt bridges | Introducing salt bridges to reinforce protein structure. | stability ↑ | RD | [12,21,115] |
| Glycosylation | Introducing sites for post translational modifications. | stability↑ | RD | [116,117] |
| Surface loop engineering | Rational remodeling of surface loops via shortening or loop grafting. | activity ↑↓ affinity ↑↓ stability ↑↓ | RD, SRD | [118,119] |
| Hydrophobic core packing | Optimized distribution of hydrophobic residues to eliminate internal cavities. | stability↑ | RD | [21,120] |
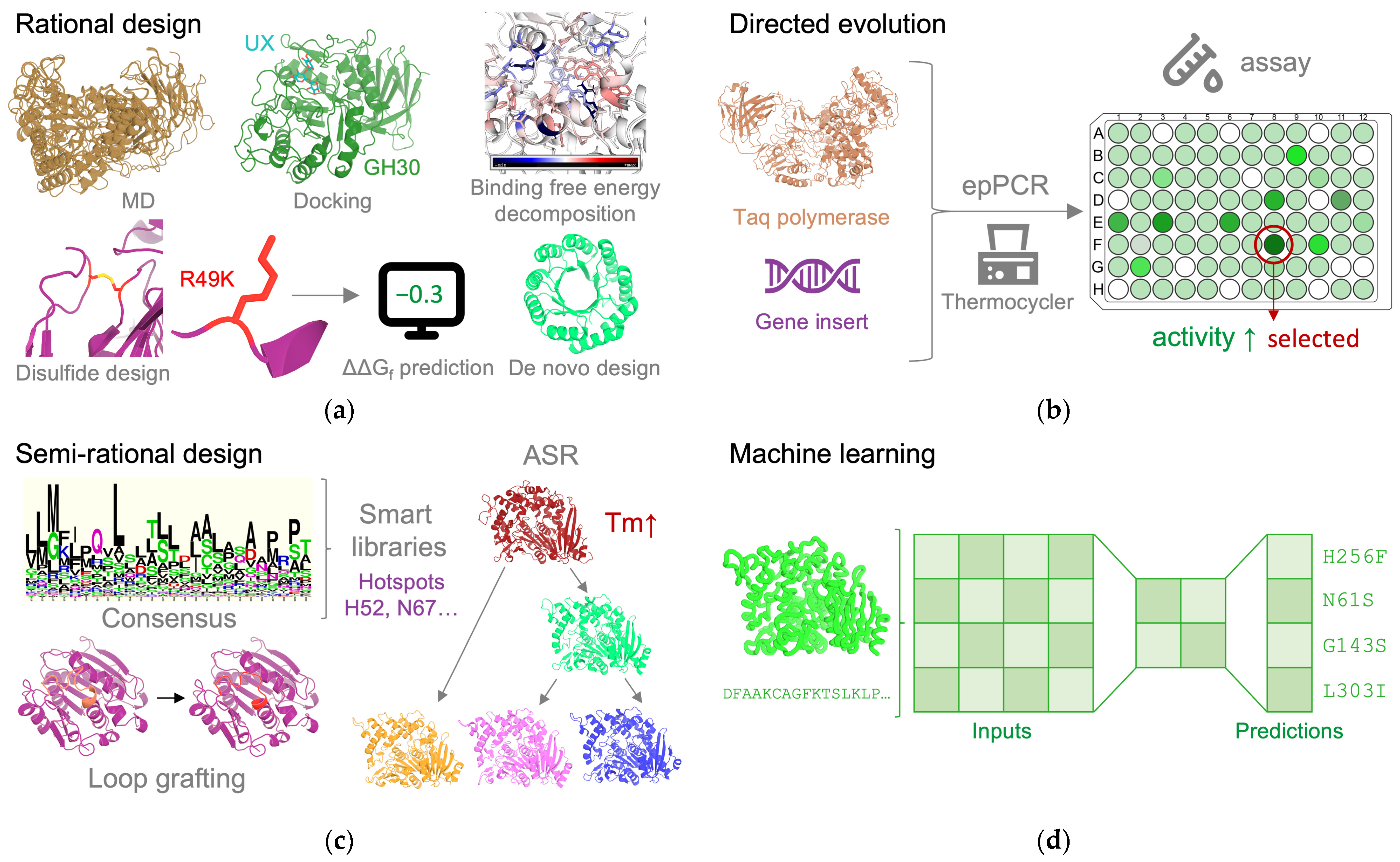
3. Protein Engineering Approaches and Strategies
3.1. Rational Design
3.1.1. Structure-Based Design
3.1.2. De Novo Design
3.2. Directed Evolution
3.3. Semi-Rational Design
3.4. Machine Learning and Deep Learning
3.4.1. ML Paradigms
3.4.2. Training Datasets
3.4.3. Model Architectures
3.4.4. Interpreting ML Models
4. Lessons from the Industrial Application of Engineered PETases
4.1. Biocatalysis of PET
4.2. Protein Engineering of PETases
| # | Enzyme | Targeted Properties | Engineering Strategies | Modifications | Results | Ref |
|---|---|---|---|---|---|---|
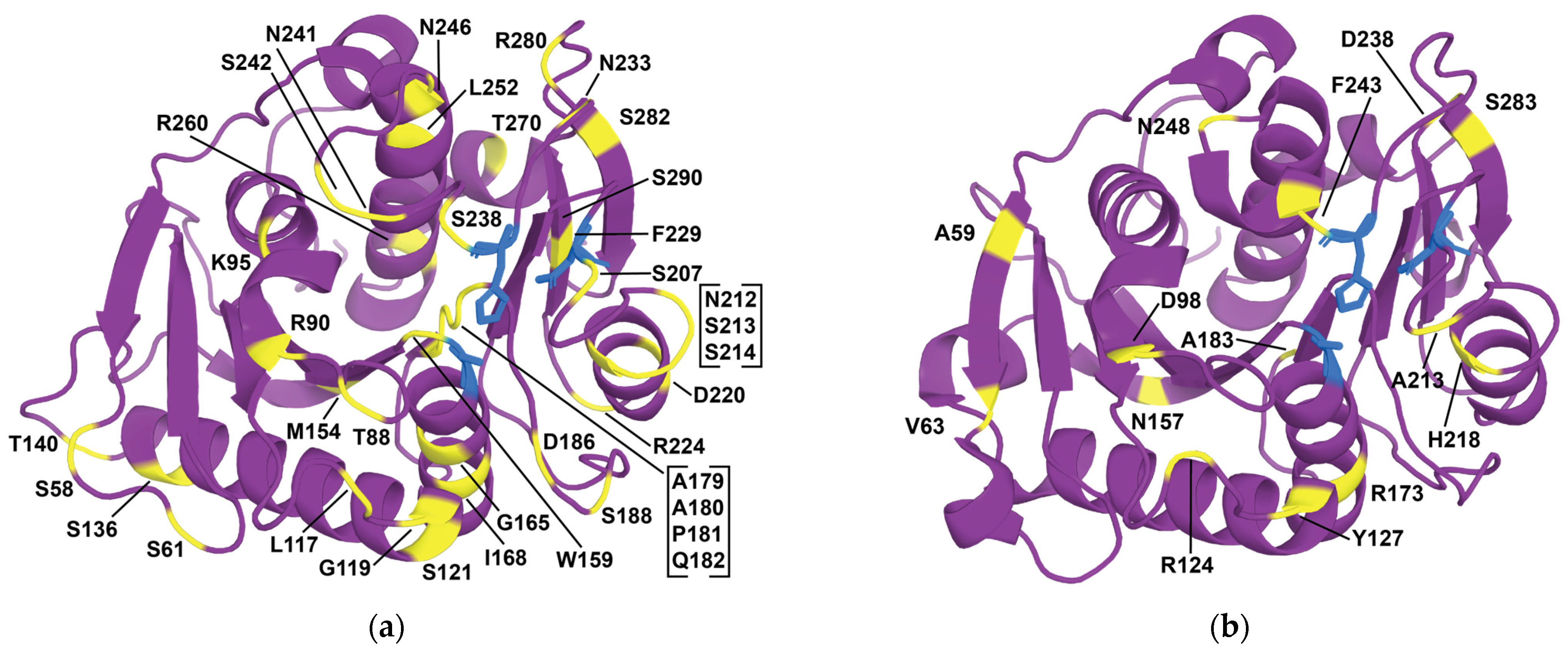
| 1 | HotPETase | stability, activity | DE | IsPETase variant: S121E, D186H, R280A, P181V, S207R, S214Y, Q119K, S213E, N233C, S282C, R90T, Q182M, N212K, R224L, S58A, S61V, K95N, M154G, N241C, K252M, T270Q | = +35.5 °C | [262] |
| 2 | DepoPETase | stability, affinity, activity | DE, SRD (focused surface charge mutations with SSM), literature | IsPETase variant: T88I, D186H, D220N, N233K, N246D, R260Y, S290P | = +23.3 °C 1407-fold more products towards amorphous PET film at 50 °C | [263] |
| 3 | Thermo-PETase | stability, activity | RD (structure-based approach), SRD (adopting features from homolog TfCUT), literature | IsPETase variant: S121E, D186H, R280A | = +8.81 °C activity enhanced by 14-fold at 40 °C | [264] |
| 4 | FAST-PETase | stability | ML | Thermo-PETase variant: N233K, R224Q | 2.4- and 38- fold higher activity at 40 and 50 °C, respectively, compared to ThermoPETase | [111] |
| 5 | IsPETase variant | affinity, stability | SRD (smart libraries from homologs), literature | IsPETase variant: S121E, D186H, S242T, N246D (based on Thermo-PETase) | = +12 °C 58-fold increased activity at 37 °C | [265] |
| 6 | DuraPETase | stability, activity | ) | IsPETase variant: S214H, I168R, W159H, S188Q, R280A, A180I, G165A, Q119Y, L117F, T140D | Enhanced degradation performance (300-fold) on semicrystalline PET films at 40 °C | [258] |
| 7 | IsPETase variant | stability, activity | SRD (position-specific amino acid probabilities) | IsPETase variant: W159H, F229Y | = +10.4 °C 40-fold activity increase at 40 °C in 24 h | [266] |
| 8 | CombiPETase | affinity, stability, activity | RD (MD, engineering flexibility engineering, disulfides, hydrophobic core packing, hydrogen bond breaking), SRD (ASR), literature | IsPETase variant: K95N, S136E, A179C, D186A, S214T, N233C, S282C | = +27.2 °C 4.25-fold increased activity when compared to WT at their respective 24.6-fold increased protein yield | [260] |
| 9 | TS-ΔIsPET | activity, affinity, stability | RD (identifying hotspots through protein-ligand interaction analysis with MD, rational mutations, salt bridge), SRD (conservation analysis followed by SSM), literature | IsPETase variant: S121E, W159H, D186H, F238A | = +4.9 °C Increased catalytic activity on PET | [261] |
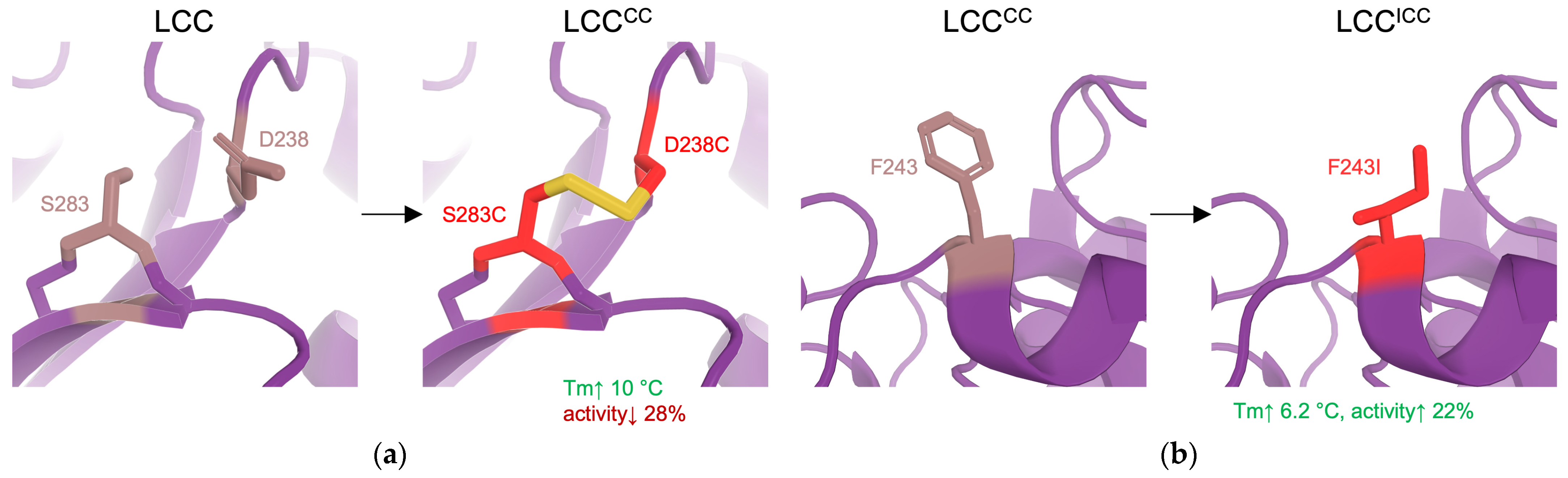
| 10 | LCCICCG | stability | RD (docking to identify hotspots followed by SSM, disulfide design) | LCC variant: F243I, D238C, S283C, Y127G | = +9.3 °C 82% PET conversion in 20 h compared to 53% of WT at 72 °C | [4] |
| 11 | LCCICCG_RIP | stability | RD (proline residues, hydrophilic surface, hydrophobic core) | LCCICCG variant: A59R, V63I, N248P | More products at 85 °C | [272] |
| 12 | LCCICCG_I6M | activity, stability | ML, SRD (coevolutionary analysis) | LCCICCG variant: S32L, D18T, S98R, T157P, E173Q, N213P | for 39% crystalline PET increased from 65 °C to 75–80 °C | [267] |
| 13 | LCC-A2 | affinity | RD (docking) | LCCICCG variant: H218Y, N248D | = +1.11 °C Increased relative activity by 80.1% at 78 °C compared to LCCICCG | [257] |
| 14 | LCC-YGA | affinity, activity | RD (remodeling hydrophilicity of binding site, correlation based accumulated mutagenesis strategy), SRD (homolog information), literature | LCCICCG variant: H183Y, L124G, S29A | 2.07-fold hydrolytic activity of LCCICCG | [271] |
| 15 | LCC-G | stability | RD (glycosylation) | Introduction of N-linked glycosylation at sites N197, N239, and N266 by expressing WT LCC in Pichia pastoris | , at 70 and 75 °C, 1.6- and 1.2-fold more active, respectively | [117] |
| 16 | TurboPETase | stability, activity | ), literature | BhrPETase variant: H218S, F222I, W104L, F243T, A209R, D238K, A251C, A281C | = 84 °C and a 3.4-fold improvement in specific activity towards GF-PET films | [259] |
| 17 | Est1 variant | stability | SRD (consensus design) | Est1 variant A68V, T253P | and activity | [273] |
| 18 | Mors1 chimera | activity | SRD (loop exchange) | Loop exchange of an active site loop from LCC | Shift in optimal temperature from 25 °C to 45 °C, increase 5x in PET hydrolysis when compared with WT at 25 °C. | [122] |
| 19 | HSH-25 | De novo PETase activity | RD (de novo) | De novo design of a 25 amino acid thermostable peptide capable of depolymerizing PET | Confirmed degradation of PET | [269] |
| 20 | IsPETase-IsMHETase chimera | activity | RD (fusion with linker to achieve synergistic action) | Construction of a bifunctional chimeric enzyme fusion of IsPETase with IsMHETase | Chimeric proteins of varying linker lengths all exhibit improved turnover relative to the free enzymes | [270] |
5. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASR | Ancestral Sequence Reconstruction |
| BLAST | Basic Local Alignment Search Tool |
| CAM | Correlation-based Accumulated Mutagenesis |
| CAZy | Carbohydrate-Active enZYmes |
| CNNs | Convolutional Neural Networks |
| CoT | Chain-of-Thought |
| DFT | Density Functional Theory |
| DL | Deep Learning |
| epPCR | error-prone PCR |
| GNNs | Graph Neural Networks |
| LCC | Leaf Compost Cutinase |
| MD | Molecular Dynamics |
| MHET | Mono(2-hydroxyethyl) terephthalate |
| MHETases | MHET hydrolases |
| ML | Machine Learning |
| MMGBSA | Molecular Mechanics Generalized Born Surface Area |
| MMPBSA | Molecular Mechanics Poisson–Boltzmann Surface Area |
| MMRT | Macromolecular Rate Theory |
| MMseq2 | Many-against-Many sequence searching |
| nanoDSF | nano-Differential Scanning Fluorimetry |
| NLP | Natural Language Processing |
| NNs | Neural Networks |
| PAZy | Plastics-Active enZYmes |
| PB | Poisson–Boltzmann |
| PCR | Polymerase Chain Reaction |
| PDB | Protein Data Bank |
| PET | Polyethylene terephthalate |
| PETases | PET hydrolases |
| PLMs | Protein Language Models |
| RL | Reinforcement Learning |
| SSM | Site Saturation Mutagenesis |
| WT | Wild-type |
References
- Dietrich, O.; Heun, M.; Notroff, J.; Schmidt, K.; Zarnkow, M. The Role of Cult and Feasting in the Emergence of Neolithic Communities. New Evidence from Göbekli Tepe, South-Eastern Turkey. Antiquity 2012, 86, 674–695. [Google Scholar] [CrossRef]
- Leek, F.F. Teeth and Bread in Ancient Egypt. J. Egypt. Archaeol. 1972, 58, 126–132. [Google Scholar] [CrossRef]
- Arnal, G.; Anglade, J.; Gavalda, S.; Tournier, V.; Chabot, N.; Bornscheuer, U.T.; Weber, G.; Marty, A. Assessment of Four Engineered PET Degrading Enzymes Considering Large-Scale Industrial Applications. ACS Catal. 2023, 13, 13156–13166. [Google Scholar] [CrossRef] [PubMed]
- Tournier, V.; Topham, C.M.; Gilles, A.; David, B.; Folgoas, C.; Moya-Leclair, E.; Kamionka, E.; Desrousseaux, M.L.; Texier, H.; Gavalda, S.; et al. An Engineered PET Depolymerase to Break down and Recycle Plastic Bottles. Nature 2020, 580, 216–219. [Google Scholar] [CrossRef]
- Xia, W.; Xu, X.; Qian, L.; Shi, P.; Bai, Y.; Luo, H.; Ma, R.; Yao, B. Engineering a Highly Active Thermophilic β-Glucosidase to Enhance Its PH Stability and Saccharification Performance. Biotechnol. Biofuels 2016, 9, 147. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.; Stadtmüller, T.H.J.; Jiang, Q.; Jaeger, K.E.; Schwaneberg, U.; Davari, M.D. How to Engineer Organic Solvent Resistant Enzymes: Insights from Combined Molecular Dynamics and Directed Evolution Study. ChemCatChem 2020, 12, 4073–4083. [Google Scholar] [CrossRef]
- McDonald, A.D.; Higgins, P.M.; Buller, A.R. Substrate Multiplexed Protein Engineering Facilitates Promiscuous Biocatalytic Synthesis. Nat. Commun. 2022, 13, 5242. [Google Scholar] [CrossRef] [PubMed]
- Victorino da Silva Amatto, I.; Gonsales da Rosa-Garzon, N.; Antônio de Oliveira Simões, F.; Santiago, F.; Pereira da Silva Leite, N.; Raspante Martins, J.; Cabral, H. Enzyme Engineering and Its Industrial Applications. Biotechnol. Appl. Biochem. 2022, 69, 389–409. [Google Scholar] [CrossRef]
- Tang, W.L.; Zhao, H. Industrial Biotechnology: Tools and Applications. Biotechnol. J. 2009, 4, 1725–1739. [Google Scholar] [CrossRef] [PubMed]
- Han, S.S.; Kyeong, H.H.; Choi, J.M.; Sohn, Y.K.; Lee, J.H.; Kim, H.S. Engineering of the Conformational Dynamics of an Enzyme for Relieving the Product Inhibition. ACS Catal. 2016, 6, 8440–8445. [Google Scholar] [CrossRef]
- Borges, P.T.; Silva, D.; Silva, T.F.D.; Brissos, V.; Cañellas, M.; Lucas, M.F.; Masgrau, L.; Melo, E.P.; Machuqueiro, M.; Frazão, C.; et al. Unveiling Molecular Details behind Improved Activity at Neutral to Alkaline pH of an Engineered DyP-Type Peroxidase. Comput. Struct. Biotechnol. J. 2022, 20, 3899–3910. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Wang, D.; Wei, N. Enzyme Discovery and Engineering for Sustainable Plastic Recycling. Trends Biotechnol. 2022, 40, 22–37. [Google Scholar] [CrossRef] [PubMed]
- Porebski, B.T.; Buckle, A.M.; By, E.; Daggett, V. Consensus Protein Design. PEDS 2016, 29, 245–251. [Google Scholar] [CrossRef]
- OECD Global Plastics Outlook-Plastics Use by Polymer. Available online: https://ourworldindata.org/grapher/plastic-production-polymer (accessed on 29 January 2025).
- Sarda, P.; Hanan, J.C.; Lawrence, J.G.; Allahkarami, M. Sustainability Performance of Polyethylene Terephthalate, Clarifying Challenges and Opportunities. J. Polym. Sci. 2022, 60, 7–31. [Google Scholar] [CrossRef]
- Del Mar Castro López, M.; Ares Pernas, A.I.; Abad López, M.J.; Latorre, A.L.; López Vilariño, J.M.; González Rodríguez, M.V. Assessing Changes on Poly(Ethylene Terephthalate) Properties after Recycling: Mechanical Recycling in Laboratory versus Postconsumer Recycled Material. Mater. Chem. Phys. 2014, 147, 884–894. [Google Scholar] [CrossRef]
- Kaabel, S.; Daniel Therien, J.P.; Deschênes, C.E.; Duncan, D.; Friščic, T.; Auclair, K. Enzymatic Depolymerization of Highly Crystalline Polyethylene Terephthalate Enabled in Moist-Solid Reaction Mixtures. Proc. Natl. Acad. Sci. USA 2021, 118, e2026452118. [Google Scholar] [CrossRef] [PubMed]
- Tournier, V.; Duquesne, S.; Guillamot, F.; Cramail, H.; Taton, D.; Marty, A.; André, I. Enzymes’ Power for Plastics Degradation. Chem. Rev. 2023, 123, 5612–5701. [Google Scholar] [CrossRef] [PubMed]
- Robinson, P.K. Enzymes: Principles and Biotechnological Applications. Essays Biochem. 2015, 59, 1. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.R. An Appraisal of the Enzyme Stability-Activity Trade-Off. Evolution 2017, 71, 1876–1887. [Google Scholar] [CrossRef] [PubMed]
- Eijsink, V.G.H.; Bjørk, A.; Gåseidnes, S.; Sirevåg, R.; Synstad, B.; Burg, B.V.D.; Vriend, G. Rational Engineering of Enzyme Stability. J. Biotechnol. 2004, 113, 105–120. [Google Scholar] [CrossRef] [PubMed]
- Wolfenden, R.; Snider, M.; Ridgway, C.; Miller, B. The Temperature Dependence of Enzyme Rate Enhancements. J. Am. Chem. Soc. 1999, 121, 7419–7420. [Google Scholar] [CrossRef]
- Kavanau, J.L. Enzyme Kinetics and the Rate of Biological Processes. J. Gen. Physiol. 1950, 34, 193–209. [Google Scholar] [CrossRef]
- Thomas, T.M.; Scopes, R.K. The Effects of Temperature on the Kinetics and Stability of Mesophilic and Thermophilic 3-Phosphoglycerate Kinases. Biochem. J. 1998, 330, 1087–1095. [Google Scholar] [CrossRef] [PubMed]
- Daniel, R.M.; Danson, M.J. A New Understanding of How Temperature Affects the Catalytic Activity of Enzymes. Trends Biochem. Sci. 2010, 35, 584–591. [Google Scholar] [CrossRef] [PubMed]
- Arcus, V.L.; Prentice, E.J.; Hobbs, J.K.; Mulholland, A.J.; Van Der Kamp, M.W.; Pudney, C.R.; Parker, E.J.; Schipper, L.A. On the Temperature Dependence of Enzyme-Catalyzed Rates. Biochemistry 2016, 55, 1681–1688. [Google Scholar] [CrossRef] [PubMed]
- Eyring, H. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Daniel, R.M.; Danson, M.J.; Eisenthal, R. The Temperature Optima of Enzymes: A New Perspective on an Old Phenomenon. Trends Biochem. Sci. 2001, 26, 223–225. [Google Scholar] [CrossRef] [PubMed]
- Hei, D.J.; Clark, D.S. Estimation of Melting Curves from Enzymatic Activity–Temperature Profiles. Biotechnol. Bioeng. 1993, 42, 1245–1251. [Google Scholar] [CrossRef]
- Daniel, R.M.; Peterson, M.E.; Danson, M.J.; Price, N.C.; Kelly, S.M.; Monk, C.R.; Weinberg, C.S.; Oudshoorn, M.L.; Lee, C.K. The Molecular Basis of the Effect of Temperature on Enzyme Activity. Biochem. J. 2010, 425, 353–360. [Google Scholar] [CrossRef]
- Klotz, I.M.; Robert, M. Rosenberg The Second Law of Thermodynamics. In Chemical Thermodynamics: Basic Concepts and Methods; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; pp. 111–157. ISBN 978-0-471-78015-1. [Google Scholar]
- Klotz, I.M.; Robert, M. Rosenberg Applications of the First Law to Gases. In Chemical Thermodynamics: Basic Concepts and Methods; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; pp. 81–109. ISBN 978-0-471-78015-1. [Google Scholar]
- Klotz, I.M.; Robert, M. Rosenberg Equilibrium and Spontaneity for Systems at Constant Temperature. In Chemical Thermodynamics: Basic Concepts and Methods; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; pp. 159–191. ISBN 978-0-471-78015-1. [Google Scholar]
- Vieille, C.; Zeikus, G.J. Hyperthermophilic Enzymes: Sources, Uses, and Molecular Mechanisms for Thermostability. Microbiol. Mol. Biol. Rev. 2001, 65, 1–43. [Google Scholar] [CrossRef]
- Johnson, C.M. Differential Scanning Calorimetry as a Tool for Protein Folding and Stability. Arch. Biochem. Biophys. 2013, 531, 100–109. [Google Scholar] [CrossRef] [PubMed]
- Greenfield, N.J. Using Circular Dichroism Collected as a Function of Temperature to Determine the Thermodynamics of Protein Unfolding and Binding Interactions. Nat. Protoc. 2006, 1, 2527. [Google Scholar] [CrossRef]
- Santiago, P.S.; Moura, F.; Moreira, L.M.; Domingues, M.M.; Santos, N.C.; Tabak, M. Dynamic Light Scattering and Optical Absorption Spectroscopy Study of PH and Temperature Stabilities of the Extracellular Hemoglobin of Glossoscolex Paulistus. Biophys. J. 2007, 94, 2228. [Google Scholar] [CrossRef] [PubMed]
- Gao, K.; Oerlemans, R.; Groves, M.R. Theory and Applications of Differential Scanning Fluorimetry in Early-Stage Drug Discovery. Biophys. Rev. 2020, 12, 85. [Google Scholar] [CrossRef] [PubMed]
- Fitter, J. Structural and Dynamical Features Contributing to Thermostability in α-Amylases. Cell. Mol. Life Sci. 2005, 62, 1925–1937. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Gupta, G.; Ahmad, T.; Mansoor, S.; Kaur, B. Enzyme Engineering: Current Trends and Future Perspectives. Food Rev. Int. 2021, 37, 121–154. [Google Scholar] [CrossRef]
- Harris, T.K.; Turner, G.J. Structural Basis of Perturbed pKa Values of Catalytic Groups in Enzyme Active Sites. IUBMB Life 2002, 53, 85–98. [Google Scholar] [CrossRef]
- Fitch, C.A.; Platzer, G.; Okon, M.; Garcia-Moreno, B.E.; McIntosh, L.P. Arginine: Its pKa Value Revisited. Protein Sci. 2015, 24, 752–761. [Google Scholar] [CrossRef] [PubMed]
- Dobrev, P.; Vemulapalli, S.P.B.; Nath, N.; Griesinger, C.; Grubmüller, H. Probing the Accuracy of Explicit Solvent Constant PH Molecular Dynamics Simulations for Peptides. J. Chem. Theory Comput. 2020, 16, 2561–2569. [Google Scholar] [CrossRef]
- Lin, J.; Cassidy, C.S.; Frey, P.A. Correlations of the Basicity of His 57 with Transition State Analogue Binding, Substrate Reactivity, and the Strength of the Low-Barrier Hydrogen Bond in Chymotrypsin. Biochemistry 1998, 37, 11940–11948. [Google Scholar] [CrossRef]
- Bender, M.L.; Killheffer, J.V.; Cohen, S. Chymotrypsin. Crit. Rev. Biochem. Mol. Biol. 1973, 1, 149–199. [Google Scholar] [CrossRef]
- Hess, G.P.; McConn, J.; Ku, E.; McConkey, G. Studies of the Activity of Chymotrypsin. Philos. Trans. R. Soc. London. B Biol. Sci. 1970, 257, 89–104. [Google Scholar] [CrossRef] [PubMed]
- Hofer, F.; Kraml, J.; Kahler, U.; Kamenik, A.S.; Liedl, K.R. Catalytic Site pKa Values of Aspartic, Cysteine, and Serine Proteases: Constant PH MD Simulations. J. Chem. Inf. Model. 2020, 60, 3030–3042. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Robertson, A.D.; Jensen, J.H. Very Fast Empirical Prediction and Rationalization of Protein pKa Values. Proteins 2005, 61, 704–721. [Google Scholar] [CrossRef] [PubMed]
- Reis, P.B.P.S.; Vila-Vicosa, D.; Rocchia, W.; Machuqueiro, M. PypKA: A Flexible Python Module for Poisson-Boltzmann-Based pKa Calculations. J. Chem. Inf. Model. 2020, 60, 4442–4448. [Google Scholar] [CrossRef] [PubMed]
- Havranek, J.J.; Harbury, P.B. Tanford-Kirkwood Electrostatics for Protein Modeling. Proc. Natl. Acad. Sci. USA 1999, 96, 11145–11150. [Google Scholar] [CrossRef]
- Thapa, B.; Schlegel, H.B. Density Functional Theory Calculation of pKa’s of Thiols in Aqueous Solution Using Explicit Water Molecules and the Polarizable Continuum Model. J. Phys. Chem. A 2016, 120, 5726–5735. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Liu, T.; Lin, Q.; He, J.; Lei, X.; Luo, F.; Huang, Y. Basis for Accurate Protein pKa Prediction with Machine Learning. J. Chem. Inf. Model. 2023, 63, 2936–2947. [Google Scholar] [CrossRef] [PubMed]
- Johnston, R.C.; Yao, K.; Kaplan, Z.; Chelliah, M.; Leswing, K.; Seekins, S.; Watts, S.; Calkins, D.; Chief Elk, J.; Jerome, S.V.; et al. Epik: pKa and Protonation State Prediction through Machine Learning. J. Chem. Theory Comput. 2023, 19, 2380–2388. [Google Scholar] [CrossRef] [PubMed]
- Ho, J.; Coote, M.L. First-Principles Prediction of Acidities in the Gas and Solution Phase. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 649–660. [Google Scholar] [CrossRef]
- Alongi, K.S.; Shields, G.C. Theoretical Calculations of Acid Dissociation Constants: A Review Article. Annu. Rep. Comput. Chem. 2010, 6, 113–138. [Google Scholar] [CrossRef]
- Seybold, P.G.; Shields, G.C. Computational Estimation of pKa Values. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 290–297. [Google Scholar] [CrossRef]
- Martins de Oliveira, V.; Liu, R.; Shen, J. Constant PH Molecular Dynamics Simulations: Current Status and Recent Applications. Curr. Opin. Struct. Biol. 2022, 77, 102498. [Google Scholar] [CrossRef] [PubMed]
- Xiang, C.; Ao, Y.F.; Höhne, M.; Bornscheuer, U.T. Shifting the PH Optima of (R)-Selective Transaminases by Protein Engineering. Int. J. Mol. Sci. 2022, 23, 15347. [Google Scholar] [CrossRef]
- Thomas, P.G.; Russell, A.J.; Fersht, A.R. Tailoring the PH Dependence of Enzyme Catalysis Using Protein Engineering. Nature 1985, 318, 375–376. [Google Scholar] [CrossRef]
- Kishore, D.; Kundu, S.; Kayastha, A.M. Thermal, Chemical and PH Induced Denaturation of a Multimeric β-Galactosidase Reveals Multiple Unfolding Pathways. PLoS ONE 2012, 7, e50380. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Song, J. Molecular Mechanism Underlying the Thermal Stability and PH-Induced Unfolding of CHABII. J. Mol. Biol. 2005, 348, 205–218. [Google Scholar] [CrossRef]
- Xiang, L.; Lu, Y.; Wang, H.; Wang, M.; Zhang, G. Improving the Specific Activity and pH Stability of Xylanase XynHBN188A by Directed Evolution. Bioresour. Bioprocess. 2019, 6, 25. [Google Scholar] [CrossRef]
- Selvaraj, C.; Rudhra, O.; Alothaim, A.S.; Alkhanani, M.; Singh, S.K. Structure and Chemistry of Enzymatic Active Sites That Play a Role in the Switch and Conformation Mechanism. Adv. Protein Chem. Struct. Biol. 2022, 130, 59–83. [Google Scholar] [CrossRef] [PubMed]
- Koshland, D.E. The Key–Lock Theory and the Induced Fit Theory. Angew. Chem. Int. Ed. Engl. 1995, 33, 2375–2378. [Google Scholar] [CrossRef]
- Paul, F.; Weikl, T.R. How to Distinguish Conformational Selection and Induced Fit Based on Chemical Relaxation Rates. PLoS Comput. Biol. 2016, 12, e1005067. [Google Scholar] [CrossRef]
- Harris, J.L.; Craik, C.S. Engineering Enzyme Specificity. Curr. Opin. Chem. Biol. 1998, 2, 127–132. [Google Scholar] [CrossRef]
- De Groeve, M.R.M.; Remmery, L.; Van Hoorebeke, A.; Stout, J.; Desmet, T.; Savvides, S.N.; Soetaert, W. Construction of Cellobiose Phosphorylase Variants with Broadened Acceptor Specificity towards Anomerically Substituted Glucosides. Biotechnol. Bioeng. 2010, 107, 413–420. [Google Scholar] [CrossRef] [PubMed]
- Li, J.X.; Fang, X.; Zhao, Q.; Ruan, J.X.; Yang, C.Q.; Wang, L.J.; Miller, D.J.; Faraldos, J.A.; Allemann, R.K.; Chen, X.Y.; et al. Rational Engineering of Plasticity Residues of Sesquiterpene Synthases from Artemisia annua: Product Specificity and Catalytic Efficiency. Biochem. J. 2013, 451, 417–426. [Google Scholar] [CrossRef]
- Ringe, D.; Petsko, G.A. How Enzymes Work. Science 2008, 320, 1428–1429. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Sharma, P.K.; Kato, M.; Xiang, Y.; Liu, H.; Olsson, M.H.M. Electrostatic Basis for Enzyme Catalysis. Chem. Rev. 2006, 106, 3210–3235. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, J.N.; Zhou, Y.; Guo, Z.; Pérez, B. Genetic and Chemical Approaches for Surface Charge Engineering of Enzymes and Their Applicability in Biocatalysis: A Review. Biotechnol. Bioeng. 2019, 116, 1795–1812. [Google Scholar] [CrossRef] [PubMed]
- Chaloupková, R.; Sýkorová, J.; Prokop, Z.; Jesenská, A.; Monincová, M.; Pavlová, M.; Tsuda, M.; Nagata, Y.; Damborský, J. Modification of Activity and Specificity of Haloalkane Dehalogenase from Sphingomonas paucimobilis UT26 by Engineering of Its Entrance Tunnel. J. Biol. Chem. 2003, 278, 52622–52628. [Google Scholar] [CrossRef]
- Morris, G.M.; Ruth, H.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated Docking with Selective Receptor Flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef] [PubMed]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization and Multithreading. J. Comput. Chem. 2010, 31, 455. [Google Scholar] [CrossRef] [PubMed]
- Miller, B.R.; McGee, T.D.; Swails, J.M.; Homeyer, N.; Gohlke, H.; Roitberg, A.E. MMPBSA.Py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. [Google Scholar] [CrossRef] [PubMed]
- Ylilauri, M.; Pentikäinen, O.T. MMGBSA as a Tool to Understand the Binding Affinities of Filamin-Peptide Interactions. J. Chem. Inf. Model. 2013, 53, 2626–2633. [Google Scholar] [CrossRef]
- Kumari, R.; Kumar, R.; Lynn, A. G_mmpbsa-A GROMACS Tool for High-Throughput MM-PBSA Calculations. J. Chem. Inf. Model. 2014, 54, 1951–1962. [Google Scholar] [CrossRef] [PubMed]
- Klvana, M.; Pavlova, M.; Koudelakova, T.; Chaloupkova, R.; Dvorak, P.; Prokop, Z.; Stsiapanava, A.; Kuty, M.; Kuta-Smatanova, I.; Dohnalek, J.; et al. Pathways and Mechanisms for Product Release in the Engineered Haloalkane Dehalogenases Explored Using Classical and Random Acceleration Molecular Dynamics Simulations. J. Mol. Biol. 2009, 392, 1339–1356. [Google Scholar] [CrossRef] [PubMed]
- Vavra, O.; Filipovic, J.; Plhak, J.; Bednar, D.; Marques, S.M.; Brezovsky, J.; Stourac, J.; Matyska, L.; Damborsky, J. CaverDock: A Molecular Docking-Based Tool to Analyse Ligand Transport through Protein Tunnels and Channels. Bioinformatics 2019, 35, 4986–4993. [Google Scholar] [CrossRef] [PubMed]
- Chovancova, E.; Pavelka, A.; Benes, P.; Strnad, O.; Brezovsky, J.; Kozlikova, B.; Gora, A.; Sustr, V.; Klvana, M.; Medek, P.; et al. CAVER 3.0: A Tool for the Analysis of Transport Pathways in Dynamic Protein Structures. PLoS Comput. Biol. 2012, 8, e1002708. [Google Scholar] [CrossRef]
- Matthews, B.W.; Nicholson, H.; Becktel, W.J. Enhanced Protein Thermostability from Site-Directed Mutations That Decrease the Entropy of Unfolding. Proc. Natl. Acad. Sci. USA 1987, 84, 6663–6667. [Google Scholar] [CrossRef] [PubMed]
- Kellogg, E.H.; Leaver-Fay, A.; Baker, D. Role of Conformational Sampling in Computing Mutation-Induced Changes in Protein Structure and Stability. Proteins 2011, 79, 830–838. [Google Scholar] [CrossRef]
- Schymkowitz, J.; Borg, J.; Stricher, F.; Nys, R.; Rousseau, F.; Serrano, L. The FoldX Web Server: An Online Force Field. Nucleic Acids Res. 2005, 33, W382. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Ding, F.; Dokholyan, N.V. Eris: An Automated Estimator of Protein Stability. Nat. Methods 2007, 4, 466–467. [Google Scholar] [CrossRef]
- Cao, H.; Wang, J.; He, L.; Qi, Y.; Zhang, J.Z. DeepDDG: Predicting the Stability Change of Protein Point Mutations Using Neural Networks. J. Chem. Inf. Model. 2019, 59, 1508–1514. [Google Scholar] [CrossRef] [PubMed]
- Pupko, T.; Bell, R.E.; Mayrose, I.; Glaser, F.; Ben-Tal, N. Rate4Site: An Algorithmic Tool for the Identification of Functional Regions in Proteins by Surface Mapping of Evolutionary Determinants within Their Homologues. Bioinformatics 2002, 18, S71–S77. [Google Scholar] [CrossRef] [PubMed]
- Bednar, D.; Beerens, K.; Sebestova, E.; Bendl, J.; Khare, S.; Chaloupkova, R.; Prokop, Z.; Brezovsky, J.; Baker, D.; Damborsky, J. FireProt: Energy- and Evolution-Based Computational Design of Thermostable Multiple-Point Mutants. PLoS Comput. Biol. 2015, 11, e1004556. [Google Scholar] [CrossRef]
- Ramanathan, A.; Agarwal, P.K. Evolutionarily Conserved Linkage between Enzyme Fold, Flexibility, and Catalysis. PLoS Biol. 2011, 9, e1001193. [Google Scholar] [CrossRef]
- Teilum, K.; Olsen, J.G.; Kragelund, B.B. Functional Aspects of Protein Flexibility. Cell Mol. Life Sci. 2009, 66, 2231–2247. [Google Scholar] [CrossRef]
- Mlynek, G.; Djinović-Carugo, K.; Carugo, O. B-Factor Rescaling for Protein Crystal Structure Analyses. Crystals 2024, 14, 443. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, Q.; Qu, G.; Feng, Y.; Reetz, M.T. Utility of B-Factors in Protein Science: Interpreting Rigidity, Flexibility, and Internal Motion and Engineering Thermostability. Chem. Rev. 2019, 119, 1626–1665. [Google Scholar] [CrossRef] [PubMed]
- Ru, W.J.; Xia, B.B.; Zhang, Y.X.; Yang, J.W.; Zhang, H.B.; Hu, X.Q. Development of Thermostable Dextranase from Streptococcus mutans (SmdexTM) through in Silico Design Employing B-Factor and Cartesian-ΔΔG. J. Biotechnol. 2022, 360, 142–151. [Google Scholar] [CrossRef]
- Mura, C. Development & Implementation of a PyMOL “putty” Representation. arXiv 2014, arXiv:1407.5211. [Google Scholar] [CrossRef]
- Roe, D.R.; Cheatham, T.E. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Alexandrov, V.; Lehnert, U.; Echols, N.; Milburn, D.; Engelman, D.; Gerstein, M. Normal Modes for Predicting Protein Motions: A Comprehensive Database Assessment and Associated Web Tool. Protein Sci. 2005, 14, 633. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Liu, Q. Aligning Experimental and Theoretical Anisotropic B-Factors: Water Models, Normal-Mode Analysis Methods, and Metrics. J. Phys. Chem. B 2014, 118, 4069–4079. [Google Scholar] [CrossRef] [PubMed]
- Fuglebakk, E.; Reuter, N.; Hinsen, K. Evaluation of Protein Elastic Network Models Based on an Analysis of Collective Motions. J. Chem. Theory Comput. 2013, 9, 5618–5628. [Google Scholar] [CrossRef]
- Pandey, A.; Liu, E.; Graham, J.; Chen, W.; Keten, S. B-Factor Prediction in Proteins Using a Sequence-Based Deep Learning Model. Patterns 2023, 4, 100805. [Google Scholar] [CrossRef] [PubMed]
- Dimarogona, M.; Topakas, E.; Christakopoulos, P.; Chrysina, E.D. The Crystal Structure of a Fusarium oxysporum Feruloyl Esterase That Belongs to the Tannase Family. FEBS Lett. 2020, 594, 1738–1749. [Google Scholar] [CrossRef] [PubMed]
- Somero, G.N. Proteins and Temperature. Annu. Rev. Physiol. 1995, 57, 43–68. [Google Scholar] [CrossRef] [PubMed]
- Svingor, Á.; Kardos, J.; Hajdú, I.; Németh, A.; Závodszky, P. A Better Enzyme to Cope with Cold. Comparative Flexibility Studies on Psychrotrophic, Mesophilic, and Thermophilic IPMDHs. J. Biol. Chem. 2001, 276, 28121–28125. [Google Scholar] [CrossRef]
- Hou, Q.; Rooman, M.; Pucci, F. Enzyme Stability-Activity Trade-Off: New Insights from Protein Stability Weaknesses and Evolutionary Conservation. J. Chem. Theory Comput. 2023, 19, 3664–3671. [Google Scholar] [CrossRef]
- Vanella, R.; Küng, C.; Schoepfer, A.A.; Doffini, V.; Ren, J.; Nash, M.A. Understanding Activity-Stability Tradeoffs in Biocatalysts by Enzyme Proximity Sequencing. Nat. Commun. 2024, 15, 1807. [Google Scholar] [CrossRef]
- Hernández, G.; Jenney, F.E.; Adams, M.W.W.; LeMaster, D.M. Millisecond Time Scale Conformational Flexibility in a Hyperthermophile Protein at Ambient Temperature. Proc. Natl. Acad. Sci. USA 2000, 97, 3166–3170. [Google Scholar] [CrossRef] [PubMed]
- Karshikoff, A.; Nilsson, L.; Ladenstein, R. Rigidity versus Flexibility: The Dilemma of Understanding Protein Thermal Stability. FEBS J. 2015, 282, 3899–3917. [Google Scholar] [CrossRef]
- Joho, Y.; Vongsouthi, V.; Gomez, C.; Larsen, J.S.; Ardevol, A.; Jackson, C.J. Improving Plastic Degrading Enzymes via Directed Evolution. Protein Eng. Des. Sel. 2024, 37, gzae009. [Google Scholar] [CrossRef] [PubMed]
- Stimple, S.D.; Smith, M.D.; Tessier, P.M. Directed Evolution Methods for Overcoming Trade-Offs between Protein Activity and Stability. AIChE J. 2020, 66, e16814. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; An, J.; Yang, G.; Wu, G.; Zhang, Y.; Cui, L.; Feng, Y. Enhanced Enzyme Kinetic Stability by Increasing Rigidity within the Active Site. J. Biol. Chem. 2014, 289, 7994–8006. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.S.; Seo, S.W.; Jang, S.; Jung, G.Y.; Kim, S. Rational Engineering of Enzyme Allosteric Regulation through Sequence Evolution Analysis. PLoS Comput. Biol. 2012, 8, e1002612. [Google Scholar] [CrossRef] [PubMed]
- Parker, M.H.; Hefford, M.A. Introduction of Potential Helix-Capping Residues into an Engineered Helical Protein. Biotechnol. Appl. Biochem. 1998, 28, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Diaz, D.J.; Czarnecki, N.J.; Zhu, C.; Kim, W.; Shroff, R.; Acosta, D.J.; Alexander, B.R.; Cole, H.O.; Zhang, Y.; et al. Machine Learning-Aided Engineering of Hydrolases for PET Depolymerization. Nature 2022, 604, 662–667. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Dong, X.; Li, X.; Liu, Z.; Liu, H. Prediction of Disulfide Bond Engineering Sites Using a Machine Learning Method. Sci. Rep. 2020, 10, 10330. [Google Scholar] [CrossRef] [PubMed]
- Mary, B.; And, T.-C.; Nielsen, J.E. Redesigning Protein pKa Values. Protein Sci. 2007, 16, 239. [Google Scholar] [CrossRef]
- Liu, H.; Ding, Y.; Mazurkewich, S.; Pei, W.; Wei, X.; Larsbrink, J.; Chipot, C.; Hong, Z.; Cai, W.; Zong, Z. Boosting Enzyme Activity in Biomass Conversion by Modulating the Hydrolysis Process of Cellobiohydrolases. ACS Catal. 2024, 14, 16044–16054. [Google Scholar] [CrossRef]
- Kordes, S.; Romero-Romero, S.; Lutz, L.; Höcker, B. A Newly Introduced Salt Bridge Cluster Improves Structural and Biophysical Properties of de Novo TIM Barrels. Protein Sci. 2021, 31, 513. [Google Scholar] [CrossRef]
- Fonseca-Maldonado, R.; Vieira, D.S.; Alponti, J.S.; Bonneil, E.; Thibault, P.; Ward, R.J. Engineering the Pattern of Protein Glycosylation Modulates the Thermostability of a GH11 Xylanase. J. Biol. Chem. 2013, 288, 25522–25534. [Google Scholar] [CrossRef] [PubMed]
- Shirke, A.N.; White, C.; Englaender, J.A.; Zwarycz, A.; Butterfoss, G.L.; Linhardt, R.J.; Gross, R.A. Stabilizing Leaf and Branch Compost Cutinase (LCC) with Glycosylation: Mechanism and Effect on PET Hydrolysis. Biochemistry 2018, 57, 1190–1200. [Google Scholar] [CrossRef] [PubMed]
- Planas-Iglesias, J.; Opaleny, F.; Ulbrich, P.; Stourac, J.; Sanusi, Z.; Pinto, G.P.; Schenkmayerova, A.; Byska, J.; Damborsky, J.; Kozlikova, B.; et al. LoopGrafter: A Web Tool for Transplanting Dynamical Loops for Protein Engineering. Nucleic Acids Res. 2022, 50, W465–W473. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; You, S.; Zha, Z.; Li, J.; Zhang, W.; Bai, Z.; Hu, Y.; Wang, X.; Chen, Y.; Chen, Z.; et al. Loop Engineering of a Thermostable GH10 Xylanase to Improve Low-Temperature Catalytic Performance for Better Synergistic Biomass-Degrading Abilities. Bioresour. Technol. 2021, 342, 125962. [Google Scholar] [CrossRef]
- Yang, J.K.; Park, M.S.; Waldo, G.S.; Suh, S.W. Directed Evolution Approach to a Structural Genomics Project: Rv2002 from Mycobacterium tuberculosis. Proc. Natl. Acad. Sci. USA 2003, 100, 455–460. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Xu, T.; Ge, Y.; Wang, L.; Tang, W.; Li, S. Hydrogen-Bond-Based Protein Engineering for the Acidic Adaptation of Bacillus acidopullulyticus Pullulanase. Enzyme Microb. Technol. 2019, 124, 79–83. [Google Scholar] [CrossRef] [PubMed]
- Blázquez-Sánchez, P.; Vargas, J.A.; Furtado, A.A.; Griñen, A.; Leonardo, D.A.; Sculaccio, S.A.; Pereira, H.D.M.; Sonnendecker, C.; Zimmermann, W.; Díez, B.; et al. Engineering the Catalytic Activity of an Antarctic PET-Degrading Enzyme by Loop Exchange. Protein Sci. 2023, 32, e4757. [Google Scholar] [CrossRef] [PubMed]
- Li, P.Y.; Chen, X.L.; Ji, P.; Li, C.Y.; Wang, P.; Zhang, Y.; Xie, B.B.; Qin, Q.L.; Su, H.N.; Zhou, B.C.; et al. Interdomain Hydrophobic Interactions Modulate the Thermostability of Microbial Esterases from the Hormone-Sensitive Lipase Family. J. Biol. Chem. 2015, 290, 11188–11198. [Google Scholar] [CrossRef] [PubMed]
- Erwin, C.R.; Barnett, B.L.; Oliver, J.D.; Sullivan, J.F. Effects of Engineered Salt Bridges on the Stability of Subtilisin BPN’. Protein Eng. Des. Sel. 1990, 4, 87–97. [Google Scholar] [CrossRef] [PubMed]
- Crooks, G.E.; Hon, G.; Chandonia, J.M.; Brenner, S.E. WebLogo: A Sequence Logo Generator. Genome Res. 2004, 14, 1188–1190. [Google Scholar] [CrossRef] [PubMed]
- Yeh, A.H.W.; Norn, C.; Kipnis, Y.; Tischer, D.; Pellock, S.J.; Evans, D.; Ma, P.; Lee, G.R.; Zhang, J.Z.; Anishchenko, I.; et al. De Novo Design of Luciferases Using Deep Learning. Nature 2023, 614, 774–780. [Google Scholar] [CrossRef] [PubMed]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly Accurate Protein Structure Prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Akin, H.; Rao, R.; Hie, B.; Zhu, Z.; Lu, W.; Smetanin, N.; Verkuil, R.; Kabeli, O.; Shmueli, Y.; et al. Evolutionary-Scale Prediction of Atomic-Level Protein Structure with a Language Model. Science 2023, 379, 1123–1130. [Google Scholar] [CrossRef]
- Jisna, V.A.; Jayaraj, P.B. Protein Structure Prediction: Conventional and Deep Learning Perspectives. Protein J. 2021, 40, 522–544. [Google Scholar] [CrossRef] [PubMed]
- WL, D. The PyMOL Molecular Graphics System (DeLano Scientific, San Carlos, CA) 2002. Available online: https://www.pymol.org/ (accessed on 29 January 2025).
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Meng, E.C.; Couch, G.S.; Croll, T.I.; Morris, J.H.; Ferrin, T.E. UCSF ChimeraX: Structure Visualization for Researchers, Educators, and Developers. Protein Sci. 2020, 30, 70. [Google Scholar] [CrossRef]
- Craig, D.B.; Dombkowski, A.A. Disulfide by Design 2.0: A Web-Based Tool for Disulfide Engineering in Proteins. BMC Bioinform. 2013, 14, 346. [Google Scholar] [CrossRef] [PubMed]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; Van Der Spoel, D.; et al. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Cerutti, D.S.; Cisneros, G.A.; Cruzeiro, V.W.D.; Forouzesh, N.; Giese, T.J.; Götz, A.W.; Gohlke, H.; et al. AmberTools. J. Chem. Inf. Model. 2023, 63, 6183–6191. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Brooks, C.L.; Mackerell, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Morales-Quintana, L.; Carrasco-Orellana, C.; Beltrán, D.; Moya-León, M.A.; Herrera, R. Molecular Insights of a Xyloglucan Endo-Transglycosylase/Hydrolase of Radiata pine (PrXTH1) Expressed in Response to Inclination: Kinetics and Computational Study. Plant Physiol. Bioch 2019, 136, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Jäckering, A.; Kamp, M.v.d.; Strodel, B.; Zinovjev, K. Influence of Wobbling Tryptophan and Mutations on PET Degradation Explored by QM/MM Free Energy Calculations. J. Chem. Inf. Model. 2024, 64, 7544–7554. [Google Scholar] [CrossRef] [PubMed]
- Berraud-Pache, R.; Garcia-Iriepa, C.; Navizet, I. Modeling Chemical Reactions by QM/MM Calculations: The Case of the Tautomerization in Fireflies Bioluminescent Systems. Front. Chem. 2018, 6, 358639. [Google Scholar] [CrossRef]
- Peng, J.H.; Wang, W.; Yu, Y.Q.; Gu, H.L.; Huang, X. Clustering Algorithms to Analyze Molecular Dynamics Simulation Trajectories for Complex Chemical and Biological Systems. CJCP 2018, 31, 404–420. [Google Scholar] [CrossRef]
- Husic, B.E.; Pande, V.S. Markov State Models: From an Art to a Science. J. Am. Chem. Soc. 2018, 140, 2386–2396. [Google Scholar] [CrossRef] [PubMed]
- Palma, J.; Pierdominici-Sottile, G. On the Uses of PCA to Characterise Molecular Dynamics Simulations of Biological Macromolecules: Basics and Tips for an Effective Use. ChemPhysChem 2023, 24, e202200491. [Google Scholar] [CrossRef]
- Lemkul, J.A. Introductory Tutorials for Simulating Protein Dynamics with GROMACS. J. Phys. Chem. B 2024, 128, 9418–9435. [Google Scholar] [CrossRef] [PubMed]
- Benrezkallah, D. Molecular Dynamics Simulations at High Temperatures of the Aeropyrum pernix L7Ae Thermostable Protein: Insight into the Unfolding Pathway. J. Mol. Graph. Model. 2024, 127, 108700. [Google Scholar] [CrossRef]
- Gattin, Z.; Riniker, S.; Hore, P.J.; Mok, K.H.; Van Gunsteren, W.F. Temperature and Urea Induced Denaturation of the TRP-Cage Mini Protein TC5b: A Simulation Study Consistent with Experimental Observations. Protein Sci. 2009, 18, 2090–2099. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Korendovych, I.V.; DeGrado, W.F. De Novo Protein Design, a Retrospective. Q. Rev. Biophys. 2020, 53, e3. [Google Scholar] [CrossRef]
- Marshall, L.R.; Zozulia, O.; Lengyel-Zhand, Z.; Korendovych, I.V. Minimalist de Novo Design of Protein Catalysts. ACS Catal. 2019, 9, 9265. [Google Scholar] [CrossRef] [PubMed]
- Leman, J.K.; Weitzner, B.D.; Lewis, S.M.; Adolf-Bryfogle, J.; Alam, N.; Alford, R.F.; Aprahamian, M.; Baker, D.; Barlow, K.A.; Barth, P.; et al. Macromolecular Modeling and Design in Rosetta: Recent Methods and Frameworks. Nat. Methods 2020, 17, 665–680. [Google Scholar] [CrossRef]
- Richter, F.; Leaver-Fay, A.; Khare, S.D.; Bjelic, S.; Baker, D. De Novo Enzyme Design Using Rosetta3. PLoS ONE 2011, 6, e19230. [Google Scholar] [CrossRef] [PubMed]
- Kaufmann, K.W.; Lemmon, G.H.; Deluca, S.L.; Sheehan, J.H.; Meiler, J. Practically Useful: What the Rosetta Protein Modeling Suite Can Do for You. Biochemistry 2010, 49, 2987–2998. [Google Scholar] [CrossRef]
- Zanghellini, A.; Jiang, L.; Wollacott, A.M.; Cheng, G.; Meiler, J.; Althoff, E.A.; Röthlisberger, D.; Röthlisberger, R.; Baker, D. New Algorithms and an in Silico Benchmark for Computational Enzyme Design. Protein Sci. 2006, 15, 2785. [Google Scholar] [CrossRef] [PubMed]
- Roda, S.; Terholsen, H.; Meyer, J.R.H.; Cañellas-Solé, A.; Guallar, V.; Bornscheuer, U.; Kazemi, M. AsiteDesign: A Semirational Algorithm for an Automated Enzyme Design. J. Phys. Chem. 2023, 127, 2661–2670. [Google Scholar] [CrossRef] [PubMed]
- Weitzner, B.D.; Kipnis, Y.; Daniel, A.G.; Hilvert, D.; Baker, D. A Computational Method for Design of Connected Catalytic Networks in Proteins. Protein Sci. 2019, 28, 2036–2041. [Google Scholar] [CrossRef]
- Khersonsky, O.; Röthlisberger, D.; Wollacott, A.M.; Murphy, P.; Dym, O.; Albeck, S.; Kiss, G.; Houk, K.N.; Baker, D.; Tawfik, D.S. Optimization of the In-Silico-Designed Kemp Eliminase KE70 by Computational Design and Directed Evolution. J. Mol. Biol. 2011, 407, 391–412. [Google Scholar] [CrossRef]
- Pan, X.; Kortemme, T. Recent Advances in de Novo Protein Design: Principles, Methods, and Applications. J. Biol. Chem. 2021, 296, 100558. [Google Scholar] [CrossRef] [PubMed]
- Siegel, J.B.; Zanghellini, A.; Lovick, H.M.; Kiss, G.; Lambert, A.R.; St. Clair, J.L.; Gallaher, J.L.; Hilvert, D.; Gelb, M.H.; Stoddard, B.L.; et al. Computational Design of an Enzyme Catalyst for a Stereoselective Bimolecular Diels-Alder Reaction. Science 2010, 329, 309–313. [Google Scholar] [CrossRef]
- Li, G.; Xu, L.; Zhang, H.; Liu, J.; Yan, J.; Yan, Y. A De Novo Designed Esterase with P-Nitrophenyl Acetate Hydrolysis Activity. Molecules 2020, 25, 4658. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Althoff, E.A.; Clemente, F.R.; Doyle, L.; Röthlisberger, D.; Zanghellini, A.; Gallaher, J.L.; Betker, J.L.; Tanaka, F.; Barbas, C.F.; et al. De Novo Computational Design of Retro-Aldol Enzymes. Science 2008, 319, 1387–1391. [Google Scholar] [CrossRef] [PubMed]
- Holst, L.H.; Madsen, N.G.; Toftgård, F.T.; Rønne, F.; Moise, I.M.; Petersen, E.I.; Fojan, P. De Novo Design of a Polycarbonate Hydrolase. Protein Eng. Des. Sel. 2023, 36, gzad022. [Google Scholar] [CrossRef] [PubMed]
- Satta, A.; Zampieri, G.; Loprete, G.; Campanaro, S.; Treu, L.; Bergantino, E.; Satta, A.; Zampieri, G.; Loprete, G.; Campanaro, S.; et al. Metabolic and Enzymatic Engineering Strategies for Polyethylene Terephthalate Degradation and Valorization. Rev. Environ. Sci. Biotechnol. 2024, 23, 351–383. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, P.; Cao, M.; Yu, T.; Lane, S.T.; Zhao, H. Directed Evolution: Methodologies and Applications. Chem. Rev. 2021, 121, 12384–12444. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.; Bao, Z.; Zhao, H. High Throughput Screening and Selection Methods for Directed Enzyme Evolution. Ind. Eng. Chem. Res. 2015, 54, 4011–4020. [Google Scholar] [CrossRef]
- Lutz, S. Beyond Directed Evolution-Semi-Rational Protein Engineering and Design. Curr. Opin. Biotechnol. 2010, 21, 734. [Google Scholar] [CrossRef] [PubMed]
- de Almeida Paiva, V.; de Souza Gomes, I.; Monteiro, C.R.; Mendonça, M.V.; Martins, P.M.; Santana, C.A.; Gonçalves-Almeida, V.; Izidoro, S.C.; de Melo-Minardi, R.C.; de Azevedo Silveira, S. Protein Structural Bioinformatics: An Overview. Comput. Biol. Med. 2022, 147, 105695. [Google Scholar] [CrossRef]
- Cantarel, B.I.; Coutinho, P.M.; Rancurel, C.; Bernard, T.; Lombard, V.; Henrissat, B. The Carbohydrate-Active EnZymes Database (CAZy): An Expert Resource for Glycogenomics. Nucleic Acids Res. 2008, 37, D233. [Google Scholar] [CrossRef] [PubMed]
- Buchholz, P.C.F.; Feuerriegel, G.; Zhang, H.; Perez-Garcia, P.; Nover, L.L.; Chow, J.; Streit, W.R.; Pleiss, J. Plastics Degradation by Hydrolytic Enzymes: The Plastics-Active Enzymes Database—PAZy. Proteins 2022, 90, 1443–1456. [Google Scholar] [CrossRef] [PubMed]
- Camacho, C.; Coulouris, G.; Avagyan, V.; Ma, N.; Papadopoulos, J.; Bealer, K.; Madden, T.L. BLAST+: Architecture and Applications. BMC Bioinform. 2009, 10, 421. [Google Scholar] [CrossRef]
- Steinegger, M.; Söding, J. MMseqs2 Enables Sensitive Protein Sequence Searching for the Analysis of Massive Data Sets. Nat. Biotechnol. 2017, 35, 1026–1028. [Google Scholar] [CrossRef] [PubMed]
- van Kempen, M.; Kim, S.S.; Tumescheit, C.; Mirdita, M.; Lee, J.; Gilchrist, C.L.M.; Söding, J.; Steinegger, M. Fast and Accurate Protein Structure Search with Foldseek. Nat. Biotechnol. 2023, 42, 243–246. [Google Scholar] [CrossRef]
- Illergård, K.; Ardell, D.H.; Elofsson, A. Structure Is Three to Ten Times More Conserved than Sequence—A Study of Structural Response in Protein Cores. Proteins 2009, 77, 499–508. [Google Scholar] [CrossRef] [PubMed]
- Musil, M.; Jezik, A.; Horackova, J.; Borko, S.; Kabourek, P.; Damborsky, J.; Bednar, D. FireProt 2.0: Web-Based Platform for the Fully Automated Design of Thermostable Proteins. Brief. Bioinform. 2023, 25, bbad425. [Google Scholar] [CrossRef]
- Risso, V.A.; Sanchez-Ruiz, J.M.; Ozkan, S.B. Biotechnological and Protein-Engineering Implications of Ancestral Protein Resurrection. Curr. Opin. Struct. Biol. 2018, 51, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Livada, J.; Vargas, A.M.; Martinez, C.A.; Lewis, R.D. Ancestral Sequence Reconstruction Enhances Gene Mining Efforts for Industrial Ene Reductases by Expanding Enzyme Panels with Thermostable Catalysts. ACS Catal. 2023, 13, 2576–2585. [Google Scholar] [CrossRef]
- Musil, M.; Khan, R.T.; Beier, A.; Stourac, J.; Konegger, H.; Damborsky, J.; Bednar, D. FireProtASR: A Web Server for Fully Automated Ancestral Sequence Reconstruction. Brief. Bioinform. 2021, 22, bbaa337. [Google Scholar] [CrossRef]
- Ashkenazy, H.; Abadi, S.; Martz, E.; Chay, O.; Mayrose, I.; Pupko, T.; Ben-Tal, N. ConSurf 2016: An Improved Methodology to Estimate and Visualize Evolutionary Conservation in Macromolecules. Nucleic Acids Res 2016, 44, W344–W350. [Google Scholar] [CrossRef]
- Pavelka, A.; Chovancova, E.; Damborsky, J. HotSpot Wizard: A Web Server for Identification of Hot Spots in Protein Engineering. Nucleic Acids Res. 2009, 37, W376–W383. [Google Scholar] [CrossRef] [PubMed]
- Kamisetty, H.; Ovchinnikov, S.; Baker, D. Assessing the Utility of Coevolution-Based Residue-Residue Contact Predictions in a Sequence- and Structure-Rich Era. Proc. Natl. Acad. Sci. USA 2013, 110, 15674–15679. [Google Scholar] [CrossRef] [PubMed]
- Hopf, T.A.; Green, A.G.; Schubert, B.; Mersmann, S.; Schärfe, C.P.I.; Ingraham, J.B.; Toth-Petroczy, A.; Brock, K.; Riesselman, A.J.; Palmedo, P.; et al. The EVcouplings Python Framework for Coevolutionary Sequence Analysis. Bioinformatics 2019, 35, 1582–1584. [Google Scholar] [CrossRef]
- Hopf, T.A.; Ingraham, J.B.; Poelwijk, F.J.; Schärfe, C.P.I.; Springer, M.; Sander, C.; Marks, D.S. Mutation Effects Predicted from Sequence Co-Variation. Nat. Biotechnol. 2017, 35, 128–135. [Google Scholar] [CrossRef] [PubMed]
- Voigt, C.A.; Martinez, C.; Wang, Z.G.; Mayo, S.L.; Arnold, F.H. Protein Building Blocks Preserved by Recombination. Nat. Struct. Biol. 2002, 9, 553–558. [Google Scholar] [CrossRef] [PubMed]
- Meyer, M.M.; Hochrein, L.; Arnold, F.H. Structure-Guided SCHEMA Recombination of Distantly Related β-Lactamases. PEDS 2006, 19, 563–570. [Google Scholar] [CrossRef]
- Schenkmayerova, A.; Pinto, G.P.; Toul, M.; Marek, M.; Hernychova, L.; Planas-Iglesias, J.; Daniel Liskova, V.; Pluskal, D.; Vasina, M.; Emond, S.; et al. Engineering the Protein Dynamics of an Ancestral Luciferase. Nat. Commun. 2021, 12, 3616. [Google Scholar] [CrossRef] [PubMed]
- Notin, P.; Rollins, N.; Gal, Y.; Sander, C.; Marks, D. Machine Learning for Functional Protein Design. Nat. Biotechnol. 2024, 42, 216–228. [Google Scholar] [CrossRef] [PubMed]
- Shinde, P.P.; Shah, S. A Review of Machine Learning and Deep Learning Applications. In Proceedings of the 2018 4th International Conference on Computing, Communication Control and Automation, ICCUBEA, Pune, India, 16–18 August 2018. [Google Scholar] [CrossRef]
- Narayanan, H.; Dingfelder, F.; Butté, A.; Lorenzen, N.; Sokolov, M.; Arosio, P. Machine Learning for Biologics: Opportunities for Protein Engineering, Developability, and Formulation. Trends Pharmacol. Sci. 2021, 42, 151–165. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Tan, C.; Wu, L.; Zheng, J.; Xia, J.; Gao, Z.; Liu, Z.; Wu, F.; Zhang, G.; Li, S.Z. Advances of Deep Learning in Protein Science: A Comprehensive Survey. arXiv 2024, arXiv:2403.05314. [Google Scholar]
- Mirdita, M.; Schütze, K.; Moriwaki, Y.; Heo, L.; Ovchinnikov, S.; Steinegger, M. ColabFold: Making Protein Folding Accessible to All. Nat. Methods 2022, 19, 679–682. [Google Scholar] [CrossRef] [PubMed]
- Wolf, T.; Debut, L.; Sanh, V.; Chaumond, J.; Delangue, C.; Moi, A.; Cistac, P.; Rault, T.; Louf, R.; Funtowicz, M.; et al. Transformers: State-of-the-Art Natural Language Processing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations; Association for Computational Linguistics: Kerrville, TX, USA, 2020; pp. 38–45. [Google Scholar] [CrossRef]
- Crisci, C.; Ghattas, B.; Perera, G. A Review of Supervised Machine Learning Algorithms and Their Applications to Ecological Data. Ecol. Modell. 2012, 240, 113–122. [Google Scholar] [CrossRef]
- Lampropoulos, A.S.; Tsihrintzis, G.A. The Learning Problem. In Machine Learning Paradigms, Intelligent Systems Reference Library 92; Springer: Cham, Switzerland, 2015; pp. 31–61. ISBN 9783319191348. [Google Scholar]
- Li, H.; Zhang, R.; Min, Y.; Ma, D.; Zhao, D.; Zeng, J. A Knowledge-Guided Pre-Training Framework for Improving Molecular Representation Learning. Nat. Commun. 2023, 14, 7568. [Google Scholar] [CrossRef] [PubMed]
- Elnaggar, A.; Heinzinger, M.; Dallago, C.; Rehawi, G.; Wang, Y.; Jones, L.; Gibbs, T.; Feher, T.; Angerer, C.; Steinegger, M.; et al. ProtTrans: Toward Understanding the Language of Life Through Self-Supervised Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 7112–7127. [Google Scholar] [CrossRef]
- Rives, A.; Meier, J.; Sercu, T.; Goyal, S.; Lin, Z.; Liu, J.; Guo, D.; Ott, M.; Zitnick, C.L.; Ma, J.; et al. Biological Structure and Function Emerge from Scaling Unsupervised Learning to 250 Million Protein Sequences. Proc. Natl. Acad. Sci. USA 2021, 118, e2016239118. [Google Scholar] [CrossRef] [PubMed]
- Chu, S.K.S.; Narang, K.; Siegel, J.B. Protein Stability Prediction by Fine-Tuning a Protein Language Model on a Mega-Scale Dataset. PLoS Comput. Biol. 2024, 20, e1012248. [Google Scholar] [CrossRef]
- Kroll, A.; Ranjan, S.; Engqvist, M.K.M.; Lercher, M.J. A General Model to Predict Small Molecule Substrates of Enzymes Based on Machine and Deep Learning. Nat. Commun. 2023, 14, 2787. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Mei, C.; Zhou, Y.; Wang, Y.; Zheng, C.; Zhen, X.; Xiong, Y.; Chen, P.; Zhang, J.; Wang, B. Semi-Supervised Prediction of Protein Interaction Sites from Unlabeled Sample Information. BMC Bioinform. 2019, 20, 699. [Google Scholar] [CrossRef] [PubMed]
- Angermueller, C.; Dohan, D.; Belanger, D.; Deshpande, R.; Murphy, K.; Colwell, L. Model-Based Reinforcement Learning for Biological Sequence Design. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Sun, H.; He, L.; Deng, P.; Liu, G.; Liu, H.; Cao, C.; Ju, F.; Wu, L.; Qin, T.; Liu, T.-Y. Accelerating Protein Engineering with Fitness Landscape Modeling and Reinforcement Learning. bioRxiv 2024. [Google Scholar] [CrossRef]
- Olivecrona, M.; Blaschke, T.; Engkvist, O.; Chen, H. Molecular De-Novo Design through Deep Reinforcement Learning. J. Cheminform 2017, 9, 48. [Google Scholar] [CrossRef]
- AlOmari, M.; AlOmari, A.; Alsmadi, I. CASP Dataset and Protein Structures Prediction. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Harding-Larsen, D.; Funk, J.; Madsen, N.G.; Gharabli, H.; Acevedo-Rocha, C.G.; Mazurenko, S.; Welner, D.H. Protein Representations: Encoding Biological Information for Machine Learning in Biocatalysis. Biotechnol. Adv. 2024, 77, 108459. [Google Scholar] [CrossRef] [PubMed]
- Sayers, E.W.; Beck, J.; Bolton, E.E.; Bourexis, D.; Brister, J.R.; Canese, K.; Comeau, D.C.; Funk, K.; Kim, S.; Klimke, W.; et al. Database Resources of the National Center for Biotechnology Information. Nucleic Acids Res. 2021, 49, D10–D17. [Google Scholar] [CrossRef] [PubMed]
- Chen, I.M.A.; Chu, K.; Palaniappan, K.; Pillay, M.; Ratner, A.; Huang, J.; Huntemann, M.; Varghese, N.; White, J.R.; Seshadri, R.; et al. IMG/M v.5.0: An Integrated Data Management and Comparative Analysis System for Microbial Genomes and Microbiomes. Nucleic Acids Res. 2019, 47, D666–D677. [Google Scholar] [CrossRef]
- Reimer, L.C.; Sardà Carbasse, J.; Koblitz, J.; Ebeling, C.; Podstawka, A.; Overmann, J. BacDive in 2022: The Knowledge Base for Standardized Bacterial and Archaeal Data. Nucleic Acids Res 2021, 50, D741. [Google Scholar] [CrossRef] [PubMed]
- Erickson, E.; Gado, J.E.; Avilán, L.; Bratti, F.; Brizendine, R.K.; Cox, P.A.; Gill, R.; Graham, R.; Kim, D.J.; König, G.; et al. Sourcing Thermotolerant Poly(Ethylene Terephthalate) Hydrolase Scaffolds from Natural Diversity. Nat. Commun. 2022, 13, 7850. [Google Scholar] [CrossRef]
- Zhang, Y.; Guan, F.; Xu, G.; Liu, X.; Zhang, Y.; Sun, J.; Yao, B.; Huang, H.; Wu, N.; Tian, J. A Novel Thermophilic Chitinase Directly Mined from the Marine Metagenome Using the Deep Learning Tool Preoptem. Bioresour. Bioprocess. 2022, 9, 54. [Google Scholar] [CrossRef]
- Hasegawa, N.; Sugiyama, M.; Igarashi, K. Random Forest Machine-Learning Algorithm Classifies White- and Brown-Rot Fungi According to the Number of the Genes Encoding Carbohydrate-Active EnZyme Families. Appl. Environ. Microbiol. 2024, 90, e0048224. [Google Scholar] [CrossRef]
- Jiang, R.; Yue, Z.; Shang, L.; Wang, D.; Wei, N. PEZy-Miner: An Artificial Intelligence Driven Approach for the Discovery of Plastic-Degrading Enzyme Candidates. Metab. Eng. Commun. 2024, 19, e00248. [Google Scholar] [CrossRef] [PubMed]
- Chang, A.; Jeske, L.; Ulbrich, S.; Hofmann, J.; Koblitz, J.; Schomburg, I.; Neumann-Schaal, M.; Jahn, D.; Schomburg, D. BRENDA, the ELIXIR Core Data Resource in 2021: New Developments and Updates. Nucleic Acids Res 2021, 49, D498–D508. [Google Scholar] [CrossRef] [PubMed]
- Wittig, U.; Rey, M.; Weidemann, A.; Kania, R.; Müller, W. SABIO-RK: An Updated Resource for Manually Curated Biochemical Reaction Kinetics. Nucleic Acids Res. 2018, 46, D656–D660. [Google Scholar] [CrossRef]
- Li, F.; Yuan, L.; Lu, H.; Li, G.; Chen, Y.; Engqvist, M.K.M.; Kerkhoven, E.J.; Nielsen, J. Deep Learning-Based Kcat Prediction Enables Improved Enzyme-Constrained Model Reconstruction. Nat. Catal. 2022, 5, 662–672. [Google Scholar] [CrossRef]
- Kroll, A.; Rousset, Y.; Hu, X.P.; Liebrand, N.A.; Lercher, M.J. Turnover Number Predictions for Kinetically Uncharacterized Enzymes Using Machine and Deep Learning. Nat. Commun. 2023, 14, 4139. [Google Scholar] [CrossRef] [PubMed]
- Lauterbach, S.; Dienhart, H.; Range, J.; Malzacher, S.; Spöring, J.D.; Rother, D.; Pinto, M.F.; Martins, P.; Lagerman, C.E.; Bommarius, A.S.; et al. EnzymeML: Seamless Data Flow and Modeling of Enzymatic Data. Nat. Methods 2023, 20, 400–402. [Google Scholar] [CrossRef]
- Charoenkwan, P.; Schaduangrat, N.; Moni, M.A.; Lio’, P.; Manavalan, B.; Shoombuatong, W. SAPPHIRE: A Stacking-Based Ensemble Learning Framework for Accurate Prediction of Thermophilic Proteins. Comput. Biol. Med. 2022, 146, 105704. [Google Scholar] [CrossRef]
- Nikam, R.; Kulandaisamy, A.; Harini, K.; Sharma, D.; Michael Gromiha, M. ProThermDB: Thermodynamic Database for Proteins and Mutants Revisited after 15 Years. Nucleic Acids Res. 2021, 49, D420–D424. [Google Scholar] [CrossRef] [PubMed]
- Stourac, J.; Dubrava, J.; Musil, M.; Horackova, J.; Damborsky, J.; Mazurenko, S.; Bednar, D. FireProtDB: Database of Manually Curated Protein Stability Data. Nucleic Acids Res. 2021, 49, D319–D324. [Google Scholar] [CrossRef]
- Dieckhaus, H.; Brocidiacono, M.; Randolph, N.Z.; Kuhlman, B. Transfer Learning to Leverage Larger Datasets for Improved Prediction of Protein Stability Changes. Proc. Natl. Acad. Sci. USA 2024, 121, e2314853121. [Google Scholar] [CrossRef]
- Gilson, M.K.; Liu, T.; Baitaluk, M.; Nicola, G.; Hwang, L.; Chong, J. BindingDB in 2015: A Public Database for Medicinal Chemistry, Computational Chemistry and Systems Pharmacology. Nucleic Acids Res 2015, 44, D1045. [Google Scholar] [CrossRef]
- Wang, R.; Fang, X.; Lu, Y.; Yang, C.Y.; Wang, S. The PDBbind Database: Methodologies and Updates. J. Med. Chem. 2005, 48, 4111–4119. [Google Scholar] [CrossRef] [PubMed]
- Velecký, J.; Hamsikova, M.; Stourac, J.; Musil, M.; Damborsky, J.; Bednar, D.; Mazurenko, S. SoluProtMutDB: A Manually Curated Database of Protein Solubility Changes upon Mutations. Comput. Struct. Biotechnol. J. 2022, 20, 6339. [Google Scholar] [CrossRef] [PubMed]
- Teufel, F.; Almagro Armenteros, J.J.; Johansen, A.R.; Gíslason, M.H.; Pihl, S.I.; Tsirigos, K.D.; Winther, O.; Brunak, S.; von Heijne, G.; Nielsen, H. SignalP 6.0 Predicts All Five Types of Signal Peptides Using Protein Language Models. Nat. Biotechnol. 2022, 40, 1023–1025. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Nie, Z.; Hong, M.; Zhao, S.; Zhou, H.; Nie, Z. MutaPLM: Protein Language Modeling for Mutation Explanation and Engineering. arXiv 2024, arXiv:2410.22949 (accessed on 13 January 2025). [Google Scholar] [CrossRef]
- Li, F.; Chen, Y.; Anton, M.; Nielsen, J. GotEnzymes: An Extensive Database of Enzyme Parameter Predictions. Nucleic Acids Res. 2023, 51, D583–D586. [Google Scholar] [CrossRef]
- Varadi, M.; Anyango, S.; Deshpande, M.; Nair, S.; Natassia, C.; Yordanova, G.; Yuan, D.; Stroe, O.; Wood, G.; Laydon, A.; et al. AlphaFold Protein Structure Database: Massively Expanding the Structural Coverage of Protein-Sequence Space with High-Accuracy Models. Nucleic Acids Res. 2022, 50, D439–D444. [Google Scholar] [CrossRef]
- Li, Y.; Fang, J. PROTS-RF: A Robust Model for Predicting Mutation-Induced Protein Stability Changes. PLoS ONE 2012, 7, e47247. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Rawi, R.; Mall, R.; Kunji, K.; Shen, C.H.; Kwong, P.D.; Chuang, G.Y. PaRSnIP: Sequence-Based Protein Solubility Prediction Using Gradient Boosting Machine. Bioinformatics 2018, 34, 1092–1098. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of Deep Learning: Concepts, CNN Architectures, Challenges, Applications, Future Directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Horne, J.; Shukla, D. Recent Advances in Machine Learning Variant Effect Prediction Tools for Protein Engineering. Ind. Eng. Chem. Res. 2022, 61, 6235–6245. [Google Scholar] [CrossRef] [PubMed]
- Petrovski, Ž.H.; Hribar-Lee, B.; Bosnić, Z. CAT-Site: Predicting Protein Binding Sites Using a Convolutional Neural Network. Pharmaceutics 2022, 15, 119. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Wang, C.; Lo, C.C.; Liu, X.; Wu, W.; Zhang, J. ProDCoNN: Protein Design Using a Convolutional Neural Network. Proteins 2020, 88, 819–829. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762 (accessed on 13 January 2025). [Google Scholar] [CrossRef]
- Pei, H.; Li, J.; Ma, S.; Jiang, J.; Li, M.; Zou, Q.; Lv, Z. Identification of Thermophilic Proteins Based on Sequence-Based Bidirectional Representations from Transformer-Embedding Features. Appl. Sci. 2023, 13, 2858. [Google Scholar] [CrossRef]
- Chen, T.; Dumas, M.; Watson, R.; Vincoff, S.; Peng, C.; Zhao, L.; Hong, L.; Pertsemlidis, S.; Shaepers-Cheu, M.; Wang, T.Z.; et al. PepMLM: Target Sequence-Conditioned Generation of Therapeutic Peptide Binders via Span Masked Language Modeling. arXiv 2023, arXiv:2310.03842v3. [Google Scholar]
- Ferruz, N.; Schmidt, S.; Höcker, B. ProtGPT2 Is a Deep Unsupervised Language Model for Protein Design. Nat. Commun. 2022, 13, 4348. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.K.; Fusi, N.; Lu, A.X. Convolutions Are Competitive with Transformers for Protein Sequence Pretraining. Cell Syst. 2024, 15, 286–294.e2. [Google Scholar] [CrossRef] [PubMed]
- Tay, Y.; Dehghani, M.; Gupta, J.; Aribandi, V.; Bahri, D.; Qin, Z.; Metzler, D. Are Pre-Trained Convolutions Better than Pre-Trained Transformers? In Proceedings of the ACL-IJCNLP 2021-59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing, Proceedings of the Conference, Virtual, 1–6 August 2021; pp. 4349–4359. [Google Scholar] [CrossRef]
- Matsoukas, C.; Haslum, J.F.; Söderberg, M.; Smith, K. Is It Time to Replace CNNs with Transformers for Medical Images? arXiv 2021, 9038. [Google Scholar] [CrossRef]
- Yim, J.; Stärk, H.; Corso, G.; Jing, B.; Barzilay, R.; Jaakkola, T.S. Diffusion Models in Protein Structure and Docking. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2024, 14, e1711. [Google Scholar] [CrossRef]
- Watson, J.L.; Juergens, D.; Bennett, N.R.; Trippe, B.L.; Yim, J.; Eisenach, H.E.; Ahern, W.; Borst, A.J.; Ragotte, R.J.; Milles, L.F.; et al. De Novo Design of Protein Structure and Function with RFdiffusion. Nature 2023, 620, 1089–1100. [Google Scholar] [CrossRef] [PubMed]
- Arts, M.; Garcia Satorras, V.; Huang, C.W.; Zügner, D.; Federici, M.; Clementi, C.; Noé, F.; Pinsler, R.; van den Berg, R. Two for One: Diffusion Models and Force Fields for Coarse-Grained Molecular Dynamics. J. Chem. Theory Comput. 2023, 19, 6151–6159. [Google Scholar] [CrossRef]
- Abramson, J.; Adler, J.; Dunger, J.; Evans, R.; Green, T.; Pritzel, A.; Ronneberger, O.; Willmore, L.; Ballard, A.J.; Bambrick, J.; et al. Accurate Structure Prediction of Biomolecular Interactions with AlphaFold 3. Nature 2024, 630, 493–500. [Google Scholar] [CrossRef]
- Jha, K.; Saha, S.; Singh, H. Prediction of Protein–Protein Interaction Using Graph Neural Networks. Sci. Rep. 2022, 12, 8360. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zheng, S.; Zhao, H.; Yang, Y. Structure-Aware Protein Solubility Prediction from Sequence through Graph Convolutional Network and Predicted Contact Map. J. Cheminform 2021, 13, 7. [Google Scholar] [CrossRef] [PubMed]
- Busk, J.; Schmidt, M.N.; Winther, O.; Vegge, T.; Jørgensen, P.B. Graph Neural Network Interatomic Potential Ensembles with Calibrated Aleatoric and Epistemic Uncertainty on Energy and Forces. PCCP 2023, 25, 25828–25837. [Google Scholar] [CrossRef] [PubMed]
- Dauparas, J.; Anishchenko, I.; Bennett, N.; Bai, H.; Ragotte, R.J.; Milles, L.F.; Wicky, B.I.M.; Courbet, A.; de Haas, R.J.; Bethel, N.; et al. Robust Deep Learning–Based Protein Sequence Design Using ProteinMPNN. Science 2022, 378, 49–56. [Google Scholar] [CrossRef] [PubMed]
- Sidak, D.; Schwarzerová, J.; Weckwerth, W.; Waldherr, S. Interpretable Machine Learning Methods for Predictions in Systems Biology from Omics Data. Front. Mol. Biosci. 2022, 9, 926623. [Google Scholar] [CrossRef]
- Hochuli, J.; Helbling, A.; Skaist, T.; Ragoza, M.; Koes, D.R. Visualizing Convolutional Neural Network Protein-Ligand Scoring. J. Mol. Graph. Model. 2018, 84, 96–108. [Google Scholar] [CrossRef]
- Vig, J.; Madani, A.; Varshney, L.R.; Xiong, C.; Socher, R.; Rajani, N.F. BERTology Meets Biology: Interpreting Attention in Protein Language Models. In Proceedings of the ICLR 2021-9th International Conference on Learning Representations, Vienna, Austria, 3–7 May 2021. [Google Scholar] [CrossRef]
- Simon, E.; Zou, J. InterPLM: Discovering Interpretable Features in Protein Language Models via Sparse Autoencoders. bioRxiv 2024. [Google Scholar] [CrossRef]
- Zhang, H.; Themelis, N.J.; Bourtsalas, A. Environmental Impact Assessment of Emissions from Non-Recycled Plastic-to-Energy Processes. Waste Dispos. Sustain. Energy 2021, 3, 1–11. [Google Scholar] [CrossRef]
- Pratiwi, O.A.; Achmadi, U.F.; Kurniawan, R. Microplastic Pollution in Landfill Soil: Emerging Threats the Environmental and Public Health. Environ. Anal. Health Toxicol. 2024, 39, e2024009. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Chen, Y.; Zhang, L.; Wu, J.; Zeng, X.; Shi, X.; Liu, L.; Chen, J. A Comprehensive Review on Enzymatic Biodegradation of Polyethylene Terephthalate. Environ. Res. 2024, 240, 117427. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, S.; Hiraga, K.; Takehana, T.; Taniguchi, I.; Yamaji, H.; Maeda, Y.; Toyohara, K.; Miyamoto, K.; Kimura, Y.; Oda, K. A Bacterium That Degrades and Assimilates Poly(Ethylene Terephthalate). Science 2016, 351, 1196–1199. [Google Scholar] [CrossRef]
- Müller, R.J.; Schrader, H.; Profe, J.; Dresler, K.; Deckwer, W.D. Enzymatic Degradation of Poly(Ethylene Terephthalate): Rapid Hydrolyse Using a Hydrolase from T. fusca. Macromol. Rapid Commun. 2005, 26, 1400–1405. [Google Scholar] [CrossRef]
- Sulaiman, S.; Yamato, S.; Kanaya, E.; Kim, J.J.; Koga, Y.; Takano, K.; Kanaya, S. Isolation of a Novel Cutinase Homolog with Polyethylene Terephthalate-Degrading Activity from Leaf-Branch Compost by Using a Metagenomic Approach. Appl. Environ. Microbiol. 2012, 78, 1556–1562. [Google Scholar] [CrossRef]
- Britton, D.; Liu, C.; Xiao, Y.; Jia, S.; Legocki, J.; Kronenberg, J.; Montclare, J.K. Protein-Engineered Leaf and Branch Compost Cutinase Variants Using Computational Screening and IsPETase Homology. Catal. Today 2024, 433, 114659. [Google Scholar] [CrossRef]
- Liu, F.; Wang, T.; Yang, W.; Zhang, Y.; Gong, Y.; Fan, X.; Wang, G.; Lu, Z.; Wang, J. Current Advances in the Structural Biology and Molecular Engineering of PETase. Front. Bioeng. Biotechnol. 2023, 11, 1263996. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Li, Q.; Liu, P.; Yuan, Y.; Dian, L.; Wang, Q.; Liang, Q.; Su, T.; Qi, Q. Dynamic Docking-Assisted Engineering of Hydrolases for Efficient PET Depolymerization. ACS Catal. 2024, 14, 3627–3639. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, Y.; Liu, X.; Dong, S.; Tian, Y.; Qiao, Y.; Mitra, R.; Han, J.; Li, C.; Han, X.; et al. Computational Redesign of a PETase for Plastic Biodegradation under Ambient Condition by the GRAPE Strategy. ACS Catal. 2021, 11, 1340–1350. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, Y.; Sun, J.; Zhu, T.; Pang, H.; Li, C.; Geng, W.C.; Wu, B. Computational Redesign of a Hydrolase for Nearly Complete PET Depolymerization at Industrially Relevant High-Solids Loading. Nat. Commun. 2024, 15, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Joho, Y.; Royan, S.; Caputo, A.T.; Newton, S.; Peat, T.S.; Newman, J.; Jackson, C.; Ardevol, A. Enhancing PET Degrading Enzymes: A Combinatory Approach. ChemBioChem 2024, 25, e202400084. [Google Scholar] [CrossRef] [PubMed]
- Pirillo, V.; Orlando, M.; Tessaro, D.; Pollegioni, L.; Molla, G. An Efficient Protein Evolution Workflow for the Improvement of Bacterial PET Hydrolyzing Enzymes. Int. J. Mol. Sci. 2022, 23, 264. [Google Scholar] [CrossRef] [PubMed]
- Bell, E.L.; Smithson, R.; Kilbride, S.; Foster, J.; Hardy, F.J.; Ramachandran, S.; Tedstone, A.A.; Haigh, S.J.; Garforth, A.A.; Day, P.J.R.; et al. Directed Evolution of an Efficient and Thermostable PET Depolymerase. Nat. Catal. 2022, 5, 673–681. [Google Scholar] [CrossRef]
- Shi, L.; Liu, P.; Tan, Z.; Zhao, W.; Gao, J.; Gu, Q.; Ma, H.; Liu, H.; Zhu, L. Complete Depolymerization of PET Wastes by an Evolved PET Hydrolase from Directed Evolution. Angew. Chem. Int. Ed. 2023, 62, e202218390. [Google Scholar] [CrossRef]
- Son, H.F.; Cho, I.J.; Joo, S.; Seo, H.; Sagong, H.Y.; Choi, S.Y.; Lee, S.Y.; Kim, K.J. Rational Protein Engineering of Thermo-Stable PETase from Ideonella sakaiensis for Highly Efficient PET Degradation. ACS Catal. 2019, 9, 3519–3526. [Google Scholar] [CrossRef]
- Son, H.F.; Joo, S.; Seo, H.; Sagong, H.Y.; Lee, S.H.; Hong, H.; Kim, K.J. Structural Bioinformatics-Based Protein Engineering of Thermo-Stable PETase from Ideonella sakaiensis. Enzym. Microb. Technol. 2020, 141, 109656. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Yang, L.; Liu, H.; Li, Q.; Xu, G.; Zhang, Y.; Guan, F.; Zhang, Y.; Zhang, W.; Wu, N.; et al. Protein Engineering of Stable IsPETase for PET Plastic Degradation by Premuse. Int. J. Biol. Macromol. 2021, 180, 667–676. [Google Scholar] [CrossRef]
- Ding, Z.; Xu, G.; Miao, R.; Wu, N.; Zhang, W.; Yao, B.; Guan, F.; Huang, H.; Tian, J. Rational Redesign of Thermophilic PET Hydrolase LCCICCG to Enhance Hydrolysis of High Crystallinity Polyethylene Terephthalates. J. Hazard. Mater. 2023, 453, 131386. [Google Scholar] [CrossRef] [PubMed]
- Kulikova, A.V.; Diaz, D.J.; Loy, J.M.; Ellington, A.D.; Wilke, C.O. Learning the Local Landscape of Protein Structures with Convolutional Neural Networks. J. Biol. Phys. 2021, 47, 435–454. [Google Scholar] [CrossRef]
- Koch, J.; Hess, Y.; Bak, C.R.; Petersen, E.I.; Fojan, P. Design of a Novel Peptide with Esterolytic Activity toward PET by Mimicking the Catalytic Motif of Serine Hydrolases. J. Phys. Chem. B 2024, 128, 10363–10372. [Google Scholar] [CrossRef] [PubMed]
- Knott, B.C.; Erickson, E.; Allen, M.D.; Gado, J.E.; Graham, R.; Kearns, F.L.; Pardo, I.; Topuzlu, E.; Anderson, J.J.; Austin, H.P.; et al. Characterization and Engineering of a Two-Enzyme System for Plastics Depolymerization. Proc. Natl. Acad. Sci. USA 2020, 117, 25476–25485. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Zhang, J.; You, S.; Lin, W.; Su, R.; Qi, W. Efficient Thermophilic Polyethylene Terephthalate Hydrolase Enhanced by Cross Correlation-Based Accumulated Mutagenesis Strategy. Bioresour. Technol. 2024, 406, 130929. [Google Scholar] [CrossRef]
- Zeng, W.; Li, X.; Yang, Y.; Min, J.; Huang, J.W.; Liu, W.; Niu, D.; Yang, X.; Han, X.; Zhang, L.; et al. Substrate-Binding Mode of a Thermophilic PET Hydrolase and Engineering the Enzyme to Enhance the Hydrolytic Efficacy. ACS Catal. 2022, 12, 3033–3040. [Google Scholar] [CrossRef]
- Thumarat, U.; Kawabata, T.; Nakajima, M.; Nakajima, H.; Sugiyama, A.; Yazaki, K.; Tada, T.; Waku, T.; Tanaka, N.; Kawai, F. Comparison of Genetic Structures and Biochemical Properties of Tandem Cutinase-Type Polyesterases from Thermobifida alba AHK119. J. Biosci. Bioeng. 2015, 120, 491–497. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigorakis, K.; Ferousi, C.; Topakas, E. Protein Engineering for Industrial Biocatalysis: Principles, Approaches, and Lessons from Engineered PETases. Catalysts 2025, 15, 147. https://doi.org/10.3390/catal15020147
Grigorakis K, Ferousi C, Topakas E. Protein Engineering for Industrial Biocatalysis: Principles, Approaches, and Lessons from Engineered PETases. Catalysts. 2025; 15(2):147. https://doi.org/10.3390/catal15020147
Chicago/Turabian StyleGrigorakis, Konstantinos, Christina Ferousi, and Evangelos Topakas. 2025. "Protein Engineering for Industrial Biocatalysis: Principles, Approaches, and Lessons from Engineered PETases" Catalysts 15, no. 2: 147. https://doi.org/10.3390/catal15020147
APA StyleGrigorakis, K., Ferousi, C., & Topakas, E. (2025). Protein Engineering for Industrial Biocatalysis: Principles, Approaches, and Lessons from Engineered PETases. Catalysts, 15(2), 147. https://doi.org/10.3390/catal15020147








