Simulation of CO2 Catalytic Absorption Process Using Amine Solutions Based on the Lattice Boltzmann Method
Abstract
1. Introduction
2. Results and Discussion
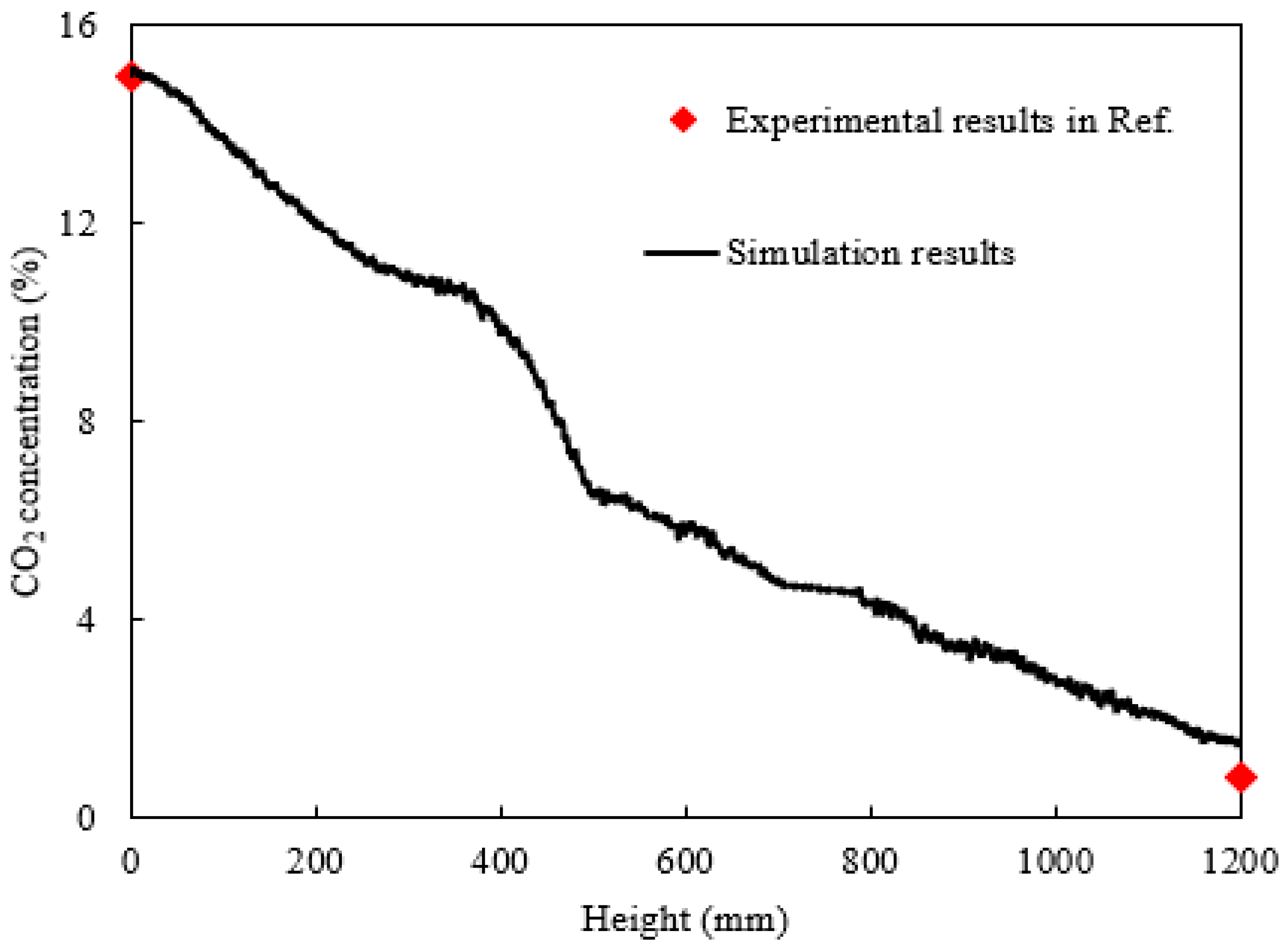
2.1. Verification of LBM Code Accuracy
2.2. Simulation Results for Full-Length Absorption Column
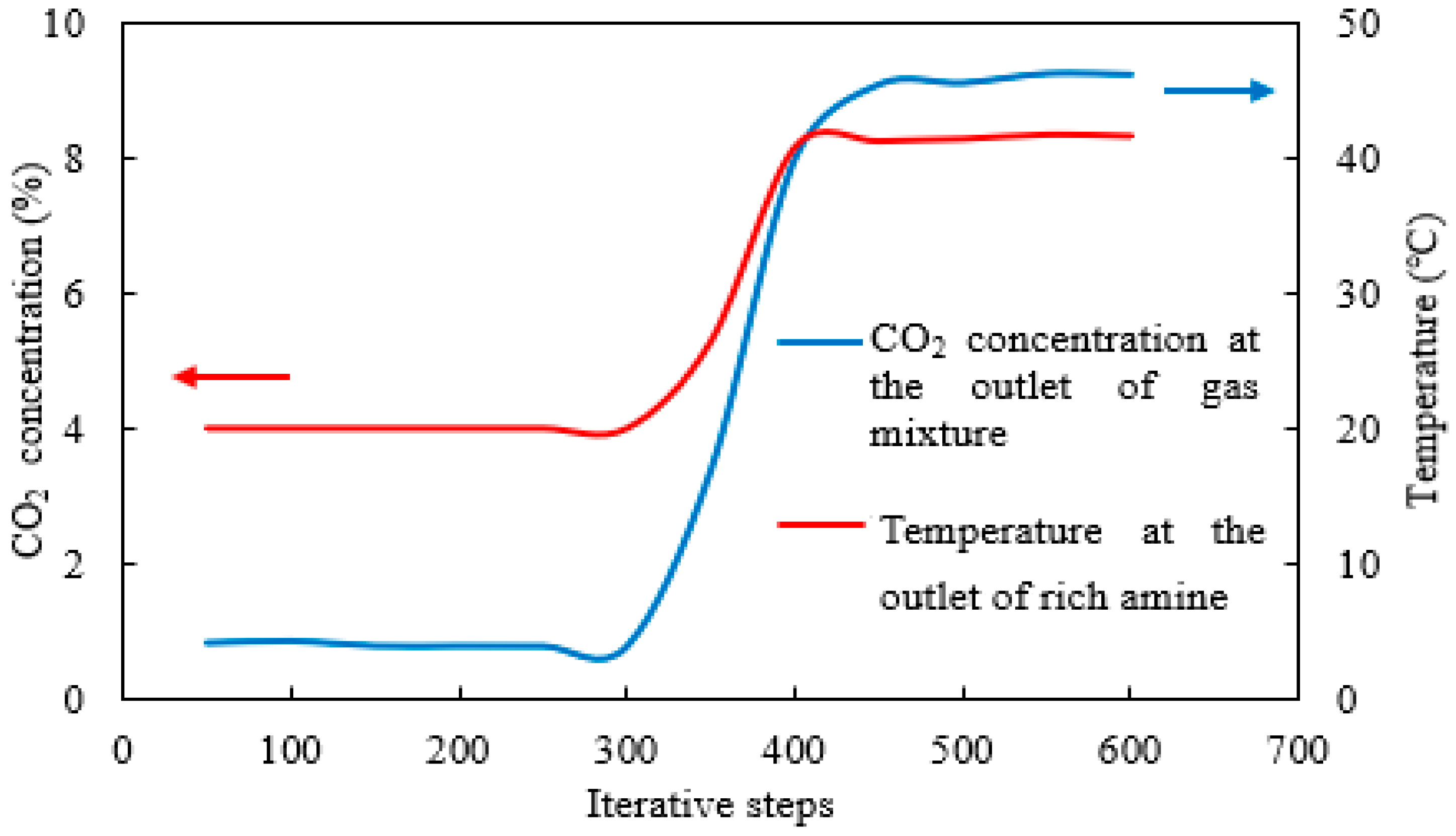
2.3. Simulation Iteration Results and Convergence Analysis
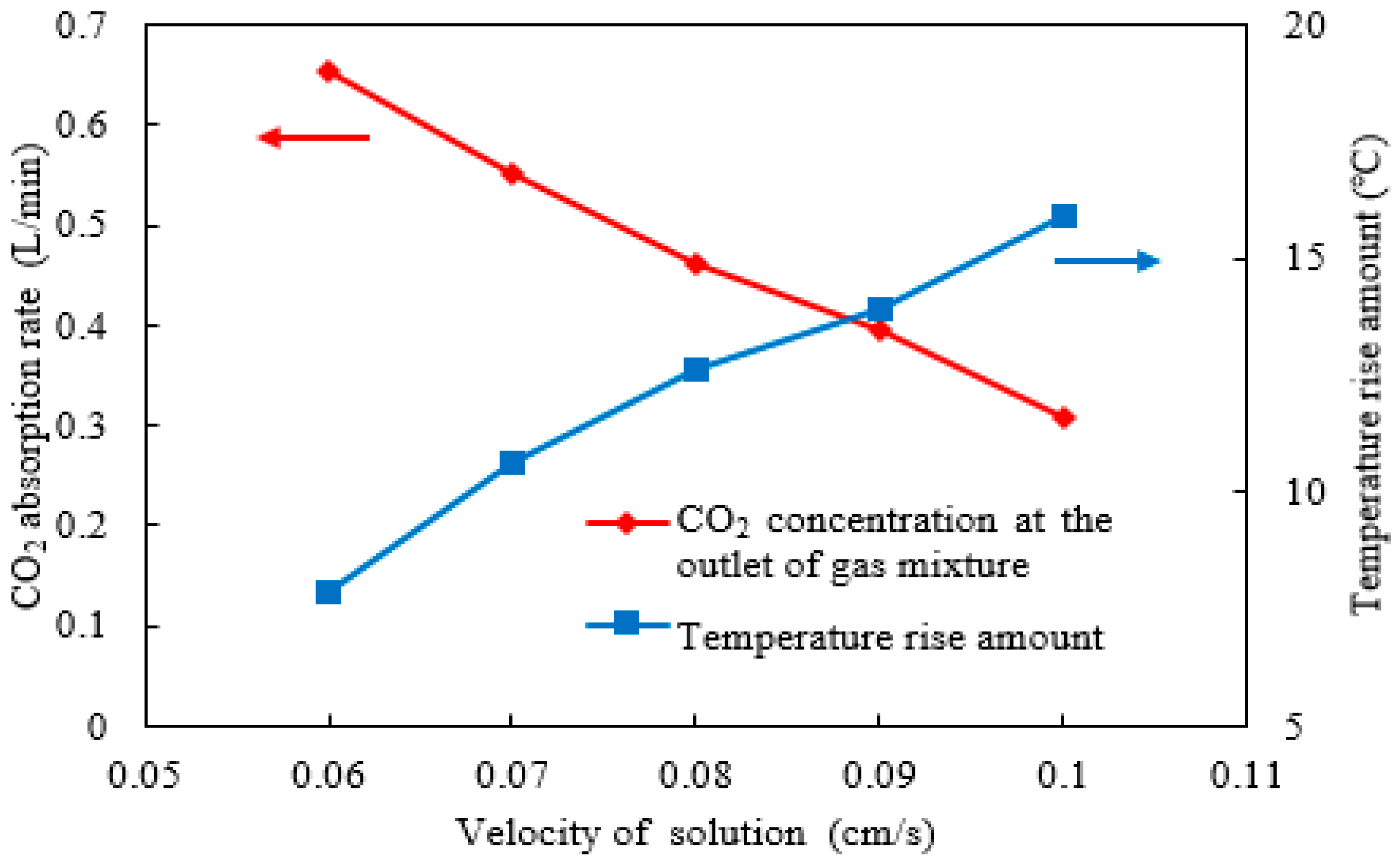
2.4. Effect of Absorbent Solution Velocity
2.5. Effect of Catalyst Volume Fraction
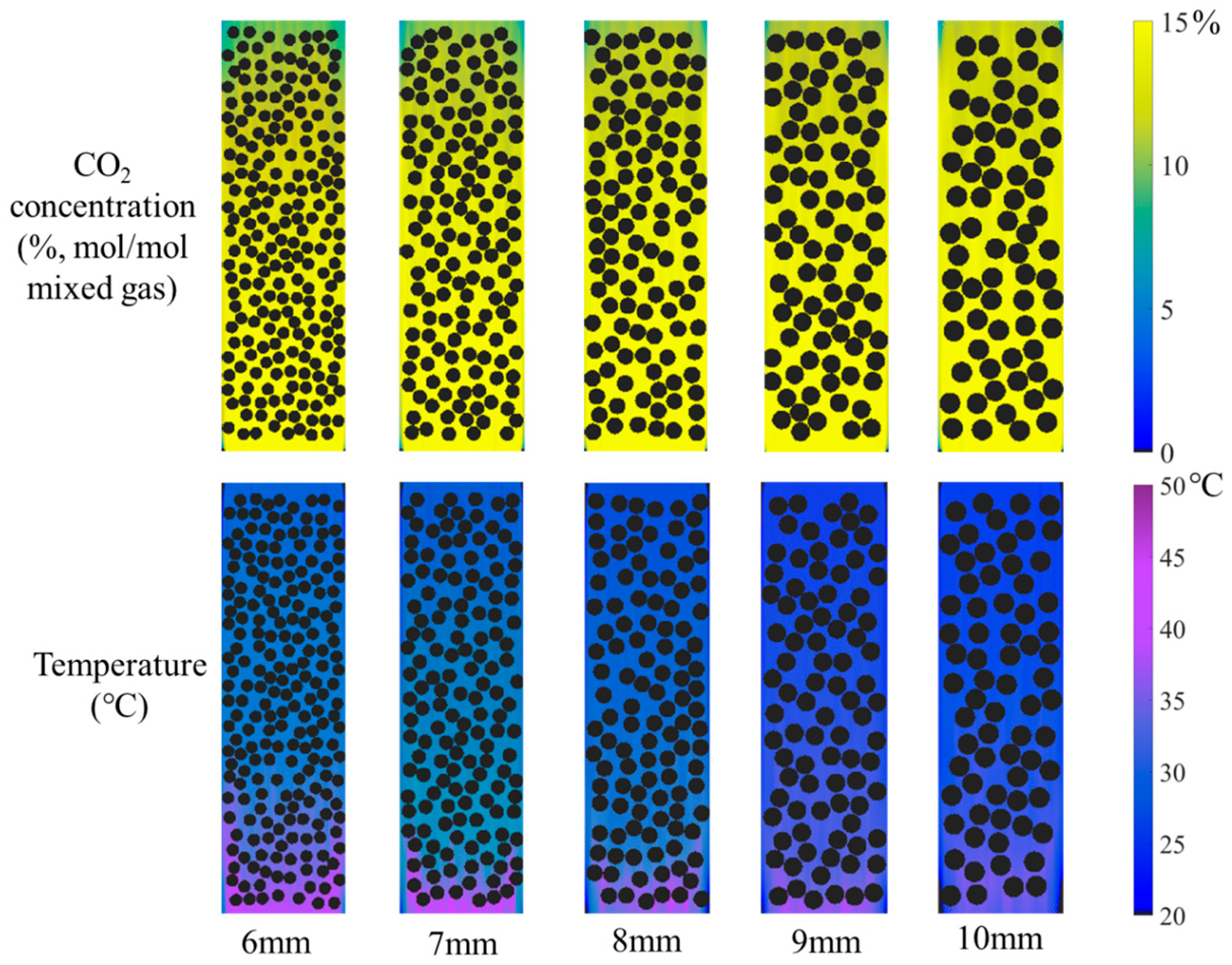
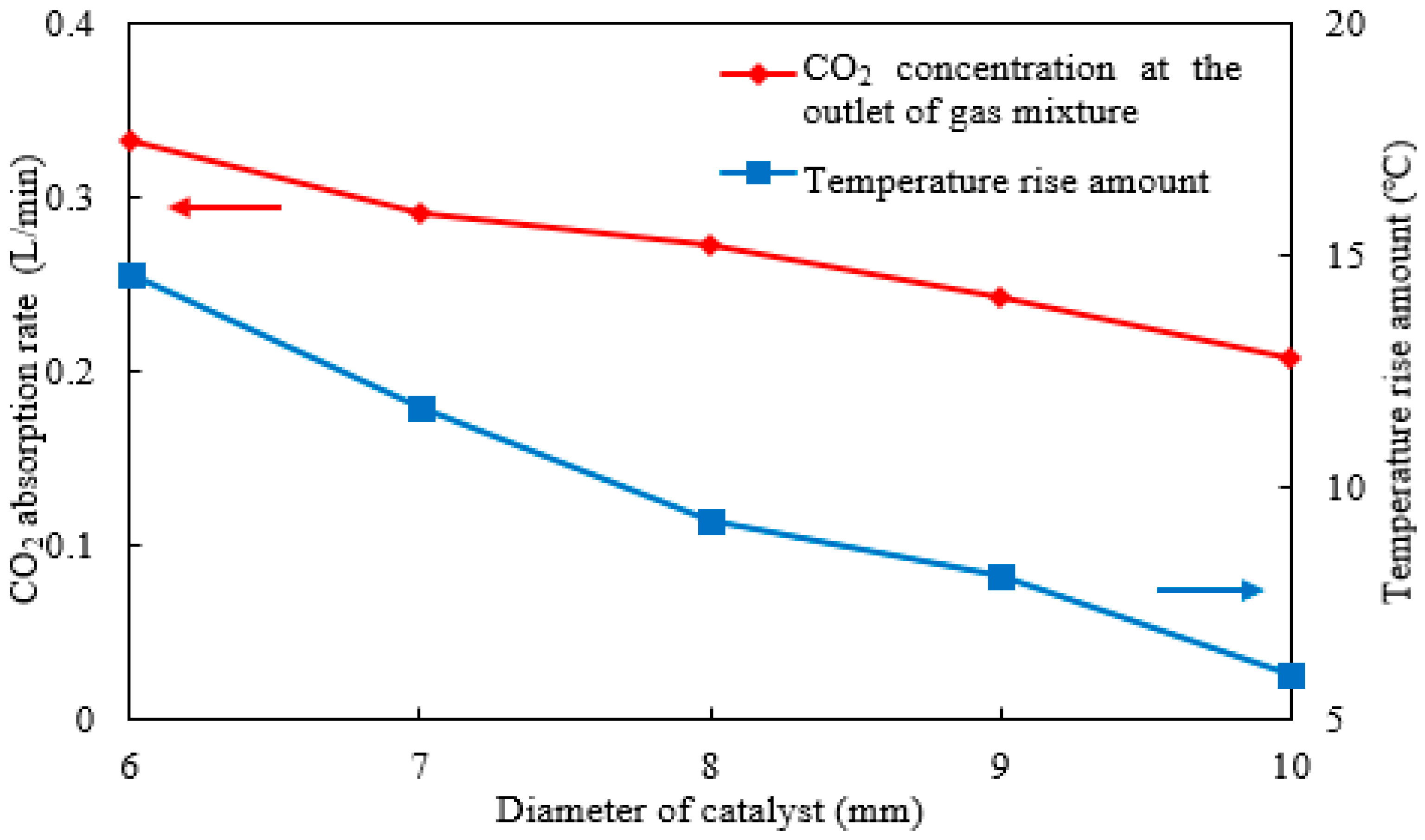
2.6. Effect of Catalyst Size
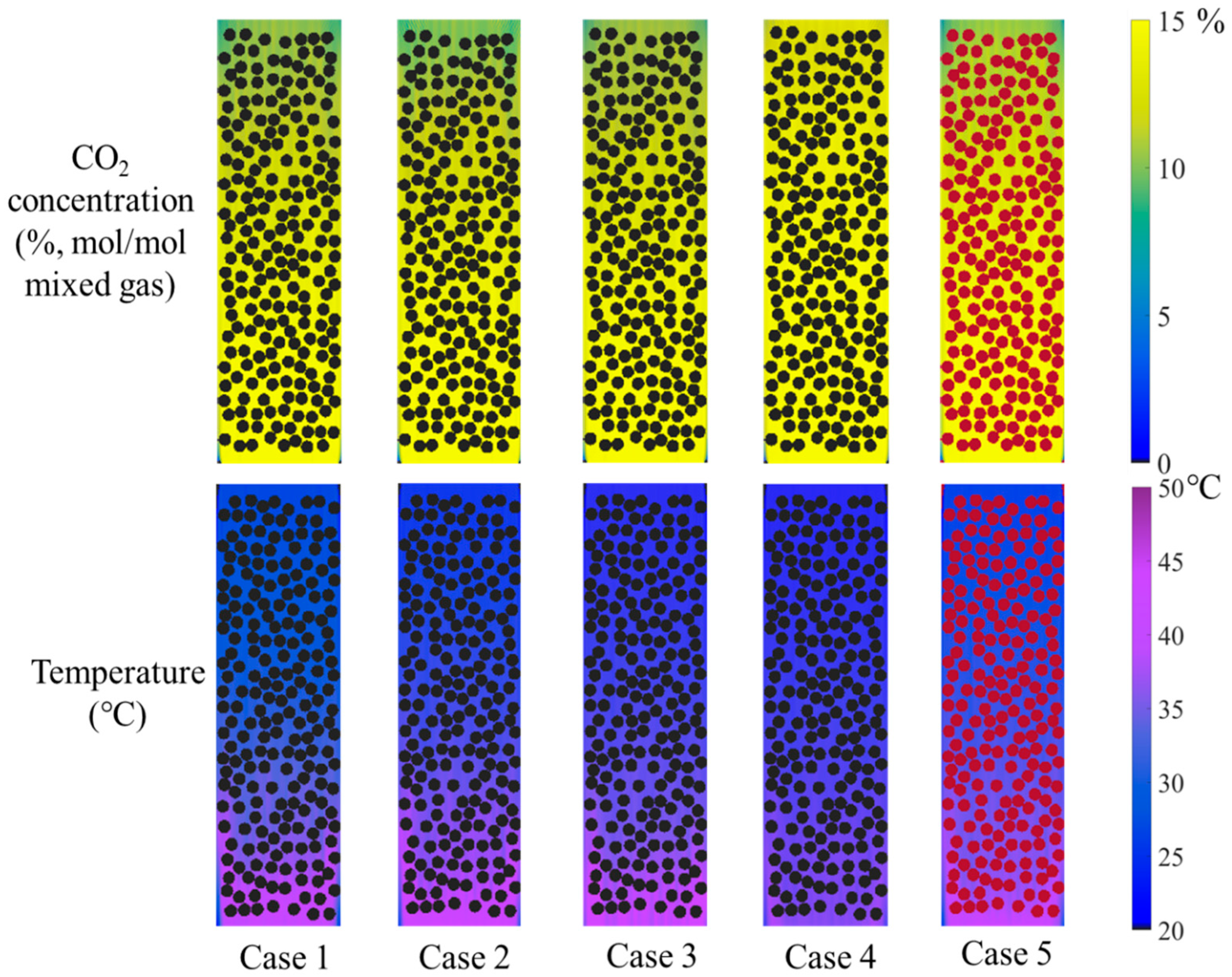
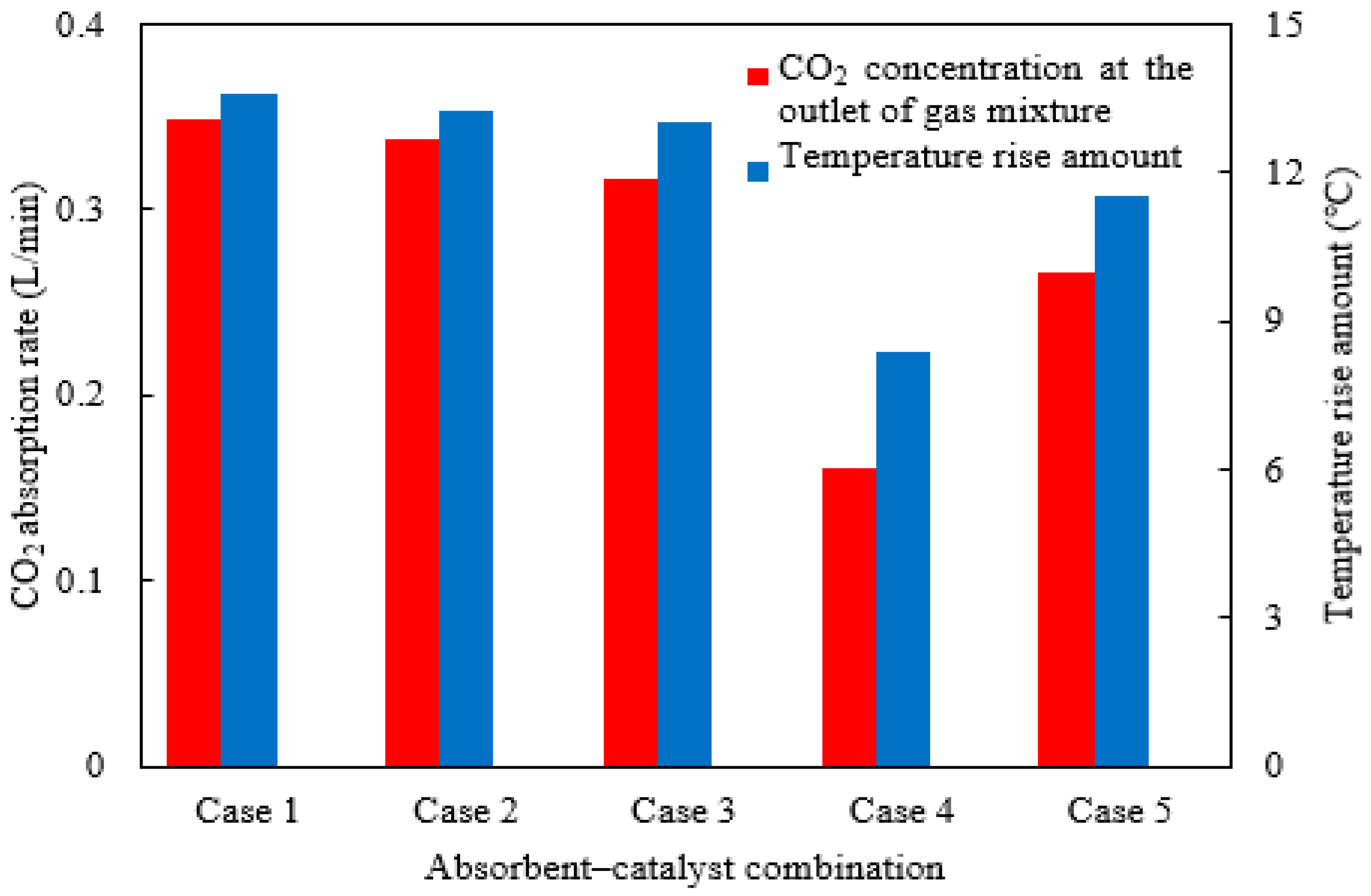
2.7. Effect of Absorbent–Catalyst Combination
3. Model Description
3.1. Lattice Boltzmann Model
3.2. Simulation Conditions
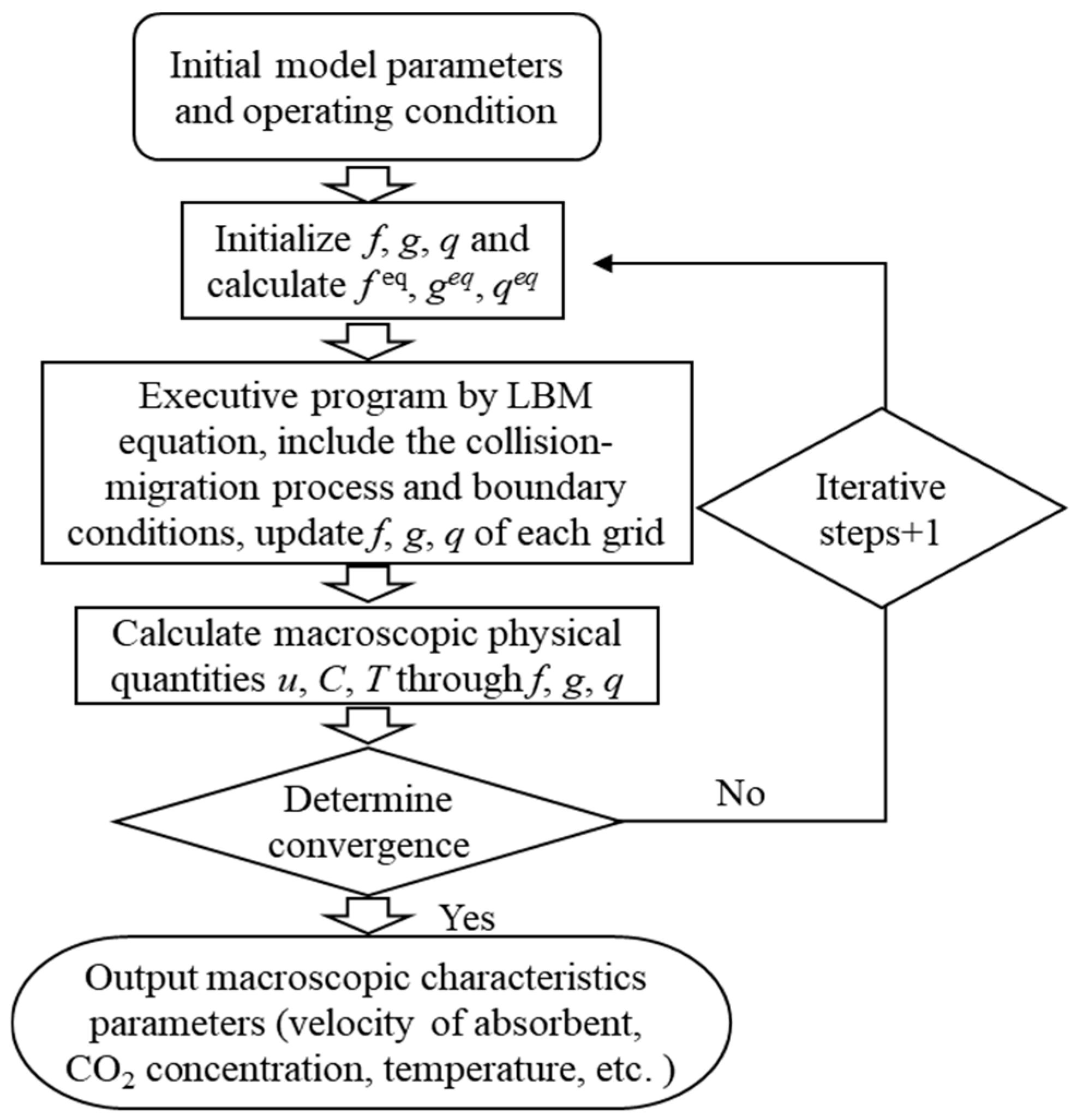
3.3. Simulation Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| C | CO2 concentration (mol/L) |
| cs | The local sound lattice speed |
| e | The lattice vector |
| α | Initial catalytic absorption efficiency (mol CO2/L·min) |
| β | Heat release or temperature increase(°C/L·min) |
| f | Probability distribution function |
| F | External forces or heat sources |
| feq | The equilibrium distribution function |
| f′ | Probability distribution functions after collision |
| f* | Probability distribution functions before collision |
| g | Probability distribution function |
| gin | Probability distribution function before collision step during normal flow |
| gout | Probability distribution function after collision step during normal flow |
| g′ | Probability distribution function after collision |
| g* | Probability distribution function before collision |
| i | The ith direction in D2Q9 model |
| N | Length of the calculation domain |
| q | Probability distribution function |
| qin | Probability distribution function before collision step during normal flow |
| qout | Probability distribution function after collision step during normal flow |
| q′ | Probability distribution function after collision |
| q* | Probability distribution function before collision |
| r | The spatial vector |
| t | Time (s) |
| T | Temperature (°C) |
| u | The macroscopic velocity (m/s) |
| ux | The macroscopic velocity in x direction (m/s) |
| uy | The macroscopic velocity in y direction (m/s) |
| xb | The grid positions at the boundary |
| Δx | The length of the grid (m) |
| Δt | The time increment (s) |
| τ0 | The relaxation time (s) |
| ρ | Density (kg/m3) |
| ω | The weight coefficient |
| κ | Increment coefficient with catalytic absorption |
| κ1 | Increment coefficient with non-catalytic absorption |
| γ | Attenuation coefficient with catalytic absorption |
| γ1 | Attenuation coefficient with non-catalytic absorption |
References
- Li, Y.; Chen, Z.; Yuan, B.; Xing, L.; Zhan, G.; Peng, Y.; Wang, L.; Li, J. Synergistic promotion for CO2 absorption and solvent regeneration by fine waste red mud particles on in amine-based carbon capture: Performance and mechanism. Sep. Purif. Technol. 2023, 304, 122380. [Google Scholar] [CrossRef]
- Rochelle, G.T. Amine Scrubbing for CO2 Capture. Science 2009, 325, 1652–1654. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, R.; Barzagli, F.; Sanku, M.G.; Li, C.; Xiao, M. CO2 absorption in blended amine solvent: Speciation, equilibrium solubility and excessive property. Chem. Eng. J. 2023, 466, 143279. [Google Scholar] [CrossRef]
- Akhdhar, A.; Al-Bogami, A.S.; Akhtar, N.; El-Said, W.A. Progress in Post-Combustion Carbon Dioxide Capture, Direct Air Capture, and Utilization. Catalysts 2025, 15, 807. [Google Scholar] [CrossRef]
- Cao, K.; Cao, K.; Abdillah, O.; Septiani, E.; Hirano, T.; Nguyen, N.; Ogi, T. Correlation between pore characteristics and high-performance carbon dioxide capture of sustainable porous carbon derived from kraft lignin and potassium carbonate. Energy Fuels 2025, 39, 6372–6387. [Google Scholar] [CrossRef]
- Bernhardsen, I.M.; Knuutila, H.K. A review of potential amine solvents for CO2 absorption process: Absorption capacity, cyclic capacity and pKa. Int. J. Greenh. Gas Control 2017, 61, 27–48. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Zhan, G.; Yuan, B.; Wang, L.; Li, J. Inducing efficient proton transfer through Fe/Ni@COF to promote aminebased solvent regeneration for achieving low-cost capture of CO2 from industrial flue gas. Sep. Purif. Technol. 2022, 298, 121676. [Google Scholar] [CrossRef]
- Sakwattanapong, R.; Aroonwilas, A.; Veawab, A. Behavior of Reboiler heat duty for CO2 capture plants using regenerable single and blended alkanolamines. Ind. Eng. Chem. Res. 2005, 44, 4465–4473. [Google Scholar] [CrossRef]
- Li, T.; Keener, T.C. A review: Desorption of CO2 from rich solutions in chemical absorption processes. Int. J. Greenh. Gas Control 2016, 51, 290–304. [Google Scholar]
- Liang, Z.; Fu, K.; Idem, R.; Tontiwachwuthikul, P. Review on current advances, future challenges and consideration issues for post-combustion CO2 capture using amine-based absorbents. Chin. J. Chem. Eng. 2016, 24, 278–288. [Google Scholar] [CrossRef]
- Liang, Z.; Rongwong, W.; Liu, H.; Fu, K.; Gao, H.; Cao, F.; Zhang, R.; Sema, T.; Henni, A.; Sumon, K. Recent progress and new developments in post-combustion carbon-capture technology with amine based solvents. Int. J. Greenh. Gas Control 2015, 40, 26–54. [Google Scholar] [CrossRef]
- Nwaoha, C.; Supap, T.; Idem, R.; Tontiwachwuthikul, P.; Al-Marri, M.J.; Benamor, A. Regeneration energy analysis of aqueous tri-solvent blends containing AMP, MDEA and DETA for CO2 capture. Energy Procedia 2017, 114, 2039–2046. [Google Scholar]
- Zhang, R.; Zhang, X.; Yang, Q.; Yu, H.; Liang, Z.; Luo, X. Analysis of the reduction of energy cost by using MEA-MDEA-PZ solvent for post-combustion CO2 capture (PCC). Appl. Energy 2017, 205, 1002–1011. [Google Scholar]
- Zhang, X.; Liu, H.; Liang, Z.; Idem, R.; Tontiwachwuthikul, P.; Al-Marri, M.J.; Benamor, A. Reducing energy consumption of CO2 desorption in CO2-loaded aqueous amine solution using Al2O3/HZSM-5 bifunctional catalysts. Appl. Energy 2018, 229, 562–576. [Google Scholar] [CrossRef]
- Alivand, M.S.; Mazaheri, O.; Wu, Y.; Stevens, G.W.; Scholes, C.A.; Mumford, K.A. Catalytic Solvent Regeneration for Ener-gyEfficient CO2 Capture. ACS Sustain. Chem. Eng. 2020, 8, 18755–18788. [Google Scholar]
- Zhang, X.; Zhang, R.; Liu, H.; Gao, H.; Liang, Z. Evaluating CO2 desorption performance in CO2-loaded aqueous tri-solvent blend amines with and without solid acid catalysts. Appl. Energy 2018, 218, 417–429. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Y.; Gao, H.; Luo, X.; Liang, Z.; Tontiwachwuthikul, P. Zeolite catalyst-aided tri-solvent blend amine regeneration: An alternative pathway to reduce the energy consumption in amine-based CO2 capture process. Appl. Energy 2019, 240, 827–841. [Google Scholar] [CrossRef]
- Shi, H.; Cui, M.; Fu, J.; Dai, W.; Huang, M.; Han, J.; Quan, L.; Tontiwachwuthikul, P.; Liang, Z. Application of “coordinative ef-fect” into tri-solvent MEA+BEA+AMP blends at concentrations of 0.1 + 2 + 2∼0.5 + 2 + 2 mol/L with absorption, desorption and mass transfer analyses. Int. J. Greenh. Gas Control 2021, 107, 103267. [Google Scholar]
- Muchan, P.; Saiwan, C.; Narku-Tetteh, J.; Idem, R.; Supap, T.; Tontiwachwuthikul, P. Screening tests of aqueous alkanolamine solutions based on primary, secondary, and tertiary structure for blended aqueous amine solution selection in post com-bustion CO2 capture. Chem. Eng. Sci. 2017, 170, 574–582. [Google Scholar] [CrossRef]
- Srisang, W.; Pouryousefi, F.; Osei, P.A.; Decardi-Nelson, B.; Akachuku, A.; Tontiwachwuthikul, P.; Idem, R. Evaluation of the heat duty of catalyst-aided amine-based post combustion CO2 capture. Chem. Eng. Sci. 2017, 170, 48–57. [Google Scholar] [CrossRef]
- Srisang, W.; Pouryousefi, F.; Osei, P.A.; Decardi-Nelson, B.; Akachuku, A.; Tontiwachwuthikul, P.; Idem, R. CO2 capture efficiency and heat duty of solid acid catalyst-aided CO2 desorption using blends of primary-tertiary amines. Int. J. Greenhouse Gas Control 2018, 69, 52–59. [Google Scholar] [CrossRef]
- Natewong, P.; Prasongthum, N.; Reubroycharoen, P.; Idem, R. Evaluating the CO2 Capture Performance Using a BEA-AMP Biblend Amine Solvent with Novel High-Performing Absorber and Desorber Catalysts in a Bench-Scale CO2 Capture Pilot Plant. Energ. Fuel 2019, 33, 3390–3402. [Google Scholar] [CrossRef]
- Afari, D.; Coker, J.; Narku-Tetteh, J.; Idem, R. Comparative Kinetic Studies of Solid Absorber Catalyst (K/MgO) and Solid Desorber Catalyst (HZSM-5)-Aided CO2 Absorption and Desorption from Aqueous Solutions of MEA and Blended Solutions of BEA-AMP and MEA-MDEA. Ind. Eng. Chem. Res. 2018, 57, 15824–15839. [Google Scholar] [CrossRef]
- Li, W.; Liang, H.; Wang, J.; Shao, L.; Chu, G.; Xiang, Y. CFD modeling on the chemical absorption of CO2 in a microporous tube-in-tube microchannel reactor. Fuel 2022, 327, 125064. [Google Scholar] [CrossRef]
- Li, W.; Liang, H.; Wang, J.; Feng, Z.; Si, C.; Shao, L.; Chu, G.; Xiang, Y. CFD simulation and experimental study of CO2 absorption in a rotating packed bed. Chem. Eng. Process 2024, 200, 109794. [Google Scholar] [CrossRef]
- Bozonc, A.; Sandu, V.; Cormos, C.; Cormos, A. 3D-CFD Modeling of Hollow-Fiber Membrane Contactor for CO2 Absorption Using MEA Solution. Membranes 2024, 14, 86. [Google Scholar] [CrossRef] [PubMed]
- Ghasem, N. Modeling and Simulation of the Simultaneous Absorption/Stripping of CO2 with Potassium Glycinate Solution in Membrane Contactor. Membranes 2020, 10, 72. [Google Scholar] [CrossRef]
- Yang, N.; Ding, Y.; Guo, L.; Zhu, X.; Wang, H.; Liao, Q. Simulation of enhanced CO2 mass transfer of nanofluid with Lattice Boltzmann method coupled cell automation probabilistic model. Chem. Eng. Res. Des. 2024, 203, 60–68. [Google Scholar] [CrossRef]
- Guo, K.; Liu, C.; Chen, S.; Liu, B. Modeling with statistical hydrodynamic quantities of mass transfer across gas–liquid interface with Rayleigh convection. Chem. Eng. Sci. 2015, 135, 33–44. [Google Scholar] [CrossRef]
- Ge, X.; Liu, B.; Liu, B.; Wang, H.; Yuan, X. Three-dimensional numerical simulation of gas-liquid interfacial mass transfer with Rayleigh convection using hybrid LBM-FDM and its mass transfer coefficient model. Chem. Eng. Sci. 2019, 197, 52–68. [Google Scholar]
- Vanka, S.; Leaf, G. Block-implicit multigrid solution of Navier-Stokes equations in primitive variables. J Comput. Phys. 1986, 65, 138–158. [Google Scholar] [CrossRef]
- Hou, S.; Zou, Q.; Chen, S.; Doolen, G.; Cogley, A.C. Simulation of cavity flow by the lattice Boltzmann method. J Comput. Phys. 1995, 118, 329–347. [Google Scholar] [CrossRef]
- Zhang, N.; Shi, H.; Wang, H.; Feng, Y.; Jin, J.; Tontiwachwuthikul, P.; Fang, M. Evaluating CO2 Capture Performance of Tri-solvent MEA-BEA-AMP with Heterogeneous catalysts in a Novel Bench-Scale Pilot Plant. ACS Omega 2023, 9, 1838–1849. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Yang, X.; Feng, H.; Fu, J.; Zou, T.; Yao, J.; Wang, Z.; Jiang, L.; Tontiwachwuthikul, P. Evaluating Energy-Efficient Solutions of CO2 Capture within Tri-solvent MEA+BEA+AMP within 0.1+2+2–0.5+2+2 mol/L Combining Heterogeneous Acid–Base Catalysts. Ind. Eng. Chem. Res. 2021, 60, 7352–7366. [Google Scholar] [CrossRef]
- Shi, H.; Huang, M.; Huang, Y.; Cui, M.; Idem, R. CO2 absorption efficiency of various MEA-DEA blend with aid of CaCO3 and MgCO3 in a batch and semi-batch processes. Sep. Purif. Technol. 2019, 220, 102–113. [Google Scholar] [CrossRef]
- Nemati, M.; Sefid, M.; Karimipour, A.; Chamkha, A. Computational thermal performance analysis by LBM for cooling a hot oval object via magnetohydrodynamics non-newtonian free convection by using magneto-ferrofluid. J. Magn. Magn. Mater. 2023, 577, 170797. [Google Scholar] [CrossRef]
- Zameni-Ghalati, S.; Mehryar, R.; Imani, G. LBM simulation of pcm melting in semi-transparent cylindrical enclosure considering conduction heat transfer with the absorption and refraction of solar radiation. J. Therm. Anal. Calorim. 2025, 150, 5249–5269. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, H.; Gao, X.; Yan, Y. Falling-Film Absorption Model Considering Surface Wave and Vibration Effects Based on Lattice Boltzmann Method. Energies 2022, 15, 7925. [Google Scholar] [CrossRef]
- Bhatnagar, P.; Gross, E.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- He, X.; Luo, L. A priori derivation of the lattice Boltamann equation. Phys. Rev. E 1997, 55, R6333–R6336. [Google Scholar] [CrossRef]
- He, X.; Luo, L. Theory of the lattice Boltzmann method: From the ioltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar]
- Qian, Y.; D’ Humieres, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
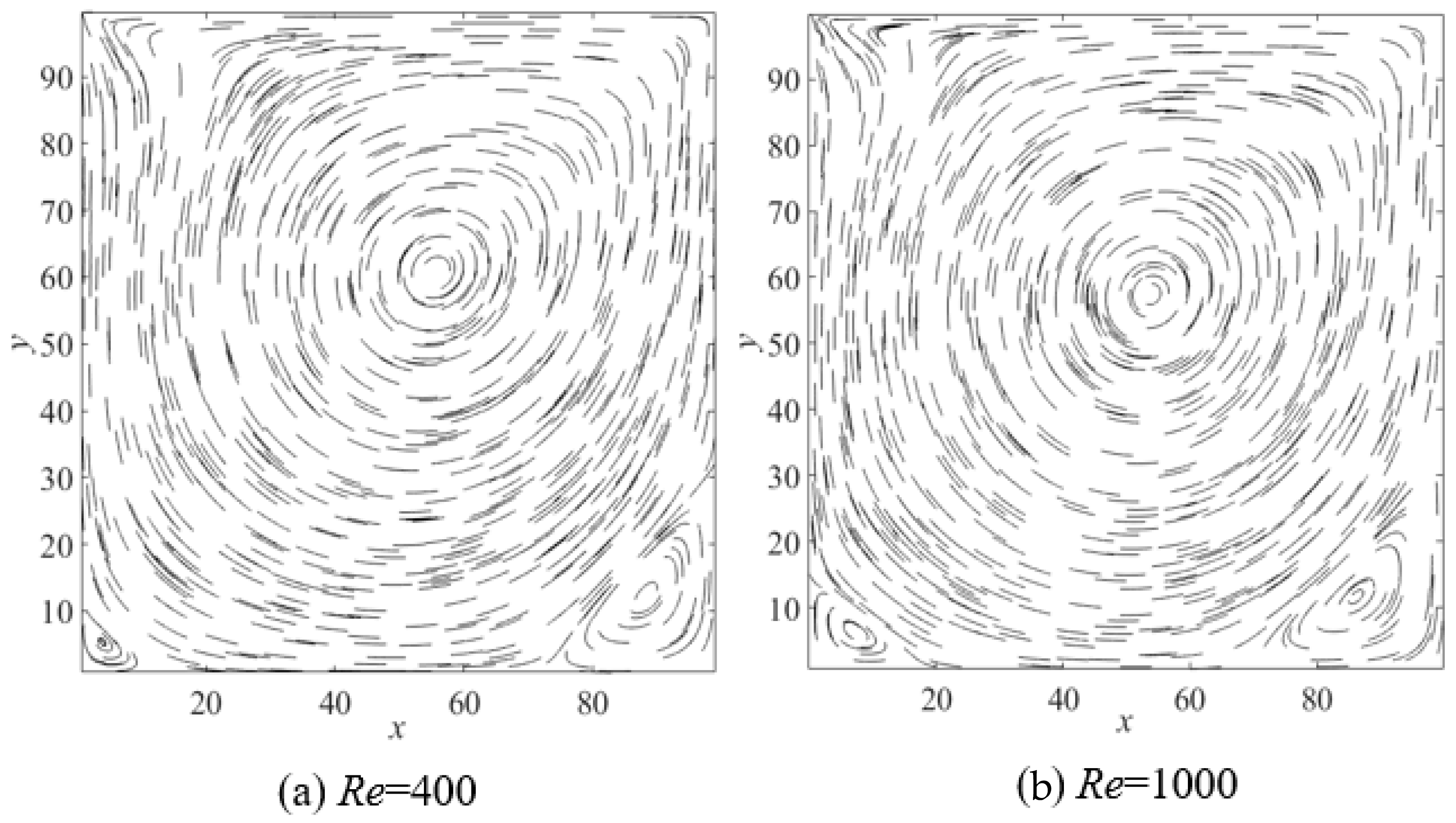






| Re | Primary Vortex | Secondary Vortex (Left) | Secondary Vortex (Right) | ||||
|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | ||
| 400 | a | 55.6 | 60.0 | 5.00 | 5.0 | 88.8 | 11.9 |
| b | 56.1 | 60.8 | 5.5 | 5.1 | 89.0 | 12.6 | |
| c | 55.9 | 60.2 | 5.2 | 4.6 | 87.6 | 12.0 | |
| 1000 | a | 54.4 | 56.3 | 7.5 | 8.1 | 86.3 | 11.0 |
| b | 53.3 | 56.5 | 9.0 | 7.8 | 86.7 | 11.4 | |
| c | 53.2 | 56.7 | 8.5 | 7.9 | 87.0 | 10.8 | |
| Parameter | Value |
|---|---|
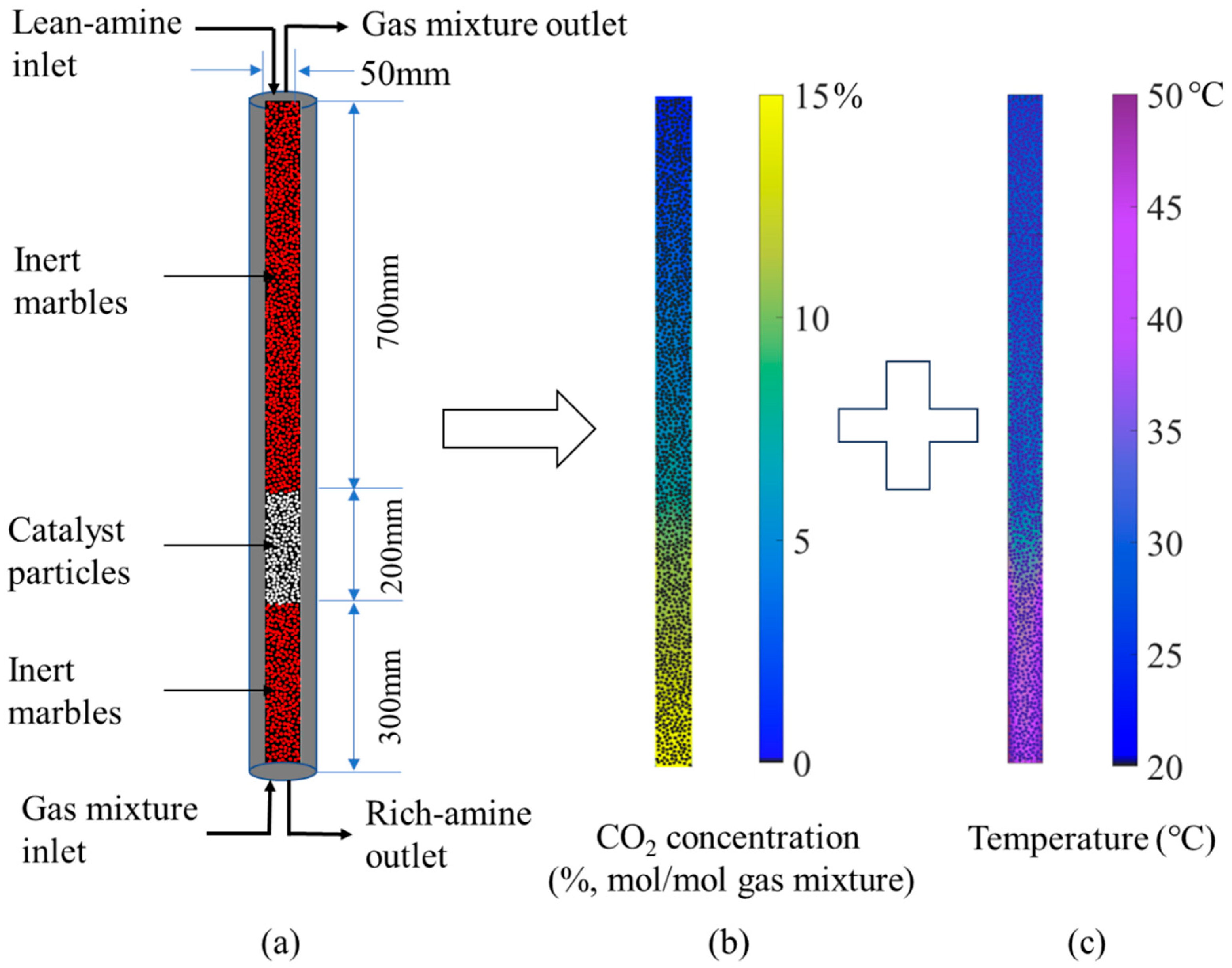
| Dimensions of absorption column | 1200 mm × 50 mm |
| Space length of catalyst particles | 200 mm |
| 2D-grid of computational domain | 2400 × 100; 400 × 100 |
| Flow rate of mixture gas | 7 L/min |
| Component of mixture gas | 15%CO2, 85%N2 |
| Temperature of lean amine | 25 °C |
| Inert marbles diameter | 6 mm |
| Porosity of the packing column | 50% |
| Parameter | Value |
|---|---|
| Catalyst particle diameters | 6, 7, 8, 9, 10 mm |
| Volume fractions of catalyst particle | 50%, 45%, 40%, 35%, 30% |
| Velocities of amine solution | 0.06, 0.07, 0.08, 0.09, 0.1 cm/s |
| Absorbent–catalyst combinations | Case 1, Case 2, Case 3, Case 4, Case 5 |
| Baseline operation conditions | 6 mm; 50%; 0.09 cm/s; Case 1 |
| Species of catalysts | H-ZSM-5, γ-Al2O3, CaCO3 |
| Classification Number | Absorbent–Catalyst Combinations | Initial CO2 Absorption Rate Determined from Batch Experiments (mol CO2/L·min) | Data Sources |
|---|---|---|---|
| Case 1 | MEA + BEA + AMP(0.4 + 2 + 2 mol/L) + H-ZSM-5/γ-Al2O3 (2:1) | 0.63 | Ref. [33] |
| Case 2 | MEA + BEA + AMP(0.3 + 2 + 2 mol/L) + CaCO3 | 0.61 | Ref. [34] |
| Case 3 | MEA + DEA(2 + 3 mol/L) + CaCO3 | 0.58 | Ref. [35] |
| Case 4 | MEA(5 mol/L) + H-ZSM-5/γ-Al2O3 (2:1) | 0.32 | Ref. [33] |
| Case 5 | MEA + BEA + AMP(0.3 + 2 + 2 mol/L), catalyst-free | 0.49 | Ref. [34] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Sun, N.; Luo, M.; Jin, J.; Wang, Q.; Shi, H. Simulation of CO2 Catalytic Absorption Process Using Amine Solutions Based on the Lattice Boltzmann Method. Catalysts 2025, 15, 1093. https://doi.org/10.3390/catal15111093
Zhang B, Sun N, Luo M, Jin J, Wang Q, Shi H. Simulation of CO2 Catalytic Absorption Process Using Amine Solutions Based on the Lattice Boltzmann Method. Catalysts. 2025; 15(11):1093. https://doi.org/10.3390/catal15111093
Chicago/Turabian StyleZhang, Binbin, Nuogeng Sun, Ming Luo, Jing Jin, Qiulin Wang, and Huancong Shi. 2025. "Simulation of CO2 Catalytic Absorption Process Using Amine Solutions Based on the Lattice Boltzmann Method" Catalysts 15, no. 11: 1093. https://doi.org/10.3390/catal15111093
APA StyleZhang, B., Sun, N., Luo, M., Jin, J., Wang, Q., & Shi, H. (2025). Simulation of CO2 Catalytic Absorption Process Using Amine Solutions Based on the Lattice Boltzmann Method. Catalysts, 15(11), 1093. https://doi.org/10.3390/catal15111093








