Abstract
A comprehensive analysis of selected DFT exchange–correlation functionals is presented, focusing on their performance in treating gold nanoclusters and on their known reliability for the description of organic species, energy barriers and dispersion interactions. To distinguish this study from the existing literature, the investigation specifically considers the practical relevance of the chosen functionals in catalytic contexts, with a particular emphasis on their potential applications in nanocatalysis for biomass valorization. Gold clusters containing 4 to 20 atoms were examined, with special attention given to the number of atoms at which the planar-to-three-dimensional-structure switch occurs. The investigation reported in this work would suggest M06 as the best exchange–correlation functional in terms of applicability and overall accuracy for computational studies of catalyzed processes involving gold nanoclusters and organic components.
1. Introduction
Driven by the increasing industrial demand for greener and more sustainable systems capable of facilitating the synthesis of a large number of molecules, the development of non-toxic, high-performance nanocatalysts has garnered significant attention. This topic has emerged as a central focus for both experimental and theoretical research. Among the systems investigated, metal clusters have shown outstanding catalytic activity and selectivity in a wide range of processes [1]. In particular, metallic nanoparticles have been widely employed as catalysts for the efficient production of valuable compounds in both academic and industrial fields [2]. The primary motivation lies in their enhanced efficiency by increasing the surface-to-volume ratio and the number of low-coordination sites, which tend to exhibit higher activity than the flat surfaces of bulk materials. Moreover, they exhibit enhanced selectivity by exposing specific facets that favor targeted catalytic transformations. As a result, significant effort has been dedicated to controlling the diameter and morphology of metal nanoparticles, a challenge that has proven to be far from simple.
Since the perception of its chemical inertness faded, gold has become one of the most extensively studied metals in catalysis [3]. Several studies have shown that gold nanoparticles display excellent catalytic performance in various reactions—notably in CO2 conversion, photo-Fenton degradation of tetracycline and in the breakdown of environmental pollutants [4,5,6]). Information on the polydispersity and size of nanoparticles clearly plays a crucial role in understanding the catalytic processes in which they participate. Consequently, the controlled synthesis of nanoparticles with a well-defined number of atoms has long been a central goal for nano-chemists. Remarkable advances have enabled the synthesis of atomically precise nanoparticles—often referred to as nanoclusters—with diameters ranging from below one to several nanometers.
In contrast to gold nanoparticles, gold nanoclusters (AuNCs) are generally smaller than 2 nm and exhibit novel catalytic properties. An ideal scenario would involve the controlled synthesis of uniform, monodispersed gold nanoclusters in high yield. This milestone was first achieved by Qian et al. [7], who successfully synthesized thiolate-protected Au25(SR)18 clusters with molecular purity and high yield. This study also highlighted the significant differences that arise from even a single-atom variation in nanocluster composition, emphasizing the difficulty of achieving precise atomic control in nanocluster synthesis [8]. More recently, Zhang et al. [9] performed the precise synthesis of the Au20 cluster, showing just the pyramidal shape predicted by computational approaches. Indeed, the interest in this kind of systems extends beyond experimental studies (which, especially for isolated neutral clusters, may be lacking [10]), involving significant theoretical investigations as well. As a matter of fact, the structure and the fluxionality of a subnanometric metal cluster play a pivotal role in determining its catalytic properties [11] so that, from a computational point of view, knowing the geometry of a catalytic system at the atomic level is an essential prerequisite for initiating a mechanistic study of its catalytic efficiency.
It has been shown [12] that a valid description of the structural and energetic properties of AuNCs requires the use of methods that accurately handle electronic correlation combined with very large basis sets. In particular, if one wishes to remain within the DFT framework, the choice should fall on doubly hybrid functionals, such as B2PLYP, which includes a contribution of the electron dynamical correlation evaluated at the second-order Moeller-Plesset perturbation theory level. Unfortunately, the heavy MP2 stage contained in this exchange–correlation functional limits its applicability, making the actual investigation of the catalytic behavior of AuNCs, applied to a specific reaction, extremely difficult if not impossible to pursue. It must also be considered that the impracticability of double-hybrid functionals (and the same is true for other approaches that include explicit calculation of the correlation energy) is made even more stringent by the need to perform the calculation of the vibration frequencies for the system under examination, essential data for a valid description of the energetics of the reaction (in terms of zero-point including electronic energy or Gibbs free energy variation) and for the correct identification of the transition states, hence of the energy barriers. Furthermore, mapping the complete mechanism of a given reaction in cluster catalysis, even the simplest, is a process that requires a very large number of calculations, in particular regarding the search for transition states. The efficiency of the chosen calculation method should also take this aspect into account. The same reasoning can be applied to the extension of the basis set; a triple-zeta valence basis set usually includes a certain number of polarization functions (for example, up to f functions for the light non-H elements) which dramatically increases the total number of functions, thus making the investigation of systems containing more than 50 atoms (as often happens) a very hard task.
It is therefore appropriate to attempt to validate the effectiveness of exchange–correlation functionals that do not go beyond the hybrid type ones in the DFT Jacob’s ladder, as these allow researchers to have reasonable confidence in the results obtained while keeping calculation times within acceptable limits.
Our research group has long been involved in the computational study of catalytic reactions for biomass valorization by metal clusters and, in particular, the mechanisms of the hydrodeoxygenation reaction of guaiacol [13,14] and isoeugenol [15,16] on subnanometer platinum clusters have been almost completely mapped. The resulting information on reaction energies and energy barriers, obtained by the application of DFT, was analyzed by means of original microkinetic algorithms [17,18], providing an example of how the scientific research of the details of a given process can lead to the development of new tools [19,20]. Just in this field, on the basis of a computational investigation [21], we recently proposed a potential catalytic system for the transformation of 5-hydroxymethylfurfural (HMF), a key molecular platform derived from lignocellulosic biomass, into furandicarboxylic acid, a renewable monomer for bioplastics [22]. The mentioned system is formed by a gold atom attached to the amino-group of the (3-amino-propyl)triethoxysilane residue covalently anchored to the external surface of the halloysite nanotube. The cheap and eco-friendly halloysite spiral nanotubes [23] have a relevant peculiarity: the outer silicic surface has basic characteristics [24,25] and can be easily functionalized [26], even with metals [27], while the inner aluminic surface, shaping the nanotube cavity, has acid properties [28]. This clay may be able to cause fructose transformation to HMF (which is catalyzed by acids) inside its channel and the oxidation of HMF (occurring in alkaline condition with the presence of a metal) in its functionalized outer surface. The proposed catalyst could solve the challenging problem of HMF intermediate separation by facilitating a one-pot reaction mechanism. One of the next steps in this project is to substitute the gold atom with a gold cluster. Therefore, considering that a systematic in-depth investigation of AuNCs is essential for advancing our understanding of their behavior and the principles underlying their catalytic activity in these kinds of systems, a theoretical analysis of clusters (–20), employing a particular set of exchange–correlation functionals within the framework of density functional theory has been performed and is here reported.
As a guideline for reading this article, it is important to keep in mind that the reported assessment study does not aim to identify the best functional for describing gold clusters as such. Rather, its goal is to propose an exchange–correlation functional capable of treating both the cluster and the catalytic environment in which it is embedded, as well as the catalyzed reaction, in a reasonably consistent manner. Achieving this balance inevitably requires certain compromises.
2. Results and Discussion
In a 2017 paper, Baek et al. [29] reported a detailed and very extensive study on the validity of 44 exchange–correlation functionals for determining the geometry (bond lengths and bond angles), the relative energetics of the structures and the ionization potential of clusters (–8). The DFT results were compared with the analogous ones obtained using coupled cluster theory at the CCSD(T) level and the conclusion was that the revTPSS functional would represent the best choice, at least in that range of cluster sizes. The extension of the reliability of revTPSS to larger cluster sizes, for which a comparison with results from heavily correlated calculations is arduous, was postulated in the present investigation.
However, it is worth recalling once again that, even if the study of AuNCs as such is an important matter, in order to computationally investigate the way they exert their catalytic action towards a given reaction, it is necessary to be able to study, with some confidence in the accuracy of the results obtained, systems and processes in which the gold cluster represents only one of the components. In a number of cases, and especially in the context of eco-sustainable catalysis such as the one our group is studying, the cluster is anchored on organic supports, which in turn can be part of a larger frame. In these types of systems, the presence of a complex network of hydrogen bonds is not uncommon, which, together with a high number of weaker interactions, can be important in determining the details of the chemical processes. Furthermore, the catalyzed reaction should be studied with methods that allow a correct description of the thermodynamics and energetics, i.e., are accurate enough in determining interactions and energy barriers. In short, it is our opinion that for the atomistic study of the catalytic aspects of systems containing AuNCs it is not acceptable (and sometimes not possible) to use computational approaches that have proven to be efficient for dealing with the cluster alone but may not be accurate for the description of the whole catalytic system or the reactions involved in the process. The best thing to do would therefore be to find a compromise that allows the homogeneous study all aspects of the process. Such a view is not restricted to the case of gold alone and can in fact be extended to any metal used for cluster catalysis.
With this in mind, it is evident from Table 1 that the revTPSS functional, although seemingly appropriate for describing the properties of subnanometer gold clusters, is not the best choice for modeling energy barriers and even less effective for noncovalent interactions. The problem related to the accuracy of the latter is partially solved by introducing the Grimme D3 correction, but the same cannot be said for the other aspects. From the table it appears that for barriers and noncovalent interactions there are exchange–correlation functionals that show definitely better performance, even without Grimme correction (it has indeed a small effect in these cases). The functionals selected in this work are in fact among those that show the best global accuracies and, according to the study by Baek et al. [29] they have been proven to be suitable for the study of AuNCs. To evaluate their reliability for a larger set of AuNCs than the one considered in the mentioned work, we decided to consider the revTPSS as a reference functional and analyzed the performance of the chosen exchange–correlation functionals in terms of the transition point between two-dimensional and three-dimensional structures, the energy difference and the free energy difference (at 1 bar pressure) between the two possibilities, and the cohesion energy, here defined as .

Table 1.
Relevant weighted total mean absolute deviations (WTMAD-1, kJ ) of all the exchange–correlation functionals used in this work. For each entry, the value without the Grimme D3 correction is shown on the left, while the value including the correction is reported on the right. Adapted from the GMTKN55 website [30,31].
The results obtained concerning the energy differences were collected in Table 2 and, for an immediate overview, the behaviors around the transition point were schematically reported in Figure 1. The overall analysis led to the conclusion that each selected exchange–correlation functional, except revTPSS and M06, gives a different result on what concerns the switching point between a 2D and a 3D geometry. It is clear that in any case, once the inversion point from the planar to the three-dimensional shape has been passed, the high positive value of demonstrates that the 3D structure is the only one to consider.

Table 2.
The energy difference (, in kJ ) between the 2D and 3D forms of the (–20) clusters calculated with the set of exchange–correlation functionals chosen in this work.
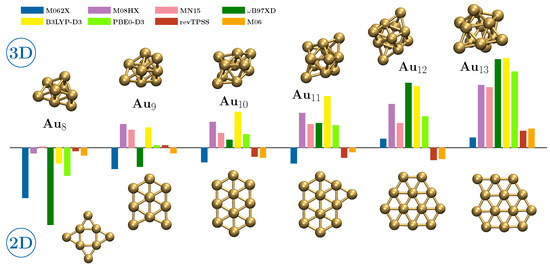
Figure 1.
Histogram-like representation of the energy difference between the planar and three-dimensional forms of the cluster from Au8 to Au13, along with their geometry. The scheme allows us to appreciate at a glance the crossing point predicted by the different functionals considered in this work. For the exact energy values, please see Table 2.
As a matter of fact, some functionals indicate that given planar geometries with high n do not represent minima in the potential energy hypersurface they describe. A notable case is the functional B97XD which, in fact, shows the largest energy imbalance between the two geometries: except in the case of Au10 which, according to this functional, is the first to have a packed structure, the values of are indeed the highest in magnitude.
MN15 is the functional that shows the 2D-3D transition for lower n values, since it describes the two Au8 structures as essentially isoenergetic and then undoubtedly gives preference to the three-dimensional geometry. M08HX also predicts a transition for quite small clusters, with the packed form of Au9 already being more stable than the planar form by more than 20 kJ ; the same behavior is shared by B3LYP-D3, while according to PBE0-D3 the 2D and 3D geometries of Au9 have inherently the same energy. The B97XD closely follows, predicting Au10 as the first three-dimensional cluster. It is worth noting that according to the M08HX, MN15 and B97XD functionals the 3D form of Au7 is not a minimum; on the other hand all functionals do not give any 3D structure for Au4, Au5 and Au6, which indeed are not worth discussing in the present work. The functionals predicting a transition point at higher values of n are M062X and M06, but between them only the latter shows a trend similar to the one resulting from the application of the revTPSS reference functional. In particular, the following similarities between M06 and revTPSS can be noted, which are not shared by any of the other Minnesota functionals:
- the existence of a three-dimensional Au7 cluster is predicted;
- the absolute value of reaches a minimum for Au9 and then rises again;
- the crossing point is from Au12 to Au13;
- near the crossing point the magnitudes of are very low: the two functionals agree in suggesting the possibility of the co-presence of the two types of geometric shape;
- finally, M06 shows the smallest deviations from revTPSS as regards the numerical values of resulting for all the clusters up to Au20.
In fact, that the 2D-3D transition occurs after Au10 has been demonstrated very recently in a paper by Kim et al. [32], where it is concluded that the agreement with the experimental spectroscopic evidence is obtained only if one assumes a Boltzmann distribution of the possible geometries of this cluster with the planar case taken as the minimum energy structure. Among other things, the need to consider the equilibrium populations of different geometries of Au10 supports point 4 above.
Regarding this point, it must be emphasized that for some functionals (in particular MN15, PBE0-D3 and B97XD to some extent) the 2D-3D transition point is not well defined, since is well below the level of confidence we can have in the DFT results. It may be that in these cases the transition point occurs one unit further ahead. However, a look at Table 2 shows that the difference between the values of and , where is the last two-dimensional cluster and Auk the first three-dimensional one according to a given functional, is in all cases in the range between 21.9 kJ (M062X) and 30.7 kJ (B3LYP-D3), with an average value of 25.9 kJ . Even if a given functional is rarely calibrated with respect to the properties of metal clusters, these values are above the absolute deviations reported in Table 1, which suggests the significance of the cluster sizes at which the 2D-3D switch occurs. Taking this into account, the fact remains that only revTPSS and M06, and perhaps M062X, predict that the transition point occurs at the largest dimension.
The thermal and entropic effects on the relative stability of the two- and three-dimensional gold clusters can be also evaluated by considering the difference between their Gibbs free energy values, . These are collected in Tables S1–S8 of the Supporting Information and shown in Figure 2 for the Au7–Au14 and for temperature values in the range 100–600 K. Excluding very specific cases (such as Au8 for M062X and B97XD), it can be noted that the becomes more negative as the temperature increases, indicating that at high temperatures the two-dimensional form should be increasingly favored. In the temperature range from 100 to 600 K, according to some functionals and with different magnitudes, a one-unit forward shift in the 2D-3D transition point is observed. It is also worth mentioning the case of Au9 which, in agreement with three out of eight functionals (B3LYP-D3, PBE0-D3 and M06), shows two irregularities: depends negligibly on the temperature and has a more positive, or less negative, value than those relating to the Au8 and Au10 clusters.
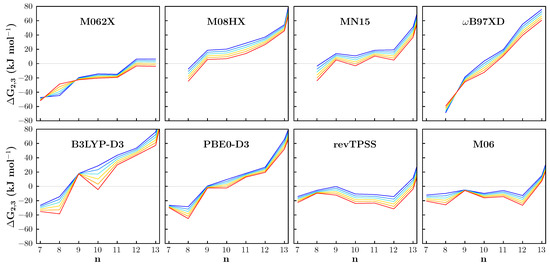
Figure 2.
The trends of the free energy difference as a function of the number of gold atoms in the cluster at various temperatures as predicted by the exchange–correlation functionals compared in this work. Temperature color code: blue (100 K), pale blue (200 K), cyan (300 K), yellow (400 K), orange (500 K) and red (600 K). Missing points correspond with unavailable data for the given functional (see Table 2).
It is necessary to mention that, while the results of our calculations would favor planar 2D isomers as temperature increases, a dedicated study from Goldsmith et al. [33] reports the opposite trend, with higher temperatures enhancing the stability of compact 3D isomers (with some exceptions). The reasons for the differences between our and Goldsmith’s data, which are based on the calculation of the Gibbs free energy from ab initio molecular dynamics simulations, may be multiple, e.g.: (i) the effects of anharmonicity, the contribution of which could be decisive for particles containing bonds between heavy atoms; (ii) the effects of sampling, at a given finite temperature, on different structures, probably needed due to the fluxionality of the metal clusters; (iii) the use, in the dynamics, of exchange–correlation functionals different from those employed in this work, to which, as also demonstrated by the present investigation, the properties of gold clusters are very sensitive. Incidentally, GGA exchange–correlation functionals, like the PBE one used by Goldsmith for the molecular dynamics simulations, have not been considered in the present investigation because, for the treatment of non-periodic systems, they are largely surpassed in both use and accuracy by hybrid ones.
It is certainly worth investigating the reasons for these behaviors in depth, but what is most relevant for the purpose of this work is the comparison of the DFT functionals. An overall look at the trends reported in Figure 2 leads us to conclude that, even in the case of the difference in free energy as a function of temperature, M06 is the functional that behaves most like the revTPSS reference. In the case in question, which involves the comparison between systems with very similar geometries, the differences between the thermal and entropic effects as predicted by the different functionals should be mainly due to the vibrational contribution and this suggests that revTPSS and M06 are more or less in agreement also in describing this aspect.
In order to study the growth trend of AuNCs for each data set obtained according to the aforementioned functionals, the cohesion energy was used. The obtained values, plotted against the number of Au atoms (see Figure 3), were analyzed by splitting the data set before and after the crossing point. The two subsets, subjected to linear fitting, clearly show a consistent change in the slope when passing from planar () to three-dimensional () structures.
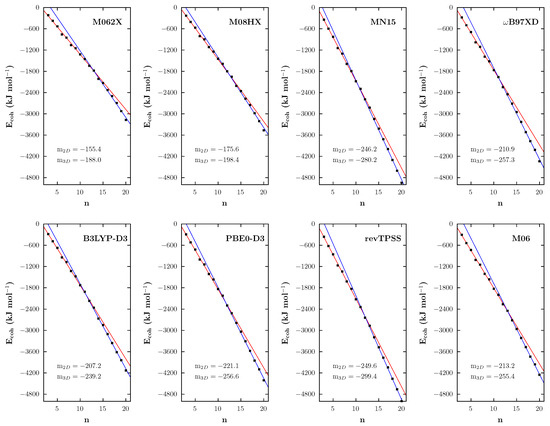
Figure 3.
In the eight panels, the cohesion energy versus the number of atoms in the Au cluster is reported. Red lines (with angular coefficients labeled as ) represent the results of the linear fit of the data sets associated with planar structures, while blue lines (with as angular coefficients) result from the fit of the data sets regarding three-dimensional structures.
It turns out that only the MN15 functional predicts cohesion energy values comparable to those of revTPSS, probably because it overestimates the covalent interaction between Au atoms (it shows indeed a marked preference for compact clusters). In fact, the values , , and a per-atom cohesion energy, , equal to and kJ for Au20, were obtained in the case of revTPSS and MN15, respectively. All other functionals predict a slower increase in the cohesion energy and smaller absolute values. Although it certainly has a much better performance than its M062X and M08HX counterparts, the M06 functional (showing in this aspect a behavior similar to those of B3LYP-D3, PBE0-D3 and B97XD) is not very close to the reference either: it seems to underestimate the Au−Au interactions, with kJ , and this probably leads to an error cancellation that determines its better performance regarding the energy difference. It also explains why M06 predicts longer Au−Au bonds (up to 0.1 Å in the considered sets of clusters) than the revTPSS functional, an issue already observed and discussed by Baek et al. [29].
3. Computational Methods
The investigations presented in this work were performed using the Gaussian 16 software package [34]. The geometry and energetics of neutral AuNCs from 4 to 20 atoms were studied by employing the following selected exchange–correlation functionals from the Minnesota group:
- M062X [35], a hybrid meta-GGA functional with 54% HF exchange, one of the most reliable choices for main group chemistry but seemingly not suitable for transition metals;
- M08HX [36], a hybrid meta-GGA functional having 52.2% of HF exchange, with good accuracy for the description of atomization energies, noncovalent interactions, barrier heights, changes of multiplicity;
- MN15 [37], one of the latest functionals from Minnesota group, it is a global meta-hybrid GGA functional (44% HF exchange) showing a good performance for systems whose electronic structure requires a multireference treatment;
- M06 [35], a hybrid meta-GGA functional with 27% HF exchange, which showed good reliability both for main group and transition metal chemistry;
plus the Tao-Perdew-Staroverov-Scuseria functional in its revised form
- revTPSS [38], a semi-local meta-GGA functional with improved treatment of condensed matter and solid state;
and
- B97X-D [39], a long-range corrected functional, characterized by 22% HF exchange and 100% long-range exchange, which include the Grimme correction for dispersion interactions [40];
- the popular B3LYP [41] and PBE0 [42] functionals, both equipped with the Grimme D3 semiempirical correction.
The cc-pVDZ-PP basis set [43], comprising relativistic effective core potentials and a (25s22p17d1f)/[4s4p3d1f] valence basis set, was employed for all calculations. As regards the spin multiplicity of the gold clusters, it seems to be a well-established fact that, in the nanometric size regime, clusters with an even number of atoms are in the singlet state, while the doublet multiplicity is preferred over the quartet one when there is an odd number of atoms. It is worth underlining here that spin–orbit coupling is certainly important for the accurate treatment of the properties of gold in all its forms, and can influence the geometry of the clusters [44]. It has not been considered in the present investigation because, in addition to the fact that a dedicated study is needed that is not necessarily applicable to large clusters, we believe it is important to treat gold with the same approaches that would potentially be used to treat catalytic systems and processes, where it is presumably difficult to afford to detail spin–orbit coupling. Further, it was assumed that the use of broken symmetry unrestricted formalisms [45,46] for clusters in singlet state would not affect the obtained results, since similar trends can be expected for the results of restricted and unrestricted calculations.
The putatively most stable geometries available in the literature for AuNCs were considered as the starting structures for the optimization procedure. In particular, the starting geometries for planar clusters up to 13 atoms were taken from Sekhar De et al. [47], while the three-dimensional structures from 14 to 20 atoms were extracted from the pioneering work of Wang et al. [48]. In order to generate the missing starting geometry of planar clusters with –20, a gold atom was attached to the lowest-coordinated site of the optimized geometry of , when possible in the position which results in the most symmetric structure. An inverse approach was followed to generate the starting geometries for the three-dimensional clusters from 4 to 13, when not available in the literature: starting from , atoms from the positions with lower coordination were gradually removed in such a way as to generate smaller clusters with the highest symmetry. The first geometry relaxation of all the 2D and 3D clusters was performed by using the revTPSS functional (see the Results and Discussion section regarding this choice); the resulting optimized geometries were then used as starting guess for all other functionals. All optimizations were performed without imposing symmetry constraints. The absence of imaginary frequencies characterizing minima in the potential energy surface was checked by inspection of the calculated harmonic vibrational frequencies; all the energy values reported in this work include the vibrational zero-point contribution. Gibbs free energies were derived by applying the standard laws of statistical thermodynamics and their values at different temperatures were calculated by using the GoodVibes code [49].
4. Conclusions
Gold catalysis plays an important role in developing sustainable routes for transforming renewable biomass into fuels, fine chemicals, and platform molecules. Since the catalytic properties of gold nanoclusters strongly depend on the coordination number and the surroundings of the atoms characterizing the active sites, in this work we explored the performance of five different, new-generation (M062X, M08HX, MN15, B97XD and M06) DFT exchange–correlation functionals, plus the popular B3LYP and PBE0 with Grimme D3 correction, in predicting, in particular, the crossing point from planar to three-dimensional structures and the cohesion energy for gold clusters up to 20 atoms. The aim of this work was to find, among those investigated, a functional that represented a compromise for a good description of both the gold clusters and all the other aspects necessary for the study of catalysts and catalytic processes involving gold, such as geometry and energetics of organic species, energy barriers, noncovalent interactions. The first issue was established through comparison with the revTPSS functional, taken as a reference for gold clusters following literature evidence; the second was evaluated based on the statistical averages contained in the GMTKN55 database.
Besides considering the fact that in most cases it is not possible to use methods that explicitly calculate the correlation energy combined with extensively large basis sets to study catalytic processes, the present work has had a pragmatic point as guideline: in the context of DFT it should not be considered appropriate to use an exchange–correlation functional that describes well only one part of the system but is not equally efficient in treating all the other important aspects. In view of this, we propose the M06 functional as the best compromise, being the one which better compares to revTPSS as regards the overall structure and energetics of the gold clusters, while at the same time it is able to describe with sufficient accuracy reaction energies, barrier heights and noncovalent interactions in a wide set of chemical species. All these features are in fact crucial when one wants to study the catalytic effects of gold nanoclusters with respect to specific reactions, when the nanocluster itself is embedded in a catalytic system of presumably organic nature.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/catal15111083/s1.
Author Contributions
Conceptualization, F.F. and L.G. (Ludovico Guercio); methodology, F.F. and L.G. (Ludovico Guercio); validation, F.F. and M.B.; formal analysis, L.G. (Ludovico Guercio) and M.B.; investigation, L.G. (Ludovico Guercio), L.G. (Laura Gueci) and L.L.; writing—original draft preparation, L.G. (Ludovico Guercio) and L.G. (Laura Gueci); writing—review and editing, F.F. and D.D.; supervision, F.F. and D.D.; project administration, F.F.; funding acquisition, F.F. and D.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “SiciliAn MicronanOTecH Research And innovation CEnter—SAMOTHRACE” (MUR, PNRR-M4C2, ECS0000002), spoke 3, Università degli Studi di Palermo. L.L. thanks the European Union for cofinancing within FESR e FSE, PON “Ricerca e Innovazione” 2014–2020—DM 1062/2021.
Data Availability Statement
The complete values and the coordinates (xyz format) corresponding to the input geometries, and to the revTPSS and M06 optimized geometries of all the investigated systems are available as Supporting Information.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AuNC | Gold NanoCluster |
| cc-pVDZ-PP | Correlation Consistent Polarized Valence Double Zeta + PseudoPotentials |
| CCSD(T) | Coupled Cluster Singles Doubles and perturbative Triples |
| DFT | Density Functional Theory |
| GGA | Generalized Gradient Approximation |
| HF | Hartree–Fock |
| HMF | 5-HydroxyMethylFurfural |
| MP2 | Möller-Plesset theory at second order |
| WTMAD | Weighted Total Mean Absolute Deviations |
References
- Li, J.; Zhao, X.; Ma, Z.; Pei, Y. Structure and Catalytic Activity of Gold Clusters Supported on Nitrogen-Doped Graphene. J. Phys. Chem. C 2021, 125, 5006–5019. [Google Scholar] [CrossRef]
- Serna-Gallén, P.; Muzina, K. Metallic Nanoparticles at the Forefront of Research: Novel Trends in Catalysis and Plasmonics. Nano Mater. Sci. 2024; in press. [Google Scholar] [CrossRef]
- Mato, M.; Franchino, A.; García-Morales, C.; Echavarren, A.M. Gold-Catalyzed Synthesis of Small Rings. Chem. Rev. 2020, 121, 8613–8684. [Google Scholar] [CrossRef]
- Cai, X.; Li, G.; Hu, W.; Zhu, Y. Catalytic Conversion of CO2 over Atomically Precise Gold-Based Cluster Catalysts. ACS Catal. 2022, 12, 10638–10653. [Google Scholar] [CrossRef]
- Qin, L.; Wang, Z.; Fu, Y.; Lai, C.; Liu, X.; Li, B.; Liu, S.; Yi, H.; Li, L.; Zhang, M.; et al. Gold Nanoparticles-Modified MnFe2O4 with Synergistic Catalysis for Photo-Fenton Degradation of Tetracycline Under Neutral pH. J. Hazard. Mater. 2021, 414, 125448. [Google Scholar] [CrossRef]
- Susan Punnoose, M.; Bijimol, D.; Mathew, B. Microwave Assisted Green Synthesis of Gold Nanoparticles for Catalytic Degradation of Environmental Pollutants. Environ. Nanotechnol. Monit. Manag. 2021, 16, 100525. [Google Scholar] [CrossRef]
- Qian, H.; Zhu, M.; Wu, Z.; Jin, R. Quantum Sized Gold Nanoclusters with Atomic Precision. Acc. Chem. Res. 2012, 45, 1470–1479. [Google Scholar] [CrossRef] [PubMed]
- Parker, J.F.; Fields-Zinna, C.A.; Murray, R.W. The Story of a Monodisperse Gold Nanoparticle: Au25L18. Acc. Chem. Res. 2010, 43, 1289–1296. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.F.; Chen, X.; Wang, L.S. Toward Solution Syntheses of the Tetrahedral Au20 Pyramid and Atomically Precise Gold Nanoclusters with Uncoordinated Sites. Acc. Chem. Res. 2018, 51, 2159–2168. [Google Scholar] [CrossRef]
- Gruene, P.; Rayner, D.M.; Redlich, B.; van der Meer, A.F.G.; Lyon, J.T.; Meijer, G.; Fielicke, A. Structures of Neutral Au7, Au19, and Au20 Clusters in the Gas Phase. Science 2008, 321, 674–676. [Google Scholar] [CrossRef] [PubMed]
- Zhai, H.; Alexandrova, A.N. Fluxionality of Catalytic Clusters: When It Matters and How to Address It. ACS Catal. 2017, 7, 1905–1911. [Google Scholar] [CrossRef]
- Ferrari, P.; Hansen, K. Computing Gold Cluster Energies with Density Functional Theory: The Importance of Correlation. Phys. Chem. Chem. Phys. 2021, 23, 14830–14835. [Google Scholar] [CrossRef]
- Nania, C.; Bertini, M.; Gueci, L.; Ferrante, F.; Duca, D. DFT Insights into Competing Mechanisms of Guaiacol Hydrodeoxygenation on a Platinum Cluster. Phys. Chem. Chem. Phys. 2023, 25, 10460–10471. [Google Scholar] [CrossRef] [PubMed]
- Nania, C.; Ferrante, F.; Bertini, M.; Gueci, L.; Duca, D. Decomposition of Guaiacol on a Subnanometric Platinum Cluster: A DFT Investigation Followed by Microkinetic Analysis. Phys. Chem. Chem. Phys. 2025, 27, 3916–3929. [Google Scholar] [CrossRef]
- Ferrante, F.; Nania, C.; Duca, D. Computational Investigation of Isoeugenol Transformations on a Platinum Cluster—I: Direct Deoxygenation to Propylcyclohexane. Mol. Catal. 2022, 529, 112541. [Google Scholar] [CrossRef]
- Nania, C.; Ferrante, F.; Bertini, M.; Gueci, L.; Duca, D. Computational Investigation of Isoeugenol Transformations on a Platinum Cluster—II: Deoxygenation through Hydrogenation to Propylcyclohexane. Mol. Catal. 2024, 564, 114298. [Google Scholar] [CrossRef]
- Gueci, L.; Ferrante, F.; Prestianni, A.; Di Chio, R.; Patti, A.F.; Duca, D.; Arena, F. DFT Insights into the Oxygen-Assisted Selective Oxidation of Benzyl Alcohol on Manganese Dioxide Catalysts. Inorg. Chim. Acta 2020, 511, 119812. [Google Scholar] [CrossRef]
- Gueci, L.; Ferrante, F.; Prestianni, A.; Arena, F.; Duca, D. Structural, Energetic and Kinetic Database of Catalytic Reactions: Benzyl Alcohol to Benzaldehyde Oxidation on MnOx Clusters. Data Brief 2021, 38, 107369. [Google Scholar] [CrossRef]
- Ferrante, F.; Bertini, M.; Gueci, L.; Duca, D. Butene Isomerization on Palladium Surfaces: Time-Dependent Monte Carlo Studies. Ind. Eng. Chem. Res. 2023, 62, 20608–20621. [Google Scholar] [CrossRef]
- Bertini, M.; Ferrante, F.; Gueci, L.; Prestianni, A.; Duca, D.; Arena, F.; Murzin, D.Y. Alternative Algebraic Perspectives on CO/H2 PROX over MnO2 Composite Catalysts. J. Chem. Inf. Model. 2025, 65, 4952–4967. [Google Scholar] [CrossRef]
- Bertini, M.; Ferrante, F.; Guercio, L.; Lisuzzo, L.; Duca, D. Modified Halloysite as Catalyst for the Conversion of Hydroxymethylfurfural to Furandicarboxylic Acid: A DFT Investigation. ChemCatChem 2024, 16, e202400179. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, K. Recent Advances in the Catalytic Synthesis of 2,5-Furandicarboxylic Acid and Its Derivatives. ACS Catal. 2015, 5, 6529–6544. [Google Scholar] [CrossRef]
- Lisuzzo, L.; Guercio, L.; Cavallaro, G.; Duca, D.; Ferrante, F. Halloysite Clay Nanotubes for Catalytic Conversion of Biomass: Synergy between Computational Modeling and Experimental Studies. ACS Catal. 2024, 14, 18167–18203. [Google Scholar] [CrossRef]
- Rozza, R.; Ferrante, F. Computational Study of Water Adsorption on Halloysite Nanotube in Different pH Environments. Appl. Clay Sci. 2020, 190, 105589. [Google Scholar] [CrossRef]
- Ferrante, F.; Bertini, M.; Ferlito, C.; Lisuzzo, L.; Lazzara, G.; Duca, D. A Computational and Experimental Investigation of Halloysite Silicic Surface Modifications after Alkaline Treatment. Appl. Clay Sci. 2023, 232, 106813. [Google Scholar] [CrossRef]
- Lisuzzo, L.; Bertini, M.; Lazzara, G.; Ferlito, C.; Ferrante, F.; Duca, D. A Computational and Experimental Investigation of the Anchoring of Organosilanes on the Halloysite Silicic Surface. Appl. Clay Sci. 2023, 245, 107121. [Google Scholar] [CrossRef]
- Massaro, M.; Colletti, C.G.; Lazzara, G.; Milioto, S.; Noto, R.; Riela, S. Halloysite Nanotubes as Support for Metal-Based Catalysts. J. Mater. Chem. A 2017, 5, 13276–13293. [Google Scholar] [CrossRef]
- Sidorenko, A.; Kurban, Y.; Aho, A.; Ihnatovich, Z.; Kuznetsova, T.; Heinmaa, I.; Murzin, D.; Agabekov, V. Solvent-Free Synthesis of Tetrahydropyran Alcohols over Acid-Modified Clays. Mol. Catal 2021, 499, 111306. [Google Scholar] [CrossRef]
- Baek, H.; Moon, J.; Kim, J. Benchmark Study of Density Functional Theory for Neutral Gold Clusters, Aun (n = 2–8). J. Phys. Chem. A 2017, 121, 2410–2419. [Google Scholar] [CrossRef]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef]
- Grimme, S. GMTKN55—A Database for General Main Group Thermochemistry, Kinetics, and Non-Covalent Interactions. 2019. Available online: https://www.chemie.uni-bonn.de/grimme/de/software/gmtkn/gmtkn55 (accessed on 11 December 2024).
- Kim, J.; Seo, W.; Park, J.; Kim, I.; Park, E.; Kim, J. Revisiting the Global Minimum of Au10 Clusters. J. Chem. Phys. 2024, 161, 184301. [Google Scholar] [CrossRef]
- Goldsmith, B.R.; Florian, J.; Liu, J.X.; Gruene, P.; Lyon, J.T.; Rayner, D.M.; Fielicke, A.; Scheffler, M.; Ghiringhelli, L.M. Two-to-three Dimensional Transition in Neutral Gold Clusters: The Crucial Role of Van der Waals Interactions and Temperature. Phys. Rev. Mater. 2019, 3, 016002. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2007, 120, 215–241. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Exploring the Limit of Accuracy of the Global Hybrid Meta Density Functional for Main-Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2008, 4, 1849–1868. [Google Scholar] [CrossRef]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn-Sham Global-Hybrid Exchange-Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Constantin, L.A.; Sun, J. Workhorse Semilocal Density Functional for Condensed Matter Physics and Quantum Chemistry. Phys. Rev. Lett. 2009, 103, 026403. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Long-range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Dorrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Peterson, K.A.; Puzzarini, C. Systematically Convergent Basis Sets for Transition Metals. II. Pseudopotential-Based Correlation Consistent Basis Sets for the Group 11 (Cu, Ag, Au) and 12 (Zn, Cd, Hg) Elements. Theor. Chem. Acc. 2005, 114, 283–296. [Google Scholar] [CrossRef]
- Shi, Y.K.; Li, Z.H.; Fan, K.N. Validation of Density Functional Methods for the Calculation of Small Gold Clusters. J. Phys. Chem. A 2010, 114, 10297–10308. [Google Scholar] [CrossRef]
- Okumura, M.; Kitagawa, Y.; Yabushita, H.; Saito, T.; Kawakami, T. Theoretical investigation of the interaction between oxygen molecules and small Au clusters using approximately spin-projected geometry optimization (AP-opt) method. Catal. Today 2009, 143, 282–285. [Google Scholar] [CrossRef]
- Dubecký, M.; Su, H. Magnetism in Thiolated Gold Model Junctions. J. Phys. Chem. C 2012, 116, 17714–17720. [Google Scholar] [CrossRef]
- Sekhar De, H.; Krishnamurty, S.; Pal, S. Understanding the Reactivity Properties of Aun (6 ≤ n ≤ 13) Clusters Using Density Functional Theory Based Reactivity Descriptors. J. Phys. Chem. C 2010, 114, 6690–6703. [Google Scholar] [CrossRef]
- Wang, J.; Wang, G.; Zhao, J. Density-Functional Study of Aun (n = 2–20) Clusters: Lowest-Energy Structures and Electronic Properties. Phys. Rev. B 2002, 66, 035418. [Google Scholar] [CrossRef]
- Luchini, G.; Alegre-Requena, J.V.; Funes-Ardoiz, I.; Paton, R.S. Goodvibes: Automated Thermochemistry for Heterogeneous Computational Chemistry Data. F1000Research 2020, 9, 291. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).