Next Article in Journal
Facile Synthesis of a Bi2WO6/BiO2−x Heterojunction for Efficient Photocatalytic Degradation of Ciprofloxacin under Visible Light Irradiation
Previous Article in Journal
An Efficient Strategy for Chemoenzymatic Conversion of Corn Stover to Furfuryl Alcohol in Deep Eutectic Solvent ChCl:PEG10000−Water Medium
Previous Article in Special Issue
Green Synthesis of Spirooxindoles via Lipase-Catalyzed One-Pot Tandem Reaction in Aqueous Media
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Catalysts
Volume 13
Issue 3
10.3390/catal13030468
catalysts-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Bayesian Optimization for an ATP-Regenerating In Vitro Enzyme Cascade

by
Regine Siedentop
1,
Maximilian Siska
2,
Niklas Möller
1,
Hannah Lanzrath
2,
Eric von Lieres
2,
Stephan Lütz
1 and
Katrin Rosenthal
1,3,*,†
1
Department of Biochemical and Chemical Engineering, TU Dortmund University, 44227 Dortmund, Germany
2
Forschungszentrum Jülich GmbH, Institute of Bio- and Geosciences, IBG-1: Biotechnology, 52428 Jülich, Germany
3
School of Science, Constructor University, 28759 Bremen, Germany
*
Author to whom correspondence should be addressed.
†
Dedicated to Karl-Erich Jaeger for his pioneering contributions in the field of molecular enzyme technology.
Catalysts 2023, 13(3), 468; https://doi.org/10.3390/catal13030468
Submission received: 3 February 2023 / Revised: 19 February 2023 / Accepted: 21 February 2023 / Published: 23 February 2023
(This article belongs to the Special Issue Biocatalytic Cascade Reactions)
Browse Figures
Versions Notes

Abstract

:
Enzyme cascades are an emerging synthetic tool for the synthesis of various molecules, combining the advantages of biocatalysis and of one-pot multi-step reactions. However, the more complex the enzyme cascade is, the more difficult it is to achieve adequate productivities and product concentrations. Therefore, the whole process must be optimized to account for synergistic effects. One way to deal with this challenge involves data-driven models in combination with experimental validation. Here, Bayesian optimization was applied to an ATP-producing and -regenerating enzyme cascade consisting of polyphosphate kinases. The enzyme and co-substrate concentrations were adjusted for an ATP-dependent reaction, catalyzed by mevalonate kinase (MVK). With a total of 16 experiments, we were able to iteratively optimize the initial concentrations of the components used in the one-pot synthesis to improve the specific activity of MVK with 10.2 U mg−1. The specific activity even exceeded the results of the reference reaction with stoichiometrically added ATP amounts, with which a specific activity of 8.8 U mg−1 was reached. At the same time, the product concentrations were also improved so that complete yields were achieved.

Graphical Abstract

1. Introduction

Reactions catalyzed by enzymes can enable syntheses with favorable features such as high selectivity and an environmentally friendly process with mild reaction conditions or low waste burdens [1]. The combination of several sequential enzymatic reactions in one-pot, called enzyme cascade, further reduces the by-product formation and the need for intermediate isolation [2]. Enzyme cascades can be used for the synthesis of a variety of compounds ranging from bulk chemicals to high value compounds, such as active pharmaceutical ingredients (APIs). Though, in spite of the examples for syntheses by enzyme cascades with impressive results [3], a common challenge is their process optimization [4]. Enzyme engineering can lead to desired properties in the catalyst’s activity or stability [5], but optimization of the whole reaction system is also required. The balancing of different catalytic properties such as pH, temperature profiles and relative concentrations, optimal reaction conditions and often the elaboration of cofactor supply are necessary and can lead to a large number of required experiments in order to determine the optimal process conditions. Here, in silico modelling can support targeting experiments and help to substantially reduce the experimental effort.
There are several methods to create these models. Design of experiments is often the method of choice to identify components that have a large impact on the system. However, the algorithms do not account for previous gained knowledge about the parameter–objective relationship [6]. Mechanistic models can then be used to study reactions in silico, e.g., to evaluate time-dependent intermediate levels of enzyme cascades. The knowledge gained through these simulations can then be used as the basis for process optimization. However, this approach requires kinetic understanding and specific data of every involved enzyme [7]. This challenge can be addressed by conducting numerous experiments or by using data of homologous enzymes, if available [8]. In both cases, knowledge is usually obtained from isolated enzymes, omitting the complexity and synergistic effects of dynamically behaving enzyme cascades with multiple involved components.
Data-driven approaches, such as Bayesian optimization [9], provide alternatives to mechanistic modeling that do not require detailed prior understanding of the underlying biological and chemical processes. Instead, probabilistic surrogate models, most commonly Gaussian process regression (GPR), are applied to model the relationship between independent variables (e.g., concentrations or pH) and dependent variables (e.g., yield or productivity). GPR inherently quantifies the uncertainty of the model predictions. Acquisition functions such as expected improvement (EI) utilize these predictions and associated uncertainty measures to propose further measurements with the highest potential of information gain. As more experimental data become available, the surrogate model is iteratively refined and new measurement points are repeatedly proposed until a stopping criterion is reached, e.g., a desired value and certainty of the process optimum. Therefore, the acquisition function balances the trade-off between parameter regions with high predicted values (exploitation) and regions with high uncertainty due to low sampling density (exploration). While Bayesian optimization does not require any mechanistic understanding of the optimized process, incorporating prior knowledge into the surrogate model substantially increases search efficiency. It allows to simultaneously adjust multiple parameters, instead of one factor at a time. Bayesian optimization has been applied across disciplines, e.g., experimental materials science or bioprocess development [10,11] and enzymatic single-step reactions [12], but never in the context of process optimization for enzyme cascades.
In this study, we have optimized an ATP-producing and -regenerating enzyme cascade by performing Bayesian optimization, combining GPR with EI. Adenosine triphosphate (ATP) as an energy-rich cofactor plays an important role in many enzyme cascades. For industrially relevant cascades, this expensive cofactor must be regenerated to provide economical syntheses [13,14]. We used mevalonate kinase (MVK) as an ATP acceptor, an enzyme that catalyzes the phosphorylation of mevalonate (MVA) to mevalonate phosphate (MVAP) using ATP as a phosphate donor. The specific activity of MVK had to be improved to reach comparable results as with stoichiometrically added ATP. Over the course of three iterations using Bayesian optimization, we were able to reach specific activities for MVK that slightly exceeded the results with stoichiometric ATP using the ATP-producing and -regenerating system. Additionally, we monitored the product concentrations, which could be improved as well.

2. Results and Discussion

2.1. Specification of the Cascade and Its Optimization

MVK is a key enzyme of the isoprenoid pathway and is found in a variety of organisms, from bacteria to mammals [15]. The enzyme has been successfully used in in vivo and in in vitro enzyme cascades to synthesize isoprenoids, such as farnesene, limonene or patchoulol [5,16,17]. In our laboratory, we also used the enzyme MVK for an enzyme cascade in which ATP is required as a cofactor in several reaction steps. We were able to show in kinetic simulations that the regeneration of ATP can have a positive effect on the performance of a farnesyl pyrophosphate (FPP)-producing cascade [18]. In the present study, we chose one of the ATP-dependent key reactions—namely, the phosphorylation of MVA to MVAP—to optimize the regeneration of ATP. In other studies, this reaction was shown to be the rate-limiting step in the isoprenoid pathway [19]. The production and regeneration of ATP are catalyzed by two polyphosphate kinases (PPKs), AjPPK2 and SmPPK2, from adenosine monophosphate (AMP) with polyphosphate (polyP) as a phosphate donor (Figure 1). These enzymes have mainly been studied for cofactor regeneration [20,21,22], but applications for (non-natural) nucleotide syntheses are reported as well [23,24,25]. MVK converts mevalonate to mevalonate phosphate while consuming ATP (Figure 1).
The goal of this study was to determine optimal initial concentrations of selected reaction components to maximize the performance of the enzyme cascade. The concentrations of the regenerating enzymes and co-substrate were chosen as variable parameters to achieve the highest specific activity of the target reaction, namely, the phosphorylation of MVA. The tested concentration ranges of the three parameters AMP, AjPPK2, and SmPPK2 are given in Table 1.
The AMP concentration was set between 10 and 50 mM. The upper limit corresponds to stoichiometric amounts of MVA. The lower limit requires the mandatory regeneration of ATP by SmPPK2 to allow for the complete conversion of MVA to MVAP. The enzyme concentrations were chosen based on previous studies, which showed a sufficient ATP supply at concentrations of 5 and 50 mg L−1 for AjPPK2 and SmPPK2, respectively [20]. A ten-fold activity of AjPPK2 with 18.7 ± 0.8 U mg−1 compared to 1.9 ± 0.4 U mg−1 for SmPPK2 was confirmed for the reaction conditions in a combined approach of both enzymes (Supplementary Materials). The concentration ranges were, therefore, set to 1–20 mg L−1 and 10–200 mg L−1 for AjPPK2 and SmPPK2, respectively. In these concentration ranges, the optimal concentrations for ATP production and regeneration were determined to achieve the highest MVK activity. The initial concentrations of the components of the target reaction MVK and MVA, as well as polyP, were kept constant in order to use this reaction as an indicator for the improvement of the ATP production and regeneration system. The concentration of MVK was set to 200 mg L−1, of MVA to 50 mM, and of polyP to 55 mM.

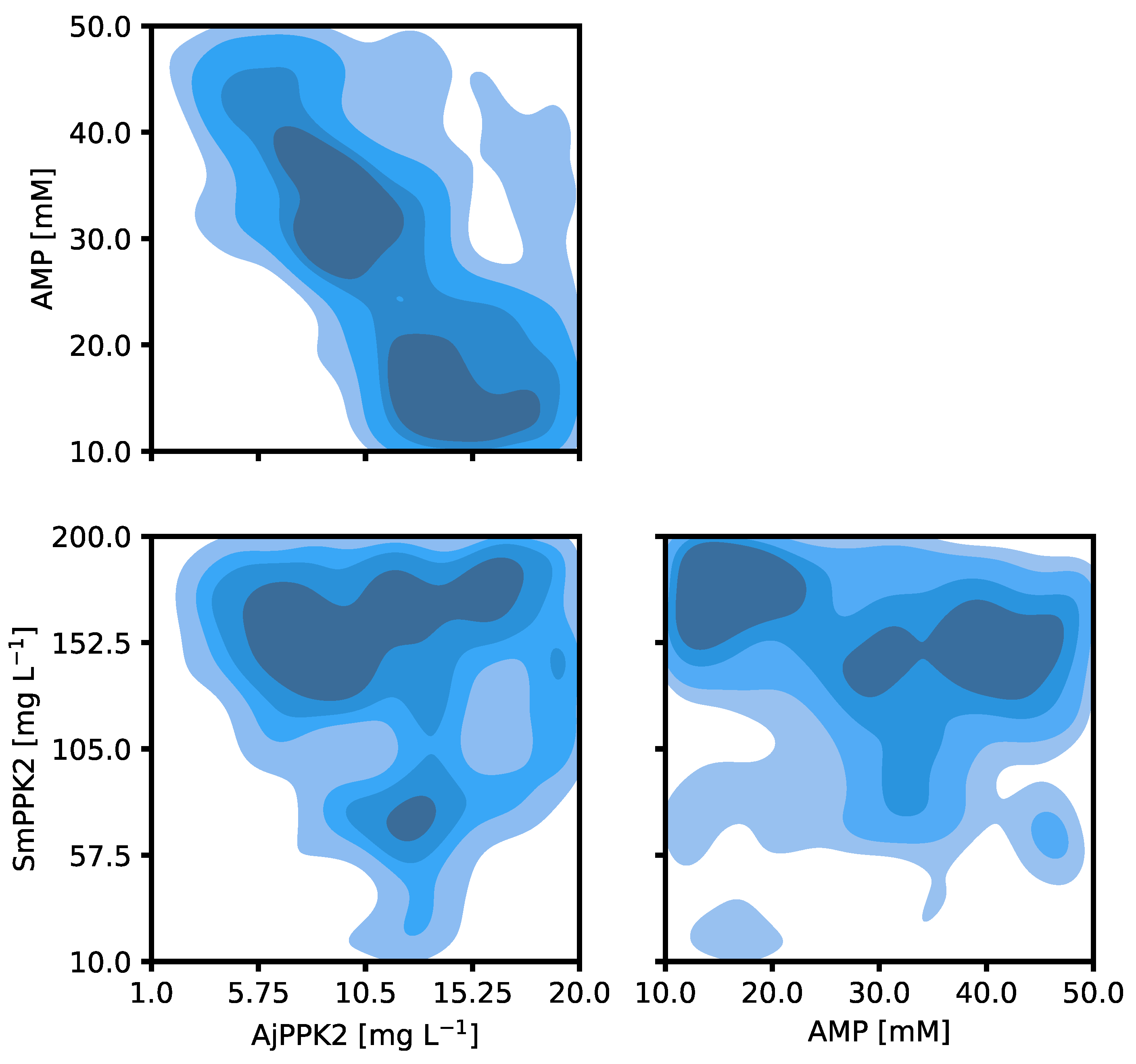
2.2. Iterative Optimization for Specific Activity of MVK

To build the first GPR model with which upcoming experiments can be designed, initial data are required. Therefore, a quasi-random Sobol sequence was used to distribute the initial data points over the parameter space (Table 2). Sobol sequences have a low discrepancy, i.e., the probability of samples to be in any subregion of the parameter space is proportional to the size of that subregion [26]. Six experiments were chosen for an appropriate level of information and a manageable number of experiments in the laboratory.
Table 2 provides an overview of the parameter concentrations of the Sobol sequence (Sobol 1–6), as well as their results. In addition, a reference experiment without cofactor regeneration, but with stoichiometric ATP amounts in a slight excess of 55 mM was conducted to gain a benchmark for the MVK activity. A specific activity of 8.8 ± 1.4 U mg−1 was reached for the MVK (Table 2, Entry 1). Furthermore, the product concentration was determined after 24 h, when the reaction was completed. For the reference experiment, a MVAP concentration of 44.0 ± 5.9 mM was reached. In the Sobol experiments, no complete conversion of substrate was observed, as MVA was still present (Supplementary Materials).
The experiments show that the enzyme and co-substrate concentrations for ATP production and regeneration have an impact on the specific activity of the ATP-dependent reaction. Three experiment designs proposed by the Sobol sequence show higher levels of activity already (Sobol 1, 2 and 5) for reactions with ATP production and the regeneration system compared to the reference experiment with a stochiometric addition of ATP. The values obtained are only slightly higher and are within the standard deviation. Nevertheless, it seems possible to achieve at least equally high specific activities compared to the reference experiment with a stoichiometric addition of ATP. Sobol 2 with 10.2 ± 0.3 U mg−1 and with 16% higher activity has the best improvement for the optimization indicator. The lowest MVK activity is observed for Sobol 4 with almost 45% reduced specific activity compared to the reference with 4.9 ± 2.9 U mg−1. The product concentrations of the Sobol experiments are mostly lower than the reference value. The lowest MVAP concentration is reached in Sobol 4 with 23.3 ± 13.7 mM and it reaches up to 44.2 ± 10.6 mM in Sobol 6, which is similar to the reference. A correlation of the achieved product concentrations to the specific activity cannot be observed and no conclusion can be made concerning the effect of the reaction conditions. Further experiments during the optimization process increase the statistical relevance of relations with which conclusions can be made.
With the data obtained by the initial Sobol experiments being the input data set, the iterative optimization using GPR and EI was performed. Each iteration used the whole data set of the previous rounds as the basis for the design of new measurement points. A number of three experiments was chosen for each iteration round and a total of three rounds were performed. The experimental conditions and results of each iteration are shown in Table 3.
In addition, for a better overview, the data were plotted in Figure 2 and presented together with the data from the Sobol experiments. In the first iteration round, a specific activity of 10.2 ± 1.5 U mg−1 was reached (Iteration 1.1), which is comparable to the Sobol experiment with the highest specific activity (Sobol 2). Interestingly, the enzyme concentration required for ATP regeneration was reduced by 20%, which improves the product-to-enzyme ratio favorably; this is also in view of the potential application on a larger scale and the environmental impact in terms of the material that has to be used to produce a certain amount of the product [27,28,29]. The experiment was conducted with low concentrations of AMP with 13.2 mM, which indicates that AMP is not a limitation if enough AjPPK2 and SmPPK2 are present. For iteration 1.2 and 1.3, the concentration limits of the enzymes were tested by the algorithm at the maximum addition of AMP, which resulted in a reduction in the specific activity to 3.9 ± 0.3 U mg−1 and 6.8 ± 0.4 U mg−1, respectively. In the second iteration, the algorithm explored a region of the parameter space with low sampling density by proposing experiments characterized by low concentration values for AjPPK2. Neither the specific activity nor the product concentration were improved. In fact, the specific activities were rather in the lower range compared to the previous experiments. Still, valuable information could be gained for the third and final iteration round. Here, specific activities were improved compared to iteration 2 and the same values as in the reference assay were achieved with 8.1 ± 1.0 U mg−1 and 8.0 ± 0.8 U mg−1, respectively. The product concentrations reached higher values than the reference assay in every experiment of the third iteration, from 50.8 ± 5.6 mM to 52.0 ± 2.1 mM MVAP. These values are slightly higher than the maximum possible 50 mM product. However, due to the standard deviation, the excess of the maximum possible concentration is not significant. Even though this was not the optimization goal, an improvement in product concentration could be achieved. This was, hence, a rather random result but could be included in Bayesian optimization in the future.
The final GPR model was applied to visualize the probability density of the maximum predicted activity, as illustrated in Figure 3. This visualization facilitates the identification of the optimal initial concentrations of the selected reaction components—namely, AMP, AjPPK2, and SmPPK2—in the presence of uncertainty. To determine the optimal concentrations, 10,000 samples of the final GPR model were analyzed. The resulting analysis allows for the identification of the regions of the parameter space which are more probable to correspond to the optimal experimental conditions. The different hues in the representation each signify 20% of the cumulative probability mass. As such, we can determine with 20% confidence that the optimum lies within the dark blue region of the parameter space. Additionally, a plateau, denoted by the darker blue hues, is predicted, where high activities can be obtained. These regions are dominant with higher amounts of SmPPK2, from ~130 to 200 mg L−1 and between ~5.75 and 18 mg L−1 of AjPPK2. AMP has less influence on the specific activity of MVK if enough enzyme is present.
With a total of 16 experiments, we succeeded in optimizing the enzymatic ATP production and regeneration system to improve the specific activity of the ATP-degrading enzyme MVK. At the same time, we were able to increase the product concentration, although it was not included as an objective function in the optimization. The simultaneous optimization of both goals could be performed using Bayesian optimization, if necessary [12]. However, the product concentration improved simultaneously, which might be due to the shift of the equilibrium by a better provision of ATP. The specific activity achieved with ATP-production and -regeneration even exceeded the reference assay, in which ATP was added in stoichiometric amounts. Therefore, the regeneration system is obviously not a limitation for the ATP-dependent reaction. As recently shown, the equilibrium of the reactions catalyzed by PPK2 is on the ATP side and thus supports the ATP-producing reaction [30]. Additionally, possible inhibitions by large amounts of ATP are bypassed by the regeneration of the nucleotide. Using low amounts of nucleotide increases the cofactor utilization in the regeneration cycle, which is an important factor for a larger scale application of regeneration systems [31]. The low impact of the amount of initial AMP concentrations on the specific activity of MVK allows for the addition of low amounts, resulting in a favorable increase in the cofactor utilization through the recycling reaction.
Interestingly, not only one optimal condition was found, but two parameter compositions were found within the measurement inaccuracy, thus leading to the same specific activity of 10.2 U mg−1 and a similar production concentration (Table 2, Sobol 2 and Table 3, Iteration 1.1). This indicates that there is not just one condition under which maximum MVK activity is achieved, but also a parameter plateau that allows for maximum activity, as also illustrated in Figure 3. The enzyme and co-substrate concentrations were not in close range, suggesting that the maximal reaction velocity was reached or that there was a different limiting factor. The specific activity might even be higher with higher amounts of substrate under these conditions. In another study, more than one optimal condition was found using Bayesian optimization [32]. Media optimization for protein production in microorganisms was performed, and as a result, an optimal parameter region was determined.
In conclusion, Bayesian optimization has successfully guided us through process optimization for an ATP-producing enzyme cascade with only few experiments. In other studies with three parameters using a traditional design of experiments approach, larger numbers of experiments were necessary to find the optimum. For the optimal nutrition supply of Streptomyces marinensis for neomycin production, 20 experiments were needed [33]. A three-step chemical synthesis of the broad-spectrum antibiotic GV143253A needed 10 experiments for the first reaction step and another 20 experiments for the second step of the reaction [34]. With our data-driven approach for optimization, a quantitative prediction with uncertainty quantification of the multi-parameter system was achieved, with collective information gained as all parameters were changed simultaneously. Interconnected influences were considered and the parameter region of the optimal composition for ATP production and regeneration was determined. Changes in the enzyme and co-substrate concentrations led to a significant variation in the enzyme cascade performance. The enzyme concentrations had a major influence on the MVK catalyzed reaction, especially.

3. Materials and Methods

3.1. Materials

Chemicals were purchased from Acros Organics (ThermoFisher Scientific, Waltham, MA, USA), AppliChem (AppliChem GmbH, Darmstadt, Germany), Merck (Merck KGaA, Darmstadt, Germany), Roth (Carl Roth, Karlsruhe, Germany), Santa Cruz Biotechnology (Santa Cruz Biotechnology, Inc., Dallas, TX, USA), ThermoFisher (ThermoFisher Scientific, Waltham, MA, USA), and VWR (VWR international GmbH, Darmstadt, Germany).

3.2. Enzyme Production

The PPKs were expressed as described by Becker et al. [20]. MVK of Methanosarcina mazei was expressed in Escherichia coli BL21 Gold (DE3). After chemical transformation, a single colony was used for the preculture. A total of 10 mL of LB medium (10 g L−1 of tryptone, 5 g L−1 of yeast extract, 10 g L−1 of NaCl, pH 7.0) was inoculated and incubated at 37 °C and 200 rpm. The main culture of 0.25 L of LB medium with 50 µg mL−1 of kanamycin and 1 mM of MgCl2 was inoculated to an OD600 of 0.01 and grown at 30 °C and 200 rpm. At an OD600 of 0.6, the culture was incubated for 15 min on ice and 0.1 mM of IPTG was added. Protein expression took place at 30 °C and 200 rpm for 9 h. The harvested cell pellets were stored at −20 °C.
Cell pellets were resuspended in 15 mL of lysis buffer (40 mM of Tris-HCl, 10 mM of NaCl, 10% glycerol, pH 8.0) for cell disruption. Sonication was performed in five cycles for 30 s on ice. Cell debris was removed by ultracentrifugation at 43,000× g for 20 min at 4 °C. The supernatant was sterile-filtered and loaded on an equilibrated 1 mL of HisTrap™ FF crude column (GE Healthcare, Solingen, Germany). After washing with five column volume of washing buffer (100 mM of K2HPO4, 500 mM of NaCl, 10 mM of imidazole, 10% glycerol, pH 8.0), protein was eluted with elution buffer (20 mM of Tris-HCl, 150 mM of NaCl, 300 mM of imidazole, pH 7.4) in 6 × 1 mL fractions. The protein concentration was determined by Bradford assay with bovine serum albumin as reference and the fractions with the highest concentrations were used for buffer exchange by size exclusion chromatography. A PD-10 column (GE Healthcare, Solingen, Germany) was equilibrated with Tris-HCl buffer (100 mM Tris-HCl, 150 mM NaCl, 10% glycerol, pH 7.5) and 2.5 mL of the protein solution was eluted with 3.5 mL of the Tris-HCl buffer. The protein solution was concentrated using Amicon® Ultra Centrifugal Filters (10 kDa, Millipore, Merck KGaA, Darmstadt, Germany) and the protein concentration was determined. Enzymes were stored at −80 °C.

3.3. Enzyme Assays

Enzyme assays were performed with purified enzymes in 1.5 mL Eppendorf tubes. They were prepared following the experiments of the reference FPP-producing cascade [18] with additional substances, which is why all enzyme assays contained 3 mM of Na3VO4, 0.043 mM of NADP+, 0.43 mM of CoA, 170 mM of glucose, 200 mM of NaOAc, and 20 mM of MgCl2 in 0.35 mL of the reaction volume, filled up with activity buffer (100 mM of Tris-HCl, 150 mM of NaCl, 10% glycerol, 20 mM of MgCl2, pH 7.5). Assays for PPK activity measurements additionally contained 50 mg L−1 of SmPPK2, 5 mg L−1 of AjPPK2, 10 mM of AMP, and 30 mM of polyP. Assays with MVK contained 0.2 mg mL−1 of MVK, 50 mM of MVA, and 55 mM of polyP with 55 mM of ATP in the reference assay. AMP, AjPPK2, and SmPPK2 were added in various concentrations. The reaction was incubated at 30 °C in a multirotator with 30 rpm. Samples were taken regularly, and enzymes were inactivated at 95 °C for 5 min.

3.4. Analytics

Samples were centrifuged and diluted with water prior to injection to fit in the linear range of the calibration curve. Nucleotides were analyzed by high performance liquid chromatography (HPLC). A Knauer Azura HPLC system (KNAUER GmbH, Berlin, Germany) consisting of an autosampler (AS 6.1L), pump (P 6.1L), column oven (CT 2.1), and a wavelength detector (MWD 2.1L) was used. The ISAspher 100-5 C18 AQ column (250 × 4 mm, Isera, Düren, Germany) was used for separation at 30 °C. The injection volume was 10 µL. The gradient consisted of mobile phase A (0.06 M K2HPO4 and 0.04 M KH2PO4) and mobile phase B (95% acetonitrile, 5% water): 0 min: 100% A; 3 min: 100% A; 10.5 min: 82% A, 18% B; 16 min: 50% A, 50% B; 18 min: 100% A; 23 min: 100% A at a flow rate of 1 mL min−1. The analytes were detected at a wavelength of 254 nm. Specific activity of AjPPK2 was determined from AMP and of SmPPK2 from ATP. MVA and MVAP were analyzed using a LC-MS (1260 Infinity II LC system combined with 6120 Quadrupole MS (Agilent, Santa Clara, CA, USA)) with a SeQuant® ZIC®-pHILIC 5 µm polymer 200 Å, 150 × 2.1 mm column (Merck KGaA, Darmstadt, Germany). The column oven was heated to 40 °C and the flow rate was set to 0.2 mL min−1. The injection volume was set to 3 µL and the following gradient of mobile phase A (10 mM NH4Ac, pH 9.2) and mobile phase B (acetonitrile) was used for separation: 0 min: 10% A; 1 min: 10% A; 26 min: 60% A; 33 min: 10% A; 50 min: 10% A. The MS measurement was performed in negative mode and the parameters for electron spray ionization (ESI) were set to the following: drying gas temperature: 350 °C, nebulizer pressure: 35 psig, drying gas flow: 12 L min−1, capillary voltage: 3500 V. Analytes were detected in the selected ion mode (SIM) with m/z of 147.0 and 147.1 during the first 15 min to detect MVA and 226.9, 227, 227.1, 455, 455.1 for monomeric and dimeric MVAP from 15 to 33 min. Specific activities were determined from substrate concentrations during the first 20 min of the reaction.

3.5. Data Analysis

GPR can be understood as a probability distribution over functions, defined by a mean function and a covariance function. The mean function encodes the prior belief on the basic behavior of the modeled process. The GPR fit to input data is influenced by a covariance function and a length scale prior, of which quantify the variation in function values. Prior to fitting the Gaussian process, experimental data were normalized on the interval [0 1]. The Gaussian process was initially parameterized by a constant zero mean function. The sum of a Matérn and a white noise kernel were used as the covariance function to account for the limited prior understanding of the relation between the varied process parameters and the observed specific activity. A length scale prior of 0.5 was chosen to sufficiently explore the parameter space by Bayesian optimization.
All processing of experimental data and the proposal experimental design configurations in this study were performed with an in-house-developed Python package, Planalyze, which is available on request. This package utilizes recent versions of Python 3.9, NumPy 1.22 [35], pandas 1.4 [36], matplotlib 3.5 [37], SciPy 1.9 [38] and related packages. GPR models were created with the GaussianProcessRegressor class of scikit-learn 1.1 [39]. Visualizations were performed with seaborn 0.12 [40].

4. Conclusions

Bayesian optimization was applied to determine the best parameters set for achieving the highest MVK activities and product titers for the studied enzyme cascade in the desired operational window. This study demonstrates the usefulness of in silico tools for the optimization of multi-parameter systems such as increasingly complex enzyme cascades. The presented approach reaches the optimization goal in an experimentally reduced and resource-efficient way. All parameters were simultaneously varied and experiments were not replicated to facilitate a better balance of exploration and exploitation of the searched parameter space. The more data are collected, the more refined the GPR model is and predictions by the acquisition function get more precise. The data obtained from the conducted experiments can even be used for further optimization tasks for the same enzyme cascade, making it even more efficient to achieve other objectives. It is demonstrated that data-driven models can boost the tedious optimization process of multi-parametric systems. Their application is not limited to enzyme cascades, but can be adapted for various other processes.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/catal13030468/s1. File: Spreadsheet with raw data and calculations.

Author Contributions

Conceptualization, R.S., E.v.L., S.L. and K.R.; software, H.L., M.S. and E.v.L.; validation, R.S.; formal analysis, R.S., M.S. and K.R.; investigation, R.S. and N.M.; resources, S.L.; data curation, R.S. and K.R.; writing—original draft preparation, R.S., M.S., E.v.L. and K.R.; writing—review and editing, R.S., M.S., E.v.L., K.R. and S.L.; visualization, R.S., M.S. and K.R.; supervision, K.R., S.L. and E.v.L.; project administration, K.R. and S.L.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.

Funding

RS received funding by Deutsche Forschungsgemeinschaft (DFG) under the priority programme SPP 2240 “eBiotech” (Bioelectrochemical and engineering fundamentals to establish electro-biotechnology for biosynthesis–Power to value-added products) (grant agreement No 445751305). The contribution of MS was performed as part of the Helmholtz School for Data Science in Life, Earth and Energy (HDS-LEE) and received funding from the Helmholtz Association of German Research Centers.

Data Availability Statement

Data are available upon request if not contained within the article or Supplementary Materials.

Acknowledgments

The authors would like to acknowledge the support with analytics by Sascha Nehring and Don Marvin Voss and support in the implementation of PPK assays by Martin Becker. We thank Frank Schulz for providing the plasmid of MVK and Jennifer Andexer for providing the plasmids of the PPKs.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Sheldon, R.A.; Brady, D.; Bode, M.L. The Hitchhiker’s guide to biocatalysis: Recent advances in the use of enzymes in organic synthesis. Chem. Sci. 2020, 11, 2587–2605. [Google Scholar] [CrossRef]
  2. Wang, Z.; Sekar, B.S.; Li, Z. Recent advances in artificial enzyme cascades for the production of value-added chemicals. Bioresour. Technol. 2021, 323, 124551. [Google Scholar] [CrossRef] [PubMed]
  3. Rosenthal, K.; Bornscheuer, U.T.; Lütz, S. Cascades of Evolved Enzymes for the Synthesis of Complex Molecules. Angew. Chem. Int. Ed. 2022, 61, e202208358. [Google Scholar] [CrossRef] [PubMed]
  4. Siedentop, R.; Claaßen, C.; Rother, D.; Lütz, S.; Rosenthal, K. Getting the Most Out of Enzyme Cascades: Strategies to Optimize In Vitro Multi-Enzymatic Reactions. Catalysts 2021, 11, 1183. [Google Scholar] [CrossRef]
  5. Zhu, F.; Zhong, X.; Hu, M.; Lu, L.; Deng, Z.; Liu, T. In vitro reconstitution of mevalonate pathway and targeted engineering of farnesene overproduction in Escherichia coli. Biotechnol. Bioeng. 2014, 111, 1396–1405. [Google Scholar] [CrossRef]
  6. Mandenius, C.-F.; Brundin, A. Bioprocess optimization using design-of-experiments methodology. Biotechnol. Prog. 2008, 24, 1191–1203. [Google Scholar] [CrossRef]
  7. Shen, L.; Kohlhaas, M.; Enoki, J.; Meier, R.; Schönenberger, B.; Wohlgemuth, R.; Kourist, R.; Niemeyer, F.; van Niekerk, D.; Bräsen, C.; et al. A combined experimental and modelling approach for the Weimberg pathway optimisation. Nat. Commun. 2020, 11, 1098. [Google Scholar] [CrossRef]
  8. Korman, T.P.; Opgenorth, P.H.; Bowie, J.U. A synthetic biochemistry platform for cell free production of monoterpenes from glucose. Nat. Commun. 2017, 8, 15526. [Google Scholar] [CrossRef]
  9. Greenhill, S.; Rana, S.; Gupta, S.; Vellanki, P.; Venkatesh, S. Bayesian Optimization for Adaptive Experimental Design: A Review. IEEE Access 2020, 8, 13937–13948. [Google Scholar] [CrossRef]
  10. Liang, Q.; Gongora, A.E.; Ren, Z.; Tiihonen, A.; Liu, Z.; Sun, S.; Deneault, J.R.; Bash, D.; Mekki-Berrada, F.; Khan, S.A.; et al. Benchmarking the performance of Bayesian optimization across multiple experimental materials science domains. NPJ Comput. Mater. 2021, 7, 188. [Google Scholar] [CrossRef]
  11. Helleckes, L.M.; Hemmerich, J.; Wiechert, W.; von Lieres, E.; Grünberger, A. Machine learning in bioprocess development: From promise to practice. Trends Biotechnol. 2022. [Google Scholar] [CrossRef]
  12. Baraibar, Á.G.; Von Lieres, E.; Wiechert, W.; Pohl, M.; Rother, D. Effective Production of (S)-α-Hydroxy ketones: An Reaction Engineering Approach. Top. Catal. 2014, 57, 401–411. [Google Scholar] [CrossRef]
  13. Schmidt, S.; Schallmey, A.; Kourist, R. Multi-Enzymatic Cascades In Vitro. In Enzyme Cascade Design and Modelling; Springer International Publishing: Cham, Switzerland, 2021; pp. 31–48. [Google Scholar]
  14. Mordhorst, S.; Andexer, J.N. Round, round we go—Strategies for enzymatic cofactor regeneration. Nat. Prod. Rep. 2020, 37, 1316–1333. [Google Scholar] [CrossRef]
  15. Cho, S.-H.; Tóth, K.; Kim, D.; Vo, P.H.; Lin, C.-H.; Handakumbura, P.P.; Ubach, A.R.; Evans, S.; Paša-Tolić, L.; Stacey, G. Activation of the plant mevalonate pathway by extracellular ATP. Nat. Commun. 2022, 13, 450. [Google Scholar] [CrossRef] [PubMed]
  16. Rolf, J.; Julsing, M.K.; Rosenthal, K.; Lütz, S. A Gram-Scale Limonene Production Process with Engineered Escherichia coli. Molecules 2020, 25, 1881. [Google Scholar] [CrossRef] [PubMed]
  17. Dirkmann, M.; Nowack, J.; Schulz, F. An in Vitro Biosynthesis of Sesquiterpenes Starting from Acetic Acid. Chembiochem 2018, 19, 2146–2151. [Google Scholar] [CrossRef] [PubMed]
  18. Siedentop, R.; Dziennus, M.; Lütz, S.; Rosenthal, K. Debottlenecking of an In Vitro Enzyme Cascade Using a Combined Model- and Experiment-Based Approach. Chem. Ing. Tech. 2023. accepted. [Google Scholar] [CrossRef]
  19. Shimane, M.; Sugai, Y.; Kainuma, R.; Natsume, M.; Kawaide, H. Mevalonate-Dependent Enzymatic Synthesis of Amorphadiene Driven by an ATP-Regeneration System Using Polyphosphate Kinase. Biosci. Biotechnol. Biochem. 2012, 76, 1558–1560. [Google Scholar] [CrossRef]
  20. Becker, M.; Nikel, P.; Andexer, J.; Lütz, S.; Rosenthal, K. A Multi-Enzyme Cascade Reaction for the Production of 2′3′-cGAMP. Biomolecules 2021, 11, 590. [Google Scholar] [CrossRef]
  21. Andexer, J.N.; Richter, M. Emerging Enzymes for ATP Regeneration in Biocatalytic Processes. Chembiochem 2015, 16, 380–386. [Google Scholar] [CrossRef]
  22. Resnick, S.M.; Zehnder, A.J.B. In Vitro ATP Regeneration from Polyphosphate and AMP by Polyphosphate:AMP Phosphotransferase and Adenylate Kinase from Acinetobacter johnsonii 210A. Appl. Environ. Microbiol. 2000, 66, 2045–2051. [Google Scholar] [CrossRef] [PubMed]
  23. Frisch, J.; Maršić, T.; Loderer, C. A Novel One-Pot Enzyme Cascade for the Biosynthesis of Cladribine Triphosphate. Biomolecules 2021, 11, 346. [Google Scholar] [CrossRef] [PubMed]
  24. Mordhorst, S.; Singh, J.; Mohr, M.K.F.; Hinkelmann, R.; Keppler, M.; Jessen, H.J.; Andexer, J.N. Several Polyphosphate Kinase 2 Enzymes Catalyse the Production of Adenosine 5′-Polyphosphates. Chembiochem 2019, 20, 1019–1022. [Google Scholar] [CrossRef] [PubMed]
  25. Sun, C.; Li, Z.; Ning, X.; Xu, W.; Li, Z. In vitro biosynthesis of ATP from adenosine and polyphosphate. Bioresour. Bioprocess. 2021, 8, 1–10. [Google Scholar] [CrossRef]
  26. Niederreiter, H. Low-discrepancy and low-dispersion sequences. J. Number Theory 1988, 30, 51–70. [Google Scholar] [CrossRef]
  27. Woodley, J.M. Accelerating the implementation of biocatalysis in industry. Appl. Microbiol. Biotechnol. 2019, 103, 4733–4739. [Google Scholar] [CrossRef]
  28. Siedentop, R.; Rosenthal, K. Industrially Relevant Enzyme Cascades for Drug Synthesis and Their Ecological Assessment. Int. J. Mol. Sci. 2022, 23, 3605. [Google Scholar] [CrossRef]
  29. Becker, M.; Lütz, S.; Rosenthal, K. Environmental Assessment of Enzyme Production and Purification. Molecules 2021, 26, 573. [Google Scholar] [CrossRef]
  30. Keppler, M.; Moser, S.; Jessen, H.J.; Held, C.; Andexer, J.N. Make or break: The thermodynamic equilibrium of polyphosphate kinase-catalysed reactions. Beilstein J. Org. Chem. 2022, 18, 1278–1288. [Google Scholar] [CrossRef]
  31. Tavanti, M.; Hosford, J.; Lloyd, R.C.; Brown, M.J.B. Recent Developments and Challenges for the Industrial Implementation of Polyphosphate Kinases. Chemcatchem 2021, 13, 3565–3580. [Google Scholar] [CrossRef]
  32. Freier, L.; Hemmerich, J.; Schöler, K.; Wiechert, W.; Oldiges, M.; von Lieres, E. Framework for Kriging-based iterative experimental analysis and design: Optimization of secretory protein production in Corynebacterium glutamicum. Eng. Life Sci. 2016, 16, 538–549. [Google Scholar] [CrossRef]
  33. Adinarayana, K.; Ellaiah, P.; Srinivasulu, B.; Devi, R.B.; Adinarayana, G. Response surface methodological approach to optimize the nutritional parameters for neomycin production by Streptomyces marinensis under solid-state fermentation. Process Biochem. 2003, 38, 1565–1572. [Google Scholar] [CrossRef]
  34. Guercio, G.; Perboni, A.; Tinazzi, F.; Rovatti, L.; Provera, S. The Synthesis of GV143253A: A Case Study for the Use of Analytical and Statistical Tools to Elucidate the Reaction Mechanism and to Optimize the Process. Org. Process Res. Dev. 2010, 14, 840–848. [Google Scholar] [CrossRef]
  35. Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
  36. McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, SciPy, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar]
  37. Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
  38. Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0 Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
  39. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
  40. Waskom, M.L. Seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
Catalysts 13 00468 g001 550
Figure 1. Enzyme cascade for adenosine triphosphate (ATP) production and regeneration and mevalonate phosphate (MVAP) production. Two polyphosphate kinases (PPKs) phosphorylate adenosine monophosphate (AMP) to ATP with polyphosphate (polyP) as phosphate donor. ATP is consumed by mevalonate kinase (MVK) to convert mevalonate (MVA) to MVAP.
Figure 1. Enzyme cascade for adenosine triphosphate (ATP) production and regeneration and mevalonate phosphate (MVAP) production. Two polyphosphate kinases (PPKs) phosphorylate adenosine monophosphate (AMP) to ATP with polyphosphate (polyP) as phosphate donor. ATP is consumed by mevalonate kinase (MVK) to convert mevalonate (MVA) to MVAP.
Catalysts 13 00468 g001
Catalysts 13 00468 g002 550
Figure 2. Results of the optimization approach with specific activities (a) and MVAP concentrations after 24 h (b) normalized to the reference assay. Enzyme assays were performed in triplicates with purified enzymes in 1.5 mL Eppendorf tubes. Enzyme assays contained 0.2 mg mL−1 of MVK, 50 mM of MVA, 55 mM of polyP, 3 mM of Na3VO4, 0.043 mM of NADP+, 0.43 mM of CoA, 170 mM of glucose, 200 mM of NaOAc, and 20 mM of MgCl2 in 0.35 mL of the reaction volume, filled up with activity buffer (100 mM Tris-HCl, 150 mM NaCl, 10% glycerol, 20 mM MgCl2, pH 7.5). AMP, AjPPK2, and SmPPK2 were added in various concentrations, except in the reference assay where 55 mM of ATP was added. The reaction was incubated at 30 °C in a multirotator with 30 rpm. Samples were taken regularly, and enzymes were inactivated at 95 °C for 5 min.
Figure 2. Results of the optimization approach with specific activities (a) and MVAP concentrations after 24 h (b) normalized to the reference assay. Enzyme assays were performed in triplicates with purified enzymes in 1.5 mL Eppendorf tubes. Enzyme assays contained 0.2 mg mL−1 of MVK, 50 mM of MVA, 55 mM of polyP, 3 mM of Na3VO4, 0.043 mM of NADP+, 0.43 mM of CoA, 170 mM of glucose, 200 mM of NaOAc, and 20 mM of MgCl2 in 0.35 mL of the reaction volume, filled up with activity buffer (100 mM Tris-HCl, 150 mM NaCl, 10% glycerol, 20 mM MgCl2, pH 7.5). AMP, AjPPK2, and SmPPK2 were added in various concentrations, except in the reference assay where 55 mM of ATP was added. The reaction was incubated at 30 °C in a multirotator with 30 rpm. Samples were taken regularly, and enzymes were inactivated at 95 °C for 5 min.
Catalysts 13 00468 g002
Catalysts 13 00468 g003 550
Figure 3. Probability density of the optimal initial concentrations of the reaction components AMP, AjPPK2, and SmPPK2. The contours encode the probability mass for the experiment conditions corresponding to the maximum specific activity derived from 10,000 samples of the final GPR model. Each shade encodes 20% of the cumulative probability mass.
Figure 3. Probability density of the optimal initial concentrations of the reaction components AMP, AjPPK2, and SmPPK2. The contours encode the probability mass for the experiment conditions corresponding to the maximum specific activity derived from 10,000 samples of the final GPR model. Each shade encodes 20% of the cumulative probability mass.
Catalysts 13 00468 g003
Table
Table 1. Optimization parameters and their tested concentration window.
Table 1. Optimization parameters and their tested concentration window.
ParameterTested Range
AMP concentration10–50 mM
AjPPK2 concentration1–20 mg L−1
SmPPK2 concentration10–200 mg L−1
Table
Table 2. Conditions of the Sobol experiments as parameter concentrations and the respective results of specific activity and product concentration. Enzyme assays were performed in triplicates with purified enzymes in 1.5 mL Eppendorf tubes. Enzyme assays contained 0.2 mg mL−1 of MVK, 50 mM of MVA, 55 mM of polyP, 3 mM of Na3VO4, 0.043 mM of NADP+, 0.43 mM of CoA, 170 mM of glucose, 200 mM of NaOAc, and 20 mM of MgCl2 in 0.35 mL of the reaction volume, filled up with activity buffer (100 mM Tris-HCl, 150 mM NaCl, 10% glycerol, 20 mM MgCl2, pH 7.5). AMP, AjPPK2, and SmPPK2 were added in various concentrations, except in the reference assay where 55 mM ATP was added. The reaction was incubated at 30 °C in a multirotator with 30 rpm. Samples were taken regularly, and enzymes were inactivated at 95 °C for 5 min.
Table 2. Conditions of the Sobol experiments as parameter concentrations and the respective results of specific activity and product concentration. Enzyme assays were performed in triplicates with purified enzymes in 1.5 mL Eppendorf tubes. Enzyme assays contained 0.2 mg mL−1 of MVK, 50 mM of MVA, 55 mM of polyP, 3 mM of Na3VO4, 0.043 mM of NADP+, 0.43 mM of CoA, 170 mM of glucose, 200 mM of NaOAc, and 20 mM of MgCl2 in 0.35 mL of the reaction volume, filled up with activity buffer (100 mM Tris-HCl, 150 mM NaCl, 10% glycerol, 20 mM MgCl2, pH 7.5). AMP, AjPPK2, and SmPPK2 were added in various concentrations, except in the reference assay where 55 mM ATP was added. The reaction was incubated at 30 °C in a multirotator with 30 rpm. Samples were taken regularly, and enzymes were inactivated at 95 °C for 5 min.
ExperimentConditionsResults
AMP
[mM]		AjPPK2
[mg L−1]		SmPPK2
[mg L−1]		Average Specific Activity
[U mg−1]		MVAP Concentration after 24 h
[mM]
Reference---8.8 ± 1.444.0 ± 5.9
Sobol 127.510.5105.09.2 ± 0.533.9 ± 14.9
Sobol 238.85.8152.510.2 ± 0.335.7 ± 8.9
Sobol 316.315.357.58.5 ± 0.626.9 ± 1.9
Sobol 444.417.633.84.9 ± 2.923.3 ± 13.7
Sobol 510.612.9176.39.9 ± 1.826.9 ± 1.0
Sobol 647.22.2116.97.2 ± 0.644.2 ± 10.6
Table
Table 3. Conditions of the experiments as parameter concentrations and the respective results of the iterative optimization approach. Enzyme assays were performed in triplicates with purified enzymes in 1.5 mL Eppendorf tubes. The enzyme assays contained 0.2 mg mL−1 of MVK, 50 mM of MVA, 55 mM of polyP, 3 mM of Na3VO4, 0.043 mM of NADP+, 0.43 mM of CoA, 170 mM of glucose, 200 mM of NaOAc, and 20 mM of MgCl2 in 0.35 mL of the reaction volume, filled up with activity buffer (100 mM Tris-HCl, 150 mM NaCl, 10% glycerol, 20 mM MgCl2, pH 7.5). AMP, AjPPK2, and SmPPK2 were added in various concentrations, except in the reference assay where 55 mM of ATP was added. The reaction was incubated at 30 °C in a multirotator with 30 rpm. Samples were taken regularly, and enzymes were inactivated at 95 °C for 5 min.
Table 3. Conditions of the experiments as parameter concentrations and the respective results of the iterative optimization approach. Enzyme assays were performed in triplicates with purified enzymes in 1.5 mL Eppendorf tubes. The enzyme assays contained 0.2 mg mL−1 of MVK, 50 mM of MVA, 55 mM of polyP, 3 mM of Na3VO4, 0.043 mM of NADP+, 0.43 mM of CoA, 170 mM of glucose, 200 mM of NaOAc, and 20 mM of MgCl2 in 0.35 mL of the reaction volume, filled up with activity buffer (100 mM Tris-HCl, 150 mM NaCl, 10% glycerol, 20 mM MgCl2, pH 7.5). AMP, AjPPK2, and SmPPK2 were added in various concentrations, except in the reference assay where 55 mM of ATP was added. The reaction was incubated at 30 °C in a multirotator with 30 rpm. Samples were taken regularly, and enzymes were inactivated at 95 °C for 5 min.
ExperimentConditionsResults
AMP
[mM]		AjPPK2
[mg L−1]		SmPPK2
[mg L−1]		Average Specific Activity
[U mg−1]		MVAP Concentration after 24 h
[mM]
Reference---8.8 ± 1.444.0 ± 5.9
Iteration 1.113.28.1118.110.2 ± 1.534.8 ± 5.0
Iteration 1.249.718.811.43.9 ± 0.322.6 ± 1.4
Iteration 1.350.01.0199.96.8 ± 0.418.5 ± 0.4
Iteration 2.124.25.031.84.1 ± 0.831.7 ± 4.5
Iteration 2.218.24.8100.63.9 ± 0.320.9 ± 0.7
Iteration 2.337.03.1107.14.5 ± 2.018.4 ± 0.4
Iteration 3.125.813.1198.08.1 ± 1.050.8 ± 5.6
Iteration 3.215.89.0138.08.0 ± 0.851.9 ± 3.6
Iteration 3.329.416.2120.65.8 ± 0.552.0 ± 2.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Siedentop, R.; Siska, M.; Möller, N.; Lanzrath, H.; von Lieres, E.; Lütz, S.; Rosenthal, K. Bayesian Optimization for an ATP-Regenerating In Vitro Enzyme Cascade. Catalysts 2023, 13, 468. https://doi.org/10.3390/catal13030468

AMA Style

Siedentop R, Siska M, Möller N, Lanzrath H, von Lieres E, Lütz S, Rosenthal K. Bayesian Optimization for an ATP-Regenerating In Vitro Enzyme Cascade. Catalysts. 2023; 13(3):468. https://doi.org/10.3390/catal13030468

Chicago/Turabian Style

Siedentop, Regine, Maximilian Siska, Niklas Möller, Hannah Lanzrath, Eric von Lieres, Stephan Lütz, and Katrin Rosenthal. 2023. "Bayesian Optimization for an ATP-Regenerating In Vitro Enzyme Cascade" Catalysts 13, no. 3: 468. https://doi.org/10.3390/catal13030468

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop