Hall Current and Soret Effects on Unsteady MHD Rotating Flow of Second-Grade Fluid through Porous Media under the Influences of Thermal Radiation and Chemical Reactions
Abstract
1. Introduction
2. Formulation of the Problem
3. Solution of the Problem
3.1. Skin Friction
3.2. Nusselt Number
3.3. Sherwood Number
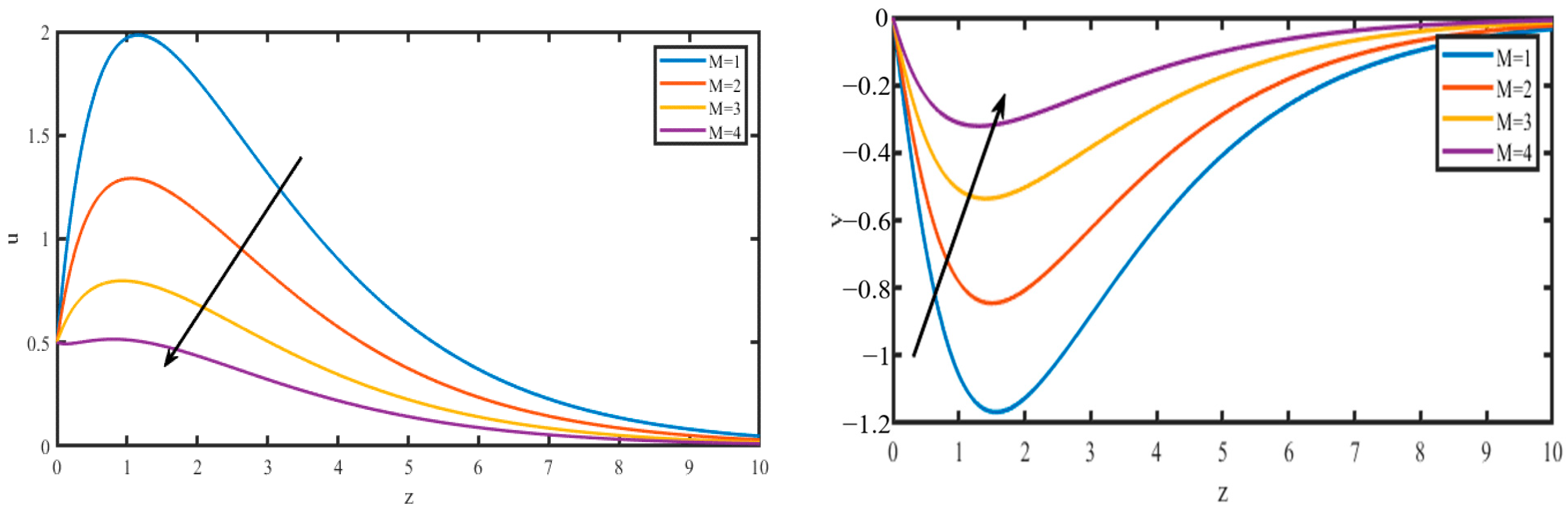
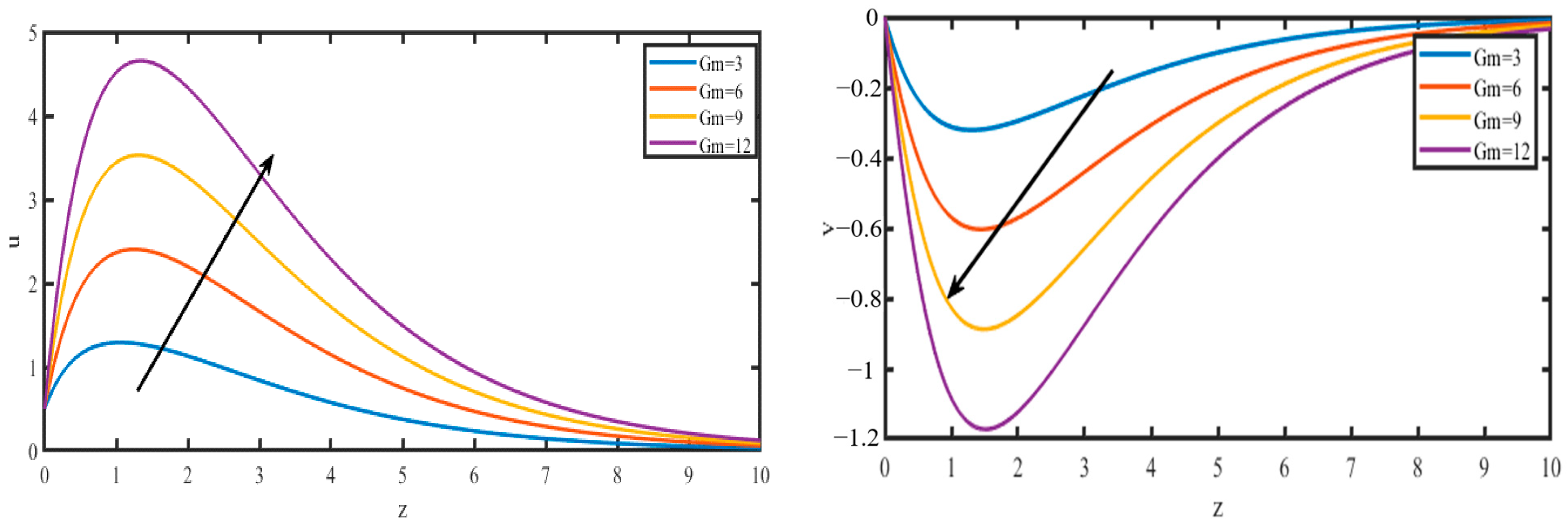
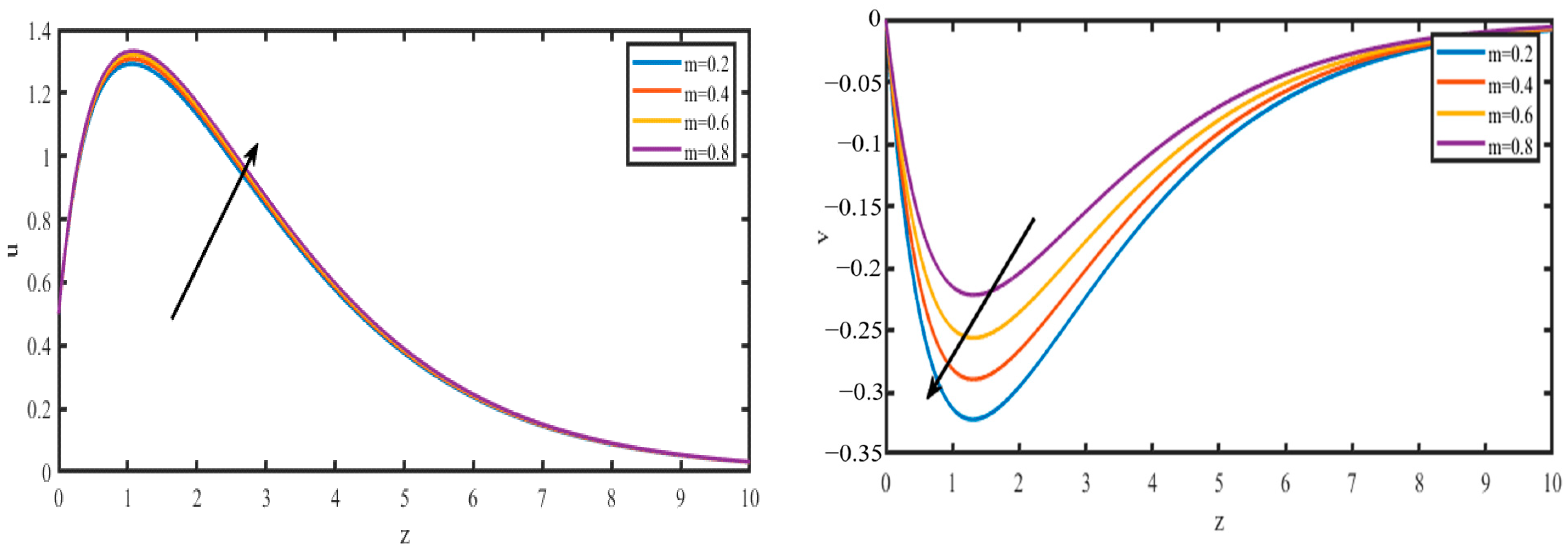
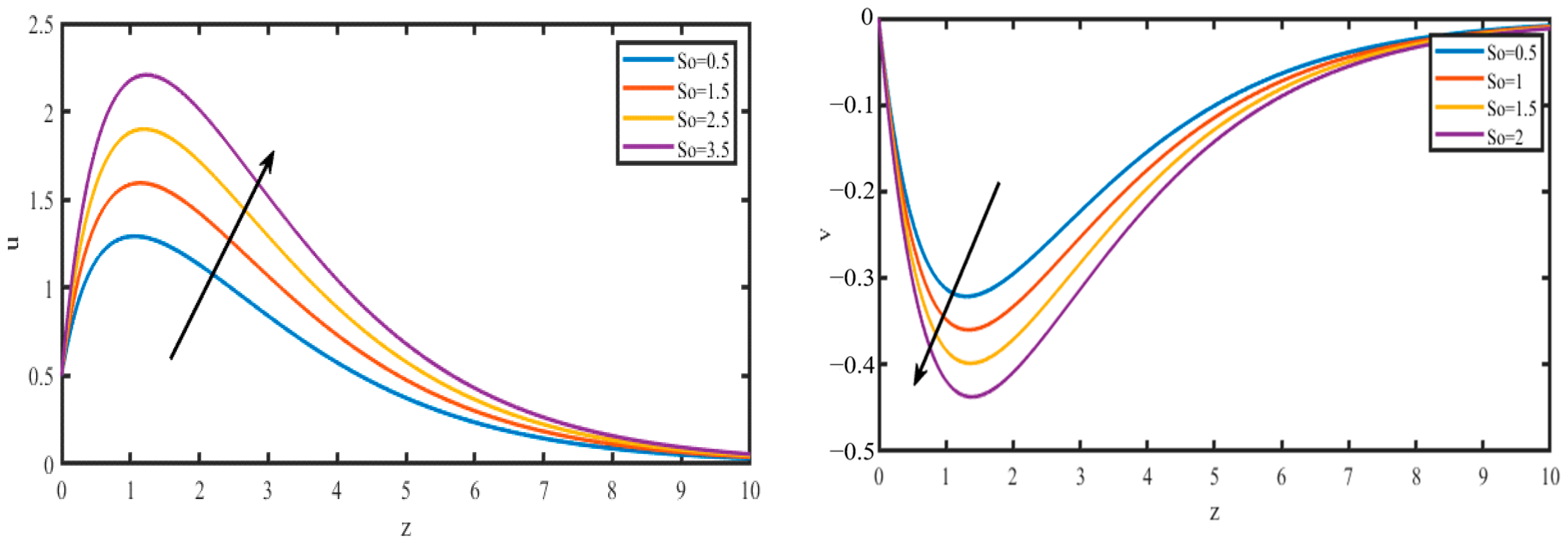
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| A | real positive constant |
| B0 | applied magnetic field (A/m) |
| x, y | dimensional co-ordinates (m) |
| u, v | velocity components in x and y directions (m/s) |
| C | non-dimensional fluid concentration (kg/m3) |
| D1 | coefficient of thermal diffusivity (m2 s−1) |
| g | acceleration due to gravity (m s−2) |
| Gr | thermal Grashof number |
| Gm | mass Grashof number |
| Cw | the uniform concentration of the fluid at the plate (kg m−3) |
| Kc | chemical reaction parameter (w/mk) |
| m | Hall parameter |
| C∞ | the concentration of the fluid far away from the plate (kg m−3) |
| B | magnetic field vector (A/m) |
| qw | local surface heat flux (W m−2) |
| Nu | local Nusselt number |
| E | electric field vector (c) |
| V | velocity vector (m/s) |
| k1 | thermal conductivity (W/m K) |
| K | permeability parameter |
| qm | local surface mass flux (kg s−1 m−2) |
| Pe | electron pressure (Pascal) |
| Pr | Prandtl number |
| Sc | Schmidt number |
| Jx, Jy | current densities in x and y directions |
| k | permeability of porous medium (m2) |
| H | heat source parameter |
| J | current density vector (A/m2) |
| Cp | specific heat at a constant pressure (J/kg·K) |
| D | coefficient of mass diffusivity (m2/s) |
| Sh | local Sherwood number |
| w | slip velocity (m s−1) |
| w0 | scale of suction velocity |
| So | Soret number |
| t | time (s) |
| u0 | plate velocity (m s−1) |
| qr | radiative heat flux |
| F | radiation parameter (cm−2) |
| Tw | the uniform temperature of the fluid on the plate (K) |
| T∞ | the temperature of the fluid far away from the plate (K) |
| R | rotation parameter |
| S | second grade fluid |
| M | Hartmann number |
| N | constant |
| Greek symbols | |
| β | coefficient of thermal expansion of the fluid |
| Ω | angular velocity (s−1) |
| τw | local wall shear stress (pascal) |
| τe | electron collision time (s) |
| ωe | cyclotron frequency (e/mB) |
| ϕ | non-dimensional concentration (mol/m3) |
| v | kinematic viscosity (m2/s) |
| τ | local skin friction coefficient |
| β * | coefficient of mass expansion of the solid |
| Θ | non-dimensional temperature (K) |
| ρ | fluid density (Kg/m3) |
| σ | electrical conductivity (S/m) |
| Subscripts and Superscripts | |
| ∞ | free stream conditions |
| i | ions |
| w | conditions on the wall |
| e | electrons |
References
- Bestman, A.R.; Adjepong, S.K. Unsteady hydromagnetic free-convection flow with radiative heat transfer in a rotating fluid. Astrophys. Space Sci. 1998, 143, 73. [Google Scholar] [CrossRef]
- Mbeledogu, I.U.; Ogulu, A. Heat and Mass Transfer of an Unsteady MHD Natural Convection Flow of a Rotating Fluid Past a Vertical Porous Flat Plate in the Presence of Radiative Heat Transfer. Int. J. Heat Mass Transf. 2007, 50, 1902–1908. [Google Scholar] [CrossRef]
- Seth, G.S.; Nandkeolyar, R.; Ansari, M.S. Effects of Thermal Radiation and Rotation on Unsteady Hydromagnetic Free Convection Flow past an Impulsively Moving Vertical Plate with Ramped Temperature in a Porous Medium. J. Appl. Fluid Mech. 2013, 6, 27. [Google Scholar]
- Sutton, G.W.; Sherman, A. Engineering Magnetohydrodynamics; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Sarkar, B.C.; Das, S.; Jana, R.N. Hall Effects on Unsteady MHD Free Convective Flow Past an Accelerated Moving Vertical Plate with Viscous and Joule Dissipations. Int. J. Comput. Appl. 2013, 70, 19–28. [Google Scholar]
- Seth, G.S.; Hussain, S.M.; Sarkar, S. Effects of Hall current and rotation on unsteady MHD natural convection flow with heat and mass transfer past an impulsively moving vertical plate in the presence of radiation and chemical reaction. Bulg. Chem. Commun. 2014, 46, 704–718. [Google Scholar]
- Farhad, A.; Norzieha, M.; Sharidan, S.; Khan, I.; Sami, U.H. Hydromagnetic rotating flow in a porous medium with slip condition and Hall current. Int. J. Phys. Sci. 2012, 7, 1540–1548. [Google Scholar] [CrossRef]
- Raghunath, K.; Mohanaramana, R. Hall, Soret, and rotational effects on unsteady MHD rotating flow of a second-grade fluid through a porous medium in the presence of chemical reaction and aligned magnetic field. Int. Commun. Heat Mass Transf. 2022, 137, 106287. [Google Scholar] [CrossRef]
- Raghunath, K.; Mohanaramana, R.; Nagesh, G.; Charankumar, G.; Khan, S.U.; Khan, M.I. Hall and ion slip radiative flow of chemically reactive second grade through porous saturated space via perturbation approach. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Deepthi, V.V.L.; Lashin, M.M.A.; Kumar, N.R.; Raghunath, K.; Ali, F.; Oreijah, M.; Guedri, K.; Tag-ElDin, E.S.M.; Khan, M.I.; Galal, A.M. Recent Development of Heat and Mass Transport in the Presence of Hall, Ion Slip and Thermo Diffusion in Radiative Second Grade Material: Application of Micromachines. Micromachines 2022, 13, 1566. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C.; Pop, I. Effects of thermal radiation on micropolar fluid flow and heat transfer over a porous shrinking sheet. Int. J. Heat Mass Transf. 2012, 55, 2945–2952. [Google Scholar] [CrossRef]
- Hussain, M.; Ashraf, M.; Nadeem, S.; Khan, M. Radiation effects on the thermal boundary layer flow of a micropolar fluid towards a permeable stretching sheet. J. Frankl. Inst. 2013, 350, 194–210. [Google Scholar] [CrossRef]
- Oahimire, J.I.; Olajuwon, B.I. Effect of Hall current and thermal radiation on heat and mass transfer of a chemically reacting MHD flow of a micropolar fluid through a porous medium. J. King Saud Univ. Eng. Sci. 2014, 26, 112–121. [Google Scholar] [CrossRef]
- Mabood, F.; Ibrahim, S.M.; Rashidi, M.M.; Shadloo, M.S.; Lorenzini, G. Non-uniform heat source/sink and Soret effects on MHD non-Darcian convective flow past a stretching sheet in a micropolar fluid with radiation. Int. J. Heat Mass Transf. 2016, 93, 674–682. [Google Scholar] [CrossRef]
- Raghunath, K.; Charankumar, G.; Giulio, L. Effects of Soret, Rotation, Hall, and Ion Slip on Unsteady MHD Flow of A Jeffrey Fluid Through A Porous Medium in The Presence of Heat Absorption and Chemical Reaction. J. Mech. Eng. Res. Dev. 2022, 45, 80–97. [Google Scholar]
- Obulesu, M.; Raghunath, K.; Reddy, P.M.; Charankumar, G.; Giulio, L.; Sidik, N.A.C. Unsteady MHD on Convective Flow of a Newtonian Fluid Past an Inclined Plate in Presence of Chemical Reaction with Radiation Absorption and Dufour Effects. CFD Lett. 2022, 14, 62–76. [Google Scholar] [CrossRef]
- Nagesh, G.; Raghunath, K. Soret Radiation and Chemical Reaction effect on MHD Jeffrey fluid flow past an inclined vertical plate Embedded in porous medium. MATERIALS Today Proc. 2022, 50 Pt 5, 2218–2226. [Google Scholar] [CrossRef]
- Muthucumaraswamy, R. Effects of a chemical reaction on a moving isothermal vertical surface with suction. Acta Mech. 2002, 155, 65–70. [Google Scholar] [CrossRef]
- Ajibade, A.O.; Umar, A.M. Effect of chemical reaction and radiation absorption on the unsteady MHD free convection Couette flow in a vertical channel filled with porous materials. Afr. Mat. 2016, 27, 201–213. [Google Scholar] [CrossRef]
- Raghunath, K.; Nagesh, G.; Reddy, V.R.C.; Obulesu, M. Unsteady MHD fluid flow past an inclined vertical porous plate in the presence of chemical reaction with aligned magnetic field, radiation, and Soret effects. Heat Transf. 2021, 51, 2742–2760. [Google Scholar] [CrossRef]
- Raghunath, K.; Obulesu, M. Unsteady MHD oscillatory Casson fluid flow past an inclined vertical porous plate in the presence of chemical reaction with heat absorption and Soret effects. Heat Transf. 2022, 51, 733–752. [Google Scholar] [CrossRef]
- Raghunath, K.; Obulesu, M.; Sujatha, S.; Venkateswaraju, K. Investigation of MHD Casson fluid flow past a vertical porous plate under the influence of thermal diffusion and chemical reaction. Heat Transf. 2022, 51, 377–394. [Google Scholar] [CrossRef]
- Reddy, V.R.; Raghunath, K.; Obulesu, M. Characteristics of MHD Casson fluid past an inclined vertical porous plate. Mater. Today Proc. 2022, 49, 2136–2142. [Google Scholar] [CrossRef]
- Ibrahim, F.; Elaiw, A.; Bakr, A. Effect of the chemical reaction and radiation absorption on the unsteady MHD free convection flow past a semi infinite vertical permeable moving plate with heat source and suction. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1056–1066. [Google Scholar] [CrossRef]
- Kesavaiah, D.C.; Satyanarayana, P.; Venkataramana, S. Effects of the chemical reaction and radiation absorption on an unsteady MHD convective heat and mass transfer flow past a semi-infinite vertical permeable moving plate embedded in a porous medium with heat source and suction. Int. J. Appl. Math. Mech. 2011, 7, 52–69. [Google Scholar]
- Narayana, P.V.S.; Venkateswarlu, B.; Venkataramana, S. Effects of Hall current and radiation absorption on MHD micropolar fluid in a rotating system. Ain Shams Eng. J. 2013, 4, 843–854. [Google Scholar] [CrossRef]
- Seth, G.S.; Mahato, G.K.; Sarkar, S. Effects of Hall current and rotation on MHD natural convection flow past an impulsively moving vertical plate with ramped temperature in the presence of thermal diffusion with heat absorption. Int. J. Energy Tech. 2013, 5, 1–12. [Google Scholar]
- Seth, G.S.; Sarkar, S.; Hussain, S.M. Effects of Hall current, radiation and rotation on natural convection heat and mass transfer flow past a moving vertical plate. Ain Shams Eng. J. 2014, 5, 489–503. [Google Scholar] [CrossRef]
- Takhar, H.S.; Chamkha, A.J.; Nath, G. MHD flow over a moving plate in a rotating fluid with magnetic field, Hall currentand free stream velocity. Int. J. Eng. Sci. 2002, 40, 1511–1527. [Google Scholar] [CrossRef]
- Cramer, K.P.; Pai, S.I. Magneto Fluid Dynamics for Engineers and Applied Physics; McGraw-Hill Book Co: New York, NY, USA, 1973. [Google Scholar]
- Grief, G.; Habib, I.S.; Lin, L.C. Laminar convection of a radiating gas in a vertical channel. J. Fluid Mech. 1971, 45, 513–520. [Google Scholar] [CrossRef]
- Cowling, G.S. Magneto Hydrodynamics; Interscience Publishers: New York, NY, USA, 1957. [Google Scholar]
- Abbasi, A.; Farooq, W.; Tag-ElDin, E.S.M.; Khan, S.U.; Khan, M.I.; Guedri, K.; Elattar, S.; Waqas, M.; Galal, A.M. Heat transport exploration for hybrid nanoparticle (Cu, Fe3O4)-based blood flow via tapered complex wavy curved channel with slip features. Micromachines 2022, 13, 1415. [Google Scholar] [CrossRef]
- Waqas, H.; Oreijah, M.; Guedri, K.; Khan, S.U.; Yang, S.; Yasmin, S.; Khan, M.I.; Bafakeeh, O.T.; Tag-ElDin, E.S.M.; Galal, A.M. Gyrotactic motile microorganisms impact on pseudoplastic nanofluid flow over a moving Riga surface with exponential heat flux. Crystals 2022, 12, 1308. [Google Scholar] [CrossRef]
- Shahid, M.; Javed, H.M.A.; Ahmad, M.I.; Qureshi, A.A.; Khan, M.I.; Alnuwaiser, M.A.; Ahmed, A.; Khan, M.A.; Tag-Eldin, E.; Shahid, A.; et al. A brief assessment on recent developments in efficient electrocatalytic Nitrogen reduction with 2D non-metallic nanomaterials. Nanomaterials 2022, 12, 3413. [Google Scholar] [CrossRef]
- Manzoor, N.; Qasim, I.; Khan, M.I.; Ahmed, M.W.; Guedri, K.; Bafakeeh, O.T.; Tag-Eldin, E.S.M.; Galal, A.M. Antibacterial applications of low pressure plasma on degradation of multidrug resistant V. Cholera. Appl. Sci. 2022, 12, 9737. [Google Scholar] [CrossRef]
- Mamatha, S.U.; Devi, R.L.V.R.; Ahammad, N.A.; Shah, N.A.; Rao, B.M.; Raju, C.S.K.; Khan, M.I.; Guedri, K. Multi-linear regression of triple diffusive convectively heated boundary layer flow with suction and injection: Lie group transformations. Int. J. Mod. Phys. B, 2022; in press. [Google Scholar] [CrossRef]
- Kiranakumar, H.V.; Thejas, R.; Naveen, C.S.; Khan, M.I.; Prasanna, G.D.; Reddy, S.; Oreijah, M.; Guedri, K.; Bafakeeh, O.T.; Jameel, M. A review on electrical and gas-sensing properties of reduced graphene oxide-metal oxide nanocomposites. Biomass Convers. Biorefinery, 2022; in press. [Google Scholar] [CrossRef]






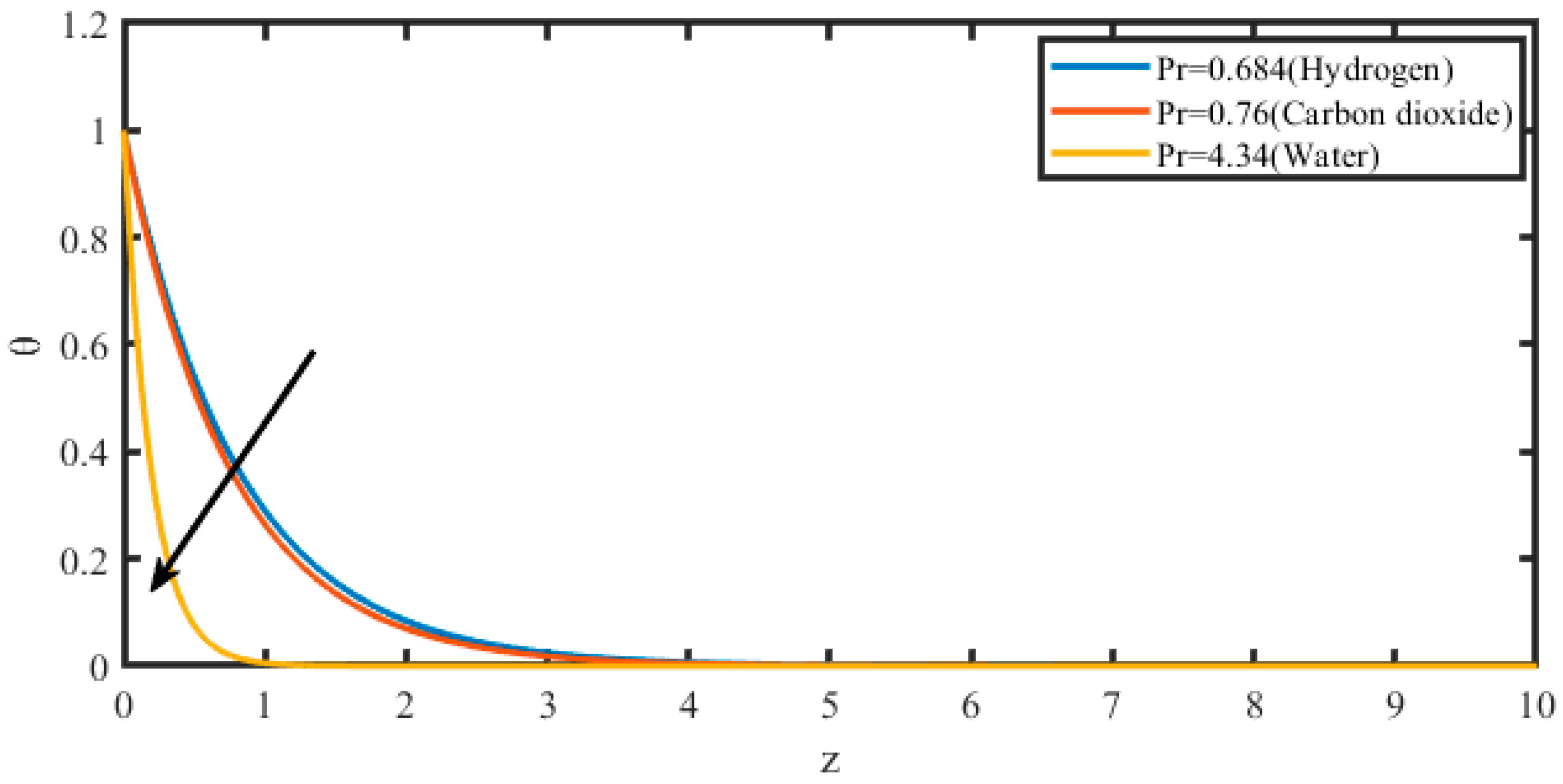

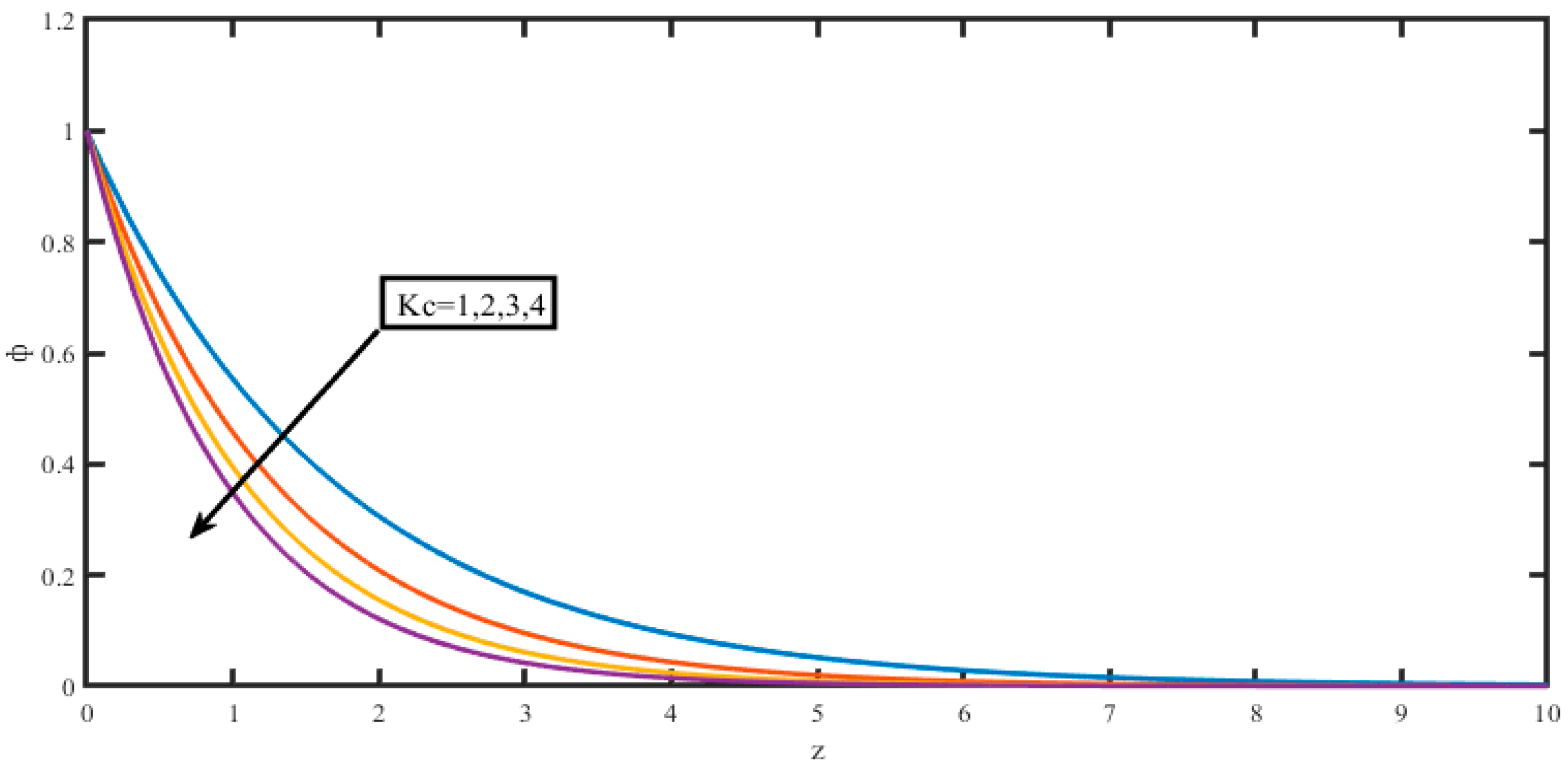

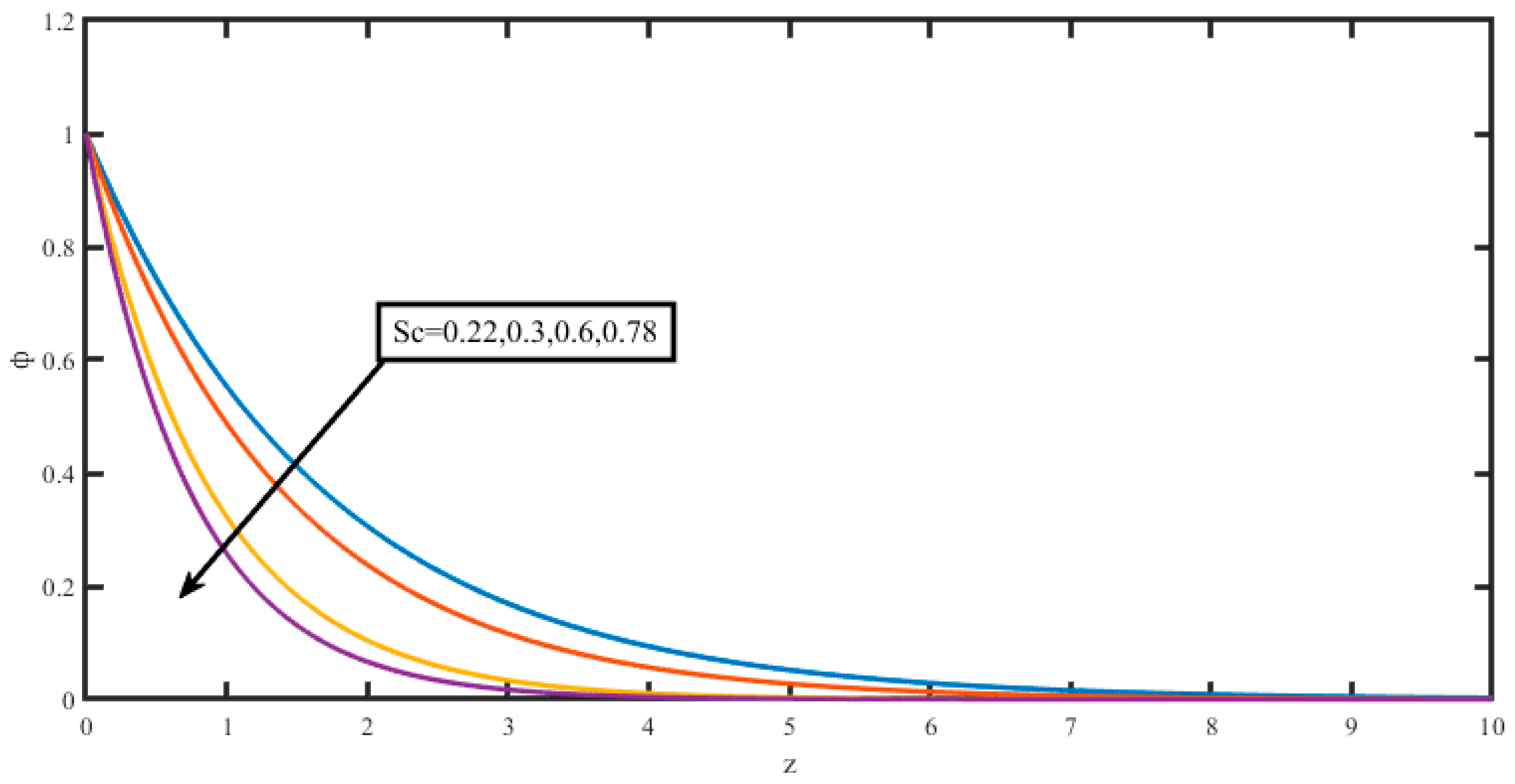
| M | k | R | Pr | Gr | Gm | Sc | Kc | H | So | m | τ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.0 | 0.50 | 1.0 | 0.710 | 3.0 | 5.0 | 0.22 | 1.0 | 1.0 | 1.0 | 0.20 | 0.6248 |
| 3.0 | 0.7245 | ||||||||||
| 4.0 | 0.7645 | ||||||||||
| 1.5 | 1.9475 | ||||||||||
| 2.0 | 2.0657 | ||||||||||
| 2.0 | 1.6578 | ||||||||||
| 3.0 | 1.7458 | ||||||||||
| 3.0 | 0.8542 | ||||||||||
| 7.0 | 0.8154 | ||||||||||
| 6 | 1.9875 | ||||||||||
| 9 | 2.2547 | ||||||||||
| 10 | 1.8752 | ||||||||||
| 15 | 2.0124 | ||||||||||
| 0.4 | 2.5479 | ||||||||||
| 0.6 | 2.9875 | ||||||||||
| 2.0 | 1.9875 | ||||||||||
| 3.0 | 2.0214 | ||||||||||
| 2.0 | 1.9647 | ||||||||||
| 3.0 | 2.6578 | ||||||||||
| 2.0 | 19875 | ||||||||||
| 3.0 | 2.2448 | ||||||||||
| 0.40 | 2.1254 | ||||||||||
| 0.60 | 2.1004 |
| Kc | H | F | Pr | Nu |
|---|---|---|---|---|
| 1.0 | 1.0 | 1.0 | 0.710 | 0.445215 |
| 2.5 | 0.645214 | |||
| 3.5 | 0.712032 | |||
| 2.5 | 1.578521 | |||
| 3.5 | 1.945214 | |||
| 2.5 | 0.978521 | |||
| 3.5 | 0.978521 | |||
| 3.5 | 3.478542 | |||
| 7.5 | 7.578512 |
| Kc | Sc | So | T | F | Sh |
|---|---|---|---|---|---|
| 1.0 | 0.220 | 0.50 | 0.50 | 1.0 | 0.578521 |
| 2.5 | 0.645876 | ||||
| 3.5 | 0.778521 | ||||
| 0.35 | 0.712014 | ||||
| 0.45 | 0.978520 | ||||
| 2.5 | 2.801234 | ||||
| 3.5 | 1.312478 | ||||
| 1.5 | 0.498741 | ||||
| 2.5 | 0.445214 | ||||
| 2.5 | 1.278521 | ||||
| 3.5 | 1.045210 |
| M | K | Gr | Gm | Previous Results Deepthi et al. [10] | Present Values |
|---|---|---|---|---|---|
| 2.0 | 0.50 | 5.0 | 3.0 | 0.70785200 | 0.7458752 |
| 3.0 | 0.44587710 | 0.4785214 | |||
| 4.0 | 0.33254700 | 0.3785214 | |||
| 1.00 | 0.75266440 | 0.7785214 | |||
| 1.50 | 0.85657100 | 0.8021448 | |||
| 10.0 | 0.97521200 | 0.9321477 | |||
| 15.0 | 1.00214700 | 1.0785214 | |||
| 6.0 | 0.76578280 | 0.7785214 | |||
| 9.0 | 0.81032570 | 0.8654785 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bafakeeh, O.T.; Raghunath, K.; Ali, F.; Khalid, M.; Tag-ElDin, E.S.M.; Oreijah, M.; Guedri, K.; Khedher, N.B.; Khan, M.I. Hall Current and Soret Effects on Unsteady MHD Rotating Flow of Second-Grade Fluid through Porous Media under the Influences of Thermal Radiation and Chemical Reactions. Catalysts 2022, 12, 1233. https://doi.org/10.3390/catal12101233
Bafakeeh OT, Raghunath K, Ali F, Khalid M, Tag-ElDin ESM, Oreijah M, Guedri K, Khedher NB, Khan MI. Hall Current and Soret Effects on Unsteady MHD Rotating Flow of Second-Grade Fluid through Porous Media under the Influences of Thermal Radiation and Chemical Reactions. Catalysts. 2022; 12(10):1233. https://doi.org/10.3390/catal12101233
Chicago/Turabian StyleBafakeeh, Omar T, Kodi Raghunath, Farhan Ali, Muhammad Khalid, El Sayed Mohamed Tag-ElDin, Mowffaq Oreijah, Kamel Guedri, Nidhal Ben Khedher, and Muhammad Ijaz Khan. 2022. "Hall Current and Soret Effects on Unsteady MHD Rotating Flow of Second-Grade Fluid through Porous Media under the Influences of Thermal Radiation and Chemical Reactions" Catalysts 12, no. 10: 1233. https://doi.org/10.3390/catal12101233
APA StyleBafakeeh, O. T., Raghunath, K., Ali, F., Khalid, M., Tag-ElDin, E. S. M., Oreijah, M., Guedri, K., Khedher, N. B., & Khan, M. I. (2022). Hall Current and Soret Effects on Unsteady MHD Rotating Flow of Second-Grade Fluid through Porous Media under the Influences of Thermal Radiation and Chemical Reactions. Catalysts, 12(10), 1233. https://doi.org/10.3390/catal12101233







