Investigation of Solid Deposit Inside L-Type Urea Injector and NOx Conversion in a Heavy-Duty Diesel Engine
Abstract
1. Introduction
2. Result and Discussion
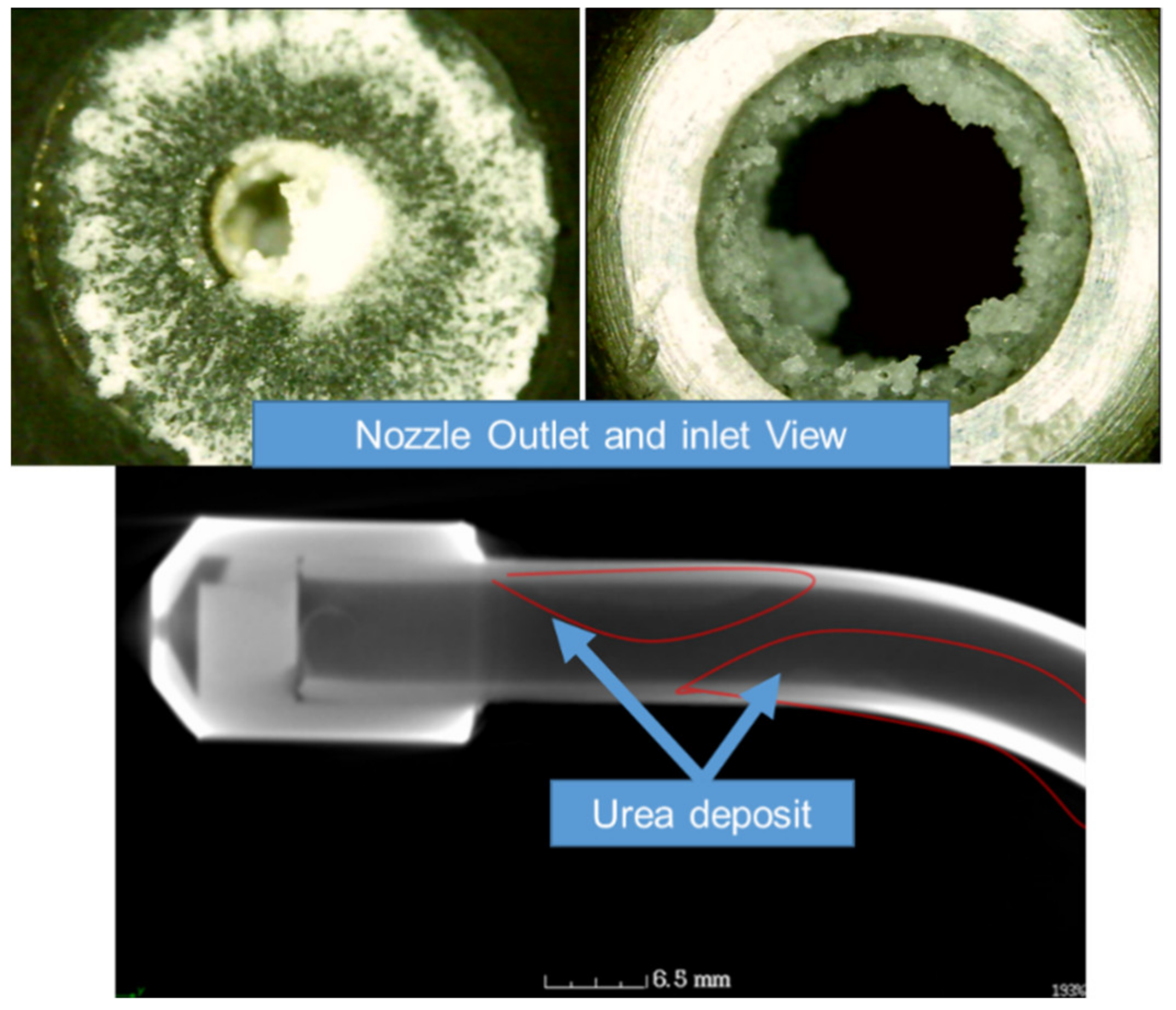
2.1. Urea Injector Phenomena
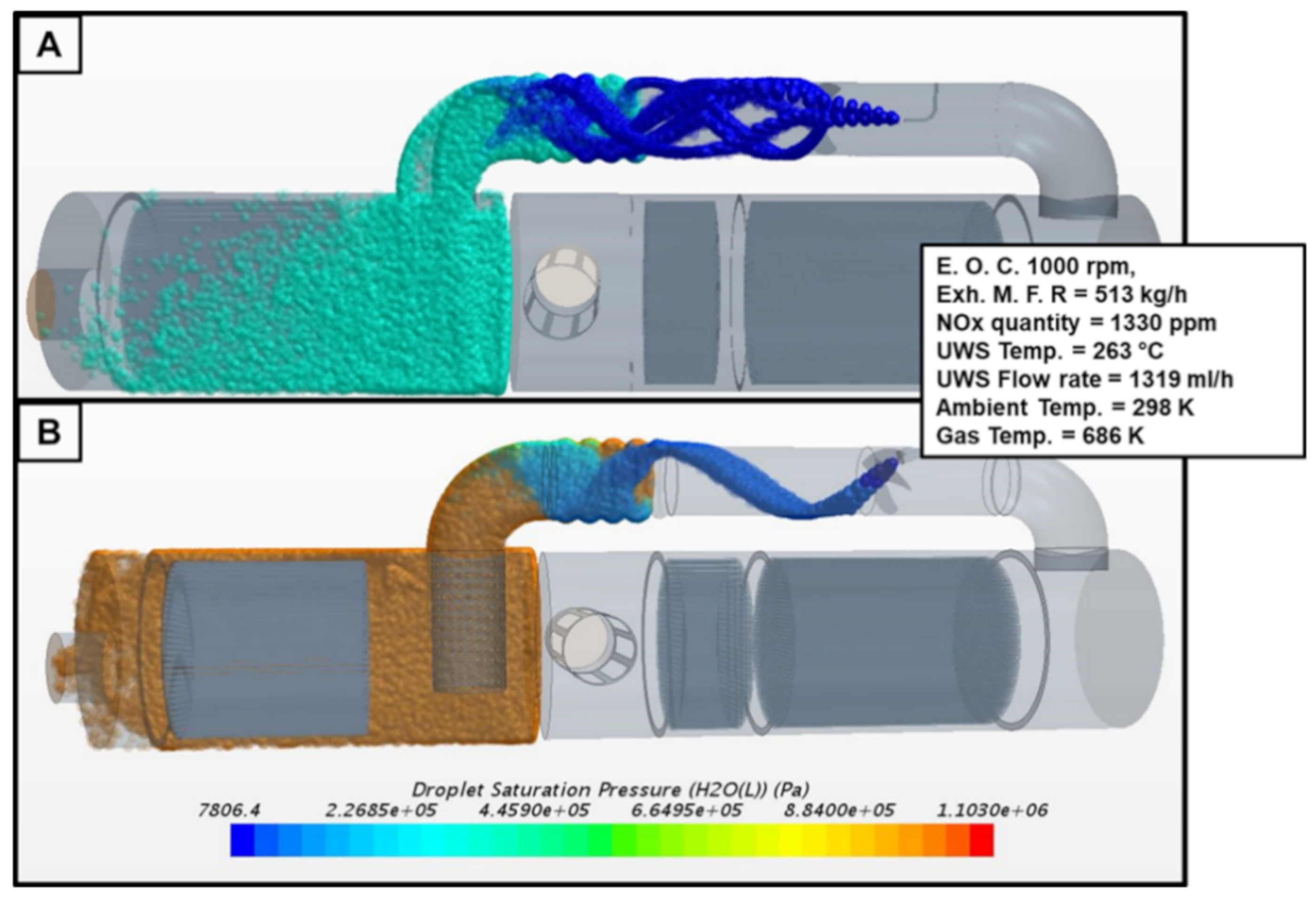
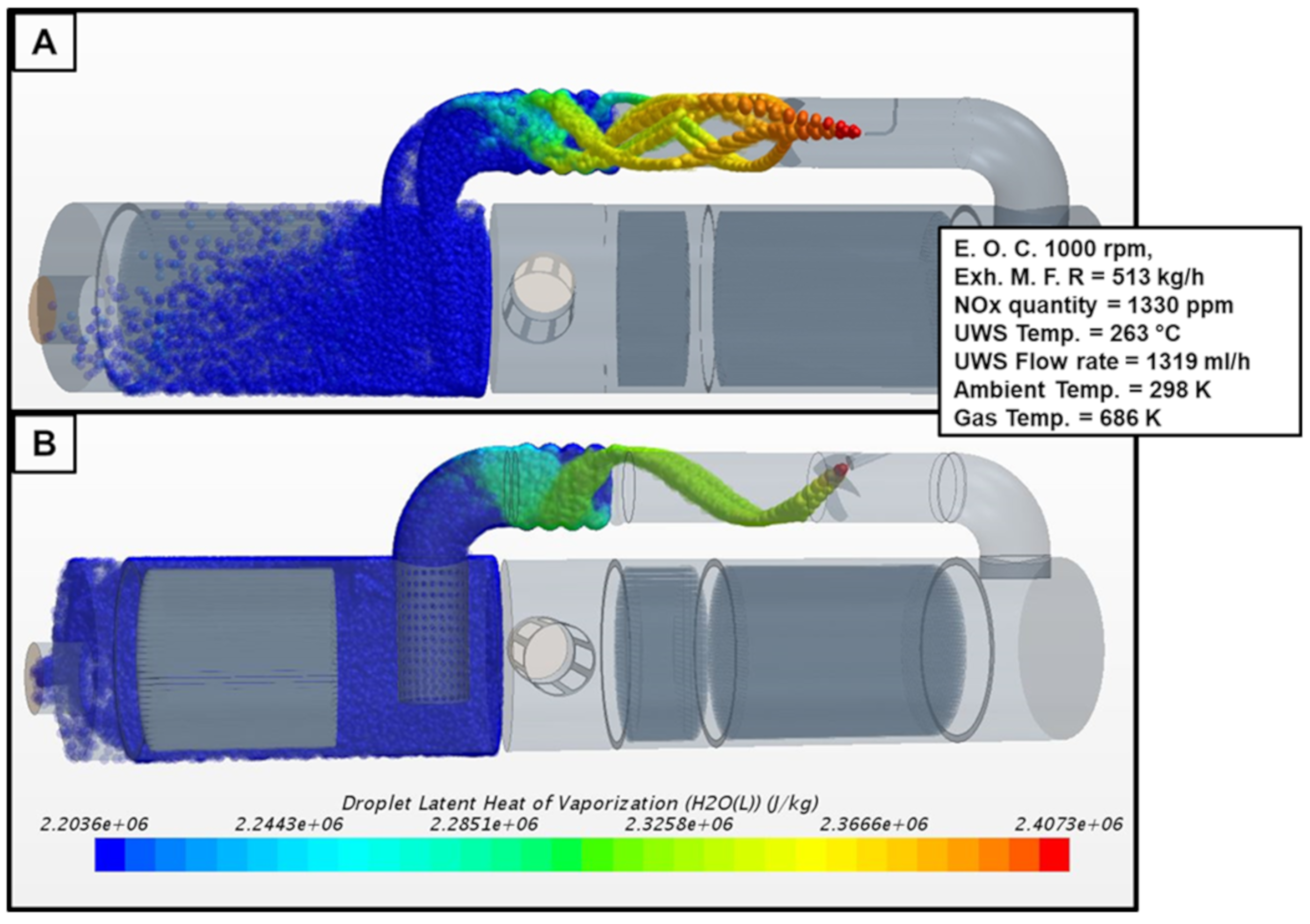
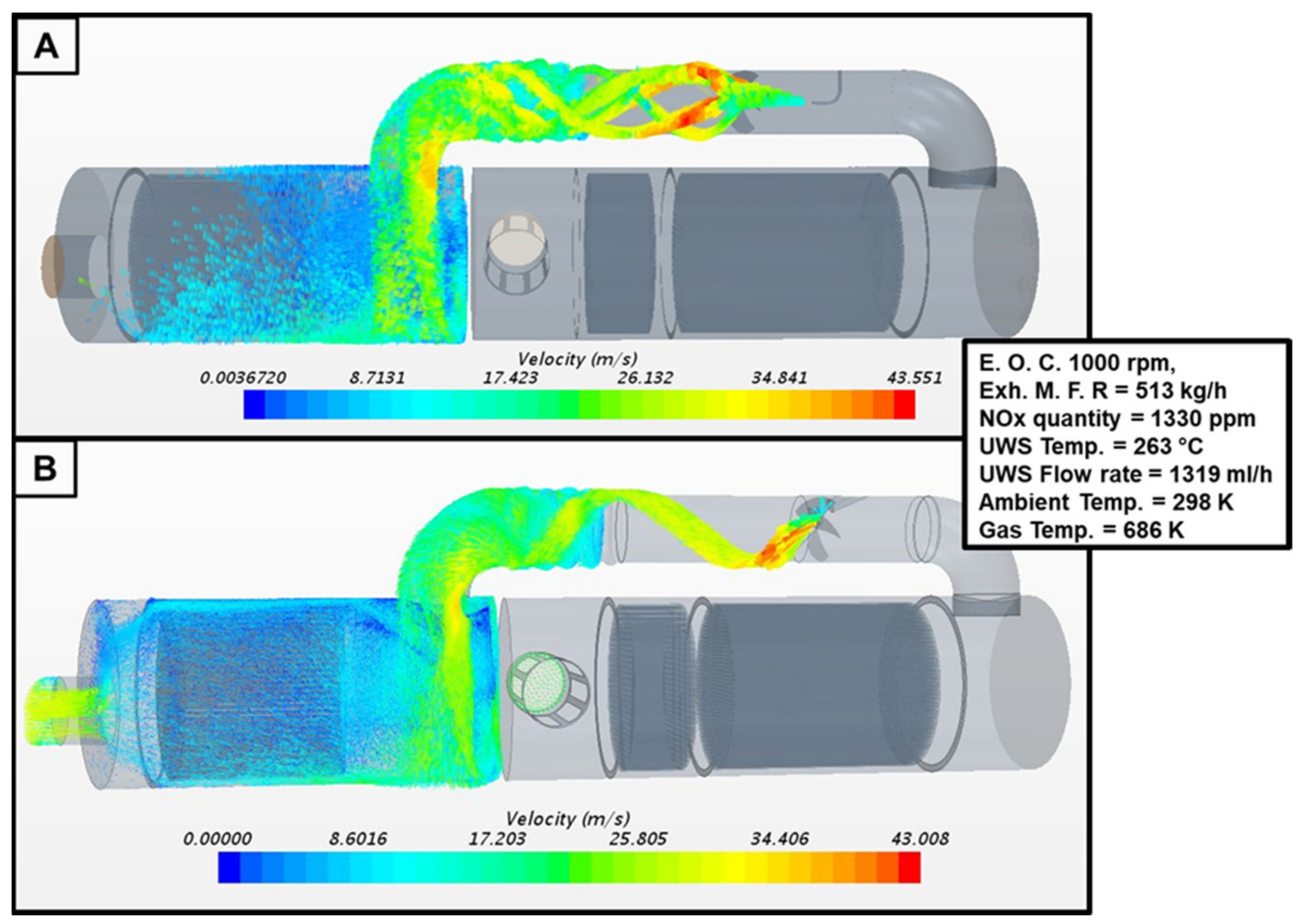
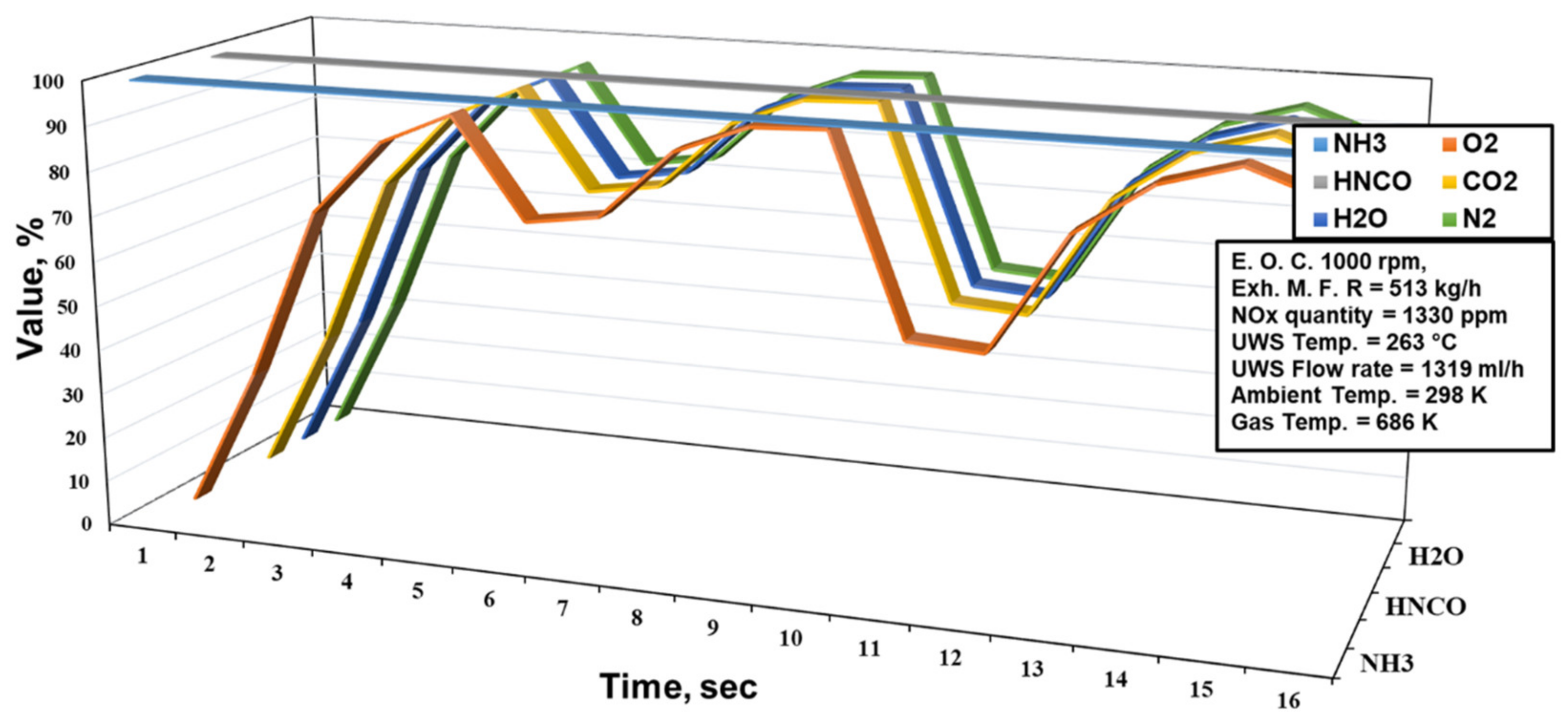
2.2. UWS Saturation and Vaporization Processes
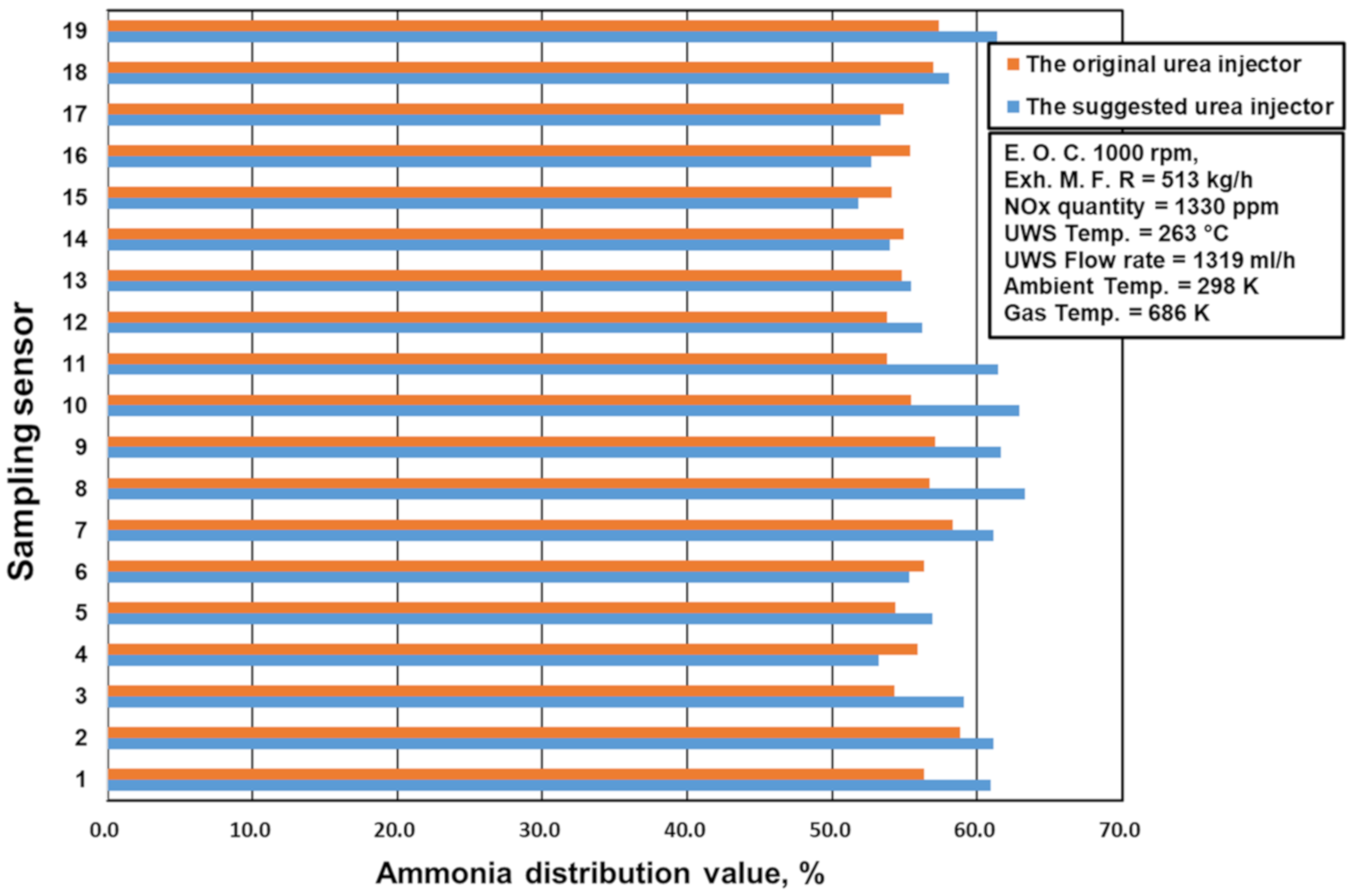
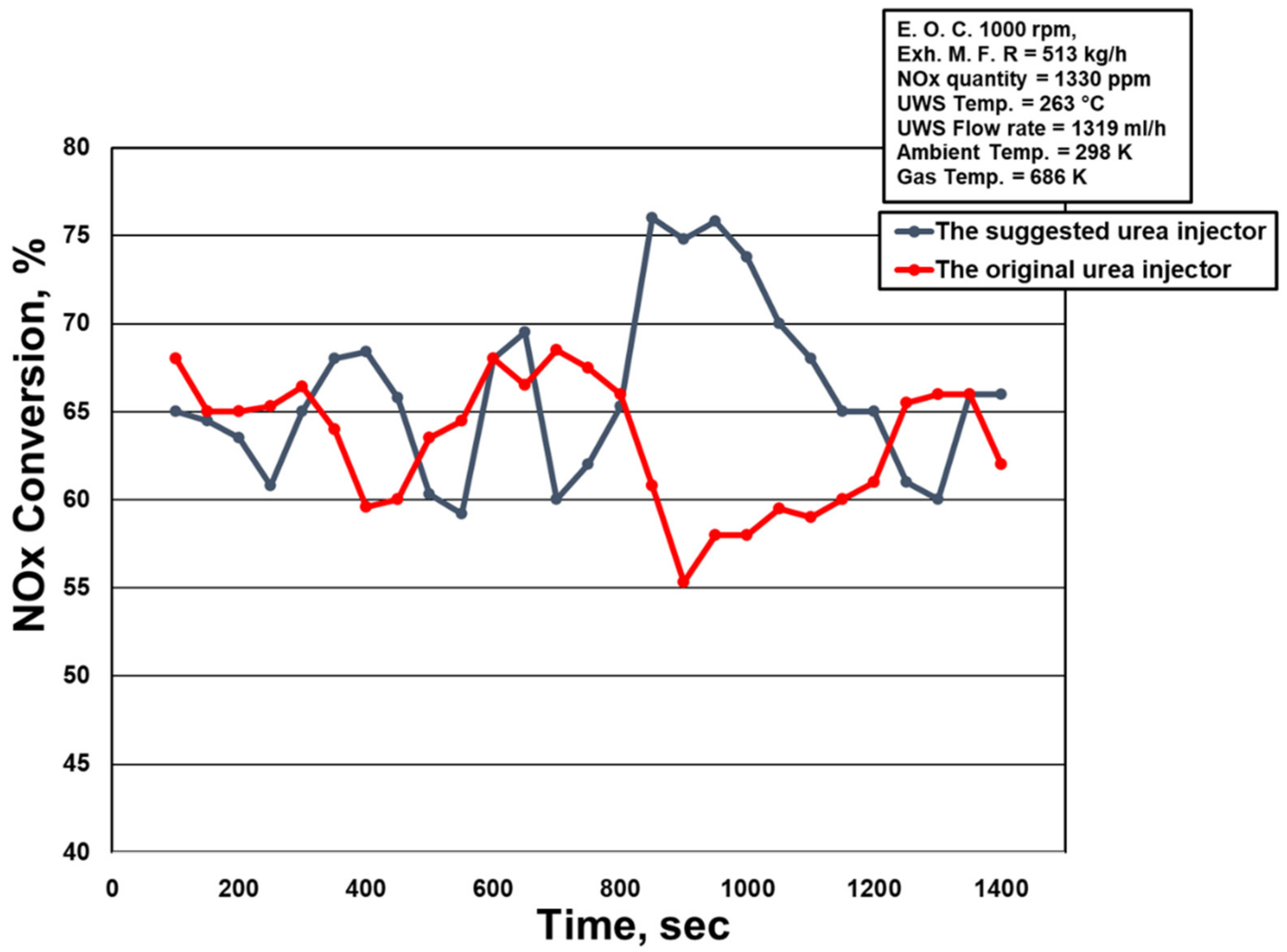
2.3. The Ammonia Distribution and NOx Conversion Value
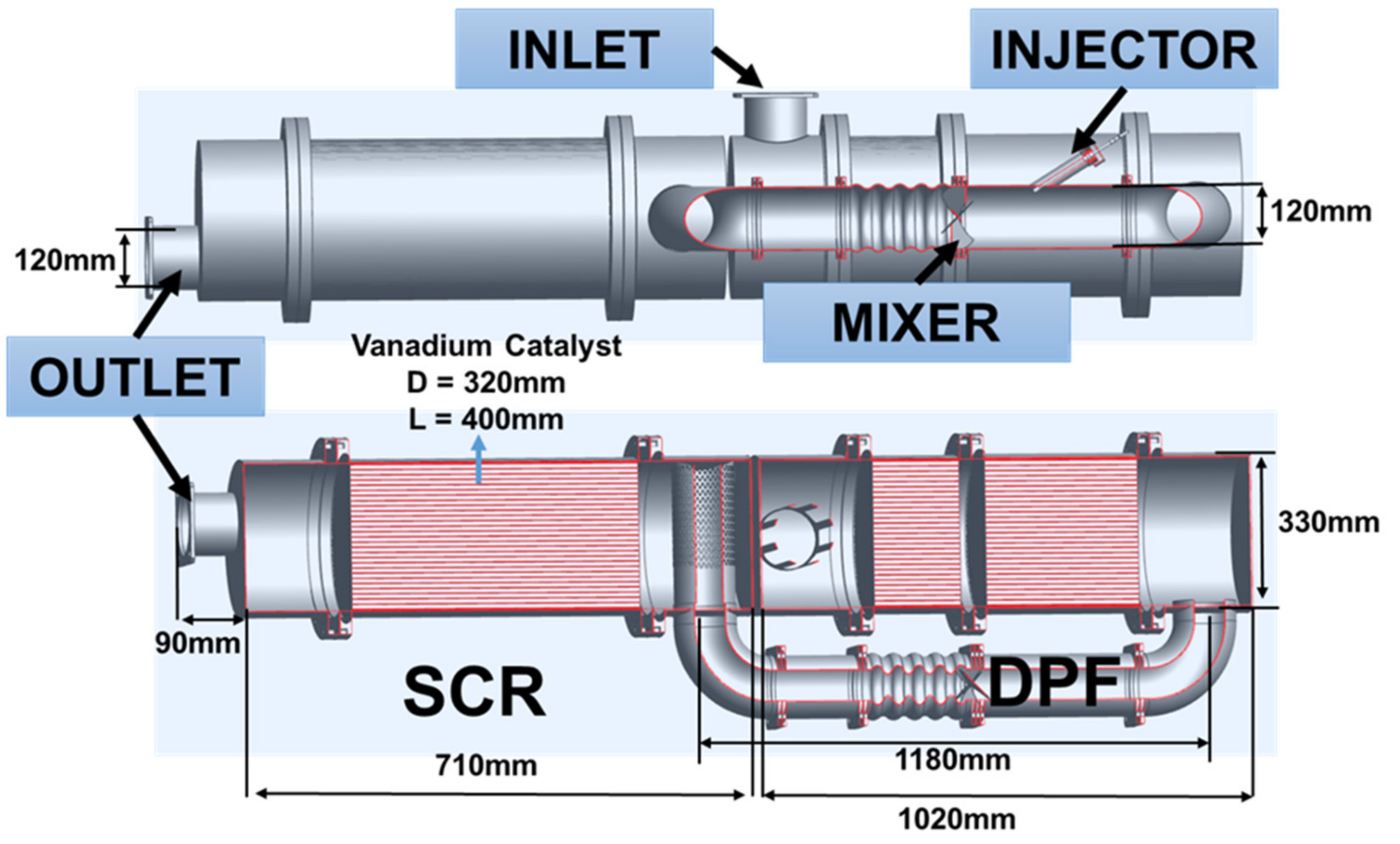
3. The CFD Model and the Parameter Condition
4. The Experimental Model and the Parameter Conditions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| RANS | Reynolds Average Navier Stokes |
| CFD | Computational Fluid Dynamics |
| UWS | Urea Water Solution |
| SCR | Selective Catalyst Reduction |
| H2O | Hydrogen |
| NOx | Nitrogen Oxide |
| N2 | Nitrogen |
| O2 | Oxygen |
| K | Kelvin temperature |
| UI | Uniformity Index |
| TKE | Turbulent kinetic energy (k) |
| RNG | Renormalization group |
| DPF | Diesel Particulate Filter |
| PM | Particular meter |
| NH3 | Ammonia gas |
References
- Shin, Y.; Jung, Y.; Cho, C.P.; Pyo, Y.D.; Jang, J.; Kim, G.; Kim, T.M. NOx abatement and N2O formation over urea-SCR systems with zeolite supported Fe and Cu catalysts in a nonroad diesel engine. Chem. Eng. J. 2020, 381, 122751. [Google Scholar] [CrossRef]
- Wardana, M.; Oh, K.; Lim, O. Investigation of Urea Uniformity with Different Types of Urea Injectors in an SCR System. Catalysts 2020, 10, 1269. [Google Scholar] [CrossRef]
- Iodice, P.; Senatore, A. Air Pollution and Air Quality State in an Italian National Interest Priority Site. Part 2: The Pollutant Dispersion. Energy Proc. 2015, 81, 637–643. [Google Scholar] [CrossRef]
- Baleta, J.; Mikulčić, H.; Vujanović, M.; Petranović, Z.; Duić, N. Numerical simulation of urea based selective non-catalytic reduction deNOx process for industrial applications. Energy Convers. Manag. 2016, 125, 59–69. [Google Scholar] [CrossRef]
- Wardana, M.K.A.; Oh, K.; Lee, Y.J.; Woo, Y.M.; Lim, O. Effects of Urea Injection Timing on Predicting NoX Conversion In SCR Systems. Int. J. Automot. Technol. 2020, 21, 137–145. [Google Scholar] [CrossRef]
- Wardana, M.K.A.; Shahariar, G.M.H.; Oh, K.; Lim, O. Ammonia Uniformity to Predict NOx Reduction Efficiency in an SCR System. Int. J. Automot. Technol. 2019, 20, 313–325. [Google Scholar] [CrossRef]
- Smith, H.; Lauer, T.; Schimik, V.; Gabel, K. Evaluation and Prediction of Deposit Severity in SCR Systems. SAE Int. J. Engines 2016, 9, 1735–1750. [Google Scholar] [CrossRef]
- Ström, H.; Lundström, A.; Andersson, B. Choice of urea-spray models in CFD simulations of urea-SCR systems. Chem. Eng. J. 2009, 150, 69–82. [Google Scholar] [CrossRef]
- Yi, Y. Development of a 3D Numerical Model for Predicting Spray, Urea Decomposition and Mixing in SCR Systems. SAE Tech. Paper Series 2007. [Google Scholar] [CrossRef]
- Maunula, T.; Kinnunen, T.; Kanniainen, K.; Viitanen, A.; Savimäki, A. Thermally Durable Vanadium-SCR Catalysts for Diesel Applications. SAE Tech. Paper Series 2013. [Google Scholar] [CrossRef]
- Koebel, M.; Strutz, E.O. Thermal and Hydrolytic Decomposition of Urea for Automotive Selective Catalytic Reduction Systems: Thermochemical and Practical Aspects. Ind. Eng. Chem. Res. 2003, 42, 2093–2100. [Google Scholar] [CrossRef]
- Langeslay, R.R.; Kaphan, D.M.; Marshall, C.L.; Stair, P.C.; Sattelberger, A.P.; Delferro, M. Catalytic Applications of Vanadium: A Mechanistic Perspective. Chem. Rev. 2019, 119, 2128–2191. [Google Scholar] [CrossRef] [PubMed]
- Fischer, S.; Bitto, R.; Lauer, T.; Krenn, C.; Tauer, J.; Pessl, G. Impact of the Turbulence Model and Numerical Approach on the Prediction of the Ammonia Homogenization in an Automotive SCR System. SAE Int. J. Engines 2012, 5, 1443–1458. [Google Scholar] [CrossRef]
- STAR-CCM + Guide. In STAR-CCM + ® Documentation; Siemens PLM Software: Plano, TX, USA, 2018.
- Stritzke, F.; Van Der Kley, S.; Feiling, A.; Dreizler, A.; Wagner, S. Ammonia concentration distribution measurements in the exhaust of a heavy-duty diesel engine based on limited data absorption tomography. Opt. Express 2017, 25, 8180–8191. [Google Scholar] [CrossRef] [PubMed]
- Marchitti, F.; Nova, I.; Tronconi, E. Experimental study of the interaction between soot combustion and NH3-SCR reactivity over a Cu–Zeolite SDPF catalyst. Catal. Today 2016, 267, 110–118. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wardana, M.K.A.; Lim, O. Investigation of Solid Deposit Inside L-Type Urea Injector and NOx Conversion in a Heavy-Duty Diesel Engine. Catalysts 2021, 11, 595. https://doi.org/10.3390/catal11050595
Wardana MKA, Lim O. Investigation of Solid Deposit Inside L-Type Urea Injector and NOx Conversion in a Heavy-Duty Diesel Engine. Catalysts. 2021; 11(5):595. https://doi.org/10.3390/catal11050595
Chicago/Turabian StyleWardana, Muhammad Khristamto Aditya, and Ocktaeck Lim. 2021. "Investigation of Solid Deposit Inside L-Type Urea Injector and NOx Conversion in a Heavy-Duty Diesel Engine" Catalysts 11, no. 5: 595. https://doi.org/10.3390/catal11050595
APA StyleWardana, M. K. A., & Lim, O. (2021). Investigation of Solid Deposit Inside L-Type Urea Injector and NOx Conversion in a Heavy-Duty Diesel Engine. Catalysts, 11(5), 595. https://doi.org/10.3390/catal11050595




