Adsorption and Photocatalytic Study of Phenol Using Composites of Activated Carbon Prepared from Onion Leaves (Allium fistulosum) and Metallic Oxides (ZnO and TiO2)
Abstract
1. Introduction
2. Results and Discussion
2.1. Characterization of Materials
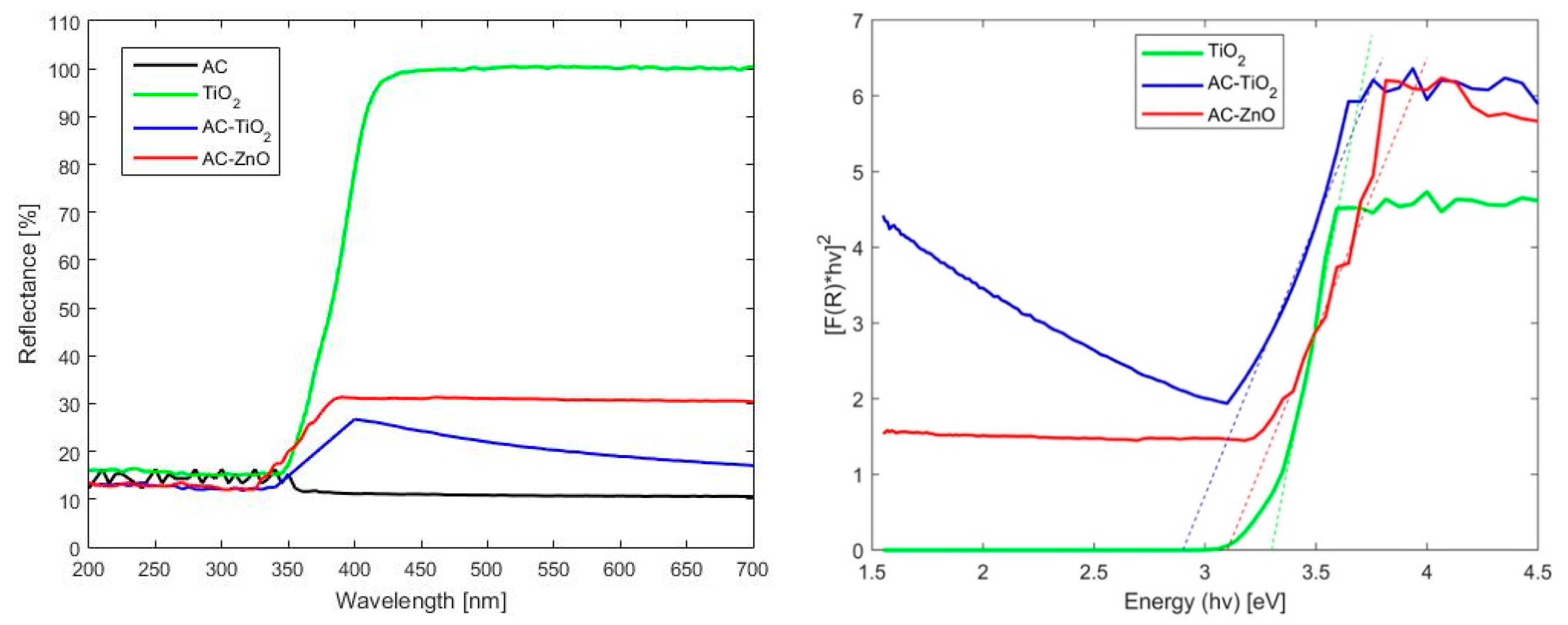
2.1.1. Physical Characterization
2.1.2. Chemical Characterization
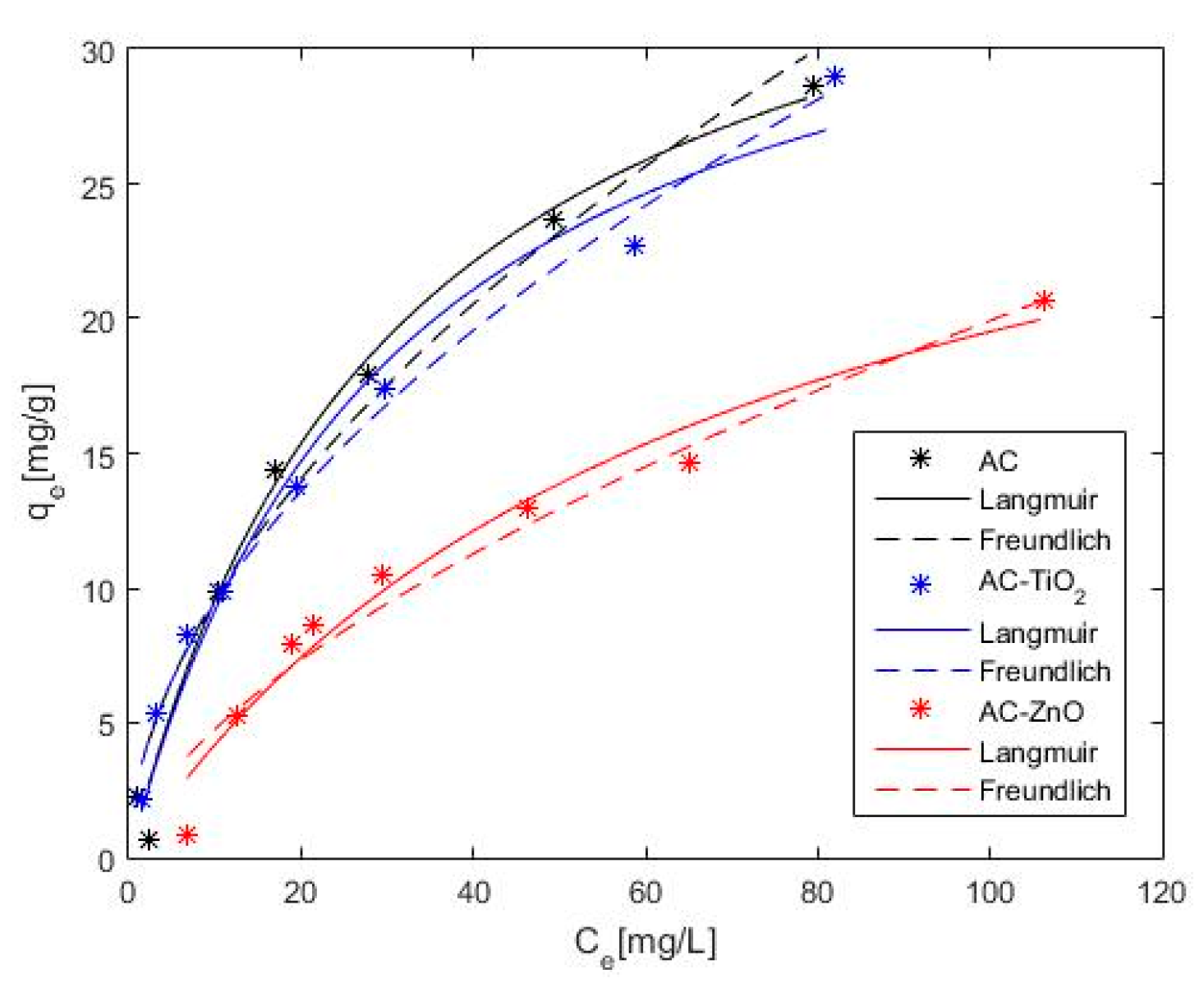
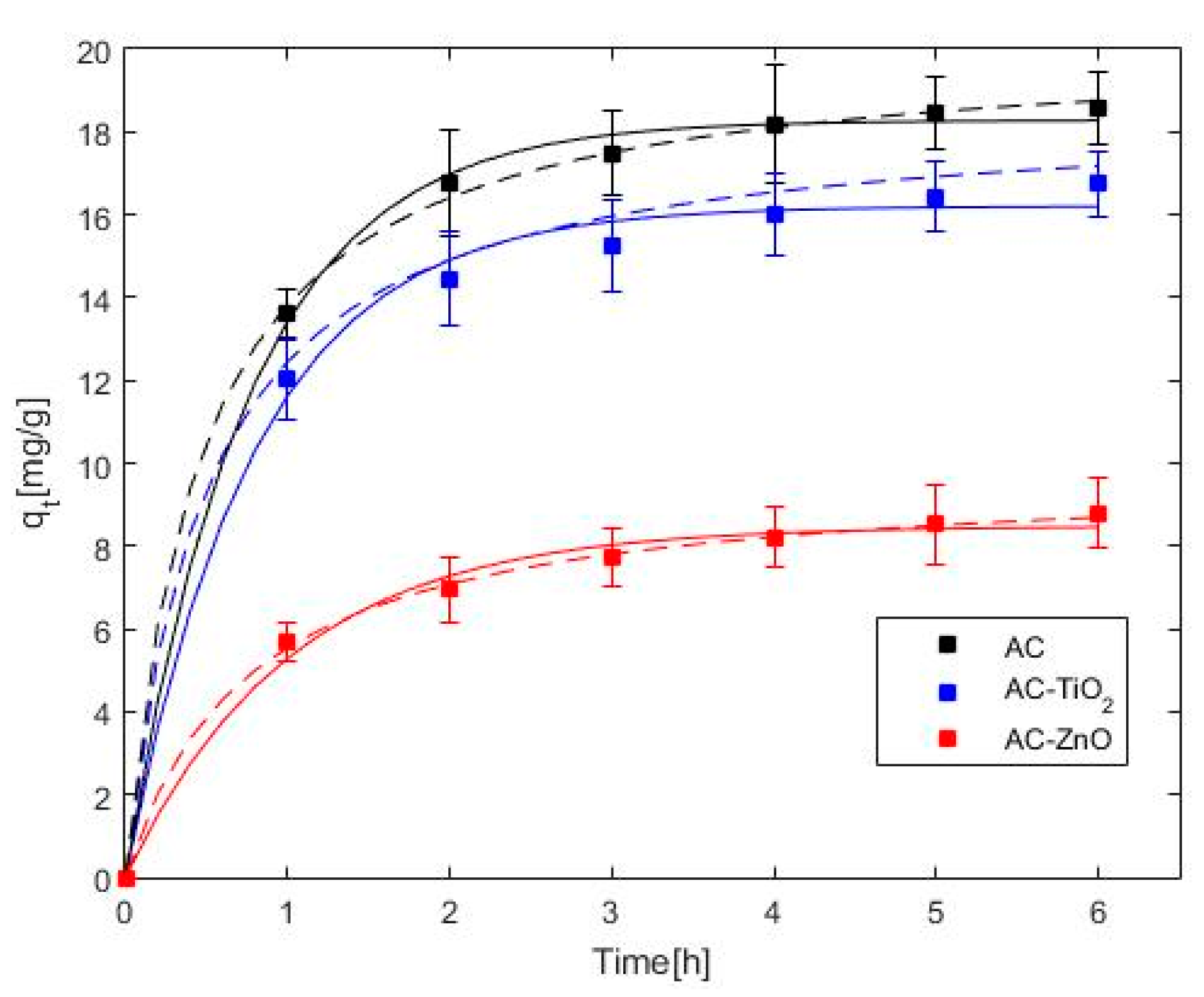
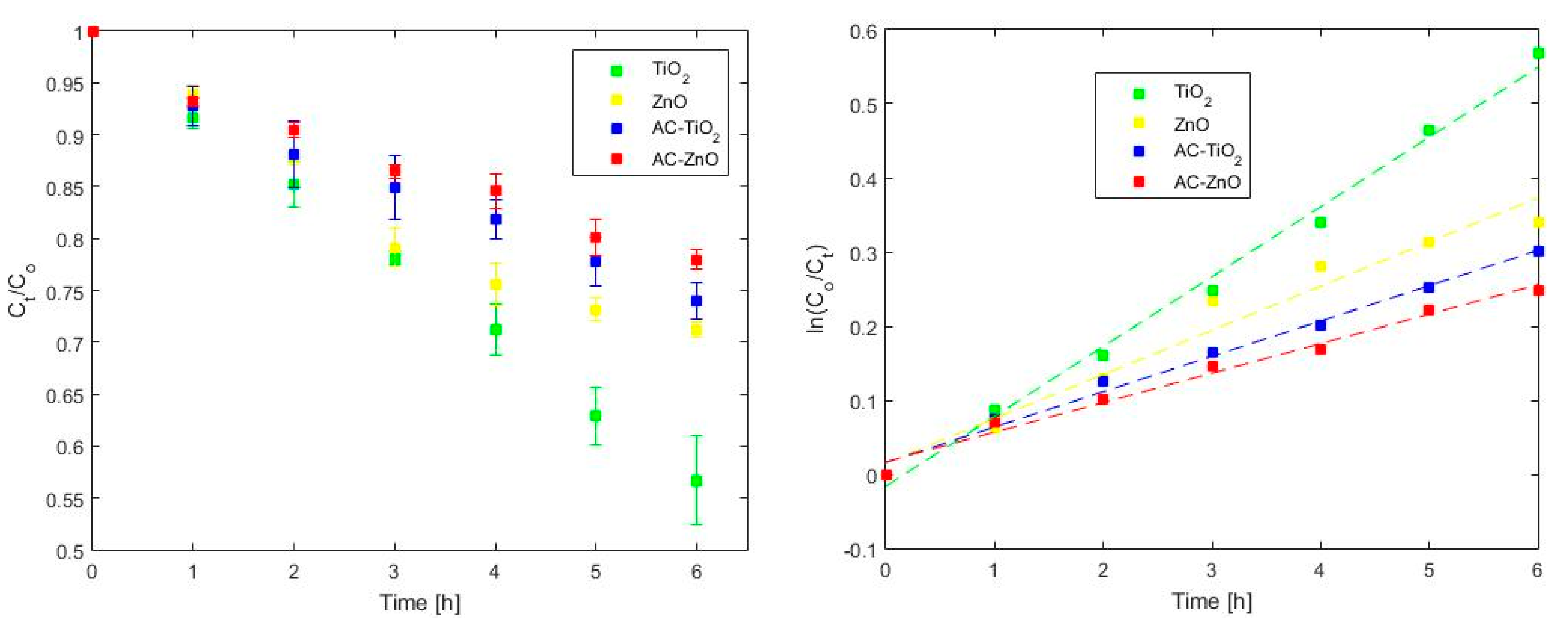
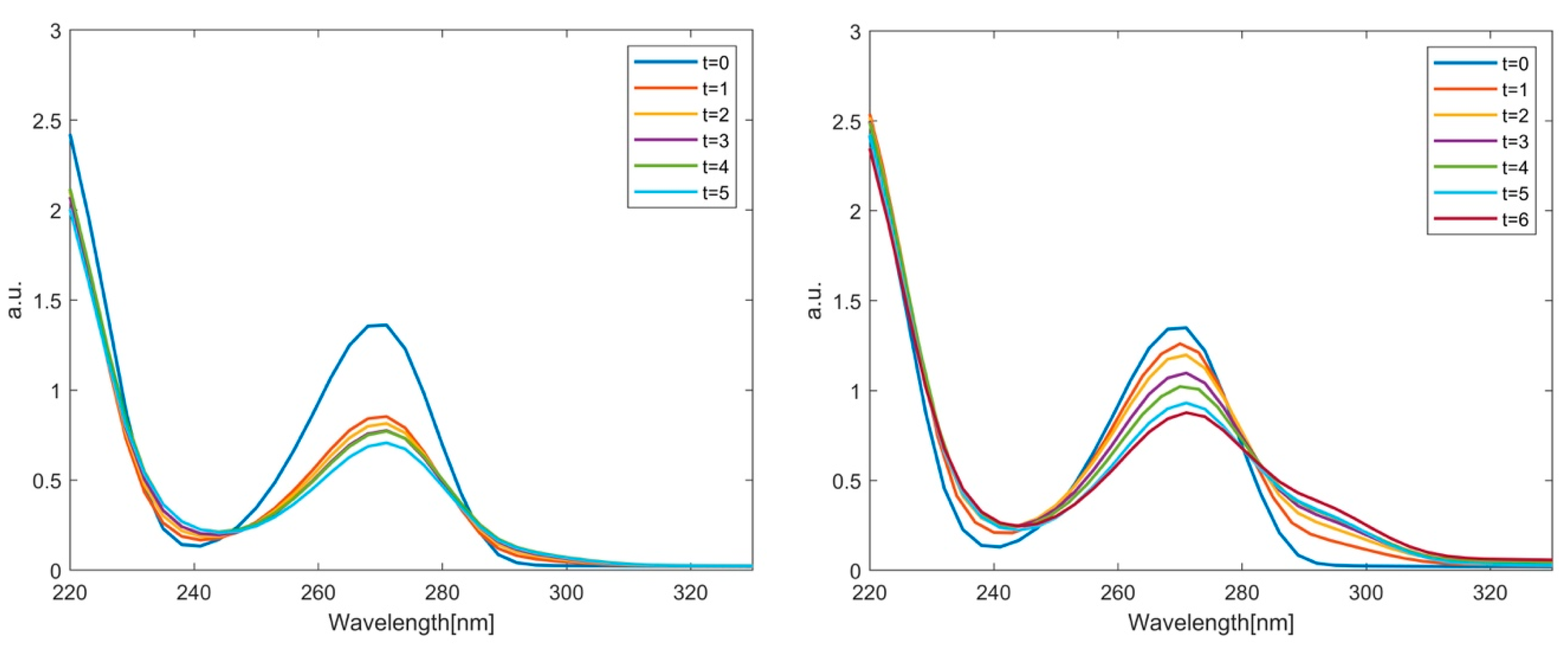
2.2. Phenol Adsorption and Photocatalysis
3. Materials and Methods
3.1. Activated Carbon Preparation
3.2. Composites Preparation
3.3. Characterization
3.3.1. Physical Characterization
3.3.2. Chemical Characterization
3.4. Adsorption Study
3.5. Photocatalysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Departamento Administrativo Nacional de Estadisticas (DANE). Boletín Mensual Insumos y Factores Asociados a la Producción Agropecuaria; Departamento Administrativo Nacional de Estadisticas: Bogotá, Colombia, 2013; Volume 17.
- Üner, O.; Bayrak, Y. The effect of carbonization temperature, carbonization time and impregnation ratio on the properties of activated carbon produced from Arundo donax. Microporous Mesoporous Mater. 2018, 268, 225–234. [Google Scholar] [CrossRef]
- Mohammed, A.A.; Chen, C.; Zhu, Z. Low-cost, high-performance supercapacitor based on activated carbon electrode materials derived from baobab fruit shells. J. Colloid Interface Sci. 2019, 538, 308–319. [Google Scholar] [CrossRef] [PubMed]
- Raj, F.R.M.S.; Boopathi, G.; Jaya, N.V.; Kalpana, D.; Pandurangan, A. N, S codoped activated mesoporous carbon derived from the Datura metel seed pod as active electrodes for supercapacitors. Diam. Relat. Mater. 2020, 102, 107687. [Google Scholar] [CrossRef]
- Hoang, V.C.; Dinh, K.N.; Gomes, V.G. Hybrid Ni/NiO composite with N-doped activated carbon from waste cauliflower leaves: A sustainable bifunctional electrocatalyst for efficient water splitting. Carbon N. Y. 2020, 157, 515–524. [Google Scholar] [CrossRef]
- Guo, Y.; Tan, C.; Sun, J.; Li, W.; Zhang, J.; Zhao, C. Porous activated carbons derived from waste sugarcane bagasse for CO2 adsorption. Chem. Eng. J. 2020, 381, 122736. [Google Scholar] [CrossRef]
- Lu, W.; Cao, X.; Hao, L.; Zhou, Y.; Wang, Y. Activated carbon derived from pitaya peel for supercapacitor applications with high capacitance performance. Mater. Lett. 2020, 264, 127339. [Google Scholar] [CrossRef]
- Nourmoradi, H.; Moghadam, K.F.; Jafari, A.; Kamarehie, B. Removal of acetaminophen and ibuprofen from aqueous solutions by activated carbon derived from Quercus Brantii (Oak) acorn as a low-cost biosorbent. J. Environ. Chem. Eng. 2018, 6, 6807–6815. [Google Scholar] [CrossRef]
- Mashile, G.P.; Mpupa, A.; Nqombolo, A.; Dimpe, K.M.; Nomngongo, P.N. Recyclable magnetic waste tyre activated carbon-chitosan composite as an effective adsorbent rapid and simultaneous removal of methylparaben and propylparaben from aqueous solution and wastewater. J. Water Process Eng. 2020, 33, 101011. [Google Scholar] [CrossRef]
- Iriarte-Velasco, U.; Sierra, I.; Zudaire, L.; Ayastuy, J.L. Preparation of a porous biochar from the acid activation of pork bones. Food Bioprod. Process. 2016, 98, 341–353. [Google Scholar] [CrossRef]
- Matos, J.; Fierro, V.; Montaña, R.; Rivero, E.; De Yuso, A.M.; Zhao, W.; Celzard, A. High surface area microporous carbons as photoreactors for the catalytic photodegradation of methylene blue under UV-vis irradiation. Appl. Catal. A Gen. 2016, 517, 1–11. [Google Scholar] [CrossRef]
- Kwiatkowski, M.; Broniek, E. An analysis of the porous structure of activated carbons obtained from hazelnut shells by various physical and chemical methods of activation. Colloids Surf. A Physicochem. Eng. Asp. 2017, 529, 443–453. [Google Scholar] [CrossRef]
- Zhang, L.; Pan, J.; Liu, L.; Song, K.; Wang, Q. Combined physical and chemical activation of sludge-based adsorbent enhances Cr(VI) removal from wastewater. J. Clean. Prod. 2019, 238, 117904. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, J.; Fan, W.; Zhong, Y.; Zhang, Y.; Deng, Q.; Zeng, Z.; Deng, S. Ultramicroporous carbons with extremely narrow pore size distribution via in-situ ionic activation for efficient gas-mixture separation. Chem. Eng. J. 2019, 375, 121931. [Google Scholar] [CrossRef]
- Il Kim, Y.; Lee, Y.J.; Yoo, J.; Kim, J.-H. High-capacitance activated bio-carbons with controlled pore size distribution for sustainable energy storage. J. Power Sources 2019, 438, 226969. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Zhao, X.; Cao, D.; Guo, T.; Yang, B. Insights into heterogeneous catalysis of peroxymonosulfate activation by boron-doped ordered mesoporous carbon. Carbon N. Y. 2018, 135, 238–247. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Z.; Zheng, H.; Fu, T.; Ju, Y.; Wang, Y. Influence of the surface oxygenated groups of activated carbon on preparation of a nano Cu/AC catalyst and heterogeneous catalysis in the oxidative carbonylation of methanol. Appl. Catal. B Environ. 2015, 179, 95–105. [Google Scholar] [CrossRef]
- Matos, I.; Bernardo, M.; Fonseca, I. Porous carbon: A versatile material for catalysis. Catal. Today 2017, 285, 194–203. [Google Scholar] [CrossRef]
- Augugliaro, V.; Palmisano, G.; Palmisano, L.; Soria, J. Heterogeneous Photocatalysis and Catalysis. Heterog. Photocatal. 2019, 1, 1–24. [Google Scholar]
- Ismael, M. Enhanced photocatalytic hydrogen production and degradation of organic pollutants from Fe (III) doped TiO2 nanoparticles. J. Environ. Chem. Eng. 2020, 8, 103676. [Google Scholar] [CrossRef]
- Ismael, M. The photocatalytic performance of the ZnO/g-C3N4 composite photocatalyst toward degradation of organic pollutants and its inactivity toward hydrogen evolution: The influence of light irradiation and charge transfer. Chem. Phys. Lett. 2020, 739, 136992. [Google Scholar] [CrossRef]
- Augugliaro, V.; Palmisano, G.; Palmisano, L.; Soria, J. Chapter 1—Heterogeneous Photocatalysis and Catalysis: An Overview of Their Distinctive Features. In Heterogeneous Photocatalysis; Marcì, G., Palmisano, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–24. ISBN 978-0-444-64015-4. [Google Scholar]
- Sadeghian, Z.; Hadidi, M.R.; Salehzadeh, D.; Nemati, A. Hydrophobic octadecylamine-functionalized graphene/TiO2 hybrid coating for corrosion protection of copper bipolar plates in simulated proton exchange membrane fuel cell environment. Int. J. Hydrog. Energy 2020. [Google Scholar] [CrossRef]
- Rouzafzay, F.; Shidpour, R.; Al-Abri, M.Z.M.; Qaderi, F.; Ahmadi, A.; Myint, M.T.Z. Graphene@ZnO nanocompound for short-time water treatment under sun-simulated irradiation: Effect of shear exfoliation of graphene using kitchen blender on photocatalytic degradation. J. Alloy. Compd. 2020, 829, 154614. [Google Scholar] [CrossRef]
- Cui, W.; Bai, H.; Shang, J.; Wang, F.; Xu, D.; Ding, J.; Fan, W.; Shi, W. Organic-inorganic hybrid-photoanode built from NiFe-MOF and TiO2 for efficient PEC water splitting. Electrochim. Acta 2020, 2012, 136383. [Google Scholar] [CrossRef]
- Cui, W.; Kang, X.; Zhang, X.; Cui, X. Gel-like ZnO/Zr-MOF(bpy) nanocomposite for highly efficient adsorption of Rhodamine B dye from aqueous solution. J. Phys. Chem. Solids 2019, 134, 165–175. [Google Scholar] [CrossRef]
- El Bekkali, C.; Bouyarmane, H.; El Karbane, M.; Masse, S.; Saoiabi, A.; Coradin, T.; Laghzizil, A. Zinc oxide-hydroxyapatite nanocomposite photocatalysts for the degradation of ciprofloxacin and ofloxacin antibiotics. Colloids Surf. A Physicochem. Eng. Asp. 2018, 539, 364–370. [Google Scholar] [CrossRef]
- Chong, R.; Fan, Y.; Du, Y.; Liu, L.; Chang, Z.; Li, D. Hydroxyapatite decorated TiO2 as efficient photocatalyst for selective reduction of CO2 with H2O into CH4. Int. J. Hydrog. Energy 2018, 43, 22329–22339. [Google Scholar] [CrossRef]
- Ali, S.; Li, Z.; Chen, S.; Zada, A.; Khan, I.; Khan, I.; Ali, W.; Shaheen, S.; Qu, Y.; Jing, L. Synthesis of activated carbon-supported TiO2-based nano-photocatalysts with well recycling for efficiently degrading high-concentration pollutants. Catal. Today 2019, 335, 557–564. [Google Scholar] [CrossRef]
- Muthirulan, P.; Meenakshisundararam, M.; Kannan, N. Beneficial role of ZnO photocatalyst supported with porous activated carbon for the mineralization of alizarin cyanin green dye in aqueous solution. J. Adv. Res. 2013, 4, 479–484. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Tran, H.N.; Fu, C.-C.; Lu, Y.-T.; Juang, R.-S. Roles of adsorption and photocatalysis in removing organic pollutants from water by activated carbon–supported titania composites: Kinetic aspects. J. Taiwan Inst. Chem. Eng. 2020. [Google Scholar] [CrossRef]
- Schäffel, F. The Atomic Structure of Graphene and Its Few-layer Counterparts. In Graphene; Elsevier: Amsterdam, The Netherlands, 2013; Volume 25, pp. 5–59. [Google Scholar]
- Warner, J.H.; Schäffel, F.; Bachmatiuk, A.; Rümmeli, M.H. Properties of Graphene. Graphene 2013, 25, 61–127. [Google Scholar]
- Varghese, S.S.; Lonkar, S.; Singh, K.K.; Swaminathan, S.; Abdala, A. Recent advances in graphene based gas sensors. Sens. Actuators B Chem. 2015, 218, 160–183. [Google Scholar] [CrossRef]
- Korkmaz, S.; Kariper, A. Graphene and graphene oxide based aerogels: Synthesis, characteristics and supercapacitor applications. J. Energy Storage 2020, 27, 101038. [Google Scholar] [CrossRef]
- Wang, J.; Song, J.; Mu, X.; Sun, M. Optoelectronic and Photoelectric Properties and Applications of Graphene-Based Nanostructures. Mater. Today Phys. 2020, 13, 100196. [Google Scholar] [CrossRef]
- Zhu, W.; Lin, Y.; Kang, W.; Quan, H.; Zhang, Y.; Chang, M.; Wang, K.; Zhang, M.; Zhang, W.; Li, Z.; et al. An aerogel adsorbent with bio-inspired interfacial adhesion between graphene and MoS2 sheets for water treatment. Appl. Surf. Sci. 2020, 512, 145717. [Google Scholar] [CrossRef]
- Gadipelli, S.; Guo, Z.X. Graphene-based materials: Synthesis and gas sorption, storage and separation. Prog. Mater. Sci. 2015, 69, 1–60. [Google Scholar] [CrossRef]
- Ismael, M.; Wu, Y.; Taffa, D.H.; Bottke, P.; Wark, M. Graphitic carbon nitride synthesized by simple pyrolysis: Role of precursor in photocatalytic hydrogen production. New J. Chem. 2019, 43, 6909–6920. [Google Scholar] [CrossRef]
- Ismael, M.; Wu, Y. A mini-review on the synthesis and structural modification of g-C3N4-based materials, and their applications in solar energy conversion and environmental remediation. Sustain. Energy Fuels 2019, 3, 2907–2925. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. IUPAC Technical Report Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Manoj, B.; Kunjomana, A.G. Study of Stacking Structure of Amorphous Carbon by X-Ray Diffraction Technique. Int. J. Electrochem. Sci. 2012, 7, 3127–3134. [Google Scholar]
- Suphankij, S.; Mekprasart, W.; Pecharapa, W. Photocatalytic of N-doped TiO2 Nanofibers Prepared by Electrospinning. Energy Procedia 2013, 34, 751–756. [Google Scholar] [CrossRef]
- Ansari, F.; Ghaedi, M.; Taghdiri, M.; Asfaram, A. Application of ZnO nanorods loaded on activated carbon for ultrasonic assisted dyes removal: Experimental design and derivative spectrophotometry method. Ultrason. Sonochem. 2016, 33, 197–209. [Google Scholar] [CrossRef] [PubMed]
- Khatami, M.; Varma, R.S.; Zafarnia, N.; Yaghoobi, H.; Sarani, M.; Kumar, V.G. Applications of green synthesized Ag, ZnO and Ag/ZnO nanoparticles for making clinical antimicrobial wound-healing bandages. Sustain. Chem. Pharm. 2018, 10, 9–15. [Google Scholar] [CrossRef]
- Ding, L.; Yang, S.; Liang, Z.; Qian, X.; Chen, X.; Cui, H.; Tian, J. TiO2 nanobelts with anatase/rutile heterophase junctions for highly efficient photocatalytic overall water splitting. J. Colloid Interface Sci. 2020, 567, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Caglar, Y.; Caglar, M.; Ilican, S. XRD, SEM, XPS studies of Sb doped ZnO films and electrical properties of its based Schottky diodes. Optik 2018, 164, 424–432. [Google Scholar] [CrossRef]
- El Mouchtari, E.M.; Daou, C.; Rafqah, S.; Najjar, F.; Anane, H.; Piram, A.; Hamade, A.; Briche, S.; Wong-Wah-Chung, P. TiO2 and activated carbon of Argania Spinosa tree nutshells composites for the adsorption photocatalysis removal of pharmaceuticals from aqueous solution. J. Photochem. Photobiol. A Chem. 2020, 388, 112183. [Google Scholar] [CrossRef]
- Omri, A.; Lambert, S.D.; Geens, J.; Bennour, F.; Benzina, M. Synthesis, Surface Characterization and Photocatalytic Activity of TiO2 Supported on Almond Shell Activated Carbon. J. Mater. Sci. Technol. 2014, 30, 894–902. [Google Scholar] [CrossRef]
- Ullattil, S.G.; Periyat, P.; Naufal, B.; Lazar, M.A. Self-Doped ZnO Microrods—High Temperature Stable Oxygen Deficient Platforms for Solar Photocatalysis. Ind. Eng. Chem. Res. 2016, 55, 6413–6421. [Google Scholar] [CrossRef]
- Gorgulho, H.F.; Mesquita, J.P.; Gonçalves, F.; Pereira, M.F.R.; Figueiredo, J.L. Characterization of the surface chemistry of carbon materials by potentiometric titrations and temperature-programmed desorption. Carbon N. Y. 2008, 46, 1544–1555. [Google Scholar] [CrossRef]
- Bandosz, T.J.; Policicchio, A.; Florent, M.; Li, W.; Poon, P.S.; Matos, J. Solar light-driven photocatalytic degradation of phenol on S-doped nanoporous carbons: The role of functional groups in governing activity and selectivity. Carbon N. Y. 2020, 156, 10–23. [Google Scholar] [CrossRef]
- Szekeres, M.; Tombácz, E. Surface charge characterization of metal oxides by potentiometric acid-base titration, revisited theory and experiment. Colloids Surf. A Physicochem. Eng. Asp. 2012, 414, 302–313. [Google Scholar] [CrossRef]
- Nagamani, B.; Srinivasu, C. Physical parameters and structural analysis of titanium doped binary boro silicate glasses by spectroscopic techniques. Mater. Today Proc. 2019, 18, 2077–2083. [Google Scholar] [CrossRef]
- Apopei, P.; Orha, C.; Popescu, M.I.; Lazau, C.; Manea, F.; Catrinescu, C.; Teodosiu, C. Diclofenac removal from water by photocatalysis- assisted filtration using activated carbon modified with N-doped TiO2. Process Saf. Environ. Prot. 2020, 138, 324–336. [Google Scholar] [CrossRef]
- Varnagiris, S.; Medvids, A.; Lelis, M.; Milcius, D.; Antuzevics, A. Black carbon-doped TiO2 films: Synthesis, characterization and photocatalysis. J. Photochem. Photobiol. A Chem. 2019, 382, 111941. [Google Scholar] [CrossRef]
- Park, Y.; Kim, W.; Park, H.; Tachikawa, T.; Majima, T.; Choi, W. Carbon-doped TiO2 photocatalyst synthesized without using an external carbon precursor and the visible light activity. Appl. Catal. B Environ. 2009, 91, 355–361. [Google Scholar] [CrossRef]
- Wu, X.; Yin, S.; Dong, Q.; Guo, C.; Li, H.; Kimura, T.; Sato, T. Synthesis of high visible light active carbon doped TiO2 photocatalyst by a facile calcination assisted solvothermal method. Appl. Catal. B Environ. 2013, 142–143, 450–457. [Google Scholar] [CrossRef]
- Ayawei, N.; Ebelegi, A.N.; Wankasi, D. Modelling and Interpretation of Adsorption Isotherms. J. Chem. 2017, 2017, 3039817. [Google Scholar] [CrossRef]
- Heiba, H.F.; Taha, A.A.; Mostafa, A.R.; Mohamed, L.A.; Fahmy, M.A. Preparation and characterization of novel mesoporous chitin blended MoO3-montmorillonite nanocomposite for Cu(II) and Pb(II) immobilization. Int. J. Biol. Macromol. 2020, 152, 554–566. [Google Scholar] [CrossRef]
- Hoque, M.A.; Guzman, M.I. Photocatalytic activity: Experimental features to report in heterogeneous photocatalysis. Materials 2018, 11, 1990. [Google Scholar] [CrossRef]
- Kisch, H. On the problem of comparing rates or apparent quantum yields in heterogeneous photocatalysis. Angew. Chem. Int. Ed. 2010, 49, 9588–9589. [Google Scholar] [CrossRef]
- Kisch, H.; Bahnemann, D. Best Practice in Photocatalysis: Comparing Rates or Apparent Quantum Yields? J. Phys. Chem. Lett. 2015, 6, 1907–1910. [Google Scholar] [CrossRef]
- Catherine, H.N.; Ou, M.H.; Manu, B.; Shih, Y.H. Adsorption mechanism of emerging and conventional phenolic compounds on graphene oxide nanoflakes in water. Sci. Total Environ. 2018, 635, 629–638. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Gong, Q.; Chen, Z.; Wang, W.D.; Huang, Q.; Song, S.; Chen, J.; Wang, X. Adsorption and competition investigation of phenolic compounds on the solid-liquid interface of three-dimensional foam-like graphene oxide. Chem. Eng. J. 2019, 378, 122085. [Google Scholar] [CrossRef]
- Pedrosa, M.; Da Silva, E.S.; Pastrana-Martínez, L.M.; Drazic, G.; Falaras, P.; Faria, J.L.; Figueiredo, J.L.; Silva, A.M.T. Hummers’ and Brodie’s graphene oxides as photocatalysts for phenol degradation. J. Colloid Interface Sci. 2020, 567, 243–255. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.C.; Juang, R.S.; Huq, M.M.; Hsieh, C. Te Enhanced adsorption and photodegradation of phenol in aqueous suspensions of titania/graphene oxide composite catalysts. J. Taiwan Inst. Chem. Eng. 2016, 67, 338–345. [Google Scholar] [CrossRef]
- Murillo-Acevedo, Y.; Bernal-Sanchez, J.; Giraldo, L.; Sierra-Ramirez, R.; Moreno-Piraján, J.C. Initial Approximation to the Design and Construction of a Photocatalysis Reactor for Phenol Degradation with TiO2 Nanoparticles. Acs Omega 2019, 4, 19605–19613. [Google Scholar] [CrossRef]
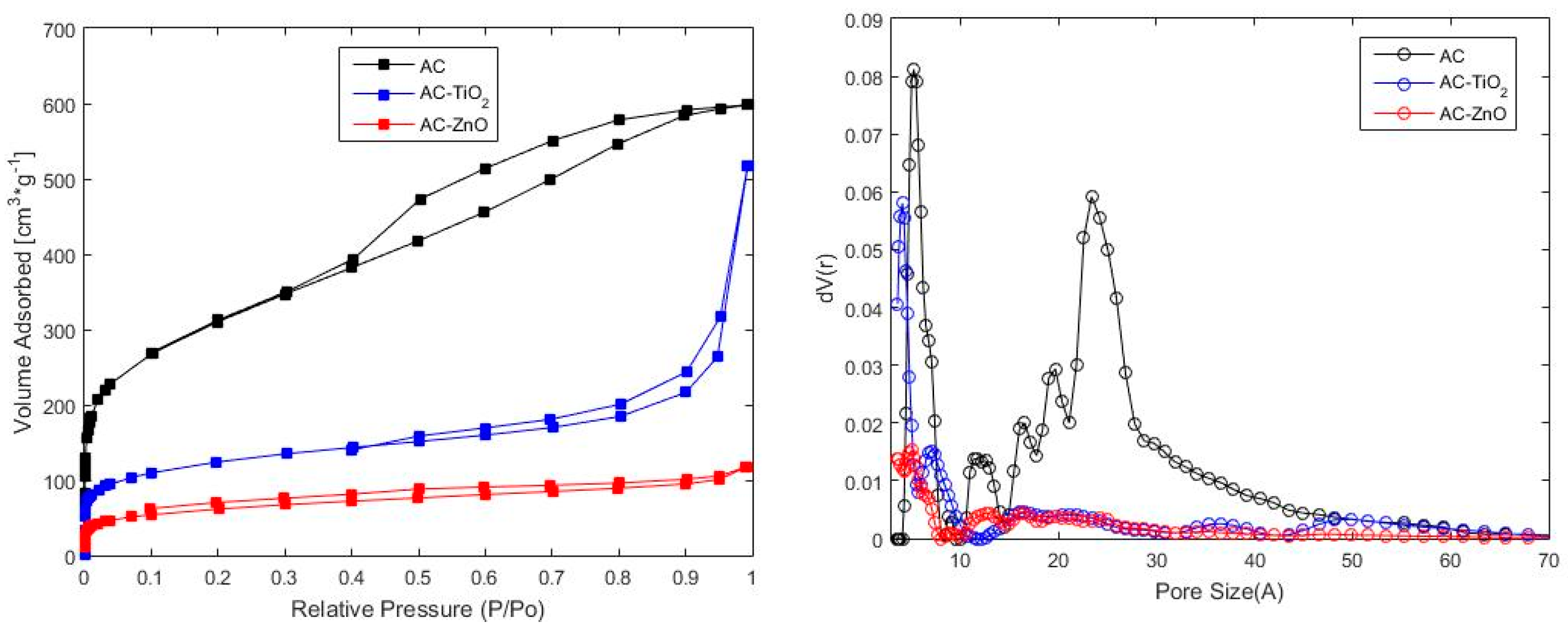
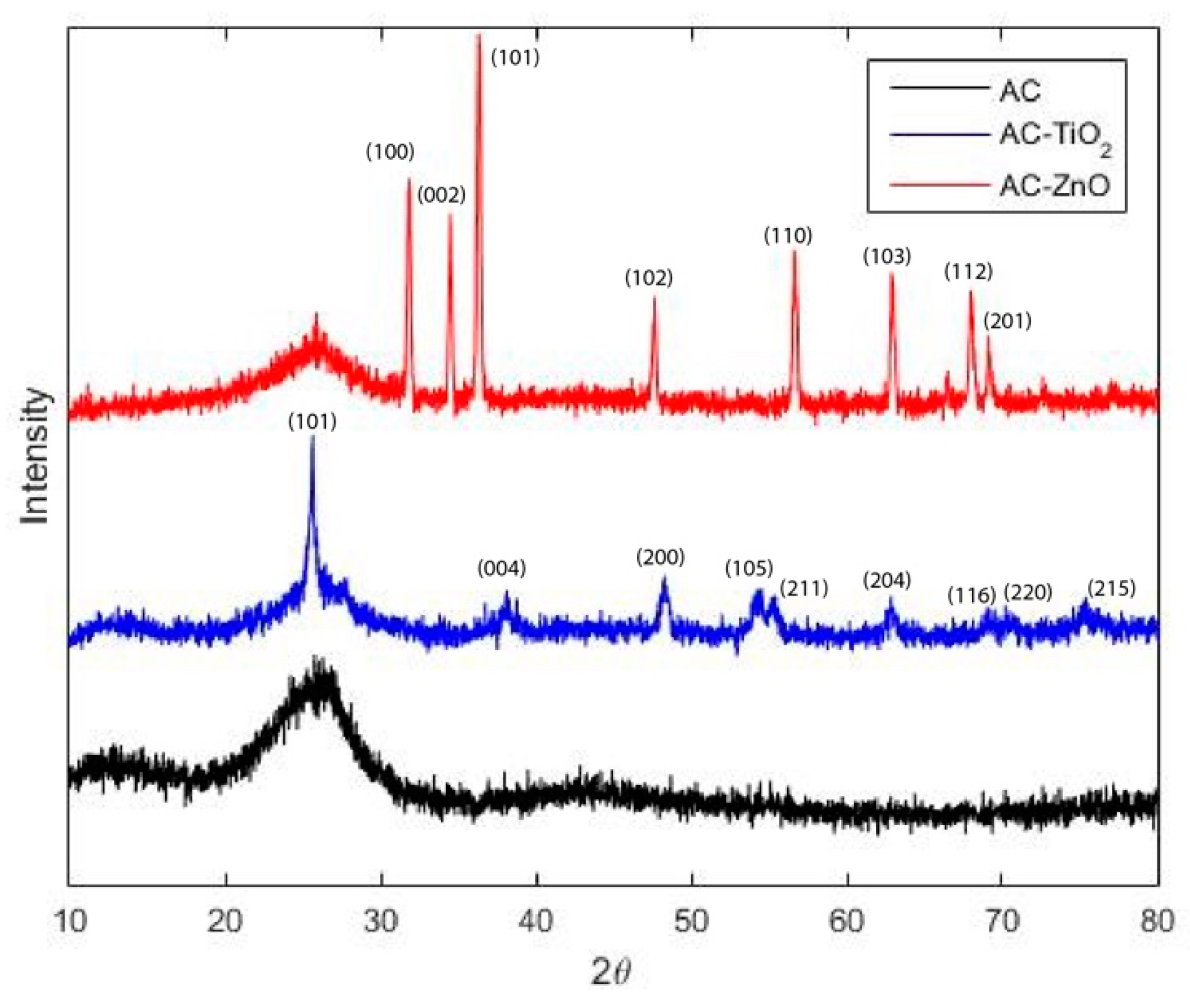


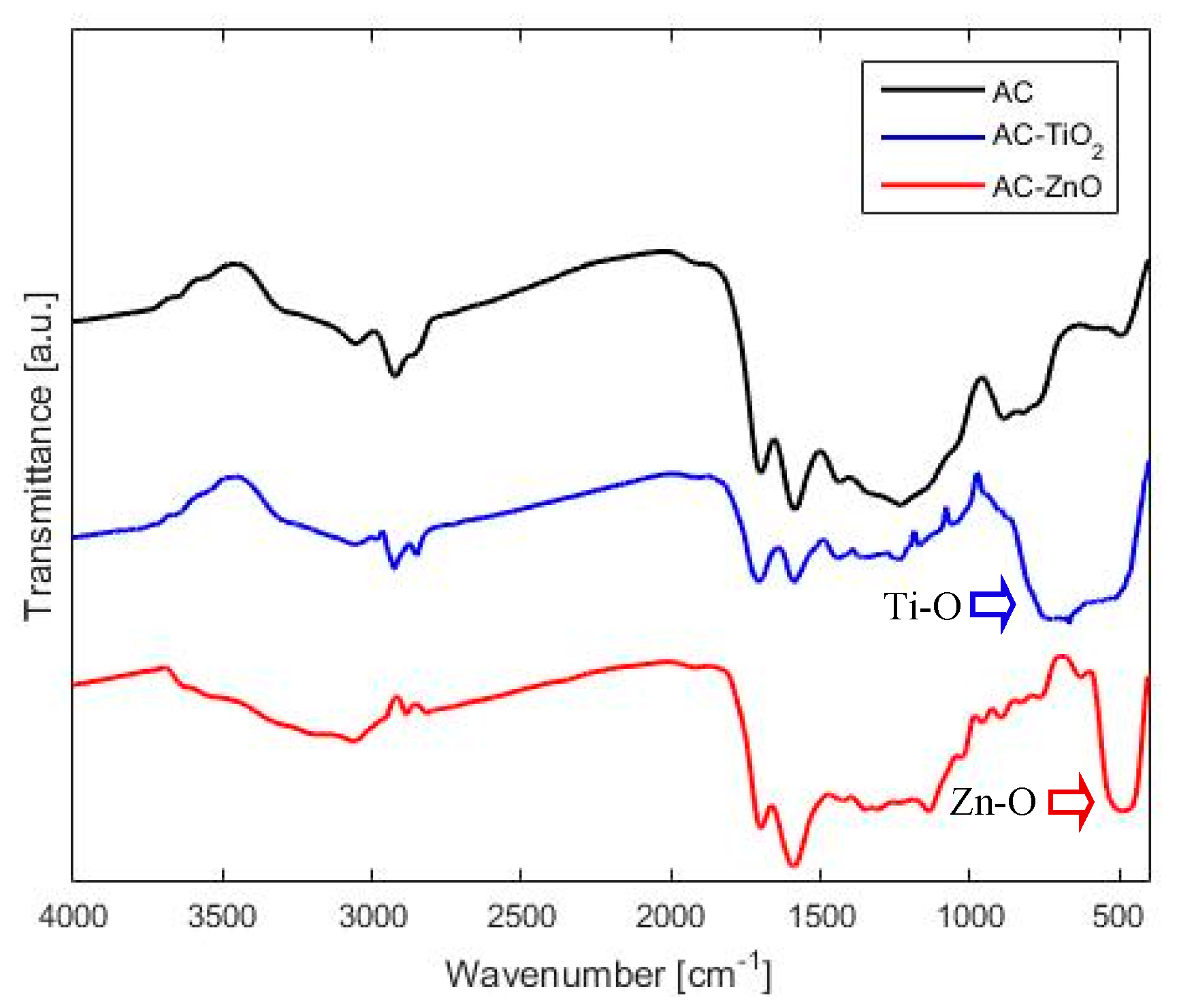
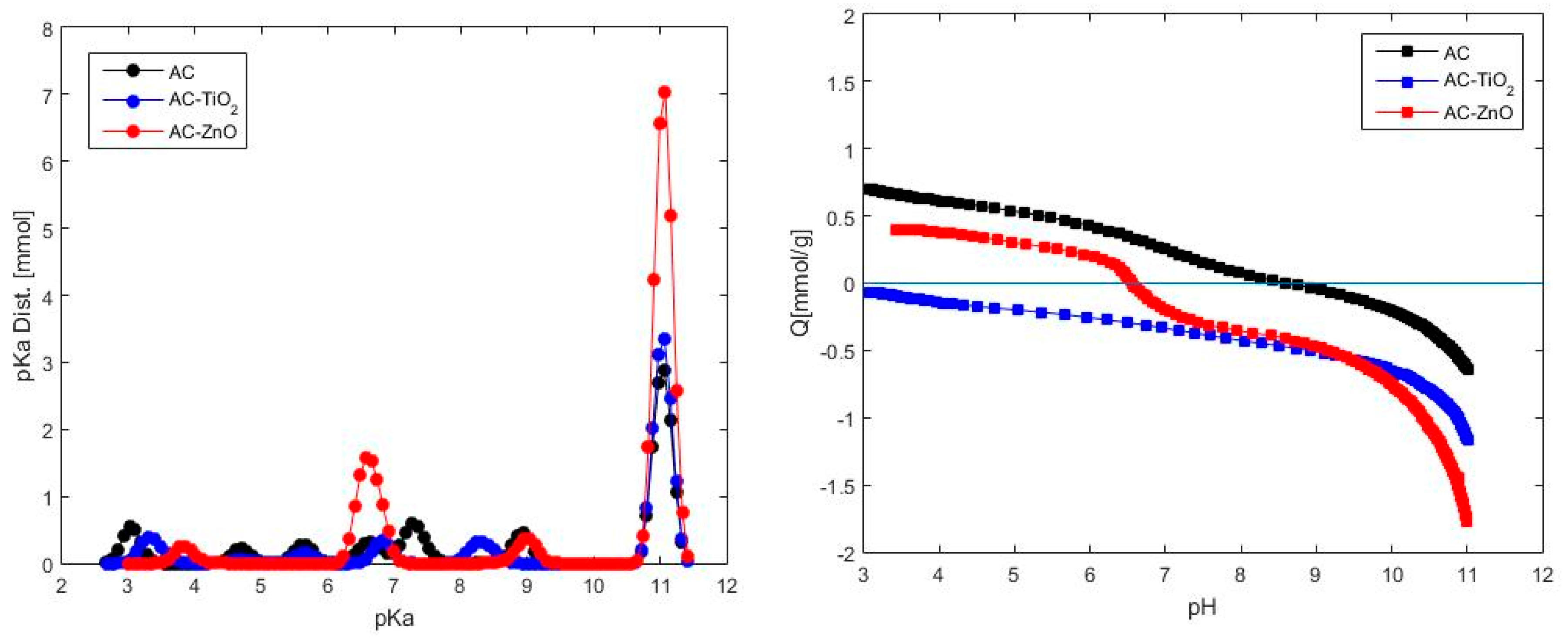
| Material | BET | QSDFT | ||
|---|---|---|---|---|
| SBET (m2∗g−1) | C (Energy Constant) | Vpore (cm3∗g−1) | Half Pore Width (Å) | |
| AC | 1100 | 203.1 | 0.879 | 5.25 |
| AC–TiO2 | 440 | 267.0 | 0.557 | 4.09 |
| AC–ZnO | 218 | 253.8 | 0.158 | 5.03 |
| Model | Parameter | AC | AC–TiO2 | AC–ZnO |
|---|---|---|---|---|
| Langmuir | qm (mg∗g−1) | 39.30 | 37.18 | 32.87 |
| KL (L∗mg−1) | 0.032 | 0.033 | 0.015 | |
| s (mg∗g−1) | 1.24 | 1.50 | 1.21 | |
| Freundlich | KF | 2.72 | 2.83 | 1.13 |
| 1/n | 0.55 | 0.52 | 0.62 | |
| s (mg∗g−1) | 1.78 | 0.86 | 1.43 |
| AC | AC–TiO2 | AC–ZnO | ||
|---|---|---|---|---|
| Pseudo-first | qe (mg·g−1) | 18.27 | 16.20 | 8.48 |
| k1 (h−1) | 1.32 | 1.26 | 0.98 | |
| s (mg·g−1) | 0.29 | 0.46 | 0.31 | |
| Pseudo-second | qe (mg·g−1) | 20.18 | 18.06 | 9.80 |
| k2 (g·mg−1h−1) | 0.11 | 0.11 | 0.13 | |
| s (mg·g−1) | 0.20 | 0.10 | 0.19 |
| Metal Oxide (MO) | CAS | Molecular Mass (g·mol−1) | Supplier | Purity | Crystalline Phase | Particle Size (nm) |
|---|---|---|---|---|---|---|
| TiO2 | 13463-67-7 | 79.87 | Sigma-Aldrich | 99% | Rutile–Anatase | 21 |
| ZnO | 1314-13-2 | 81.39 | Sigma-Aldrich | 99% | Wurtzite | 50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Barreto, D.F.; Rodriguez-Estupiñán, J.P.; Moreno-Piraján, J.C.; Sierra Ramírez, R.; Giraldo, L. Adsorption and Photocatalytic Study of Phenol Using Composites of Activated Carbon Prepared from Onion Leaves (Allium fistulosum) and Metallic Oxides (ZnO and TiO2). Catalysts 2020, 10, 574. https://doi.org/10.3390/catal10050574
Hernández-Barreto DF, Rodriguez-Estupiñán JP, Moreno-Piraján JC, Sierra Ramírez R, Giraldo L. Adsorption and Photocatalytic Study of Phenol Using Composites of Activated Carbon Prepared from Onion Leaves (Allium fistulosum) and Metallic Oxides (ZnO and TiO2). Catalysts. 2020; 10(5):574. https://doi.org/10.3390/catal10050574
Chicago/Turabian StyleHernández-Barreto, Diego Felipe, Jenny Paola Rodriguez-Estupiñán, Juan Carlos Moreno-Piraján, Rocío Sierra Ramírez, and Liliana Giraldo. 2020. "Adsorption and Photocatalytic Study of Phenol Using Composites of Activated Carbon Prepared from Onion Leaves (Allium fistulosum) and Metallic Oxides (ZnO and TiO2)" Catalysts 10, no. 5: 574. https://doi.org/10.3390/catal10050574
APA StyleHernández-Barreto, D. F., Rodriguez-Estupiñán, J. P., Moreno-Piraján, J. C., Sierra Ramírez, R., & Giraldo, L. (2020). Adsorption and Photocatalytic Study of Phenol Using Composites of Activated Carbon Prepared from Onion Leaves (Allium fistulosum) and Metallic Oxides (ZnO and TiO2). Catalysts, 10(5), 574. https://doi.org/10.3390/catal10050574






