Abstract
The metabolic engineering of pathways has been used extensively to produce molecules of interest on an industrial scale. Methods like gene regulation or substrate channeling helped to improve the desired product yield. Cell-free systems are used to overcome the weaknesses of engineered strains. One of the challenges in a cell-free system is selecting the optimized enzyme concentration for optimal yield. Here, a machine learning approach is used to select the enzyme concentration for the upper part of glycolysis. The artificial neural network approach (ANN) is known to be inefficient in extrapolating predictions outside the box: high predicted values will bump into a sort of “glass ceiling”. In order to explore this “glass ceiling” space, we developed a new methodology named glass ceiling ANN (GC-ANN). Principal component analysis (PCA) and data classification methods are used to derive a rule for a high flux, and ANN to predict the flux through the pathway using the input data of 121 balances of four enzymes in the upper part of glycolysis. The outcomes of this study are i. in silico selection of optimum enzyme concentrations for a maximum flux through the pathway and ii. experimental in vitro validation of the “out-of-the-box” fluxes predicted using this new approach. Surprisingly, flux improvements of up to 63% were obtained. Gratifyingly, these improvements are coupled with a cost decrease of up to 25% for the assay.
1. Introduction
Many chemical molecules like peptides, organic acids, etc., are synthesized by different methods such as chemical reactions [1,2,3,4,5] and fermentation process for their application in everyday life. Due to the depletion of non-renewable resources, synthesis of these molecules through a biological system is essential on an industrial scale [6,7]. For decades, scientists have been successful in producing different chemical molecules through microbial fermentation by optimizing the process [7,8,9,10]. The costs of microbial fermentation are low, for instance, in comparison to mammalian cell cultures. Microbial systems are easily scalable, use inexpensive synthetic media and have lower batch-to-batch variability [11]. However, microbial systems such as Escherichia coli or yeasts have no or only limited capacity for post-translational modifications. Microbial biosynthesis may show low productivity and the coproduction of by-products is possible, which make product recovery complex and protracted [12]. With the advancement of science and technology, there is a continuous effort to improve productivity through novel techniques like gene regulation, which helps to channel the pathway in particular directions, substrate channeling where reactants are directed to the active site of enzymes [13,14], quorum sensing [15], enzyme engineering, etc. However, even after numerous studies, synthesizing some molecules on an industrial scale through microbial fermentation is not cost-effective.
Nobel laureate Eduard Buchner laid the foundation for the cell-free system (CFS) of biomolecule production by converting sugar into ethanol in 1897. It has been successfully used in the synthesis of many products like bio-hydrogen [16,17], bio-ethanol [18,19], antibodies [20], vaccines [21], proteins [22], etc. The CFS is classified into two broad categories: i) cell-extract based: in which the host cells are lysed [23,24] and ii) purified-enzyme based: a mixture of purified enzymes and cofactors are in the system [25]. The CFS has high toxic tolerance, rapid development timeline, easy incorporation of unnatural amino acids and easy purification of the product. The disadvantages of CFS include poor scalability, and post-translation modification of proteins is challenging [22]. The selection of enzymes is crucial in metabolic engineering since low performing enzymes result in poor titer and yield. Homology based methodologies like Selenzyme [26] have been developed to select better performing enzymes. One of the main challenges of purified enzyme-based CFS is the selection of optimum enzyme concentrations for maximum product formation. The experimental selection of optimum enzyme concentrations is expensive and tedious.
Researchers became more interested in the mathematical modeling of biological systems due to the availability of data from omics studies [27]. The modeling helps to organize the system information, to simulate and hence optimize the experiment and to understand system characteristics. Out of many different kinds of modeling methods, constraints-based and statics-based models, as well as kinetics-based or dynamic models have been used extensively to study metabolic pathways. The constraints-based methods such as the flux balance analysis [28] depend on physicochemical constraints like mass and energy balance [29]. However, the constraint-based method does not provide information about the concentration of metabolites. Kinetic modeling depends on the kinetic parameters of the enzymes involved in the pathway and provides information about their concentrations [30]. Kinetic modeling of pathways helps to better understand their behavior and replicate the system. Since the kinetic parameters are essential for this kind of modeling, it is not always easy to replicate the system. Finding the kinetic parameters is expensive, tedious [31], and some parameters are difficult to estimate experimentally [32]. For example, phosphofructokinase requires more than ten parameters to model [33]. Hence, the development of a computational method for selecting optimum enzyme concentrations without detailed knowledge of their kinetic parameters, using other existing experimental data, is helpful.
Machine learning methods help to predict the outcome based on the existing experimental data. The artificial neural network (ANN) is one such method inspired by brain architecture [34]. The neural network consists of connections between three layers: input, hidden and output layer. An activation function for the hidden layer is used to define the output. The neural network has been widely used in different fields of science for system identification and control, pattern recognition, medical diagnosis, weather prediction, etc. In particular, the ANN has been used for the selection of optimized medium components in the fermentation process for producing different molecules such as lipids from Chlorella vulgaris [35] and Spinosyns from Saccharopolyspora spinose [36]. ANN was employed, for instance, for the prediction of the flux through mammalian gluconeogenesis, using the simulated data from metabolite isotopic labeling [37]. Glycolysis, one of the central carbon metabolism pathways, is not only important for organisms, but also in biotechnology for producing different biomolecules [38]. Many chemicals such as organic acids [39,40] and biofuels [41,42] have been successfully produced with high titer using engineered microorganisms including Saccharomyces cerevisiae or Escherichia coli. Glycolysis is widely studied from various perspectives. The availability of data from Fievet et al. [43] for flux prediction with different enzyme concentrations makes it a good candidate for developing a new approach to select optimum enzyme concentrations.
Previously, ANN was used to predict the flux through the upper part of glycolysis using enzyme concentrations, i.e., phosphogluco isomerase (PGI), phosphofructokinase (PFK), fructose biphosphate aldolase (FBA), and triosephosphate isomerase (TPI) as the input to the model [44]. The predicted flux has a root mean square error (RMSE) of 0.84 and an R2 of 0.93, with 13 hidden units. Since the ANN is a training-based method, the new prediction depends on the training dataset. Since ANN is not efficient in extrapolating predictions [45,46], the new predictions will always lie in the range of the known output predictions; in other words, we could say that they will remain “in-the-box”. High predicted output values will bump into a sort of “glass ceiling”. Our working hypothesis was that, in reality, actual flux values could be higher than the predicted ones. So, in order to explore this “glass ceiling” space, we developed a new methodology (GC-ANN, for glass ceiling ANN) to predict the flux for the upper part of glycolysis, given enzyme concentrations using an artificial neural network. The outcomes of this study are i. in silico selection of optimum enzyme concentrations for maximum flux through the pathway and ii. experimental in vitro validation of the “out-of-the-box” flux predicted using this new approach. Initially, we expected to obtain slight improvements, i.e., improved flux values close to the highest one that we fed into the model. Surprisingly, improvements up to 63% were obtained. Moreover, these improvements are coupled with a cost decrease of up to 25% for the assay.
2. Methodology
2.1. Data for New Methodology
The data from Fievet et al. [43] were used to develop the new methodology for selecting optimum enzyme concentrations using ANN. The dataset consisted of 121 combinations of four enzymes (PGI, PFK, FBA and TPI) for the upper stage of glycolysis for a flux value of 0.74–12.9 µM/s. The total enzyme concentration was kept constant for four enzymes of 101.9 mg/L. The flux was measured as NADH consumption through G3PDH. For more details about the data, please refer to the experimental section of the research article by Fievet et al. [43].
2.2. ANN-Based Flux Prediction Workflow
The new GC-ANN methodology is explained in three steps: i.) the preparation stage: the data dimension is reduced to find the possibly correlated variable, the rule for obtaining higher flux (>12 µM/s) is derived from the data, and a neural network model is built to predict the flux using the enzyme concentrations; ii.) execution stage: new enzyme concentrations are generated using the rule obtained and the flux is predicted for the new concentration using ANN; and iii.) validation of the methodology: the new methodology of predicting flux using ANN is validated through simulation and experiment.
2.2.1. Preparation stage
Reduction of Data Dimensionality
Principal component analysis (PCA) is one of the methods for the reduction of dimensionality of the dataset [47,48]. For datasets with a high degree of freedom, PCA is very useful to find possible correlations between the variables. PCA is performed using the R (V 3.4.3; R Development Core Team (2008)) package FactoMineR [49].
Visualization of Data
Three-dimensional viewing of data could provide insight into the distribution of flux in the space. Therefore, the fluxes in the 3D space of concentrations PGI, PFK, and TPI were visualized using R statistical packages plot3D [50] and plot3Drgl [51].
Classification of Data for Higher Flux (> 12 µM/s)
Data classification is the process of categorizing data into various homogeneous groups or types based on common characteristics. Decision tree analysis is a method of data classification helping to search for possible associations within the dataset. The decision tree is a simple tree-like graph method to understand and interpret the observations. The discriminant analysis helps to discriminate between the groups of data. The classification is supported by a discriminant analysis.
The data were classified into 5 groups, i.e., flux value from 0.728–3.17, 3.17–5.6, 5.6–8.04, 8.04–10.5 and 10.5–12.9. Approximately, 40% of the data are in the final group, which consists of higher flux concentrations (greater than 10.5 µM/s). The R packages klaR [52] and rpart [53] were used for discriminant analysis and decision tree respectively. The results from the decision tree and discriminant analysis were used to derive the concentration rule for higher flux values (> 12 µM/s) through the pathway.
Neural Network Model
The artificial neural network for predicting the flux through the upper part of glycolysis is built using the data described earlier in the section “Data for new methodology”. The model predicts flux as an NADH consumption through the pathway. The model is built using the R package neuralnet [54], which gives us the freedom to choose two different activation functions: logistic and tanh [44].
2.2.2. Execution Stage
Generation of New Enzyme Concentration
The new enzyme concentrations were generated between the highest (PGI = 70, PFK = 70, FBA = 86.1, TPI = 66.1 mg/L) and lowest (PGI = 1, PFK = 1, FBA = 2, TPI = 1.66 mg/L) concentrations of the data from Fievet et al. [43], with a step size of 1 mg/L using R script. The total enzyme concentration of four enzymes was kept constant at 101.9 mg/L as in Fievet et al. [43]. The newly generated concentrations were used in the additional analysis.
Flux Prediction Using ANN
Newly generated enzyme concentrations were fed to the ANN model to predict the flux. The data consisted of flux values ranging from 0.74 to 12.9 µM/s. Since ANN is not good for extrapolation, these values limit the prediction to this range. Nevertheless, it is likely that new enzyme concentrations could provide higher flux. However, ANN prediction will remain in the glass ceiling space. Hence, we decided to explore this space with squeezed flux, i.e., the flux that lies in this particular space. Thus, for our study, fluxes > 12 µM/s predicted by ANN and the concentrations that obeyed the rule derived to obtain possible higher flux values from data classification were retained.
2.2.3. Validation of Methodology
The artificial neural network-based methodology for flux prediction was validated in two steps. In the first step of validation, the available kinetic parameters from Fievet et al. [43] helped us to build the model and replicate the experimental conditions. In the second step, the methodology was experimentally validated.
Simulation of Upper Part of Glycolysis
In CellDesigner (ver4.4) [55,56], the kinetic model of the upper part of glycolysis was built using the kinetic parameters from Fievet et al. [43] and the parameters for cofactors chosen from the BRENDA [57] database (Table 1). The model was built to replicate the experimental condition with the Michaelis-Menten equation (Table 1). ATP is regenerated using the creatine kinase system. The hexokinase concentration was kept constant at 0.1 µM and flux was measured as NADH consumption, as catalyzed by 1 µM of G3PDH. The concentrations of PGI, PFK, FBA and TPI were varied according to the selected balance from Section 2.2.2. (i.e., with concentrations that provide a flux ≥ 12 µM/s as predicted by the ANN model). The concentrations were converted from mg/L to µM using the molecular weight as suggested by Fievet et al.

Table 1.
The kinetic equations and parameters used to build the kinetic model of the upper part of glycolysis. Glu: glucose; G6P: glucose-6-phosphate; F6P: fructose-6-phosphate; FBP: fructose bisphosphate; DHAP: dihydroxyacetone phosphate.
The model was simulated for 120 s using COPASI [58] to measure NADH consumption. The slope of NADH decay between 60 and 120 s was estimated as flux through the pathway 182 enzyme balances yielding flux ≥ 15 µM/s from simulation using an in silico model were selected as the potential higher flux balances.
Experimental Validation
The upper part of glycolysis was reconstructed as described in Fievet et al. [43] (Figure 1). The in vitro system consisted of varied concentrations of PGI, PFK, FBA and TPI. The HK and G3PDH were kept constant and creatine kinases were used to regenerate ATP in the system. The NADH decay was measured as flux through the pathway. The slope of the linear NADH decay was used to calculate the flux in μM/s.
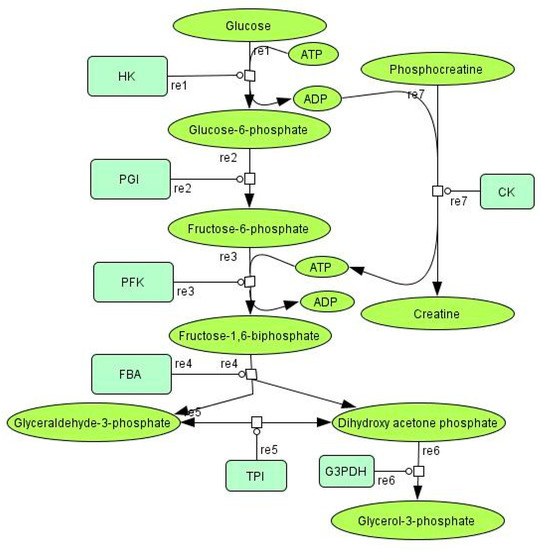
Figure 1.
CellDesigner diagram for the upper part of glycolysis, which replicates the experimental conditions described by Fievet et al. [41]. HK: hexokinase, PGI: glucose 6- phosphate isomerase, PFK: phosphofructokinase, FBA: aldolase, TPI: triose-phosphate Isomerase, G3PDH: glycerol-3-phosphate dehydrogenase, CK: creatine kinase, re: reaction.
2.2.4. The Workflow of the Proposed Methodology
Based on the data listed in Fievet et al. [43], the ANN model was built to predict the flux using enzyme balances, and the rule for enzyme balance for higher flux was obtained by data classification. The fluxes for newly generated enzyme balances were predicted using the ANN model. The balances with a flux value > 12 µM/s (balances from the glass-ceiling) and the balances obeying the derived rule for higher flux were selected as potential higher flux balances. These selected balances were validated using the kinetic model and by experiments. The methodology that followed for exploring the glass-ceiling of ANN (GC-ANN) is represented diagrammatically in Figure 2.
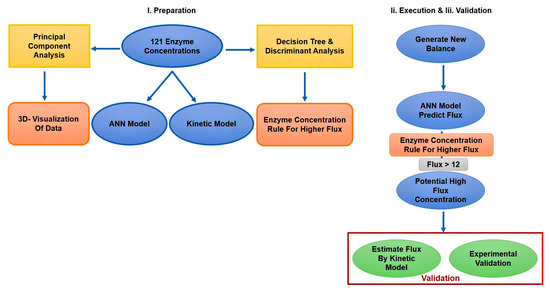
Figure 2.
The methodology followed to obtain the new flux values from the generated enzyme concentration.
3. Application and Results
3.1. Preparation
3.1.1. Data Dimension Reduction
In our study, PCA did not provide much information regarding the data. The total four-enzyme concentration was constant in the system, which reduced the degree of freedom to limit the enzyme concentrations to three. If the total enzyme concentration is not constant or the dataset presents a high degree of freedom, PCA will be more useful for obtaining uncorrelated variables: this is why we mentioned PCA as a useful tool in the framework of this methodology.
3.1.2. Visualization of Data
After the PCA, data was visualized in 3D (Figure 3). We could observe on the plot that the higher flux (red dots) was quite distinct. This is a good indication that a quantitative method could be applied and should provide good results. Indeed, this is verified in the section “Flux prediction using ANN” (Figure 3). In this methodology, we were exploring the space around those higher flux concentrations to obtain new concentrations of PGI, PFK and TPI.
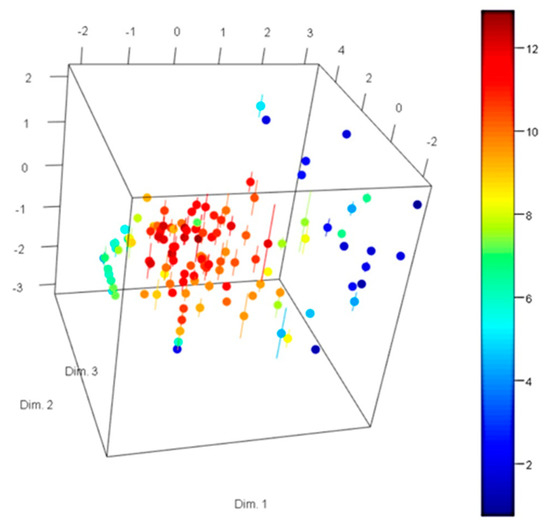
Figure 3.
Three-dimensional visualization of Fievet et al. [43] enzyme balances after PCA (Dim1: 43.55%, Dim2: 23.78% and Dim 3: 17.56%). The change from blue to red indicates the gradient from low to high fluxes, respectively. Standard deviation of experimental flux is represented on the third-dimension.
3.1.3. Enzyme Concentration Rule
Decision tree analysis was performed using the R package rpart by dividing the data into five groups; this provides the best compromise on the gain in inter-class inertia. The five groups were determined using kmeans clustering.
Figure 4 represents the classification of data where the percentage of data belongs to the branch of tree and fraction represents the distribution into different groups. For example, 89% of the data had FBA concentration > 11 and is distributed in five groups as a fraction of 0.01, 0.09, 0.17, 0.29 and 0.44 (Figure 4, node 3).
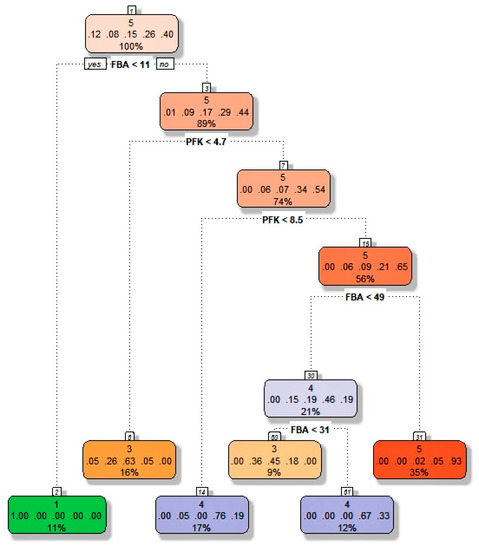
Figure 4.
Decision tree analysis for Fievet et al. [43] data to obtain the rule for higher flux (≥ 12 µM/s). The data is classified into 5 groups (i.e., flux value from (0.728–3.17), (3.17–5.6), (5.6–8.04), (8.04–10.5) and (10.5–12.9).
Among the different methods of discriminant analysis studied, rpart performed the best with an approximate error rate of 0.1. The different methods studied were LDA (linear discriminant analysis), QDA (quadratic discriminant analysis), SKNN (simple k nearest neighbors), RDA (regularized discriminant analysis) and naïve Bayes (under R package). For the SKNN method, the error rate was low but it led to an over-classification (data not shown). Figure 5 represents the discriminant analysis for the classification of data from Fievet et al. [43] using the rpart [53] method from R.
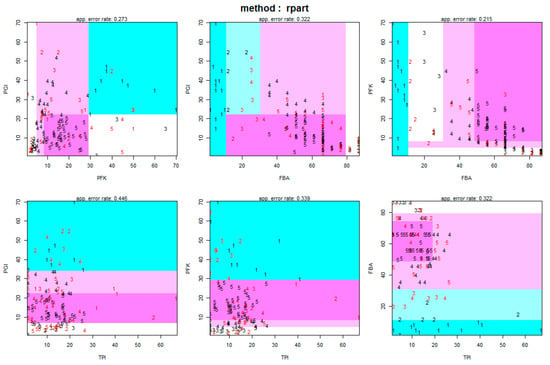
Figure 5.
Discriminant analysis for the classification of data from Fievet et al. [43] using the rpart50 method from R. Color code according to the feature space of data, where group 1 (flux: 0.728–3.17 µM/s) is shown in light blue, group 2 (flux: 3.17–5.6 µM/s) in dark blue, group 3 (flux: 5.6–8.04 µM/s) in white, group 4 (flux: 8.04–10.5 µM/s) in light pink and group 5 (flux: 10.5–12.9 µM/s) in dark pink. Numbers in black represent the data classified to the same group, and in red represent data misclassified into the other groups.
After using the decision tree (Figure 4) and discriminant analysis (Figure 5), the following rule was derived to obtain a flux ≥ 12 µM/s:
PGI < 11; 10 < PFK < 16; TPI < 18; 59 >FBA (mg/L), which corresponds to PGI < 15.07 U/mL; 0.7 U/mL < PFK < 1.12 U/mL; TPI < 264.42 U/mL; 2.48 U/mL > FBA.
The conversion from mg/L to U/mL is given in Methods S1 in Supplementary Materials. The derived rule is applied for the selection of the best concentrations of the enzymes PFK, PGI, TPI, and FBA to obtain a high flux through the pathway.
3.1.4. Neural Network Model
ANN is a training-based method, the structure of the neural network needs to be chosen carefully since it depends on the number of inputs, sampling in the training dataset and the outputs. The structure was determined based on our previous study [44]. The neuralnet package from R statistical tool with the logistic activation function was used. It has 13 hidden units in a single layer. The ANN model used has an RMSE value of 0.84 and an R2 value of 0.93, using leave-one-out cross-validation [44].
3.2. Execution
3.2.1. Generation of New Enzyme Concentrations
The new concentrations of PFK, PGI, TPI and FBA were generated as explained in the methodology section. These new balances were used for further analysis to predict the flux.
3.2.2. Flux Prediction Using ANN
The new balances were fed into the previously built neural network to predict the flux. The ANN predicted flux from the newly generated data was visualized in 3-dimensions (Figure 6).
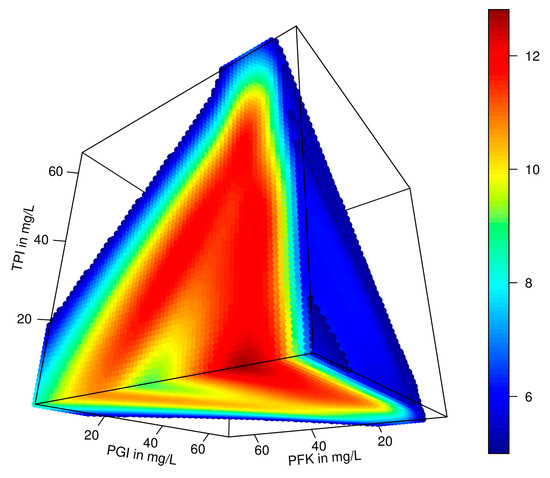
Figure 6.
Three-dimensional visualization of flux predicted by an artificial neural network (ANN) for newly generated enzyme concentrations. The color gradient is from the lowest (blue) to the highest (red) predicted flux.
As expected, the new prediction remained in the box (see the maximum value of the color gradient bar in Figure 6) since ANN is a training-based method that depends on the training dataset. The high predicted values bump into the “glass ceiling”. Our hypothesis was that even though they remain in the roof of the “glass ceiling”, the experimental values could be higher than the predicted ones. By exploring this space, we could obtain new balances with higher flux values.
In order to explore the “glass ceiling” space, we developed this new methodology (named GC-ANN) using the artificial neural network to predict the flux through the upper part of glycolysis for given enzyme concentrations. In this study, we showed (see below in the section validation) that by careful selection of enzyme concentrations from the “glass-ceiling” space, it is possible to obtain higher flux values “out-of-the-box”.
For all the enzyme concentrations generated between minimum and maximum of experimental data, only flux values above 12 µM/s predicted by neural network, and only enzyme balances (total of 335 balances, a balance being defined as a mixture of the four enzymes PGI, PFK, FBA and TPI) obeying the enzyme concentration rule were selected as potential high-flux balances.
3.3. Validation
The methodology for exploring the glass-ceiling using ANN (GC-ANN) was validated in two steps: first using the kinetic model and second, in vitro.
3.3.1. Simulation of Upper Part of Glycolysis
The kinetic model is built using CellDesigner [55,56] (Figure 1) and validated with COPASI [58] using the 121 concentrations from Fievet et al. [43]. The model has an RMSE value of 1.58 and R2 of 0.84 in a cross-validation procedure, compared to the experimentally determined flux (Figure 7). Figure 7 proves that the kinetic model was good and could be used for the validation of the new approach. The highest flux predicted by the kinetic model of the reconstituted upper part of glycolysis was 14.93 µM/s, where the highest experimentally observed flux was 12.9 µM/s. The flux predicted by ANN for new enzyme balances from the section “Flux prediction using ANN” was compared with the simulated flux for each enzyme (Figure 8). Figure 8 shows that the balances that were predicted with higher flux through GC-ANN were also estimated to have higher flux using the kinetic model. This validates the good quality of the kinetic model.
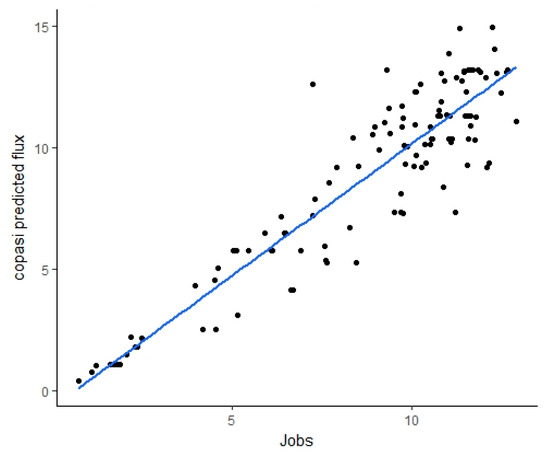
Figure 7.
Relationship between experimental flux (JFievet) estimated by Fievet et al. [43] and COPASI [58] estimated by the kinetic model.
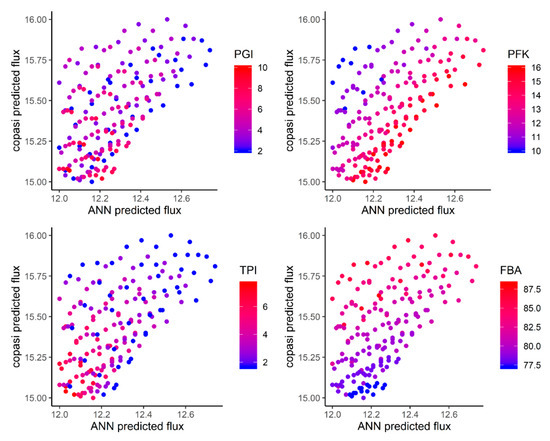
Figure 8.
The relationship between flux values predicted by ANN vs COPASI for newly generated enzyme balances. The enzymes considered are: upper, left (PGI), right (PFK), lower left (TPI), right (FBA). The color gradient from blue to red represents the particular enzyme concentration from low to high, respectively.
3.3.2. Experimental Validation of the Methodology
To validate this new approach to exploring the glass-ceiling (GC-ANN), the new enzyme balances generated were assayed in vitro. For the control experiment, 10 enzyme balances from previously used Fievet et al. [43] enzyme concentrations (Figure 9) were selected (Figure 10; Table S1). These selected balances have a correlation R2 of 0.99 and an RMSE of 0.17 between the predicted flux from our kinetic model and the experimental flux assessed by Fievet et al. [43]. Figure 9 shows that balances selected for the control study are an appropriate choice. Two of these selected Fievet’s balances were tested experimentally. The resulting fluxes for these two balances were 0.59 (±0.10) µM/s and 8.03 (±0.56) µM/s (see Table S2 in the Supporting Information) while Fievet et al. had determined 1.22 (±0.08) µM/s and 11.05 (±0.29) µM/s, respectively.
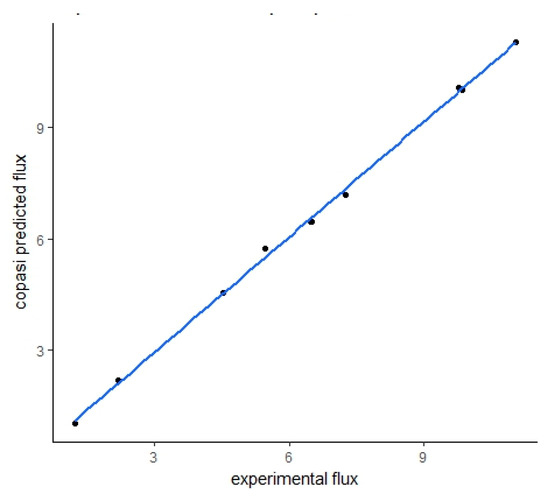
Figure 9.
Correlation between Fievet et al. [43] experimental flux and Copasi predicted flux. The balances corresponding to these flux values are selected as experimental control.
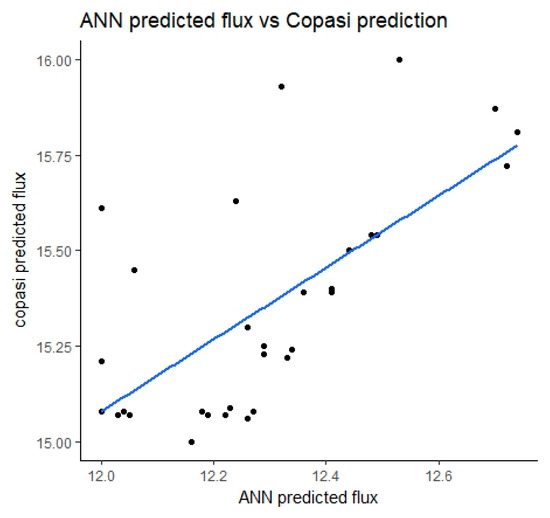
Figure 10.
Comparison between glass ceiling ANN (GC-ANN) predicted flux and simulated flux. The enzyme balance corresponding to these flux values are selected for experimental validation of the methodology.
From the GC-ANN approach, 31 new balances were selected (Figure 10; Table S1) for experimental validation. The flux values associated with the selected balances had a coefficient of determination R2 of 0.44, between GC-ANN predictions and simulated flux. This low R2 between ANN and Copasi prediction is due to the glass-ceiling effect: the underestimation of the flux due to the inability to obtain “out-of-the-box” values for the ANN was expected.
Enzyme Assays for Measurement of Kinetic Parameters
HK activity was assessed using glucose-6-phosphate dehydrogenase (G6PDH) in a coupled reaction. The substrate glucose was converted to 6-phosphogluconate, the formation of NADPH was followed spectrophotometrically at 340 nm (Figure 11A).
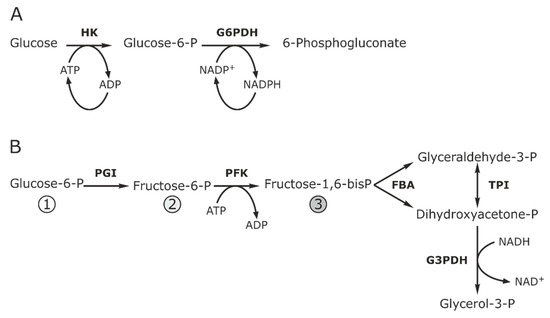
Figure 11.
(A) Coupled HK/G6PDH assay to assess the HK activity. (B) Coupled NADH assay to assess the activities of PGI, PFK, and FBA. The individual reactions were started with substrates indicated by the numbers in circles.
We assessed the activities of PGI, PFK and FBA using a coupled NADH assay applied to the upper part of glycolysis (Figure 11B). To determine the activity of PGI, we started the assay with glucose-6-P (Figure 11B, reaction 1); for the measurement of the activities of PFK and FBA, fructose 6-P and fructose 1,6-bisP were used as the substrates (Figure 11B, reactions 2 and 3). All reactions were monitored by reading the absorbance of NADH at 340 nm and the initial rates were used to calculate the Michaelis constant Km and the maximal velocity Vmax. The kinetic parameters Km for HK, PGI, PFK and FBA corresponded well to the values listed by the manufacturer (Sigma) or by the Enzyme Database Brenda (Table 2). Nevertheless, some enzymes, particularly HK and FBA, showed lower specific activity compared to the Sigma reference. The loss of activity could have occurred during delivery and/or storage of the enzymes or could be attributed to a different enzyme assay.

Table 2.
Summary of the kinetic parameters of HK, PGI, PFK, and FBA. The experimentally assessed values were deduced from Lineweaver-Burk and Eadie-Hofstee plots. Reference values for Km and Vmax from Brenda and Sigma’s product data sheets are indicated, respectively. Lot No., lot number; sp. act., specific activity.
Flux Determinations
The reaction mixtures for the measurements of the flux through the upper part of glycolysis were based on Fievet et al. [43] (Table 3). In contrast to Fievet et al., we based our mixtures on relative enzyme activities rather than enzyme concentrations. Calculations are explained in Method S1, in the Supplementary Materials.

Table 3.
Comparison of ANN predicted flux (JANN in µM/s), simulated flux (JCopasi in µM/s) and experimentally assessed flux (JExp in µM/s). The four enzymes PGI, PFK, FBA and TPI were used at the indicated concentrations for the experimental assessment of the flux with mean deviation (M.D) of triplicates.
Out of 41 selected balances, 31 newly predicted enzyme concentrations were tested experimentally to estimate flux. All 31 new enzyme balances experimentally tested were estimated with flux values greater than 12 µM/s (Table 3). Table 3 shows that 28 out of 31, i.e., 90.3%, had a value above 15.0 µM/s, as expected according to the kinetic model. Moreover, 31 out of 31, i.e., 100%, had a value above 12.0 µM/s, as expected according to our methodology.
3.4. Application: Selection of Cost-Efficient Enzyme Balances
For industrial-scale production, the selection of best enzyme concentrations in terms of cost is essential. Therefore, we estimated the cost per µM of NADH consumed per second for all the enzyme balances generated (Figure 12) and for those selected balances from ANN prediction that obey the enzyme concentration rule (flux greater than 12 µM/s), i.e., 335 balances from the section “Flux prediction using ANN” (Figure 13). The calculations were described in Method S2 in the Supplementary Materials. The cost calculation for each reaction observed in the selection of enzymes could help to reduce cost. Figure 12 and Figure 13 show the variation in cost according to each balance and its flux and allow the selection of balances with higher flux at low cost.
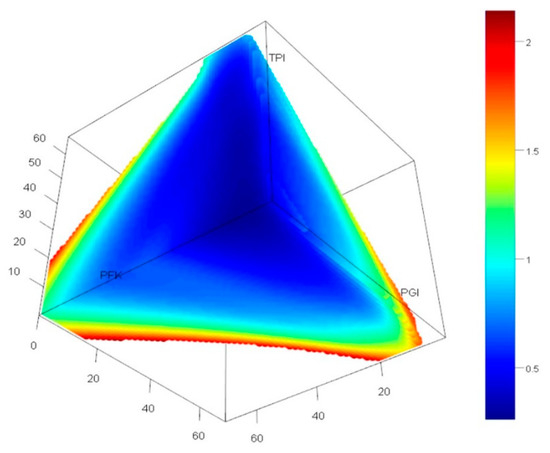
Figure 12.
3D-representation of cost estimated for all the enzyme concentrations generated. The color gradient is according to the cost required for each balance: blue is the lowest and red is the highest cost for a selected balance of the four enzymes PGI, PFK, FBA and TPI.
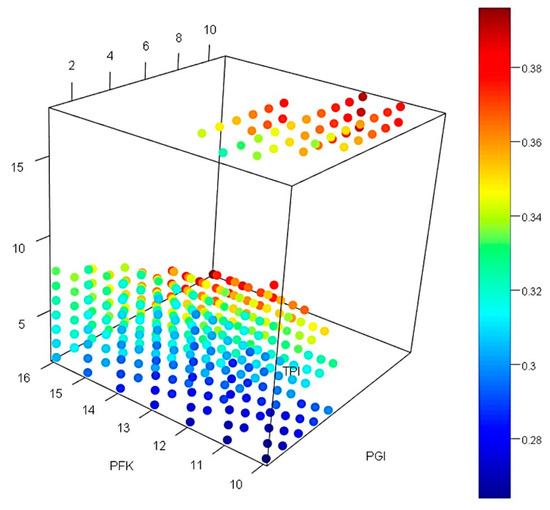
Figure 13.
3D-representation of the cost estimated for the enzyme concentration that obeys the rule obtained for higher flux values. The color gradient is according to the cost required for each balance, blue is the lowest and red is the highest cost for a selected balance of the four enzymes PGI, PFK, FBA and TPI.
As an example: the enzyme balance (in mg/L) with PGI = 2, PFK = 12, FBA = 81.24 and TPI = 4.66 (index 13 in Table S6 of the Supporting Information) could give a flux of 12.1 µM/s with a cost of 3.79 EUR.
4. Discussion
Traditionally, chemical molecules are synthesized by the chemical reaction of petroleum-based products. Due to the depletion of petroleum products, in-vivo biosynthesis has gained a lot of attention. Limitations of the cellular production system, such as low productivity, by-product formation, and low host cell tolerance to toxins moved the focus towards development of cell-free systems. Compared to cell systems, cell-free systems have high productivity and high toxin tolerance [22]. The selection of optimal enzyme concentrations for maximal productivity is a crucial step for industrial scale, cell-free production of biomolecules. The modeling of metabolic pathways helps to study and predict the behavior of the biological system. Constraint-based methods facilitate the understanding of the system but do not provide information about the concentration of the individual metabolites. In contrast, kinetic models provide information about individual metabolite concentrations but require kinetic parameters of enzymes, which are tedious and expensive to determine [32]. Design of experiment (DOE) is a systematic approach to optimize the conditions for biomolecule production in the field of biotechnology [63]. In DOE, multiple variables are studied to find the correlation between the variables and the final outcome. The main objective of DOE is to reduce the number of experiments, time and cost; our study has the same objective. The benefit of GC-ANN is that the objective optimum can be “out-of-the-box” but will nevertheless be found without additional experiments.
4.1. GC-ANN Approach Could be Used to Predict “Out-of-the-Box” Values
In this study, a new methodology, GC-ANN, to select the optimum enzyme balances for industrial biotechnology is devised. This approach aims to see beyond the “glass ceiling”, using an artificial neural network and different statistical methods like PCA and data classification. The method was designed and validated for the upper part of glycolysis but could be applied to any other natural or reconstituted biosynthesis pathway.
The workflow of the methodology used in the upper part of glycolysis is summarized in Figure 2. In the first step, for selecting the optimum concentrations of the four relevant enzymes PGI, PFK, FBA and TPI, a rule was devised for high flux values (supported by Figure 3, Figure 4 and Figure 5). We generated all possible balances using a step of 1 mg/L in terms of variation for each enzyme concentration. The balances newly generated in the present study have higher and lower limits than those in Fievet et al. [43]. These new enzyme balances were used to predict the flux through the upper glycolysis using ANN, and the predicted fluxes were depicted in 3D representation (Figure 6); we observed a zone (Figure 6, brown zone) with predicted flux > 12 µM/s. To explore this space in order to obtain even higher fluxes, the high-flux-rule was applied, i.e., 10 < PFK < 16; PGI < 11; TPI < 18; 59 < FBA (in mg/L), and 335 enzyme balances were scrutinized. The main idea behind our approach is based on the fact that: i. ANN is known to be a good tool for predicting class and/or quantitative values inside the box (i.e., prediction close to training data), ii. the brown region in Figure 6 contains values that are all very close to 12 µM/s (from 12 to 12.9 µM/s) because ANN is not useful for extrapolation and new predictions remain inside the box; and iii. we postulate that among these flux values, in fact, some could be higher than predicted.
In the second step, to validate our hypothesis we conducted in silico and in vitro experiments.
4.1.1. In-Silico Validation
Due to the availability of kinetic parameters, to avoid unnecessary expenses linked to in vitro assays:
First, we built a kinetic model. Figure 7 shows good agreement (R2 = 0.84) between the fluxes predicted by the kinetic model and all the flux values experimentally assessed by Fievet et al. [41]. Then, we selected 10 balances associated with experimental values between 0.74 and 12.9 µM/s of Fievet’s data for the benchmark study. Figure 9 shows excellent correlation with R2 of 0.99 and an RMSE of 0.17 between the predicted flux from our kinetic model and the experimental flux assessed by Fievet et al. Taken together, these first results were a good validation of our kinetic model.
Second, we intended to validate our in vitro assay by reproducing the results obtained by Fievet et al. [43]. We decided to carry out in vitro experiments for the balances that had a good correlation between simulated and experimental flux. The experimentally determined fluxes using the balances selected from the Fievet data were lower than those previously determined by these authors (Table S3). Nevertheless, the fold-increase was comparable (approximately 9-fold, this study vs. 13-fold, Fievet et al. [43]). The deviation of the absolute flux values could be attributed to experimental settings, i.e., NADH depletion assay in cuvettes at 390 nm (Fievet et al. [43]) vs. in 96 well plates at 365 nm, in this study; or to differences in the assays performed to measure kinetic parameters of the individual enzymes.
Finally, as our kinetic model has been validated, we used it to conduct the first verification, in silico, of our hypothesis. For 31 new balances selected according to the methodology described above (Section 3.3.2), Figure 10 shows how flux values predicted by the kinetic model fit with the simulated values. All the balances selected from the brown zone (Figure 6) were indeed superior to 12.0 µM/s. Moreover, the flux should be above 15.0 µM/s. So, this is a first, in silico, validation of our hypothesis, i.e., the ANN-based approach could be used to predict “out-of-the-box” values.
At this point, we had to keep in mind that this preliminary verification was conducted because the kinetic model was possible to establish, but this step is not mandatory in the proposed methodology. Indeed, the 31 balances were chosen first, based only on the outcome of GC-ANN methodology that combines ANN and different statistical methods like PCA and data classification.
4.1.2. In Vitro Validation
The 31 new enzyme balances were assessed experimentally. Table 3 proves our hypothesis: with careful selection of enzyme concentrations from the glass ceiling, it is possible to obtain higher flux values. For the 27 best enzyme balances, the improvement of flux ranged from 20% (observed flux: 15.4, original flux: 12.9) to 63% (observed flux: 21.0, original flux: 12.9). This clearly demonstrates that exploring the predicted values, which hit the “glass ceiling” using the GC-ANN approach is a good way to select the optimum enzyme concentration.
Since artificial neural networks do not require much information regarding experimental conditions, and particularly, in our case, kinetic parameters hard to obtain, they are easy to apply in different fields of science. Our GC-ANN approach could be applied to any pathway provided the experimental data are available. Currently, we are looking for other experimental datasets to which this methodology can be applied.
4.2. The Proposed Methodology Is Cost-Efficient
From an industrial perspective, production costs per quantity of product are very important. Choosing an enzyme balance that results in maximum flux at a very low cost per given quantity of product is essential. The ANN-based methodology makes it easy to estimate the total cost. The approximate price for each reaction was calculated using the details provided by the manufacturer, such as specific activity and units of enzyme in the sample. We could calculate the approximate cost required for 1 µM of product formation per second through the pathway. This would help us to decide which is the most suitable enzyme balance for maximum flux in terms of cost minimization, which is important for industrial-scale production. For example, to obtain a flux of 12.1 µM/s, the approximate cost should be 6.28 EUR, whereas we could achieve the same flux value with a cheaper rate of 3.79 EUR (40%). Figure 12 clearly shows how costs vary. Details are provided in Table S6 and Figure S1. Among the enzyme combinations selected for the validation of our methodology, PGI = 3, PFK = 16, FBA = 80.24 and TPI = 2.66 (mg/L) had an estimated flux value of 20.6 µM/s with the lowest cost of 0.197 EUR per µM of NADH consumed per second using GC-ANN methodology for the selection of enzyme balances (Figure S2). In contrast, the lowest price in Fievet et al. [43] with the selected balance PGI = 7, PFK = 12, FBA = 66.23 and TPI = 16.66 (mg/L) was 0.349 EUR per µM/s with an experimentally estimated flux value of 12.35 µM/s (Figure S2). This method, therefore, makes it possible to identify the production costs of 1 µM of product from 0.197 to 6.28 € in order to choose the best compromise between the cost and speed of the reaction.
Lastly and interestingly, the validated kinetic model makes it possible to generate a huge amount of data so as to feed our ANN-based model with more flux values from the newly predicted enzyme balances. This should be explored in future studies.
5. Materials and Methods
All enzymes as well as phosphocreatine, glucose-6-phosphate, fructose-6-phosphate and fructose-1,6-bisphosphate were purchased from Sigma-Aldrich (St. Louis, MO, USA). D-Glucose, ATP, NADH, and NADP were obtained from Carl Roth GmbH (Karlsruhe, Germany). Hexokinase (HK), phosphoglucoisomerase (PGI), triose-phosphate isomerase (TPI), and glucose-6-phosphate dehydrogenase (G6PDH) originated from baker’s yeast; fructose biphosphate aldolase (FBA), glycerol-3-phosphate dehydrogenase (G3PDH), and creatine kinase (CK) were obtained from rabbit muscle and phosphofructokinase (PFK) originated from Bacillus stearothermophilus. The enzymes were obtained as lyophilized powder except for PGI and TPI, which were ammonium sulphate suspensions. Detailed information on the enzymes used is provided in Table S1 of Supplementary Materials.
5.1. Determination of Protein Concentration
Protein concentrations were determined using the Bradford protein assay [64] from Bio-Rad Laboratories (Hercules, CA). Of the protein solutions 10 μL was mixed with 200 μL of Bio-Rad Protein Assay Dye Reagent, incubated for 5 minutes at room temperature, and the absorbance was measured spectrophotometrically at 595 nm. A dilution series of 0.06–0.5 mg/mL BSA (Carl Roth GmbH) was used for calibration.
5.2. Enzyme Assays for the Determination of Kinetic Parameters
Enzyme assays were performed in 96-well UV-STAR® microplates (Greiner Bio-One GmbH, Kremsmünster, Austria) in a total volume of 100 μL at 25 °C. The reaction buffer contained 50 mM PIPES (pH 7.5), 100 mM KCl, and 5 mM magnesium acetate. The cofactors for the reactions were 1 mM ATP and 1 mM NADH or NADP.
HK activity was measured with 0.05 U HK, 2.5 U G6PDH, and glucose concentrations from 10 to 0.01 mM. PGI activity was measured with 0.02–0.01 U PGI, 1–0.5 U PFK, 0.5 U FBA, 2 U G3PDH, 5 U TPI, and glucose 6-phosphate concentrations ranging from 30 to 0.03 mM. PFK activity was measured with 0.02 U PFK, 0.5 U FBA, 2 U G3PDH, 5 U TPI, and fructose 6-phosphate concentrations from 10 to 0.01 mM. FBA activity was measured with 0.01–0.05 U FBA, 2 U G3PDH, 5 U TPI, and fructose 1,6-phosphate concentrations from 10 to 0.01 mM. All reactions were monitored by recording the absorption at a wavelength of 340 nm (molar extinction coefficient ε340 nm, 25 °C 6.22 L mmol−1 cm−1). For calculation of the kinetic parameters Vmax, Km, and kcat we used Lineweaver-Burk as well as Eadie-Hofstee representations.
5.3. Flux Measurements
The total reaction volume of 100 μL contained fixed concentrations of 3 mM NADH, 20 mM phosphocreatine, 1 μM CK, 0.1 μM HK, and 1 μM G3PDH. The concentrations of PGI, PFK, FBA, and TPI were varied as indicated (Section 3.3.2). The reactions were started with 1 mM ATP and 100 mM glucose. Blank reactions contained all ingredients except ATP and glucose. Each condition was measured in triplicates. The NADH decay was monitored every 3 s at 365 nm using a SynergyMxSMATBLD(+) Gen5 SW plater reader (SZABO-SCANDIC, Vienna, Austria). The slope of NADH decay was measured as the flux through the pathway (molar extinction coefficient ε365 nm, 25 °C 3.4 L mmol−1 cm−1).
6. Conclusions
The selection of enzymes is an important step in the production of biomolecules. Methods based on homology are widely used to select the best performing enzymes. In addition, the selection of optimum enzyme balances is also crucial. Most methods use kinetic information for concentration selection via modeling. However, the determination of kinetic parameters is not always easy; therefore, developing new methodologies for selecting the optimum enzyme balances is of great interest.
In this study, we developed a new approach, GC-ANN, which uses an artificial neural network along with different statistical methods (PCA and data classification) to select enzyme balances that improve the flux as well as the costs. The selected balances might not be the balances with the highest flux, but they would be among the best. This approach allows cost-efficient selection of enzyme balances using a small existing dataset, and it opens the door for rapid optimization of cell-free systems in an industrial environment.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4344/10/3/291/s1, Figure S1: The cost predicted (in EUR) for the four-enzyme concentration (PGI, PFK, FBA, and TPI) selected for experimental validation. The blue is lowest, to highest in red; Figure S2: The cost predicted (in EUR) for the four-enzyme concentration (PGI, PFK, FBA, and TPI) selected by Fievet et al. (2006). The blue is lowest, to highest in red; Table S1: Enzymes used in this study for the upper part of glycolysis. All enzymes were from Sigma; Table S2: The measured enzyme activities for the enzymes involved in the upper part of glycolysis (see also Table 2 in the main text); Table S3: The enzyme concentrations (mg/L) predicted from ANN and in-silico modeling to have higher flux values. For the experimental validation, we used relative concentrations of enzymes obtained as explained in Method S1; Table S4: Specification of enzymes used for the calculation of cost for the preparatory stage of glycolysis from sigma. Specific activities are calculated by Fievet et al; Table S5: Comparison of flux predicted between Fievet et al. selected concentration (JFievet) and new estimation during current work (Jobs); Table S6: The calculated price for the µM of NADH consumed per second by the enzyme concentration selected for the experiment; Methods S1: concentration based on relative activity; Method S2: Cost Calculation.
Author Contributions
F.C., C.D. and P.C. designed the method. A.A.N., P.C., X.F.C., N.F., M.D., B.W., A.V., B.O., C.D., B.G.-P. and F.C. participated in the design of the study and performed the analysis. A.A.N. and M.D. wrote algorithms. A.A.N., P.C., X.F.C., C.D. and F.C. wrote and corrected the manuscript. All authors read and approved the final version of the manuscript.
Funding
AAN is supported by a PhD grant from the Region Reunion and European Union (FEDER) under European operational program INTERRG V-2014-2020, file number 20161449, tiers 234273. We gratefully acknowledge support from: i. the Federal Ministry for Digital and Economic Affairs (bmwd), the Federal Ministry for Transport, Innovation and Technology (bmvit), the Styrian Business Promotion Agency SFG, the Standortagentur Tirol, Government of Lower Austria and ZIT—Technology Agency of the City of Vienna through the COMET-Funding Program managed by the Austrian Research Promotion Agency FFG.; ii. Peaccel via a research program co-funded by the European Union (UE) and Region Reunion (FEDER). The funding agencies had no influence on the research process.
Conflicts of Interest
Authors declare no conflict of interest.
Availability of Data and Materials
R-scripts used for the analysis are found at https://github.com/DSIMB/GC-ANN-Enzyme-Concentration-Selection.
References
- Borgia, J.A.; Fields, G.B. Chemical synthesis of proteins. Trends Biotechnol. 2000, 18, 243–251. [Google Scholar] [CrossRef]
- Hojo, H. Recent progress in the chemical synthesis of proteins. Curr. Opin. Struct. Biol. 2014, 26, 16–23. [Google Scholar] [CrossRef]
- Liu, F.; Zaykov, A.N.; Levy, J.J.; Dimarchi, R.D.; Mayer, J.P. Chemical synthesis of peptides within the insulin superfamily. J. Pept. Sci. 2016, 22, 260–270. [Google Scholar] [CrossRef] [PubMed]
- Graf, M.; Mardirossian, M.; Nguyen, F.; Seefeldt, A.C.; Guichard, G.; Scocchi, M.; Innis, C.A.; Wilson, D.N. Proline-rich antimicrobial peptides targeting protein synthesis. Nat. Prod. Rep. 2017, 34, 702–711. [Google Scholar] [CrossRef] [PubMed]
- Arora, K.; Program, B.; Arbor, A. Total Synthesis of Glycosylated Proteins Alberto; Springer: Berlin/Heidelberg, Germany, 2015; Volume 200, pp. 165–187. [Google Scholar]
- Zhang, Y.H.P. Renewable carbohydrates are a potential high-density hydrogen carrier. Int. J. Hydrogen Energy 2010, 35, 10334–10342. [Google Scholar] [CrossRef]
- Yim, H.; Haselbeck, R.; Niu, W.; Pujol-Baxley, C.; Burgard, A.; Boldt, J.; Khandurina, J.; Trawick, J.D.; Osterhout, R.E.; Stephen, R.; et al. Metabolic engineering of Escherichia coli for direct production of 1,4-butanediol. Nat. Chem. Biol. 2011, 7, 445–452. [Google Scholar] [CrossRef]
- Martínez, J.A.; Bolívar, F.; Escalante, A. Shikimic Acid Production in Escherichia coli: From Classical Metabolic Engineering Strategies to Omics Applied to Improve Its Production. Front. Bioeng. Biotechnol. 2015, 3, 1–16. [Google Scholar] [CrossRef]
- Lee, J.W.; Na, D.; Park, J.M.; Lee, J.; Choi, S.; Lee, S.Y. Systems metabolic engineering of microorganisms for natural and non-natural chemicals. Nat. Chem. Biol. 2012, 8, 536–546. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Wang, Y.; Dong, X.; Hu, G.; Liu, L. Engineering rTCA pathway and C4-dicarboxylate transporter for l-malic acid production. Appl. Microbiol. Biotechnol. 2017, 101, 4041–4052. [Google Scholar] [CrossRef]
- Stanton, D. Microbial or Mammalian? Biosilta Backs the Former Licensing E. Coli platform. Biopharma Reporter. Available online: https://www.biopharma-reporter.com/Article/2016/04/08/Microbial-or-mammalian-BioSilta-licenses-E.-Coli-tech (accessed on 20 February 2020).
- Theisen, M.; Liao, J.C. Industrial Biotechnology: Escherichia coli as a Host. Ind. Biotechnol. 2016, 1, 149–181. [Google Scholar]
- Zhang, Y.H.P. Substrate channeling and enzyme complexes for biotechnological applications. Biotechnol. Adv. 2011, 29, 715–725. [Google Scholar] [CrossRef]
- Wheeldon, I.; Minteer, S.D.; Banta, S.; Barton, S.C.; Atanassov, P.; Sigman, M. Substrate channelling as an approach to cascade reactions. Nat. Chem. 2016, 8, 299–309. [Google Scholar] [CrossRef]
- Tan, S.Z.; Prather, K.L. Dynamic pathway regulation: Recent advances and methods of construction. Curr. Opin. Chem. Biol. 2017, 41, 28–35. [Google Scholar] [CrossRef]
- Fontaine, N.; Grondin-Perez, B.; Cadet, F.; Offmann, B. Modeling of a Cell-Free Synthetic System for Biohydrogen Production. J. Comput. Sci. Syst. Biol. 2015, 8, 132–139. [Google Scholar]
- Ye, X.; Wang, Y.; Hopkins, R.C.; Adams, M.W.W.; Evans, B.R.; Mielenz, J.R.; Zhang, Y.H.P. Spontaneous high-yield production of hydrogen from cellulosic materials and water catalyzed by enzyme cocktails. ChemSusChem 2009, 2, 149–152. [Google Scholar] [CrossRef]
- Khattak, W.A.; Ul-Islam, M.; Ullah, M.W.; Yu, B.; Khan, S.; Park, J.K. Yeast cell-free enzyme system for bio-ethanol production at elevated temperatures. Process. Biochem. 2014, 49, 357–364. [Google Scholar] [CrossRef]
- Zhang, Y.H.P. Production of biofuels and biochemicals by in vitro synthetic biosystems: Opportunities and challenges. Biotechnol. Adv. 2015, 33, 1467–1483. [Google Scholar] [CrossRef]
- Huang, L.; Sheng, J.; Xu, Z.; Zhu, X.; Cai, J. Reconstitution of the peptidoglycan cytoplasmic precursor biosynthetic pathway in cell-free system and rapid screening of antisense oligonucleotides for Mur enzymes. Appl. Microbiol. Biotechnol. 2014, 98, 1785–1794. [Google Scholar]
- Yang, J.; Voloshin, A.; Swartz, J.R.; Velkeen, H.; Levy, R.; Michel-Reydellet, N. Rapid expression of vaccine proteins for B-cell lymphoma in a cell-free system. Biotechnol. Bioeng. 2005, 89, 503–511. [Google Scholar] [CrossRef]
- Lu, Y. Cell-free synthetic biology: Engineering in an open world. Synth. Syst. Biotechnol. 2017, 2, 23–27. [Google Scholar] [CrossRef]
- Schoborg, J.A.; Hodgman, C.E.; Anderson, M.J.; Jewett, M.C. Substrate replenishment and byproduct removal improve yeast cell-free protein synthesis. Biotechnol. J. 2014, 9, 630–640. [Google Scholar] [CrossRef]
- Shrestha, P.; Holland, T.M.; Bundy, B.C. Streamlined extract preparation for Escherichia coli-based cell-free protein synthesis by sonication or bead vortex mixing. Biotechniques 2012, 53, 163–174. [Google Scholar] [CrossRef]
- Zhang, Y.-H.P. Production of biocommodities and bioelectricity by cell-free synthetic enzymatic pathway biotransformations: Challenges and opportunities. Biotechnol. Bioeng. 2009, 105, 663–677. [Google Scholar] [CrossRef]
- Carbonell, P.; Wong, J.; Swainston, N.; Takano, E.; Turner, N.J.; Scrutton, N.S.; Kell, D.B.; Breitling, R.; Faulon, J.-L. Selenzyme: Enzyme selection tool for pathway design. Bioinformatics 2018, 34, 2153–2154. [Google Scholar] [CrossRef]
- Stelling, J. Mathematical models in microbial systems biology. Curr. Opin. Microbiol. 2004, 7, 513–518. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.O. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef]
- Covert, M.W.; Famili, I.; Palsson, B.O. Identifying Constraints that Govern Cell Behavior: A Key to Converting Conceptual to Computational Models in Biology? Biotechnol. Bioeng. 2003, 84, 763–772. [Google Scholar] [CrossRef]
- Smallbone, K.; Simeonidis, E.; Broomhead, D.S.; Kell, D.B. Something from nothing-Bridging the gap between constraint-based and kinetic modelling. FEBS J. 2007, 274, 5576–5585. [Google Scholar] [CrossRef]
- Schmeier, S.; Hakenberg, J.; Klipp, E.; Leser, U.; Kowald, A. Finding Kinetic Parameters Using Text Mining. Omi. A J. Integr. Biol. 2004, 8, 131–152. [Google Scholar]
- Bisswanger, H. Enzyme assays. Perspect. Sci. 2014, 1, 41–55. [Google Scholar] [CrossRef]
- Teusink, B.; Passarge, J.; Reijenga, C.A.; Esgalhado, E.; van der Weijden, C.C.; Schepper, M.; Walsh, M.C.; Bakker, B.M.; van Dam, K.; Westerhoff, H.V.; et al. Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry. Eur. J. Biochem. 2000, 267, 5313–5329. [Google Scholar] [CrossRef] [PubMed]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods. 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Morowvat, M.H.; Ghasemi, Y. Medium optimization by artificial neural networks for maximizing the triglycerides-rich lipids from biomass of Chlorella vulgaris. Int. J. Pharm. Clin. Res. 2016, 8, 1414–1417. [Google Scholar]
- Lan, Z.; Zhao, C.; Guo, W.; Guan, X.; Zhang, X. Optimization of culture medium for maximal production of spinosad using an artificial neural network-genetic algorithm modeling. J. Mol. Microbiol. Biotechnol. 2015, 25, 253–261. [Google Scholar] [CrossRef]
- Antoniewicz, M.R.; Stephanopoulos, G.; Kelleher, J.K. Evaluation of regression models in metabolic physiology: Predicting fluxes from isotopic data without knowledge of the pathway. Metabolomics 2006, 2, 41–52. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.; Shin, H.D.; Liu, L.; Du, G.; Chen, J. Protein and metabolic engineering for the production of organic acids. Bioresour. Technol. 2017, 239, 412–421. [Google Scholar] [CrossRef]
- Song, C.W.; Kim, D.I.; Choi, S.; Jang, J.W.; Lee, S.Y. Metabolic engineering of Escherichia coli for the production of fumaric acid. Biotechnol. Bioeng. 2013, 110, 2025–2034. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Z.; Zhu, N.; Wang, B.; Chen, T.; Zhao, X. Metabolic engineering of Escherichia coli and in silico comparing of carboxylation pathways for high succinate productivity under aerobic conditions. Microbiol. Res. 2014, 169, 432–440. [Google Scholar] [CrossRef]
- Clomburg, J.M.; Gonzalez, R. Biofuel production in Escherichia coli: The role of metabolic engineering and synthetic biology. Appl. Microbiol. Biotechnol. 2010, 86, 419–434. [Google Scholar] [CrossRef]
- Yang, X.; Xu, M.; Yang, S.T. Metabolic and process engineering of Clostridium cellulovorans for biofuel production from cellulose. Metab. Eng. 2015, 32, 39–48. [Google Scholar] [CrossRef]
- Fiévet, J.B.; Dillmann, C.; Curien, G.; de Vienne, D. Simplified modelling of metabolic pathways for flux prediction and optimization: Lessons from an in vitro reconstruction of the upper part of glycolysis. Biochem. J. 2006, 396, 317–326. [Google Scholar] [CrossRef][Green Version]
- Ajjolli Nagaraja, A.; Fontaine, N.; Delsaut, M.; Charton, P.; Damour, C.; Offmann, B.; Grondin-Perez, B.; Cadet, F. Flux prediction using artificial neural network (ANN) for the upper part of glycolysis. PLoS ONE 2019, 14, 1–15. [Google Scholar] [CrossRef]
- Minns, A.W.; Hall, M.J. Artificial neural networks as rainfall- runoff models. Hydrol. Sci. J. 1996, 41, 399–417. [Google Scholar] [CrossRef]
- Balabin, R.M.; Smirnov, S.V. Interpolation and extrapolation problems of multivariate regression in analytical chemistry: Benchmarking the robustness on near-infrared (NIR) spectroscopy data. Analyst 2012, 137, 1604–1610. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal Component Analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Ringnér, M. What is principal component analysis? Nat. Biotechnol. 2008, 26, 303–304. [Google Scholar] [CrossRef]
- Le, S.; Josse, J.; Husson, F. FactoMineR: An R Package for Multivariate Analysis. J. Stat. Softw. 2008, 25, 1–18. [Google Scholar] [CrossRef]
- Soetaert, K. plot3D: Plotting Multi-Dimensional Data, 2017. Available online: https://CRAN.R-project.org/package=plot3D (accessed on 2 March 2020).
- Soetaert, K. plot3Drgl: Plotting Multi-Dimensional Data-Using “rgl”. 2016. Available online: https://CRAN.R-project.org/package=plot3Drgl (accessed on 2 March 2020).
- Weihs, C.; Ligges, U.; Luebke, K.; Raabe, N. klaR Analyzing German Business Cycles. In Data Analysis and Decision Support; Baier, D., Decker, R., Schmidt-Thieme, L., Eds.; Springer-Verlag: Berlin, Germany, 2005; pp. 335–343. [Google Scholar]
- Therneau, T.; Atkinson, B.; Ripley, B. rpart: Recursive Partitioning and Regression Trees. R Package 2018, 4, 1–9. [Google Scholar]
- Günther, F.; Fritsch, S. Neuralnet: Training of Neural Networks. R. J. 2010, 2, 30–38. [Google Scholar] [CrossRef]
- Funahashi, A.; Morohashi, M.; Kitano, H.; Tanimura, N. CellDesigner: A process diagram editor for gene-regulatory and biochemical networks. Biosilico 2003, 1, 159–162. [Google Scholar] [CrossRef]
- Funahashi, A.; Matsuoka, Y.; Jouraku, A.; Morohashi, M.; Kikuchi, N.; Kitano, H. CellDesigner 3.5: A Versatile Modeling Tool for Biochemical Networks. Proc IEEE. 2008, 96, 1254–1265. [Google Scholar] [CrossRef]
- Schomburg, I.; Chang, A.; Schomburg, D. BRENDA, enzyme data and metabolic information. Nucleic. Acids Res. 2002, 30, 47–49. [Google Scholar] [CrossRef]
- Lee, C.; Pahle, J.; Singhal, M.; Gauges, R.; Sahle, S.; Mendes, P.; Kummer, U.; Hoops, S. COPASI—A COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar]
- BRENDA-Information on EC 2.7.1.1-hexokinase. Available online: https://www.brenda-enzymes.org/enzyme.php?ecno=2.7.1.1 (accessed on 22 May 2019).
- BRENDA-Information on EC 5.3.1.9-glucose-6-phosphate isomerase. Available online: https://www.brenda-enzymes.org/enzyme.php?ecno=5.3.1.9 (accessed on 22 May 2019).
- BRENDA-Information on EC 2.7.1.11-6-phosphofructokinase. Available online: https://www.brenda-enzymes.org/enzyme.php?ecno=2.7.1.11 (accessed on 22 May 2019).
- BRENDA-Information on EC 4.1.2.13-fructose-bisphosphate aldolase. Available online: https://www.brenda-enzymes.org/enzyme.php?ecno=4.1.2.13 (accessed on 22 May 2019).
- Kumar, V.; Bhalla, A.; Rathore, A.S. Design of experiments applications in bioprocessing: Concepts and approach. Biotechnol. Prog. 2014, 30, 86–99. [Google Scholar] [CrossRef]
- Bradford, M.M. A rapid and sensitive method for the quantitation of microgram quantities of protein utilizing the principle of protein-dye binding. Anal. Biochem. 1976, 72, 248–254. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).