The aggregate results show that people differentiate among charities. We now focus on the relationship between subjects’ characteristics and their donation behavior. First, we use the comparative dictator game (CDG) subject-level panel to analyze the full sample. Second, we break the regressions apart by CDG level to investigate level-specific heterogeneous behavior among characteristics. Third, we discuss the consistent givers who gave the same amount to each recipient level. Last, we examine what subjects choose in the SDG and offer explanations for this behavior.
4.1. Comparative Dictator Game: Pooled Sample
Donating behavior was truncated between (
$0,
$60), so we use a Tobit model to account for subjects who might have preferred to give less than
$0 or more than
$60 in the absence of this restriction. We use four different specifications to evaluate the relationship between these characteristics and giving
where
is a vector of level controls (state, local, and person);
is a vector of demographic variables (age, male, high church attendance, college, and low income); and
is a vector of our constructed trust indices (government and people).
is the subject-specific error term.
will capture any level-specific differences in giving, independent of demographics, with state as the control variable. Based on
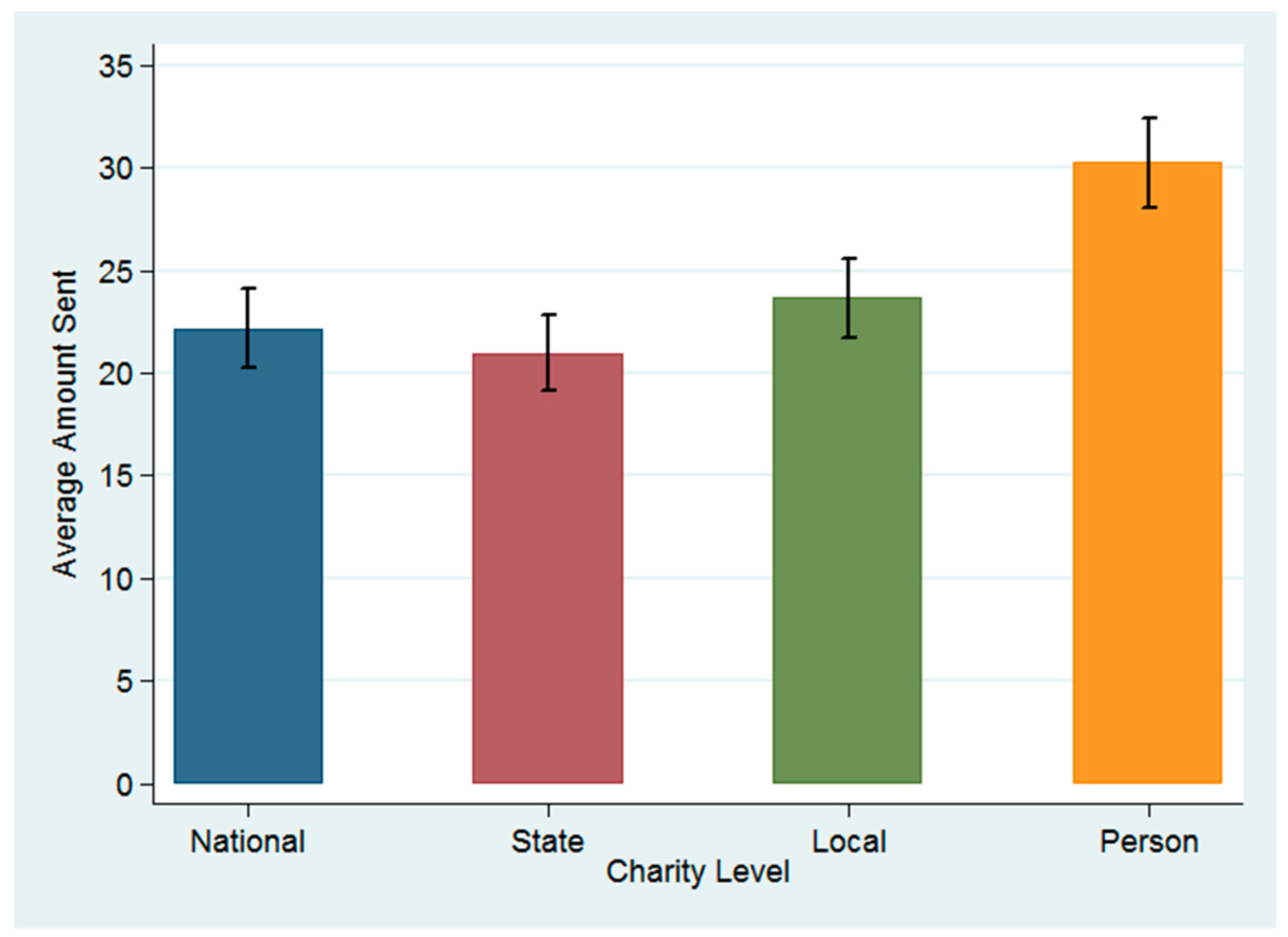
Figure 3 and Panel A of
Table A1, we expect the coefficients on national, local, and person to be positive and significant.
There is a large, existing, literature on individual differences in altruistic behavior in the lab, typically measured by variations on dictator games. Gender has been extensively studied: in standard dictator games, where the recipient is an anonymous individual, women give more than men [
17,
18], although the gender difference may reverse if the relative price of giving is sufficiently low [
19]. In “real donation” experiments [
2], women also tend to give more than men, though this difference may vary by context. Two papers survey studies of charitable giving across methodologies and summarize findings on many factors including gender, age, education, religiosity, etc. [
20,
21]. Age, education, and income are consistently positively correlated with giving, but gender and religiosity show mixed results. From this literature, we predict age, education, and household income will have a consistent, significant, positive effect on giving. Since the literature is not entirely clear on how our other demographic covariates correlate with dictator game decisions, especially across each of our three non-human recipients (charities), we use the summary information in Panel B of
Table A1 to guide our predictions: we expect gender and our measures of religiosity to have no effect. Though race is commonly and reasonably included as a control variable, our sample is predominantly white and therefore does not have enough variation to detect any racial effects. Including race in the analysis did not meaningfully change our results in any way.
The results for Specifications (1)–(4) are displayed in
Table 4. The state-level charity is omitted for comparison. Consistent with the identifiable victim literature and Hypothesis 1, the coefficient on the person in town is significant and large in all specifications: subjects give considerably more to the person than to other levels (e.g., subjects give on average
$11.50 more than to the state organization). We conclude from this that when an individual is included in the consideration set the relative impact of a donation becomes more salient than its geographic reach, in comparison to giving to other (organization) recipients.
Hypothesis 2 posits that the organizations will be considered differently than the individual recipient and, following [
7], we will observe donation magnitude to correlate with organizations’ reach. We do not find consistent support for this hypothesis in
Table 4. Subjects tend to give more to the national (
$1.58) and local (
$3.34) charities than to the state charity. Importantly, our full model (4) shows subjects giving a statistically significant amount more to every level than to state.
This causes a U-shaped giving curve across geographic level of operation. The relationship between ‘National’ and ‘State’ is consistent with [
7] but the relationship between ‘State’ and ‘Local’ is exactly the opposite. There are two potential explanations for this difference: sample composition and consideration set. Our sample consists of adults aged 18–86 (mean of 45.48) instead of students, which (under Hypothesis 3b) we believe affects beliefs about the effectiveness of organizations operating at each level that informs charitable behavior. We test this more formally below. Another potential explanation is that we have added an individual to the subjects’ consideration set. Though each decision was made independently, simply adding the individual could affect how subjects consider giving to the other charities, possibly by shifting some internal reference point. We do not claim this as fact but offer it as conjecture, as our experiment is not designed to test how an additional recipient in the consideration set affects reference points.
There is markedly little evidence of significant demographic effects on giving across these specifications. Consistent with the literature and Hypothesis 3b, age is consistently positive and significant (
p < 0.01) and economically meaningful: 10 additional years of age corresponds to a
$2.40–
$2.50 increase in giving. Considering our sample spans ages 18–84 there is room for considerable differences in giving behavior.
3 Men give slightly less than women, but the difference is insignificant. Church attendance (religiosity) has a weak positive relationship to giving behavior here, which is possibly driven by giving to the Salvation Army (a religiously affiliated charity). People earning less than
$30,000 a year give less than those earning more but not in a statistically meaningful way. Having at least some college education is negatively correlated with the amount given. Though this relationship is not statistically significant (
p < 0.1), the sign is counterintuitive: education is typically positively correlated with giving.
Columns 3 and 4 include the trust survey measures, which are a preliminary test of Hypothesis 3a. Trust in institutions does not have a significant effect on giving. Trust in people, however, has an economically and statistically significant relationship with giving across both specifications: when accounting for other factors, an additional point increase in trusting people corresponds to approximately a $5 increase in sending (p < 0.01). We do not draw any definitive conclusions on Hypothesis 3a from these results, because we suspect that these indices will have a clearer relationship with giving when analysis is disaggregated. Still, it is surprising that “Trust in People” has an effect on the pooled data because it is likely to be isolated to lower levels (local and person). This suggests that people who score high on this index either always give large amounts (to all levels) or the effect is so strong in the lower levels that it is not washed out by pooling the data. Results below suggest that the former explanation is correct.
As discussed above, subjects gave approximately $10 more to the individual than any other level. This supports the importance of impact over reach when giving to an identifiable victim. Beyond this, however, rejecting Hypothesis 2 means impact and reach are related to each other. Subjects likely respond to some mixture of these two factors heterogeneously at each level, so we now turn to the disaggregated analysis.
4.2. Comparative Dictator Game: Disaggregated Analysis
We retain similar Tobit models as in
Section 4.1, but restrict each specification by level (
j) which necessarily means we no longer include level controls:
where
and
are the demographics and trust indices vectors defined as above for each level
j and
is the subject-level specific error term. The results for Equation (7) are displayed in
Table 5. Results for Specifications (5) and (6) are not meaningfully different from (7) and are available in
Table A2 in the
Appendix A.
As with the aggregate analysis, age has a persistent, significant, positive relationship with giving, further confirming Hypothesis 3b. Across all levels, an additional 10 years corresponds to sending between
$2.10–
$3.32 more. Surprisingly, when controlling for all factors this age effect is strongest with the state-level charity. This likely means that though it is important that our sample includes adults, the sample’s age composition is not the primary driver behind our U-shaped giving curve and, therefore, our contradiction with [
7].
There is also level-specific heterogeneity in other demographic characteristics. Consistent with the findings from
Section 4.1, the coefficients on gender, church attendance, and income are not statistically distinguishable from zero at the national, state, or local level. This changes when people make allocation decisions with a person. Subjects with high church attendance give
$7.56 more (
p < 0.05), on average, to a person than subjects with low church attendance, when including all relevant covariates. This further supports our conclusion that measuring organization-level preferences are not confused with
organization preferences in our experiment (e.g., religious subjects do not display a preference for the Salvation Army
because it is a religious organization).
Subjects who make less than $30,000 a year give $6.38 less (p < 0.05), on average, than subjects with a higher income. This implies that the identifiable victim effect is stronger for people with higher church attendance and higher incomes. Likewise, this implies that, if reach is a dimension on which subjects make charitable decisions, it is uncorrelated with most demographics or, at least, they do not systematically move together (i.e., men do not systematically value the reach of national over state charities more than women). The coefficient on college education is negative and significant (p < 0.05) at the national level, meaning that subjects with more education gave approximately $5 less to the national level charity. There is no such effect at other levels, with the exception of column 4 results (though this effect goes away when including our trust indices in column 6). This implies there is some relationship between education and beliefs about the efficacy of national-level charities. Since education is almost always an endogenous choice, we do not make any causal claims.
The trust indices offer additional insights. In columns 2 and 3, we observe that an additional point on the institutional trust index corresponds to sending approximately
$5 more to the national charity (
p < 0.01). This means that an increased trust in institutions is meaningfully expressed in giving behavior, supporting Hypothesis 3a that subjects hold underlying beliefs about the efficiency of different charity-levels. Contrary to Hypothesis 3a, institutional trust does not carry over to affect giving to the state charity. Consistent with intuition, however, the magnitude of the institutional trust effect monotonically diminishes as the recipient becomes ‘closer’ to the subject where ‘trust in people’ instead takes over as the operating behavioral mechanism. The institutional trust index is uncorrelated with political party affiliation (covariance = 0.0687) or political ideology (covariance = 0.0533), and the effect documented in
Table 4 is unchanged by the inclusion of party and ideology controls.
The coefficient on the index for trusting in people is similarly consistent with intuition and Hypothesis 3a. An increased trust in people (by one point on our index) corresponds to a
$6.70,
$6.40, and
$6.43 increase in giving to the state charity (
p < 0.01), local charity (
p < 0.01), and person (
p < 0.05), respectively, when controlling for other demographic characteristics. As noted in
Section 4.1, subjects who score higher on the ‘people trust’ measurement likely give more in general, though it is apparently limited to ‘lower level’ recipients. We would expect a trust in people to most strongly affect giving to a person, but interestingly it does not. This is likely because other factors take over at the person level (religiosity or income). Overall, we find strong support for Hypothesis 3a between our two trust indices with a slight modification—beliefs about how trustworthy institutions and people are map into donative behavior in a statistically significant way.
4.4. Selected Dictator Game
We now turn to the selected dictator game (SDG), the second task, where subjects chose one recipient out of the four levels from the CDG. If the SDG was selected for payment, subjects received the allocation for their chosen level from the CDG, with the remainder going to the selected organization. Subjects were unaware of the SDG when making allocation decisions in the CDG. The SDG is a form of revealed preference. However, it has three implications. First, it can indicate which charity the subject most prefers, independent of their allocation choice. Second, it could reveal an income-enhancing preference in which subjects chose the charity to which they gave the least (thereby maximizing what they earned if the task were selected for payment). Finally, it could reveal the subject’s desire to maximize their contribution to a charity in which the subject chose the charity to which they gave the most. Disentangling this from the first implication is difficult except for those subjects who always gave the same amount to each charity. As stated in Hypothesis 4 and consistent with [
3], we expect subjects to be income-enhancing and choose the charity to which they gave the least in the CDG.
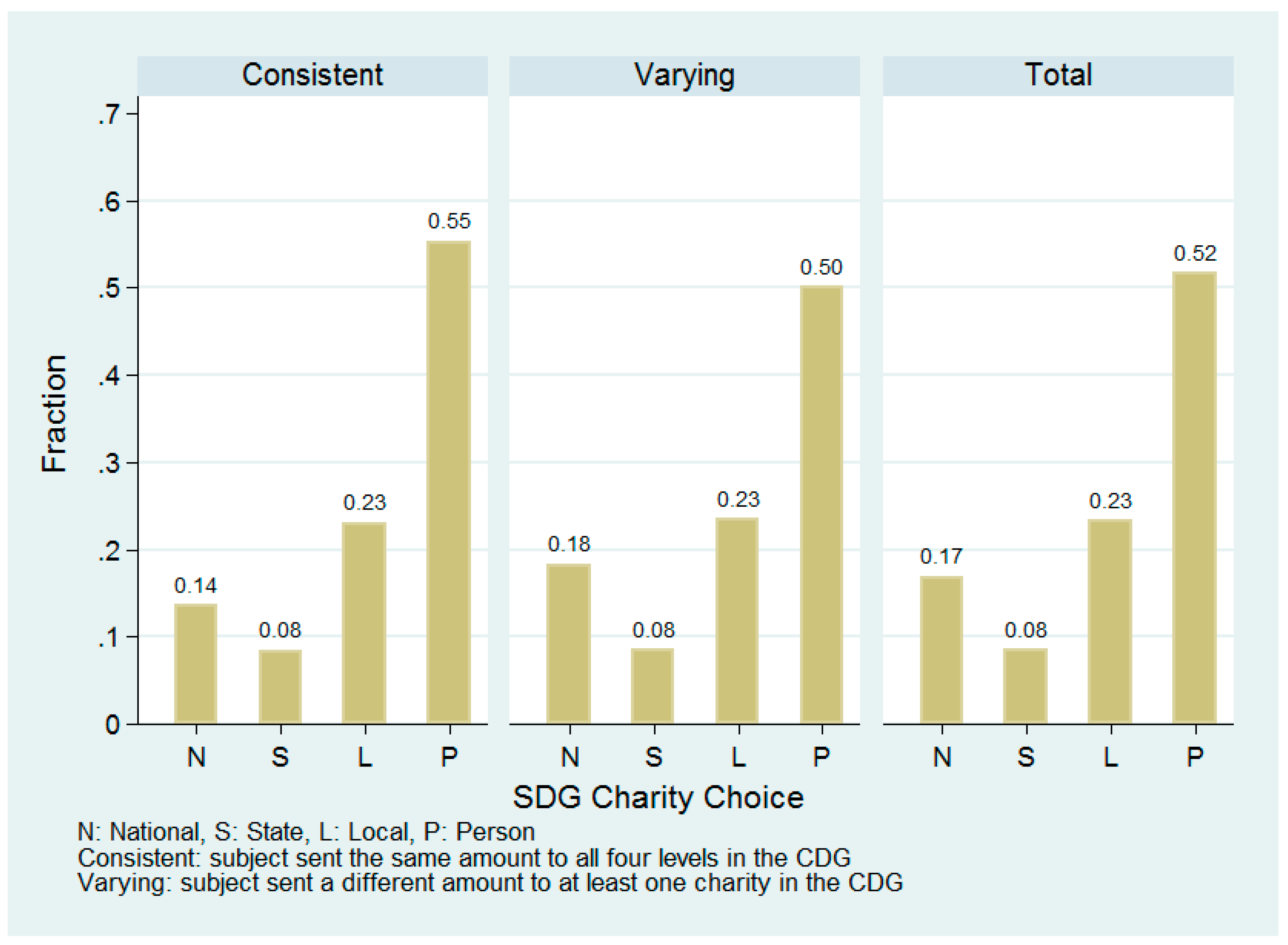
Figure 4 shows what proportion of subjects chose each level (panel C), as well as the distributions for consistent givers who gave the same amount in each decision (panel A) and varying givers who gave different amounts to each organization (panel B). Consistent with giving patterns observed in
Section 4.1, the majority of subjects prefer the individual person to be the recipient followed by local, national, and then state charities. Revealed preference theory tells us that consistent givers are indifferent between each of the levels. If that were true, we should see a uniform distribution in panel A. Not only is the consistent givers’ distribution not uniform, but it is remarkably similar to the varying givers’ and total distributions. This implies that consistent givers are not truly indifferent between levels and are not so different from varying givers but have a similar behavioral response mechanism (weighing impact and reach).
Following the results from
Section 4.2, there are plausibly heterogeneous preferences for SDG choice by demographic characteristics. For example, if people who attend church more give more to a person recipient, we can hypothesize that they will also be more likely to choose that level in the SDG. We test these choice and demographic relationships using an ordered logit model. We are interested in estimating the probability of choosing each level given some control variables, or
, where
and
are defined as above and
is a vector containing the amount each subject sent to each level and
is defined as
we calculate this using the latent variable models
An ordered logit model is particularly well-suited for this estimation because our charities’ levels retain a natural ordering (where 1 = national, 2 = state, 3 = local, and 4 = individual). Estimating this model gives us the predicted probability that subject
i selects charity
j from their decisions in the CDG, conditional on their characteristics (i.e., age, gender, church attendance, income, education), their trust indices, and the amounts they sent to each level. The results are displayed in
Table 7.
We find little evidence of demographics influencing charity choice in the SDG. The only variable that is significant at conventional levels is age: There is a negative relationship between age and the level chosen (p < 0.05), meaning that older persons are less likely to select local organizations.
We now turn to the analysis testing Hypothesis 4. In their CDG study, [
3] observed this purely selfish behavior. They argue that subjects must compete internally between financial self-interest and the desire to feel charitable by giving some amount away, and show that in their case, financial self-interest ultimately overpowered subjects’ altruism. We do not observe this: the coefficients on the donations to each recipient are small and statistically insignificant, and uncorrelated with their choice in the SDG.
We examine this more closely in
Table 8 and
Figure 5. We restrict our analysis here to varying givers only, since the minimum and maximum charities are equivalent for consistent givers.
Table 8 is a tabulation of how many subjects chose each level in the SDG and breaks this down by those who chose the charity where they sent the least (min charity) and the most (max charity). We define a subject’s min (max) charity as the recipient to which they gave less (greater) than or equal to the next lowest (highest) amount sent to all other recipients by that subject.
Figure 5 shows this information as a percentage of the total within each panel. For example, 23.73% (69.05%) of the subjects who chose their min (max) charity in the SDG selected the ‘person’ level.
Table A5 in
Appendix A shows probit results for the probability of choosing the min (columns 1–2) and max (columns 3–4) charity for each of our main covariates (demographics and indices).
Table 8 shows that substantially more people chose their max charity (126) in the SDG than their min charity (59). This further supports the rejection of our Hypothesis 4.
Additional analysis (see columns 1 and 2 of
Table A5) show that no socio-demographic variables are correlated with the probability of choosing one’s min charity in the SDG. The coefficient on the people trust index is negative and statistically significant (
p < 0.05): An additional point of trust on the index corresponds to a 36.2% decrease in the probability of choosing the min charity. This is unsurprising given the strong, positive relationship between this index and the amount sent (as described in
Table 5). Those with higher trust in people are likely much more generous donors. They are not so altruistic, however, as to choose the max charity as shown in column 4. The coefficient on the people trust index is positive but is not significant at conventional levels (
p < 0.1). Interestingly, men are much more likely than women (54%,
p < 0.01) to choose their max charity in the SDG. This is surprising considering there were no gender differences in the amounts given across levels. Furthermore, the literature typically posits women as behaving more altruistically than men while we find the opposite here.