Learning Dynamics and Norm Psychology Supports Human Cooperation in a Large-Scale Prisoner’s Dilemma on Networks

Abstract

In this work, we explore the role of learning dynamics and social norms in human cooperation on networks. We study the model recently introduced in [Physical Review E, 97, 042321 (2018)] that integrates the well-studied Experience Weighted Attraction learning model with some features characterizing human norm psychology, namely the set of cognitive abilities humans have evolved to deal with social norms. We provide further evidence that this extended model—that we refer to as Experience Weighted Attraction with Norm Psychology—closely reproduces cooperative patterns of behavior observed in large-scale experiments with humans. In particular, we provide additional support for the finding that, when deciding to cooperate, humans balance between the choice that returns higher payoffs with the choice in agreement with social norms. In our experiment, agents play a prisoner’s dilemma game on various network structures: (i) a static lattice where agents have a fixed position; (ii) a regular random network where agents have a fixed position; and (iii) a dynamic lattice where agents are randomly re-positioned at each game iteration. Our results show that the network structure does not affect the dynamics of cooperation, which corroborates results of prior laboratory experiments. However, the network structure does seem to affect how individuals balance between their self-interested and normative choices.

1. Introduction

Human cooperation is both powerful and puzzling. Large-scale cooperation among genetically unrelated individuals makes humans unique with respect to all other animal species. As such, it has played an important role in most major transitions in society [1,2]. Therefore, learning how cooperation emerges and persists and why individuals sacrifice their own narrow self-interest to help others is still a very active area of research and in recent years a considerable amount of effort has been invested in better understanding these questions. Several mechanisms for the promotion of cooperation have been identified [3,4]: direct, indirect and network reciprocity; multi-level selection; kin selection; and social norms with their enforcement strategies [3,4,5,6].

These mechanisms are usually studied in the framework of game theory, a mathematical formalism used to study cooperation and strategic interactions between rational decision-makers [7]. The general social structure in these games can be described as follows: consider two agents, say Alice and Bob, interacting strategically. Each agent can either cooperate (C) or defect (D). Alice’s payoff depends not only on her action but also on Bob’s; the same applies to Bob. We can arrange Alice’s information in a table, i.e., payoff matrix, as shown in

Table 1. Payoff matrix of a two-player game. C and D on the left column are Alice’s choices, while C and D on the top row are Bob’s.

	C	D
C	R	S
D	T	P

.

Here, Alice picks a row, Bob picks a column, and the corresponding entry is Alice’s payoff. We are interested in symmetric games, thus Bob’s payoff matrix is obtained from Alice’s by simply swapping the roles of rows and columns. If $T>R>P>S$, we have a well-known game called the Prisoner’s Dilemma (PD) (and, in addition, $2R>T+S$ for iterated PD games), which has been extensively used to study the emergence of cooperation [8]. In this case, when both agents cooperate, they both obtain the reward’s payoff R; if both defect, they both get the punishment’s payoff P; or, if one cooperates and the other defects, the former gets the sucker’s payoff S and the latter the temptation’s payoff T. Here is the dilemma: although the best individual choice for both is to defect, mutual cooperation yields a better payoff than mutual defection ($R>P$).

Some assumptions behind traditional game theory, however, have been challenged [8,9]. In particular, it has been argued that humans do not necessarily have enough cognitive capabilities to compute an optimal strategy in every situation, but rather they learn how to play from repeated interactions [10,11]. It is for this reason that a variety of learning models have been used to study this problem, among which the model called Experience Weighted Attraction (EWA) is of particular interest to us [11,12,13]. EWA is a combination of model-free and model-based reinforcement learning [14]. This hybrid approach has been extensively explored in the field of behavioral economics and it has been rather successful in explaining the interactive learning of humans in games [11,12,15,16].

The different learning dynamics that have been studied, however, have sometimes yielded contradictory predictions. For instance, whether the existence of an underlying network of contacts affects cooperation, something usually termed network reciprocity in the field of evolutionary game theory [3], has been under debate lately [17,18,19]. This debate has prompted the realization of large-scale laboratory experiments with humans that have provided valuable insights into the nature of human strategic behavior and learning processes [20,21,22,23,24,25]. Nonetheless, as pointed out by one of the leading scientist in the field: “there are many relevant experimental results on cooperation on structured populations published in widely read journals while, unfortunately, many models are introduced in the literature without taking into account [such experimental] facts” [19]. Some of the most relevant experimental findings are (see [19]): (i) networks or lattices do not promote cooperation, which suggests that network structure does not significantly influence cooperative behavior [22]; (ii) individuals follow a rule called Moody Conditional Cooperation (MCC)1; (iii) individuals do not take into account the earnings of their neighbors when deciding to cooperate [24], which disagrees with typical evolutionary rules based on the comparison between how well an individual does against others, e.g., how much earning an agent receives in comparison to others; and (iv) cooperation can be sustained in dynamic networks. In this work, we investigate a cognitive-inspired model [26] that by design is in agreement with Observation (iii). Additionally, we provide evidence that the model is also in agreement with Observation (i), i.e., there is no significant influence of network structure on cooperation, with Observation (ii), i.e., the model reproduces the MCC behavior, and other general experimental observations. We leave for future work the study on dynamic networks related to Observation (iv).

That human cooperation depends on people’s mood and their social context (Observation (ii)) has also been reported by other authors, who in addition have highlighted the importance of social norms in promoting cooperative behavior [27,28]. Social norms are rules or informal principles that indicate what is socially appropriate in a certain context and are typically enforced through social sanctions [29,30,31,32,33]. They have been shown to play a crucial role in promoting cooperation and more generally in shaping humans’ decisions in a variety of contexts [5,30,33,34,35]. To detect, reason, and decide whether to comply with social norms, humans have evolved a norm psychology [27,34]. This cognitive machinery allows humans to overcome rational egoistic impulses and interact with others in a way that may favor the emergence and stabilization of cooperation [27]. In recent years, agent-based models with a varying degree of complexity have been proposed to explore the role of social norms in promoting human cooperation [27,31,36].

In this work, we study an agent-based implementation of the Experience Weighted Attraction with Norm Psychology (EWAN) model, a cognitive-inspired model recently introduced in [26] that incorporates some important features of norm psychology into the EWA formalism [13] to better account for humans’ decision processes leading to cooperative behavior. In particular, Realpe-Gómez et al. [26] propose that humans always take into account what others do, even when they defected in the past, yet the importance ascribed to others’ actions depends on their immediate past behavior; this is in contrast with previous studies [21]. Recently, EWAN has also received the attention of experts in other fields where the interplay between conformism, individuality and leadership is important to achieve cooperation [37].

This study differs from [26] in which the authors did not explicitly implement the full stochastic agent-based model on networks proposed in the EWAN model. They rather concentrated on studying an analytically-tractable simplified EWAN version based on a so-called mean field approximation. Thus, they assumed that network structure does not significantly influence cooperation and stochastic fluctuations are negligible. This allowed them to effectively represent the whole population via a single representative agent and obtain an effective deterministic equation that simplified the analysis. However, they did not provide any evidence that these assumptions were indeed valid when studying the full stochastic agent-based EWAN model on networks.

Here, we partially fill this gap by providing evidence that indeed the full EWAN model is consistent with the assumption that network structure does not significantly influence cooperation. We also provide evidence that the results obtained with the full model are qualitatively similar to those obtained with the simplified model. Furthermore, the study in [26] left open the question about the effect of the distribution of cooperation, as well as other more granular properties of the individuals inside the group. In particular, our results suggest that, while network structure does not seem to significantly influence cooperation, it does seem to influence how individuals balance between self-interested and normative considerations when making their decision to cooperate.

2. Experience Weighted Attraction with Norm Psychology Model

Building on recent work attesting the interplay between egoism and conformism in promoting cooperation in human and animal societies [26,38,39], Experience Weighted Attraction with Norm Psychology (EWAN) assumes that at any given time the utility of an agent depends both on the material rewards she obtains (i.e., the individual drive) and on the degree to which her action is in accordance with the social norms of the group (i.e., the normative drive). Thus, the utility function of an agent can be written as

$$\Delta U^t=\Delta I^t+h\Delta N^t.$$

(1)

If $\Delta U^t>0$, the agent prefers to cooperate; if $\Delta U^t<0$, she prefers to defect; and, if $\Delta U^t=0$, she is indifferent. The individual drive, $\Delta I^t$, models material payoffs-based motivations, independent of what the norm prescribes. It is the difference between the material rewards that an agent would receive if she was to cooperate and those she would receive if she was to defect, given the actions taken by her neighbors and herself at round t, normalized over the number of neighbors (i.e., in this work, divided by 4). The normative drive $\Delta N^t$, on the other hand, models the motivation to comply with the norm as a function of the norm salience, i.e., a measure of how strong a norm is perceived within a group [27]. The parameter h describes the relative strength of the normative component in comparison to the individual component: if $h=0$ agents do not care about normative information, while if h is very large agents’ behavior is dominated by the norm. The impact that the norms have on an agent’s decision is a function of how salient the norm is perceived by agent i at round t within the social group. The higher is the salience of the social norm, the stronger is its impact on the motivation to comply with it. The norm salience is determined by two factors and their interaction: first, by the behavior of the agent at round t, i.e., her choice to comply with or violate the norm; and, second, by the share of agents among her neighbors that comply with (or violate) the norm at round t. The more neighbors comply with the norm, the more salient the norm becomes, and vice versa. Then, there is the interaction between the behavior of the agent and the actions of her neighbors. The agent discounts the salience of those norms that she violated in the immediate past and increases the salience of the norms that she complied with.

The relative importance of the own compliance (defection) with the norm, the compliance (defection) of neighbors and the interaction of both in the estimation of the norm salience is weighted, respectively, by the non-negative parameters $w_c$, $w_o$, and $w_i$. Formally,

$$\Delta N^t=w_c\left(2c^t-1\right)+w_o{O}^t+w_i{c}^t{O}^t,$$

(2)

where $O^t$ refers to the number of neighbors who cooperated at the same round t, also referred to as the observed cooperation. The first term is the only one that can be either added ($+w_c$) or subtracted ($-w_c$) to the estimation of the salience of the norm depending on whether at round t the agent has cooperated (i.e., $c^t=1$) or defected (i.e., $c^t=0$), respectively. This means that, if the agent complied with the norm in the immediate past, she will perceive the norm as more salient than if she had violated it. This is justified by the fact that humans have a strong need to enhance their self-concepts by behaving consistently with their own statements, commitments, beliefs and self-ascribed habits2 [40,41]. This human attitude to be consistent can also be explained as a desire to avoid ethical dissonance [42,43,44]. The second and third terms are always non-negative, the third term being zero if the agent did not cooperate at round t (i.e., if $c^t=0$). While not present in [27], this last term was introduced in [26] to account for the recent experimental observations that support the MCC rule, which assumes that in taking decisions individuals are responsive to the behavior of others but only after having cooperated themselves [21]. The second term containing $w_o$, however, relaxes the assumption behind the MCC rule by positing that individuals always take into account what others do, even though the overall importance ascribed to their actions depends on the individual’s “mood”. In this sense, EWAN assumes that when deciding how to act individuals are always sensitive to what their neighbors do and consider as socially appropriate, i.e., to the social norms of their group and their influence is a function of the norm salience. However, the salience ascribed to social norms is also modulated by the agent’s past behavior.

Taking as a starting point the EWA formalism, the EWAN model introduced in [26] is defined by the following equations

$$P^{t+1}=\frac{1}{1+e^{-\beta D^{t+1}}},$$

(3)

$$D^{t+1}=\left(1-\alpha \right)D^t+\Delta I^t+h\Delta N^t.$$

(4)

Here, $P^{t+1}$ is the probability of an agent to cooperate at round $t+1$ and $D^{t+1}$ is a term that incorporates the individual and normative drives; we call it here the drive. The non-negative parameter $\beta$ is sometimes called the intensity of choice. When $\beta =0$, the agent does not care about the drive and just picks an action at random, i.e., she cooperates with 50% probability. When $\beta$ is very large, the agent always cooperates (defects) if her drive is positive (negative); if her drive is at zero, she returns to act randomly again. Intermediate values of $\beta$ interpolate between those two extremes—rational optimization and random behavior. The update rule for the drive depends on the parameters h and $\alpha$. The parameter $\alpha$ describes memory loss: if $\alpha =1$, the agent only has information about the previous round, while, if $\alpha =0$, the agent has cumulative information of the full history of play. The case $0<\alpha <1$, economically speaking, amounts to an exponential discount of utilities in time. Finally, it is necessary to specify an initial value for the total drive ($D^0$) that in our case is inferred from laboratory experiments [21] (see Section 3). In Section 5, we discuss previous work related to the EWAN model we study here.

3. Methodology

We have studied the EWAN model on iterated weak Prisoner’s Dilemma games on networks using the payoffs and some network structures that have been investigated in large-scale laboratory experiments with humans [21,24]. Here, we focus on the experiment performed by Garcia-Lázaro and colleagues in Zaragoza [17], which to this date is still the one with the largest number of participants, i.e., 625 agents arranged in a square lattice $25\times 25$. Therefore, we expect this experiment to offer better statistics than other similar experiments.

Our numerical simulations of the experiment assume that 625 agents are positioned in a network structure and they interact for n rounds with their k neighbors. In our simulations, we conducted three treatments that differ with respect to their network structure: dynamic lattice, static lattice and regular random network. In the dynamic lattice treatment, agents are randomly re-positioned in the square lattice at each round, causing them to adapt to the average behavior of others3. In the static lattice treatment, agents remain on the same square lattice position, thus they interact with the same neighbors during the whole duration of the game. In the regular random network treatment, agents also remain on the same position during the whole duration of the game, but they form a network instead of a square lattice. In all treatments, the agents have the same number of neighbors, i.e., $k=4$.

The experimental settings assume yet that the agents interact for n rounds with their four neighbors (i.e., the four nearest orthogonal neighbor agents, von Neumann neighborhood, in the square lattices), using the payoff matrix values $T=10$, $R=7$, $P=0$ and $S=0$. The fact that P and S are equal gives this PD game its weak character, which means that it is not costly to cooperate when the agent’s neighbor defects. Agents receive information about the actions and normalized payoffs of their neighbors in the previous round, whose may also differ from the current neighbors depending on the treatment applied (see dynamic vs. static treatments in Section 4). This experiment was investigated in a mean field approximation to EWAN in [26], which neglects network structure by focusing on the probable actions of a single representative agent. In [26], it was found that the experimental human group appears to be near criticality, a special point where the system develops long correlations and may enhance its adaptability and resilience to external variability [26,45].

Our initial value for the total drive ($D^0$) was inferred from [17] by fitting the initial probability of cooperation to the experimental data, estimated to be around 60%, and it was set to be the same for all agents. The parameter $w_c$ in Equation (1) has been fixed to 1 as it can be absorbed by the parameter h from Equation (3)—yet it is very close to the value of 0.99 used in [27,36]. The parameter $w_o$ has been set to $0.33$ to respect the $w_c/w_o=3$ ratio, as also assumed in [27,36]4 5. In an attempt to fit the experimental results in [17], the other cognitive parameters of our model have been determined via an extensive brute-force parametric exploration. More precisely, we ran a few thousand simulations scanning parameter values restricted to a range of meaningful cognitive values to produce the best visual qualitative results relative to those reported in [17]. The parameter values that produced the best qualitative results were the following ones: $\alpha =0.21$, $\beta =0.31$, $h=0.31$, and $w_i=3.2$. This method differs from [26], where more sophisticated Bayesian inference techniques were utilized. However, given the complexity of the full stochastic agent-based EWAN model on networks, we decided to keep it simple in this first exploration of the model. We expect to use more sophisticated techniques in the future to better study the full EWAN model. However, the values we found for $\alpha$ and $\beta$ are consistent with experimental values. The value of $\alpha =0.21$ is consistent with the experimental values reported in [12] (Table 4), which are given in terms of a parameter $\varphi =1-\alpha$ (see also [46]), while the value of $\beta =0.31$ (called $\lambda$ in [12]), which is game-specific and a direct comparison is not possible, is close to the value obtained in one of the experiments reported in [10]. Finally, the value of $h=0.31$ is also consistent with the range of values of the corresponding term in [27,36], called $1/\Phi$ in [36], (p. 344), with $3\lesssim \Phi \lesssim 6$.

4. Results

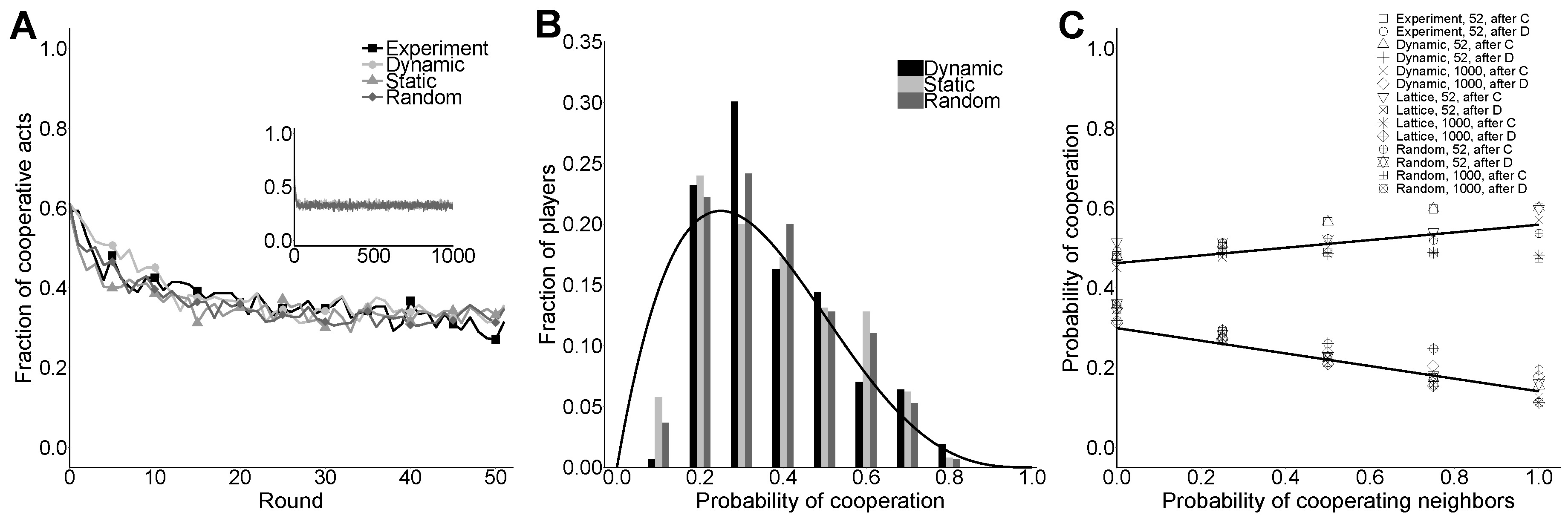
Figure 1 shows that the main results of one generic realization of a simulation conducted using EWAN on different network structures: (i) dynamic lattice (Dynamic); (ii) static lattice (Static); and (iii) regular random network (Random). Since the dynamic treatment is closer than the static and random ones to what is known in physics as a mean field scenario, where the topology of interactions is expected to be irrelevant, its results allow us to check the robustness of the results obtained in [26].

Figure 1A shows the fraction of cooperative actions for all the 52 rounds of all treatments, and displays a decay in cooperation from the initial value of 60% to a stabilized value around 35% in all treatments. This result is in good agreement with the one observed in laboratory experiments (cf. Figure 1 in [24]). Likewise, in [17], the network structure does not seem to have any appreciable influence on the evolution of the level of cooperation. During a preliminary parameter exploration with EWAN, we noticed that the experimental global level of cooperation was not very difficult to reproduce with different sets of parameter values. More delicate was the reproduction of the full distribution of agents according to the probability of cooperation that they have reached at the end of the simulation (cf. Figure 1 in [24]), shown in Figure 1B. The black curve was obtained from a mean field analysis as done in [26] (see Appendix A).

Similar to [21], we also analyzed the way subjects behave by considering that they might be influenced by the previous actions of their neighbors, i.e., the observed cooperation. Figure 1C displays the calculated probabilities for an agent to cooperate given the fraction of her neighbors that cooperated in a generic round, depending on her “mood”. Each cooperation probability is calculated by dividing the number of occurrences of a given “mood” pattern (after C or after D) and the number of cooperative neighbors over all rounds by the total number of occurrences. This indicates the probability of cooperation for an agent picked at random and at any given round, with the conditions stated above. We observed that these probabilities are very sensitive to the choice of model parameters. This last type of characterization of the cooperative behavior of a population is also obtained in the experimental studies and constitutes an additional and demanding test for our model. Overall, our results show good agreement with the results observed in the laboratory experiments with humans (cf. Figure 3 in [24]). In particular, it reproduces human cooperative behavior obtained in laboratory experiments more accurately than the MCC behavioral rule in [21]. A heuristic parameter search has shown that MCC is not able to reproduce the slow decay of the cooperation level when the agents did not cooperate in the immediate past [17].

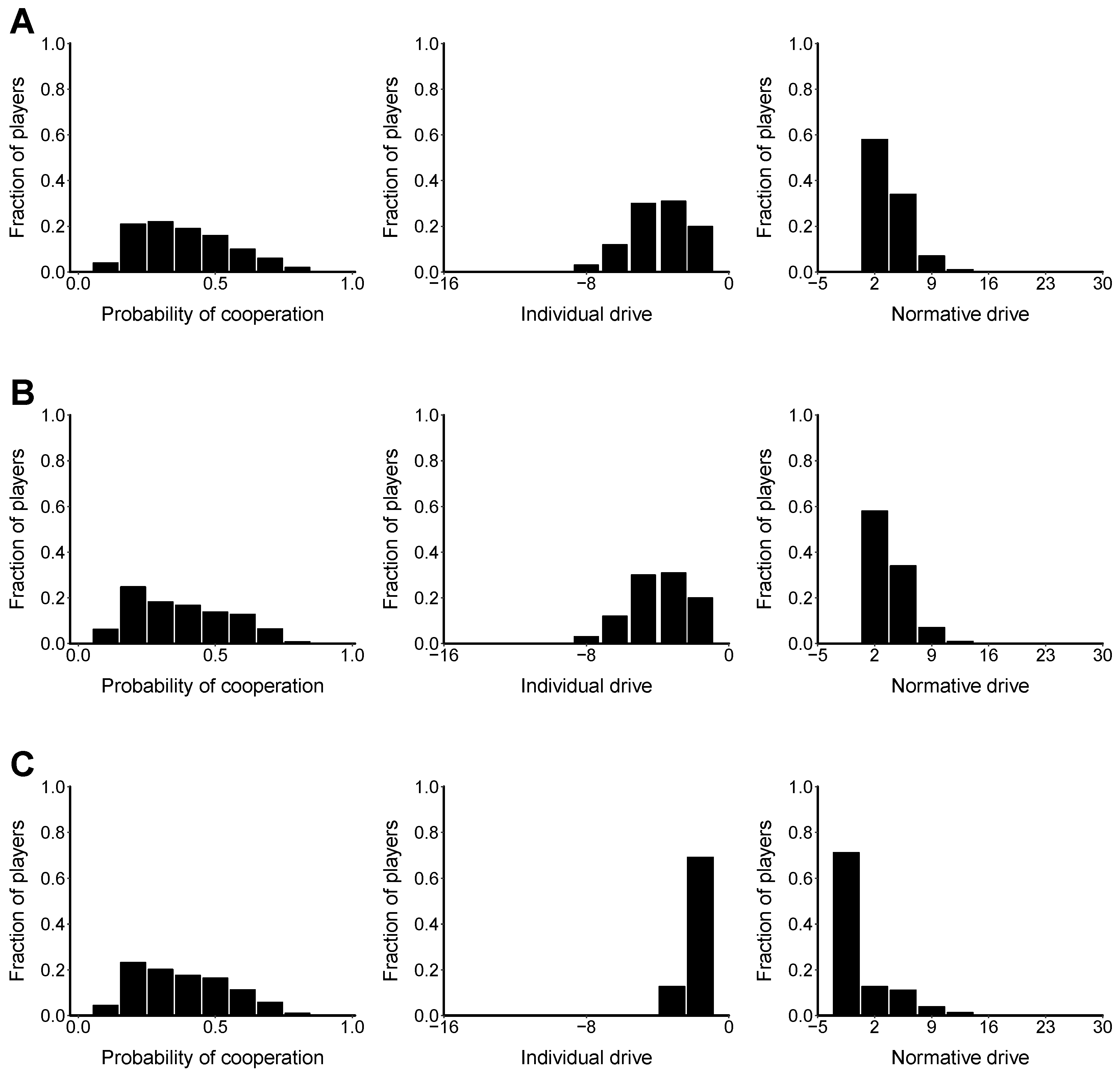
Figure 2 shows the final stationary state reached for several of the characteristics of the model on: (i) the dynamic lattice (Figure 2A); (ii) static lattice (Figure 2B); and (iii) regular random network (Figure 2C) treatments. The middle and right histograms show the global distribution of the individual drive and normative drive, respectively, accumulated during the iterated game for each treatment. Since the initial drive $D^0$ is defined by the initial cooperation probability, and how it is distributed between the individual and normative components is arbitrary, these figures show the individual and normative drives that have been accumulated during the game but leave out the initial value, i.e., starting from an initial value of zero.

5. Related Work

The EWAN model [26] has been inspired by an agent-based model that incorporates a normative architecture, described in [31], which is defined there in a more computational fashion if compared against statistical models such as EWAN. The agent-based model in [31] assumes that the decision of an agent to cooperate or defect varies as a function of material payoffs-based and normative-based considerations, namely the individual drive and the normative drive. The individual drive of an agent at round $t+1$ equals $+1$ if cooperation yields a higher payoff to her, given the actions taken by her neighbors at round t; otherwise, it equals $-1$. Neglecting additional terms associated to the existence of punishment and related concepts, the agent’s normative drive is commonly given by an expression that is similar to Equation (1), except for the term with weight $w_i$. This term has been introduced in [26] to account for the recent experimental observations that players behave in a moody manner, being significantly less likely to cooperate after a defection of their own, and constitutes the most important conceptual difference between the model mentioned in [27] and the one presented in [26]. In this sense, it is also worth emphasizing at this point that, strictly speaking, Equation (1) does not represent a pure MCC rule because in the decision to cooperate (or more technically in the calculation of the norm salience) we take into account the fraction of cooperating neighbors, even if the agent herself did not cooperate in the previous step ($c^t=0$). Coming back to the model introduced in [31], the resulting probability $P^{t+1}$ for an agent to cooperate at round $t+1$ is typically updated as $P^{t+1}=P^t+\left(\Delta I^t+\Delta N^t\right)/2$, as long as the right hand side is between zero and one. Otherwise, $P^{t+1}$ is set equal to zero or to one, depending on whether the right hand side is lower than zero or greater than one, respectively. This way of updating cooperation probability, which involves truncation, introduces some mathematical non-analyticities that are automatically avoided by working in an EWA-like formalism instead.

To compare the EWAN model [26] with the standard EWA formalism, some observations are in order. First, to the best of our knowledge, the focus of EWA studies has mostly been on models based exclusively on economic incentives, i.e., with $h=0$. Second, the EWA approach is defined in terms of the “attraction” of an agent towards cooperation or defection, based on the performance of one of these actions in the past. In these terms, the drive is the excess attraction towards cooperation, i.e., the difference between the attraction to cooperate and the attraction to defect. Indeed, it is not difficult to reformulate the EWAN model in terms of attractions, which works for games with any number of strategies. The EWA dynamics is typically specified by the update rules for the attractions. Under certain reasonable assumptions [46], the attraction of a given action is governed by an update rule like that expressed by Equation (3). In this case, the EWA modeling framework coincides with that introduced in [47,48]. The assumptions are essentially that actions actually played and those not played are equally weighted in the learning process and that the type of reinforcement is cumulative reinforcement.

Recent research has explored the possible relationship between an EWA-like modeling framework and the MCC rule [18]. However, in that work, the authors attempted a sort of convex combination of belief learning and reinforcement learning: an approach that does not necessarily coincide in spirit with EWA [49]. The authors mentioned that it is neither clear nor easy to say how to generalize the MCC rule to the EWA framework.

Finally, Horita et al. [50] showed that (model-free) reinforcement learning algorithms where agents have no access to information about decisions made by their neighbors can account for the observed human behavior roughly as accurately as algorithms where agents can directly encode the MCC rule. The model presented in [50] is able to well reproduce results from laboratory experiments, such as Prisoner’s Dilemma and Public Goods Games, in which subjects interact with different people at every stage. However, Horita et al. [50] do not reproduce as well data obtained in experimental settings with repeated interactions, the typical conditions in which social norms are more likely to emerge and influence people’s behavior. Due to a number of differences between the EWAN model [26] and the one in [50], e.g., the latter is a model-free learning, while the former integrates model-free with model-based reinforcement learning, a careful comparison between the two models is difficult. In the future, it would be interesting to make these models more comparable in order to better evaluate the similarities and differences between them.

6. Summary and Discussion

In this work, we have explored the relationship between reinforcement and belief learning and norm psychology in explaining cooperative human behavior observed in large-scale laboratory experiments with humans on different network structures. In particular, we have considered the EWAN model introduced in [26], which extends the well-known modeling framework called Experience Weighted Attraction (EWA) to incorporate some features of the norm psychology. The EWAN modeling framework can be conceived as a non-trivial hybrid between belief learning and cumulative reinforcement learning that gives equal weight to what could have happened and what actually happened. This learning model is based on the utilities that agents can obtain in playing the game. We have assumed that the utility function describing agents’ decision-making is composed of both the material rewards and the degree to which the action is in agreement with the social norms of the group in which the individual is located. The norm-based motivation is a function of the salience of the cooperation norm, which is estimated on the basis of the acts of compliance with the norm, performed both by the agent herself and her neighbors.

Previous computational work on norm psychology [27,31] has usually assumed the effect of own compliance and of others’ compliance on norm salience to be independent of each other, or to be mixed in a linear fashion. We, however, build on the model introduced in [26] and consider the possibility of a nonlinear interaction between them, so that the agent’s past experience with the norm affects her perception regarding the salience of the norm. This is supported by work on ethical dissonance [42,43], suggesting that individuals seek to feel good about themselves and maintain a positive self-image, which presumably includes viewing themselves as conforming to the salient social norms of their group. One cognitive strategy that enables individuals to resolve the tension between their own unethical behavior and ethical self-image is by adjusting their perception of the salience of the norm in order to render it consistent with their behavior. Thus, the salience of the norm is discounted (increased) if the individual violated (complied with) the norm.

In this work, we have presented results from computer simulations using EWAN that are in good agreement, both qualitatively and quantitatively, with the large-scale laboratory experiment with humans performed by Garcia-Lázaro and colleagues in Zaragoza [17]. Additionally, the EWAN model allowed us to reproduce the slow decay of the cooperation level observed in [17] when the individuals did not cooperate in the immediate past, a result that the original MCC rule failed to match. Both results are consistent with the ones presented in [26].

We have then presented results of simulations aimed to test the effect of network structure on cooperation. In particular, we do not observe a significant difference between the two-dimensional lattice and the regular random network structure on the type of statistics that are usually considered in the literature, aside from slight variations in the histograms (see Figure 1B). We see more peaked histograms in the dynamic lattice treatment with respect to the static lattice treatment (see Figure 1B and Figure 2A,B, left). This is what one should expect from a model that is closer to a mean field approach, where fluctuations are neglected: indeed, the distribution of cooperation probability in the pure mean field case is simply a Dirac delta function, as shown in [26]. Thus, similarly to [22], we can affirm that a significant influence of network structure on cooperation is not evident in our analyses. However, the network structure does seem to influence how agents balance between their individual and normative reasoning, as suggested by the different histograms in the lattice and a random network (see Figure 2A–C, middle and right columns). We hope future work will clarify further this point. The results presented in this work are interesting in several respects. First, as acknowledged in [18], “the original formulation of EWA cannot be trivially generalized to [the] MCC scenario”. However, there is some evidence that EWA actually performs better than previous implementations [49]. For instance, in [20], the authors used the linear MCC results to motivate the parameterization of agents’ mixed strategies allowing the learning dynamics to operate on the internal parameters. Here, instead, we have opted for an approach which is more “microscopic” than the one explored in [26] wherein the learning dynamics operates directly on the agent’s binary actions (Cooperate or Defect), while the learning parameters are kept fixed. In other words, we have incorporated this and other aspects of norm psychology by directly affecting the utility function that encodes the agents’ behavioral preferences. In this way, the standard EWA formalism remains almost intact and, at the same time, we make direct contact with research done in cognitive sciences aimed to better understand the mechanisms underlying humans’ decision to cooperate. Notice that, although we have worked here with a simplified version of the EWA formalism, which is more common to physicists, it is straightforward to extend these ideas to the more general case [13] as the model proposed here only implies to express the utility function as a combination of economic and normative components.

Additionally, we have focused our comparisons on some of the features that have been reported in the literature to characterize experimental results, i.e., the dynamics of the global cooperation level, the MCC rule and, to some extent, the influence of network structure on cooperation [17,21]. Clearly, the EWAN modeling framework is very recent and still needs careful scrutiny before reaching more general and solid conclusions. In particular, other statistical analyses and checks of the numerically obtained data could be done and compared with new experimental data to extend the present results. However, the absence of a significant influence of network structure on cooperation is expected to be the general case according to previous related work [18]. Before doing this, it will be necessary to clarify whether the normative component should take into account the actual number or rather the fraction of neighbors observed to comply with the norm. This is particularly important when dealing with network structures with a varying number of neighbors (e.g., random graphs or complex networks) or with a large number of them (e.g., large fully connected networks). Another aspect that would be interesting to explore in the future is whether EWAN supports Fermi-rule-like behavior such as that observed in [24]. This is also expected to be so, due to the similarity of the (logit) functional form that defines the probability of cooperating in both models (cf. Equation (1) in [24] and Equation (1) here). Notice, however, that, while the Fermi rule compares actual payoffs of different agents, EWAN compares actual or potential payoffs of the same agent.

One common criticism to the EWA modeling framework is that it needs many parameters. Even though, following [26], we have used a simplified version of the EWA model that leaves only two relevant parameters ($\alpha$ and $\beta$, memory-loss and the intensity of choice, respectively), we have also introduced three auxiliary parameters ($w_c$, $w_o$, and $w_i$) to use a cognitive approach in estimating the impact of norms. Hence, in this sense, this criticism could also be applied to our modeling framework and some sophisticated statistical tools could be used to assess the mathematical relevance of each parameter used in our current approach. Another possibility could be to explore some ways to aggregate some of the current normative parameters in higher-level mechanisms represented by functions, as has been done with EWA in [12].

Finally, the assumptions we have used imply that agents perform cumulative reinforcement in contrast to average reinforcement. Notwithstanding, as pointed out in [26], the EWAN modeling framework is general enough and allows more clearly specifying the different assumptions on the cognitive processes involved in the decision to cooperate made by humans. We expect that this approach might shed light and motivate further research on human cooperation and its underlying cognitive mechanisms.