Cooperation of Pairs
Abstract
1. Introduction
2. Experimental Design
3. Results
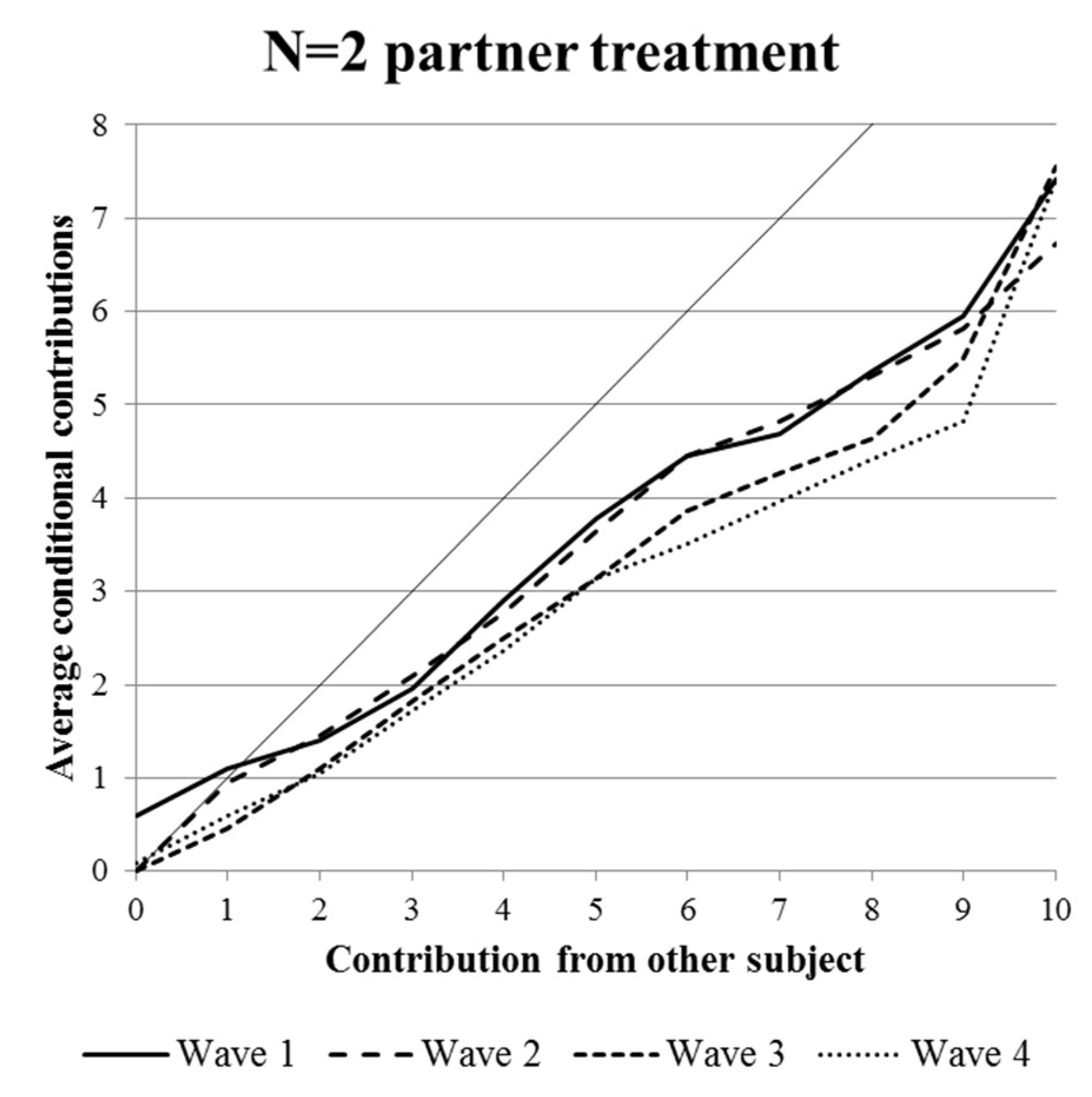
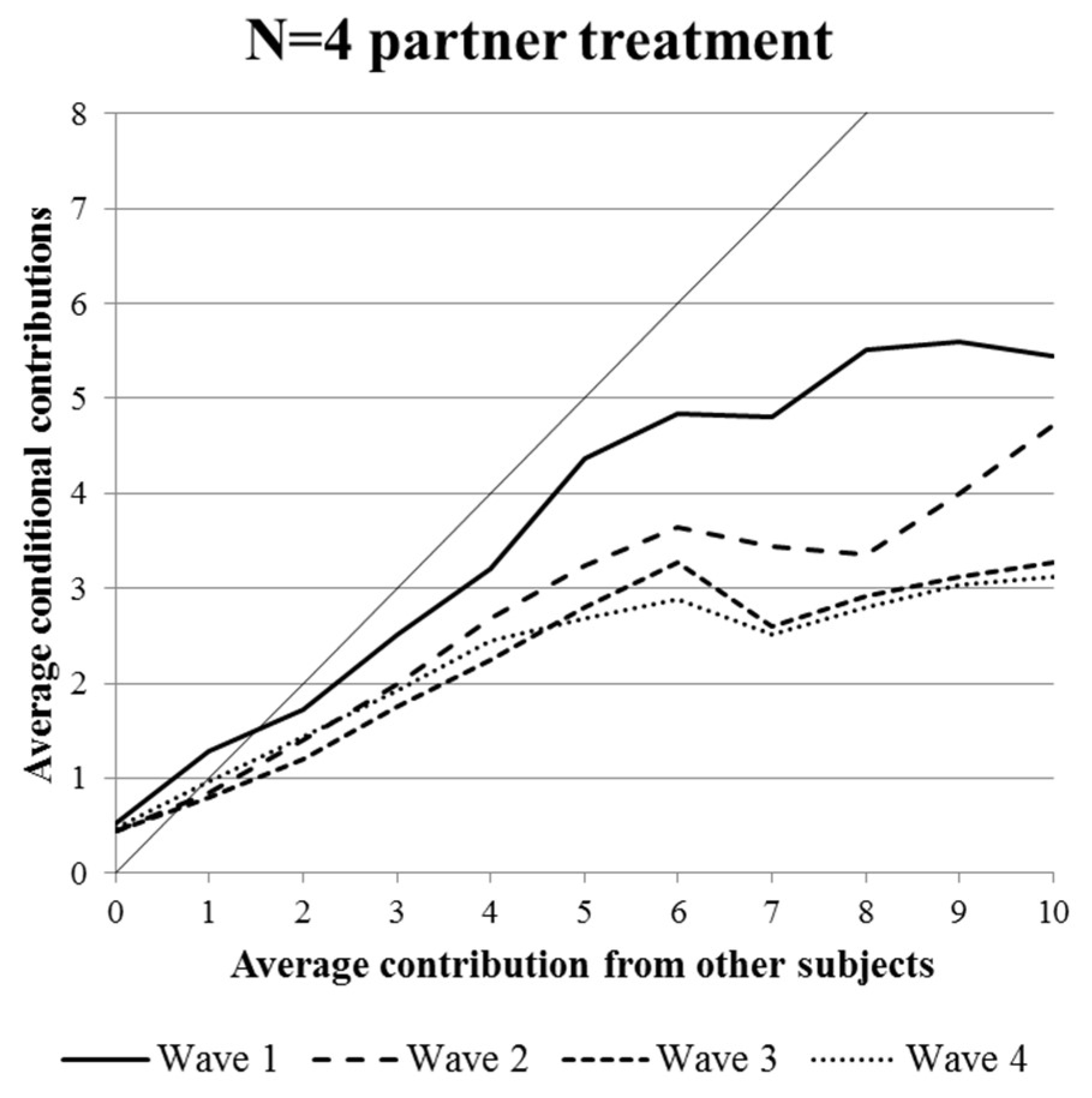
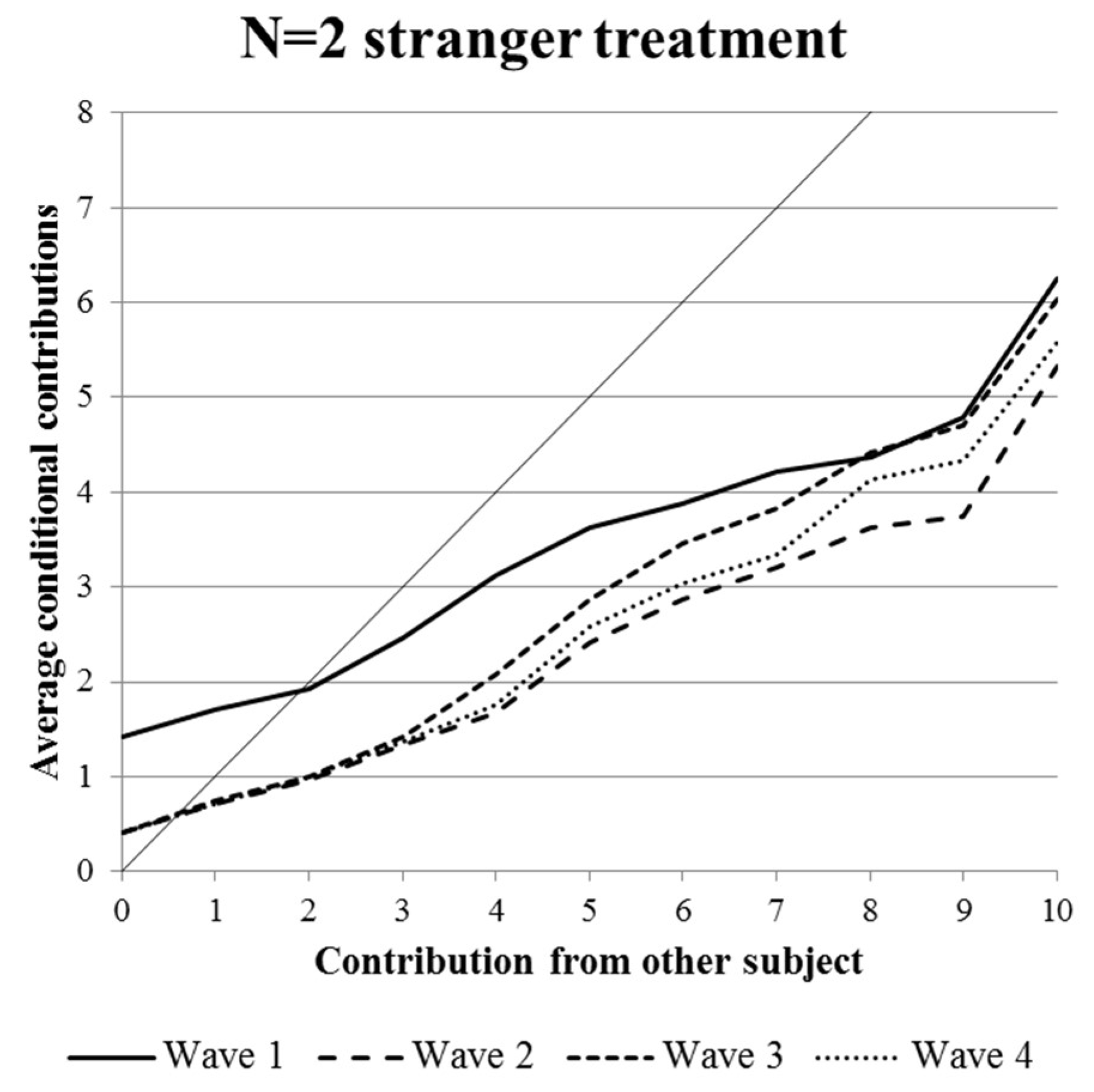
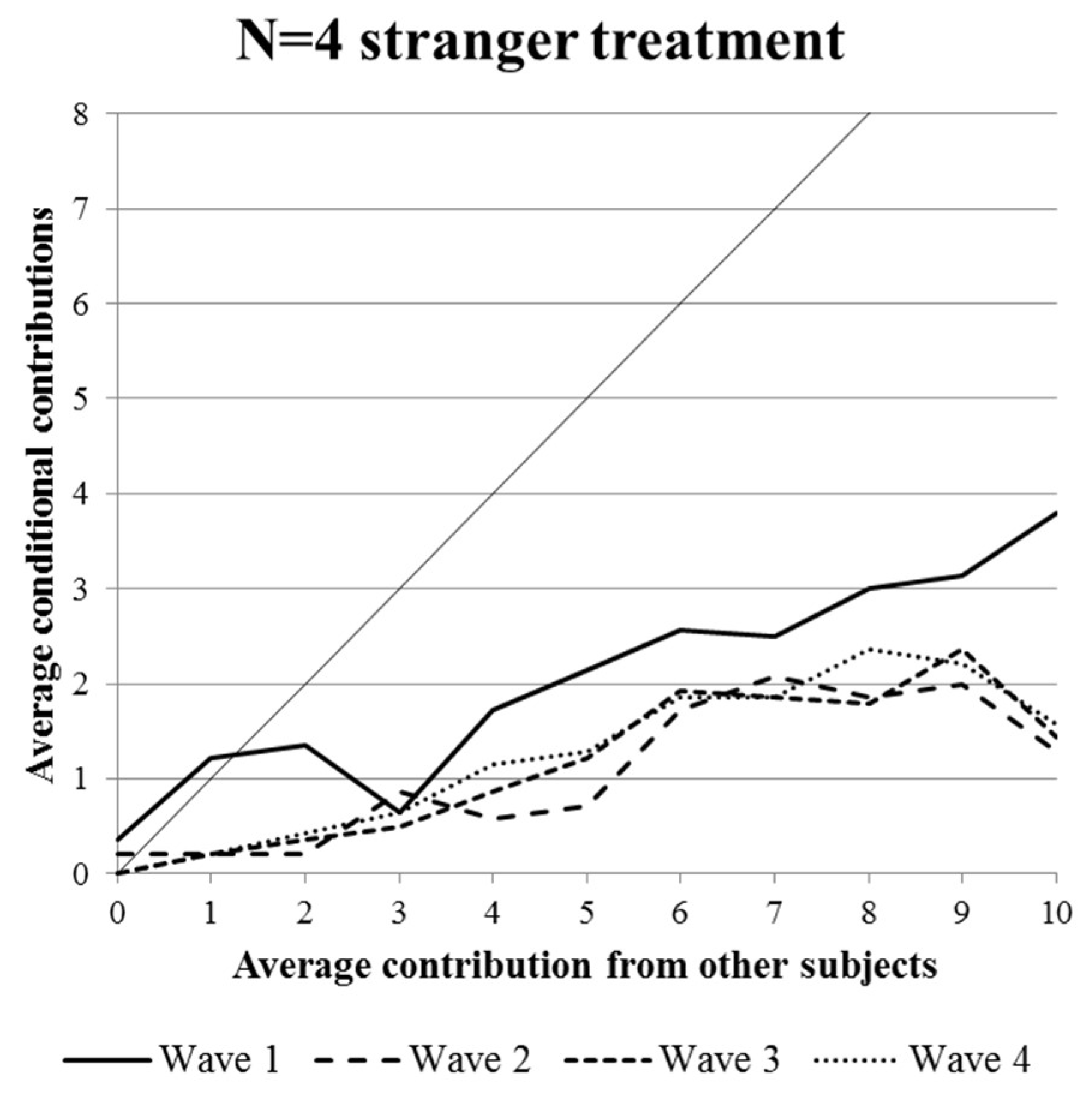
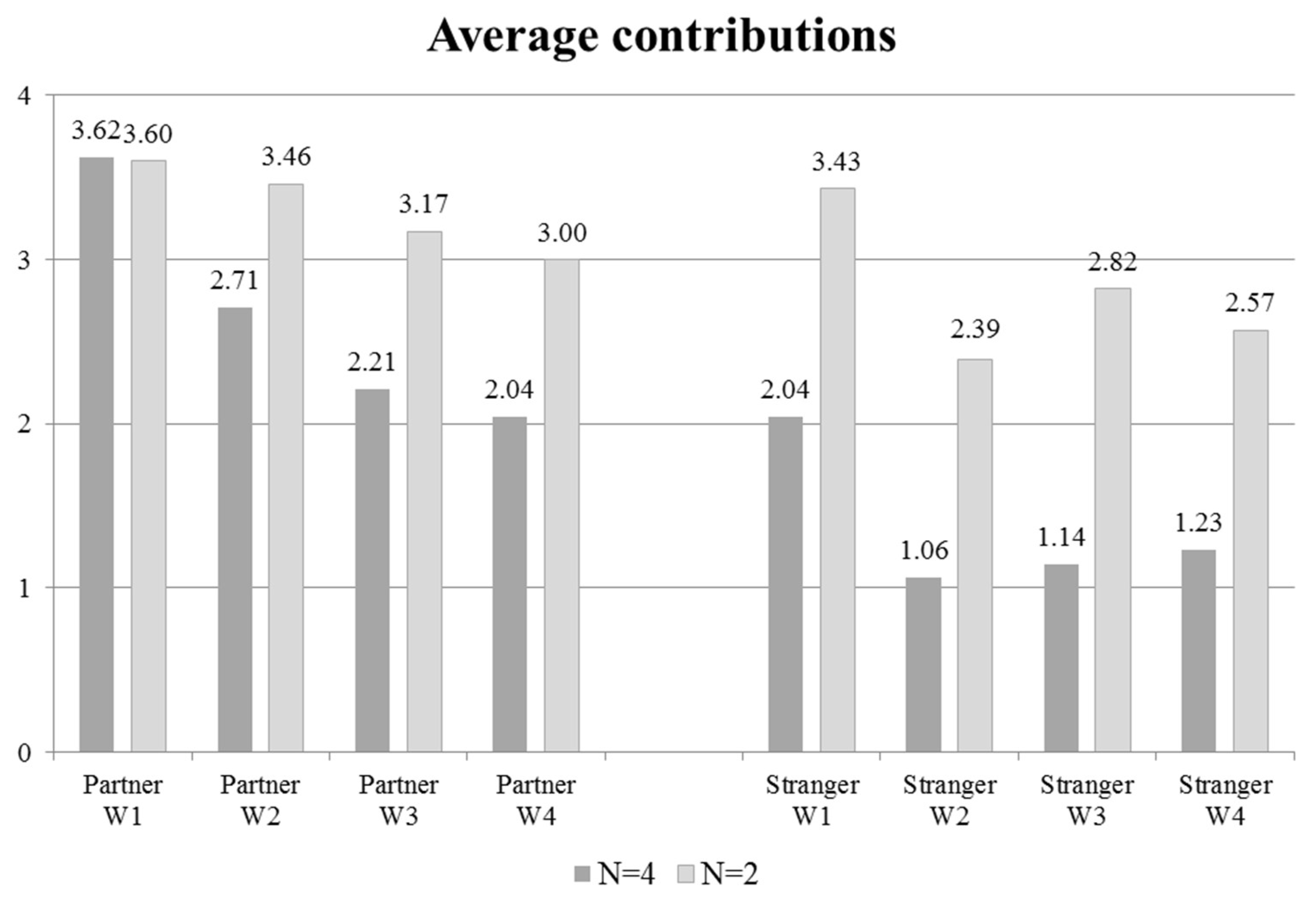
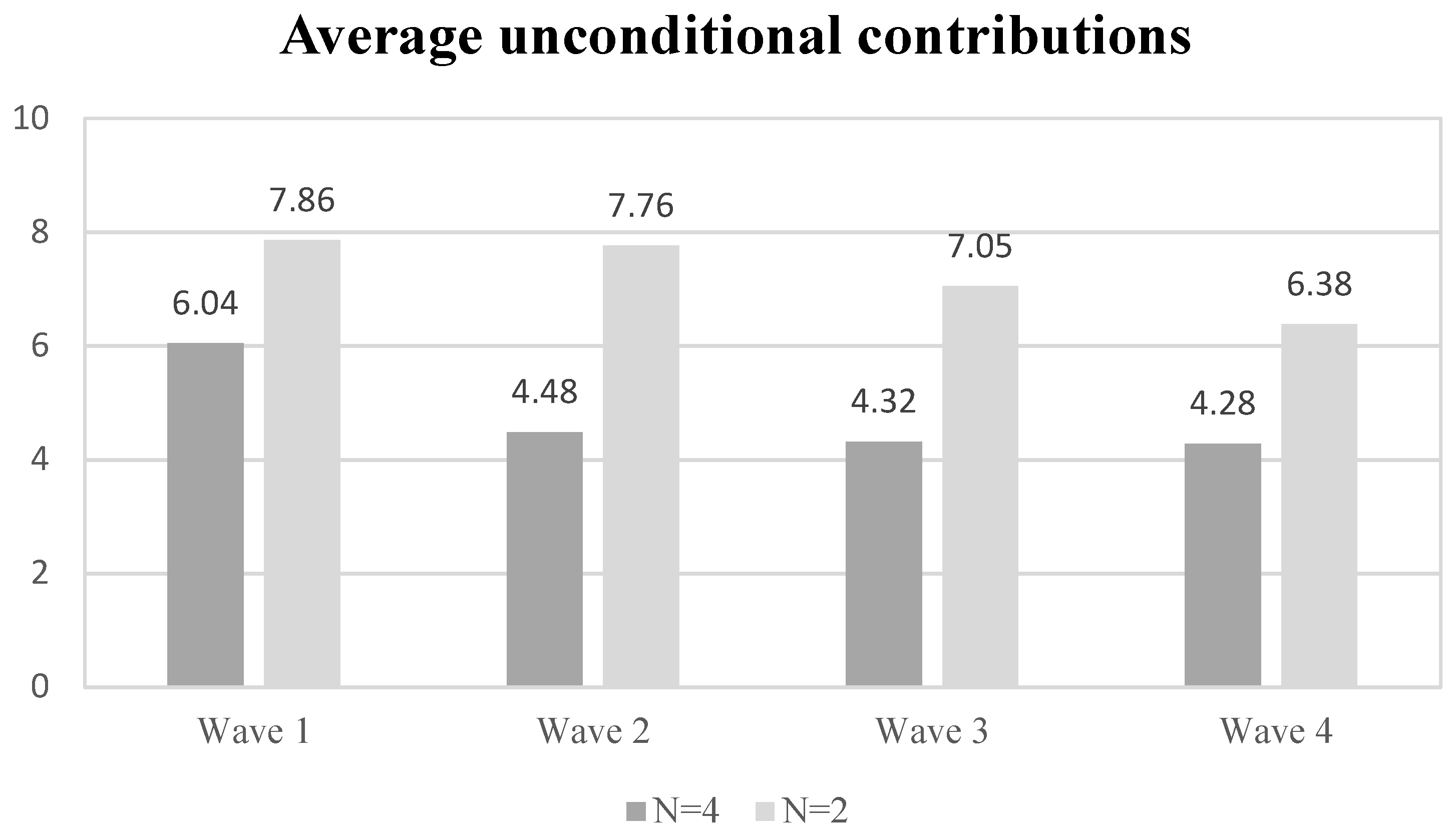
- Despite having designed the experiment in a way that promotes stable behavior, we generally find declining prosocial behavior in all treatments.
- There is a strong norm demanding subjects to engage in cooperative behavior in the first wave. Under partner conditions, this norm is similar in groups and pairs. Under stranger conditions, this norm is stronger in pairs.
- The norm mentioned in 2 apparently allows pairs a much more stable cooperation over time. This result is backed by both the partner and the stranger treatment in terms of conditional cooperation and for unconditional cooperation in the stranger treatment.
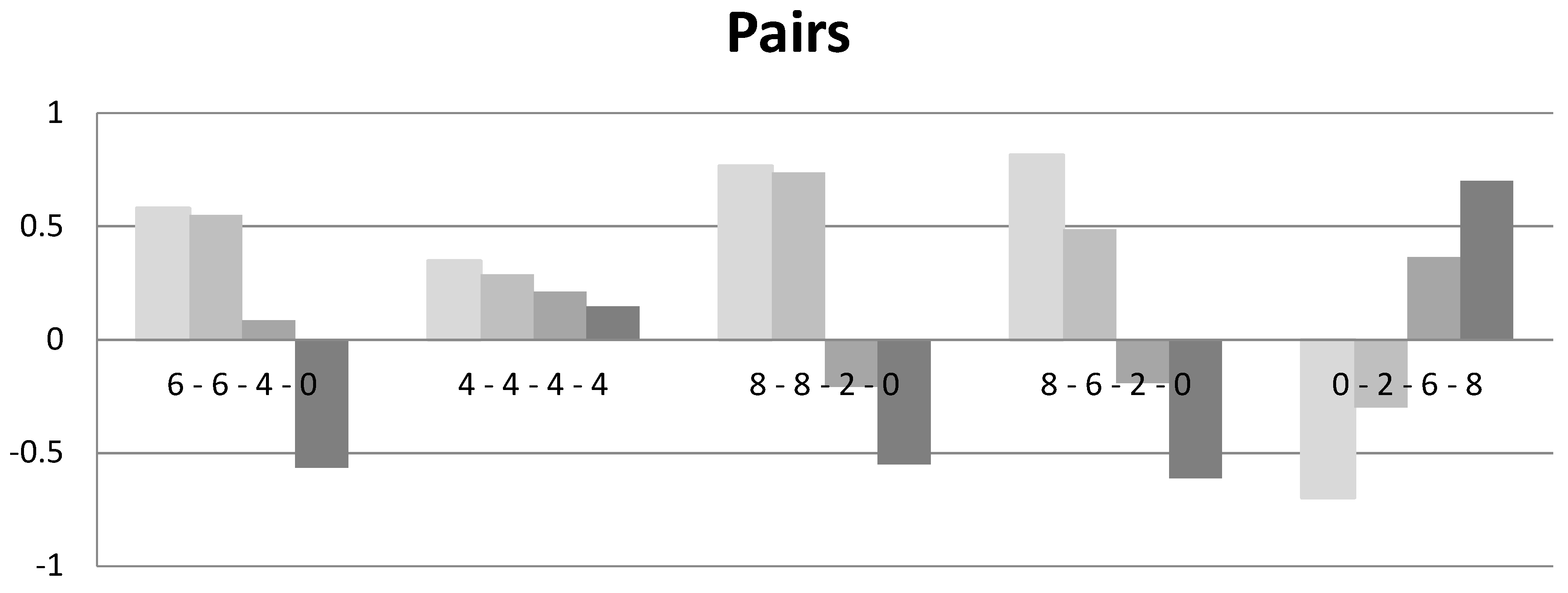
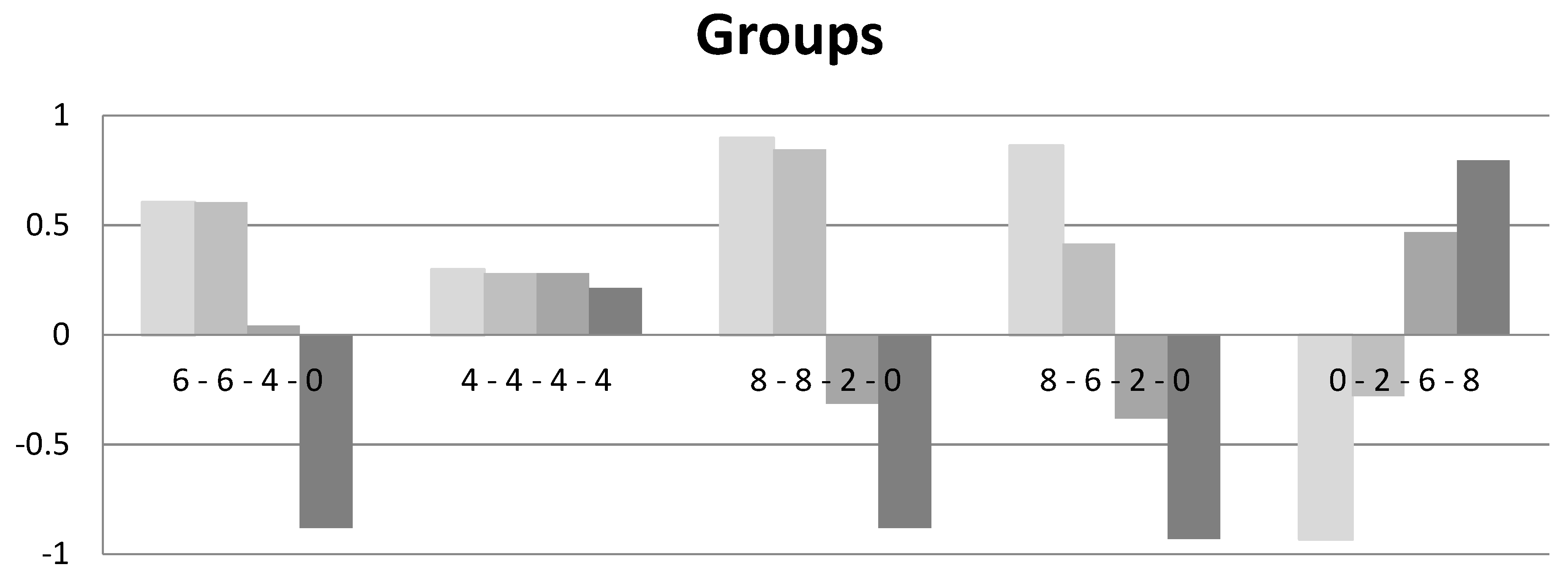
4. Norm Elicitation
4.1. Description of the Experiment
4.2. Results
5. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A1. Instructions & Data Sheet N = 4 Partner Treatment
- You will now take part in an experiment within the context of experimental economics. In this experiment you can earn money that will be paid out to you in cash at the end of the experiment. The amount of money depends on your decisions and the decisions of other subjects.
- The experiment has a duration of four weeks. The peculiarities that result from this experimental setup are explained in detail in the following instructions. Please read them carefully. Thank you!
- You and three other subjects are part of the following decision situation. You will be interacting with the exact same three other subjects each week. The other subjects’ identities will not be revealed to you at any point in time. Likewise, your identity will not be revealed to the other subjects. Thus, the interaction is always completely anonymous.
The Decision Situation of Today’s Experiment
- The decision situation is completely symmetrical, so the exact same information and choices are available to you and the other subjects.
- You and the other subjects each receive a monetary endowment of EUR 10.
- You and the other subjects each decide individually on how much of this endowment (integer values only) you wish to contribute to a public account for all four subjects. In the first step you will be asked to indicate this amount directly. In the second step you will be asked to indicate your preferred choice of contribution subject to the level of average contribution by the other three subjects (please also note the instruction on the data sheet).
- For each EUR 1 contributed by any group member to the public account, every group member will each receive a payoff of EUR 0.40. Each EUR 1 contributed to the public account thus yields a payoff of 4 × 0.40 EUR = EUR 1.60 to the group in total. Each group member will receive the same share of EUR 0.40.
- For each EUR 1 not contributed to the public account, you will receive EUR 1 at the end of the experiment.
- Each group member’s individual payoff (in EUR) is thus calculated as follows:10 − contribution to public account + 0.40 × sum of all contributions to public account
- A few numeric examples
- ○
- The other three subjects contribute on average EUR 5 to the public account. You contribute EUR 3 to the public account. Total contribution to the public account is therefore 3 × EUR 5 + 1 × EUR 3 = EUR 18.
- ▪
- Your payoff: 10 − 3 + 0.40 × 18 = EUR 14.20
- ▪
- Average payoff to other subjects: 10 − 5 + 0.40 × 18 = EUR 12.20
- ○
- All subjects (including you) contribute EUR 10 each to the public account. Total contribution to the public account is therefore 4 × EUR 10 = EUR 40.
- ▪
- Payoff to each subject: 10 − 10 + 0.40 × 40 = EUR 16
- ○
- All subjects (including you) contribute EUR 0 each to the public account. Total contribution to the public account is therefore EUR 0.
- ▪
- Payoff to each subject: 10 − 0 + 0.40 × 0 = EUR 10
- ○
- The other three subjects contribute EUR 10 each to the public account. You contribute EUR 0 to the public account. Total contribution to the public account is therefore 3 × EUR 10 + 1 × EUR 0 = EUR 30.
- ▪
- Your payoff: 10 − 0 + 0.40 × 30 = EUR 22
- ▪
- Payoff to other subjects: 10 − 10 + 0.40 × 30 = EUR 12
Payment Mechanism & Feedback
- You will receive no information on what the other subjects did until after the end of the four week experiment. The same applies to all other subjects.
- Likewise, you will not receive your payment until after the end of the experiment, i.e., you will only be paid when the final experiment is completed. The same applies to all other subjects.
- At the end of the experiment you will not receive the sum of the earnings from all the individual weeks. Instead, an individual week will be randomly drawn to be payoff relevant. The payment from that week will be multiplied by four and paid out to you in cash.
- It is important to us that you show up for all four experiments. If you fail to show up for any of the experiments, you forfeit all earnings.
- Example 1:
- ○
- You took part in all four weeks of the experiment. Your earnings were EUR 10 in week 1, EUR 14 in week 2, EUR 18 in week 3 and EUR 22 in week 4. The draw determines that you will be paid the earnings from week 3 multiplied by four. Your total payment in this illustrative example is thus 4 × EUR 18 = EUR 72.
- Example 2:
- ○
- You took part in the first three weeks of the experiment, but you failed to show up in week 4. In this case, you forfeit all earnings. Your total payment in this illustrative example is thus EUR 0.
- If the other three subjects contribute EUR 0 on average, I contribute: ___________.
- If the other three subjects contribute EUR 1 on average, I contribute: ___________.
- If the other three subjects contribute EUR 2 on average, I contribute: ___________.
- If the other three subjects contribute EUR 3 on average, I contribute: ___________.
- If the other three subjects contribute EUR 4 on average, I contribute: ___________.
- If the other three subjects contribute EUR 5 on average, I contribute: ___________.
- If the other three subjects contribute EUR 6 on average, I contribute: ___________.
- If the other three subjects contribute EUR 7 on average, I contribute: ___________.
- If the other three subjects contribute EUR 8 on average, I contribute: ___________.
- If the other three subjects contribute EUR 9 on average, I contribute: ___________.
- If the other three subjects contribute EUR 10 on average, I contribute: ___________.
Appendix A2. Instructions & Data Sheet N = 4 Stranger Treatment
- You will now take part in an experiment within the context of experimental economics. In this experiment, you can earn money that will be paid out to you in cash at the end of the experiment. The amount of money depends on your decisions and the decisions of other subjects.
- The experiment has a duration of four weeks. The peculiarities that result from this experimental setup are explained in detail in the following instructions. Please read them carefully. Thank you!
- You and three other subjects are part of the following decision situation. In each weak, you will be matched with three freshly recruited new subjects, who will only take part once in this experiment. Thus, you will be interacting with three freshly recruited new subjects in each weak. The other subjects’ identities will not be revealed to you at any point in time. Likewise, your identity will not revealed to the other subjects. Thus, the interaction is always completely anonymous.
The Decision Situation of Today’s Experiment
- The decision situation is completely symmetrical, so the exact same information and choices are available to you and the other subjects.
- You and the other subjects each receive a monetary endowment of EUR 10.
- You and the other subjects each decide individually on how much of this endowment (integer values only) you wish to contribute to a public account of all four subjects. Each of the other subjects will indicate their choice directly. You on the other hand will be asked to indicate your preferred choice of contribution subject to the level of average contribution by the other three subjects (please also note the instructions on the data sheet).
- For each EUR 1 contributed by any group member to the public account, every group member will each receive a payoff of EUR 0.40. Each EUR 1 contributed to the public account thus yields a payoff of 4 × 0.40 EUR = EUR 1.60 to the group in total. Each group member will receive the same share of EUR 0.40.
- For each EUR 1 not contributed to the public account, you will receive EUR 1 at the end of the experiment.
- Each group member’s individual payoff (in EUR) is thus calculated as follows:10 − contribution to public account + 0.40 × sum of all contributions to public account
- A few numeric examples
- ○
- The other three subjects contribute on average EUR 5 to the public account. You contribute EUR 3 to the public account. Total contribution to the public account thus is 3 × EUR 5 + 1 × EUR 3 = EUR 18.
- ▪
- Your payoff: 10 − 3 + 0.40 × 18 = EUR 14.20
- ▪
- Average payoff of other subjects: 10 − 5 + 0.40 × 18 = EUR 12.20
- ○
- All subjects (including you) contribute EUR 10 each to the public account. Total contribution to the public account thus is 4 × EUR 10 = EUR 40.
- ▪
- All subject’s payoff: 10 − 10 + 0.40 × 40 = EUR 16
- ○
- All subjects (including you) contribute EUR 0 each to the public account. Total contribution to the public account thus is EUR 0.
- ▪
- All subject’s payoff: 10 − 0 + 0.40 × 0 = EUR 10
- ○
- The other three subjects contribute EUR 10 each to the public account. You contribute EUR 0 to the public account. Total contribution to the public account thus is 3 × EUR 10 + 1 × EUR 0 = EUR 30.
- ▪
- Your payoff: 10 − 0 + 0.40 × 30 = EUR 22
- ▪
- Payoff of other subjects: 10 − 10 + 0.40 × 30 = EUR 12
Payment Mechanism & Feedback
- You will receive no information on what the other subjects did until after the end of the four week long experiment.
- Likewise, you will not receive your payment until after the end of the experiment. Only after the end of the final experiment you will be paid.
- The other subjects receive their payment at the end of today’s experiment, since (unlike you) they only take part once in this experiment.
- At the end of the experiment, you will not receive the sum of the earnings from all the individual weeks. Instead, an individual week will be randomly drawn to be payoff relevant. The payment from that week will be multiplied by four and paid out to you in cash.
- It is important to us that you show up for all four experiments. If you fail to show up for any of the experiments, you forfeit all earnings.
- Example 1:
- ○
- You took part in all four weeks of the experiment. Your earnings were EUR 10 in week 1, EUR 14 in week 2, EUR 18 in week 3 and EUR 22 in week 4. The draw determines that you will be paid the earnings from week 3 multiplied by four. Your total payment in this illustrative example is thus 4 × EUR 18 = EUR 72.
- Example 2:
- ○
- You took part in the first three weeks of the experiment, but you failed to show up in week 4. In this case, you forfeit all earnings. Your total payment in this illustrative example is thus EUR 0.
- If the other three subjects contribute EUR 0 on average, I contribute: ___________.
- If the other three subjects contribute EUR 1 on average, I contribute: ___________.
- If the other three subjects contribute EUR 2 on average, I contribute: ___________.
- If the other three subjects contribute EUR 3 on average, I contribute: ___________.
- If the other three subjects contribute EUR 4 on average, I contribute: ___________.
- If the other three subjects contribute EUR 5 on average, I contribute: ___________.
- If the other three subjects contribute EUR 6 on average, I contribute: ___________.
- If the other three subjects contribute EUR 7 on average, I contribute: ___________.
- If the other three subjects contribute EUR 8 on average, I contribute: ___________.
- If the other three subjects contribute EUR 9 on average, I contribute: ___________.
- If the other three subjects contribute EUR 10 on average, I contribute: ___________.
Appendix A3. Instructions & Data Sheet N = 2 Partner Treatment
- You will now take part in an experiment within the context of experimental economics. In this experiment, you can earn money that will be paid out to you in cash at the end of the experiment. The amount of money depends on your decisions and the decisions of other subjects.
- The experiment has a duration of four weeks. The peculiarities that result from this experimental setup are explained in detail in the following instructions. Please read them carefully. Thank you!
- You and another subject are part of the following decision situation. You will be interacting with the exact same other subject in each week. The other subject’s identity will not be revealed to you at any point in time. Likewise, your identity will not be revealed to the other subject. Thus, the interaction is always completely anonymous.
The Decision Situation of Today’s Experiment
- The decision situation is completely symmetrical, so the exact same information and choices are available to you and the other subject.
- You and the other subject each receive a monetary endowment of EUR 10.
- You and the other subject each decide individually on how much of this endowment (integer values only) you wish to contribute to a public account of both subjects. In a first step, you will be asked to indicate this amount directly. In a second step, you will be asked to indicate your preferred choice of contribution subject to the level of contribution by the other subject (please also note the instructions on the data sheet).
- For each EUR 1 contributed by you or the other subject to the public account, you and the other subject will each receive a payoff of EUR 0.80. Each EUR 1 contributed to the public account thus yields a payoff of 2 × 0.80 EUR = EUR 1.60 to you and the other subject in total. Each subject will receive the same share of EUR 0.80.
- For each EUR 1 not contributed to the public account, you will receive EUR 1 at the end of the experiment.
- Individual payoff for you and the other subject (in EUR) is thus calculated as follows:10 − contribution to public account + 0.80 × sum of all contributions to public account
- A few numeric examples
- ○
- The other subject contributes EUR 5 to the public account. You contribute EUR 3 to the public account. Total contribution to the public account thus is EUR 5 + EUR 3 = EUR 8.
- ▪
- Your payoff: 10 − 3 + 0.80 × 8 = EUR 13.40
- ▪
- Others subject’s payoff: 10 − 5 + 0.80 × 8 = EUR 11.40
- ○
- Both you and the other subject contribute EUR 10 each to the public account. Total contribution to the public account thus is 2 × EUR 10 = EUR 20.
- ▪
- Your payoff and payoff of other subject: 10 − 10 + 0.80 × 20 = EUR 16
- ○
- Both you and the other subject contribute EUR 0 each to the public account. Total contribution to the public account thus is EUR 0.
- ▪
- Your payoff and payoff of other subject: 10 − 0 + 0.80 × 0 = EUR 10
- ○
- The other subject contributes EUR 10 to the public account. You contribute EUR 0 to the public account. Total contribution to the public account thus is EUR 10 + EUR 0 = EUR 10.
- ▪
- Your payoff: 10 − 0 + 0.80 × 10 = EUR 18
- ▪
- Others subject’s payoff: 10 − 10 + 0.80 × 10 = EUR 8
Payment Mechanism & Feedback
- You will receive no information on what the other subjects did until after the end of the four week long experiment. The same applies to the other subject.
- Likewise, you will not receive your payment until after the end of the experiment. Only after the end of the final experiment you will be paid. The same applies to the other subject.
- At the end of the experiment, you will not receive the sum of the earnings from all the individual weeks. Instead, an individual week will be randomly drawn to be payoff relevant. The payment from that week will be multiplied by four and paid out to you in cash.
- It is important to us that you show up for all four experiments. If you fail to show up for any of the experiments, you forfeit all earnings.
- Example 1:
- ○
- You took part in all four weeks of the experiment. Your earnings were EUR 10 in week 1, EUR 12 in week 2, EUR 14 in week 3 and EUR 16 in week 4. The draw determines that you will be paid the earnings from week 3 multiplied by four. Your total payment in this illustrative example is thus 4 × EUR 14 = EUR 56.
- Example 2:
- ○
- You took part in the first three weeks of the experiment, but you failed to show up in week 4. In this case, you forfeit all earnings. Your total payment in this illustrative example is thus EUR 0.
- If the other subject contributes EUR 0, I contribute: ___________.
- If the other subject contributes EUR 1, I contribute: ___________.
- If the other subject contributes EUR 2, I contribute: ___________.
- If the other subject contributes EUR 3, I contribute: ___________.
- If the other subject contributes EUR 4, I contribute: ___________.
- If the other subject contributes EUR 5, I contribute: ___________.
- If the other subject contributes EUR 6, I contribute: ___________.
- If the other subject contributes EUR 7, I contribute: ___________.
- If the other subject contributes EUR 8, I contribute: ___________.
- If the other subject contributes EUR 9, I contribute: ___________.
- If the other subject contributes EUR 10, I contribute: ___________.
Appendix A4. Instructions & Data Sheet N = 2 Stranger Treatment
- You will now take part in an experiment within the context of experimental economics. In this experiment, you can earn money that will be paid out to you in cash at the end of the experiment. The amount of money depends on your decisions and the decisions of other subjects.
- The experiment has a duration of four weeks. The peculiarities that result from this experimental setup are explained in detail in the following instructions. Please read them carefully. Thank you!
- You and another subject are part of the following decision situation. In each weak, you will be interacting with a freshly recruited new subject in each week, who will only take part once in this experiment. Thus, you will be interacting with a different, new subject in each weak. The other subjects’ identities will not be revealed to you at any point in time. Likewise, your identity will not be revealed to the other subjects. Thus, the interaction is always completely anonymous.
The Decision Situation of Today’s Experiment
- The decision situation is completely symmetrical, so the exact same information and choices are available to you and the other subject.
- You and the other subject each receive a monetary endowment of EUR 10.
- You and the other subject each decide individually on how much of this endowment (integer values only) you wish to contribute to a public account of both subjects. The others subject will indicate his or her choice directly. You on the other hand will be asked to indicate your preferred choice of contribution subject to the level of contribution by the other subject (please also note the instructions on the data sheet).
- For each EUR 1 contributed by you or the other subject to the public account, you and the other subject will each receive a payoff of EUR 0.80. Each EUR 1 contributed to the public account thus yields a payoff of 2 × 0.80 EUR = EUR 1.60 to you and the other subject in total. Each subject will receive the same share of EUR 0.80.
- For each EUR 1 not contributed to the public account, you will receive EUR 1 at the end of the experiment.
- Individual payoff for you and the other subject (in EUR) is thus calculated as follows:10 − contribution to public account + 0.80 × sum of all contributions to public account
- A few numeric examples
- ○
- The other subject contributes EUR 5 to the public account. You contribute EUR 3 to the public account. Total contribution to the public account thus is EUR 5 + EUR 3 = EUR 8.
- ▪
- Your payoff: 10 − 3 + 0.80 × 8 = EUR 13.40
- ▪
- Others subject’s payoff: 10 − 5 + 0.80 × 8 = EUR 11.40
- ○
- Both you and the other subject contribute EUR 10 each to the public account. Total contribution to the public account thus is 2 × EUR 10 = EUR 20.
- ▪
- Your payoff and payoff of other subject: 10 − 10 + 0.80 × 20 = EUR 16
- ○
- Both you and the other subject contribute EUR 0 each to the public account. Total contribution to the public account thus is EUR 0.
- ▪
- Your payoff and payoff of other subject: 10 − 0 + 0.80 × 0 = EUR 10
- ○
- The other subject contributes EUR 10 to the public account. You contribute EUR 0 to the public account. Total contribution to the public account thus is EUR 10 + EUR 0 = EUR 10.
- ▪
- Your payoff: 10 − 0 + 0.80 × 10 = EUR 18
- ▪
- Others subject’s payoff: 10 − 10 + 0.80 × 10 = EUR 8
Payment Mechanism & Feedback
- You will receive no information on what the other subjects did until after the end of the four week long experiment. The same applies to the other subject.
- Likewise, you will not receive your payment until after the end of the experiment. Only after the end of the final experiment you will be paid. The same applies to the other subject.
- The other subject receives his or her payment at the end of today’s experiment, since (unlike you) he or she only takes part once in this experiment.
- At the end of the experiment, you will not receive the sum of the earnings from all the individual weeks. Instead, an individual week will be randomly drawn to be payoff relevant. The payment from that week will be multiplied by four and paid out to you in cash.
- It is important to us that you show up for all four experiments. If you fail to show up for any of the experiments, you forfeit all earnings.
- Example 1:
- ○
- You took part in all four weeks of the experiment. Your earnings were EUR 10 in week 1, EUR 12 in week 2, EUR 14 in week 3 and EUR 16 in week 4. The draw determines that you will be paid the earnings from week 3 multiplied by four. Your total payment in this illustrative example is thus 4 × EUR 14 = EUR 56.
- Example 2:
- ○
- You took part in the first three weeks of the experiment, but you failed to show up in week 4. In this case, you forfeit all earnings. Your total payment in this illustrative example is thus EUR 0.
- If the other subject contributes EUR 0, I contribute: ___________.
- If the other subject contributes EUR 1, I contribute: ___________.
- If the other subject contributes EUR 2, I contribute: ___________.
- If the other subject contributes EUR 3, I contribute: ___________.
- If the other subject contributes EUR 4, I contribute: ___________.
- If the other subject contributes EUR 5, I contribute: ___________.
- If the other subject contributes EUR 6, I contribute: ___________.
- If the other subject contributes EUR 7, I contribute: ___________.
- If the other subject contributes EUR 8, I contribute: ___________.
- If the other subject contributes EUR 9, I contribute: ___________.
- If the other subject contributes EUR 10, I contribute: ___________.
Appendix B1. Control Questions N = 4 Treatments
- Each member of your group is given an endowment of EUR 10. Suppose that nobody (including you) contributes to the public account.What is your payoff? EUR __________________What is the payoff of all other group members? EUR __________________
- Each member of your group is given an endowment of EUR 10. Suppose that everybody (including you) contributes EUR 10 to the public account.What is your payoff? EUR __________________What is the payoff of all other group members? EUR __________________
- Each member of your group is given an endowment of EUR 10. Suppose that each of the other group members contributes EUR 10 to the public account, whereas you contribute EUR 0.What is your payoff? EUR __________________What is the payoff of all other group members? EUR __________________
- Each member of your group is given an endowment of EUR 10. Suppose that each of the other group members contributes EUR 0 to the public account, whereas you contribute EUR 10.What is your payoff? EUR __________________What is the payoff of all other group members? EUR __________________
- Each member of your group is given an endowment of EUR 10. Suppose that the other group members contribute EUR 10 in total to the public account.What is your payoff if you contribute EUR 0?EUR __________________What is your payoff if you contribute EUR 5?EUR __________________What is your payoff if you contribute EUR 10?EUR __________________
Appendix B2. Control Questions N = 2 Treatments
- You and the other subject are given an endowment of EUR 10. Suppose that neither you nor the other subject contributes to the public account.What is your payoff? EUR __________________What is the payoff of the other subject? EUR __________________
- You and the other subject are given an endowment of EUR 10. Suppose both you and the other subject each contribute EUR 10 to the public account.What is your payoff? EUR __________________What is the payoff of the other subject? EUR __________________
- You and the other subject are given an endowment of EUR 10. Suppose that the other subject contributes EUR 10 to the public account, whereas you contribute EUR 0.What is your payoff? EUR __________________What is the payoff of the other subject? EUR __________________
- You and the other subject are given an endowment of EUR 10. Suppose that the other subject contributes EUR 0 to the public account, whereas you contribute EUR 10.What is your payoff? EUR __________________What is the payoff of the other subject? EUR __________________
- You and the other subject are given an endowment of EUR 10. Suppose that the other group members contribute EUR 5 to the public account.What is your payoff if you contribute EUR 0?EUR __________________What is your payoff if you contribute EUR 5?EUR __________________What is your payoff if you contribute EUR 10?EUR __________________
Appendix C1. Elicitation Experiment N = 2
Page 1: Instructions (ID: 1)
- Please read the description of the base game on page 2 carefully.
- Answer the question on page 3 (data sheet).
- Separate page 3 from these instructions, fold it once and hand it to an experimenter when asked to do so.
- The data sheets will be evaluated immediately after collection.
- You will find an ID on each page in the top right corner. After the evaluation of the data sheets, we will list all IDs and the corresponding payment. Please line up at the payment desk when asked to do so.
Page 2: Description of the Base Game (ID:1)
The Decision Situation of Today’s Experiment
- The decision situation is completely symmetrical, so the exact same information and choices are available to you and the other subject.
- You and the other subject each receive a monetary endowment of EUR 10.
- You and the other subject each decide individually on how much of this endowment (integer values only) you wish to contribute to a public account of both subjects. In a first step, you will be asked to indicate this amount directly. In a second step, you will be asked to indicate your preferred choice of contribution subject to the level of contribution by the other subject (please also note the instructions on the data sheet).
- For each EUR 1 contributed by you or the other subject to the public account, you and the other subject will each receive a payoff of EUR 0.80. Each EUR 1 contributed to the public account thus yields a payoff of 2 × 0.80 EUR = EUR 1.60 to you and the other subject in total. Each subject will receive the same share of EUR 0.80.
- For each EUR 1 not contributed to the public account, you will receive EUR 1 at the end of the experiment.
- Individual payoff for you and the other subject (in EUR) is thus calculated as follows:10 − contribution to public account + 0.80 × sum of all contributions to public account
- A few numeric examples
- ○
- The other subject contributes EUR 5 to the public account. You contribute EUR 3 to the public account. Total contribution to the public account thus is EUR 5 + EUR 3 = EUR 8.
- ▪
- Your payoff: 10 − 3 + 0.80 × 8 = EUR 13.40
- ▪
- Others subject’s payoff: 10 − 5 + 0.80 × 8 = EUR 11.40
- ○
- Both you and the other subject contribute EUR 10 each to the public account. Total contribution to the public account thus is 2 × EUR 10 = EUR 20.
- ▪
- Your payoff and payoff of other subject: 10 − 10 + 0.80 × 20 = EUR 16
- ○
- Both you and the other subject contribute EUR 0 each to the public account. Total contribution to the public account thus is EUR 0.
- ▪
- Your payoff and payoff of other subject: 10 − 0 + 0.80 × 0 = EUR 10
- ○
- The other subject contributes EUR 10 to the public account. You contribute EUR 0 to the public account. Total contribution to the public account thus is EUR 10 + EUR 0 = EUR 10.
- ▪
- Your payoff: 10 − 0 + 0.80 × 10 = EUR 18
- ▪
- Others subject’s payoff: 10 − 10 + 0.80 × 10 = EUR 8
Page 3: Data Sheet (ID:1)
- The experiment described on page 2 is conducted in a laboratory.
- The following table consists of different possibilities on how a player could behave in the two experiments. In the first column you find the contributions of the other player and in the second column you find your own contributions. You are asked to indicate for each possibility, what you believe a majority of your co-participants thinks of the “appropriateness” or “social desirability” of the behavior in the second experiment. Options range between “very desirable/very appropriate” to “somewhat desirable/somewhat appropriate” to “somewhat undesirable/inappropriate” to “very undesirable/very inappropriate”.
- Note: Only one of the 16 possibilities is chosen for evaluation. You will receive the additional EUR 5 if you match the choice made by the majority of participants in the randomly drawn row.
| Amount Given by the Other Player | Amount Given by the Yourself | Very Desirable/Very Appropriate | Somewhat Desirable/Somewhat Appropriate | Somewhat Undesirable/Somewhat Inappropriate | Very Undesirable/Very Inappropriate |
| 2 EUR | 2 EUR | ||||
| 4 EUR | |||||
| 6 EUR | |||||
| 8 EUR | |||||
| 4 EUR | 2 EUR | ||||
| 4 EUR | |||||
| 6 EUR | |||||
| 8 EUR | |||||
| 6 EUR | 2 EUR | ||||
| 4 EUR | |||||
| 6 EUR | |||||
| 8 EUR | |||||
| 8 EUR | 2 EUR | ||||
| 4 EUR | |||||
| 6 EUR | |||||
| 8 EUR |
Appendix C2. Elicitation Experiment N = 4
Appendix C2.1. Page 1: Instructions (ID: 1)
- 6
- Please read the description of the base game on page 2 carefully.
- 7
- Answer the question on page 3 (data sheet).
- 8
- Separate page 3 from these instructions, fold it once and hand it to an experimenter when asked to do so.
- 9
- The data sheets will be evaluated immediately after collection.
- 10
- You will find an ID on each page in the top right corner. After the evaluation of the data sheets, we will list all IDs and the corresponding payment. Please line up at the payment desk when asked to do so.
Appendix C2.2. Page 2: Description of the Base Game (ID: 1)
The Decision Situation of Today’s Experiment
- You and the other three subjects each receive a monetary endowment of EUR 10.
- You and the other subjects each decide individually on how much of this endowment (integer values only) you wish to contribute to a public account of all four subjects. In a first step, you will be asked to indicate this amount directly. In a second step, you will be asked to indicate your preferred choice of contribution subject to the level of contribution by the other subjects (please also note the instructions on the data sheet).
- For each EUR 1 contributed by you or the other subject to the public account, you and the other subjects will each receive a payoff of EUR 0.40. Each EUR 1 contributed to the public account thus yields a payoff of 4 × 0.40 EUR = EUR 1.60 to you and the other subjects in total. Each subject will receive the same share of EUR 0.40.
- For each EUR 1 not contributed to the public account, you will receive EUR 1 at the end of the experiment.
- Individual payoff for you and the other subject (in EUR) is thus calculated as follows:10 − contribution to public account + 0.40 × sum of all contributions to public account
- A few numeric examples
- ○
- The other subjects contribute EUR 5 to the public account. You contribute EUR 3 to the public account. Total contribution to the public account thus is EUR 5 + EUR 3 = EUR 18.
- ▪
- Your payoff: 10 − 3 + 0.40 × 8 = EUR 14.20
- ▪
- Others subject’s payoff: 10 − 5 + 0.40 × 18 = EUR 12.20
- ○
- Both you and the other subject contribute EUR 10 each to the public account. Total contribution to the public account thus is 4 × EUR 10 = EUR 40.
- ▪
- Your payoff and payoff of other subject: 10 − 10 + 0.40 × 40 = EUR 16
- ○
- Both you and the other subject contribute EUR 0 each to the public account. Total contribution to the public account thus is EUR 0.
- ▪
- Your payoff and payoff of other subject: 10 − 0 + 0.40 × 0 = EUR 10
- ○
- The other subject contributes EUR 10 to the public account. You contribute EUR 0 to the public account. Total contribution to the public account thus is 3 × EUR 10 + 1 × EUR = EUR 30.
- ▪
- Your payoff: 10 − 0 + 0.40 × 30 = EUR 22
- ▪
- Others subject’s payoff: 10 − 10 + 0.40 × 30 = EUR 12
Appendix C2.3. Page 3: Data Sheet (ID:1)
- The experiment described on page 2 is conducted in a laboratory.
- The following table consists of different possibilities on how a player could behave in the two experiments. In the first column you find the average contribution of the other players and in the second column you find your own contributions. You are asked to indicate for each possibility, what you believe a majority of your co-participants thinks of the “appropriateness” or “social desirability” of the behavior in the second experiment. Options range between “very desirable/very appropriate” to “somewhat desirable/somewhat appropriate” to “somewhat undesirable/inappropriate” to “very undesirable/very inappropriate”.
- Note: Only one of the 16 possibilities is chosen for evaluation. You will receive the additional EUR 5 if you match the choice made by the majority of participants in the randomly drawn row.
| Average Amount Given by the Other Players | Amount Given by the Yourself | Very Desirable/Very Appropriate | Somewhat Desirable/Somewhat Appropriate | Somewhat Undesirable/Somewhat Inappropriate | Very Undesirable/Very Inappropriate |
| 2 EUR | 2 EUR | ||||
| 4 EUR | |||||
| 6 EUR | |||||
| 8 EUR | |||||
| 4 EUR | 2 EUR | ||||
| 4 EUR | |||||
| 6 EUR | |||||
| 8 EUR | |||||
| 6 EUR | 2 EUR | ||||
| 4 EUR | |||||
| 6 EUR | |||||
| 8 EUR | |||||
| 8 EUR | 2 EUR | ||||
| 4 EUR | |||||
| 6 EUR | |||||
| 8 EUR |
Appendix C3. Elicitation Sequence
Page 4: Additional Sheet I ID (Copy from Page 1/2)
| Sequence: 6 6 4 0 | Very Desirable/Very Appropriate | Somewhat Desirable/Somewhat Appropriate | Somewhat Undesirable/Somewhat Inappropriate | Very Undesirable/Very Inappropriate |
| Contribution week 1. Woche: 6 | ||||
| Contribution week 2 | ||||
| Contribution week 3 | ||||
| Contribution week 4 |
| Sequence: 4 4 4 4 | Very Desirable/Very Appropriate | Somewhat Desirable/Somewhat Appropriate | Somewhat Undesirable/Somewhat Inappropriate | Very Undesirable/Very Inappropriate |
| Contribution week 1. Woche: 6 | ||||
| Contribution week 2 | ||||
| Contribution week 3 | ||||
| Contribution week 4 |
| Sequence: 8 8 2 0 | Very Desirable/Very Appropriate | Somewhat Desirable/Somewhat Appropriate | Somewhat Undesirable/Somewhat Inappropriate | Very Undesirable/Very Inappropriate |
| Contribution week 1. Woche: 6 | ||||
| Contribution week 2 | ||||
| Contribution week 3 | ||||
| Contribution week 4 |
| Sequence: 8 6 2 0 | Very Desirable/Very Appropriate | Somewhat Desirable/Somewhat Appropriate | Somewhat Undesirable/Somewhat Inappropriate | Very Undesirable/Very Inappropriate |
| Contribution week 1. Woche: 6 | ||||
| Contribution week 2 | ||||
| Contribution week 3 | ||||
| Contribution week 4 |
| Sequence: 0 2 6 8 | Very Desirable/Very Appropriate | Somewhat Desirable/Somewhat Appropriate | Somewhat Undesirable/Somewhat Inappropriate | Very Undesirable/Very Inappropriate |
| Contribution week 1. Woche: 6 | ||||
| Contribution week 2 | ||||
| Contribution week 3 | ||||
| Contribution week 4 |
Appendix C4: Elicitation Direct
Appendix C4.1. Page 5: Additional Sheet II ID (Copy from Page 1/2)
The Decision Situation of Today’s Experiment (Group A)
- You play with one other subject.
- You and the other subject each receive a monetary endowment of EUR 10.
- You and the other subject each decide individually on how much of this endowment (integer values only) you wish to contribute to a public account of both subjects.
- For each EUR 1 contributed by you or the other subject to the public account, you and the other subject will each receive a payoff of EUR 0.80. Each EUR 1 contributed to the public account thus yields a payoff of 2 × 0.80 EUR = EUR 1.60 to you and the other subject in total. Each subject will receive the same share of EUR 0.80.
- For each EUR 1 not contributed to the public account, you will receive EUR 1 at the end of the experiment.
- Individual payoff for you and the other subject (in EUR) is thus calculated as follows:10 − contribution to public account + 0.80 × sum of all contributions to public account
The Decision Situation of Today’s Experiment (Group B)
- You play with three other subjects.
- You and the other subjects each receive a monetary endowment of EUR 10.
- You and the other subjects each decide individually on how much of this endowment (integer values only) you wish to contribute to a public account of both subjects.
- For each EUR 1 contributed by you or the other subjects to the public account, you and the other subject will each receive a payoff of EUR 0.40. Each EUR 1 contributed to the public account thus yields a payoff of 4 × 0.40 EUR = EUR 1.60 to you and the other subjects in total. Each subject will receive the same share of EUR 0.40.
- For each EUR 1 not contributed to the public account, you will receive EUR 1 at the end of the experiment.
- Individual payoff for you and the other subject (in EUR) is thus calculated as follows:10 − contribution to public account + 0.40 × sum of all contributions to public account
| Average Contribution of Other Players | Contribution 2-Player Group (A) | Contribution 2-Player Group (B) | The Behavior of the Player from 2-Player Group Is Socially More Desirable | The Behavior of Both Players Is Equally Desirable | The Behavior of the Player from 4-Player Group Is Socially More Desirable |
| 2 EUR | 2 EUR | 2 EUR | |||
| 4 EUR | 4 EUR | ||||
| 6 EUR | 6 EUR | ||||
| 8 EUR | 8 EUR | ||||
| 4 EUR | 2 EUR | 2 EUR | |||
| 4 EUR | 4 EUR | ||||
| 6 EUR | 6 EUR | ||||
| 8 EUR | 8 EUR | ||||
| 6 EUR | 2 EUR | 2 EUR | |||
| 4 EUR | 4 EUR | ||||
| 6 EUR | 6 EUR | ||||
| 8 EUR | 8 EUR | ||||
| 8 EUR | 2 EUR | 2 EUR | |||
| 4 EUR | 4 EUR | ||||
| 6 EUR | 6 EUR | ||||
| 8 EUR | 8 EUR |
References
- Isaac, R.M.; Walker, J.M.; Thomas, S.H. Divergent evidence on free riding: An experimental examination of possible explanations. Public Choice 1984, 43, 113–149. [Google Scholar] [CrossRef]
- Weimann, J.; Brosig-Koch, J.; Heinrich, T.; Hennig-Schmidt, H.; Keser, C. The Logic of Collective Actions Revisited; CESifo Working Paper No. 5039; CESifo Group: Munich, Germany, 2017. [Google Scholar]
- Grujić, J.; Fosco, C.; Araujo, L.; Cuesta, J.A.; Sánchez, A. Social Experiments in the Mesoscale: Humans Playing a Spatial Prisoner’s Dilemma. PLoS ONE 2010, 5, e13749. [Google Scholar] [CrossRef] [PubMed]
- Fischbacher, U.; Gächter, S. Social Preferences, Beliefs, and the Dynamics of Free Riding in Public Goods Experiments. Am. Econ. Rev. 2010, 100, 541–556. [Google Scholar] [CrossRef]
- Brosig, J.; Riechmann, T.; Weimann, J. The dynamics of behavior in modified dictator games. PLoS ONE 2017, 12, e0176199. [Google Scholar] [CrossRef] [PubMed]
- Fouraker, L.E.; Siegel, S. Bargaining Behavior; McGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Holt, C.A. Industrial Organization: A Survey of Laboratory Research. In Handbook of Experimental Economics; Kagel, J., Roth, A., Eds.; Princeton University Press: Princeton, NJ, USA, 1995; pp. 349–443. [Google Scholar]
- Huck, S.; Normann, H.-T.; Oechssler, J. Two are few and four are many: Number effects in experimental oligopolies. J. Econ. Behav. Organ. 2004, 53, 435–446. [Google Scholar] [CrossRef]
- Potters, J.; Suetens, S. Oligopoly experiments in the current millennium. J. Econ. Surv. 2013, 27, 439–460. [Google Scholar] [CrossRef]
- Marwell, G.; Schmitt, D.R. Cooperation in a three-person Prisoner’s Dilemma. J. Personal. Soc. Psychol. 1972, 21, 376–383. [Google Scholar] [CrossRef]
- Nosenzo, D.; Quercia, S.; Sefton, M. Cooperation in small groups: The effect of group size. Exp. Econ. 2015, 18, 4–14. [Google Scholar] [CrossRef]
- Suzuki, S.; Akiyama, E. Reputation and the evolution of cooperation in sizable groups. Proc. R. Soc. Lond. B Biol. Sci. 2005, 272, 1373–1377. [Google Scholar] [CrossRef] [PubMed]
- Krupka, E.L.; Weber, R.A. Identifying social norms using coordination games: Why does dictator game sharing vary? J. Eur. Econ. Assoc. 2013, 11, 495–524. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gächter, S.; Fehr, E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar] [CrossRef]
- Isaac, R.M.; Walker, J.M. Group Size Effects in Public Goods Provision: The Voluntary Contribution Mechanism. Q. J. Econ. 1988, 103, 179–199. [Google Scholar] [CrossRef]
- Greiner, B. The Online Recruitment System ORSEE 2.0—A Guide for the Organization of Experiments in Economics; Working Paper Series in Economics 10; University of Cologne: Köln, Germany, 2004. [Google Scholar]
- Bock, O.; Nicklisch, A.; Baetge, I. hroot: Hamburg registration and organization online tool. Eur. Econ. Rev. 2014, 71, 117–120. [Google Scholar] [CrossRef]
- Selten, R. Die Strategiemethode zur Erforschung des eingeschränkt rationalen Verhaltens im Rahmen eines Oligopolexperimentes. In Beiträge zur Experimentellen Wirtschaftsforschung; Sauermann, H., Ed.; Mohr-Siebeck: Tübingen, Germany, 1967; pp. 136–168. [Google Scholar]
- Gino, F.; Ayal, S.; Ariely, D. Contagion and Differentiation in Unethical Behavior: The Effect of One Bad Apple on the Barrel. Psychol. Sci. 2009, 20, 393–398. [Google Scholar] [CrossRef] [PubMed]
- Sass, M.; Timme, F.; Weimann, J. The Dynamics of Dictator Behavior; CESifo Working Paper No. 5348; CESifo Group: Munich, Germany, 2015. [Google Scholar]
- Cartwright, E.J.; Lovett, D. Conditional cooperation and the marginal per capita return in public good games. Games 2014, 5, 234–256. [Google Scholar] [CrossRef]
- Sturm, B.; Weimann, J. Unilateral Emissions Abatement: An Experiment. In Experimental Methods, Environmental Economics; Todd, L.C., Kroll, S., Shogren, J.F., Eds.; Routledge: Abingdon-on-Thames, UK, 2008; pp. 157–183. [Google Scholar]
| 1 | This is also true for prisoner dilemma games (e.g., [3]). |
| 2 | Each subject is one independent observation in the partner treatment. In the stranger treatment, only the subject who participates in all waves is an observation. |
| 3 | We tested this stabilizing effect with a series of four repeated dictator game experiments at intervals of one week, once using the payoff mechanism described above and once paying subjects immediately after each wave. Prosocial behavior was indeed significantly more stable when the payoff mechanism “one out of four” was used. |

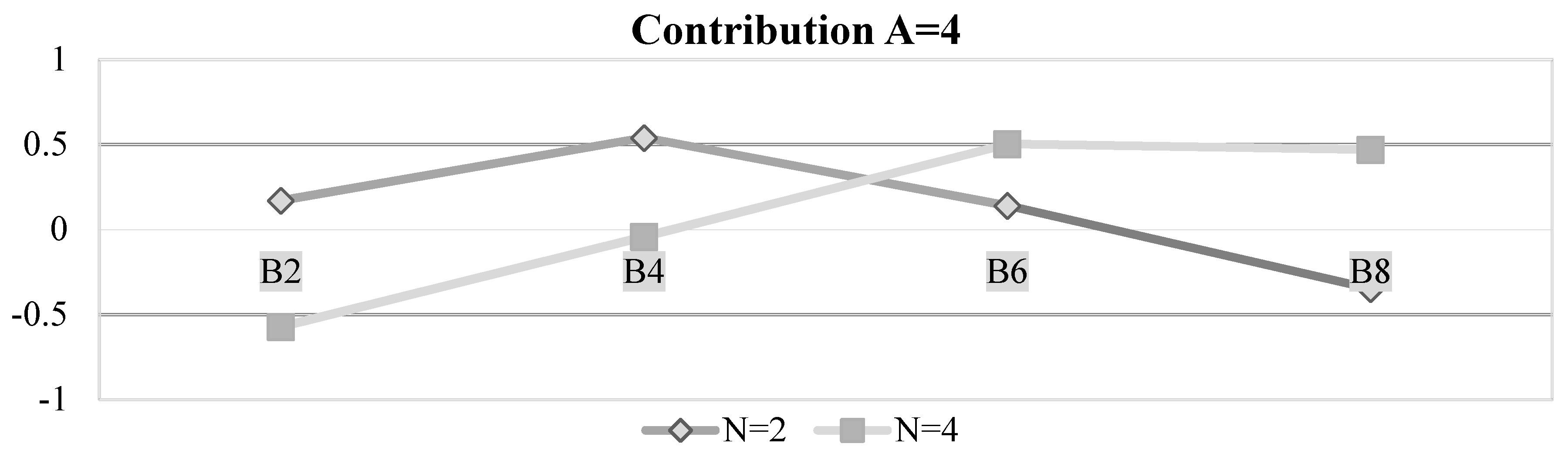
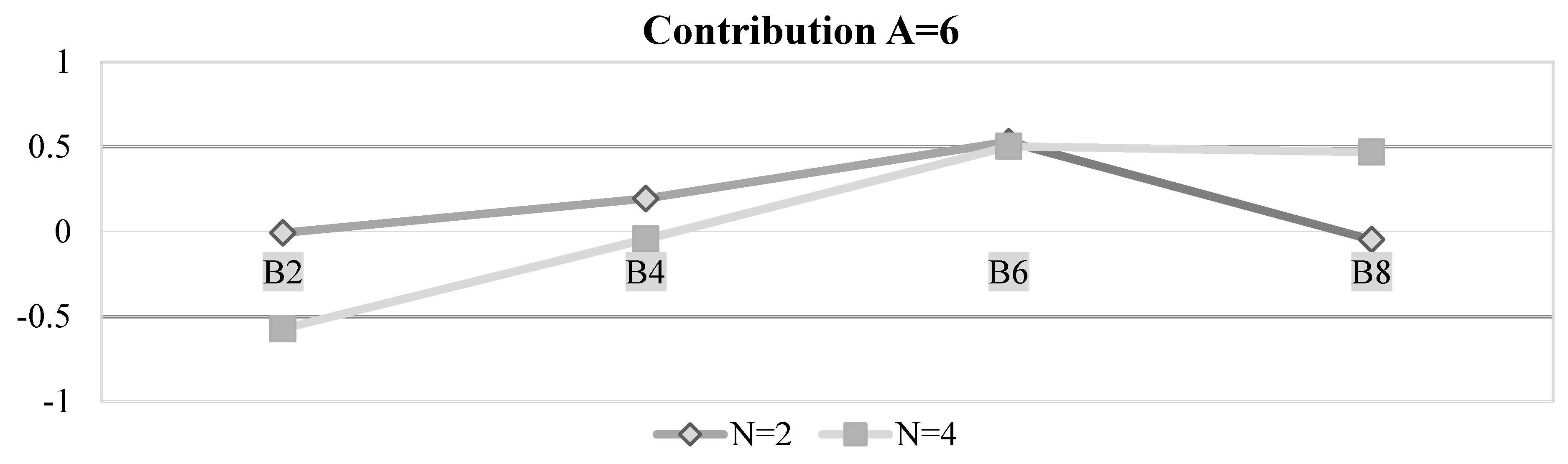
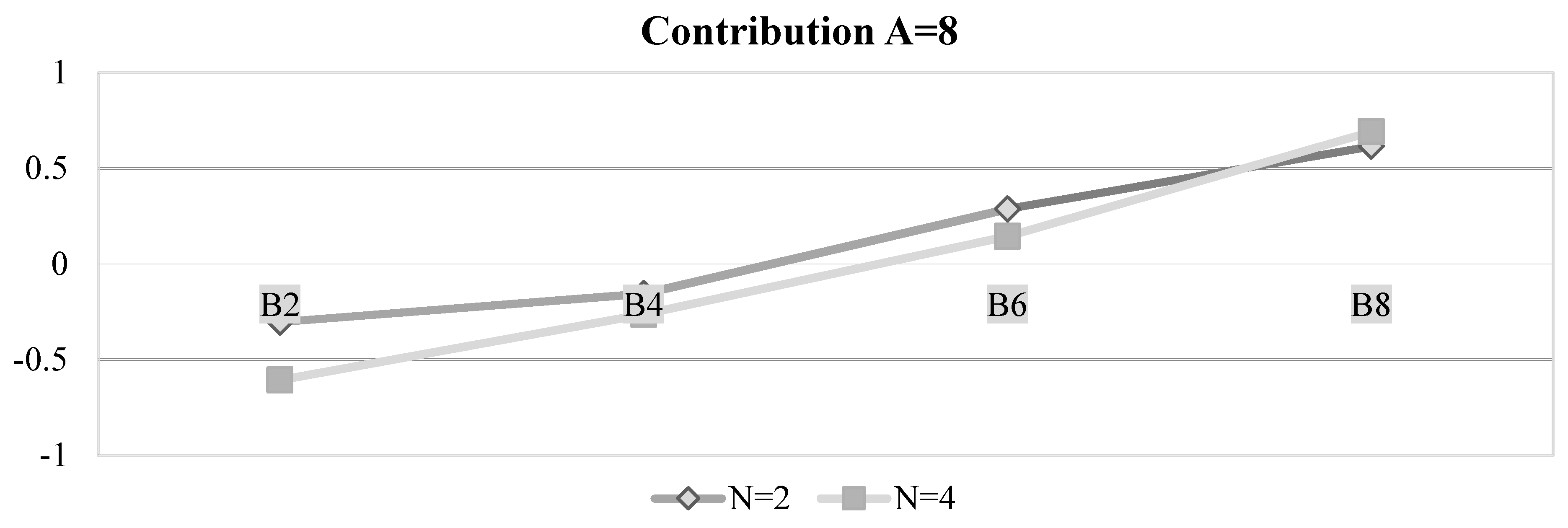
| Group Composition | |||
|---|---|---|---|
| Partner Treatments | Stranger Treatments | ||
| Group size | N = 2 | Independent observations: 22 ⌀ Earnings per wave: EUR 12.71 | Independent observations: 24 ⌀ Earnings per wave: EUR 13.13 |
| N = 4 | Independent observations: 25 ⌀ Earnings per wave: EUR 11.75 | Independent observations: 21 ⌀ Earnings per wave: EUR 13.09 | |
| Treatment | ⌀ = 0 | ⌀ = 1 | ⌀ = 2 | ⌀ = 3 | ⌀ = 4 | ⌀ = 5 | ⌀ = 6 | ⌀ = 7 | ⌀ = 8 | ⌀ = 9 | ⌀ = 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) | W1 vs. W2 | 0.084 ↓ | 0.894 | 0.985 | 0.741 | 0.753 | 0.985 | 0.769 | 0.741 | 0.752 | 0.504 | 0.900 |
| (b) | W2 vs. W3 | 1.000 | 0.099 ↓ | 0.259 | 0.171 | 0.095 ↓ | 0.052 ↓ | 0.015 ↓ | 0.046 ↓ | 0.026 ↓ | 0.123 | 0.900 |
| (c) | W3 vs. W4 | 0.317 | 0.306 | 0.961 | 0.961 | 0.755 | 0.478 | 0.851 | 0.859 | 0.828 | 0.927 | 0.602 |
| (d) | W1 vs. W3 | 0.084 ↓ | 0.091 ↓ | 0.805 | 0.898 | 0.714 | 0.476 | 0.426 | 0.663 | 0.448 | 0.917 | 0.721 |
| (e) | W2 vs. W4 | 0.317 | 0.083 ↓ | 0.284 | 0.167 | 0.348 | 0.251 | 0.048 ↓ | 0.099 ↓ | 0.108 | 0.227 | 0.330 |
| (f) | W1 vs. W4 | 0.528 | 0.579 | 0.791 | 0.844 | 0.475 | 0.638 | 0.402 | 0.454 | 0.329 | 0.541 | 0.491 |
| Treatment | ⌀ = 0 | ⌀ = 1 | ⌀ = 2 | ⌀ = 3 | ⌀ = 4 | ⌀ = 5 | ⌀ = 6 | ⌀ = 7 | ⌀ = 8 | ⌀ = 9 | ⌀ = 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) | W1 vs. W2 | 0.157 | 0.026 ↓ | 0.089 ↓ | 0.028 ↓ | 0.052 ↓ | 0.001 ↓ | 0.010 ↓ | 0.015↓ | 0.007 ↓ | 0.036 ↓ | 0.830 |
| (b) | W2 vs. W3 | 1.000 | 0.564 | 0.207 | 0.432 | 0.233 | 0.141 | 0.204 | 0.070↓ | 0.596 | 0.368 | 0.078 ↓ |
| (c) | W3 vs. W4 | 0.977 | 0.548 | 0.328 | 0.641 | 0.632 | 0.957 | 0.844 | 0.712 | 0.655 | 0.986 | 0.564 |
| (d) | W1 vs. W3 | 0.157 | 0.008 ↓ | 0.016 ↓ | 0.009 ↓ | 0.003 ↓ | 0.000 ↓ | 0.004 ↓ | 0.001 ↓ | 0.003 ↓ | 0.005 ↓ | 0.144 |
| (e) | W2 vs. W4 | 0.977 | 0.966 | 0.655 | 0.681 | 0.426 | 0.418 | 0.169 | 0.066 ↓ | 0.238 | 0.257 | 0.219 |
| (f) | W1 vs. W4 | 0.580 | 0.069 ↓ | 0.075 ↓ | 0.015 ↓ | 0.017 ↓ | 0.003 ↓ | 0.002 ↓ | 0.002 ↓ | 0.003 ↓ | 0.016 ↓ | 0.139 |
| Treatment | ⌀ = 0 | ⌀ = 1 | ⌀ = 2 | ⌀ = 3 | ⌀ = 4 | ⌀ = 5 | ⌀ = 6 | ⌀ = 7 | ⌀ = 8 | ⌀ = 9 | ⌀ = 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) | W1 vs. W2 | 0.083 ↓ | 0.044 ↓ | 0.056 ↓ | 0.055 ↓ | 0.024 ↓ | 0.013 ↓ | 0.059 ↓ | 0.040 ↓ | 0.111 | 0.083 ↓ | 0.401 |
| (b) | W2 vs. W3 | 1.000 | 0.564 | 0.965 | 0.655 | 0.150 | 0.275 | 0.060 ↑ | 0.072 ↑ | 0.091 ↑ | 0.145 | 0.307 |
| (c) | W3 vs. W4 | 1.000 | 0.564 | 1.000 | 0.564 | 0.096 ↓ | 0.099 ↓ | 0.032 ↓ | 0.031 ↓ | 0.096 ↓ | 0.026 ↓ | 0.046 ↓ |
| (d) | W1 vs. W3 | 0.083 ↓ | 0.084 ↓ | 0.065 ↓ | 0.039 ↓ | 0.091 ↓ | 0.114 | 0.575 | 0.432 | 0.656 | 0.471 | 0.728 |
| (e) | W2 vs. W4 | 1.000 | 1.000 | 0.581 | 0.581 | 0.581 | 0.680 | 0.563 | 0.779 | 0.290 | 0.410 | 0.598 |
| (f) | W1 vs. W4 | 0.083 ↓ | 0.027 ↓ | 0.037 ↓ | 0.034 ↓ | 0.014 ↓ | 0.057 ↓ | 0.209 | 0.160 | 0.459 | 0.311 | 0.643 |
| Treatment | ⌀ = 0 | ⌀ = 1 | ⌀ = 2 | ⌀ = 3 | ⌀ = 4 | ⌀ = 5 | ⌀ = 6 | ⌀ = 7 | ⌀ = 8 | ⌀ = 9 | ⌀ = 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) | W1 vs. W2 | 0.604 | 0.026 ↓ | 0.026 ↓ | 0.959 | 0.009 ↓ | 0.123 | 0.155 | 0.133 | 0.070 ↓ | 0.181 | 0.491 |
| (b) | W2 vs. W3 | 0.157 | 1.000 | 0.317 | 0.046 ↓ | 0.046 ↑ | 0.895 | 0.589 | 0.416 | 0.547 | 0.834 | 0.631 |
| (c) | W3 vs. W4 | 1.000 | 1.000 | 0.564 | 0.545 | 0.622 | 0.672 | 0.786 | 0.277 | 0.323 | 0.414 | 1.000 |
| (d) | W1 vs. W3 | 0.3173 | 0.026 ↓ | 0.026 ↓ | 0.046↓ | 0.368 | 0.450 | 0.303 | 0.103 | 0.087 ↓ | 0.408 | 0.200 |
| (e) | W2 vs. W4 | 0.157 | 1.000 | 0.545 | 0.106 | 0.166 | 0.251 | 0.296 | 0.747 | 0.240 | 0.468 | 0.446 |
| (f) | W1 vs. W4 | 0.317 | 0.026 ↓ | 0.026 ↓ | 0.213 | 0.600 | 0.508 | 0.453 | 0.587 | 0.719 | 0.139 | 0.050 ↓ |
| Treatment | ⌀ = 0 | ⌀ = 1 | ⌀ = 2 | ⌀ = 3 | ⌀ = 4 | ⌀ = 5 | ⌀ = 6 | ⌀ = 7 | ⌀ = 8 | ⌀ = 9 | ⌀ = 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) | N = 2 partner vs. N = 4 partner | 0.869 | 0.789 | 0.406 | 0.149 | 0.389 | 0.333 | 0.679 | 0.862 | 0.957 | 0.905 | 0.212 |
| (b) | N = 2 stranger vs. N = 4 stranger | 0.196 | 0.313 | 0.298 | 0.009 | 0.046 | 0.016 | 0.040 | 0.027 | 0.108 | 0.118 | 0.031 |
| (c) | N = 2 partner vs. N = 2 stranger | 0.686 | 0.560 | 0.536 | 0.332 | 0.536 | 0.775 | 0.599 | 0.780 | 0.425 | 0.328 | 0.455 |
| (d) | N = 4 partner vs. N = 4 stranger | 0.404 | 0.430 | 0.162 | 0.001 | 0.010 | 0.001 | 0.001 | 0.008 | 0.007 | 0.021 | 0.109 |
| Treatment | Wave 1 | Wave 2 | Wave 3 | Wave 4 |
|---|---|---|---|---|
| N = 2 Stranger | 0.909 ** | 0.912 ** | 0.961 *** | 0.966 *** |
| N = 2 Partner | 0.959 *** | 0.985 *** | 0.930 ** | 0.898 ** |
| N = 4 Stranger | 0.938 ** | −0.467 | −0.237 | −0.116 |
| N = 4 Partner | 0.815 * | 0.776 | 0.286 | 0.676 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sass, M.; Timme, F.; Weimann, J. Cooperation of Pairs. Games 2018, 9, 68. https://doi.org/10.3390/g9030068
Sass M, Timme F, Weimann J. Cooperation of Pairs. Games. 2018; 9(3):68. https://doi.org/10.3390/g9030068
Chicago/Turabian StyleSass, Markus, Florian Timme, and Joachim Weimann. 2018. "Cooperation of Pairs" Games 9, no. 3: 68. https://doi.org/10.3390/g9030068
APA StyleSass, M., Timme, F., & Weimann, J. (2018). Cooperation of Pairs. Games, 9(3), 68. https://doi.org/10.3390/g9030068





