Peer-Punishment in a Cooperation and a Coordination Game

Abstract

We elicit individual-level peer-punishment types in a cooperation (social dilemma) and a coordination (weakest link) problem. In line with previous literature, we find heterogeneity in peer-punishment in both environments. Comparing punishment behavior across the two environments within subject, we observe a high degree of individuals’ punishment type stability. However, the aggregate punishment demand is higher in the weakest-link game. The difference between the two environments is driven by subjects whose behavioral types are inconsistent rather than by a change in the punishment demand of those who punish in both environments.

1. Introduction

An extensive body of research documents human failure to cooperate in order to jointly provide goods if societal and individual interests are at odds (e.g., [1,2,3]). However, despite Nash equilibrium predictions of complete absence of cooperation in the presence of egocentric payoff maximizers, (some) individuals cooperate at least to some degree (e.g., [4,5]). Furthermore, if available, individuals and groups make use of an extensive set of institutions to mitigate these tragedies of the commons (e.g., [6,7,8]). Reputation (e.g., [9]), trust (e.g., [10]), pre-play communication (cheap talk) (e.g., [11]), or mutual monitoring (e.g., [12]) are such effective countermeasures, improving cooperation levels in the lab and in the field. Similarly, the availability of sanctions via peer-punishment (e.g., [3,13,14,15]) or as a centralized system (e.g., [16,17,18]) can lead to improvements in cooperation, resulting in higher provision of public goods.

While in public goods games the Nash equilibrium prediction is zero cooperation, there exist multiple Nash equilibria in coordination games. Therefore, a problem of tacit coordination on one of these many equilibria arises, which is not easily resolved (e.g., [19]). The literature investigates various mechanisms to overcome the potential coordination failures. For example, implementing incentives in coordination problems facilitates improvements in tacit coordination which persist even after the subsequent removal of these incentives [20]. Similarly pre-play communication fosters coordination and can be interpreted as self-commitment to previously conveyed statements [21]. Given the potential effectiveness of peer-punishment in cooperation problems, Le Lec et al. [22] examine costly social sanctions for their efficacy to overcome coordination failures in a Pareto ranked coordination setting. Social sanctions appear enhance tacit coordination and, in the long run, the accruing gain even make up for the initial social costs of punishment. These social sanctions in coordination problems are primarily implemented by high effort players [22]. Both findings, a potential increase in social efficiency and heterogeneity in punishment behavior, are mirrored in the literature studying the effectiveness of peer-punishment in public-good experiments (e.g., [4,14,23]). Naturally, the question arises if there is a link at the individual level between punishment behavior in the coordination and the cooperation environment—and our paper tries to shed light on this question.

The basic idea of our approach mirrors parts of the work by Peysakhovich et al. [24]. They have subjects play a variety of games and observe that subjects display behavioral “phenotypes”. Individual behavior seems to be consistent across cooperation games which they dub “cooperative phenotype”. Studying the minimum acceptance threshold in an ultimatum game and punishment decisions in a prisoner’s dilemma, they further show that phenotypical behavior also exists in the norm-enforcement domain. Moreover, behavior in the cooperation and the punishment domain seem to be only very weakly linked. Knowing about the existence of punishment phenotypes in social dilemmas [15,25,26], the consistency across games where cooperation interests are at play [24], and having observed the potential efficacy of peer-punishment in coordination problems, we investigate whether punishment phenotypes transmit to domains where selfish players might also be interested in using costly peer punishment. Thus, instead of looking at norm-enforcement within different cooperation environments, we analyze behavioral differences in norm-enforcement by varying the type of the underlying environment between games.

To this end, we had subjects play a cooperation dilemma in the form of a public goods game and a tacit coordination problem in the form of a weakest link game. Both games allow to observe others’ action and to subsequently apply costly peer punishment. Peer-punishment is implemented in a way that we can study individual level peer-punishment inclinations in these two environments. We do so by using an approach that entails a fine-grained elicitation of punishment decision and relies on the strategy method technology [4,27]. This allow us to classify punishment types in the spirit of Albrecht et al. [15] for each individual in each game separately and, consequently, to examine the robustness of punishment phenotypes (henceforth “types”) across the two settings.

We find that individual peer-punishment behavior is fairly consistent across the two games. Even more, observed differences in aggregate peer-punishment between the two games can be attributed almost exclusively to those subjects who change their peer-punishment type between games, i.e., who adjust their behavior on the extensive margin. In contrast, we observe only minor adjustments on the intensive margin, i.e., subjects who punish in both situations do so to a similar extent rather than applying (ceteris paribus) different amounts of punishment.

Our findings contribute to the recent literature that advances the strategy-method design to allow for the elicitation of individual level peer-punishment behavior in social dilemmas [15,25,26]. Differences in peer-punishment inclinations have been shown to have important economic implications, as group compositions (with respect to punishment types) significantly affect group outcomes in public goods games [15]. We show that the same could potentially apply to coordination games, too, since our results depict a large degree of heterogeneity in individual inclinations to apply costly sanctions in the coordination environment as well. Additionally, by comparing behavior at the individual level between coordination and cooperation environments, we further inform the question whether norm-enforcement is “generic”, i.e., if it is idiosyncratic to the individual (phenotype) rather than being environment-specific. While the aggregate effects suggest the latter, the individual level comparisons speak more in favor of a punishment phenotype which is domain-unspecific. This, in turn, might also be interesting in light of the ongoing debate about the fundamentals of peer punishment (e.g., [28] and the corresponding open peer commentaries). Moving away from the focus on whether individuals take costs to punish others and instead investigating what influences one’s willingness to punish seems crucial to gain a better understanding of the mechanisms underlying punishment in laboratory studies of cooperation.

This paper continues as follows: Section 2 describes the experimental setup and the implementation of the punishment strategy method (as first used by Kube and Traxler [18]). Section 3 explains the individual level peer-punishment type classification. Section 4 presents the results. Finally, Section 5 summarizes our findings and concludes.

2. Design and Implementation

The experiment consists of a public-goods game (VCM) and a weakest-link game (WL) with peer-punishment, both played repeatedly for 10 periods in stable groups of four but random rematching between games.1

2.1. VCM Game

We implemented a linear public goods game (VCM) with costly peer-punishment in the spirit of Fehr and Gächter [1] and Fehr et al. [2]. At the beginning of the game, subjects are randomly assigned into groups of four. Each subject $i\in \{1,2,3,4\}$ is endowed with 20 tokens and has to decide how many tokens to contribute to a public good, $g_i$, and how many to keep for herself, $20-g_i$. Each token allocated to the public good yields a marginal per capita return of $0.4$ tokens for each player of the group. At the second stage of the game, each subject i can assign punishment points to the other group members $j\ne i$, $d_{ij}\ge 0$. Assigning 1 punishment point costs 1 token for the punisher (1) and reduces the payoff of the punished subject by three tokens (2) (e.g., [2,23]). The payoff function is therefore:

$$\begin{array}{c}\hfill {\pi }_i=\underset{\mathrm{VCM}}{\underbrace{20-g_i+0.4\sum _{j=1}^4{g}_j}}\underset{\left(1\right)}{\underbrace{-1\sum _{j\ne i}{d}_{ij}}}\underset{\left(2\right)}{\underbrace{-3\sum _{j\ne i}{d}_{ji}}}.\end{array}$$

(1)

The unique subgame-perfect Nash equilibrium assuming self-centered money maximization is zero punishment and thus zero contributions to the public good.

We innovate on Albrecht et al. [15] and Kube and Traxler [18] by implementing the strategy method at the punishment stage in the first period of a repeated game rather than playing only a pure one-shot game.2 Throughout the 10 periods, subjects make their contribution decisions in the first stage of the game without knowledge of the contribution decisions of their peers in the current period. In the second stage, subjects receive information about the individual contributions by the other three players and can decide how many points to deduct from them.

The second stage of the first period varies in its setup from the subsequent nine periods by including the punishment strategy method as it is used in Kube and Traxler [18]. In the VCM, subjects are confronted with a sequence of contribution triples of the other group members and have to decide on assigning punishment points to the other subjects. The details of the procedure are as follows: each subject i faces 11 screens, where each screen presents one contribution triple: $\{g_j^t,g_k^t,g_l^t\}$, with $t\in [1,11]$; the subindices denote the contributions of the other group members, $i\ne j\ne k\ne l$. One of the 11 triples presents the “real” contribution decisions made by the other group members. The remaining ten triples are hypothetical combinations of contributions, each being randomly drawn from a pre-defined set of combinations (see below), shown to subjects in individually randomized sequence. For each triple, a subject has to decide how many punishment points (if any) to allocate to the other subjects. Each point that is assigned costs 1 to the punisher and reduces the punished player’s payoff by 3. We want subjects to face contributions from the entire strategy space while at the same time avoiding boredom and overstraining people with too many situations. The strategy space is thus partitioned into three intervals: low (L), intermediate (M), and high (H) contributions with $g^L\in \{0,\dots ,4\}$, $g^M\in \{5,\dots ,15\}$, and $g^H\in \{16,\dots ,20\}$. Based on these partitions, we consider 10 hypothetical combinations of low, intermediate and high contributions, as shown in

Table 1. Composition of contribution triplets.

Hypothetical:
$\{g^L,g^L,g^L\}$	$\{g^L,g^L,g^M\}$	$\{g^L,g^L,g^H\}$	$\{g^L,g^M,g^M\}$	$\{g^L,g^M,g^H\}$
$\{g^L,g^H,g^H\}$	$\{g^M,g^M,g^M\}$	$\{g^M,g^M,g^H\}$	$\{g^M,g^H,g^H\}$	$\{g^H,g^H,g^H\}$
+ Real:$\{{\mathbf{g}}_{\mathbf{j}},{\mathbf{g}}_{\mathbf{k}},{\mathbf{g}}_{\mathbf{l}}\}$

.

Within each of the 10 hypothetical contribution combinations, we randomly draw from a set of eight different triples.3 Therefore, one subject could face $\{0,2,3\}$ for the combination $\{g^L,g^L,g^L\}$ and $\{1,2,10\}$ for $\{g^L,g^L,g^M\}$, while a different subject might face $\{1,3,3\}$ for the former and $\{0,2,14\}$ for the latter.4

Once subjects complete their punishment decisions for all 11 screens, they are informed about the payoffs for Period 1 and continue to Period 2. For the duration of the VCM game, subjects remain in the same groups of four and interact repeatedly (which is known to the subjects). In the subsequent Periods 2–10, subjects do not play the strategy method but only see (and potentially punish) the real contributions of the other subjects.

Subjects are thoroughly instructed about the set up of the first period of the treatment and are made aware that 10 out of the 11 contribution triples are hypothetical. Further, it is common knowledge that only the punishment decisions for the real contribution triple are payoff-relevant. However, subjects neither know which one is the “real” triple, nor are they instructed on the procedure to generate the hypothetical triples. Following this protocol, we observe $3\times 11$ punishment decisions for each subject. Our analysis will explore only the choices made for the 30 hypothetical contributions.5

2.2. WL Game

The structure of the second game (WL) is identical to the VCM game but distinct in its implemented payoff function. We construct the payoff function for the WL game in the form of a coordination game. In this weakest-link game structure, solely the smallest individual contribution, rather than the sum of all contributions, determines the size of the group project. The individual payoff function is therefore defined as:

$$\begin{array}{c}\hfill {\pi }_i=\underset{\mathrm{Weakest}\mathrm{Link}}{\underbrace{\phantom{\sum _{j\ne i}{d}_{ij}}20-g_i+1.6\times \underset{i,j,k,l}{\min }\left(g_j\right)}}\underset{\mathrm{Punishment}}{\underbrace{-1\sum _{j\ne i}{d}_{ij}-3\sum _{j\ne i}{d}_{ji}}}.\end{array}$$

(2)

The weakest link game differs from a linear public goods game with respect to its monetary incentives and Nash-equilibria. While in VCM the subgame perfect Nash equilibrium of zero contributions is unique, it is only one of many Nash-equilibria in the weakest link game. In WL, every common effort level chosen by all members of a group $(g_i=g_j=g_k=g_l)$ are part of a Nash-equilibrium. Moreover, equilibria in the WL game can be ranked with $g_{i,j,k,l}=20$ being the most efficient and payoff dominant and $g_{i,j,k,l}=0$ being the least efficient and risk dominant equilibrium.

Apart from the payoff function, and thus the standard equilibrium predictions, everything else is kept constant between treatments. Again, subjects play repeatedly for 10 periods in fixed groups of four, contribute to a common group project on the first stage of the game and can sanction their peers on the second stage of the game (at the identical costs as in VCM to isolate the potential differences in demand for punishment, which we are interested in, from potential price effects, e.g., [30]). Subjects once more face a punishment stage strategy method in the first period of the repeated WL game, again consisting of 11 screens. The hypothetical triples were randomly drawn from the same predefined contribution triple space that was employed for the VCM game (again, see Appendix A for the complete list of triples).

2.3. Implementation

We evaluated data for 228 subjects collected in 10 sessions at the BonnEconLab in Bonn, Germany. For every subject, we observed $2\times 30$ (excluding the $2\times 3$ real) peer-punishment decisions from the strategy methods implemented in the first period of the VCM and WL, respectively. The treatment order was counterbalanced between subjects. As both games only differ in their payoff functions, we took great care to ensure that subjects thoroughly understood the treatment differences.6 The treatments were implemented using ztree [31] and subjects were recruited using Hroot [32]. Including a follow-up questionnaire, a session lasted $\approx 140$ min. Subjects earned on average $\approx 22$ Euros in total, including a show-up fee.

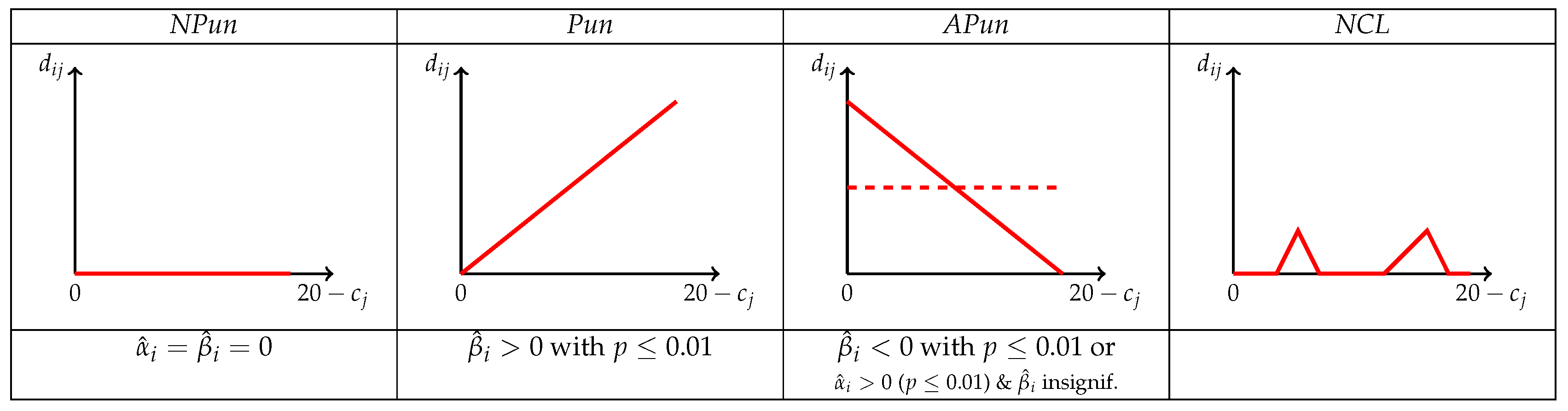
3. Punishment Types

In line with Albrecht et al. [15], we classify punishment types with respect to their punishment assigned to tokens not contributed ($20-g_j$) to the group project in the VCM or WL game. For each of the 228 individuals, we estimate the model

$$\begin{array}{c}\hfill d_{ij}={\alpha }_i+{\beta }_i(20-g_j)+{\epsilon }_i\end{array}$$

(3)

twice, using the 30 punishment observations obtained in the respective strategy methods, where $d_{ij}$ is the punishment assigned by i to peer j and ${\beta }_i$ is the demand for punishment conditional on tokens not contributed by j.

Subjects are classified into three behavioral categories:

• A subject is classified as a “non-punisher” (NPun) if zero punishment points are assigned in each of the 30 punishment decisions, i.e., $d_{ij}=0$ for all $g_j$. In Equation (3), this is depicted by ${\widehat{\alpha }}_i={\widehat{\beta }}_i=0$.
• Subjects that target their punishment primarily towards those that contribute little or nothing to the public good have a punishment pattern that is upward sloping in $(20-g_i)$. These subjects, with ${\widehat{\beta }}_i>0$ and $p\le 0.01$, are classified as “pro-social punishers” (Pun).
• Subjects are classified as “anti-social punishers” (APun) if their punishment is either increasing in the other’s contribution $g_j$, i.e., if ${\widehat{\beta }}_i<0$ and $p\le 0.01$, or if they display a significant positive but otherwise unsystematic level of punishment, i.e., ${\widehat{\alpha }}_i>0$ with $p\le 0.01$ and an insignificant slope coefficient ${\widehat{\beta }}_i$ with $p>0.01$.7

Punishment patterns that cannot be assigned to one of these three types are summarized in a group of non-classified (NCL) patterns. The different punishment types and their stylized punishment patterns are illustrated in Figure 1.

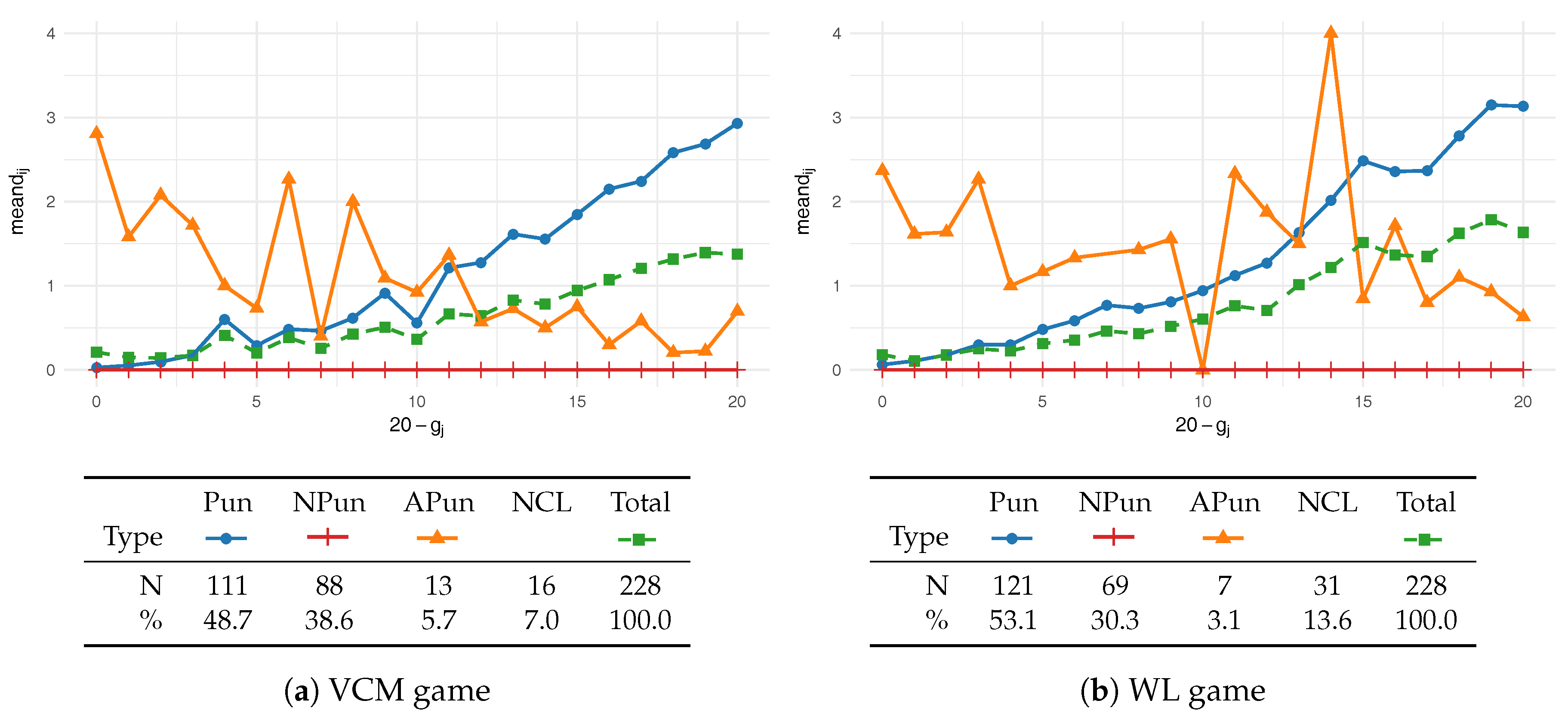
4. Results

Figure 2a presents the distribution of punishment patterns for the 228 subjects classified based on VCM observations. Overall, 48.7% show pro-social punishment patterns, punishing low contributors more severely than high contributors; 38.6% of subjects do not invest in peer-punishment in any of the 30 decision situations and are classified as NPun; 5.7% of subjects classify as APun; 7% do not fit into one of the three classifications and remain non-classified.

Figure 2b shows the distribution of punishment patterns classified for the same individuals but playing the WL game. We observe an increase in pro-socially punishing Pun-types (53.1%) and non-classifiable individuals (13.6%). This increase goes along with a reduction in non-punishing NPun (30.3%) and anti-socially punishing APun (3.1%) individuals. A Fisher’s exact test, significant on the 1% level, supports the observed differences in type distributions between treatments.

Combining the two punishment classifications across the two games within subjects allows us to elicit the individual punishment type stability.

Table 2. Individual punishment type stability.

	WL-Game
VCM↓	Pun	NPun	APun	NCL	Total
Pun	90	9	0	12	111
%	[39.5]	[3.9]	[0.0]	[5.3]	[48.7]
NPun	21	57	0	10	88
%	[9.2]	[25.0]	[0.0]	[4.4]	[38.6]
APun	2	1	7	3	13
%	[0.9]	[0.4]	[3.1]	[1.3]	[5.7]
NCL	8	2	0	6	16
%	[3.5]	[0.9]	[0.0]	[2.6]	[7.0]
Total	121	69	7	31	228
%	[53.1]	[30.3]	[3.1]	[13.6]	[100.0]

Note: The vertical axis presents the individual classification for VCM, the horizontal for WL. More than 65% of subjects are consistent across the two settings in their punishment behavior. The largest type-inconsistent group is formed by subjects who are Non-Punishers in VCM but Punishers in WL (9.2%).

presents the results. The majority of subjects (67.7%, main diagonal) show a consistent punishment type across the two games, i.e., subjects classified as Pun, NPun, and APun in VCM remain as such in WL. Among subjects changing their behavior on the extensive margin, the single largest group (NPun × Pun) increases their pro-social punishment in WL compared to VCM (21 subjects). Intriguingly, no subject punishes anti-socially in WL that did not do so already in VCM.

Result 1.

Within each game setting, there is heterogeneity in individual-level punishment behavior. Across game settings, a majority of subjects shows a consistent inclination for punishment behavior.

Figure 2 also presents the average punishment observed in the respective games. The figures hint at a slight increase in punishment demand in WL over VCM.

Table 3. Punishment demand across games.

	Assigned Punishment ${\mathit{d}}_{\mathbf{ij}}$
	All	Intensive	Extensive		${\mathbf{m}\mathbf{i}\mathbf{n}}_{\mathit{i},\mathit{j},\mathit{k},\mathit{l}}\left({\mathit{g}}_{\mathit{j}}\right)$
	(1)	(2)	(3)		(4)
$(20-g_j)$	0.068 ***	0.086 ***	0.031 ***		0.051 ***
	(0.007)	(0.009)	(0.008)		(0.007)
$D.WL$	−0.017	0.030	−0.114		−0.030
	(0.031)	(0.029)	(0.070)		(0.031)
$D.WL\times (20-g_j)$	0.017 **	0.001	0.050 ***		0.020 ***
	(0.007)	(0.006)	(0.018)		(0.007)
${\min }_{i,j,k,l}\left(g_j\right)$					0.460 ***
					(0.051)
$D.WL\times {\min }_{i,j,k,l}\left(g_j\right)$					−0.094
					(0.064)
Constant	−0.000	−0.055	0.114		0.034
	(0.062)	(0.083)	(0.077)		(0.061)
N	228	154	74		228
Obs.	13,680	9240	4440		13,680
adj.$R^2$	0.201	0.263	0.135		0.217

Note: Individual level fixed effects estimation for 228 subjects. Screen order is used as time variance to capture potential ordering effects. Column 1 estimates the model for the full dataset. Column 2 estimates the model for type-consistent subjects and Column 3 for subjects exhibiting behavioral changes on the extensive margin. Column 2 only includes subjects exhibiting Pun × Pun, NPun × NPun, and APun × APun classifications across games. The six NCL × NCL subjects are not included in Column 2 estimations. Cluster robust standard errors in parentheses. **, and *** represent p ≤ 0.1, p ≤ 0.05, and p ≤ 0.01, respectively.

presents individual level fixed effects regressions for the model in Equation (4),8 investigating aggregate changes between the two settings.

$$\begin{array}{c}\hfill d_{ij}={\alpha }^{\prime }+{\beta }_1^{\prime }(20-g_j)+{\beta }_2^{\prime }D.WL+{\beta }_3^{\prime }D.WL\times (20-g_j)+\epsilon \end{array}$$

(4)

where ${\beta }_1$ captures the average punishment demand for one-token kept privately in the VCM, ${\beta }_2$ indicates level changes between VCM and WL, and ${\beta }_3$ captures changes in the slope of punishment demand per privately kept token.

Column 1 shows the results for estimating the model in Equation (4) for the complete sample, supporting the visual findings. The coefficient for the interaction effect $D.WL\times (20-g_j)$ is significant at the 5% level and of considerable magnitude $({\widehat{\beta }}_2=0.017)$ when compared to the coefficient $({\widehat{\beta }}_1=0.068)$ of $(20-g_j)$. In fact, the increase in punishment demand from VCM to WL is about 25%.

However, it is unclear whether the 25% increase in the average peer-punishment demand observed in Column 1 of Table 3 is driven by changes on the extensive or intensive margins (or both). Changes on the intensive margins can be identified by looking at adjustments in the punishment demand of those subjects that show a consistent peer-punishment phenotype across games (Pun × Pun, NPun × NPun, and APun × APun). Recall that, for these subjects, our classification approach still allows for changes in the demand for punishment per token not contributed (${\widehat{\beta }}_i$ in the model in Equation (3)), as long as no sign change occurs and the respective p-value remains significant (≤0.01). By contrast, changes along the extensive margins are driven by all other subjects, i.e., those that change their types between games or are not classifiable at all (NCL). Column 2 presents the results for the former group (“type-consistent”) and Column 3 for the latter group (“type-inconsistent” subjects), respectively.

The interaction effect $D.WL\times (20-g_j)$ for changes in punishment demand between VCM and WL is not significant on any conventional level for type-consistent subjects. Individuals with stable peer-punishment inclinations therefore show no significant changes in their demand for peer-punishment across these two settings. As expected, given the aggregate findings, the picture is different for inconsistent types. On average, subjects that change their punishment behavior across games show a significant increase in punishment demand in the WL game.

Result 2.

Average demand for punishment in a weakest link game increases compared to punishment demand in a public goods game. The increased punishment demand is caused by changes on the extensive rather than by changes on the intensive margin.

A potential cause for the increase in average punishment demand in the WL could be the, ceteris paribus, lower expected payoff in the WL, resulting in higher penalties for the lowest contributor in the group, as she determines the payoff in the coordination setting of the WL game. To test this assumption, we extended the model in Equation (4) by including a dummy for the lowest contribution ${\min }_{i,j,k,l}\left(g_j\right)$ and an interaction effect $D.WL\times {\min }_{i,j,k,l}\left(g_j\right)$ capturing changes in sanctions for the lowest contribution in the WL compared to the VCM.

$$\begin{array}{cc}\hfill d_{ij}={\alpha }^{″}& +{\beta }_1^{″}(20-g_j)+{\beta }_2^{″}D.WL+{\beta }_3^{″}D.WL\times (20-g_j)\hfill \\ \hfill & +{\beta }_4^{″}\underset{i,j,k,l}{\min }\left(g_j\right)+{\beta }_5^{″}D.WL\times \underset{i,j,k,l}{\min }\left(g_j\right)+\epsilon \hfill \end{array}$$

(5)

The results are shown in Column 4 of Table 3. It is apparent that the lowest contribution in VCM is sanctioned at a considerable premium $({\min }_{i,j,k,l}\left(g_j\right)=0.460)$. However, subjects do not take the changed payoff importance of the lowest contribution under the WL-regime into special considerations. The interaction effect $D.WL\times {\min }_{i,j,k,l}\left(g_j\right)$ is insignificant and, if anything, its sign indicates a reduction of the punishment premium.

Result 3.

Despite its increased importance for payoff formation in the weakest-link game, we find no evidence that ${\min }_{i,j,k,l}\left(g_j\right)$ is sanctioned differently in WL compared to VCM.

5. Summary

Innovating on the peer-punishment strategy method implemented by Kube and Traxler [18] and Albrecht et al. [15], we set up both a cooperation and a coordination problem with peer-punishment to examine individual-level heterogeneity in peer-punishment behavior across the two games. Both games only differ in the structure of their payoff function and otherwise share the same game parameters, allowing for a high degree of comparability.

We show that heterogeneity in peer-punishment behavior, as observed in social dilemma games (e.g., [15,23,24,25,26]), also occurs in coordination problems and that a majority of subjects exhibits a consistent peer-punishment phenotype that transfers from one domain to the other, despite differences in the monetary incentive structure.

On the aggregate level, we still observe significant differences in demand for peer-punishment. Aggregate demand for peer-punishment is higher in the weakest link game compared to a linear public-goods game. We show that the increase in aggregate sanctions is attributable to those subjects that display an inconsistent peer-punishment phenotype. Individuals with a consistent phenotype transfer their peer-punishment demand between domains without significant changes in the aggregate peer-punishment intensity.

Lastly, we investigate whether the higher demand for peer-punishment could also stem from a higher level of sanctions towards the lowest contributions in the weakest link game, given that the lowest contribution exclusively determines the group payoff in that setting. Even though there is a significant additional penalty on the lowest contribution in both settings, we find no evidence for altered peer-punishment behavior towards the lowest contributions in the weakest link game compared to the VCM.

Having shown a large degree of consistency of punishment behavior, in line with Peysakhovich et al. [24], future research might focus on determining factors that cause inconsistent behavior across domains. Moreover, as (not only) Albrecht et al. [15] showed that pro-social punishers can positively affect group outcomes, and given the malleability of some persons’ punishment type shown here, it might be worthwhile to study nudges towards social sanctions as to induce non-punishers to engage in pro-social punishment, too. Furthermore, the existence of cross-domain consistent phenotypes might also be of use for algorithmic modeling approaches by helping to determine the efficacy of phenotypes across game settings. Finally, the applied strategy method [15,18] would allow for determining individual peer-punishment profiles and could provide a rich set of information to model agents for evolutionary approaches.