1. Introduction
A voluntary contribution mechanism (VCM) is a decision environment where each individual makes a decision about how to allocate an endowment of a productive factor between private goods (where consumption benefits accrue only to the individual) and public goods or a joint project that benefits all group members. The individual contributions are collected through some aggregating mechanism, and the aggregated contributions are then distributed to the participants, usually in equal shares. The linear voluntary contribution mechanism, in which the individual contributions are added up and then multiplied by some constant, is the most common public goods institution in economic experiments, as noted by [
1].
Consequently, the linear public goods games with dominating strategy equilibria at the boundary of the action set have been extensively studied by experimenters (for a meta-analysis, see [
2]). However, designs implementing non-linearities in the production of either the private goods or the public goods are less common, and there are only a few studies that employ a nonlinear earnings function in both the private and the public goods.
While simple aggregation of individual contributions through summing them up is familiar and intuitively appealing, joint production or team work organized towards a common goal can be characterized by a broad range of production technologies differing in their degree of complementarity, of which standard summation technology is but one example. Consequently, the technology aggregating individual contributions can play a major role in deciding how much effort a group exerts toward a common goal. This is not without real-life parallels: For an academic reader, a not too unfamiliar situation is one where the coauthors writing a scientific article consider how much effort to put in designing, analyzing and reporting the results of the study, a case in which their actions can be either strategic complements or substitutes, depending on their personal skill sets and the characteristics of the paper, and it is ultimately these factors that determine the success of the whole endeavor. Other such examples can be found in a wide variety of situations requiring joint effort, ranging from team sports to the operation of a surgical team, to name a few. In short, complementarities can be found in any situation where a team of experts with different specializations works towards a common goal.
In the games where actions are strategic complements, the change in one player’s choice gives the other player an incentive to move in the same direction. In other words, the increased activity level of a player has a positive effect on the marginal payoff of the other players, whereas in games with strategic substitutes, the opposite is true. That is, in a game with strategic complementarities, the best response to increased cooperation by one player is to increase his/her own level of cooperation, but in the case of strategic substitutes, the increased activity level of one individual is offset by less activity by the other players.
In the limiting case, the actions that are strategic complements have the weakest link property: the minimum effort determines the overall level of production. At the other extreme, strategic substitutes converge to the best shot actions, where the highest effort level determines the yield from the public goods [
3]. When the canonical public goods model of [
4] is generalized by specifying a more general CES social composition function (SCF) for aggregating individual contributions, it is possible to construct a whole spectrum of production technologies ranging from the weakest link to the best shot in their degree of complementarity [
5]
1.
This paper reports results from an experiment designed to examine an intermediate case: We study a team production game in which private consumption has diminishing marginal benefits and the individual contributions to the joint project exhibit pairwise strategic complementarities, which means that the production technology is essentially a Cobb–Douglas function with increasing returns to scale. We compare the observed behavior under strategic complementarities to a baseline treatment, where the public goods game has quadratic private payoffs and the standard social composition function is linear, i.e., the unweighted sum of the individual contributions. In both settings, partial contribution is a unique equilibrium action. We specify the coefficient for the return from the public goods in the linear setup and the degree of complementarity between actions in the game with strategic complements in such a manner that the respective payoffs from both the minimum action and the maximum action profiles and the equilibrium contribution level to the joint project are the same under both production technologies when the group size is n = 5.
The experimental evidence suggests that the strategic complementarity of Bertrand markets induces more cooperative (collusive) behavior than the case with strategic substitutes of Cournot markets [
6,
7,
8]. However, the costs of deviating from the best response in Bertrand markets are higher than in Cournot markets, and consequently, the former converge to Nash equilibrium predictions more quickly and more completely [
9]. For a theoretical overview of Cournot and Bertrand oligopolies and supermodular games, see [
10]. Our experiment contributes to this research by examining the behavior under strategic complementarity in a public goods or a team production environment, where in contrast to competitive oligopoly experiments, there is a conflict between individually-rational and socially-optimal activity. The work in [
11] observed that there is significantly more cooperation with actions exhibiting strategic complementarities than with strategic substitutes in finitely-repeated two-player games with a Pareto-inefficient Nash equilibrium. We find that in our experiment, the level of over-contribution in a team production game with strategic complementarities and interior Nash equilibrium is much higher than in a public goods game with the same interior equilibrium action, but the standard linear social composition function.
In addition to the form of the composition function, we manipulate the group size in both treatments. The group size effect in VCM games with the unique Nash equilibrium at the lower boundary of the action set (full free-riding) is well documented (see, e.g., the survey by [
12]). The first systematic studies documenting the effects of the group size (or lack thereof) while holding the other variables constant was conducted by [
13,
14], who carefully carried out experiments that were designed so that the group size effect could be isolated from the effects of changes in the marginal incentive to contribute towards the joint project, which they called marginal per capita return (MPCR). They found that the MPCR multiplier has a strong effect, but that group size has little effect if the MPCR is large.
In the present study, we keep the MPCR constant in the baseline treatment by adjusting the multiplier when the group size is altered from n = 5 to n = 2. This is necessary in order to keep the equilibrium action the same within the baseline treatment. We observe a weak numbers effect: on average, the subjects contribute slightly more in the linear public goods game in groups of five. In contrast, the numbers effect is much stronger in the game with strategic complementarities.
2. The Social Dilemma Games with Diminishing Private Benefits
In
Section 2.1 and
Section 2.2, we will define the earnings functions for each treatment so that the equilibrium level of contribution is two or 20% of the initial endowment (
) in both treatments, when the group size is five. In the larger groups (
n = 5), also the minimum and maximum action profiles yield the same payoff for each group member in each treatment.
Section 2.3 will provide details for how these experimental parameters are obtained. Moreover, when the group size is reduced to two, the game theoretic equilibrium contribution drops considerably in the treatment with complementarities, but remains the same in the linear baseline treatment. This is shown in
Section 2.4, which presents the comparative statics predictions with respect to experimental parameters. Respective hypotheses are presented in
Section 2.5, which concludes
Section 2.
2.1. Linear Baseline VCM Game
The games studied belong to the class of voluntary contribution mechanism games with the equilibrium action in the interior of the action set. Individuals decide how much of their endowment to invest in a private project A and how much to contribute towards a joint project B. As noted by [
15], the simplest way to introduce non-linearity in the private goods is by using a quadratic payoff function:
where
e denotes the endowments given to the subjects,
the contribution to the public goods by subject
i and
a and
b are constant parameters. In the experiment, this is called a payoff from the investment in the private project A. The earnings function determining payoffs from the private activity is kept the same throughout the experiment, whereas the functional form of the social composition function that determines the payoff from the joint project varies between the treatments.
In the standard linear summation treatment, the experimenter multiplies the sum of the contributions by the subjects by some constant
M and divides this equally by the entire group,
:
In the experiment, we call this a payoff from the investment in the joint project B.
Combining the private and the public earnings functions, we obtain the VCM with diminishing returns from private consumption:
where:
is the dominating equilibrium action equalizing marginal return from private and public goods, independent of other players’ choices.
2.2. Treatment with Pairwise Complementarities in Joint Production
Also in this treatment, the private benefits are given by an identical quadratic payoff function as in the linear treatment. However, the investment in the joint project with the complementary earnings function is defined as follows:
that is, for each subject in the group, the investments by the other members are summed up and then multiplied by her contribution and some constant
w, reflecting the degree of complementarity between their actions. Collecting the private and public parts, we obtain the following general earnings function:
By expanding and rearranging Equation (
2), we obtain the linear quadratic payoff function:
where
and
.
To solve for the Nash equilibrium action for any weight
in Equation (
3), we employ the results provided in Ballester et al. [
16]; also see Jackson [
17]. This is obtained by differentiating Equation (
3) with respect to
and setting this equal to zero, which gives us a solution for any VCM game with pairwise complementarities:
Given that in our case,
a,
b and
w are the same for every player, we can write an equation in vector form characterizing the solution to Equation (
4) as:
where
I is the identity matrix and 1 a vector of ones. Because the action set is bounded above by the size of the initial endowment, we know that the interior solution to a game with strategic complementarities and linear best reply is unique [
18].
Assuming symmetric parameters for each agent, we can straightforwardly solve the symmetric Nash equilibrium level of individual action:
2.3. Experimental Parameters
In order to ensure that the observed variation between treatments is due to the differences in the form of the production function and does not result from the difference in the scale of payoffs, the outcome of both the minimum and the maximum action profiles should match between the treatments, in addition to both games having the same equilibrium action (but not necessarily the same equilibrium payoff). The outcome from the minimum action profile is identical in both treatments by definition. Fixing the parameter
e, the initial endowment, the parameter
a, the multiplier of the investment in the private project A, and the cost parameter
b, we obtain a system of two equations in two unknowns (multipliers
w and
m):
and:
where Equation (
7) imposes the restriction that the equilibrium action is the same in both treatments and Equation (
8) ensures that the payoff from the maximum action is the same across treatments
2. Solving for
w in Equation (
8) and substituting it into Equation (
7), it is possible to define the group payoff multipliers
m and
w as follows:
2.4. Comparative Static Predictions
Given the specification of the linear earnings function Equation (
1), we can make some comparative static predictions: If the coefficient
a is increased or cost parameter
b is decreased, the equilibrium contribution level falls as the private project becomes more profitable. In contrast, the equilibrium action is increasing in the public goods multiplier
m. In the game with strategic complements, given by Equation (
2), the equilibrium contribution levels are also decreasing in
a and increasing in
b. Furthermore, the equilibrium contribution level is increasing in
w, assuming that it is non-negative (see [
17], p. 291–292, for a sketch of the proof). However, the group size has an effect only in the game with strategic complementarities, where the level of the equilibrium action is increasing in group size, whereas the dominant action in the linear game is the same irrespective of the group size.
We set the endowment parameter
e to 10 (tokens). Choosing
for the quadratic multiplier, the maximum value of parameter
a approaches 20 at the limit, given the restriction
. Given these parameters,
a and
b, we fix the multiplier
a to the largest possible integer value (i.e., [
19]) satisfying this constraint. Given Solution (1), this parametrization yields multiplier values
or
in the linear social composition function (SCF) treatment and
in the complementary SCF treatment with five group members. In order to avoid implementing an unintended focal point at the middle of the strategy space to which the subjects might feel attracted, we choose parameters so that the game theoretic solution is less than half of the endowment (e.g., [
19]; see also [
20]). With the chosen parameters, the resulting symmetric interior Nash action is equal to two, or 20% of the initial endowment.
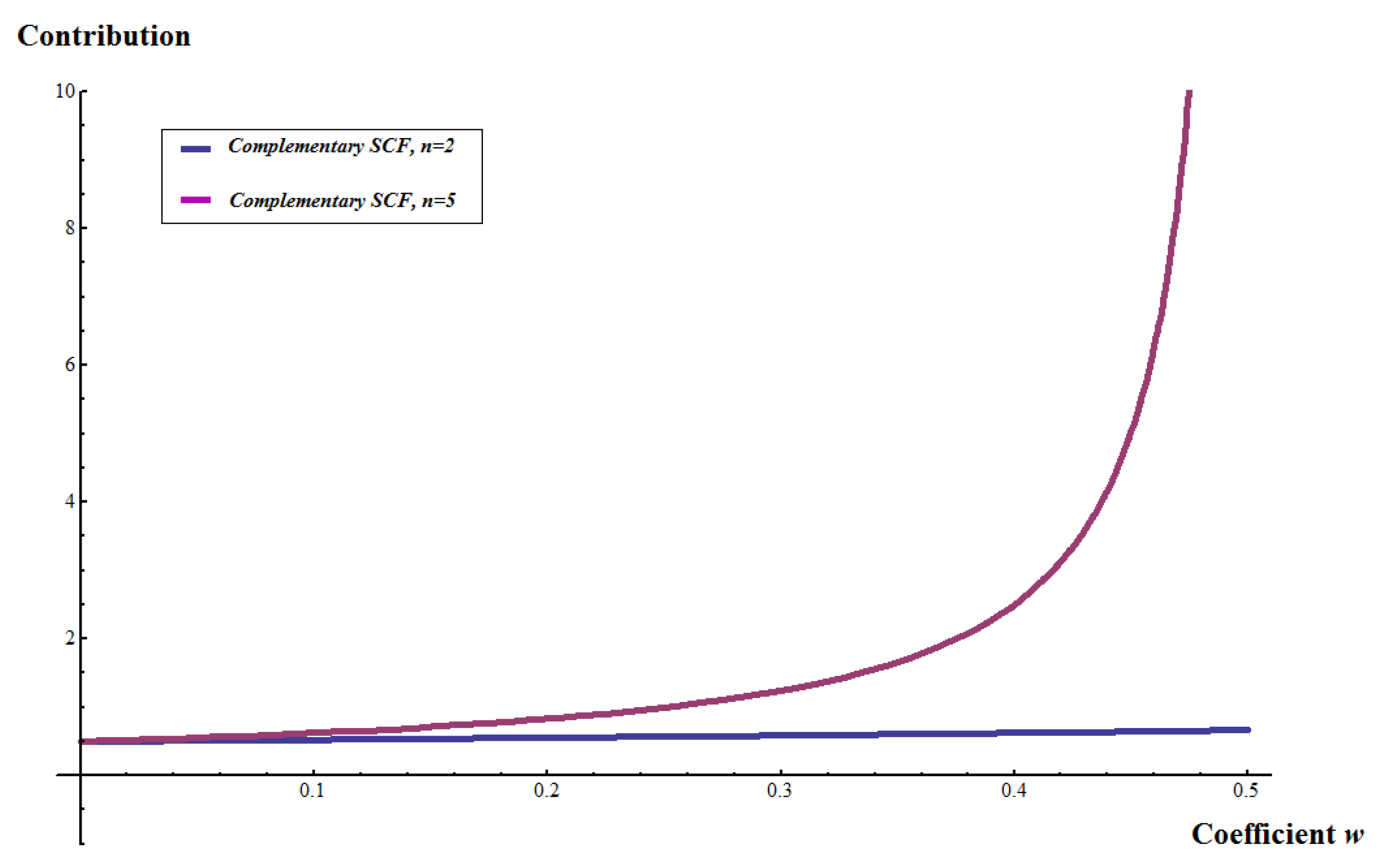
The multiplier
w in the game with complementary SCF is interpreted here as the degree of the complementarity between the actions of the group members in their joint production. Naturally, the larger the group, the more bite this has in determining the equilibrium action level. Already with a group size of
members, the equilibrium action is very sensitive to the magnitude of
w, as can be seen in
Figure 1. Note that when
, the system has a boundary solution where everyone contributes every token towards the public goods in groups of five,
. Assuming
, in groups with five members, the limiting value for the multiplier is 0.5, as any larger value would not lead to a well-defined or non-negative equilibrium action.
However, in small groups with two members, the size of
w has a very small effect on the level of the equilibrium action, which is shown by the nearly horizontal blue line in
Figure 1. Given this negligible variation in the level of equilibrium action with respect to parameter
w in small groups, we concentrate on studying experimentally how the group size affects observed behavior, while keeping the parameter
w constant.
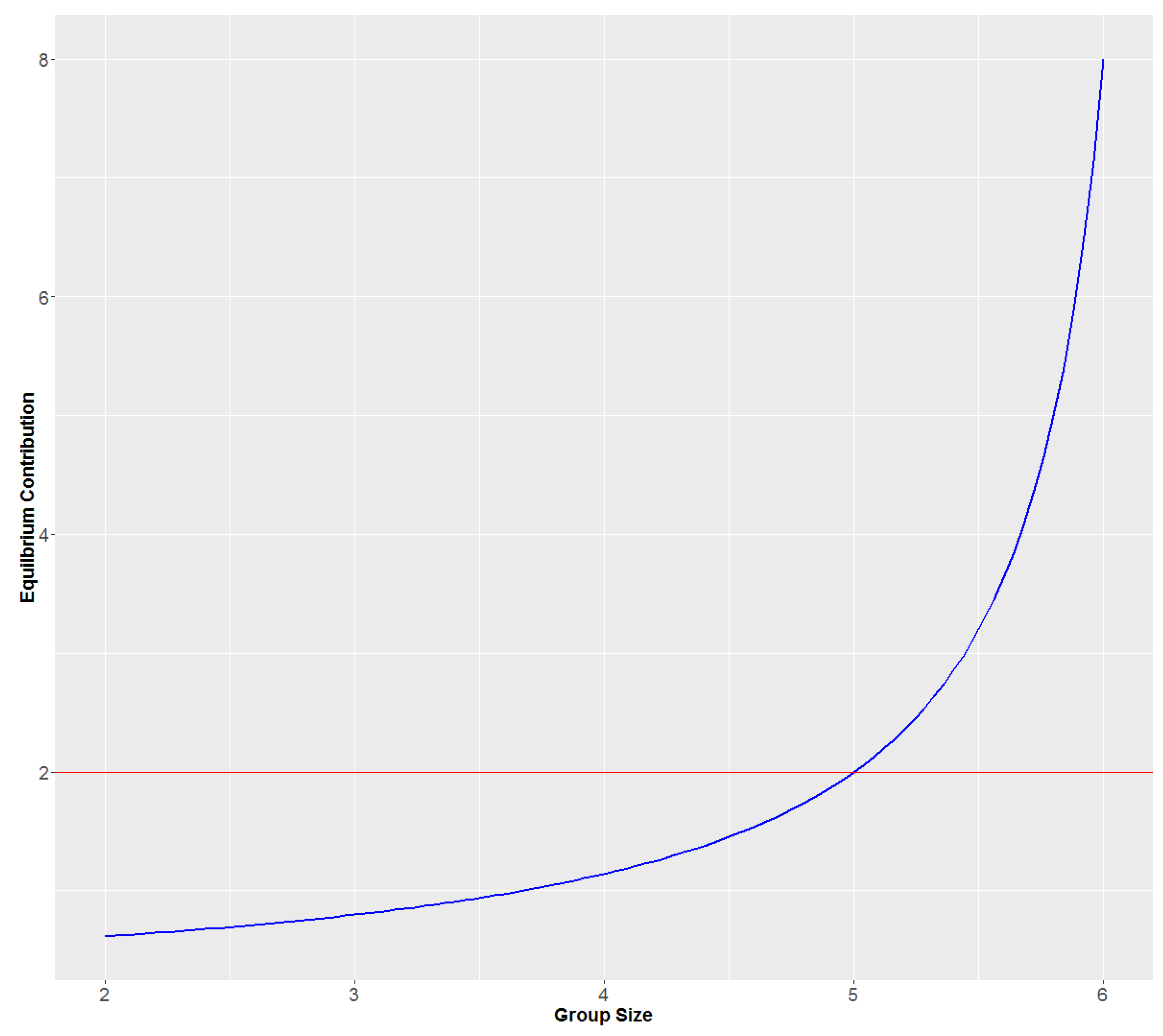
In the treatment with complementarities in the public goods production, the larger the group size is, the higher is the respective equilibrium action, as is depicted by the blue line in
Figure 2. However, the group size has no effect on the equilibrium level when the aggregation technology is linear, as is illustrated by the red line plotted in the same figure. It is also worth noting the solution to Equation (
7) at group size
n = 5.
In the small groups, fixing w at 3/8, the equilibrium action is 8/13 or 0.615 tokens with group size , and the corresponding return from the public goods is 0.14, whereas the action level (0.80 tokens) maximizing joint payoffs is very close to this. As noted above, in the linear baseline treatment, the equilibrium action remains two also in the small groups.
2.5. Hypotheses
Given the multiplicative effect of group size on the equilibrium action and assuming monetary payoff maximizing agents, we can make the following game-theoretic predictions:
We should:
Hypothesis 1 (H1). Under the complementary aggregation technology (pairwise complementary treatment VCM), observe a decrease in contributions to the joint project when the group size is reduced from five to two.
Hypothesis 2 (H2). Under the linear technology (baseline control VCM), observe no change in contributions to the joint project when the group size is reduced from five to two.
The rationale of using the standard linear production VCM as a control treatment is based on the detected group size effect in the previous literature: contrary to the classical theoretical predictions [
21], in public goods games with a boundary solution, larger groups seem to be more efficient in public goods production [
14]. We compare the average and individual contribution levels under different group sizes (
n = 5 or
n = 2 individuals per group) within a treatment. Any difference in this difference between treatments should reflect also the effect of the functional form of the production function and not only the `behavioral’ group size effect.
A relevant theoretical model for our work is posited by [
22], who employed the well-known quantal response equilibrium of [
23] in explaining the group size effect. In particular, the authors in [
22] note that when the equilibrium level of contributions is in the interior, the average contribution is likely to be sandwiched between the Nash equilibrium and half the endowment, and contributions should (stochastically) increase with the marginal value of the public goods and with the endowment. Furthermore, assuming altruism, i.e., a positive weight that subjects attach to the payoff of others, total contributions should be increasing in the number of participants. In particular, for public goods games with quadratic private goods and linear SCF, the expected contribution per person is sandwiched between the symmetric Nash equilibrium level and half of the endowment.
However, since there is no dominating strategy available, it is harder to predict behavior in the game with complementary SCF relative to the game with standard linear VCM with
n = 5 individuals per group. On the one hand, the complementary actions may feed each other, and we might see higher contribution levels than in the standard game, but on the other hand, cooperating is more risky since one might lose all in case other group members deviate. It has been argued that risk and trust are closely-related constructs in the economic context of personal exchange, where the uncertainty is often of a strategic nature, as opposed to mere state-dependent risk (see, e.g., [
24,
25]). However, there is evidence suggesting that trusting behavior is not tightly connected to a person’s risk attitudes [
26]. To control for this, a Holt–Laury [
27] risk aversion instrument was run in both treatments after the main treatments had taken place.
The payoffs in the pairwise complementary SCF treatment are shown in
Table 1,
Table 2, and
Table 3 in
Section 3 (respective payoff Tables for the linear baseline treatment are included in the
Supplementary Materials, pages 9–16)). Deviating from the maximum action profile (shown in the bottom right corner of
Table 3 in
Section 3) yields the subjects very little in the complementary SCF treatment compared to the baseline treatment with standard linear production, where free-riding is potentially very lucrative. By looking at the payoff
Table 3, it can be seen that this complementary game exhibits features typical to stag hunt and other coordination games. Furthermore, the best response to minimum action by other group members is not zero contribution, but investing 0.5 tokens in the public project B. This feature could possibly kick start a cooperative spell of increasing best replies and direct the overall behavior away from mutual defection.
Finally, in the treatment with pairwise complementary SCF, within certain ranges of the action set, it is possible for a subject to grant others rather large marginal gains in payoff with relatively little marginal cost to himself/herself, in particular at the higher end of the payoff table. This means that, should we assume the same level of possible altruism between treatments, this payoff mechanism might induce much more cooperative behavior.
3. Experimental Design
The experiment was conducted at the Decision Making Laboratory of the Public Choice Research Centre (PCRClab) at the University of Turku. The experiment was programmed using the Z-Tree software [
28]. Participants were recruited from a pool (
n = 1070) of mostly undergraduate students using ORSEE software [
29]. A total of 80 individuals participated in 4 sessions, with 20 individuals participating in each session. Both treatments consisted of two sessions or 40 subjects, and each individual took part in one session only. Some subjects had participated in other decision making experiments that were unrelated to this research, and a few individuals had previous experience with the Holt and Laury task. The median age of the participants was 25 years, and 69% (55) of the participants were female. A copy of the instructions (translated from Finnish) is included in the
Supplementary Materials.
In each session, the subjects were randomly seated at a computer terminal. The instructions were read out by the experimenter, after which the participants had a few minutes to read them at their own pace, followed by a few control questions and two practice rounds of a five-player VCM game (with the aggregating mechanism respective to each treatment). Once the experiment was started, no talking was allowed; if a participant had a question, he/she would have to raise his/her hand, and the experimenter would come to consult him/her individually in private.
The subjects were told that the experiment consisted of three independent parts. In each part, the subjects would take part in a different task: (i) a 20-fold repetition of a VCM game with a group size of five and random matching, where the technology aggregating individual contributions to the public account was either a standard linear or a pairwise complementary production function, depending on the assigned treatment; (ii) the same game as in Part (i), but with group size
n = 2, so that subjects were randomly paired in each round; and finally, (iii) Holt and Laury’s [
27] risk instrument. The instructions for Parts (ii) and (iii) were dealt to the subjects only after the preceding part was completed by every subject (see the
Supplementary Materials for the specific instructions for each part.)
After each period, each group member was told how much income he/she gained from each respective project, the individual investments made by the members of his/her group (including his/her own investment) in a random order and also the average of and the total of these contributions. We did not provide information about individual earnings of the other group members.
At the end of the experiment, each subject rolled a 20-sided die twice outside the classroom, choosing one period out of 20 from Game (i) and one period out of 20 from Game (ii) for payment. The payoffs from the Holt and Laury lottery were determined by letting each subject roll a 10-sided die twice. Experimental currency units were used in Tasks (i) and (ii), with a conversion rate of 15 points = 1 EUR, whereas the Holt and Laury lottery payoffs were in Euros. The subjects earned 19.86 EUR on average, including a show-up fee of 3 EUR. The sessions lasted approximately 2 h, including instruction time.
At the beginning of each period in Games (i) and (ii), the group members were each endowed with 10 tokens (), which they were asked to allocate between the private project A and the public project B with a precision of up to two decimals (so the action set in each period consisted of any amount between [0.00, 10.00]).
Table 1 shows the marginal and cumulative payoffs from tokens allocated to the activity A, or payoffs from investing in the private project. The return from the private project was the same irrespective of the group size.
Table 2 shows the separate payoffs ensuing from various allocations between the private and public goods in the complementarity SCF treatment with a group size of five and
Table 3 the respective total payoffs. The linear treatment has also similarly constructed payoff tables (shown in the
Supplementary Materials, pages 9–16) under the respective instructions. These tables were handed out to subjects in the experiment to help them in making the allocation decision. In addition, the subjects were provided with programmed sliders shown on their display each period, with which they could experiment by trying out different allocation profiles and the respective payoffs.
With n = 5 individuals per group, the payoff from maximum action profile is 150 tokens in both treatments, and the payoff from the dominant equilibrium action profile is 118 tokens in the linear treatment, whereas each member of the group would earn 94 tokens from the symmetric Nash equilibrium in the complementary treatment. Ending up being the sole contributor to the public goods still pays off 30 tokens in the linear treatment, but yields nothing in the complementary treatment. Benefits from free-riding grow in the sum of contributions of other members of the group in the linear treatment, but the payoff remains zero in the complementary SCF treatment.
To summarize, our main design consists of a setting where we vary the group size from two to five for both SCF games, and the parameters are specified so that donating two tokens to Activity B is either dominating or a Nash strategy when the group size is
n = 5 individuals. The design and respective equilibrium contribution levels are summarized in
Table 4 and
Table 5. From the tables, one can see that in groups of two, the parametrization does not allow much variation between the complementary SCF treatment, as Nash contribution, group optimum action and minimum action profile yield payoffs very close to each other in terms of real money.
The third part of the experiment replicates the experiment in Holt and Laury: Subjects faced a questionnaire with ten decisions, where each decision consisted of a choice between two paired lotteries, Option A and Option B. The payoffs for Choice A were always 2 EUR or 1.60 EUR and for Choice B 3.85 EUR or 0.10 EUR. The probabilities for high and low payoffs were the same for both alternatives for each decision. In the first decision, the probability of the high payoff in both decisions was 1/10. This probability gradually rose as a subject moved down the decision sheet. The expected pay off from Option A was higher for the first four choices and for Option B after that, implying that a risk-neutral subject would switch from Option A to Option B after the fourth decision, whereas risk-loving subjects would switch earlier and risk-averse subjects later. The options are shown in the
Supplementary Materials, pages 17–18.
4. Results
In this section, we first describe our subjects’ risk attitudes as elicited by the Holt and Laury task, before analyzing how the behavior in public goods games of Parts (i) and (ii) is related to risk aversion preferences.
4.1. Subjects’ Risk Attitudes
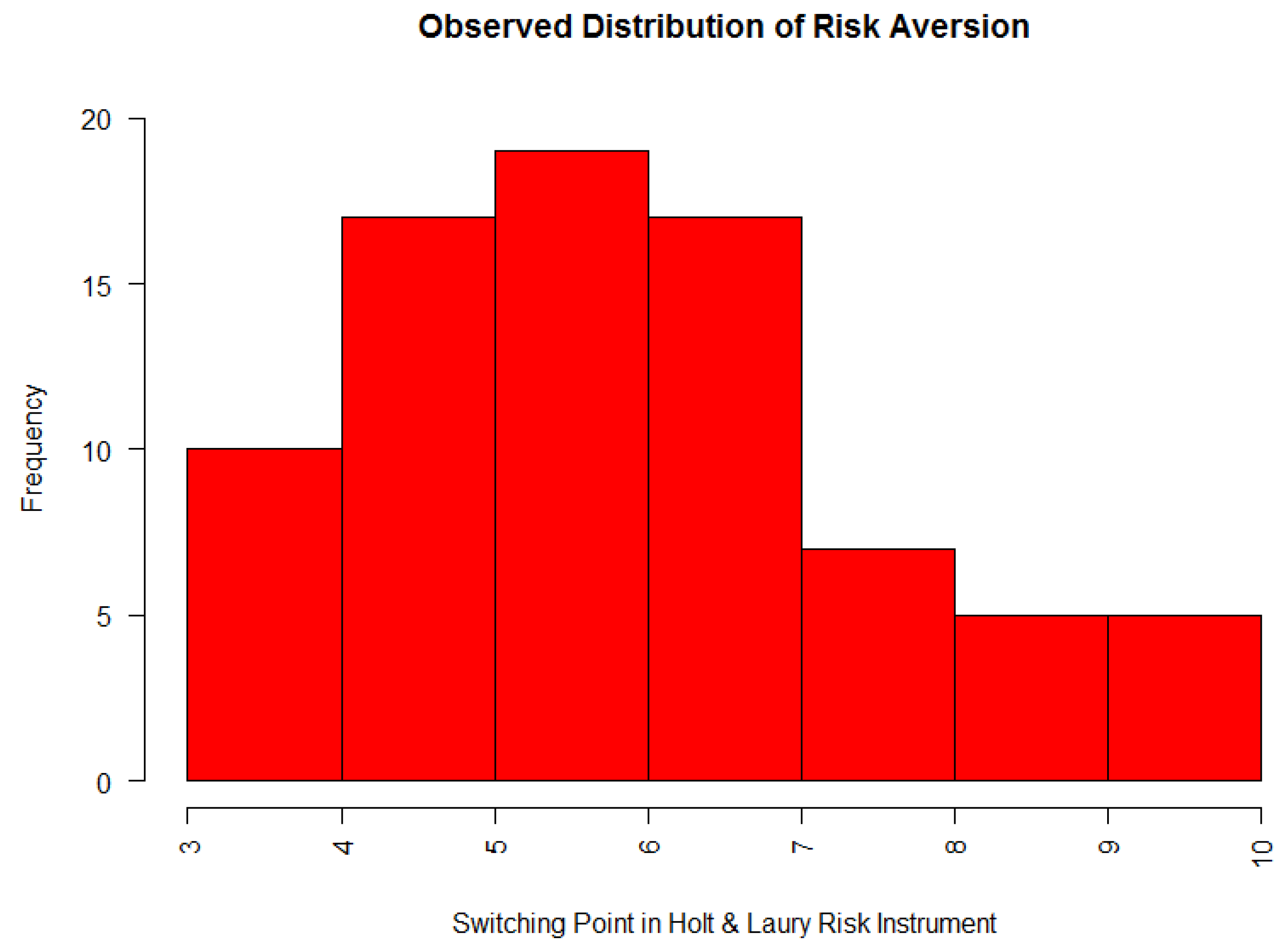
We find that 10% (n = 8) of the subjects had inconsistent risk attitudes, switching back and forth between risky and safe options at least once. Excluding this subsample from the analysis does not change the statistical significance of any reported results.
Figure 3 shows the distribution of risk preferences. Data are coded by the number of safe (A) choices. The risk aversion is measured as the (last) point where a subject switches from the safe option A to the risky option B. Our experimental subjects were on average quite risk averse, with a mean switching point of 6.34 (s.d. 1.70). This finding is partially explained by the large share of female subjects, as women have been found to be more risk averse than men in the previous risk literature. We also find this difference between genders, although it is not statistically significant at conventional significance levels. The distribution of risk attitudes did not differ between our two experimental treatments (Kolmogorov–Smirnov test,
).
4.2. Public Goods Game with the Dominant Interior Solution and Linear Social Composition Function
In this section, we report the results for each treatment separately, after which at the end of the section, the results for the pooled observations are reported and discussed. For each treatment, we begin the analysis by looking at the average behavior aggregated over all rounds and individuals, before analyzing individual level behavior, or taking into account the possible dynamics created by the repetition of the single-shot VCM game.
In the linear SCF treatment, the individual payoff of agent
i is given by:
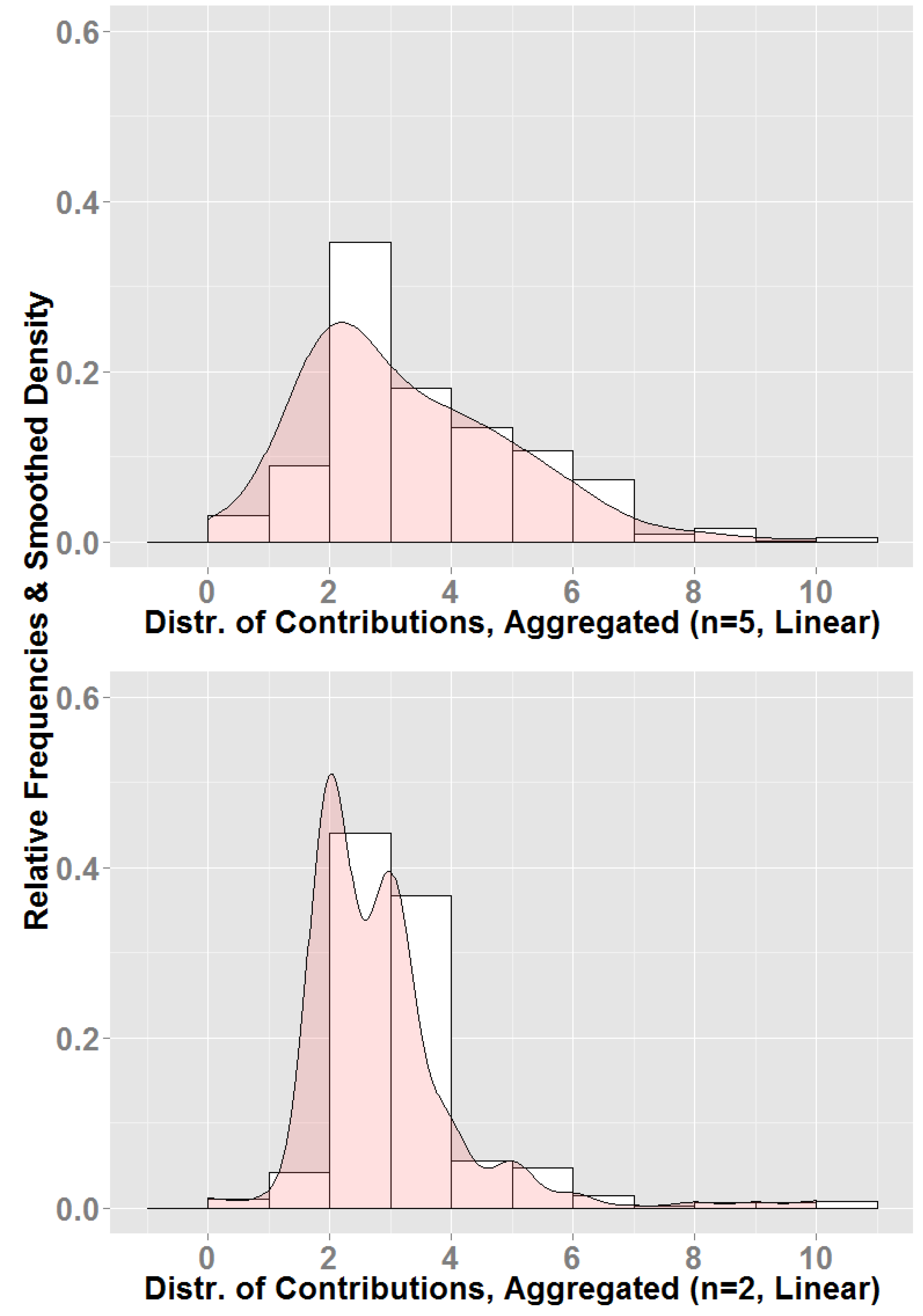
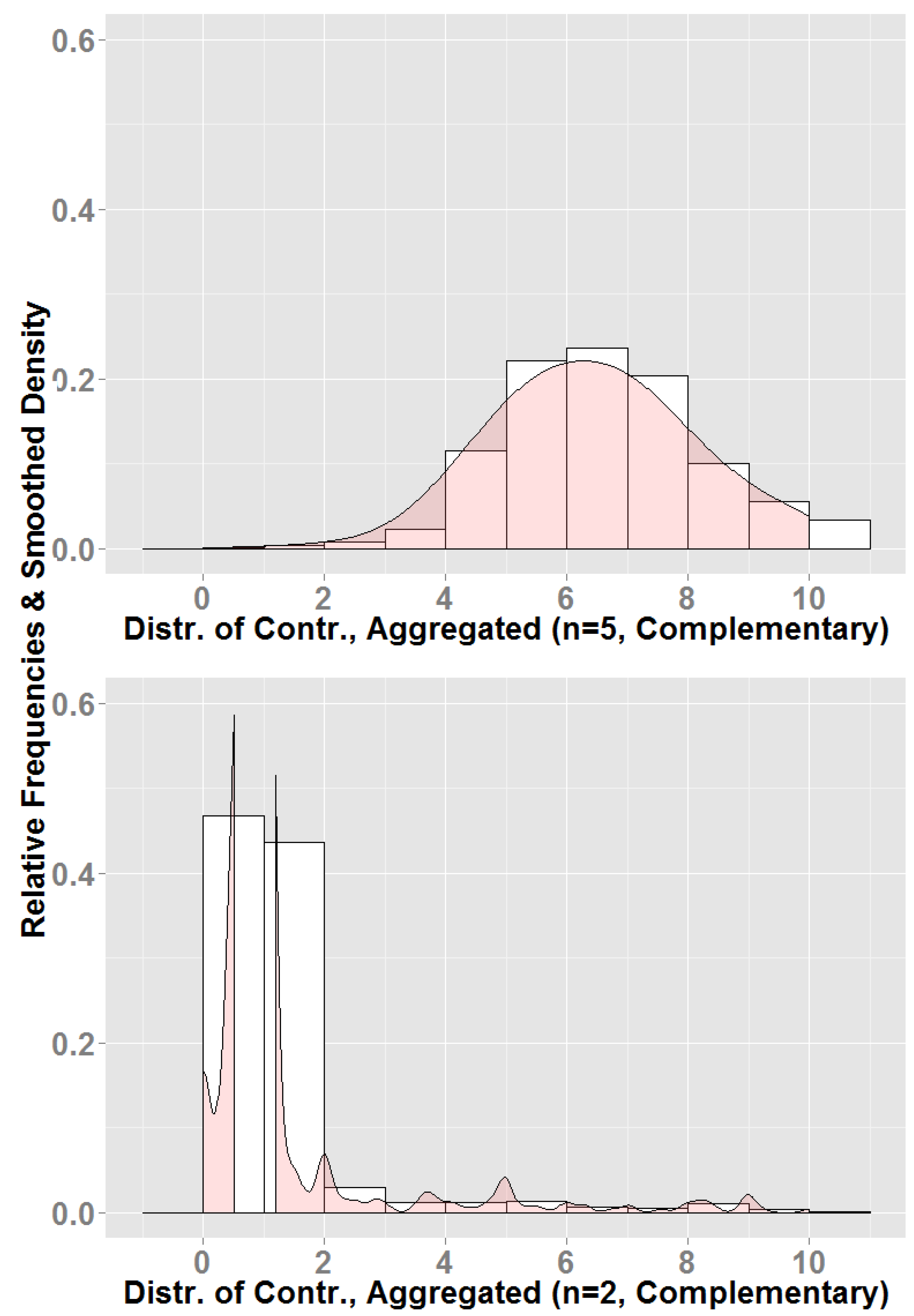
In
Figure 4, we can see that in the groups of five, the average contribution is somewhat spread (the upper panel), although there is a slight spike near 2.00, the dominant equilibrium action. The contributions are even more concentrated around the equilibrium action when the group size is two (the lower panel). Interestingly, the equilibrium action of 2.00 was a modal choice in both cases: It was chosen as 243 out of 800 (30.38% of the time) rounds with groups of five and allowing for a tolerance of 0.07 tokens
3, 306/800 times (38.25% of the time). In groups of two, the dominant action was chosen as 305 out of 800 times (38.13%) (343/800 (42.88%), allowing for a tolerance of 0.07).
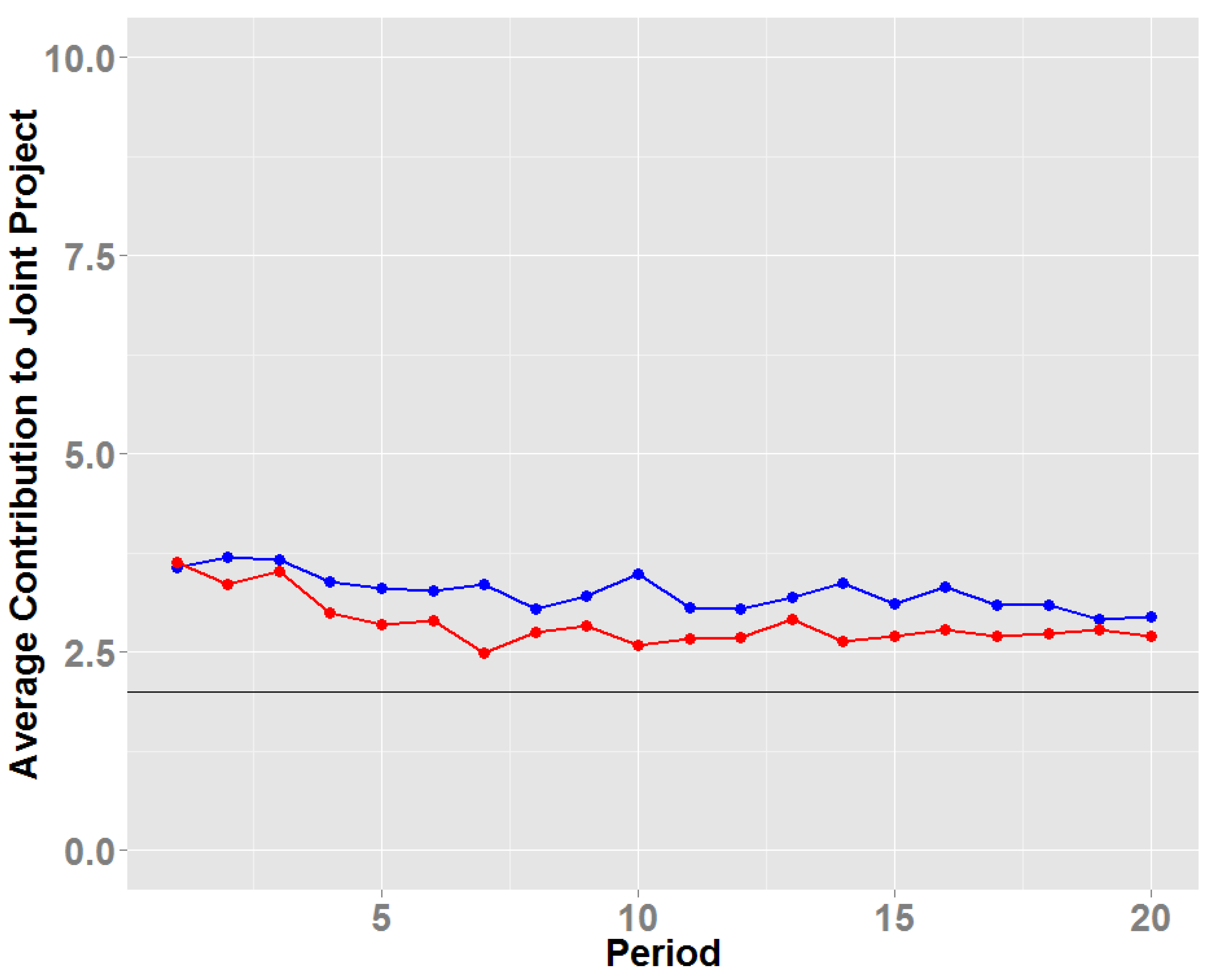
In
Figure 5, the blue line depicts the time path of the contributions averaged over all subjects (
n = 40) each period in the linear treatment with five players. The red line shows the respective average contributions when the group size is two, and the dominant equilibrium contribution level is marked with a black horizontal line.
In groups of five, we observe that the overall average contribution level over rounds and individuals is 3.26 tokens, which corresponds to an average over-contribution rate of 15.75% compared to the dominant action of contributing two tokens towards the joint project B
4. With smaller groups, the average contribution over all rounds to the joint project is 2.86 (an average over-contribution of 10.75%), and the spike around the equilibrium action level is more pronounced, reflecting the modal action.
Our finding that a larger group size induces more cooperative behavior is consistent with the results obtained in earlier literature [
14]. The difference in the distribution of subjects’ average contributions over all periods is statistically significant (Kolmogorov–Smirnov test,
). That is, ignoring possible temporal dynamics within the data, we compute each subject’s mean contribution and then compare the distribution of these averages.
Next, we explore the dynamic structure of the linear SCF games with five and two members by specifying a fixed effects panel regression. As control variables, we include the gender and and the risk attitude variables and their interaction term. The dependent measure is individual
i’s contribution to the public goods in period
t. In
Table 6, we can observe a gender effect: men tend to contribute significantly more (almost three tokens), albeit this coefficient is only borderline significant. After controlling for gender, risk aversion does not seem to affect the contribution amount chosen, as less risk-averse subjects contribute as much as others.
When the group size is decreased (right panel, Regression (2)) in
Table 6, the gender is no longer a significant regressor, once we cluster the standard errors on individual choice and group.
4.3. Public Goods Game with the Interior Solution and Pairwise Complementary Social Composition Function
With complementary aggregation technology, the individual payoff of agent
iis given by:
in our experiment.
In
Figure 6, the average contribution levels are depicted as in
Figure 4. In groups of five, the average contribution over all rounds was 6.43 tokens, reflecting an over-contribution rate of 55.38%. The average contribution in groups with
n = 2 individuals was 1.19 or an over-contribution of 15.38%. We see that when the group size was larger (
n = 5), the contributions were somewhat spread around the average contribution. In particular, the contributions at the Nash equilibrium level (2.00) were very few (this action was chosen a total of 14 times in 800 rounds).
Admittedly, in terms of real monetary compensation, the payoffs from the joint project were so small in the n =2 group treatment, that one can rightfully suspect whether the subjects are properly incentivized, as making a contribution of one token instead of nothing would yield at most 0.25 euros, and 0.02 euros if the other group member donated one token similarly. However, choosing one was precisely the modal action, since out of 800 individual decisions, 237 or 30% involved contributing one token to the joint project (cf. one chosen as the action in 13 out of 800 choices, when n = 5).
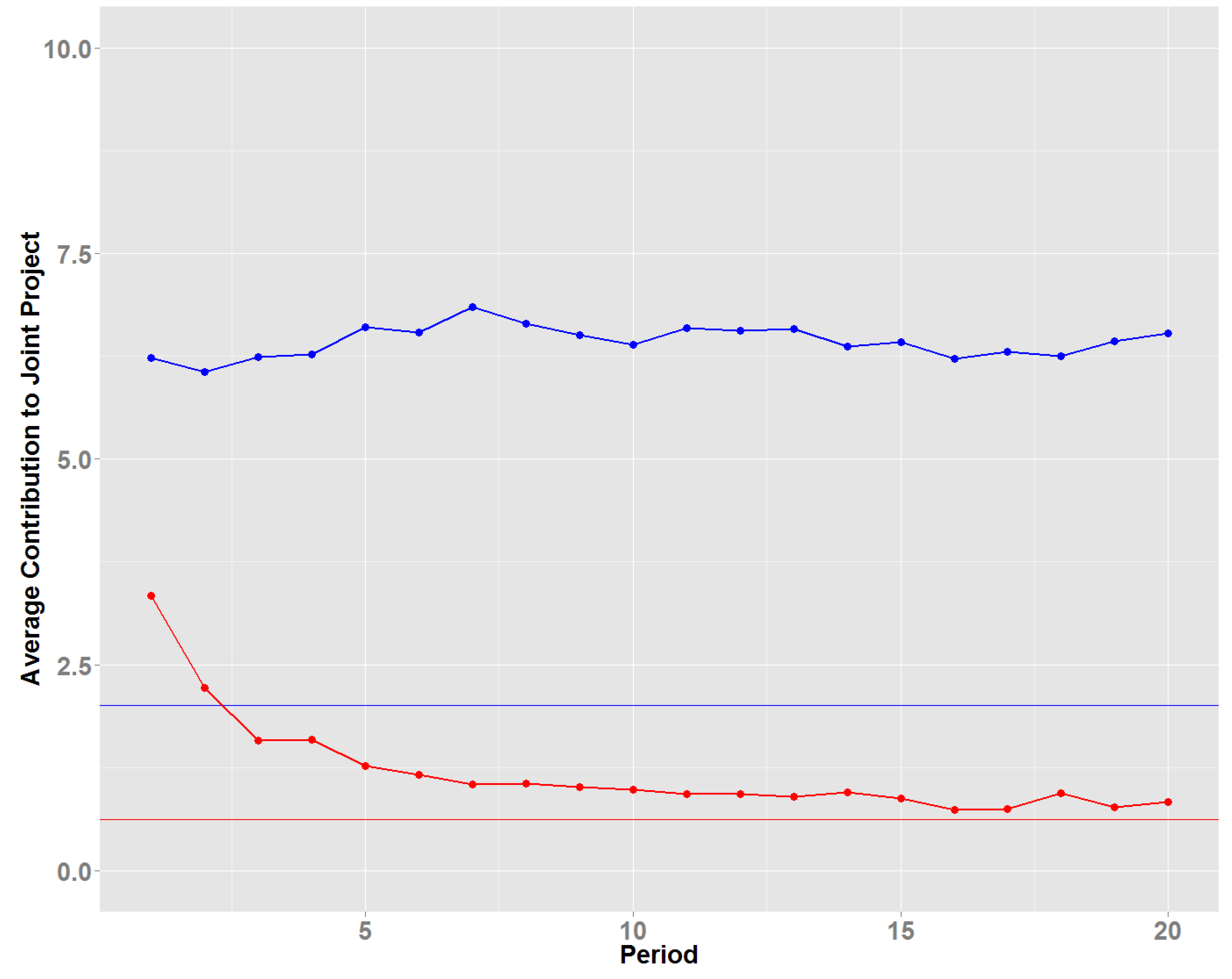
As in
Figure 5 in the linear SCF treatment, in
Figure 7, the blue line depicts the time path of the contributions averaged over all subjects each period (
n = 40) with five players in the complementary SCF treatment. The red line shows the respective average contributions when the group size is two. However, the respective Nash equilibria contribution levels are marked with straight lines bearing the respective colors. That is, the blue line illustrates the Nash contribution level 2.00 in the treatment with groups of five, and the red line shows the Nash equilibrium level in the
n = 2 treatment. Examining time paths, we see that in the larger groups (
n = 5), the average contribution remains way over its Nash equilibrium throughout the 20 rounds, and more remarkably, there is no end game effect to be seen. In the smaller groups (
n = 2), the average contribution converges relatively quickly very close to the respective Nash equilibrium level.
By our regression analysis, we find that contrary to the linear baseline treatment, when the group size was five, men contributed about 2.3 tokens less towards the public goods on average after controlling for risk aversion, but this coefficient was not statistically significant (Regression (1) in
Table 7). However, as the risk aversion increased amongst male subjects, so did their contributions, albeit the significance of the respective interaction coefficient was weak
. Risk aversion itself had no significant effect on contributions.
In groups of two with complementary SCF, gender, risk aversion and their interaction term had no statistically significant effect when clustering the observations on groups and individual subjects.
Having examined both treatments separately, we studied the data on the aggregate level. First we studied the aggregate descriptive statistics for the contribution, whereafter we estimated a regression for the whole sample by pooling the observations from each treatment together.
Table 8 summarizes the average contributions (standard deviations in parenthesis) and rates of over-contribution per treatment: there is a slight difference between contribution levels between groups of two and five in the linear treatment, and that same difference between groups of different sizes in the complementary SCF treatment is much larger. This is also reflected in the right-hand side columns, which show that the rate of over-contribution is much higher in the complementary treatment and group size
n = 5 than in other cells.
Next, we estimate a pooled OLS-regression, where the explained variable is the amount contributed towards the joint project, and the explanatory variables are the main treatment (linear vs. complementary) and group size. Individual and time period effects are controlled by time and individual specific dummy variables
5. The results are presented in
Table 9. We observe that both the treatment effect and the group size effect are highly significant, as is their interaction term. The sign of the treatment effect coefficient is negative; however, this is not to be interpreted as complementarity being harmful for cooperative behavior: This is explained by the large positive coefficient for the interaction term between (large group) and complementarity treatment: on the aggregate level, the high level of contributions in the groups of five more than offsets the more modest contributions in small groups under complementary production, compared to the baseline.
The regression analysis confirms the impressions obtained by a casual look at the aggregate descriptive statistics: both the aggregation technology and the group size have a strong effect on contributions. As expected by the comparative static predictions, the contributions increase in the complementary treatment when the group size is increased. We also detect a group size effect present in the linear baseline treatment, albeit a small one compared to the treatment group.
5. Summary and Discussion
This paper extends the research on public goods in nonlinear environments by specifying a VCM game where both the private earning mechanism and the social composition function aggregating individual outputs are nonlinear. We compared this weaker link-type VCM game to the baseline treatment with the standard linear aggregating function. Interestingly, the familiar numbers effect, or contributions increasing in group size, is present in both of our treatments. Neither risk attitudes nor gender were prominent in predicting the contribution behavior; the former (lack of) effect could be attributed to the characteristics of the experiment: even under neutral framing, the subjects may interpret this setting involving interpersonal trust and moral choices rather than a neutral, recurrent investment opportunity (see [
26]).
Our results indicate that increasing the group size in the linear SCF treatment results in a higher level of average contribution towards the public goods. The average contribution over all rounds is 3.26, which is sandwiched between the Nash equilibrium (2.00) and half of the endowment (5.00). Having pairwise complementarity in the SCF production induces more cooperative behavior than what is the case in the linear SCF treatment. However, if we assume altruism, this is to be expected. Given our setup, we must be cautious when comparing the differences in differences between treatments, as changing the group size, but keeping the multiplier parameters the same in the pairwise complementarity treatment actually changes the marginal rate per capita yield from the joint production. However, the statistical results reported in the respective section confirm what can be seen by casual observation in the graphs alone: the effect of increasing the group size is stronger in the treatment group with strategic complementarity in contrast to the difference detected within the baseline treatment.
In particular, we found out that the positive feedback resulting from pairwise complementarities in production enhances cooperative behavior, radically in groups of five. The production technology aggregating individual contributions favors increasing activity levels and coordinating actions, as even a weak preferences for altruism or conditional cooperation might induce a virtuous cycle, in which high levels of contribution in the current period also pave the way to successful future cooperation.
A somewhat puzzling phenomenon is the lack of decline in the contributions over the periods and the respective absence of the end game effect in both treatments when the group size was five. Among factors affecting the evolution of the contribution behavior over the periods are the matching protocol used and the form of feedback provided to the subjects. In our experiment, we employed stranger matching and, after each round, reported to each group member how much income he/she gained from each respective project, the individual investments made by the members in his/her group (including his/her own investment) in a random order and also the average of these investments and their total amount.
The work in [
31] found that in the strangers design, the subjects give more on average. This result was also found by [
32] and [
33] in Italy, but not in the U.K., where partners gave more, on average. The work in [
34] found that strangers gave more in their experiment in Spain, but the opposite was true in the U.S., whereas there is no difference to be found in their experiment in Japan or in the Netherlands, and the differences in behavior across countries are minor. The work in [
35] found no difference, and in [
36,
37,
38], the partners design was more conducive to cooperative behavior. The work in [
39] provided a discussion on the results. As is expected, no satisfactory and definite conclusion can be drawn from the results surveyed, and they note that “if a prediction is based on a single-shot equilibrium, then a Strangers condition will be most appropriate.” This is also the rationale for us choosing the strangers design.
In terms of feedback provided to the subjects, in experiments with the stranger design, the evidence is also mixed. The work in [
40] found no effect, whereas in the experiment reported in [
41], aggregate level feedback resulted in subjects making higher contributions to the public goods. The work in [
42] ran a design varying framing (give vs. take), matching (partners vs. strangers) and feedback (individual vs. aggregate). They found that in a partners setup with the give framing, there was significantly more free-riding with individual feedback compared to aggregate feedback. However, no such difference is found in the strangers setup, which is closer to our design.
Due to the conflicting and mixed results in the existing literature, I believe we are justified to conclude that the magnitude of the effects observed was not exaggerated by design features that would be especially conducive to cooperative behavior, but it was rather a genuine result of the manipulated treatment variables. However, the possible interaction between the matching, feedback and various forms of non-linear social composition functions remains an interesting open question.