Cyber–Physical Correlation Effects in Defense Games for Large Discrete Infrastructures

Abstract

In certain critical infrastructures, correlations between cyber and physical components can be exploited to launch strategic attacks, so that disruptions to one component may affect others and possibly the entire infrastructure. Such correlations must be explicitly taken into account in ensuring the survival of the infrastructure. For large discrete infrastructures characterized by the number of cyber and physical components, we characterize the cyber–physical interactions at two levels: (i) the cyber–physical failure correlation function specifies the conditional survival probability of the cyber sub-infrastructure given that of the physical sub-infrastructure (both specified by their marginal probabilities), and (ii) individual survival probabilities of both sub-infrastructures are characterized by first-order differential conditions expressed in terms of their multiplier functions. We formulate an abstract problem of ensuring the survival probability of a cyber–physical infrastructure with discrete components as a game between the provider and attacker, whose utility functions are composed of infrastructure survival probability terms and cost terms, both expressed in terms of the number of components attacked and reinforced. We derive Nash equilibrium conditions and sensitivity functions that highlight the dependence of infrastructure survival probability on cost terms, correlation functions, multiplier functions, and sub-infrastructure survival probabilities. We apply these analytical results to characterize the defense postures of simplified models of metro systems, cloud computing infrastructures, and smart power grids.

1. Introduction

The operation of critical infrastructures such as metro systems, smart power grids, high-performance computing complexes, and cloud computing infrastructures requires the continued functioning of cyber components such as signals, servers, supervisory control and data acquisition (SCADA) systems, routers, and switches, and also physical components such as tracks, power lines, fiber lines, cooling systems, and power systems. Components of both types must be operational as individual units, and must also be available (i.e., accessible to other infrastructure components). The individual components are subject to direct attacks in that cyber attacks will disable individual cyber components and physical attacks will disable individual physical components, when the components have not been reinforced. Furthermore, critical correlations or inter-dependencies exist between cyber and physical components, which may be exploited to launch strategic component attacks that propagate the disruptions to several others. To counter such attacks, infrastructure providers have to explicitly account for the underlying cyber–physical correlations and adopt strategies that ensure the continued operation of both cyber and physical sub-infrastructures.

In this paper, we consider a discrete component model of infrastructures with a large number of cyber and physical components, such as a metro system with hundreds of signals and sensors, a cloud computing infrastructure with thousands of servers, or a power grid with hundreds to thousands of sensors. The notations for various quantities are provided in

Table 1. Notation.

Symbol	Explanation
$x_C,x_P$	number of cyber and physical components reinforced, respectively
$y_C,y_P$	number of cyber and physical components attacked, respectively
$P_{CP}\left(x_C,x_P,y_C,y_P\right)$	survival probability of the infrastructure
$P_C$, $P_P$	marginal survival probabilities of cyber and physical sub-infrastructures, respectively
$f(P_C,P_P)$	failure correlation function (i.e., the failure probability of cyber sub-infrastructure given the other’s failure)
${\mathrm{\Lambda }}_C(x_C,x_P,y_C,y_P)$, ${\mathrm{\Lambda }}_P(x_C,x_P,y_C,y_P)$	multiplier functions of cyber and physical sub-infrastructures
$U_D\left(x_C,x_P,y_C,y_P\right)$, $U_A\left(x_C,x_P,y_C,y_P\right)$	provider’s and attacker’s composite utility function, respectively
$F_{D,G}(x_C,x_P,y_C,y_P)$, $F_{D,L}(x_C,x_P,y_C,y_P)$	provider’s reward and cost multiplier functions, respectively
$F_{A,G}(x_C,x_P,y_C,y_P)$, $F_{A,L}(x_C,x_P,y_C,y_P)$	attacker’s reward and cost multiplier functions, respectively
$g_D\left(x_C,x_P,y_C,y_P\right)$	reward for rendering the infrastructure operational in the provider’s sum-form utility function
$L_D(x_C,x_P)$, $L_A(y_C,y_P)$	provider’s and attacker’s total cost of cyber and physical attacks, respectively
$G_D(x_C,x_P,y_C,y_P)$, $G_A(x_C,x_P,y_C,y_P)$	provider’s and attacker’s reward, respectively
$a_C$, $b_C$	coefficients in the linear correlation function
$p_{C|R}$, $p_{C|N}$	conditional survival probability of a cyber component with and without reinforcement, respectively
$p_{P|R}$, $p_{P|N}$	conditional survival probability of a physical component with and without reinforcement, respectively
$p_{C|R}^i$, $p_{P|R}^j$	survival probabilities of reinforced cyber component of type i and reinforced physical component of type j, respectively
$p_{C|N}^i$, $p_{P|N}^j$	survival probabilities of cyber component of type i and physical component of type j without reinforcement, respectively
$N_C^i$, $N_P^j$	number of type i cyber components and type j physical components, respectively
$\xi$	coefficient of inherent robustness of cyber component
$\alpha$	coefficient representing a partial effect of cyber–physical correlation
$N_L$	number of trains running on a line, or the number of sensors connected using a communication node
$N_S$	number of servers connected through a fiber
$f_P$	normalization factor in the survival probability of metro system and smart power grid infrastructure
$f_C$	normalization factor in the survival probability of cloud computing infrastructure
$L_{G,L}^D(x_C,x_P,y_C,y_P)$	composite gain–cost term
$F_{G,L}^{D,B}(x_C,x_P,y_C,y_P)$	provider’s gain–cost gradient with respect to $x_B$, where $B=C,P$, for cyber and physical components, respectively
${\mathsf{\Theta }}_C\left(·\right)$, ${\mathsf{\Theta }}_P\left(·\right)$	cyber and physical scaled gain–cost gradients, respectively
$x_C^T$, $x_C^S$	number of reinforced control centers and signals in metro system, respectively
$x_C^S$, $x_C^R$	number of reinforced servers and routers in cloud computing infrastructure, respectively
$x_C^S$, $x_C^M$	number of reinforced communication nodes and smart meters in smart power grid infrastructure, respectively
$P_A^S$, $P_A^M$	probabilities of an attack on a communication node and smart meter in smart power grid infrastructure, respectively

. The attacker launches $y_C$ cyber or $y_P$ physical component attacks but not both, and the provider reinforces $x_C$ cyber and $x_P$ physical components. The cyber–physical interactions may render the otherwise operational components unavailable, whether they are reinforced or not. 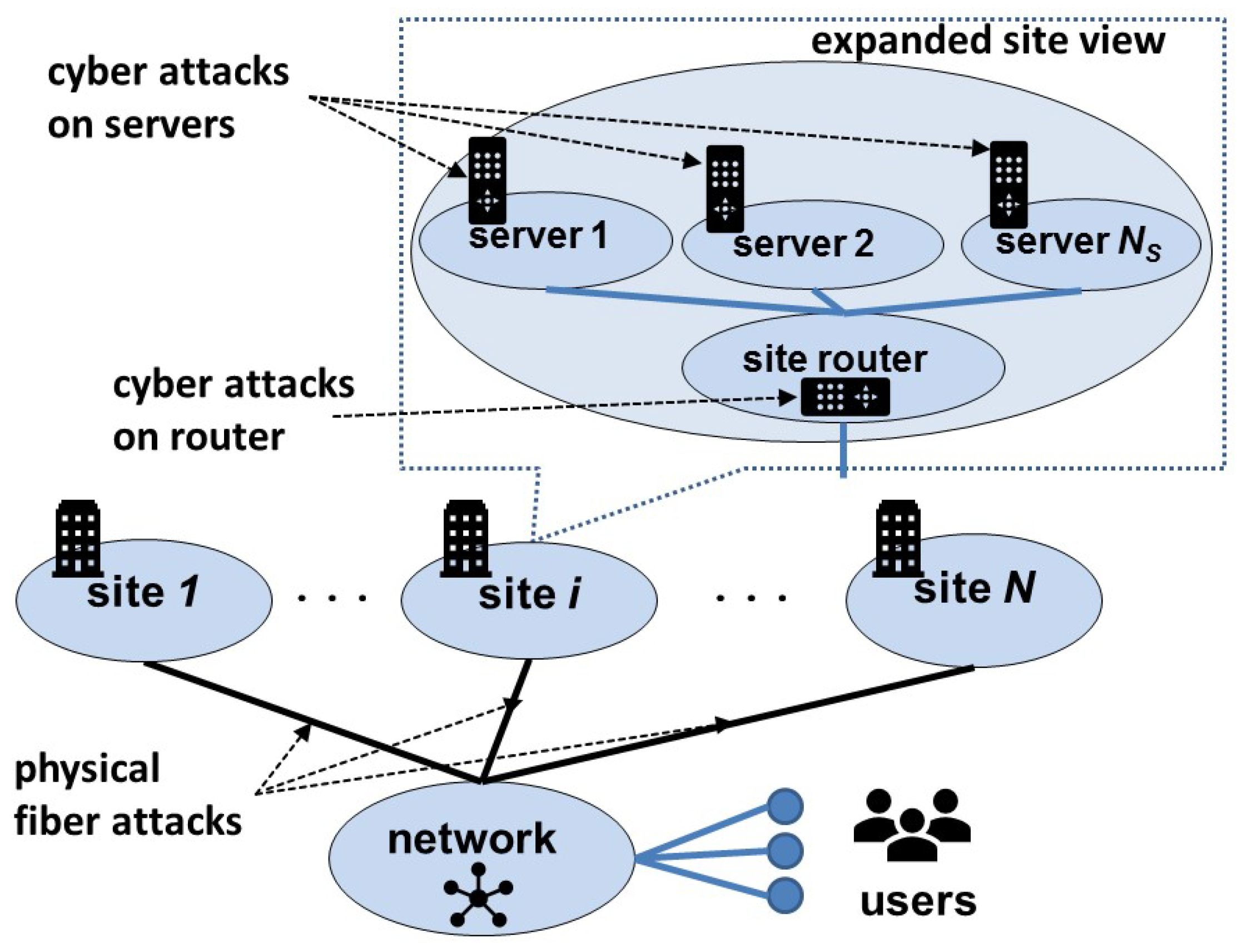For example, a physical attack on a fiber connection to a server site of a cloud computing infrastructure shown in Figure 1 may disconnect all servers (thousands in some cases) from the network, even if they are all fortified against cyber attacks.

In addition to component-level characterizations, the cyber and physical sub-infrastructures can be separately identified in several cases. Indeed, they may be operated by different domain experts. For example, in a power grid, SCADA systems are maintained by operations staff, and the power routes are maintained by power engineering staff. We consider the cyber and physical sub-infrastructures consisting entirely of cyber and physical components, respectively. Disruptions to either could disrupt the entire infrastructure. Let $P_{CP}$ denote the survival probability of the infrastructure, and $P_C$ and $P_P$ denote the marginal survival probabilities of cyber and physical sub-infrastructures, respectively. The cyber–physical failure correlation function $f(P_C,P_P)$ is the failure probability of cyber sub-infrastructure given the other’s failure, and is estimated using the structural properties of the infrastructure. Furthermore, we consider that $P_C$ and $P_P$ satisfy first-order differential conditions based on the multiplier functions [1] of cyber and physical sub-infrastructures, denoted by ${\mathrm{\Lambda }}_C$ and ${\mathrm{\Lambda }}_P$, respectively, which are derived based on their component-level considerations. Together, these two characterizations [2,3] generalize the linearity and statistical independence conditions used in previous works [4,5] for this class of infrastructures with discrete cyber and physical components. The multiplier functions depend on $x_C$, $x_P$, $y_C$, and $y_P$, and also on additional infrastructure parameters (e.g., the number of power lines controlled by a SCADA system), and they provide an insightful abstraction. They appear in the estimates of survival probabilities of sub-infrastructures at Nash equilibrium (NE) and provide insights into the defense posture of the infrastructure.

We formulate a game between the provider and attacker with the following considerations:

(a)

knowledge about the infrastructure is available to the attacker which is sufficient to launch component attacks;

(b)

costs of attacks and reinforcements of components, denoted by $L_A(y_C,y_P)$ and $L_D(x_C,x_P)$, respectively, are not available to the other player;

(c)

components chosen by the provider to reinforce, and by the attacker to attack, are not revealed; and

(d)

incidents and results of attacks on components are known to the provider and attacker.

The information in items (a) and (d) is available to both the provider and attacker, and that in item (b) is private. The provider and attacker minimize their respective utility functions, which are based on both types of information.

The composite utility function [1] to be minimized by the provider is the sum of two terms, representing the reward for keeping the infrastructure operational and the corresponding cost, respectively. It is given by

$$U_D\left(x_C,x_P,y_C,y_P\right)=F_{D,G}(x_C,x_P,y_C,y_P)G_D(x_C,x_P,y_C,y_P)+F_{D,L}(x_C,x_P,y_C,y_P)L_D(x_C,x_P),$$

where $F_{D,G}$ and $F_{D,L}$ are the reward and cost multiplier functions, respectively, of the provider, $G_D$ represents the reward of keeping the infrastructure operational, and $L_D$ is the total cost of reinforcing cyber and physical components. The composite utility function to be minimized by the attacker is given by

$$U_A\left(x_C,x_P,y_C,y_P\right)=F_{A,G}(x_C,x_P,y_C,y_P)G_A(x_C,x_P,y_C,y_P)+F_{A,L}(x_C,x_P,y_C,y_P)L_A(y_C,y_P),$$

where $F_{A,G}$ and $F_{A,L}$ are the reward and cost multiplier functions, respectively, $G_A$ is the reward for rendering the infrastructure non-operational, and $L_A$ is the total cost of cyber or physical attacks. These utility functions can be specialized to capture different provider and attacker considerations as shown in

Table 2. Gain and cost terms for sum-form and product-form utilities of the provider.

	${\mathit{F}}_{\mathit{D},\mathit{G}}$	${\mathit{G}}_{\mathit{D}}$	${\mathit{F}}_{\mathit{D},\mathit{L}}$
sum-form: $U_{D+}$	$\left[1-P_{CP}\right]$	$g_D$	1
product-form: $U_{D\times }$	0	0	$\left[1-P_{CP}\right]$

, in particular by expressing them in terms of the survival probability of the infrastructure $P_{CP}(x_C,x_P,y_C,y_P)$. The sum-form utility [2] for the cyber–physical infrastructure provider is given by

$$U_{D+}\left(x_C,x_P,y_C,y_P\right)=\left[1-P_{CP}(x_C,x_P,y_C,y_P)\right]g_D+L_D(x_C,x_P),$$

where $P_{CP}(x_C,x_P,y_C,y_P)g_D$ is the expected reward in return for the reinforcement cost $L_D(x_C,x_P)$ of cyber and physical components. In certain infrastructures, players focus on the cost term only, and the reward of operating the infrastructure is not explicit. In such cases, the product-form utility [3] of the provider is given by

$$U_{D\times }\left(x_C,x_P,y_C,y_P\right)=\left[1-P_{CP}(x_C,x_P,y_C,y_P)\right]L_D(x_C,x_P),$$

which represents the expected cost under infrastructure failure and thus represents the “wasted” effort.

The NE of this game represents the state of the infrastructure under the reinforcement and attack actions of the provider and attacker that attempt to minimize their respective utility functions based on their individual information (from which neither has a motivation to unilaterally deviate [6]). The choices of provider and attacker, given by $(x_C,x_P)$ and $(y_C,y_P)$, respectively, can be obtained using various available methods [6,7], which typically involves exploiting the scenario-specific details. Indeed, because of the large-scale and complexity feature of cyber–physical infrastructures, most game models obtain Nash equilibrium using numerical methods. Our objective in this paper is to show that critical insights about the infrastructure survival can be gained by deriving estimates of survival probabilities in terms of various correlations and multiplier functions, without requiring explicit solutions for $(x_C,x_P)$ and $(y_C,y_P)$. To this end, we derive NE conditions that highlight the dependence of $P_{CP}$ on the cost terms, correlation function, multiplier functions, and cyber and physical sub-infrastructure survival probabilities, as well as their partial derivatives. Indeed, the effects of infrastructure parameters will be reflected in estimates of $P_{CP}$ via the multiplier functions, while the correlation effects are “separated” from them. In particular, the impacts of the two players’ strategies are captured using the composite gain–cost terms and gain–cost gradients that depend on gain and cost terms and their derivatives with respect to $x_C$ and $x_P$ ($y_C$ and $y_P$), respectively, which are specialized versions of those proposed for systems of systems [1]. The NE conditions reveal a direct dependence of $P_{CP}$ on the parameters of cyber and physical components and sub-infrastructures, as well as a close coupling between them through the correlation function. We also estimate the sensitivity functions of $P_{CP}$ using the partial derivatives of parameters $L_A(·)$, $L_D(·)$, $P_C$, $P_P$, and $f(P_C,P_P)$ that indicate their relative importance in the defense posture of the infrastructure.

The contributions of this paper are as follows. We unify the analysis of previously separate sum-form [2] and product-form [3] formulations, and provide a deeper treatment of NE, including second-order conditions which are not considered in prior work. Although a special case of a system of systems [1], our formulation provides a more focussed treatment of cyber and physical sub-infrastructures. Our results provide insights into the defense postures of (simplified models) three infrastructures, including metro systems and smart power grids (new here), and cloud computing infrastructures from [8]. We first consider cases where both cyber and physical components are uniform (Section 3.2), namely, signals and trains of metro systems, servers and fiber connections for cloud infrastructures, and SCADA system and power lines for smart power grids. Then, we consider different types of cyber components (Section 5), namely signals and the centralized traffic controls for a metro system, servers and routers for the cloud infrastructure, and SCADA system components and smart meters for the smart power grid. We explicitly derive NE conditions and sensitivity functions for these scenarios.

The organization of this paper is as follows. We compare our formulation with other related work in Section 2. In Section 3, we present a discrete component model for cyber–physical infrastructures, and discuss the failure correlation function and the differential conditions on sub-infrastructure survival probabilities. We present the game theoretic formulation in Section 4, and derive NE conditions and sensitivity estimates. We also describe two special cases, OR systems in Section 4.2 and statistically independent sub-infrastructures in Section 4.3, wherein the cyber–physical correlation effects are somewhat simplified. We discuss NE conditions for applications of metro systems, cloud computing infrastructures, and smart power grids in Section 5. We conclude in Section 6.

2. Related Work

Critical infrastructures are vital to national security [9], and there are numerous published reports, books, and studies on identifying [10] and securing [11,12,13,14] critical infrastructures. A detailed scientific analysis of critical infrastructures is provided in [15]. The author draws insights that critical infrastructures are complex systems, and their architecture is the most crucial factor in deciding their reliability and resilience. Securing cyber–physical networks has been studied extensively from various perspectives [16,17,18,19,20]. A risk assessment approach is used in [21] to identify and address the vulnerabilities of a cyber–physical system, without explicitly using the interactions between the attacker and the provider. Consequently, the quantification of risk and correlations is somewhat limited. Although cyber–physical networks form an integral part of many critical infrastructures such as energy, information technology, and transportation systems, these works primarily cater to applications on power systems and smart power grids. To our best knowledge, there has not been any study that rigorously models the correlations between cyber and physical components in a general system. Our objective is to develop such a general formulation and illustrate its generality by using models of various applications, such as metro systems, cloud computing infrastructures, and smart power grids.

Game-theoretic methods have been extensively applied to capture the interactions between providers and attackers of critical infrastructures [22] to develop strategies to ensure their continued operation in the presence of evolving threats. Such interactions are being increasingly analyzed ever since the 9/11 attacks [23], after which there has been an increased emphasis on protecting critical infrastructures. Most of these studies use sequential models with the provider as the first mover and the attacker as the second. This is useful in enabling analysts to draft preemptive recommendations [24]. Game theory has been used widely in the field of cyber–physical network security [25,26,27]. An overview of the game-theoretic models in network security is provided in [28]. However, these works do not consider the physical components that are critical to the functioning of cyber networks.

Several infrastructures to support power distribution, transportation, and agriculture have been analyzed using game-theoretic approaches. They typically employ complex dynamic models of the underlying physical systems [11]—in particular, using partial differential equations. Both game-theoretic formulations and their solutions are quite extensive for such infrastructures, including: multiple-period games [29] that address multiple time-scales of system dynamics; incomplete information games [30,31,32] that account for partial knowledge about the system dynamics and attack models; and multiple-target games [33,34] that account for possibly competing objectives. A comprehensive review of the defense and attack models in various game-theoretic formulations has been presented in [35].

Game-theoretic methods have been developed specifically to address the system reliability and robustness for several applications [22], which are particularly applicable to critical infrastructures. Recently, there have been increasing levels of integration of cyber components, including computing and networking devices, into several critical infrastructures. This contributes to faster information transmission and processing, but also lead to unprecedented security vulnerabilities due to the underlying cyber–physical correlations [36]. While many existing formulations utilize detailed dynamic infrastructure models, the cyber–physical correlations have only recently been explicitly addressed, and in a limited way [36]. Because of the large scale and complexity of cyber–physical systems, most game models obtain Nash equilibrium using numerical methods. The current paper analytically presents players’ best responses and provides insights for defense strategy at NE.

Due to the wide spectrum of the game-theoretic methods used for critical infrastructures, we now briefly consider the ones that are directly related to our discrete cyber–physical component models. These are much simpler than others used in infrastructures such as power distribution, transportation, and agriculture [11]. For example, partial differential equations that model traffic dynamics. In terms of overall goals, they belong to formulations that integrate system reliability and robustness parameters [22], which are applied for example to smart power grids [37], cloud computing infrastructures [38], and power systems [39]. Within this class, Stackelberg games are an important subclass, wherein the provider chooses actions based on instantaneous information. They lead to more reactive and sensitive responses to dynamic disruptions compared to long-term strategies used in Markov game models [37,40].

Stackelberg formulations have been applied to discrete models of cyber–physical infrastructures in various forms [36], and an important subset is formulated using the number of cyber and physical components that are attacked or reinforced. These formulations capture infrastructures with a large number of components, and are coarser than formulations that consider the attack and defense of individual cyber and physical components [41]. The correlation function was proposed in [2] to capture the dependencies between the survival probabilities of cyber and physical sub-infrastructures; this is a generalization of simple linear forms studied earlier in [4,5]. First-order differential conditions on the sub-infrastructure survival probabilities are proposed in [2] as a generalization of the statistical independence and contest survival functions [42], and the role of multiplier functions on these conditions has been further expanded in [1].

We now place our formulation and results within the broader context above. The composite utility functions described in the introduction generalize the sum-form [2] and product-form [3] utility functions used for infrastructures with discrete components. The composite utility functions have been applied to more general systems of systems (SOS) in [1,43], and here we customize them to cyber–physical sub-infrastructures. The resultant NE conditions unify the previous results by using composite gain–cost terms (Theorem 1), and also provide second-order NE derivative conditions (Theorem 2), which together enable us to apply them to more detailed and newer (metro system) infrastructure models. SOS have been studied under a similar formulation [43,44], and also under additional conditions due to an asymmetric role played by the inter-connection network [1,45,46]. The current paper explicitly targets the cyber and physical sub-infrastructures, provides in-depth results based on cyber–physical correlations, and also addresses the second-order NE conditions that have not been addressed in earlier works on cyber–physical infrastructures [2,3]. To make the presentation self-contained, we provide or re-state definitions of various terms needed for our formulation (Section 3) from the references.

3. Discrete System Models

A cyber–physical infrastructure (CPI) consists of cyber and physical sub-infrastructures with $N_C$ cyber components and $N_P$ physical components. Both components must be operational and available as parts of the infrastructure, but they can be functionally disabled or operationally disconnected from the infrastructure through attacks. In particular, cyber attacks may render physical components unavailable even if they are functional. For example, cyber attacks on a power grid’s SCADA system might disable power flows on the lines it controls. Physical component attacks may also render cyber components unavailable, as in the case of fiber cuts in a cloud infrastructure described in the previous section. We capture these cyber–physical interactions using the survival probabilities of cyber and physical sub-infrastructures using: (i) the cyber–physical failure correlation function $f(P_C,P_P)$ that captures the correlations at the sub-infrastructure level (Section 3.1), and (ii) the differential conditions on $P_C$ and $P_P$ using the multiplier functions that capture the component-level correlations (Section 3.2).

3.1. Cyber–Physical Structural Interactions

The failure probabilities of cyber and physical sub-infrastructures are $P_{\overline{C}}=1-P_C$ and $P_{\overline{P}}=1-P_P$, respectively. The probability that a CPI is operational is given by

$$P_{CP}=1-\left(P_{\overline{C}}+P_{\overline{P}}-P_{\overline{C}\cap \overline{P}}\right)=P_C+P_P-1+P_{\overline{C}\cap \overline{P}}.$$

The joint failure probability $P_{\overline{C}\cap \overline{P}}$ is expressed in terms of the conditional failure probability as $P_{\overline{C}\cap \overline{P}}=P_{\overline{C}|\overline{P}}{P}_{\overline{P}}$, which leads to the following definition.

Condition 1.

Cyber–Physical Correlation Function:The survival probability a CPI is given by

$$P_{CP}=P_C+P_P-1+f\left(P_C,P_P\right)(1-P_P),$$

where $f\left(P_C,P_P\right)=P_{\overline{C}|\overline{P}}$ is the cyber–physical failure correlation function of cyber and physical sub-infrastructures.

The failure correlation function captures the dependence of cyber sub-infrastructure failure on that of physical sub-infrastructure. For example, in a cloud computing infrastructure with $N_S$ servers at each site, disabling the fiber would disconnect all servers at the site, which can be reflected by choosing $f\left(P_C,P_P\right)=N_S(1-P_P)$. This shows that the physical failure rate is amplified by $N_S$ in rendering the servers unavailable. The following are two illustrative forms of $f\left(P_C,P_P\right)$.

(a)

OR Systems: A special class called the OR systems are defined in [4,5] to illustrate cases where cyber and physical parts can be independently analyzed. For these systems, the probability of failure of cyber or physical sub-infrastructure is $P_{\overline{C}\cup \overline{P}}=P_{\overline{C}}+P_{\overline{P}}$ or equivalently $P_{\overline{C}\cap \overline{P}}=0$. That is, the failure of the physical sub-infrastructure is guaranteed not to cause the failure of the cyber sub-infrastructure. Thus, we have $P_{CP}=P_C+P_P-1$ and $f\left(P_C,P_P\right)=0$. These systems are of mostly academic interest.

(b)

Linear Forms: The linear form

$$f(P_C,P_P)=a_C(1-P_C)+b_C$$

expresses the correlation in terms of multiplicative and additive coefficients, denoted by $a_C$ and $b_C$, respectively, and is used in [5] (in [4] only $a_C$ is used). Here, $a_C$ represents a proportional change in $P_{\overline{C}}$ due to the physical sub-infrastructure failure, whereas $b_C$ represents an independent factor. There are two special cases under this form:

(i)

Statistical Independence: We have $f\left(P_C,P_P\right)=1-P_C$. That is, $a_C=1$ and $b_C=0$, so that $P_{\overline{C}\cap \overline{P}}=P_{\overline{C}}{P}_{\overline{P}}$ or equivalently $P_{CP}=P_C{P}_P$, and

(ii)

Failure Certainty: When physical failures lead to cyber failures with certainty, we have $f\left(P_C,P_P\right)=1$. That is, $a_C=0$ and $b_C=1$, such that $P_{CP}=P_C$ (i.e., infrastructure survival probability solely depends on cyber sub-infrastructure).

More generally, if $a_C>1$ and $b_C\ge 0$, or $a_C\ge 1$ and $b_C>0$, the cyber failures are positively correlated to physical failures. That is, they occur with higher probability following physical failures (i.e., $P_{\overline{C}|\overline{P}}>P_{\overline{C}}$). If $a_C<1$ and $b_C\le 0$, or $a_C\le 1$ and $b_C<0$, i.e., $f\left(P_C,P_P\right)<1-P_C$, cyber failures are negatively correlated to physical failures (i.e., $P_{\overline{C}|\overline{P}}<P_{\overline{C}}$).

We now consider that the effects of reinforcements and attacks can be separated at the sub-infrastructure level such that $\frac{\partial P_P}{\partial z_C}=0$ and $\frac{\partial P_C}{\partial z_P}=0$, where $z=x,y$. Intuitively, these conditions indicate that only direct impacts are dominant at the level of sub-infrastructures. For example, cyber reinforcements contribute to improving the cyber sub-infrastructure but not directly to physical sub-infrastructure. We capture the sub-infrastructure correlations for the provider using the following conditions.

Condition 2.

De-Coupled Reinforcement Effects:The partial derivatives of $P_{CP}$ in Condition 1 satisfy the following conditions

$$\frac{\partial P_{CP}}{\partial x_C}=\left[1+(1-P_P)\frac{\partial f}{\partial P_C}\right]\frac{\partial P_C}{\partial x_C}and\frac{\partial P_{CP}}{\partial x_P}=\left[1-f(P_C,P_P)+(1-P_P)\frac{\partial f}{\partial P_P}\right]\frac{\partial P_P}{\partial x_P}$$

for the provider.

3.2. Sub-Infrastructure Survival Probabilities

We consider that the sub-infrastructure survival probabilities satisfy the following differential conditions.

Condition 3.

Cyber and Physical Multiplier Functions:The derivatives of survival probabilities of cyber and physical sub-infrastructures can be expressed as

$$\begin{array}{c}\hfill \frac{\partial P_C}{\partial x_C}={\mathrm{\Lambda }}_C(x_C,x_P,y_C,y_P)P_{C}and\frac{\partial P_P}{\partial x_P}={\mathrm{\Lambda }}_P(x_C,x_P,y_C,y_P)P_P\end{array}$$

in terms of the cyber and physical multiplier functions ${\mathrm{\Lambda }}_C$ and ${\mathrm{\Lambda }}_P$, respectively.

These multiplier functions capture the underlying details of cyber and physical sub-infrastructures (specialized systems of [1]) after factoring out the corresponding survival probabilities. They depend on the the parameters of cyber and physical sub-infrastructures, in addition to game variables $x_C$, $x_P$, $y_C$, and $y_P$. For example, for the cloud computing infrastructure described in Example 1, ${\mathrm{\Lambda }}_C$ depends on the number of servers $N_S$ at each site, and for the metro system in Example 2, ${\mathrm{\Lambda }}_P$ depends on the number of lines $N_L$ controlled by a signal. These somewhat abstract functions enable us to encapsulate some of the sub-infrastructure details so that the multiplier functions appear explicitly in various estimates at NE (including the survival probability estimates in Theorem 1), and provide valuable insights into the underlying dependencies. These multiplier functions can take simple forms in the following two important cases, which have been studied extensively in the literature.

(a)

Statistically Independent Components: Let $p_{C|R}$ and $p_{C|N}$ denote the conditional survival probability of a cyber component with and without reinforcement, respectively. Under the assumption of statistical independence of component failures, the probabilities that the cyber and physical parts survive the attacks are given by [4]

$$P_C=p_{C|R}^{x_C}{p}_{C|N}^{N_C-x_C}\mathrm{and}{P}_P=p_{P|R}^{x_P}{p}_{P|N}^{N_P-x_P},$$

respectively. In this case, we have $\frac{\partial P_C}{\partial x_C}=P_{C}ln\left(\frac{p_{C|R}}{p_{C|N}}\right).$

(b)

Contest Survival Functions: The contest survival functions are used to characterize $P_C$ and $P_P$ in [42] such that $P_C=\frac{\xi +x_C}{\xi +x_C+y_C}$, for which we have

$$\frac{\partial P_C}{\partial x_C}=P_C\left[\frac{y_C}{(\xi +x_C+y_C)(\xi +x_C)}\right].$$

We now describe three simplified illustrative cyber–physical infrastructure models for which we derive estimates for the multiplier functions ${\mathrm{\Lambda }}_B(·)$, where $B=C,P$ under uniform selection of components to reinforce and attack. We will expand further on these examples in Section 5 by taking additional details into account.

Example 1.

Cloud Computing Infrastructure: A cloud computing infrastructure (Figure 1) consisting of multiple sites can be simply modeled with $N_S$ servers at each site. Cyber attacks may bring down the individual servers, and the communication fiber routes to the sites may be physically cut. Reinforcements to these components may be in the form of replicated stand-by servers, and redundant physically-separated fiber routes. Since a physical fiber cut disconnects all servers at the site from the network, a first-order model is $f\left(P_C,P_P\right)=N_S(1-P_P)$, which indicates the multiplicative effect of physical attacks. There are ${[y_P-x_P]}_{+}$ non-reinforced fiber connections that are vulnerable to physical attacks, where ${[·]}_{+}$ represent the non-negative part. That is, ${\left[z\right]}_{+}=z$ for $z>0$, and ${\left[z\right]}_{+}=0$ otherwise. Under a uniform distribution of attacks and reinforcements, the probability that a cyber-reinforced server survives $y_P$ fiber attacks is estimated by

$$p_{C|R}=\frac{f_C}{1+N_S{[y_P-x_P]}_{+}},$$

where $0\le f_C\le 1$ is an appropriately chosen normalization factor. This estimate decreases with higher values of ${[y_P-x_P]}_{+}$. If a server is not reinforced, it will be brought down by a direct cyber attack, or disconnected through a fiber attack. Thus, the survival probability of such a non-reinforced server is

$$p_{C|N}=\frac{f_C}{1+y_C+N_S{[y_P-x_P]}_{+}},$$

which reflects a decrease due to $y_C$ compared to a reinforced server. For example, in an infrastructure with 10,000 servers at each site with a non-reinforced fiber, a single fiber attack has an effect similar to 10,000 individual server cyber attacks. Using these formulae, we have

$${\mathrm{\Lambda }}_C(x_P,y_C,y_P)=ln\left(1+\frac{y_C}{1+N_S{[y_P-x_P]}_{+}}\right)$$

for the cyber sub-infrastructure, which interestingly does not depend on cyber $x_C$ but depends on physical $x_P$.

Example 2.

Metro System: A metro system (Figure 2) consists of many components, including trains, tracks, perway, telecommunication systems, and electrical systems. The system operates normally when trains are running smoothly, being controlled by the signals located along the lines. A simplified model of a metro system may be based on abstracting its signaling system. The model consists of $N_S$ signals along the tracks and the actuators on $N_T$ trains, which are centrally controlled. The communication between the signals and the control center may be interrupted through cyber means, while the actuators on trains may be damaged physically. Reinforcements to these components may be in the form of redundant communication routes for the signals and better physical protection of the actuators on trains. Since a cyber attack on a signal along the tracks partially disrupts the smooth running of all the trains running the line through that signal, a first-order model is given by $P_{\overline{P}|\overline{C}}=\alpha N_L(1-P_C)$, which captures the multiplicative effect of cyber attacks, where $0<\alpha <1$ is properly chosen to represent a partial effect and $N_L$ indicates the number of trains running on a line.

Then, by using the Bayes formula $P_{\overline{C}|\overline{P}}=P_{\overline{P}|\overline{C}}{P}_{\overline{C}}/P_{\overline{P}}$, we have $f(P_C,P_P)=\frac{\alpha N_L{(1-P_C)}^2}{(1-P_P)}$. Typically, $N_L$ is on the order of tens, whereas $N_S$ in the previous example could be in the thousands.

We now consider that the attacker and provider choose components to attack and reinforce, respectively, according to uniform distribution. Then, there are ${[y_C-x_C]}_{+}$ non-reinforced signals. The probability that a reinforced actuator survives the cyber attacks is estimated by

$$p_{P|R}=\frac{f_P}{1+\alpha N_L{[y_C-x_C]}_{+}},$$

where $0\le f_P\le 1$ is a normalization factor. This estimate reflects that cyber attacks are more likely to disrupt the actuator functioning for higher values of ${[y_C-x_C]}_{+}$, and the physical attacks have no effect on a reinforced actuator. If the actuator is not reinforced, it will be brought down by a direct physical attack, or indirectly through a cyber attack. Thus, we estimate its survival probability as

$$p_{P|N}=\frac{f_P}{1+y_P+\alpha N_L{[y_C-x_C]}_{+}},$$

which is inversely proportional to the number of physical attacks $y_P$. Using these formulae, we have

$${\mathrm{\Lambda }}_P(x_C,y_C,y_P)=ln\left(1+\frac{y_P}{1+\alpha N_L{[y_C-x_C]}_{+}}\right)$$

for the physical sub-infrastructure, which interestingly does not depend on physical $x_P$ but captures the dependence on cyber $x_C$. Note that the roles of cyber and physical components are switched in this example compared to the cloud computing infrastructure.

Example 3.

Smart Power Grid Infrastructure:A power grid infrastructure (Figure 3) is controlled by a SCADA system using information collected by a network of sensors that monitor transmission and distribution lines. The sensors are placed at strategic locations for effective flow control, and they have good connectivity to the SCADA system via communication nodes. We assume that each communication node relays information from sensors of $N_L$ lines to the SCADA system, and it may be disabled by a direct cyber attack, which will disrupt the information flow from all $N_L$ lines. Typically, $N_L$ is of the order of tens. When the monitoring information of a line is lost, the SCADA system may assume the line to be down for safety reasons, and hence disrupting a node will also disrupt the power flow on all $N_L$ lines. By using reasoning analogous to the previous two examples, we have $P_{\overline{P}|\overline{C}}=N_L(1-P_C)$. Then, by using the Bayes formula $P_{\overline{C}|\overline{P}}=P_{\overline{P}|\overline{C}}{P}_{\overline{C}}/P_{\overline{P}}$, we have $f(P_C,P_P)=\frac{N_L{(1-P_C)}^2}{(1-P_P)}$. We then estimate the survival probability of a reinforced line, which can be disconnected by ${[y_C-x_C]}_{+}$ cyber attacks, as

$$p_{P|R}=\frac{f_P}{1+N_L{[y_C-x_C]}_{+}},$$

where $0\le f_P\le 1$ is appropriately chosen under uniform attack and reinforcement distributions. Meanwhile, a power line can be directly disrupted by physical means if it is not reinforced, and it is more likely to be unavailable if there are more physical attacks (i.e., higher $y_P$). Thus, an attack on a communication node will have an amplified effect on power lines compared to direct physical attacks, such that

$$p_{P|N}=\frac{f_P}{1+y_P+N_L{[y_C-x_C]}_{+}},$$

which provides an estimate of the probability of survival of a non-reinforced power line. Using the above formulae, we have

$${\mathrm{\Lambda }}_P(x_C,y_C,y_P)=ln\left(1+\frac{y_P}{1+N_L{[y_C-x_C]}_{+}}\right),$$

which does not depend on $x_P$ as in the case of the metro system.

4. Game-Theoretic Formulation

The provider’s objective is to make the infrastructure resilient by reinforcing $x_C$ and $x_P$ cyber and physical components, respectively, to minimize the utility function. For uniform component reinforcement costs, we have $L_D\left(x_C,x_P\right)=c_{CD}{x}_C+c_{PD}{x}_P$, where $c_{CD}$ and $c_{PD}$ are reinforcement costs of cyber and physical components, respectively. The attacker’s objective is to disrupt the infrastructure by attacking $y_C$ or $y_P$ cyber and physical components, respectively (but not both), in order to minimize the utility function. For uniform component attack costs, we use $L_A\left(y_C,y_P\right)=c_{CA}{y}_C+c_{PA}{y}_P$, where $c_{CA}$ and $c_{PA}$ are the attack costs of cyber and physical components, respectively, and only one of $y_C$ and $y_P$ is non-zero.

4.1. Nash Equilibrium Conditions

The Nash equilibrium conditions are derived by equating the corresponding derivatives of the utility functions (as shown in Section 1) to zero, which yields

$$\frac{\partial U_D}{\partial x_B}=\left(G_D\frac{\partial F_{D,G}}{\partial P_{CP}}+L_D\frac{\partial F_{D,L}}{\partial P_{CP}}\right)\frac{\partial P_{CP}}{\partial x_B}+F_{D,G}\frac{\partial G_D}{\partial x_B}+F_{D,L}\frac{\partial L_D}{\partial x_B}=0,$$

where $B=C,P$ for the provider. We define $L_{G,L}^D=G_D\frac{\partial F_{D,G}}{\partial P_{CP}}+L_D\frac{\partial F_{D,L}}{\partial P_{CP}}$ as the composite gain–cost term, and $F_{G,L}^{D,B}=F_{D,G}\frac{\partial G_D}{\partial x_B}+F_{D,L}\frac{\partial L_D}{\partial x_B}$ as the gain–cost gradient with respect to $x_B$, $B=C,P$. For the attacker, we similarly obtain, for $B=C,P$,

$$\frac{\partial U_A}{\partial y_B}=\left(G_A\frac{\partial F_{A,G}}{\partial P_{CP}}+L_A\frac{\partial F_{A,L}}{\partial P_{CP}}\right)\frac{\partial P_{CP}}{\partial y_B}+F_{A,G}\frac{\partial G_A}{\partial y_B}+F_{A,L}\frac{\partial L_A}{\partial y_B}=0.$$

4.2. OR Systems

The OR subsystems are a special case where the probability of simultaneous failures of cyber and physical sub-infrastructures is negligible. [4]. Here, the infrastructure will fail if either of the cyber or physical sub-infrastructures fail, such that $P_{\overline{C}\cup \overline{P}}=P_{\overline{C}}+P_{\overline{P}}$, or equivalently $P_{CP}=P_C+P_P-1$. In these (theoretical) systems, the dependence of $P_{CP}$ on system parameters at NE is easier to derive and interpret, since it is determined entirely by Condition 3 without involving $f(P_C,P_P)$. We have a much simpler form of Condition 2 given by $\frac{\partial P_{CP}}{\partial x_C}=\frac{\partial P_C}{\partial x_C}$ and $\frac{\partial P_{CP}}{\partial x_P}=\frac{\partial P_P}{\partial x_P}$. At NE, we have

$$\frac{\partial P_C}{\partial x_C}=-\frac{F_{D,G}\frac{\partial G_D}{\partial x_C}+F_{D,L}\frac{\partial L_D}{\partial x_C}}{G_D\frac{\partial F_{D,G}}{\partial P_{CP}}+L_D\frac{\partial F_{D,L}}{\partial P_{CP}}}=-\frac{F_{G,L}^{D,C}\left(x_C,x_P,y_C,y_P\right)}{L_{G,L}^D\left(x_C,x_P,y_C,y_P\right)}=-{\mathsf{\Theta }}_C\left(x_C,x_P,y_C,y_P\right),$$

$$\frac{\partial P_P}{\partial x_P}=-\frac{F_{D,G}\frac{\partial G_D}{\partial x_P}+F_{D,L}\frac{\partial L_D}{\partial x_P}}{G_D\frac{\partial F_{D,G}}{\partial P_{CP}}+L_D\frac{\partial F_{D,L}}{\partial P_{CP}}}=-\frac{F_{G,L}^{D,P}\left(x_C,x_P,y_C,y_P\right)}{L_{G,L}^D\left(x_C,x_P,y_C,y_P\right)}=-{\mathsf{\Theta }}_P\left(x_C,x_P,y_C,y_P\right),$$

wherein ${\mathsf{\Theta }}_C\left(·\right)$ and ${\mathsf{\Theta }}_P\left(·\right)$ are called the cyber and physical scaled gain–cost gradients, respectively. Using Condition 3, we obtain the following estimates for the survival probabilities of cyber and physical sub-infrastructures:

$$\begin{array}{c}\hfill {\tilde{P}}_{C;D}\left(x_C,x_P,y_C,y_P\right)=-\frac{{\mathsf{\Theta }}_C\left(x_C,x_P,y_C,y_P\right)}{{\mathrm{\Lambda }}_C(x_C,x_P,y_C,y_P)}\mathrm{and}{\tilde{P}}_{P;D}\left(x_C,x_P,y_C,y_P\right)=-\frac{{\mathsf{\Theta }}_P\left(x_C,x_P,y_C,y_P\right)}{{\mathrm{\Lambda }}_P(x_C,x_P,y_C,y_P)}.\end{array}$$

These estimates for cyber and physical sub-infrastructures depend mainly on the corresponding scaled gain–cost gradients, and thus represent a “separation” of the cyber and physical parts at this level. In this sense, OR systems constitute an important analytical case wherein the cyber–physical correlations between the sub-infrastructures may be ignored. In addition, these estimates provide the sensitivity information of the survival probabilities of cyber and physical sub-infrastructures, and they depend only on the derivatives of the corresponding probabilities. Although they do not involve the failure correlation function $f(P_C,P_P)$, the cyber–physical interactions are still captured by ${\mathrm{\Lambda }}_C(·)$ and ${\mathrm{\Lambda }}_P(·)$ at the component level. Both survival probability estimates ${\tilde{P}}_{C;D}$ and ${\tilde{P}}_{P;D}$ are proportional to the corresponding weighted cost and reward functions, and are inversely proportional to their weighted derivatives. This seemingly counter-intuitive trend applies only to the set of Nash equilibria, and not to the overall system behavior.

4.3. Statistical Independence of Cyber and Physical Sub-Infrastructures

We consider that the cyber sub-infrastructure failures are statistically independent such that $P_{CP}=P_C{P}_P$ and $f\left(P_C,P_P\right)=1-P_C$. At NE, we have

$$\begin{array}{c}\hfill P_P\frac{\partial P_C}{\partial x_C}=-{\mathsf{\Theta }}_C\left(x_C,x_P,y_C,y_P\right)\mathrm{and}{P}_C\frac{\partial P_P}{\partial x_P}=-{\mathsf{\Theta }}_P\left(x_C,x_P,y_C,y_P\right).\end{array}$$

We now substitute expressions for $\frac{\partial P_C}{\partial x_C}$ and $\frac{\partial P_P}{\partial x_P}$ based on Condition 3, and obtain the system of equations:

$$\begin{array}{c}\hfill {\overline{P}}_{C;D}{\overline{P}}_{P;D}=-\frac{{\mathsf{\Theta }}_C\left(x_C,x_P,y_C,y_P\right)}{{\mathrm{\Lambda }}_C(x_C,x_P,y_C,y_P)}\mathrm{and}{\overline{P}}_{C;D}{\overline{P}}_{P;D}=-\frac{{\mathsf{\Theta }}_P\left(x_C,x_P,y_C,y_P\right)}{{\mathrm{\Lambda }}_P(x_C,x_P,y_C,y_P)}.\end{array}$$

Qualitatively, at NE, the survival probability estimates of cyber and physical sub-infrastructures ${\overline{P}}_{C;D}$ and ${\overline{P}}_{P;D}$ have an inverse relationship, but their product is determined by ${\mathrm{\Lambda }}_C(·)$ and ${\mathrm{\Lambda }}_P(·)$ in a manner similar to the individual probabilities ${\tilde{P}}_{C;D}$ and ${\tilde{P}}_{P;D}$ of OR systems. However, unlike OR systems, statistical independence is not sufficient to decouple the estimates ${\overline{P}}_{C;D}$ and ${\overline{P}}_{P;D}$ so that they depend solely on ${\mathrm{\Lambda }}_C(·)$ and ${\mathrm{\Lambda }}_P(·)$, respectively.

4.4. NE Sensitivity Functions

We now derive estimates for $P_C$ and $P_P$ at NE using the scaled gain–cost gradients and failure correlation function to obtain qualitative information about their sensitivities to different parameters from the provider’s perspective.

Theorem 1.

Under Conditions 1, 2, and 3, an estimate of the survival probability of physical sub-infrastructure at the Nash equilibrium for $\frac{\partial f}{\partial P_P}\ne 0$ is

$${\widehat{P}}_{P;D}\left(x_C,x_P,y_C,y_P\right)=\frac{1-f\left(P_C,P_P\right)+\frac{\partial f}{\partial P_P}}{2\frac{\partial f}{\partial P_P}}\pm \sqrt{{\left(\frac{1-f\left(P_C,P_P\right)+\frac{\partial f}{\partial P_P}}{2\frac{\partial f}{\partial P_P}}\right)}^2-\frac{{\mathsf{\Theta }}_P(x_C,x_P,y_C,y_P)}{{\mathrm{\Lambda }}_P(x_C,x_P,y_C,y_P)\frac{\partial f}{\partial P_P}}},$$

and, for $\frac{\partial f}{\partial P_P}=0$, is

$${\widehat{P}}_{P;D}\left(x_C,x_P,y_C,y_P\right)=-\frac{{\mathsf{\Theta }}_P(x_C,x_P,y_C,y_P)}{{\mathrm{\Lambda }}_P(x_C,x_P,y_C,y_P)\left[1-f\left(P_C,P_P\right)\right]}.$$

An estimate of the survival probability of cyber sub-infrastructure is

$${\widehat{P}}_{C;D}\left(x_C,x_P,y_C,y_P\right)=-\frac{{\mathsf{\Theta }}_C(x_C,x_P,y_C,y_P)}{{\mathrm{\Lambda }}_C(x_C,x_P,y_C,y_P)\left[1+(1-{\widehat{P}}_{P;D})\frac{\partial f}{\partial P_C}\right]}.$$

Proof: 

At NE, we have $\frac{\partial P_{CP}}{\partial x_C}=-{\mathsf{\Theta }}_C(x_C,x_P,y_C,y_P)$ and $\frac{\partial P_{CP}}{\partial x_P}=-{\mathsf{\Theta }}_P(x_C,x_P,y_C,y_P)$. By using the formulae in Condition 2, we have

$$\left[1+(1-P_P)\frac{\partial f}{\partial P_C}\right]\frac{\partial P_C}{\partial x_C}=-{\mathsf{\Theta }}_C(x_C,x_P,y_C,y_P),$$

$$\left[1-f(P_C,P_P)+(1-P_P)\frac{\partial f}{\partial P_P}\right]\frac{\partial P_P}{\partial x_P}=-{\mathsf{\Theta }}_P(x_C,x_P,y_C,y_P).$$

We now substitute expressions for $\frac{\partial P_C}{\partial x_C}$ and $\frac{\partial P_P}{\partial x_P}$ based on Condition 3, and obtain the system of equations:

$$\left[1+(1-P_P)\frac{\partial f}{\partial P_C}\right]P_C=-\frac{{\mathsf{\Theta }}_C(x_C,x_P,y_C,y_P)}{{\mathrm{\Lambda }}_C(x_C,x_P,y_C,y_P)},$$

$$\left[1-f(P_C,P_P)+(1-P_P)\frac{\partial f}{\partial P_P}\right]P_P=-\frac{{\mathsf{\Theta }}_P(x_C,x_P,y_C,y_P)}{{\mathrm{\Lambda }}_P(x_C,x_P,y_C,y_P)}.$$

The expression for ${\widehat{P}}_{P;D}$ is obtained by solving for $P_P$ using the above quadratic equation, and the expression for ${\widehat{P}}_{C;D}$ follows from the equation above it. □

Compared to OR Systems, there are significant cyber–physical interactions at the sub-infrastructure level in both ${\widehat{P}}_{P;D}\left(x_C,x_P,y_C,y_P\right)$ and ${\widehat{P}}_{C;D}\left(x_C,x_P,y_C,y_P\right)$. In particular, ${\widehat{P}}_{P;D}\left(x_C,x_P,y_C,y_P\right)$ depends on both $f(·)$ and its partial derivatives with respect to $P_P$, and the partial derivatives of $G_D$ and $L_D$ with respect to $x_P$ and ${\mathrm{\Lambda }}_P$, as expected. Its dependence on $P_C$ is implicit through the failure correlation function $f(P_C,P_P)$. The qualitative behavior of ${\widehat{P}}_{C;D}\left(x_C,x_P,y_C,y_P\right)$ is quite similar with respect to $L_D$, but its dependence on $P_P$ is also through f. They are both affected by ${\mathrm{\Lambda }}_C(·)$ and ${\mathrm{\Lambda }}_P(·)$, and each of them in turn depends on the number of both cyber and physical component attacks and reinforcements. Thus, the estimates ${\widehat{P}}_{P;D}$ and ${\widehat{P}}_{C;D}$ reflect the correlations between the sub-infrastructures explicitly through f, as well as those captured by the survival probabilities of individual sub-infrastructures.

Theorem 1 utilizes $P_{\overline{C}|\overline{P}}=f(P_C,P_P)$, which captures the failure effects of physical sub-infrastructure on the cyber sub-infrastructure. Alternatively, we can utilize $P_{\overline{P}|\overline{C}}=g(P_C,P_P)$, which captures the failure effects of cyber sub-infrastructure on the physical sub-infrastructure. In this case, we obtain a quadratic expression in $P_C$. Then, we can estimate ${\widehat{P}}_{C;D}\left(x_C,x_P,y_C,y_P\right)$ in terms of $g(P_C,P_P)$ by solving the quadratic equation as in Theorem 1. Additionally, results expressed in terms of $f(P_C,P_P)$ and $g(P_C,P_P)$ can be converted between each other using the following expression:

$$\begin{array}{cc}\hfill f(P_C,P_P)=& P_{\overline{C}\overline{P}}/(1-P_P)=P_{\overline{P}|\overline{C}}(1-P_C)/(1-P_P)\hfill \\ \hfill =& g(P_C,P_P)(1-P_C)/(1-P_P).\hfill \end{array}$$

The qualitative effects of $f(·)$ and $g(·)$ on the sensitivity function estimates is quite similar, and their choice is determined by their functional forms and the accuracy with which they can be estimated.

The estimates in Theorem 1 are based on the first-order derivatives of utility functions, and their minimization leads to second-order derivative conditions, which in turn provides an upper bound on $P_P$ as follows:

Theorem 2.

Under Conditions 1, 2, and 3, an upper bound on the survival probability of physical sub-infrastructure at the Nash equilibrium for $\frac{\partial f}{\partial P_P}\ne 0$ is

$$P_P\le 1+\left[1-f(P_C,P_P)\right]/\frac{\partial f}{\partial P_P}+\frac{1}{\frac{\partial f}{\partial x_P}}\left[\left(L_{G,L}^D\frac{{\partial }^2{P}_{CP}}{\partial x_P^2}+\frac{\partial F_{G,L}^{D,P}}{\partial x_P}\right)/\left(\frac{\partial L_{G,L}^D}{\partial x_P}\right)\right].$$

Proof: 

At NE, the first derivative of the utility function is given by

$$\frac{\partial U_D}{\partial x_B}=\left(G_D\frac{\partial F_{D,G}}{\partial P_{CP}}+L_D\frac{\partial F_{D,L}}{\partial P_{CP}}\right)\frac{\partial P_{CP}}{\partial x_B}+F_{D,G}\frac{\partial G_D}{\partial x_B}+F_{D,L}\frac{\partial L_D}{\partial x_B}=L_{G,L}^D\frac{\partial P_{CP}}{\partial x_B}+F_{G,L}^{D,B},$$

where $B=C,P$. The second derivative condition is given by

$$\frac{{\partial }^2{U}_D}{\partial x_B^2}=L_{G,L}^D\frac{{\partial }^2{P}_{CP}}{\partial x_B^2}+\frac{\partial L_{G,L}^D}{\partial x_B}\frac{\partial P_{CP}}{\partial x_B}+\frac{\partial F_{G,L}^{D,B}}{\partial x_B}>0,$$

which in turn provides a bound on $\frac{\partial P_{CP}}{\partial x_B}$ as follows,

$$\frac{\partial P_{CP}}{\partial x_B}>-\left(L_{G,L}^D\frac{{\partial }^2{P}_{CP}}{\partial x_B^2}+\frac{\partial F_{G,L}^{D,B}}{\partial x_B}\right)/\frac{\partial L_{G,L}^D}{\partial x_B}.$$

The upper bound on $P_P$ then follows from Condition 2 by using $x_B=x_P$ and $\frac{\partial f}{\partial P_P}\frac{\partial P_P}{\partial x_P}=\frac{\partial f}{\partial x_P}$ . □

This theorem indicates that the ratio of the correlation function and its derivatives $\frac{\partial f}{\partial P_P}$ and $\frac{\partial f}{\partial x_P}$ could limit the achievable $P_P$. The cost term $L_{G,L}^D$ and $\frac{\partial F_{G,L}^{D,P}}{\partial x_P}$ can counter this effect somewhat, but $\frac{\partial L_{G,L}^D}{\partial x_P}$ can add to this effect.

4.5. Sum-Form and Product-Form Utility Functions

The utility functions can be specialized to reflect different aspects of the infrastructure, in particular explicitly expressing the terms using $P_{CP}(x_C,x_P,y_C,y_P)$. Corresponding to the sum-form in Section 1, the utility of the attacker is given by

$$U_{A+}\left(x_C,x_P,y_C,y_P\right)=\left[P_{CP}(x_C,x_P,y_C,y_P)\right]g_A+L_A(y_C,y_P),$$

where $[1-P_{CP}(x_C,x_P,y_C,y_P)]g_A$ is the expected reward for the cost $L_A(y_C,y_P)$ of cyber or physical attacks. Similarly, the product-form utility of the attacker is given by

$$U_{A\times }\left(x_C,x_P,y_C,y_P\right)=P_{CP}(x_C,x_P,y_C,y_P)L_A(y_C,y_P),$$

which represents the expected cost when the infrastructure survives the attacks and thus represents “wasted” effort. The individual terms of the utility functions for sum- and product-forms are simplified as shown in

Table 3. Gain and cost terms and their multipliers for sum-form and product-form utilities of the provider.

	${\mathit{F}}_{\mathit{D},\mathit{G}}$	${\mathit{G}}_{\mathit{D}}$	${\mathit{F}}_{\mathit{D},\mathit{L}}$	${\mathit{L}}_{\mathit{D}}$	$\frac{\mathit{\partial }{\mathit{F}}_{\mathit{D},\mathit{G}}}{\mathit{\partial }{\mathit{P}}_{\mathbf{CP}}}$	$\frac{\mathit{\partial }{\mathit{G}}_{\mathit{D}}}{\mathit{\partial }{\mathit{x}}_{\mathit{B}}}$	$\frac{\mathit{\partial }{\mathit{F}}_{\mathit{D},\mathit{L}}}{\mathit{\partial }{\mathit{P}}_{\mathbf{CP}}}$
sum-form: $U_{D+}$	$\left[1-P_{CP}\right]$	$g_D$	1	$L_D$	−1	0	0
product-form: $U_{D\times }$	0	0	$\left[1-P_{CP}\right]$	$L_D$	0	0	−1

for the provider.

Special cases of Theorem 1 for sum- and product-forms are presented in [2,4], and the second-order condition in Theorem 2 provides us with additional conditions on achievable $P_P$. In particular, for the sum-form utility of the provider, the second derivative condition is

$$\frac{{\partial }^2{U}_D}{\partial x_B^2}=-\frac{{\partial }^2{P}_{CP}}{\partial x_B^2}{g}_D+\frac{{\partial }^2{L}_D}{\partial x_B^2}>0,$$

which provides an upper bound on $\frac{{\partial }^2{P}_{CP}}{\partial x_B^2}$. And for the product-form utility of the provider, the second derivative condition is

$$\frac{{\partial }^2{U}_D}{\partial x_B^2}=-2\frac{\partial P_{CP}}{\partial x_B}\frac{\partial L_D}{\partial x_B}-L_D\frac{{\partial }^2{P}_{CP}}{\partial x_B^2}+(1-P_{CP})\frac{{\partial }^2{L}_D}{\partial x_B^2}>0,$$

which provides an upper bound on $P_{CP}$.

4.6. Survival Probabilities of Sub-Infrastructures

It is instructive to compare the individual survival probabilities of cyber and physical sub-infrastructures $P_C$ and $P_P$, respectively, since the minimum of the two determines the survival probability of the infrastructure. Using the equations from the proof of Theorem 1, we have

$$\begin{array}{cc}\hfill \left[1+(1-P_P)\frac{\partial f}{\partial P_C}\right]P_C=& -\frac{{\mathsf{\Theta }}_C\left(x_C,x_P,y_C,y_P\right)}{{\mathrm{\Lambda }}_C\left(x_C,x_P,y_C,y_P\right)}\hfill \\ \hfill \left[1-f(P_C,P_P)+(1-P_P)\frac{\partial f}{\partial P_P}\right]P_P=& -\frac{{\mathsf{\Theta }}_P\left(x_C,x_P,y_C,y_P\right)}{{\mathrm{\Lambda }}_P\left(x_C,x_P,y_C,y_P\right)}.\hfill \end{array}$$

In this section, for simplicity we denote ${\mathrm{\Lambda }}_C\left(x_C,x_P,y_C,y_P\right)$, ${\mathrm{\Lambda }}_P\left(x_C,x_P,y_C,y_P\right)$, ${\mathsf{\Theta }}_C\left(x_C,x_P,y_C,y_P\right)$, and ${\mathsf{\Theta }}_P\left(x_C,x_P,y_C,y_P\right)$ by ${\mathrm{\Lambda }}_C$, ${\mathrm{\Lambda }}_P$, ${\mathsf{\Theta }}_C$, and ${\mathsf{\Theta }}_P$, respectively. By dividing the above two equations by $\frac{\partial f}{\partial P_C}$ and $\frac{\partial f}{\partial P_P}$, respectively, and eliminating the term $(1-P_P)$ by subtraction, we obtain the following condition:

$$\left(\frac{{\mathsf{\Theta }}_P}{P_P{\mathrm{\Lambda }}_P}\right)-\frac{\frac{\partial f}{\partial P_P}}{\frac{\partial f}{\partial P_C}}\left(\frac{{\mathsf{\Theta }}_C}{P_C{\mathrm{\Lambda }}_C}\right)=-\left[1-f\left(P_C,P_P\right)-\frac{\frac{\partial f}{\partial P_P}}{\frac{\partial f}{\partial P_C}}\right].$$

Then, by using $\frac{\partial P_C}{\partial P_P}=-\frac{\frac{\partial f}{\partial P_P}}{\frac{\partial f}{\partial P_C}}$, we obtain the following relationship between $P_P$ and $P_C$:

$$P_P=\frac{P_C{\mathrm{\Lambda }}_C{\mathsf{\Theta }}_P}{{\mathrm{\Lambda }}_P\left\{-P_C{\mathrm{\Lambda }}_C\left[1-f(P_C,P_P)+\frac{\partial P_C}{\partial P_P}\right]-\frac{\partial P_C}{\partial P_P}{\mathsf{\Theta }}_C\right\}}.$$

By comparing the right hand side to $P_C$, the condition $P_P\ge P_C$ is equivalent to

$$P_C\doteq -\frac{\left(\frac{{\mathrm{\Lambda }}_C}{{\mathrm{\Lambda }}_P}{\mathsf{\Theta }}_P+\frac{\partial P_C}{\partial P_P}{\mathsf{\Theta }}_C\right)}{{\mathrm{\Lambda }}_C\left[1-f(P_C,P_P)+\frac{\partial P_C}{\partial P_P}\right]},$$

where ≐ is either ≤ or ≥ based on the sign of the denominator above. If ≐ is ≤, then the above condition is not satisfied if the right hand side is negative, which in turn corresponds to the signs of the two terms $\left(\frac{{\mathrm{\Lambda }}_C}{{\mathrm{\Lambda }}_P}{\mathsf{\Theta }}_P+\frac{\partial P_C}{\partial P_P}{\mathsf{\Theta }}_C\right)$ and $\left[1-f(P_C,P_P)+\frac{\partial P_C}{\partial P_P}\right]$ being the opposite. On the other hand, if ≐ is ≥, then this condition is not true if the right hand side is greater than 1. These two boundary conditions determine that one of the two conditions $P_P\ge P_C$ and $P_P\le P_C$ is true. In the other cases, this relationship is not that simply determined, and can take a more complicated form.

For the special case $f\left(P_C,P_P\right)=a_C(1-P_C)+b_C$, we have

$$P_P=-\frac{{\mathsf{\Theta }}_P}{{\mathrm{\Lambda }}_P\left(1-a_C+a_C{P}_C-b_C\right)}.$$

Then, the condition $P_P\ge P_C$ leads to a quadratic equation with the following solution:

$$P_C=\frac{-(1-a_C-b_C)}{2a}\pm \frac{1}{2a}\sqrt{{(1-a_C-b_C)}^2-\frac{4a_C{\mathsf{\Theta }}_P}{{\mathrm{\Lambda }}_P}}.$$

The boundary conditions in this case can be derived as in the general case. However, a different line of analysis done in this case in [5] provides a much simpler characterization of the relationship between $P_C$ and $P_P$. It yields the following simpler condition:

$$P_C=\left(1-\frac{b_C}{1-a_C}\right)P_P+\frac{d_{CD}-d_{PD}}{(1-a_C)},$$

where $d_{CD}=\frac{\partial L_D}{\partial x_C}/\left[g_{D}ln\left(\frac{p_{P|R}}{p_{P|N}}\right)\right]$ and $d_{PD}=\frac{\partial L_D}{\partial x_P}/\left[g_{D}ln\left(\frac{p_{C|R}}{p_{C|N}}\right)\right]$. Then, the relationship between $P_C$ and $P_P$ is described by 12 different regions determined solely by $a_C$, $b_C$, $d_{CD}$, and $d_{PD}$ such that in each region exactly one of the two conditions $P_P\ge P_C$ and $P_P\le P_C$ is true.

5. Application Examples

In this section, we expand the three examples from Section 3.2 by taking more component details into account. First, we consider different types of cyber and physical components such that $x_C^i$, $i\in {\mathcal{A}}_C$ is the number of cyber components of type i, and $x_P^j$, $j\in {\mathcal{A}}_P$ is the number of physical components of type j. Thus, in terms of the original indices, we have $x_C={\displaystyle \sum _{i\in {\mathcal{A}}_C}}{x}_C^i$ and $x_P={\displaystyle \sum _{j\in {\mathcal{A}}_P}}{x}_P^j$. We define sub-infrastructures consisting of only cyber components of type i and physical components of type j, with their survival probabilities denoted by $P_C^i$ and $P_P^j$, respectively. Now we generalize Condition 3 as follows.

Condition 4.

The survival probabilities of cyber and physical sub-infrastructures are given by

$$\frac{\partial P_C^i}{\partial x_C^i}=h_C^i\left(P_C^i,x_C,x_P,y_C,y_P\right)={\mathrm{\Lambda }}_C^i(x_C,x_P,y_C,y_P)P_C^i$$

for $x_C^i$, $i\in {\mathcal{A}}_C$, corresponding to cyber components of type i, and

$$\frac{\partial P_P^j}{\partial x_P^j}=h_P^j\left(P_P^j,x_C,x_P,y_C,y_P\right)={\mathrm{\Lambda }}_P^j(x_C,x_P,y_C,y_P)P_P^j$$

for $x_P^j$, $j\in {\mathcal{A}}_P$, corresponding to physical components of type j.

The component failures are considered statistically independent for different types in [5] such that

$$P_C=\prod _{i\in {\mathcal{A}}_C}{P}_C^i=\prod _{i\in {\mathcal{A}}_C}{\left(p_{C|R}^i\right)}^{x_C^i}{\left(p_{C|N}^i\right)}^{N_C^i-x_C^i},$$

$$P_P=\prod _{j\in {\mathcal{A}}_P}{P}_P^j=\prod _{j\in {\mathcal{A}}_P}{\left(p_{P|R}^j\right)}^{x_P^j}{\left(p_{P|N}^j\right)}^{N_P^j-x_P^j},$$

where $p_{C|R}^i$ and $p_{P|R}^j$ denote the probabilities of reinforced cyber component of type i and reinforced physical component of type j, respectively; $p_{C|N}^i$ and $p_{P|N}^j$ denote the probabilities of cyber component of type i and physical component of type j without reinforcement, respectively; and $N_C^i$ and $N_P^j$ denote the number of type i cyber components and type j physical components, respectively. These conditions in turn lead to the special case of Condition 4: for $i\in {\mathcal{A}}_C$, $j\in {\mathcal{A}}_P$,

$$\frac{\partial P_C}{\partial x_C^i}=P_{C}ln\left(\frac{p_{C|R}^i}{p_{C|N}^i}\right)\mathrm{and}\frac{\partial P_P}{\partial x_P^j}=P_{P}ln\left(\frac{p_{P|R}^j}{p_{P|N}^j}\right).$$

We consider that these conditions are satisfied in both of the following examples.

5.1. Cloud Computing Infrastructure

The simple cloud computing infrastructure model of Example 1 in Section 3.2 is expanded to include a gateway router at each site, which connects to all servers at the site. A cyber attack on a gateway router will also have essentially the same effect as a physical fiber attack—namely, disconnecting all servers at the site. A fiber attack requires physical proximity, whereas a router cyber attack may be remotely launched, thereby representing different types of costs. Cyber components now belong to two classes, namely, servers and routers, such that $x_C=x_C^S+x_C^R$ where $x_C^S$ and $x_C^R$ denote the number of reinforced servers and routers, respectively. Similarly, we have $y_C=y_C^S+y_C^R$, where $y_C^S$ and $y_C^R$ denote the number of servers and routers attacked, respectively. Then, for the two cyber sub-infrastructures, we have the failure correlation functions $f^S\left(P_C^S,P_P\right)=N_S(1-P_P)$ and $f^R\left(P_C^R,P_P\right)=(1-P_P)$, wherein the physical failures are amplified by $N_S$ for the servers but are the same for routers. Thus, the composite failure correlation function $f(P_C,P_P)$ is given as follows:

$$f\left(P_C,P_P\right)=\sum _{B\in \{S,R\}}{P}_{\overline{C}|\overline{P}}^B=f^S\left(P_C^S,P_P\right)+f^R\left(P_C^R,P_P\right)=(N_S+1)(1-P_P).$$

Then, the survival probabilities of cyber-reinforced components are computed separately for the servers and routers, which are denoted by $p_{C|R}^S$ and $p_{C|R}^R$, respectively. The probability that a cyber-reinforced server survives fiber or router attacks is given by

$$p_{C|R}^S=\frac{f_C^S}{1+N_S{[y_P-x_P]}_{+}+N_S{[y_C^R-x_C^R]}_{+}},$$

which now depends on both physical attacks on fiber and cyber attack on routers. An estimate of the probability that a cyber-reinforced router survives a physical fiber attack is given by $p_{C|R}^R=\frac{f_C^R}{1+{[y_P-x_P]}_{+}},$ since a cyber attack on a reinforced router has no impact and a fiber attack will disconnect only one router. If the router is not cyber-reinforced, then we have $p_{C|N}^R=\frac{f_C^R}{1+{[y_P-x_P]}_{+}+y_C^R},$ which additionally depends on $y_C^R$. By using these estimates for the router, we have

$${\mathrm{\Lambda }}_C^R\left(x_P,y_C^R,y_P\right)=ln\left(1+\frac{y_C^R}{1+{[y_P-x_P]}_{+}}\right),$$

which increases in the number of cyber router attacks but decreases in the number of attacks on non-reinforced routers. If the cyber component, server or router, is not reinforced, it will be brought down by a direct cyber attack or indirectly by fiber attack, but the latter will have a greater impact. However, cyber attacks on servers and routers will have different impacts on the availability of the infrastructure. That is, a server attack will only bring it down, but a router attack will make all $N_S$ servers unavailable. In some current infrastructures, $N_S$ could be on the order of thousands. Thus, for a server that is not cyber-reinforced, we use the estimate

$$p_{C|N}^S=\frac{f_C^S}{1+N_S{[y_P-x_P]}_{+}+N_S{[y_C^R-x_C^R]}_{+}+y_C^S},$$

which reflects the additional lowering of survival probability inversely proportional to the level of cyber attack $y_C^S$, and to $y_C^R$ but amplified by a factor $N_S$. Thus, for servers, we have

$${\mathrm{\Lambda }}_C^S\left(x_C^R,x_P,y_C^S,y_C^R,y_P\right)=ln\left(1+\frac{y_C^S}{1+N_S{[y_P-x_P]}_{+}+N_S{[y_C^R-x_C^R]}_{+}}\right),$$

which increases in the number of server attacks but decreases in the attacks on non-reinforced routers and fibers.

The survival probabilities of physical fiber components depend on $y_P$ such that $p_{P|R}=f_P$ and $p_{P|N}=\frac{f_P}{1+y_P}.$ By combining the two formulae for fiber, we have ${\mathrm{\Lambda }}_P\left(y_P\right)=ln\left(1+y_P\right),$ which increases in the number of physical attacks. Similar to the case of the metro system, in addition to ${\mathrm{\Lambda }}_P(·)$ and ${\mathrm{\Lambda }}_C^B(·)$, where $B=S,R$, the survival probabilities of cyber and physical sub-infrastructures are determined by the correlation function $f(P_C,P_P)$, as described in Section 4.6.

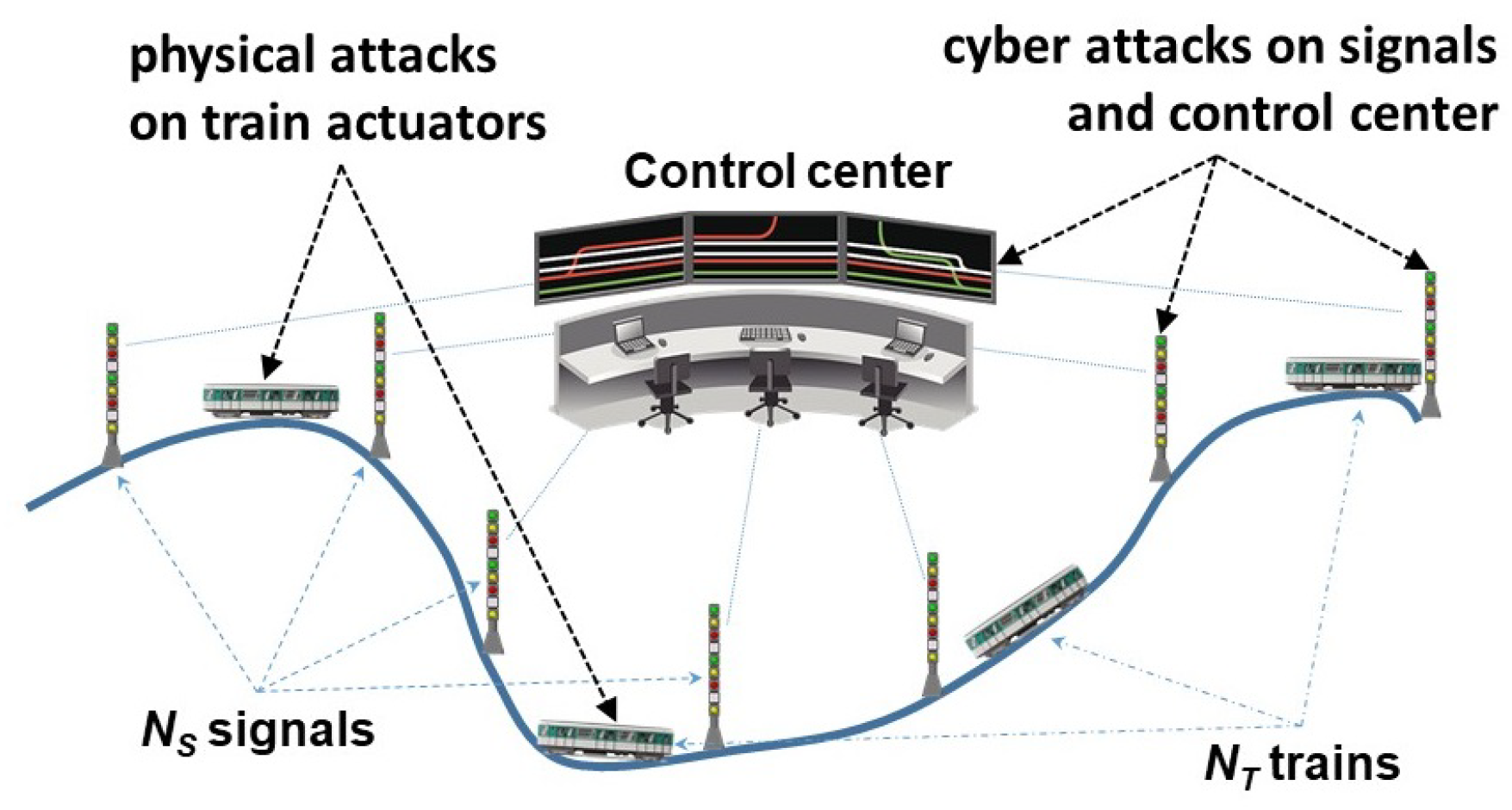
5.2. Metro System

We refine the metro system model of Example 2 in Section 3.2 to include multiple traffic control centers, each connecting to all signals of a single line. A cyber attack on a control center will disconnect all signals of its line and disrupt all trains running on that line. Now, we separate the cyber components into two classes, namely, control centers and signals, and $x_C=x_C^T+x_C^S$ such that $x_C^T$ and $x_C^S$ denote the number of reinforced control centers and signals, respectively. Similarly, $y_C=y_C^T+y_C^S$, such that $y_C^T$ and $y_C^S$ denote the number of control centers and signals attacked, respectively. Since we focus on the smooth running of the trains, it is more instructive to carry out the analysis in terms of the failure correlation function $g(P_C,P_P)=P_{\overline{P}|\overline{C}}$. Then, for the sub-infrastructures, we have the failure correlation functions $g^T\left(P_C^T,P_P\right)=N_L\left(1-P_C^T\right)$ and $g^S\left(P_C^S,P_P\right)=\alpha N_L\left(1-P_C^S\right)$, wherein the physical failures are amplified by $N_L$ for control centers and by $\alpha N_L$ for the signals. We now estimate the composite failure correlation function $g(P_C,P_P)$ as follows:

$$g\left(P_C,P_P\right)=g^T\left(P_C^T,P_P\right)\frac{P_A^T}{P_A^T+P_A^S}+g^S\left(P_C^S,P_P\right)\frac{P_A^S}{P_A^T+P_A^S}=N_L\left(1-P_C^T\right)\frac{P_A^T}{P_A^T+P_A^S}+\alpha N_L\left(1-P_C^S\right)\frac{P_A^S}{P_A^T+P_A^S},$$

where $P_A^T$ and $P_A^S$ are the probabilities of a cyber attack on a control center and a signal of the metro system, respectively, and $\frac{P_A^T}{P_A^T+P_A^S}$ and $\frac{P_A^S}{P_A^T+P_A^S}$ are conditional failure probabilities of the control center and signal, respectively, given that the cyber sub-infrastructure of the metro system failed.

The probability that a physically-reinforced actuator on a train survives cyber attacks on a control center or signal is given by

$$p_{P|R}=\frac{f_P}{1+N_L{\left[y_C^T-x_C^T\right]}_{+}+\alpha N_L{[y_C^S-x_C^S]}_{+}},$$

which now depends on both cyber attacks on control centers and signals. If the actuator is not physically-reinforced, then we have

$$p_{P|N}=\frac{f_P}{1+y_P+N_L{[y_C^T-x_C^T]}_{+}+\alpha N_L{[y_C^S-x_C^S]}_{+}},$$

which additionally decreases with respect to $y_P$. By using these estimates for an actuator, we have

$${\mathrm{\Lambda }}_P\left(x_C^T,x_C^S,y_C^T,y_C^S,y_P\right)=ln\left(1+\frac{y_P}{1+N_L{[y_C^T-x_C^T]}_{+}+\alpha N_L{[y_C^S-x_C^S]}_{+}}\right),$$

which increases in the number of physical attacks on actuators, but decreases in the number of cyber attacks on control centers and signals. Since the term ${\mathrm{\Lambda }}_P$ appears in the denominator, ${\widehat{P}}_{P;D}$ in Theorem 1 decreases with the number of physical attacks $y_P$, and increases with ${[y_C^T-x_C^T]}_{+}$ and ${[y_C^S-x_C^S]}_{+}$, which are the number of cyber attacks on the control centers and signals exceeding the reinforcements, respectively. The latter condition may appear counter-intuitive at the surface, but note that it only characterizes the states that satisfy NE conditions. An analogous dependence of ${\widehat{P}}_{P;D}$ on the parameters $x_C$, $x_P$, $y_C$, and $y_P$ (shown in Theorem 1) is less direct, since ${\mathrm{\Lambda }}_P$ appears inside the square root but is qualitatively somewhat similar since they appear in the denominator.

The cyber component survival probabilities are computed separately for the reinforced control centers and signals, denoted by $p_{C|R}^T$ and $p_{C|R}^S$, respectively. The survival probabilities of cyber components are given by $p_{C|R}^B=f_C^B$ and $p_{C|N}^B=\frac{f_C^B}{1+y_C^B},$ where $B=T,S$. Then we have ${\mathrm{\Lambda }}_C^B\left(y_C^B\right)=ln\left(1+y_C^B\right),$ where $B=T,S$, which increases in the total number of cyber attacks on the specific type of component. Since the term ${\mathrm{\Lambda }}_C^B$ appears in the denominator, ${\widehat{P}}_{C;D}$ in Theorem 1 decreases with the number of cyber attacks $y_C^B$, where $B=T,S$.

Note that the net effect of the number of attacks and reinforcements on the survival probabilities of cyber and physical sub-infrastructures is also determined by the correlation function as described in Section 4.6, in addition to ${\mathrm{\Lambda }}_P$ and ${\mathrm{\Lambda }}_C^B$, where $B=T,S$.

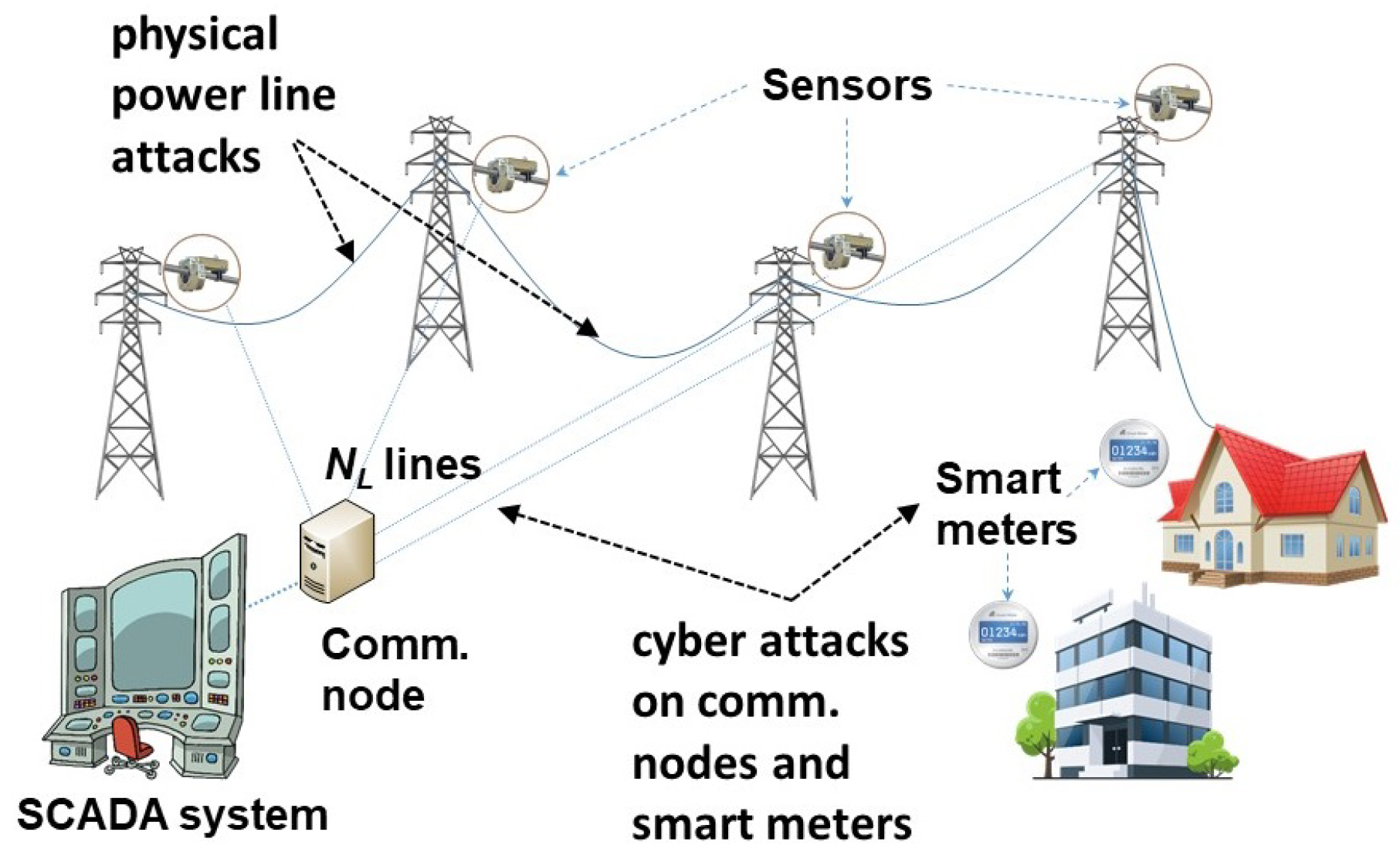
5.3. Smart Power Grid Infrastructure

The power grid model described in Example 3 in Section 3.2 is expanded to include smart meters on the lines that provide the demand information to generation and distribution control systems. The smart meters can be attacked by cyber means to manipulate the demand information (e.g., to make it zero). We group the cyber components into two classes, namely, communication nodes and smart meters, such that $x_C=x_C^S+x_C^M$, where $x_C^S$ and $x_C^M$ are the number of reinforced communication nodes and smart meters, respectively. Similarly, we have $y_C=y_C^S+y_C^M$, where $y_C^S$ and $y_C^M$ are the number of communication nodes and smart meters attacked, respectively. Since the electricity transmission in the grid takes place on the physical sub-infrastructure, it is more instructive to carry out the analysis in terms of the failure correlation function $g(P_C,P_P)=P_{\overline{P}|\overline{C}}$. As in the metro system example, for the sub-infrastructures, we have the failure correlation functions $g^S\left(P_C^S,P_P\right)=N_L\left(1-P_C^S\right)$ and $g^M\left(P_C^M,P_P\right)=\left(1-P_C^M\right)$, wherein the attacks on communication nodes are amplified by the number of lines $N_L$ controlled by each of them, but are the same for smart meter attacks. Then, we utilize the estimate

$$g(P_C,P_P)=\left[N_L\left(1-P_C^S\right)\frac{P_A^S}{P_A^S+P_A^M}+\left(1-P_C^M\right)\frac{P_A^M}{P_A^S+P_A^M}\right],$$

where $P_A^S$ and $P_A^M$ are the probabilities of an attack on a communication node and smart meter, respectively, and $\frac{P_A^S}{P_A^S+P_A^M}$ and $\frac{P_A^M}{P_A^S+P_A^M}$ are conditional failure probabilities of a communication node and smart meter, respectively, given that the cyber sub-infrastructure failed.

Then, the survival probabilities of cyber components are estimated separately for the communication nodes and smart meters. The survival probabilities of the power supply lines with and without reinforcement are denoted by $p_{P|R}$ and $p_{P|N}$, respectively. A communication node or a smart meter may be disabled by cyber means, which will disrupt the power flow on the lines so that

$$p_{P|R}=\frac{f_P}{1+N_L{[y_C^S-x_C^S]}_{+}+{[y_C^M-x_C^M]}_{+}},$$

for physically-reinforced power lines. Note that cyber attacks on communication nodes are amplified by $N_L$ times compared to attacks on smart meters. Each power line can be directly disrupted by physical means such that it can be brought down if not reinforced, and thus we have

$$p_{P|N}=\frac{f_P}{1+y_P+N_L{[y_C^S-x_C^S]}_{+}+{[y_C^M-x_C^M]}_{+}},$$

which reflects the amplified effect of cyber attacks on communication nodes compared to physical line attacks. Combining the two formulae, we have

$${\mathrm{\Lambda }}_P\left(x_C^S,x_C^M,y_C^S,y_C^M,y_P\right)=ln\left(1+\frac{y_P}{1+N_L{[y_C^S-x_C^S]}_{+}+{[y_C^M-x_C^M]}_{+}}\right),$$

which increases in the number of attacks on non-reinforced power lines and decreases in the number of attacks on non-reinforced communication nodes and non-reinforced smart meters, but the former effect is amplified $N_L$ times. The survival probabilities of cyber components are given by $p_{C|R}^B=f_C^B$ and $p_{C|N}^B=\frac{f_C^B}{1+y_C^B},$ where $B=S,M$. Then, we have ${\mathrm{\Lambda }}_C^B\left(y_C^B\right)=ln\left(1+y_C^B\right),$ where $B=S,M$, which increases in the total number of cyber attacks. As in the previous examples, the net effect of the number of attacks and reinforcements on the survival probabilities of cyber and physical sub-infrastructures is also determined by the correlation function (in addition to ${\mathrm{\Lambda }}_P$ and ${\mathrm{\Lambda }}_C^B$, where $B=S,M$) as described in Section 4.6.

6. Conclusions

We studied a class of infrastructures characterized by the number of discrete components that can be disrupted by either cyber or physical attacks, and are protected by cyber and physical reinforcements. We characterized the cyber–physical interactions in these infrastructures at two levels: (i) the failure correlation function specifies the conditional survival probability of a cyber sub-infrastructure given that of the physical sub-infrastructure as a function of their marginal probabilities, and (ii) the individual survival probabilities of both sub-infrastructures are characterized by first-order differential conditions. We derived Nash equilibrium conditions in terms of partial derivatives of cost terms, failure correlation function, multiplier functions, and survival probabilities of sub-infrastructures and their partial derivatives. We then estimated the sensitivity functions that indicate the dependence of infrastructure survival probability on these parameters. We applied this approach to models of metro systems, cloud computing infrastructures, and smart power grids at different levels of abstraction when all have a large number of components. These results generalize previous results using simpler utility functions in [2,3,4,5], and specialize the results on systems of systems in [8,43,44,45,46,47,48]. Together, our results enable us to unify the previous results and consider more detailed models of the correlations between the sub-infrastructures in the metro systems, cloud computing infrastructures, and smart power grids, with sharpened focus on cyber and physical sub-infrastructures.

Several extensions of this formulation could be pursued in future studies, including the cases where the effects of attacks and reinforcements of specific components are explicitly accounted for. In such formulations, $x_C$ and $x_P$ may be replaced by vectors whose components are Boolean representing the reinforcement of a component or a fraction representing the probability of reinforcement. It would also be of future interest to explicitly model various redundancies incorporated by infrastructures to avoid single-point failures (e.g., abstracted by fiber cuts). Such extensions may also require a more refined characterizations of attacks (e.g., single- or multiple-fiber attacks) and defenses, which may lead to their partial successes. Indeed, the attack and defense models can be extended to include their success probabilities to capture cases wherein the attacks and reinforcements are not always guaranteed to fully fail or succeed. It would be interesting to study sequential game formulations of this problem, and cases where different levels of knowledge are available to the attacker and provider. Other future formulations could include multiple attackers and hybrid infrastructure models. For example, physical sub-infrastructure represented by partial differential equations and cyber sub-infrastructures represented by graphs. Applications of our approach to more detailed models of metro systems, cloud computing infrastructures, smart power grids, and high-performance computing complexes would be of future interest.