Voluntary Leadership and Asymmetric Endowments in the Investment Game
Abstract
1. Introduction
2. Experimental Game and Theoretical Predictions
2.1. The Trust Game with Endogenous Leadership and Asymmetric Endowments
- Stage 1
- Player H (“high endowment player”) is endowed with 50 money units and decides upon the sequencing of moves in the investment game that follows in stages 2 and 3. H has two options, either become first mover in the investment game, and let player L who is endowed with 10 money units (“low endowment player”) be second mover. Or H may become second mover and let’s player L be first mover.
- Stage 2
- The first mover decides upon investment x with . Then, the second mover receives the amount .
- Stage 3
- The second mover decides upon backtransfer y with . Then, the first mover receives the amount .
2.2. Game Variants/Experimental Treatments
2.3. Theoretical Benchmark Solutions
2.4. Empirical Hypotheses
3. Experimental Procedures
4. Experimental Results
4.1. Descriptive Statistics
4.2. Regression Analyses: Backtransfer
4.3. Regression Analyses: Investment
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Instructions
Appendix A.1. General Introduction
Appendix A.2. Exogenous Treatment of Sym
- (1)
- Each participant receives an endowment.
- Participant A receives 10 points
- B receives 10 points
- (2)
- Participant B transfers an amount x (0 ≤ x ≤ 10) to participant A.
- (3)
- Participant A gains 3x, i.e., participant A receives three times the amount transferred by B.
- (4)
- Participant A transfers an amount y (0 ≤ y ≤ 10) to participant B.
- (5)
- Participant B gains 3y, i.e., participant B receives three times the transferred amount.
- (6)
- The experiment is done.
Appendix A.3. Endogenous Treatment of Sym
- (1)
- Each participant receives an endowment.
- Participant A receives 10 points
- Participant B receives 10 points
- (2)
- Participant B decides about the sequence of choices. There are two possible sequences. B–A or A–B. If B–A is chosen, the experiment continues as described in (3a) to (7a). If A–B is chosen, the experiment continues as described in (3b) to (7b).
- (3a)
- Participant B transfers an amount x (0 ≤ x ≤ 10) to participant A.
- (4a)
- Participant A gains 3x, i.e., participant A receives three times the amount transferred by B.
- (5a)
- Participant A transfers an amount y (0 ≤ y ≤ 10) to participant B.
- (6a)
- Participant B gains 3y, i.e., participant B receives three times the transferred amount.
- (7a)
- The experiment is done.
- (3b)
- Participant A transfers an amount x (0 ≤ x ≤ 10) to participant B.
- (4b)
- Participant B gains 3x, i.e., participant B receives three times the amount transferred by participant A
- (5b)
- Participant B transfers an amount y (0 ≤ y ≤ 10) to participant A.
- (6b)
- Participant A gains 3y, i.e., participant A receives three times the amount transferred by participant B.
- (7b)
- The experiment is done.
Appendix A.4. Exogenous Treatment of AsymHigh
- (3)
- Each participant receives an endowment.
- Participant A receives 10 points
- receives 50 points
- (4)
- Participant B transfers an amount x (0 ≤ x ≤ 10) to participant A.
- (5)
- Participant A gains 3x, i.e., participant A receives three times the amount transferred by B.
- (6)
- Participant A transfers an amount y (0 ≤ y ≤ 10) to participant B.
- (7)
- Participant B gains 3y, i.e., participant B receives three times the transferred amount.
- (8)
- The experiment is done.
Appendix A.5. Endogenous Treatment of AsymHigh
- (1)
- Each participant receives an endowment.
- Participant A receives 10 points
- Participant B receives 50 points
- (2)
- Participant B decides about the sequence of choices. There are two possible sequences. B–A or A–B. If B–A is chosen, the experiment continues as described in (3a) to (7a). If A–B is chosen, the experiment continues as described in (3b) to (7b).
- (3a)
- Participant B transfers an amount x (0 ≤ x ≤ 10) to participant A.
- (4a)
- Participant A gains 3x, i.e., participant A receives three times the amount transferred by B.
- (5a)
- Participant A transfers an amount y (0 ≤ y ≤ 10) to participant B.
- (6a)
- Participant B gains 3y, i.e., participant B receives three times the transferred amount.
- (7a)
- The experiment is done.
- (3b)
- Participant A transfers an amount x (0 ≤ x ≤ 10) to participant B.
- (4b)
- Participant B gains 3x, i.e., participant B receives three times the amount transferred by participant A
- (5b)
- Participant B transfers an amount y (0 ≤ y ≤ 10) to participant A.
- (6b)
- Participant A gains 3y, i.e., participant A receives three times the amount transferred by participant B.
- (7b)
- The experiment is done.
Appendix A.6. Exogenous Treatment of AsymLow
- (3)
- Each participant receives an endowment.
- Participant A receives 50 points
- B receives 10 points
- (4)
- Participant B transfers an amount x (0 ≤ x ≤ 10) to participant A.
- (5)
- Participant A gains 3x, i.e., participant A receives three times the amount transferred by B.
- (6)
- Participant A transfers an amount y (0 ≤ y ≤ 10) to participant B.
- (7)
- Participant B gains 3y, i.e., participant B receives three times the transferred amount.
- (8)
- The experiment is done.
Appendix A.7. Endogenous Treatment of SymLow
- (1)
- Each participant receives an endowment.
- Participant A receives 50 points
- Participant B receives 10 points
- (2)
- Participant B decides about the sequence of choices. There are two possible sequences. B–A or A–B. If B–A is chosen, the experiment continues as described in (3a) to (7a). If A–B is chosen, the experiment continues as described in (3b) to (7b).
- (3a)
- Participant B transfers an amount x (0 ≤ x ≤ 10) to participant A.
- (4a)
- Participant A gains 3x, i.e., participant A receives three times the amount transferred by B.
- (5a)
- Participant A transfers an amount y (0 ≤ y ≤ 10) to participant B.
- (6a)
- Participant B gains 3y, i.e., participant B receives three times the transferred amount.
- (7a)
- The experiment is done.
- (3b)
- Participant A transfers an amount x (0 ≤ x ≤ 10) to participant B.
- (4b)
- Participant B gains 3x, i.e., participant B receives three times the amount transferred by participant A
- (5b)
- Participant B transfers an amount y (0 ≤ y ≤ 10) to participant A.
- (6b)
- Participant A gains 3y, i.e., participant A receives three times the amount transferred by participant B.
- (7b)
- The experiment is done.
Appendix A.8. Side Experiment 1
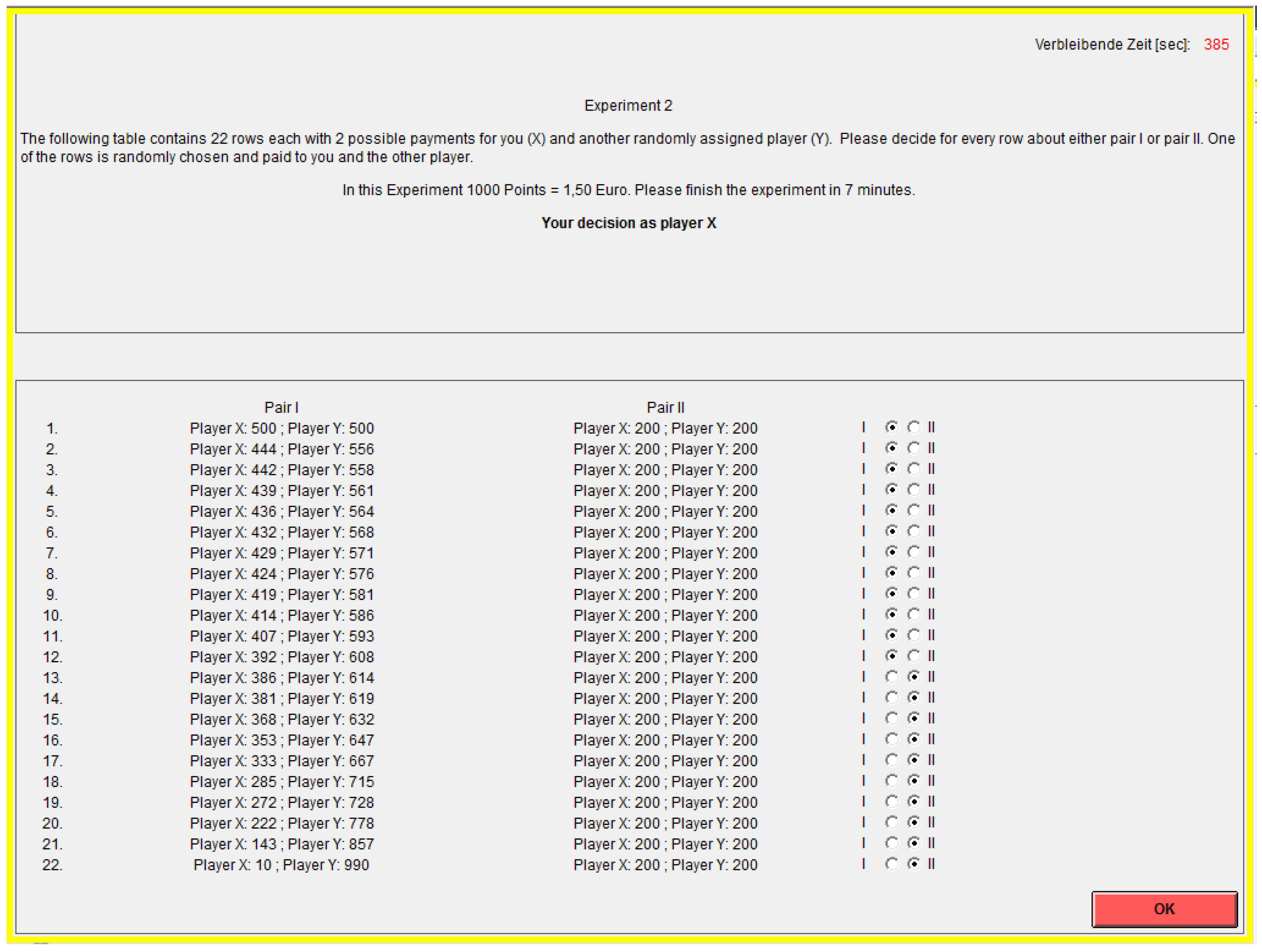
Appendix A.9. Side Experiment 2
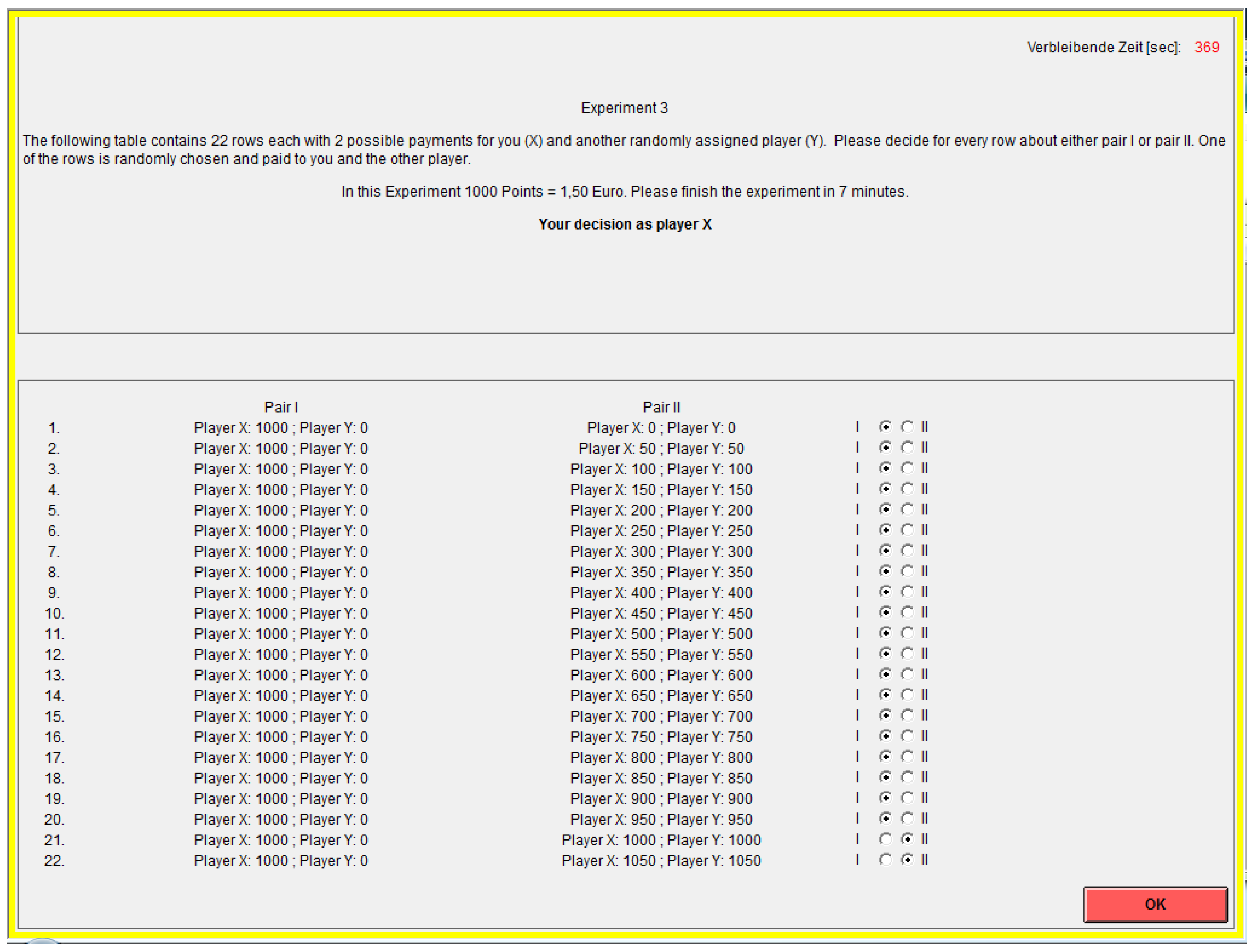
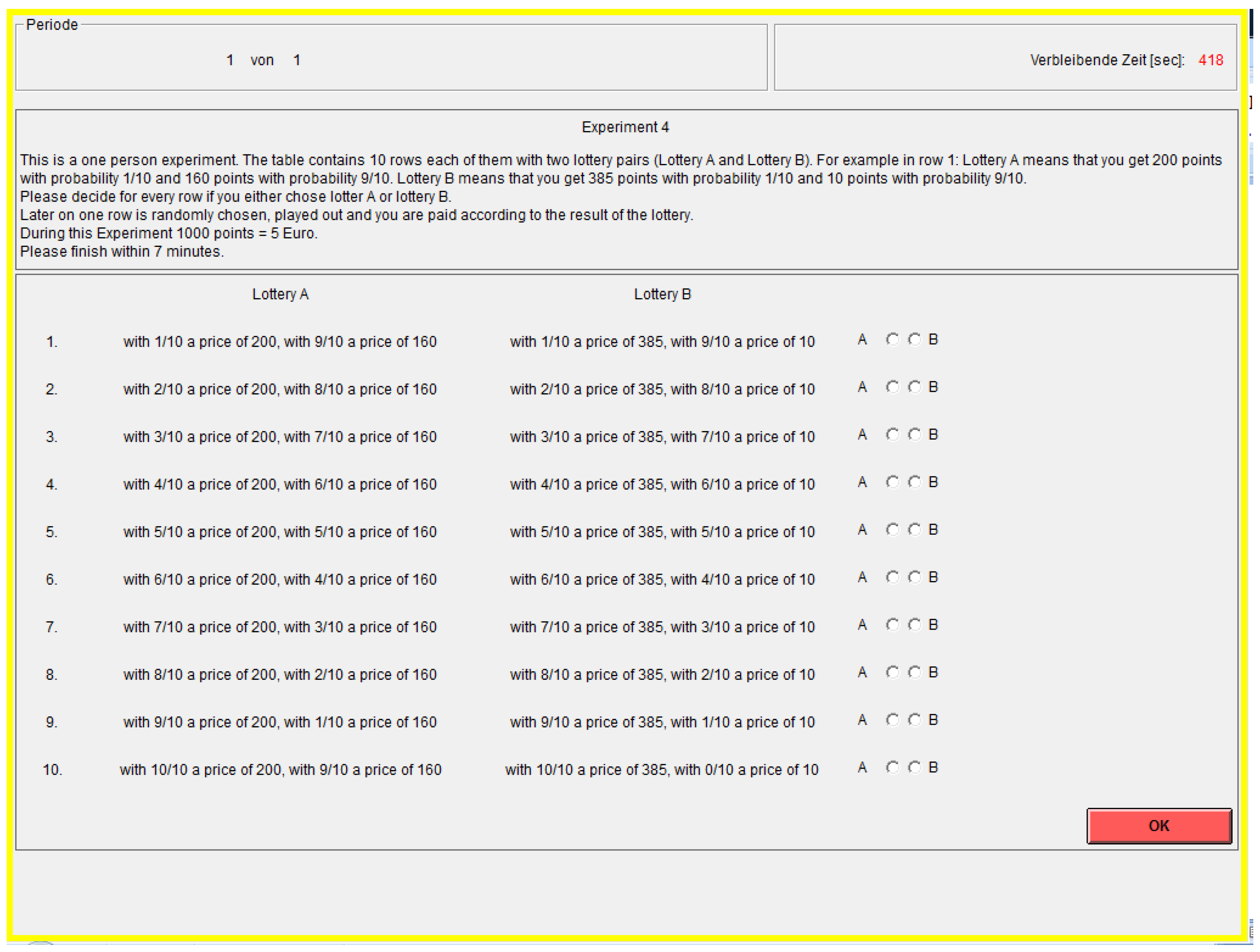
Appendix A.10. Side Experiment 3
References
- Berg, J.; Dickhaut, J.; McCabe, K. Trust, Reciprocity and Social History. Games Econ. Behav. 1995, 10, 122–142. [Google Scholar] [CrossRef]
- Kleine, F.; Königstein, M.; Rozsnyói, B. Voluntary Leadership in an Experimental Trust Game. J. Econ. Behav. Organ. 2014, 108, 442–452. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A Theory of Fairness, Competition, and Cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Xiao, E.; Bicchieri, C. When equality trumps reciprocity. J. Econ. Psychol. 2010, 31, 456–470. [Google Scholar] [CrossRef]
- Arbak, E.; Villeval, M.C. Voluntary leadership: Motivation and influence. Soc. Choice Welf. 2013, 40, 635–662. [Google Scholar] [CrossRef]
- Rivas, M.F.; Sutter, M. Leadership in Public Goods Experiments—On the Role of Reward, Punishment and Endogenous Leadership. Available online: http://campus.usal.es/ehe/Papers/Leadership_FernandaRivas.pdf (accessed on 27 April 2018).
- Fonseca, M.A.; Huck, S.; Normann, H.T. Endogenous Timing in Duopoly: Experimental Evidence. Int. J. Game Theory 2006, 34, 443–456. [Google Scholar] [CrossRef]
- Fonseca, M.A.; Huck, S.; Normann, H.T. Playing Cournot although they shouldn’t. Econ. Theory 2006, 25, 669–677. [Google Scholar]
- Huck, S.; Müller, W.; Normann, H.T. To Commit or Not to Commit: Endogenous Timing in Experimental Duopoly Markets. Games Econ. Behav. 2002, 38, 240–264. [Google Scholar] [CrossRef]
- Potters, J.; Sefton, M.; Vesterlund, L. After You—Endogenous Sequencing in Voluntary Contribution Games. J. Public Econ. 2005, 89, 1399–1419. [Google Scholar] [CrossRef]
- Nosenzo, D.; Sefton, M. Endogenous Move Structure and Voluntary Provision of the Public Goods: Theory and Experiment. J. Public Econ. Theory 2011, 13, 721–754. [Google Scholar] [CrossRef]
- Collins, S. Relay the Right Way: Harnessing Heterogeneity in Sequential Team Production. Manag. Decis. Econ. 2016, 37, 407–423. [Google Scholar] [CrossRef]
- Dasgupta, U.; Orman, W.H. Does Heterogeneity Help in Overcoming the Public Goods Dilemma in a Sequential Contribution Environment? Group Decis. Negot. 2013, 23, 1219–1239. [Google Scholar] [CrossRef]
- Güth, W.; Levati, M.V.; Sutter, M.; van der Heijden, E. Leading by example with and without exclusion power in voluntary contribution experiments. J. Public Econ. 2007, 91, 1023–1042. [Google Scholar] [CrossRef]
- Levati, M.V.; Sutter, M. Leading by Example in a Public Goods Experiment with Heterogeneity and Incomplete Information. J. Confl. Resolut. 2007, 51, 793–818. [Google Scholar] [CrossRef]
- Au, W.T.; Chung, M.W. Effect of Order of Contribution in a Sequential Public Goods Dilemma. Group Decis. Negot. 2007, 16, 437–449. [Google Scholar] [CrossRef]
- Reuben, E.; Riedl, A. Enforcement of contribution norms in public good games with heterogeneous populations. Games Econ. Behav. 2013, 77, 122–137. [Google Scholar] [CrossRef]
- Cox, J.C. How to identify trust and reciprocity. Games Econ. Behav. 2004, 46, 260–281. [Google Scholar] [CrossRef]
- Rabin, M. Incorporating Fairness into Game Theory and Economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Charness, G.; Rabin, M. Understanding Social Preferences with Simple Tests. Q. J. Econ. 2002, 117, 817–869. [Google Scholar] [CrossRef]
- Dufwenberg, M.; Kirchsteiger, G. A Theory of Sequential Reciprocity. Games Econ. Behav. 2004, 47, 268–298. [Google Scholar] [CrossRef]
- Falk, A.; Fischbacher, U. A Theory of Reciprocity. Games Econ. Behav. 2006, 54, 293–315. [Google Scholar] [CrossRef]
- Danneberg, A.; Reichmann, T.; Sturm, B.; Vogt, C. Inequality Aversion and Individual Behavior in Public Good Games: An Experimental Investigation. ZEW Discuss. Pap. 2007. [Google Scholar] [CrossRef]
- Bolton, G.E.; Ockenfels, A. ERC: A theory of equity, reciprocity, and competition. Am. Econ. Rev. 2000, 90, 166–193. [Google Scholar] [CrossRef]
- Pratt, J.M. Risk Aversion in the Small and in the Large. Econometrica 1964, 32, 122–136. [Google Scholar] [CrossRef]
- World Value Survey: WVS 2005 Questionnaire. Available online: http://www.worldvaluessurvey.org/WVSDocumentationWV5.jsp (accessed on 27 April 2018).
- Fischbacher, U. Z-Tree Zurich Toolbox for ready-made Economic Experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Greiner, B. Subject Pool Recruitment Procedures: Organizing Experiments with ORSEE. J. Econ. Sci. Assoc. 2015, 1, 114–125. [Google Scholar] [CrossRef]
- Brier, G. Verification of forecasts expressed in terms of probability. Month. Weather Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Offerman, T.; Sonnemans, J.; van de Kuilen, G.; Wakker, P. A Truth Serum for Non-Bayesians: Correcting Proper Scoring Rules for Risk Attitudes. Rev. Econ. Stud. 2009, 76, 1461–1489. [Google Scholar] [CrossRef]
- Holt, C.A.; Laury, S.K. Risk Aversion and Incentive Effects. Am. Econ. Rev. 2002, 92, 1644–1655. [Google Scholar] [CrossRef]
- Brandstätter, H. Sechzehn Persönlichkeits-Adjektivskalen (16 PA) als Forschungsinstrument anstelle des 16 PF. Z. Exp. Angew. Psychol. 1988, 25, 370–391. [Google Scholar]
- Maniadis, Z.; Tufano, F.; List, J.A. One Swallow Doesn’t Make a Summer: New Evidence on Anchoring Effects. Am. Econ. Rev. 2014, 104, 277–290. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Cox, J.C. Trust and reciprocity: Implications of game triads and social contexts. N. Z. Econ. Pap. 2009, 43, 89–104. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Ali Khan, S.; Lakshmiratan, A.; Py, A.-L.; Shah, L. Trust and trustworthiness in a sequential bargaining game. J. Behav. Decis. Mak. 2003, 16, 331–340. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Gangadharan, L. An Experimental Analysis of Trust and Trustworthiness. South. Econ. J. 2007, 73, 959–985. [Google Scholar]
- Dasgupta, U.; Menon, A. Trust and Trustworthiness among Economics Majors. Econ. Bull. 2011, 31, 2799–2815. [Google Scholar]
| 1 | |
| 2 | Fonseca et al. (2006a) [7], (2006b) [8] and Huck et al. (2002) [9] study duopoly games with endogenous timing. Firms can choose their quantities in one of two periods. Potters et al. (2005) [10] study a public good game with endogenous sequencing when some donors do not know the value of the public good. Nosenzo and Sefton (2009) [11] study a public good game with endogenous move structure. Players can choose their contribution in one of two periods. Furthermore players receive different returns of the public good. |
| 3 | |
| 4 | We refer to this as two treatments even though the distinction was not implemented exogenously by us as experimenters but endogenously by the player’s sequencing choice. However, it is advantageous to discriminate and label this as two experimental conditions since all empirical analyses will be done conditional on this distinction. The same applies to other cases of endogenous sequencing. |
| 5 | Investors with the same degree of constant relative risk aversion invest the same share of wealth into risky assets. Thus, a rich player invests a larger absolute amount into a risky asset than a poor player (see Pratt (1964) [25]). |
| 6 | The participants had to state probabilities for each possible backtransfer. Using these responses we calculated the expected backtransfer and paid the participants based on the squared difference between expected and received payoff. The Quadratic Scoring Rule was introduced by Brier (1950) [29]. For a methodological discussion of this and other scoring rules see Offerman et al. (2009) [30]. |
| 7 | The question is: Generally speaking, would you say that most people can be trusted or that you need to be very careful in dealing with people? Participants may answer “yes” or “no”. |
| 8 | An average earning for a student job at the time of the experiment was about 8 EUR per hour. |
| 9 | A Binomial test for the frequency of voluntary leadership by the rich player versus voluntary leadership under equal endowments also supports this (p < 0.001, n = 176). |
| 10 | We also estimated this and all the other models reported in the paper with median regression in order to check for robustness. All of the effects were qualitatively the same as those of the Tobit regressions. |
| 11 | In all tests we report p-values for two-tailed tests. The values may be adjusted for our directional hypotheses. |
| 12 | |
| 13 | To save on notation, we simply formulate hypotheses using variable names instead of coefficients of these variables. |
| 14 | Hypothesis 1.a is also supported by a Mann-Whitney U-test (MWU) when comparing the backtransfer y between the two treatments HighEndoHighLow and Mid1EndoMid1Mid2 (p < 0.003, n = 55). Maniadis [33] et al. consider the problem of false positives and present a model of the post-study probability of a result which hinges among other things on the power of individual studies. Therefore, for our Hypothesis 1 to 4, we report post-hoc measures of statistical power in addition to the p-values of statistical tests. Regarding Hypothesis 1.a we get a power value of 0.88 for a simple two-sample t-test (two-sided) for a value of Cohen’s d of 0.949 (Cohen [34]) and assuming a significance level α = 0.05. This is a more conservative calculation of power than one based on the regression model since the two-sample t-test relies on the sample sizes of the two-treatments rather than all treatments. To calculate power values we use the R Package pwr, Version 1.2-2, which refers to Cohen [34]. |
| 15 | This effect is also significant according to MWU-tests of backtransfer: ExoLowHigh vs. ExoMidMid (p < 0.006, n = 39), ExoLowHigh vs. ExoHighLow (p < 0.003, n = 46). The power of a two-sample, two-sided t-test is 0.854 (Cohen’s d = 0.991, α = 0.05) for the test ExoLowHigh vs. ExoMidMid. The power is 0.910 (Cohen’s d = 1.011, α = 0.05) for the test ExoLowHigh vs. ExoHighLow. |
| 16 | MWU-tests of backtransfer: HighEndoLowHigh vs. Mid1EndoMid2Mid1 (n.s., n = 123), HighEndoLowHigh vs. LowEndoHighLow (p = 0.036, n = 103). |
| 17 | Specifically, Alpha-High and Beta-High are 0/1-dummies for above-median values of the respective parameter conditional on the respective parameter being relevant. E.g., Alpha-High is equal to 1 when the second mover is poor and his/her value of α is above median. Alpha-High is equal to 0 when the value is below median (or missing/inconsistent) or if the second mover is rich. When endowments are equal unfavorable inequality aversion is relevant if investment is zero. Similar definitions apply to the variables Beta-High, Alpha-Missing, and Beta-Missing. E.g., Alpha-Missing is equal to 1 only when unfavorable inequality aversion is relevant and α is missing (incomplete or inconsistent measurement); otherwise, it is zero. When endowments are equal favorable inequality aversion is relevant if investment is greater than zero. |
| 18 | Note that in Table 5 all the estimated treatment coefficients are negative while they are all positive in Table 6. This should not be confusing because it simply comes from the change in the reference category. In Table 5 the reference category is Mid1EndoMid1Mid2 since this is the relevant category according to the main Hypothesis 1.b. In Table 6, we cannot use this reference category since Table 6 uses only asymmetric treatments. Here, we choose the treatment with the lowest investment (HighEndoLowHigh) as reference category. |
| 19 | The effect is also supported by a MWU-test of investment in treatments HighEndoHighLow vs. Mid1EndoMid1Mid2 (p < 0.009, n = 55). The power of a two-sample, two-sided t-test is 0.801 (Cohen’s d = 0.848, α = 0.05). |
| 20 | Also a Spearman rank correlation is highly significant: ρ = 0.67, p < 0.001, n = 202). The power of a two-sided correlation test (Pearson correlation) is 1 (α = 0.05). |
| 21 | As in the analysis of backtransfer the influence of Alpha-High, Beta-High, Alpha-Missing, Beta-Missing are measured for relevant conditions. E.g., Alpha-High is relevant when the first mover is poor or equally endowed. |
| 22 | While we think that expectations cause backtransfer, we agree to the comment of an anonymous referee that the reversed causality is possible if players exhibit a false consensus effect. In this case players who intend to choose high backtransfer will develop high expectations. |
| 23 | In these cases unfavorable inequality aversion is relevant. |
| 24 | In these cases favorable inequality aversion is relevant. |
| Endogenous/Exogenous Sequencing | Treatment Label | Asymmetric/Symmetric Endowments |
|---|---|---|
| Endogenous Sequencing “Voluntary Leadership” | HighEndoHighLow | asymmetric |
| Mid1EndoMid1Mid2 | symmetric | |
| LowEndoLowHigh | asymmetric | |
| Endogenous Sequencing “Delegation of Responsibility” | HighEndoLowHigh | asymmetric |
| Mid1EndoMid2Mid1 | symmetric | |
| LowEndoHighLow | asymmetric | |
| Exogenous Sequencing | ExoHighLow | asymmetric |
| ExoMidMid | symmetric | |
| ExoLowHigh | asymmetric |
| Sequencing | Treatment | Investment x | Expected Backtransfer | Backtransfer | Backtransfer Rate y/x | # Obs. |
|---|---|---|---|---|---|---|
| Voluntary Leadership | HighEndoHighLow | 6.84 (3.03) | 5.06 (1.90) | 4.95 (3.49) | 0.82 (0.73) | 39 |
| Mid1EndoMid1Mid2 | 9.13 (1.50) | - | 8.06 (2.70) | 0.89 (0.26) | 16 | |
| LowEndoLowHigh | 6.71 (2.84) | 5.40 (2.15) | 6.07 (2.99) | 1.01 (0.46) | 14 | |
| Delegation of Responsibility | HighEndoLowHigh | 4.94 (3.30) | 4.53 (2.08) | 5.39 (3.42) | 1.38 (1.16) | 57 |
| Mid1EndoMid2Mid1 | 6.83 (3.09) | - | 5.19 (3.09) | 0.88 (0.64) | 64 | |
| LowEndoHighLow | 6.13 (3.53) | 4.20 (2.59) | 3.96 (3.42) | 0.89 (1.39) | 46 | |
| Exogenous Sequencing | ExoHighLow | 6.70 (2.74) | 4.59 (1.72) | 4.19 (2.84) | 0.66 (0.39) | 27 |
| ExoMidMid | 5.40 (2.76) | - | 4.10 (3.09) | 0.94 (0.86) | 20 | |
| ExoLowHigh | 5.53 (3.20) | 4.71 (1.75) | 7.16 (3.08) | 1.57 (1.12) | 19 |
| Sequencing | Treatment | Investment x | Expected Backtransfer | Backtransfer | Backtransfer Rate y/x | # Obs. |
|---|---|---|---|---|---|---|
| Voluntary Leadership | HighEndoHighLow | 7.0 (5.0) | 5.0 (2.01) | 5.0 (6.0) | 0.8 (0.5) | 39 |
| Mid1EndoMid1Mid2 | 10.0 (2.0) | - | 9.0 (3.0) | 1.00 (0.17) | 16 | |
| LowEndoLowHigh | 5.5 (5.0) | 5.0 (2.88) | 6.0 (3.0) | 1.0 (0.2) | 14 | |
| Delegation of Responsibility | HighEndoLowHigh | 5.0 (6.0) | 4.78 (2.88) | 5 (6) | 1.0 (0.5) | 57 |
| Mid1EndoMid2Mid1 | 7.5 (5.75) | - | 5.0 (4.75) | 1.00 (0.50) | 64 | |
| LowEndoHighLow | 6.5 (7.0) | 4.14 (2.87) | 3.0 (5.0) | 0.8 (0.8) | 46 | |
| Exogenous Sequencing | ExoHighLow | 7.0 (5.0) | 4.63 (1.31) | 4.0 (6.0) | 0.66 (0.57) | 27 |
| ExoMidMid | 5.0 (5.0) | - | 3.0 (4.0) | 0.67 (0.57) | 20 | |
| ExoLowHigh | 5.0 (7.0) | 4.55 (1.97) | 9.0 (5.0) | 1.2 (1.33) | 19 |
| Variable | Coefficient | Std. Error | p-Value (Two-Tailed) |
|---|---|---|---|
| Investment | 0.660 | 0.072 | <0.001 |
| HighEndoHighLow | −2.119 | 1.222 | 0.084 |
| LowEndoLowHigh | −1.405 | 1.378 | 0.309 |
| ExoHighLow | −2.663 | 1.243 | 0.033 |
| ExoMidMid | −2.648 | 1.272 | 0.038 |
| ExoLowHigh | 1.353 | 1.320 | 0.306 |
| LowEndoHighLow | −2.864 | 1.221 | 0.020 |
| Mid1EndoMid2Mid1 | −2.268 | 1.072 | 0.035 |
| HighEndoLowHigh | −0.432 | 1.115 | 0.698 |
| Alpha | 1.857 | 0.797 | 0.020 |
| Alpha-Missing | −2.230 | 1.126 | 0.049 |
| Beta | 1.582 | 0.597 | 0.008 |
| Beta-Missing | 0.702 | 0.784 | 0.371 |
| Constant | 2.302 | 1.213 | 0.059 |
| Number of Observations | 302 | ||
| Pseudo R2 | 0.085 |
| Variable | Coefficient | Std. Error | p-Value (Two-Tailed) |
|---|---|---|---|
| HighEndoHighLow | −5.190 | 1.567 | 0.001 |
| LowEndoLowHigh | −5.383 | 1.742 | 0.002 |
| ExoHighLow | −5.682 | 1.603 | <0.001 |
| ExoMidMid | −6.302 | 1.576 | <0.001 |
| ExoLowHigh | −6.110 | 1.601 | <0.001 |
| LowEndoHighLow | −5.958 | 1.514 | <0.001 |
| Mid1EndoMid2Mid1 | −4.774 | 1.389 | 0.001 |
| HighEndoLowHigh | −7.396 | 1.400 | <0.001 |
| Alpha | −1.524 | 0.692 | 0.028 |
| Alpha-Missing | −1.260 | 0.989 | 0.204 |
| Beta | 0.374 | 0.872 | 0.668 |
| Beta-Missing | −0.861 | 1.255 | 0.493 |
| Male | 2.502 | 0.543 | <0.001 |
| Constant | 12.160 | 1.319 | <0.001 |
| Number of Observations | 302 | ||
| Pseudo R2 | 0.044 |
| Variable | Coefficient | Std. Error | p-Value (Two-Tailed) |
|---|---|---|---|
| HighEndoHighLow | 1.389 | 0.790 | 0.080 |
| LowEndoLowHigh | 1.079 | 0.965 | 0.265 |
| ExoHighLow | 1.649 | 0.820 | 0.046 |
| ExoLowHigh | 0.847 | 0.835 | 0.312 |
| LowEndoHighLow | 2.033 | 0.746 | 0.007 |
| Alpha | −1.471 | 0.716 | 0.041 |
| Alpha-Missing | −2.050 | 1.179 | 0.084 |
| Beta | −0.152 | 0.645 | 0.814 |
| Beta-Missing | −0.354 | 0.973 | 0.707 |
| Male | 1.346 | 0.485 | 0.006 |
| Expected-Backtransfer | 1.483 | 0.128 | <0.001 |
| Constant | −1.441 | 0.734 | 0.051 |
| Number of Observations | 202 | ||
| Pseudo R² | 0.164 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleine, F.; Königstein, M.; Rozsnyói, B. Voluntary Leadership and Asymmetric Endowments in the Investment Game. Games 2018, 9, 51. https://doi.org/10.3390/g9030051
Kleine F, Königstein M, Rozsnyói B. Voluntary Leadership and Asymmetric Endowments in the Investment Game. Games. 2018; 9(3):51. https://doi.org/10.3390/g9030051
Chicago/Turabian StyleKleine, Fabian, Manfred Königstein, and Balázs Rozsnyói. 2018. "Voluntary Leadership and Asymmetric Endowments in the Investment Game" Games 9, no. 3: 51. https://doi.org/10.3390/g9030051
APA StyleKleine, F., Königstein, M., & Rozsnyói, B. (2018). Voluntary Leadership and Asymmetric Endowments in the Investment Game. Games, 9(3), 51. https://doi.org/10.3390/g9030051




