Evolutionary Game Theory: A Renaissance
Abstract
Table of contents
1. Introduction
1.1. The Shadow of Nash Equilibrium
1.2. Renaissance and the Scope of This Survey
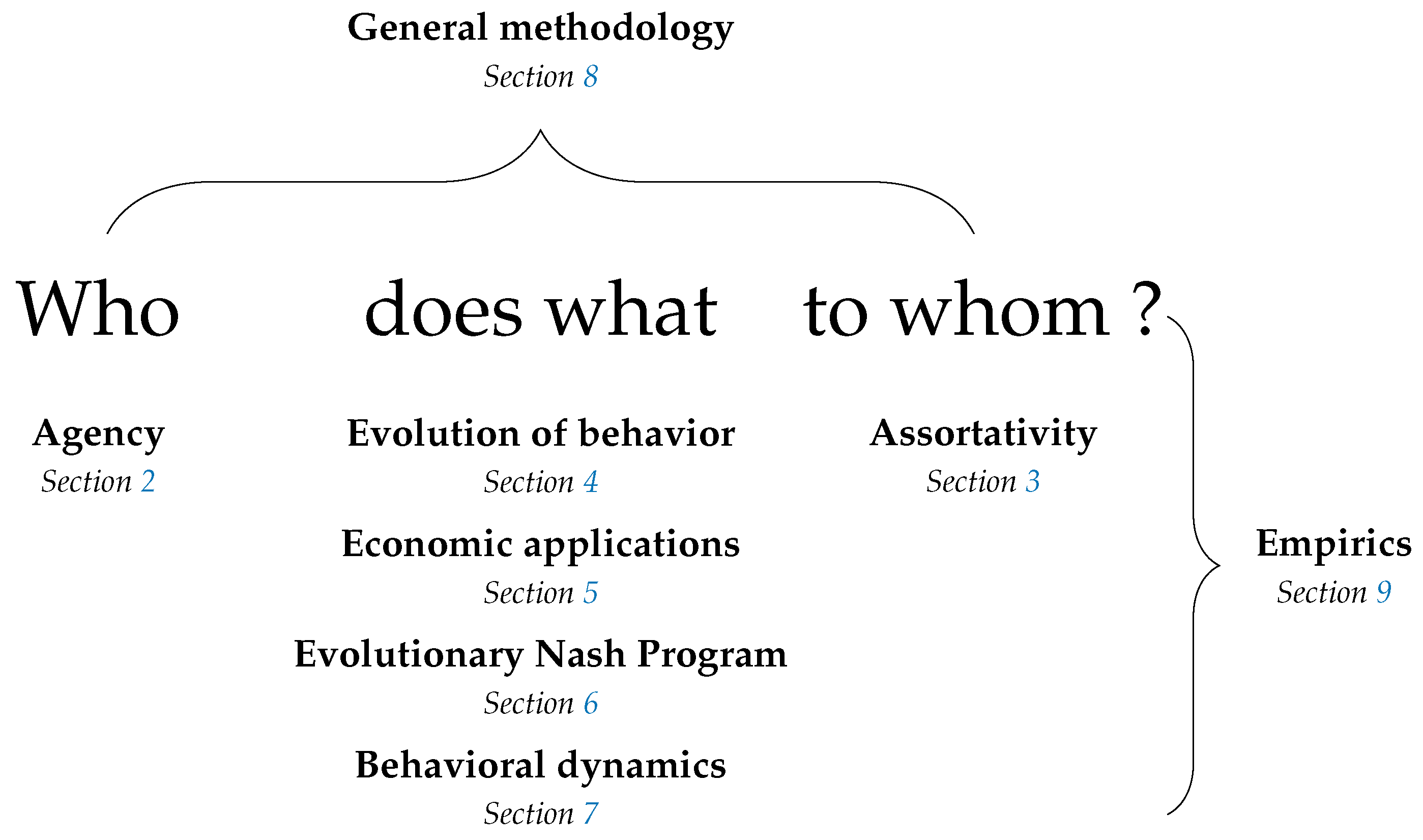
1.3. Structure of the Survey
2. Agency—Who Makes Decisions?
“... humans are able to coordinate with others, in a way that other primates seemingly are not, to form a “we” that acts as a kind of plural agent to create everything from a collaborative hunting party to a cultural institution.”—Tomasello[342]
2.1. Advances in Methodology
2.1.1. Coalitional Stochastic Stability
2.1.2. Coalitional Logit Choice
2.1.3. Frequent or Infrequent Coalitional Behavior
2.2. Implications of Collective Agency
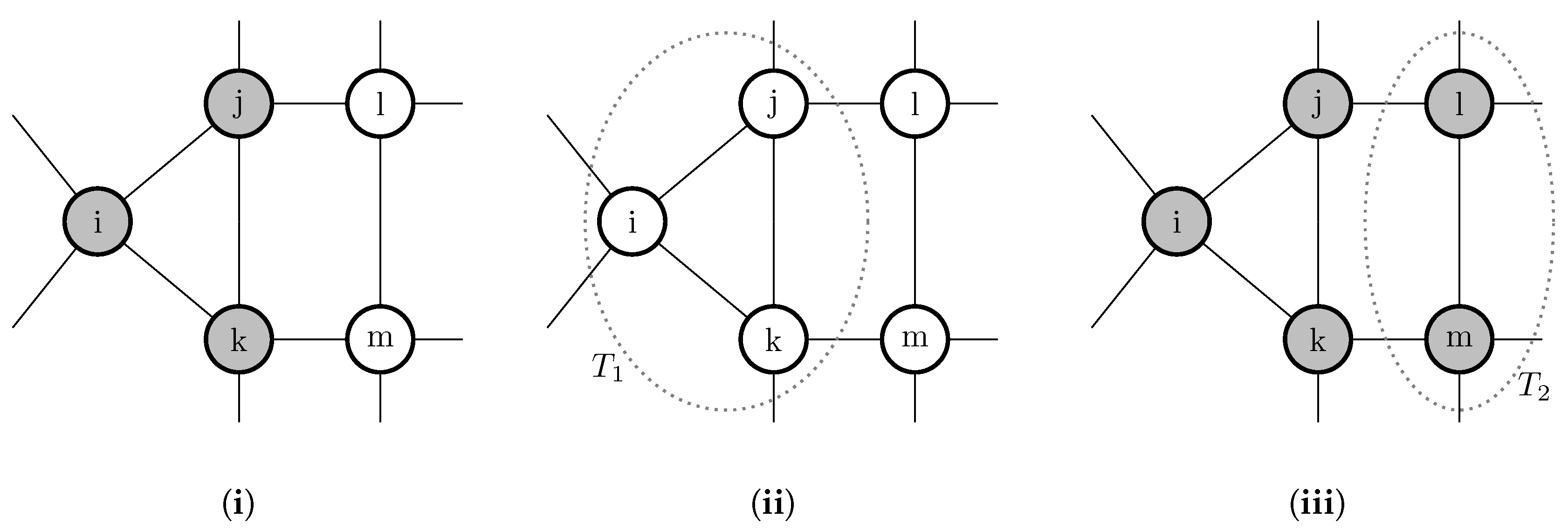
2.2.1. Coordination Games on Networks.
2.2.2. Matching
2.2.3. Social Choice Rules
2.3. The Evolution of Collective Agency
2.4. Links between Individual and Collective Agency
3. Assortativity—With Whom Does Interaction Occur?
3.1. Assortativity and Preferences
3.2. Evolution of Assortativity
3.2.1. Individual Types and Assortativity
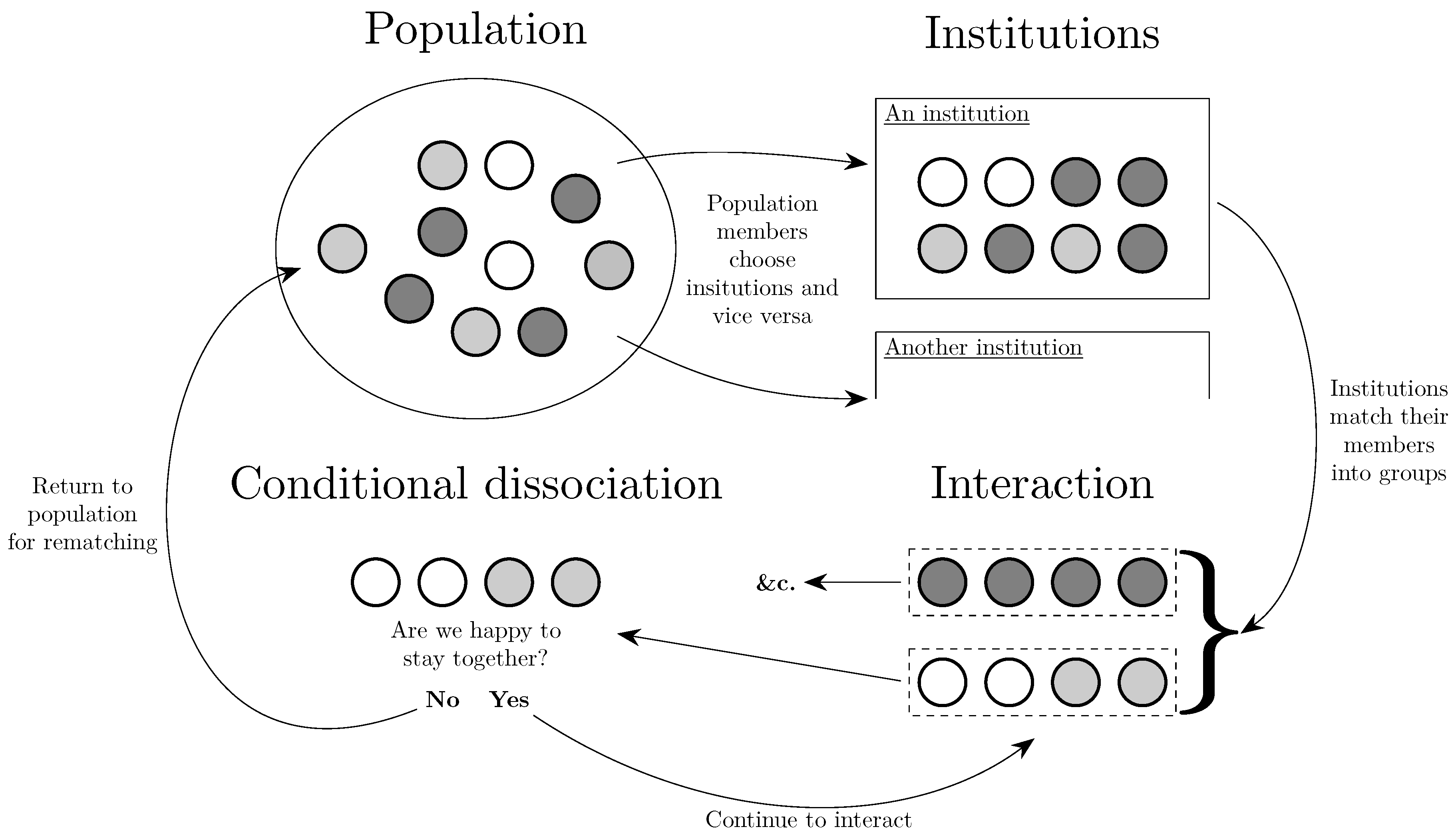
3.2.2. Institutions that Determine Assortativity
3.2.3. Choosing an Institution
3.3. Generalized Assortative Matching Protocols
3.4. Conditional Dissociation
3.5. Network Formation
4. Evolution of Behavior
4.1. Evolution of Traits
4.1.1. Self-Confirming Beliefs
4.1.2. Level k Thinking
4.1.3. Foresight
4.1.4. Competing Cognition
4.1.5. Biases: Overconfidence and Endowment Effects
4.2. Conventions—Culture Embodied in Society
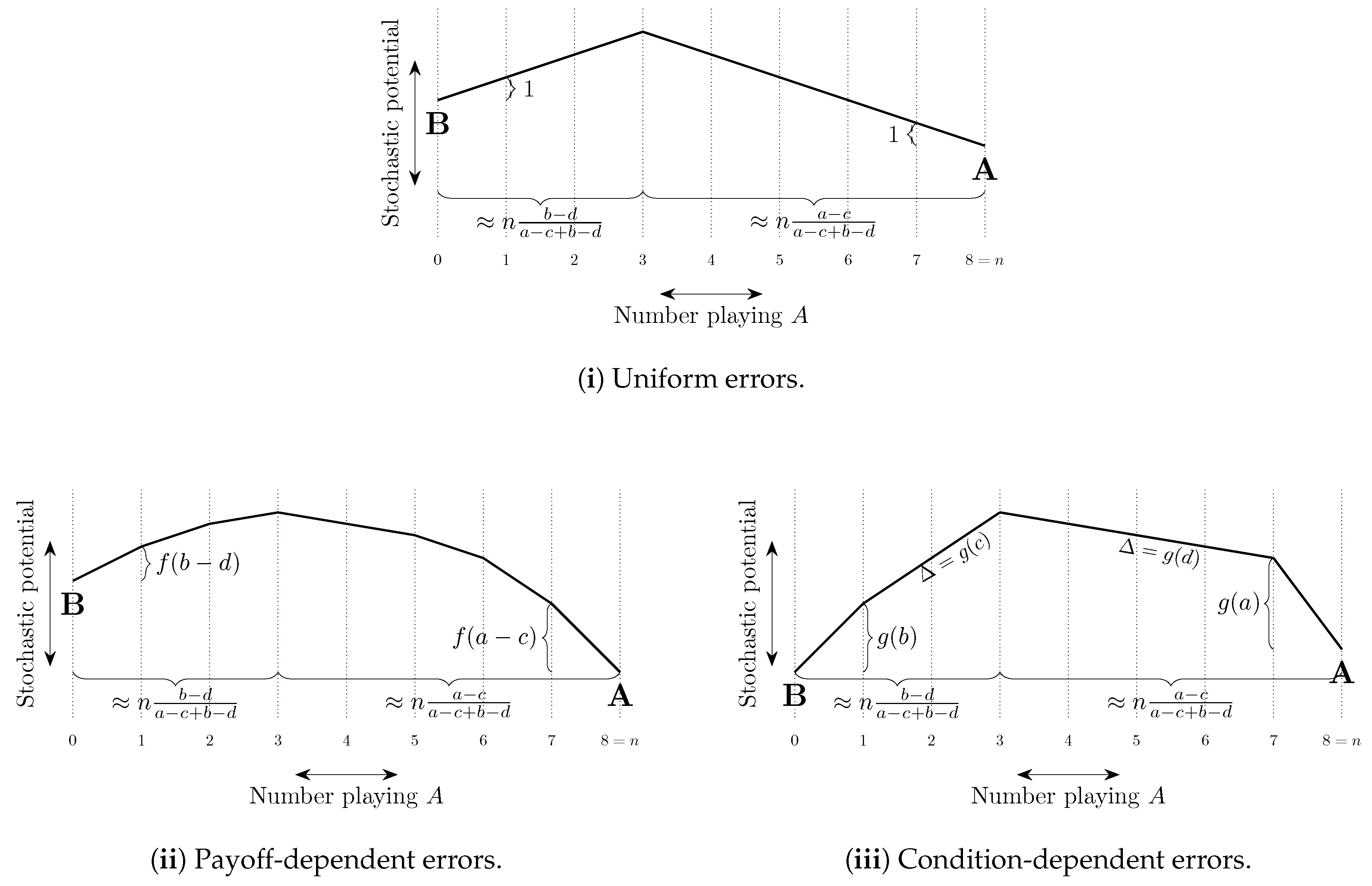
4.2.1. Perturbed Dynamics and Stochastic Stability
4.2.2. Coordination Games
4.2.3. Communication and Language
4.2.4. Best Shot and Minimum Effort Games
4.2.5. Cournot Oligopoly
4.2.6. Prisoner’s Dilemmas
4.3. Culture Embodied in Individuals
4.4. Interaction of Culture Embodied in Individuals and Society
5. Economic Applications
5.1. Macroeconomics, Market Selection and Finance
5.2. Industrial Organization
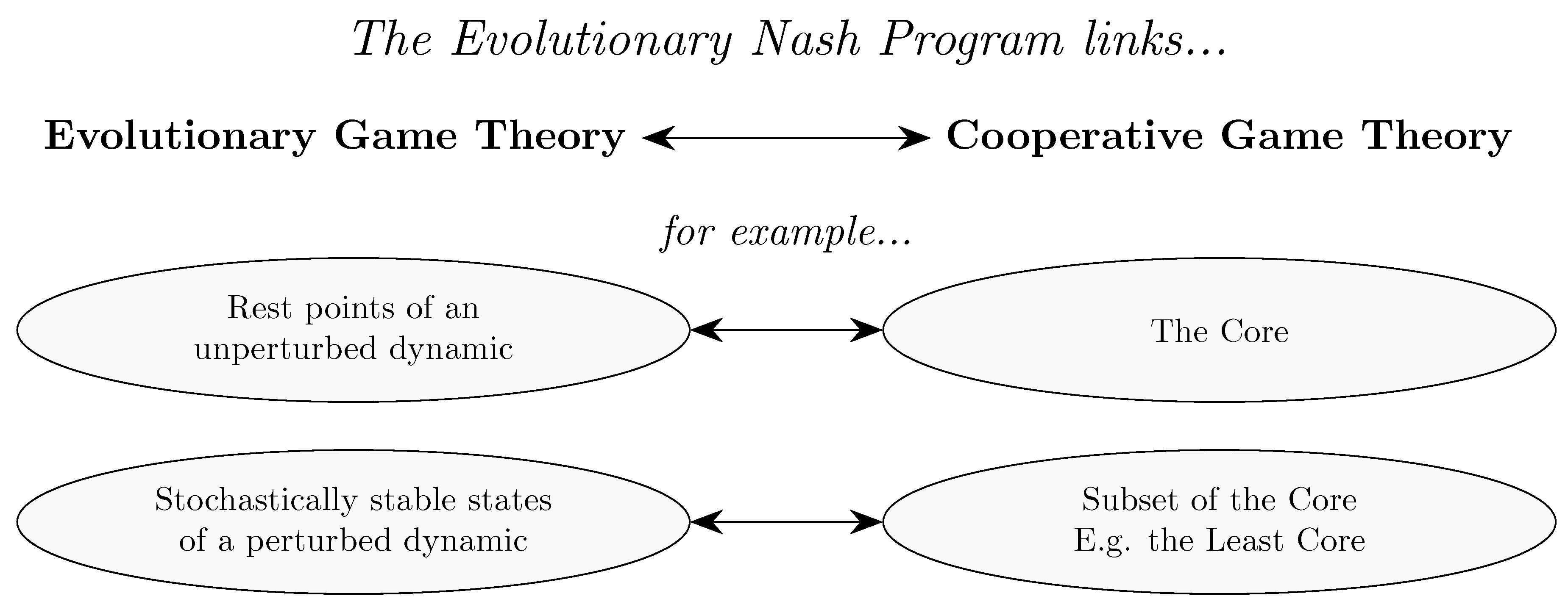
6. The Evolutionary Nash Program
6.1. Recontracting and Nash Demand Games
6.2. Transferable Utility Matching—The Assignment Game
6.3. Non-Transferable Utility Matching—Marriage, College Admissions
6.4. Bargaining Solutions and Coordination Games
7. Behavioral Dynamics
7.1. Reinforcement Learning
7.2. Imitation
7.3. Sampling Equilibrium and Best Experienced Payoff Dynamics
7.4. Best and Better Response
7.5. Continuous Strategy Sets
7.6. Completely Uncoupled Dynamics
8. General Methodology
8.1. Perturbed Dynamics and Stochastic Stability
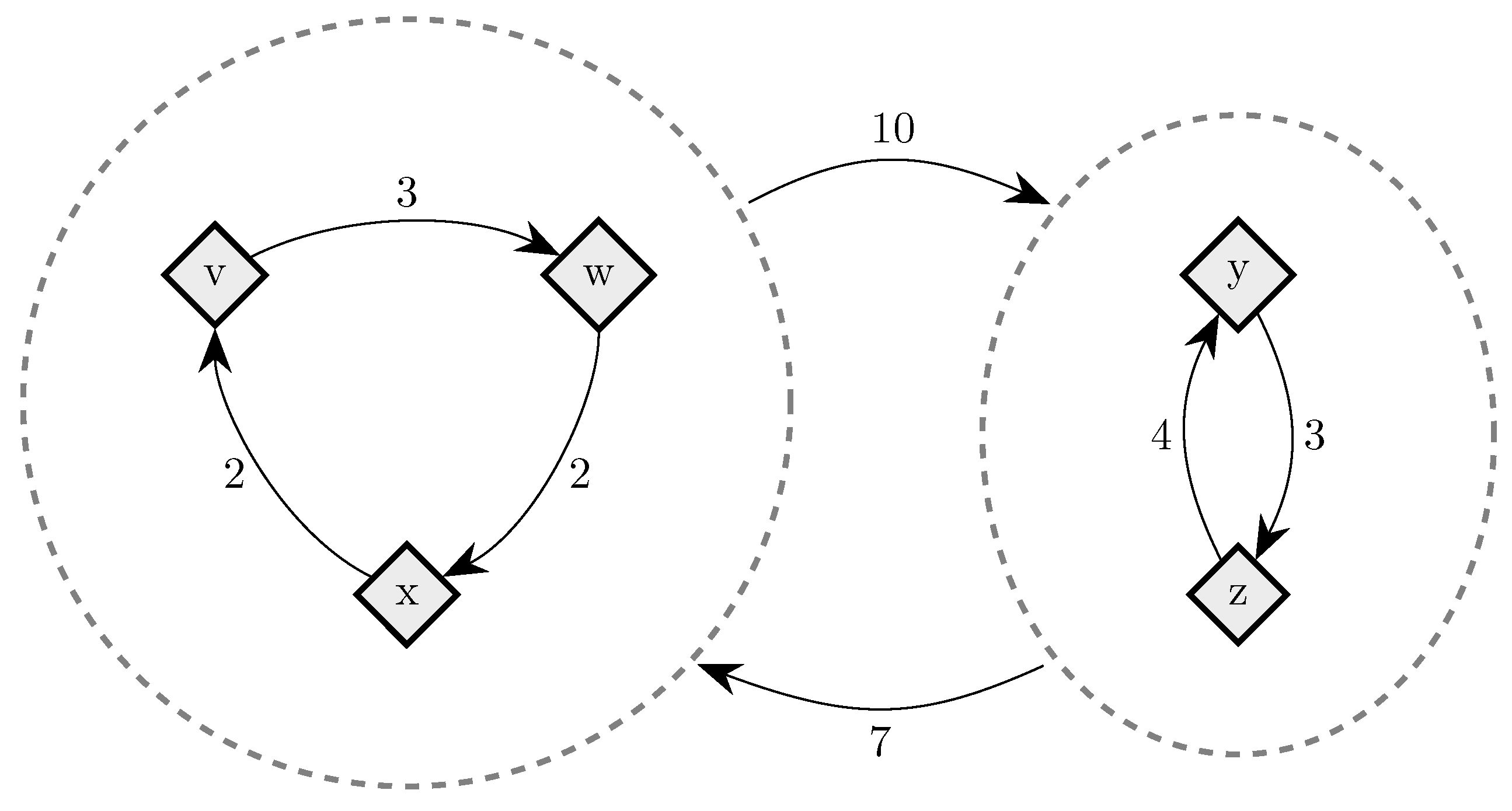
8.1.1. Least Cost Transition Paths
8.1.2. Cyclic Decomposition
8.1.3. Convergence Time
8.1.4. Elimination of Weakly Dominated Strategies
8.2. Further Stability Results
8.3. Further Convergence Results
8.4. Distributed control
8.5. Software and Simulations
9. Empirics
9.1. Best and Better Response
9.2. Imitation
9.3. Completely Uncoupled Dynamics
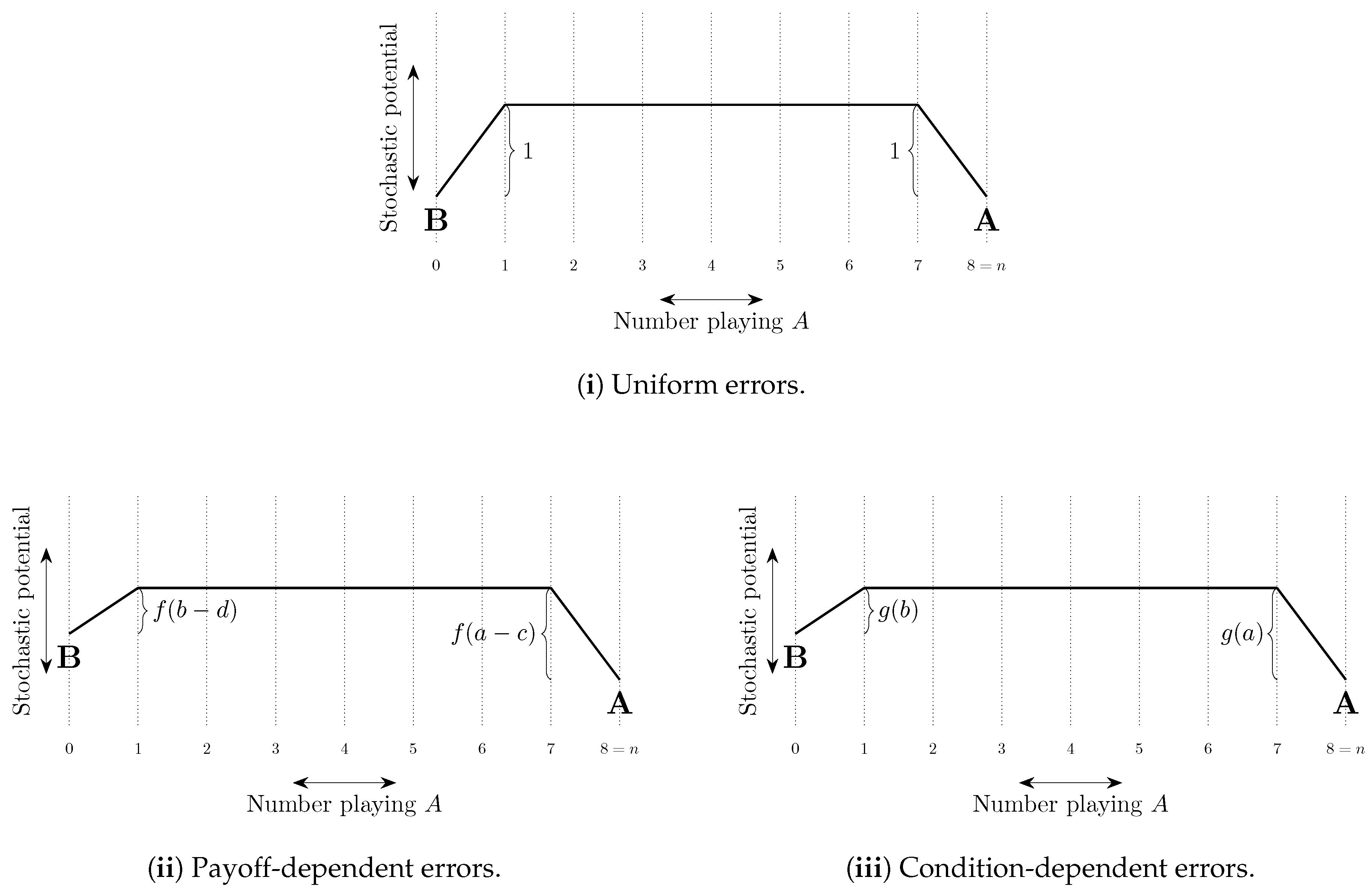
9.4. Errors in Perturbed Dynamics
- (a)
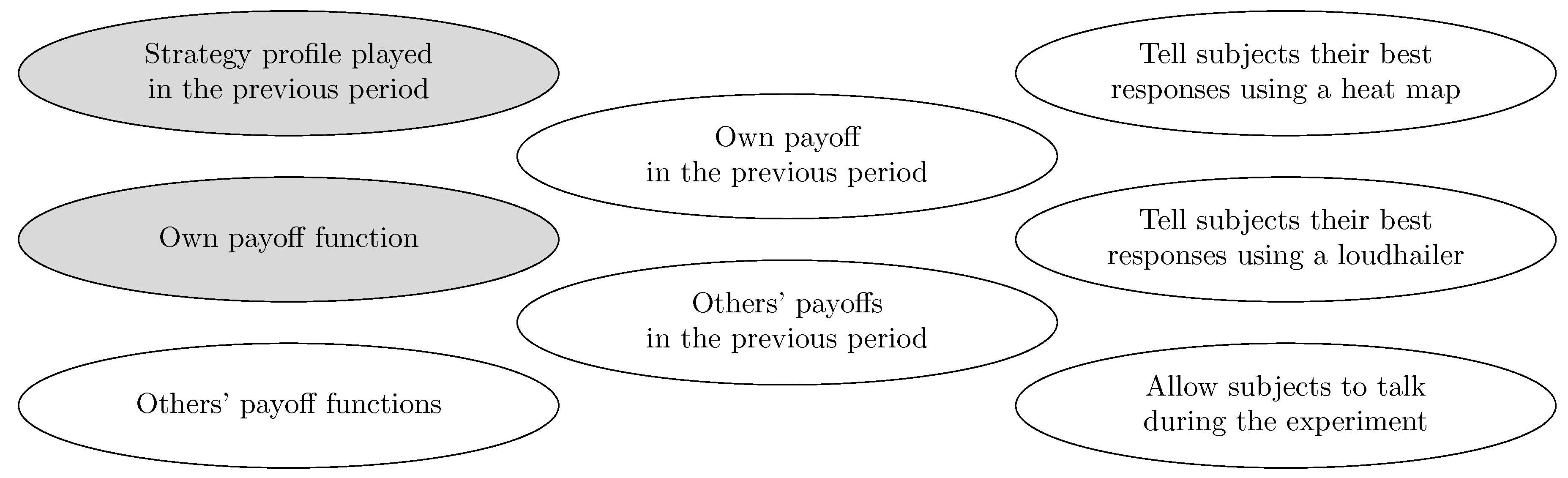
- That the behavior of subjects in context X is approximated by dynamic Y may be non-generic in the sense that small changes to X may lead to the connection being broken. This is one reason, beyond the usual reasons, that replication is important, as any replication will never replicate X exactly (e.g., the weather outside the laboratory will be different). An important question is then the size of the set of contexts containing X that can be approximated by Y. This can be examined by including or excluding elements such as those of Figure 17. Resources permitting, for any positive results (i.e., mapping), X can be adjusted until the mapping fails.
- (b)
- Further study of separate attributes and features of decision rules, as discussed in several papers in Section 9.3 and Section 9.4, could be promising. In particular, the cues and information that influence each feature could be studied.
- (c)
- There is much real world time series data that could be considered using evolutionary models.
- (d)
- Theories of the evolution of traits, including preferences, should be tested, as suggested in Open Topic 5.
10. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Abbot, P.; Abe, J.; Alcock, J.; Alizon, S.; Alpedrinha, J.A.; Andersson, M.; Andre, J.B.; Van Baalen, M.; Balloux, F.; Balshine, S.; et al. Inclusive fitness theory and eusociality. Nature 2011, 471, E1. [Google Scholar] [CrossRef] [PubMed]
- Agastya, M. Adaptive Play in Multiplayer Bargaining Situations. Rev. Econ. Stud. 1997, 64, 411–426. [Google Scholar] [CrossRef]
- Agastya, M. Perturbed Adaptive Dynamics in Coalition Form Games. J. Econ. Theory 1999, 89, 207–233. [Google Scholar] [CrossRef]
- Alexander, J.; Skyrms, B. Bargaining with Neighbors: Is Justice Contagious? J. Philos. 1999, 96, 588–598. [Google Scholar] [CrossRef]
- Alger, I.; Weibull, J.W. Kinship, incentives, and evolution. Am. Econ. Rev. 2010, 100, 1725–1758. [Google Scholar] [CrossRef]
- Alger, I.; Weibull, J.W. A generalization of Hamilton’s rule—Love others how much? J. Theor. Biol. 2012, 299, 42–54. [Google Scholar] [CrossRef] [PubMed]
- Alger, I.; Weibull, J.W. Homo Moralis–Preference Evolution Under Incomplete Information and Assortative Matching. Econometrica 2013, 81, 2269–2302. [Google Scholar]
- Alger, I.; Weibull, J.W. Evolution and Kantian morality. Games Econ. Behav. 2016, 98, 56–67. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Ania, A.B. The asset market game. J. Math. Econ. 2005, 41, 67–90. [Google Scholar] [CrossRef]
- Alos-Ferrer, C.; Ania, A.B. The evolutionary stability of perfectly competitive behavior. Econ. Theory 2005, 26, 497–516. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Buckenmaier, J. Trader matching and the selection of market institutions. J. Math. Econ. 2017, 69, 118–127. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Kirchsteiger, G. General equilibrium and the emergence of (non) market clearing trading institutions. Econ. Theory 2010, 44, 339–360. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Netzer, N. The logit-response dynamics. Games Econ. Behav. 2010, 68, 413–427. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Shi, F. Imitation with asymmetric memory. Econ. Theory 2012, 49, 193–215. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Weidenholzer, S. Imitation and the role of information in overcoming coordination failures. Games Econ. Behav. 2014, 87, 397–411. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Ania, A.; Vega-Redondo, F. An evolutionary model of market structure. In The Theory of Markets; van der Laan, G., Herings, P., Talman, A., Eds.; Number 177 in KNAW Series; North Holland: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Alós-Ferrer, C.; Ania, A.B.; Schenk-Hoppé, K.R. An evolutionary model of Bertrand oligopoly. Games Econ. Behav. 2000, 33, 1–19. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Kirchsteiger, G.; Walzl, M. On the evolution of market institutions: The platform design paradox. Econ. J. 2010, 120, 215–243. [Google Scholar] [CrossRef]
- Alós-Ferrer, C. Cournot versus Walras in dynamic oligopolies with memory. Int. J. Ind. Organ. 2004, 22, 193–217. [Google Scholar] [CrossRef]
- Amir, R.; Evstigneev, I.V.; Hens, T.; Schenk-Hoppé, K.R. Market selection and survival of investment strategies. J. Math. Econ. 2005, 41, 105–122. [Google Scholar] [CrossRef]
- Angus, S.; Masson, V. The Effects of Information and Interactions on Contagion Processes; University of Adelaide: Adelaide, Australia, 2010. [Google Scholar]
- Angus, S.D.; Newton, J. Emergence of Shared Intentionality Is Coupled to the Advance of Cumulative Culture. PLOS Comput. Biol. 2015, 11, e1004587. [Google Scholar] [CrossRef] [PubMed]
- Argiento, R.; Pemantle, R.; Skyrms, B.; Volkov, S. Learning to signal: Analysis of a micro-level reinforcement model. Stoch. Process. Their Appl. 2009, 119, 373–390. [Google Scholar] [CrossRef]
- Arieli, I.; Young, H.P. Stochastic learning dynamics and speed of convergence in population games. Econometrica 2016, 84, 627–676. [Google Scholar] [CrossRef]
- Arnold, T.; Schwalbe, U. Dynamic coalition formation and the core. J. Econ. Behav. Organ. 2002, 49, 363–380. [Google Scholar] [CrossRef]
- Aumann, R. Acceptable Points in General Cooperative n-Person Games. In Contributions to the Theory of Games IV; Tucker, A.W., Luce, R.D., Eds.; Princeton University Press: Princeton, NJ, USA, 1959; pp. 287–324. [Google Scholar]
- Avrachenkov, K.; Singh, V.V. Stochastic coalitional better-response dynamics and stable equilibrium. Autom. Remote Control 2016, 77, 2227–2238. [Google Scholar] [CrossRef]
- Babichenko, Y. Completely uncoupled dynamics and Nash equilibria. Games Econ. Behav. 2012, 76, 1–14. [Google Scholar] [CrossRef]
- Babichenko, Y. Best-Reply Dynamic in Large Aggregative Games; Mimeo: New York, NY, USA, 2013. [Google Scholar]
- Babichenko, Y. Best-reply dynamics in large binary-choice anonymous games. Games Econ. Behav. 2013, 81, 130–144. [Google Scholar] [CrossRef]
- Balkenborg, D.; Schlag, K.H. Evolutionarily stable sets. Int. J. Game Theory 2001, 29, 571–595. [Google Scholar] [CrossRef]
- Balkenborg, D.; Hofbauer, J.; Kuzmics, C. Refined best reply correspondence and dynamics. Theor. Econ. 2013, 8, 165–192. [Google Scholar] [CrossRef]
- Basu, K.; Weibull, J.W. Strategy subsets closed under rational behavior. Econ. Lett. 1991, 36, 141–146. [Google Scholar] [CrossRef]
- Bednarik, P.; Hofbauer, J. Discretized best-response dynamics for the rock-paper-scissors game. J. Dyn. Games 2017, 4, 75–86. [Google Scholar] [CrossRef]
- Beggs, A.W. On the convergence of reinforcement learning. J. Econ. Theory 2005, 122, 1–36. [Google Scholar] [CrossRef]
- Belloc, M.; Bowles, S. The Persistence of Inferior Cultural-Institutional Conventions. Am. Econ. Rev. 2013, 103, 93–98. [Google Scholar] [CrossRef]
- Benaïm, M.; Hirsch, M.W. Stochastic approximation algorithms with constant step size whose average is cooperative. Ann. Appl. Probab. 1999, 216–241. [Google Scholar]
- Benaım, M.; Hirsch, M.W. Mixed equilibria and dynamical systems arising from fictitious play in perturbed games. Games Econ. Behav. 1999, 29, 36–72. [Google Scholar] [CrossRef]
- Benaïm, M.; Weibull, J.W. Deterministic approximation of stochastic evolution in games. Econometrica 2003, 71, 873–903. [Google Scholar] [CrossRef]
- Bendor, J.; Swistak, P. Types of evolutionary stability and the problem of cooperation. Proc. Natl. Acad. Sci. USA 1995, 92, 3596–3600. [Google Scholar] [CrossRef] [PubMed]
- Bergstrom, T.C. On the evolution of altruistic ethical rules for siblings. Am. Econ. Rev. 1995, 85, 58–81. [Google Scholar]
- Bergstrom, T.C. The algebra of assortative encounters and the evolution of cooperation. Int. Game Theory Rev. 2003, 5, 211–228. [Google Scholar] [CrossRef]
- Bilancini, E.; Boncinelli, L. The co-evolution of cooperation and defection under local interaction and endogenous network formation. J. Econ. Behav. Organ. 2009, 70, 186–195. [Google Scholar] [CrossRef]
- Bilancini, E.; Boncinelli, L. Social coordination with locally observable types. Econ. Theory 2015, 65, 975–1009. [Google Scholar] [CrossRef]
- Bilancini, E.; Boncinelli, L. The Evolution of Conventions under Condition-Dependent Mistakes; Working Paper; Universita’degli Studi di Firenze: Firenze, Italia, 2016. [Google Scholar]
- Bilancini, E.; Boncinelli, L.; Wu, J. The interplay of cultural intolerance and action-assortativity for the emergence of cooperation and homophily. Eur. Econ. Rev. 2018, 102, 1–18. [Google Scholar] [CrossRef]
- Binmore, K.; Samuelson, L. Drift. Eur. Econ. Rev. 1994, 38, 859–867. [Google Scholar] [CrossRef]
- Binmore, K.; Samuelson, L. Evolutionary drift and equilibrium selection. The Rev. Econ. Stud. 1999, 66, 363–393. [Google Scholar] [CrossRef]
- Binmore, K.G. Game Theory and the Social Contract: Just Playing; MIT Press: Cambridge, MA, USA, 1998; Volume 2. [Google Scholar]
- Binmore, K. Natural Justice; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Biró, P.; Bomhoff, M.; Golovach, P.A.; Kern, W.; Paulusma, D. Solutions for the Stable Roommates Problem with Payments. In Graph-Theoretic Concepts in Computer Science; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2013; pp. 69–80. [Google Scholar]
- Bisin, A.; Verdier, T. The economics of cultural transmission and the dynamics of preferences. J. Econ. Theory 2001, 97, 298–319. [Google Scholar] [CrossRef]
- Blume, A.; Arnold, T. Learning to communicate in cheap-talk games. Games Econ. Behav. 2004, 46, 240–259. [Google Scholar] [CrossRef]
- Blume, L.; Easley, D. Evolution and market behavior. J. Econ. Theory 1992, 58, 9–40. [Google Scholar] [CrossRef]
- Blume, L.; Easley, D. If you’re so smart, why aren’t you rich? Belief selection in complete and incomplete markets. Econometrica 2006, 74, 929–966. [Google Scholar] [CrossRef]
- Blume, A.; Kim, Y.G.; Sobel, J. Evolutionary stability in games of communication. Games Econ. Behav. 1993, 5, 547–575. [Google Scholar] [CrossRef]
- Blume, A.; DeJong, D.V.; Kim, Y.G.; Sprinkle, G.B. Experimental evidence on the evolution of meaning of messages in sender-receiver games. Am. Econ. Rev. 1998, 88, 1323–1340. [Google Scholar]
- Blume, A.; DeJong, D.V.; Kim, Y.G.; Sprinkle, G.B. Evolution of communication with partial common interest. Games Econ. Behav. 2001, 37, 79–120. [Google Scholar] [CrossRef]
- Blume, L.E. The Statistical Mechanics of Strategic Interaction. Games Econ. Behav. 1993, 5, 387–424. [Google Scholar] [CrossRef]
- Blume, L.E. Population Games; Working Papers 96-04-022; Santa Fe Institute: Santa Fe, NM, USA, 1996. [Google Scholar]
- Blume, A. Communication, risk, and efficiency in games. Games Econ. Behav. 1998, 22, 171–202. [Google Scholar] [CrossRef]
- Bomze, I.M. Non-cooperative two-person games in biology: A classification. Int. J. Game Theory 1986, 15, 31–57. [Google Scholar] [CrossRef]
- Boncinelli, L.; Pin, P. Stochastic stability in best shot network games. Games Econ. Behav. 2012, 75, 538–554. [Google Scholar] [CrossRef]
- Boncinelli, L.; Pin, P. The stochastic stability of decentralized matching on a graph. Games Econ. Behav. 2017. [Google Scholar] [CrossRef]
- Börgers, T.; Sarin, R. Learning through reinforcement and replicator dynamics. J. Econ. Theory 1997, 77, 1–14. [Google Scholar] [CrossRef]
- Börgers, T.; Morales, A.J.; Sarin, R. Expedient and monotone learning rules. Econometrica 2004, 72, 383–405. [Google Scholar] [CrossRef]
- Bowles, S.; Gintis, H. A Cooperative Species: Human Reciprocity and Its Evolution; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Bowles, S. Microeconomics: Behavior, Institutions, and Evolution; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Bowles, S. Is inequality a human universal. In The Social Economics of Poverty; Barrett, C.B., Ed.; Routledge: Abingdon, UK, 2005; pp. 125–145. [Google Scholar]
- Bowles, S. Group competition, reproductive leveling, and the evolution of human altruism. Science 2006, 314, 1569–1572. [Google Scholar] [CrossRef] [PubMed]
- Bowles, S. Institutional poverty traps. In Poverty Traps; Bowles, S., Durlauf, S.N., Hoff, K., Eds.; Princeton University Press: Princeton, NJ, USA, 2006; pp. 116–138. [Google Scholar]
- Boyd, R.; Lorberbaum, J.P. No pure strategy is evolutionarily stable in the repeated prisoner’s dilemma game. Nature 1987, 327, 58. [Google Scholar] [CrossRef]
- Brambilla, M.; Ferrante, E.; Birattari, M.; Dorigo, M. Swarm robotics: a review from the swarm engineering perspective. Swarm Intell. 2013, 7, 1–41. [Google Scholar] [CrossRef]
- Brown, G.W. Iterative solution of games by fictitious play. Act. Anal. Prod. Alloc. 1951, 13, 374–376. [Google Scholar]
- Burdett, K.; Judd, K.L. Equilibrium price dispersion. Econometrica 1983, 955–969. [Google Scholar] [CrossRef]
- Burton-Chellew, M.N.; Nax, H.H.; West, S.A. Payoff-based learning explains the decline in cooperation in public goods games. Proc. R. Soc. Lond. B Biol. Sci. 2015, 282, 20142678. [Google Scholar] [CrossRef] [PubMed]
- Cara, M.A.R.d.; Barton, N.H.; Kirkpatrick, M. A Model for the Evolution of Assortative Mating. Am. Nat. 2008, 171, 580–596. [Google Scholar] [CrossRef] [PubMed]
- Cárdenas, J.C.; Mantilla, C.; Sethi, R. Stable sampling equilibrium in common pool resource games. Games 2015, 6, 299–317. [Google Scholar] [CrossRef]
- Carvalho, J.P. Veiling. Q. J. Econ. 2012, 128, 337–370. [Google Scholar] [CrossRef]
- Cason, T.N.; Friedman, D.; Hopkins, E. Cycles and instability in a rock–paper–scissors population game: A continuous time experiment. Rev. Econ. Stud. 2013, 81, 112–136. [Google Scholar] [CrossRef]
- Cavalli-Sforza, L.L.; Feldman, M.W. Cultural Transmission and Evolution: A Quantitative Approach; Princeton University Press: Princeton, NJ, USA, 1981. [Google Scholar]
- Chakrabarti, A.S.; Lahkar, R. An Evolutionary Analysis of Growth and Fluctuations with Negative Externalities. Dyn. Games Appl. 2017. [Google Scholar] [CrossRef]
- Chakrabarti, A.S.; Lahkar, R. Productivity dispersion and output fluctuations: An evolutionary model. J. Econ. Behav. Organ. 2017, 137, 339–360. [Google Scholar] [CrossRef]
- Chen, B.; Fujishige, S.; Yang, Z. Random decentralized market processes for stable job matchings with competitive salaries. J. Econ. Theory 2016, 165, 25–36. [Google Scholar] [CrossRef]
- Cheung, M.W.; Wu, J. On the probabilistic transmission of continuous cultural traits. J. Econ. Theory 2018, 174, 300–323. [Google Scholar] [CrossRef]
- Cheung, M.W. Pairwise comparison dynamics for games with continuous strategy space. J. Econ. Theory 2014, 153, 344–375. [Google Scholar] [CrossRef]
- Cheung, M.W. Imitative dynamics for games with continuous strategy space. Games Econ. Behav. 2016, 99, 206–223. [Google Scholar] [CrossRef]
- Cho, I.K.; Kasa, K. Learning and model validation. Rev. Econ. Stud. 2014, 82, 45–82. [Google Scholar] [CrossRef]
- Choi, J.K.; Bowles, S. The coevolution of parochial altruism and war. Science 2007, 318, 636–640. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.J.; Liu, T.H. On the shortest arborescence of a directed graph. Sci. Sin. 1965, 14, 1396–1400. [Google Scholar]
- Clemm von Hohenberg, B.; Maes, M.; Pradelski, B.S. Micro Influence and Macro Dynamics of Opinions; SSRN Working Paper Series 2974413; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Cross, J.G. A stochastic learning model of economic behavior. Q. J. Econ. 1973, 87, 239–266. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, R. Collaboration in networks with randomly chosen agents. J. Econ. Behav. Organ. 2016, 129, 129–141. [Google Scholar] [CrossRef]
- Cui, Z.; Zhai, J. Escape dynamics and equilibria selection by iterative cycle decomposition. J. Math. Econ. 2010, 46, 1015–1029. [Google Scholar] [CrossRef]
- Daskalakis, C.; Goldberg, P.W.; Papadimitriou, C.H. The complexity of computing a Nash equilibrium. SIAM J. Comput. 2009, 39, 195–259. [Google Scholar] [CrossRef]
- Dawid, H.; Hellmann, T. The evolution of R&D networks. J. Econ. Behav. Organ. 2014, 105, 158–172. [Google Scholar]
- De Borda, J.C. Mémoire sur les élections au scrutin. In Histoire de l’Academie Royale des Sciences pour 1781; Royal Society: London, UK, 1784. [Google Scholar]
- De Giorgi, E. Evolutionary portfolio selection with liquidity shocks. J. Econ. Dyn. Control 2008, 32, 1088–1119. [Google Scholar] [CrossRef]
- Dekel, E.; Ely, J.C.; Yilankaya, O. Evolution of preferences. Rev. Econ. Stud. 2007, 74, 685–704. [Google Scholar] [CrossRef]
- Demichelis, S.; Weibull, J.W. Language, meaning, and games: A model of communication, coordination, and evolution. Am. Econ. Rev. 2008, 98, 1292–1311. [Google Scholar] [CrossRef]
- Diamantoudi, E.; Xue, L.; Miyagawa, E. Random paths to stability in the roommate problem. Games Econ. Behav. 2004, 48, 18–28. [Google Scholar] [CrossRef]
- Dieckmann, U.; Doebeli, M. On the origin of species by sympatric speciation. Nature 1999, 400, 354–357. [Google Scholar] [CrossRef] [PubMed]
- Dindoš, M.; Mezzetti, C. Better-reply dynamics and global convergence to Nash equilibrium in aggregative games. Games Econ. Behav. 2006, 54, 261–292. [Google Scholar] [CrossRef]
- Dokumaci, E.; Sandholm, W.H. Large deviations and multinomial probit choice. J. Econ. Theory 2011, 146, 2151–2158. [Google Scholar] [CrossRef]
- Doraszelski, U.; Lewis, G.; Pakes, A. Just starting out: Learning and equilibrium in a new market. Am. Econ. Rev. 2018, 108, 565–615. [Google Scholar] [CrossRef]
- Duersch, P.; Oechssler, J.; Schipper, B.C. Unbeatable imitation. Games Econ. Behav. 2012, 76, 88–96. [Google Scholar] [CrossRef]
- Edmonds, J. Optimum branchings. J. Res. Natl. Bureau Stand. 1967, 71, 233–240. [Google Scholar] [CrossRef]
- Ellison, G. Basins of Attraction, Long-Run Stochastic Stability, and the Speed of Step-by-Step Evolution. Rev. Econ. Stud. 2000, 67, 17–45. [Google Scholar] [CrossRef]
- Ely, J.C.; Sandholm, W.H. Evolution in Bayesian games I: theory. Games Econ. Behav. 2005, 53, 83–109. [Google Scholar] [CrossRef]
- Ely, J.C.; Hörner, J.; Olszewski, W. Belief-free equilibria in repeated games. Econometrica 2005, 73, 377–415. [Google Scholar] [CrossRef]
- Erev, I.; Roth, A.E. Predicting how people play games: Reinforcement learning in experimental games with unique, mixed strategy equilibria. Am. Econ. Rev. 1998, 88, 848–881. [Google Scholar]
- Eshel, I.; Cavalli-Sforza, L.L. Assortment of encounters and evolution of cooperativeness. Proc. Natl. Acad. Sci. USA 1982, 79, 1331–1335. [Google Scholar] [CrossRef] [PubMed]
- Evans, G.W.; Honkapohja, S. Learning and Expectations in Macroeconomics; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Evstigneev, I.V.; Hens, T.; Schenk-Hoppé, K.R. Market Selection Of Financial Trading Strategies: Global Stability. Math. Financ. 2002, 12, 329–339. [Google Scholar] [CrossRef]
- Evstigneev, I.V.; Hens, T.; Schenk-Hoppé, K.R. Evolutionary stable stock markets. Econ. Theory 2006, 27, 449–468. [Google Scholar] [CrossRef]
- Farrell, J.; Ware, R. Evolutionary stability in the repeated Prisoner’s Dilemma. Theor. Popul. Biol. 1989, 36, 161–166. [Google Scholar] [CrossRef]
- Feldman, A.M. Recontracting Stability. Econometrica 1974, 42, 35–44. [Google Scholar] [CrossRef]
- Ferriere, R.; Michod, R.E. Inclusive fitness in evolution. Nature 2011, 471, E6. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. The Genetical Theory of Natural Selection, Variorum Edition (2000); Oxford University Press: Oxford, UK, 1930. [Google Scholar]
- Flåm, S.D.; Morgan, J. Newtonian mechanics and Nash play. Int. Game Theory Rev. 2004, 6, 181–194. [Google Scholar] [CrossRef]
- Foster, D.; Young, H.P. Stochastic Evolutionary Game Dynamics. Theor. Popul. Biol. 1990, 38, 219–232. [Google Scholar] [CrossRef]
- Foster, D.P.; Young, H.P. On the impossibility of predicting the behavior of rational agents. Proc. Natl. Acad. Sci. USA 2001, 98, 12848–12853. [Google Scholar] [CrossRef] [PubMed]
- Foster, D.P.; Young, H.P. Learning, hypothesis testing, and Nash equilibrium. Games Econ. Behav. 2003, 45, 73–96. [Google Scholar] [CrossRef]
- Foster, D.P.; Young, H.P. Regret testing: Learning to play Nash equilibrium without knowing you have an opponent. Theor. Econ. 2006, 1, 341–367. [Google Scholar]
- Freidlin, M.I.; Wentzell, A.D. Random Perturbations of Dynamical Systems, 2nd ed.; Springer: Berlin, Germany, 1984. [Google Scholar]
- Frenkel, S.; Heller, Y.; Teper, R. The Endowment Effect as blessing. Int. Econ. Rev. 2018. (online first). [Google Scholar] [CrossRef]
- Friedman, J.; Mezzetti, C. Learning in Games by Random Sampling. J. Econ. Theory 2001, 98, 55–84. [Google Scholar] [CrossRef]
- Friedman, D.; Huck, S.; Oprea, R.; Weidenholzer, S. From imitation to collusion: Long-run learning in a low-information environment. J. Econ. Theory 2015, 155, 185–205. [Google Scholar] [CrossRef]
- Friedman, D. Evolutionary games in economics. Econometrica 1991, 59, 637–666. [Google Scholar] [CrossRef]
- Fudenberg, D.; Kreps, D.M. Learning mixed equilibria. Games Econ. Behav. 1993, 5, 320–367. [Google Scholar] [CrossRef]
- Fudenberg, D.; Levine, D.K. Self-confirming equilibrium. Econometrica 1993, 61, 523–545. [Google Scholar] [CrossRef]
- Fujiwara-Greve, T.; Okuno-Fujiwara, M. Voluntarily separable repeated prisoner’s dilemma. Rev. Econ. Stud. 2009, 76, 993–1021. [Google Scholar] [CrossRef]
- Fujiwara-Greve, T.; Okuno-Fujiwara, M.; Suzuki, N. Voluntarily separable repeated Prisoner’s Dilemma with reference letters. Games Econ. Behav. 2012, 74, 504–516. [Google Scholar] [CrossRef]
- Gale, D.; Shapley, L.S. College Admissions and the Stability of Marriage. Am. Math. Mon. 1962, 69, 9–15. [Google Scholar] [CrossRef]
- Gamba, A. Learning and evolution of altruistic preferences in the Centipede Game. J. Econ. Behav. Organ. 2013, 85, 112–117. [Google Scholar] [CrossRef]
- García, J.; van Veelen, M. In and out of equilibrium I: Evolution of strategies in repeated games with discounting. J. Econ. Theory 2016, 161, 161–189. [Google Scholar] [CrossRef]
- Germano, F.; Lugosi, G. Global Nash convergence of Foster and Young’s regret testing. Games Econ. Behav. 2007, 60, 135–154. [Google Scholar] [CrossRef]
- Gilboa, I.; Matsui, A. Social stability and equilibrium. Econometrica 1991, 59, 859–867. [Google Scholar] [CrossRef]
- Golman, R.; Page, S.E. Basins of attraction and equilibrium selection under different learning rules. J. Evol. Econ. 2010, 20, 49–72. [Google Scholar] [CrossRef]
- Goyal, S.; Hernández, P.; Martínez-Cánovas, G.; Moisan, F.; Muñoz Herrera, M.; Sánchez, A. Integration and Segregation; CWPE Working Paper 1721; Faculty of Economics, University of Cambridge: Cambridge, UK, 2017. [Google Scholar]
- Granovetter, M. Threshold Models of Collective Behavior. Am. J. Sociol. 1978, 83, 1420–1443. [Google Scholar] [CrossRef]
- Green, J.R. The Stability of Edgeworth’s Recontracting Process. Econometrica 1974, 42, 21–34. [Google Scholar] [CrossRef]
- Güth, W.; Kliemt, H. The indirect evolutionary approach: Bridging the gap between rationality and adaptation. Ration. Soc. 1998, 10, 377–399. [Google Scholar] [CrossRef]
- Haldane, J.B.S. The Causes of Evolution; Princeton University Press: Princeton, NJ, USA, 1932. [Google Scholar]
- Hamilton, W.D. The evolution of altruistic behavior. Am. Nat. 1963, 97, 354–356. [Google Scholar] [CrossRef]
- Hamilton, W. The genetical evolution of social behaviour I. J. Theor. Biol. 1964, 7, 1–16. [Google Scholar] [CrossRef]
- Hamilton, W. The genetical evolution of social behaviour II. J. Theor. Biol. 1964, 7, 17–52. [Google Scholar] [CrossRef]
- Harsanyi, J.C. Games with Incomplete Information Played by “Bayesian” Players, I-III. Part I. The Basic Model. Manag. Sci. 1967, 14, 159–182. [Google Scholar] [CrossRef]
- Hart, S.; Mansour, Y. How long to equilibrium? The communication complexity of uncoupled equilibrium procedures. Games Econ. Behav. 2010, 69, 107–126. [Google Scholar] [CrossRef]
- Hart, S.; Mas-Colell, A. A simple adaptive procedure leading to correlated equilibrium. Econometrica 2000, 68, 1127–1150. [Google Scholar] [CrossRef]
- Hart, S.; Mas-Colell, A. Uncoupled dynamics do not lead to Nash equilibrium. Am. Econ. Rev. 2003, 93, 1830–1836. [Google Scholar] [CrossRef]
- Hart, S.; Mas-Colell, A. Stochastic uncoupled dynamics and Nash equilibrium. Games Econ. Behav. 2006, 57, 286–303. [Google Scholar] [CrossRef]
- Hart, S. Commentary: Nash equilibrium and dynamics. Games Econ. Behav. 2011, 71, 6–8. [Google Scholar] [CrossRef]
- Heifetz, A.; Shannon, C.; Spiegel, Y. What to maximize if you must. J. Econ. Theory 2007, 133, 31–57. [Google Scholar] [CrossRef]
- Heller, Y.; Mohlin, E. Coevolution of Deception and Preferences: Darwin and Nash Meet Machiavelli; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Heller, Y.; Mohlin, E. Observations on cooperation. Rev. Econ. Stud. 2017. Available online: http://www.restud.com/wp-content/uploads/2017/12/MS24086manuscript.pdf (accessed on 24 May 2018).
- Heller, Y. Overconfidence and diversification. Am. Econ. J. Microecon. 2014, 6, 134–153. [Google Scholar] [CrossRef]
- Heller, Y. Language, meaning, and games: A model of communication, coordination, and evolution: Comment. Am. Econ. Rev. 2014, 104, 1857–1863. [Google Scholar] [CrossRef]
- Heller, Y. Stability and trembles in extensive-form games. Games Econ. Behav. 2014, 84, 132–136. [Google Scholar] [CrossRef]
- Heller, Y. Three steps ahead. Theor. Econ. 2015, 10, 203–241. [Google Scholar] [CrossRef]
- Heller, Y. Instability of belief-free equilibria. J. Econ. Theory 2017, 168, 261–286. [Google Scholar] [CrossRef]
- Hellmann, T.; Staudigl, M. Evolution of Social Networks. Eur. J. Oper. Res. 2014, 234, 583–596. [Google Scholar] [CrossRef]
- Hens, T.; Schenk-Hoppé, K.R. Evolutionary stability of portfolio rules in incomplete markets. J. Math. Econ. 2005, 41, 43–66. [Google Scholar] [CrossRef]
- Herold, F.; Kuzmics, C. Evolutionary stability of discrimination under observability. Games Econ. Behav. 2009, 67, 542–551. [Google Scholar] [CrossRef]
- Herold, F. Carrot or stick? The evolution of reciprocal preferences in a haystack model. Am. Econ. Rev. 2012, 102, 914–940. [Google Scholar] [CrossRef]
- Herre, E.A.; Wcislo, W.T. In defence of inclusive fitness theory. Nature 2011, 471, E8. [Google Scholar] [CrossRef] [PubMed]
- Hofbauer, J.; Sandholm, W.H. Evolution in games with randomly disturbed payoffs. J. Econ. Theory 2007, 132, 47–69. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary game dynamics. Bull. Am. Math. Soc. 2003, 40, 479–519. [Google Scholar] [CrossRef]
- Hofbauer, J.; Weibull, J.W. Evolutionary selection against dominated strategies. J. Econ. Theory 1996, 71, 558–573. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sorin, S.; Viossat, Y. Time average replicator and best-reply dynamics. Math. Oper. Res. 2009, 34, 263–269. [Google Scholar] [CrossRef]
- Hopkins, E.; Seymour, R.M. The stability of price dispersion under seller and consumer learning. Int. Econ. Rev. 2002, 43, 1157–1190. [Google Scholar] [CrossRef]
- Hopkins, E. Two competing models of how people learn in games. Econometrica 2002, 70, 2141–2166. [Google Scholar] [CrossRef]
- Huck, S.; Normann, H.T.; Oechssler, J. Learning in Cournot oligopoly—An experiment. Econ. J. 1999, 109, 80–95. [Google Scholar] [CrossRef]
- Hurkens, S.; Schlag, K.H. Evolutionary insights on the willingness to communicate. Int. J. Game Theory 2003, 31, 511–526. [Google Scholar] [CrossRef]
- Hurkens, S. Learning by forgetful players. Games Econ. Behav. 1995, 11, 304–329. [Google Scholar] [CrossRef]
- Hwang, S.H.; Newton, J. Payoff-dependent dynamics and coordination games. Econ. Theory 2017, 64, 589–604. [Google Scholar] [CrossRef]
- Hwang, S.; Rey-Bellet, L. Positive feedback in coordination games: stochastic evolutionary dynamics and the logit choice rule. arXiv, 2017; arXiv:1701.0487. [Google Scholar]
- Hwang, S.H.; Lim, W.; Neary, P.; Newton, J. Conventional contracts, intentional behavior and logit choice: Equality without symmetry. Games Econ. Behav. 2018. forthcoming. [Google Scholar] [CrossRef]
- Ianni, A. Learning strict Nash equilibria through reinforcement. J. Math. Econ. 2014, 50, 148–155. [Google Scholar] [CrossRef]
- Izquierdo, S.S.; Izquierdo, L.R.; Vega-Redondo, F. The option to leave: Conditional dissociation in the evolution of cooperation. J. Theor. Biol. 2010, 267, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Izquierdo, L.R.; Izquierdo, S.S.; Vega-Redondo, F. Leave and let leave: A sufficient condition to explain the evolutionary emergence of cooperation. J. Econ. Dyn. Control 2014, 46, 91–113. [Google Scholar] [CrossRef]
- Izquierdo, L.R.; Izquierdo, S.S.; Sandholm, W.H. An Introduction to ABED: Agent-Based Simulation of Evolutionary Game Dynamics; Mimeo: New York, NY, USA, 2018. [Google Scholar]
- Jackson, M.O.; Watts, A. The Evolution of Social and Economic Networks. J. Econ. Theory 2002, 106, 265–295. [Google Scholar] [CrossRef]
- Jackson, M.O. Social and Economic Networks; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Jensen, M.K.; Rigos, A. Evolutionary Games and Matching Rules; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision under Risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Kalai, E.; Smorodinsky, M. Other Solutions to Nash’s Bargaining Problem. Econometrica 1975, 43, 513–518. [Google Scholar] [CrossRef]
- Kalai, E. Proportional Solutions to Bargaining Situations: Interpersonal Utility Comparisons. Econometrica 1977, 45, 1623–1630. [Google Scholar] [CrossRef]
- Kandori, M.; Rob, R. Bandwagon effects and long run technology choice. Games Econ. Behav. 1998, 22, 30–60. [Google Scholar]
- Kandori, M.; Mailath, G.J.; Rob, R. Learning, Mutation, and Long Run Equilibria in Games. Econometrica 1993, 61, 29–56. [Google Scholar] [CrossRef]
- Kaniovski, Y.M.; Young, H.P. Learning dynamics in games with stochastic perturbations. Games Econ. Behav. 1995, 11, 330–363. [Google Scholar] [CrossRef]
- Khan, A. Coordination under global random interaction and local imitation. Int. J. Game Theory 2014, 43, 721–745. [Google Scholar] [CrossRef]
- Kifer, Y. Random Perturbations of Dynamical Systems; Birkhauser: Basel, Switzerland, 1988. [Google Scholar]
- Kim, N.; Hwang, S.H. Evolution of Altruistic Preferences among Boundedly Rational Agents. Korean Econ. Rev. 2015, 31, 239–266. [Google Scholar]
- Kim, Y.G.; Sobel, J. An evolutionary approach to pre-play communication. Econometrica 1995, 63, 1181–1193. [Google Scholar] [CrossRef]
- Kipling, R. Just So Stories; Macmillan and Co.: London, UK, 1902. [Google Scholar]
- Klaus, B.; Klijn, F. Paths to Stability for Matching Markets with Couples. Games Econ. Behav. 2007, 36, 154–171. [Google Scholar] [CrossRef]
- Klaus, B.; Newton, J. Stochastic stability in assignment problems. J. Math. Econ. 2016, 62, 62–74. [Google Scholar] [CrossRef]
- Klaus, B.; Payot, F. Paths to Stability in the Assignment Problem; Cahiers de recherches economiques du département d’econométrie et d’economie politique (deep); Universitéde Lausanne Facultédes HEC; DEEP: Lausanne, Suisse, 2013. [Google Scholar]
- Klaus, B.; Klijn, F.; Walzl, M. Stochastic stability for roommate markets. J. Econ. Theory 2010, 145, 2218–2240. [Google Scholar] [CrossRef]
- Koch, C.M.; Nax, H.H. Theory and Evidence of Common-Pool Resource Usage; Mimeo, Dept. of Humanities, Social and Political Sciences, ETH: Zurich, Switzerland, 2017. [Google Scholar]
- Kojima, F.; Ünver, M. Random paths to pairwise stability in many-to-many matching problems: A study on market equilibration. Int. J. Game Theory 2008, 36, 473–488. [Google Scholar] [CrossRef]
- Kreindler, G.E.; Young, H.P. Fast convergence in evolutionary equilibrium selection. Games Econ. Behav. 2013, 80, 39–67. [Google Scholar] [CrossRef]
- Kreindler, G.E.; Young, H.P. Rapid innovation diffusion in social networks. Proc. Natl. Acad. Sci. USA 2014, 111, 10881–10888. [Google Scholar] [CrossRef] [PubMed]
- Kuzmics, C. On the elimination of dominated strategies in stochastic models of evolution with large populations. Games Econ. Behav. 2011, 72, 452–466. [Google Scholar] [CrossRef]
- Lahkar, R.; Riedel, F. The logit dynamic for games with continuous strategy sets. Games Econ. Behav. 2015, 91, 268–282. [Google Scholar] [CrossRef]
- Lahkar, R.; Sandholm, W.H. The projection dynamic and the geometry of population games. Games Econ. Behav. 2008, 64, 565–590. [Google Scholar] [CrossRef]
- Lahkar, R.; Seymour, R.M. The dynamics of generalized reinforcement learning. J. Econ. Theory 2014, 151, 584–595. [Google Scholar] [CrossRef]
- Lahkar, R. The dynamic instability of dispersed price equilibria. J. Econ. Theory 2011, 146, 1796–1827. [Google Scholar] [CrossRef]
- Lahkar, R. Equilibrium selection in the stag hunt game under generalized reinforcement learning. J. Econ. Behav. Organ. 2017, 138, 63–68. [Google Scholar] [CrossRef]
- Laraki, R.; Mertikopoulos, P. Higher order game dynamics. J. Econ. Theory 2013, 148, 2666–2695. [Google Scholar] [CrossRef]
- Laslier, J.F.; Topol, R.; Walliser, B. A behavioral learning process in games. Games Econ. Behav. 2001, 37, 340–366. [Google Scholar] [CrossRef]
- Leshno, J.D.; Pradelski, B.S.R. Efficient Price Discovery and Information in the Decentralized Assignment Game; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Leslie, D.S.; Perkins, S.; Xu, Z. Best-Response Dynamics in Zero-Sum Stochastic Games; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Levine, D.K.; Modica, S. Dynamics in stochastic evolutionary models. Theor. Econ. 2016, 11, 89–131. [Google Scholar] [CrossRef]
- Lewis, D. Convention: A Philosophical Study; Harvard University Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Lewontin, R.C.; Cohen, D. On population growth in a randomly varying environment. Proc. Natl. Acad. Sci. USA 1969, 62, 1056–1060. [Google Scholar] [CrossRef] [PubMed]
- Lim, W.; Neary, P.R. An experimental investigation of stochastic adjustment dynamics. Games Econ. Behav. 2016, 100, 208–219. [Google Scholar] [CrossRef]
- Littlestone, N.; Warmuth, M.K. The weighted majority algorithm. Inf. Comput. 1994, 108, 212–261. [Google Scholar] [CrossRef]
- Mantilla, C.; Sethi, R.; Cárdenas, J.C. Efficiency and Stability of Sampling Equilibrium in Public Good Games; SSRN Working Paper Series 3081506; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Marden, J.R.; Roughgarden, T. Generalized Efficiency Bounds in Distributed Resource Allocation. IEEE Trans. Autom. Control 2014, 59, 571–584. [Google Scholar] [CrossRef]
- Marden, J.R.; Shamma, J.S. Game theory and distributed control. In Handbook of Game Theory; Elsevier: Amsterdam, The Netherlands, 2012; Volume 4, pp. 861–900. [Google Scholar]
- Marden, J.R.; Shamma, J.S. Revisiting log-linear learning: Asynchrony, completeness and payoff-based implementation. Games Econ. Behav. 2012, 75, 788–808. [Google Scholar] [CrossRef]
- Marden, J.R.; Wierman, A. Distributed welfare games. Operations Research 2013, 61, 155–168. [Google Scholar] [CrossRef]
- Marden, J.R.; Arslan, G.; Shamma, J.S. Joint strategy fictitious play with inertia for potential games. IEEE Trans. Autom. Control 2009, 54, 208–220. [Google Scholar] [CrossRef]
- Marden, J.R.; Young, H.P.; Pao, L.Y. Achieving Pareto optimality through distributed learning. SIAM J. Control Optim. 2014, 52, 2753–2770. [Google Scholar] [CrossRef]
- Marden, J.R. State based potential games. Automatica 2012, 48, 3075–3088. [Google Scholar] [CrossRef]
- Mäs, M.; Nax, H.H. A behavioral study of “noise” in coordination games. J. Econ. Theory 2016, 162, 195–208. [Google Scholar] [CrossRef]
- Maschler, M.; Peleg, B.; Shapley, L.S. Geometric Properties of the Kernel, Nucleolus, and Related Solution Concepts. Math. Oper. Res. 1979, 4, 303–338. [Google Scholar] [CrossRef]
- Massari, F. Comment on If You’re so Smart, Why Aren’t You Rich? Belief Selection in Complete and Incomplete Markets. Econometrica 2013, 81, 849–851. [Google Scholar]
- Massari, F. Market Selection in Large Economies: A Matter of Luck; Mimeo: New York, NY, USA, 2015. [Google Scholar]
- Massari, F. Markets with heterogeneous beliefs: A necessary and sufficient condition for a trader to vanish. J. Econ. Dyn. Control 2017, 78, 190–205. [Google Scholar] [CrossRef]
- Matessi, C.; Gimelfarb, A.; Gavrilets, S. Long-term buildup of reproductive isolation promoted by disruptive selection: how far does it go? Selection 2002, 2, 41–64. [Google Scholar] [CrossRef]
- Mertikopoulos, P.; Moustakas, A.L. The emergence of rational behavior in the presence of stochastic perturbations. Ann. Appl. Probab. 2010, 20, 1359–1388. [Google Scholar] [CrossRef]
- Mertikopoulos, P.; Sandholm, W.H. Learning in games via reinforcement and regularization. Math. Oper. Res. 2016, 41, 1297–1324. [Google Scholar] [CrossRef]
- Mertikopoulos, P.; Sandholm, W.H. Riemannian game dynamics. arXiv, 2016; arXiv:1603.09173. [Google Scholar]
- Mohlin, E.; Östling, R.; Wang, J.T.Y. Learning by Similarity-Weighted Imitation in Games; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Mohlin, E. Evolution of theories of mind. Games Econ. Behav. 2012, 75, 299–318. [Google Scholar] [CrossRef]
- Monderer, D.; Shapley, L.S. Potential Games. Games Econ. Behav. 1996, 14, 124–143. [Google Scholar] [CrossRef]
- Montgomery, J.D. Intergenerational cultural transmission as an evolutionary game. Am. Econ. J. Microecon. 2010, 2, 115–136. [Google Scholar] [CrossRef]
- Nachbar, J.H. “Evolutionary” selection dynamics in games: Convergence and limit properties. Int. J. Game Theory 1990, 19, 59–89. [Google Scholar] [CrossRef]
- Nagurney, A.; Zhang, D. Projected dynamical systems in the formulation, stability analysis, and computation of fixed-demand traffic network equilibria. Transp. Sci. 1997, 31, 147–158. [Google Scholar] [CrossRef]
- Naidu, S.; Hwang, S.H.; Bowles, S. Evolutionary bargaining with intentional idiosyncratic play. Econ. Lett. 2010, 109, 31–33. [Google Scholar] [CrossRef]
- Naidu, S.; Hwang, S.H.; Bowles, S. The Evolution of Egalitarian Sociolinguistic Conventions. Am. Econ. Rev. Papers Proc. 2017, 107, 572–577. [Google Scholar] [CrossRef]
- Nash, John F., Jr. The Bargaining Problem. Econometrica 1950, 18, 155–162. [Google Scholar]
- Nash, J. Non-cooperative games. Ann. Math. 1951, 286–295. [Google Scholar] [CrossRef]
- Nash, J. Two-person cooperative games. Econometrica 1953, 21, 128–140. [Google Scholar] [CrossRef]
- Nax, H.H.; Perc, M. Directional learning and the provisioning of public goods. Sci. Rep. 2015, 5, 8010. [Google Scholar] [CrossRef] [PubMed]
- Nax, H.H.; Pradelski, B.S.R. Evolutionary dynamics and equitable core selection in assignment games. Int. J. Game Theory 2015, 44, 903–932. [Google Scholar] [CrossRef]
- Nax, H.H.; Pradelski, B.S.R. Core Stability and Core Selection in a Decentralized Labor Matching Market. Games 2016, 7, 10. [Google Scholar] [CrossRef]
- Nax, H.H.; Rigos, A. Assortativity evolving from social dilemmas. J. Theor. Biol. 2016, 395, 194–203. [Google Scholar] [CrossRef] [PubMed]
- Nax, H.H.; Pradelski, B.S.R.; Young, H.P. Decentralized dynamics to optimal and stable states in the assignment game. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 2391–2397. [Google Scholar]
- Nax, H.H.; Burton-Chellew, M.N.; West, S.A.; Young, H.P. Learning in a black box. J. Econ. Behav. Organ. 2016, 127, 1–15. [Google Scholar] [CrossRef]
- Nax, H.H. Uncoupled Aspiration Adaptation Dynamics Into the Core. Ger. Econ. Rev. 2018. (online first). [Google Scholar] [CrossRef]
- Neary, P.R.; Newton, J. Heterogeneity in Preferences and Behavior in Threshold Models. J. Mech. Inst. Des. 2017, 2, 141–159. [Google Scholar]
- Neary, P.R. Competing conventions. Games Econ. Behav. 2012, 76, 301–328. [Google Scholar] [CrossRef]
- Nemitz, M.P.; Sayed, M.E.; Mamish, J.; Ferrer, G.; Teng, L.; McKenzie, R.M.; Hero, A.O.; Olson, E.; Stokes, A.A. HoverBots: Precise Locomotion Using Robots That Are Designed for Manufacturability. Front. Robot. AI 2017, 4, 55. [Google Scholar] [CrossRef]
- Newton, J.; Angus, S. Coalitions, Tipping Points and the Speed of Evolution; Working Papers Series 2013-02; University of Sydney Economics: Sydney, NSW, Australia, 2013. [Google Scholar]
- Newton, J.; Angus, S.D. Coalitions, tipping points and the speed of evolution. J. Econ. Theory 2015, 157, 172–187. [Google Scholar] [CrossRef]
- Newton, J.; Sawa, R. A one-shot deviation principle for stability in matching problems. J. Econ. Theory 2015, 157, 1–27. [Google Scholar] [CrossRef]
- Newton, J.; Sercombe, D. Agency, Potential and Contagion; SSRN Working Paper Series 3035245; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Newton, J.; Wait, A.; Angus, S.D. Watercooler Chat, Organizational Structure and Corporate Culture; SSRN Working Paper Series 3053174; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Newton, J. Coalitional stochastic stability. Games Econ. Behav. 2012, 75, 842–854. [Google Scholar] [CrossRef]
- Newton, J. Recontracting and stochastic stability in cooperative games. J. Econ. Theory 2012, 147, 364–381. [Google Scholar] [CrossRef]
- Newton, J. Stochastic stability on general state spaces. J. Math. Econ. 2015, 58, 46–60. [Google Scholar] [CrossRef]
- Newton, J. Shared intentions: The evolution of collaboration. Games Econ. Behav. 2017, 104, 517–534. [Google Scholar] [CrossRef]
- Newton, J. The preferences of Homo Moralis are unstable under evolving assortativity. Int. J. Game Theory 2017, 46, 583–589. [Google Scholar] [CrossRef]
- Norman, T.W. Rapid evolution under inertia. Games Econ. Behav. 2009, 66, 865–879. [Google Scholar] [CrossRef]
- Norman, T.W. Learning, hypothesis testing, and rational-expectations equilibrium. Games Econ. Behav. 2015, 90, 93–105. [Google Scholar] [CrossRef]
- Norman, T.W. Endogenous Market Selection; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Nowak, M.A.; Tarnita, C.E.; Wilson, E.O. The evolution of eusociality. Nature 2010, 466, 1057. [Google Scholar] [CrossRef] [PubMed]
- Okada, A.; Sawa, R. An Evolutionary Approach to Social Choice Problems with Q-Quota Rules; Kyoto Institute of Economic Research Discussion Paper 936; Kyoto University: Kyoto, Japan, 2016. [Google Scholar]
- Oprea, R.; Henwood, K.; Friedman, D. Separating the Hawks from the Doves: Evidence from continuous time laboratory games. J. Econ. Theory 2011, 146, 2206–2225. [Google Scholar] [CrossRef]
- Osborne, M.J.; Rubinstein, A. Games with procedurally rational players. Am. Econ. Rev. 1998, 88, 834–847. [Google Scholar]
- Östling, R.; Wang, J.T.Y.; Chou, E.Y.; Camerer, C.F. Testing game theory in the field: Swedish LUPI lottery games. Am. Econ. J. Microecon. 2011, 3, 1–33. [Google Scholar] [CrossRef]
- Otto, S.P.; Servedio, M.R.; Nuismer, S.L. Frequency-dependent selection and the evolution of assortative mating. Genetics 2008, 179, 2091–2112. [Google Scholar] [CrossRef] [PubMed]
- Oyarzun, C.; Ruf, J. Convergence in models with bounded expected relative hazard rates. J. Econ. Theory 2014, 154, 229–244. [Google Scholar] [CrossRef]
- Pennings, P.S.; Kopp, M.; Meszéna, G.; Dieckmann, U.; Hermisson, J. An analytically tractable model for competitive speciation. Am. Nat. 2008, 171, E44–E71. [Google Scholar] [CrossRef] [PubMed]
- Perkins, S.; Leslie, D.S. Stochastic fictitious play with continuous action sets. J. Econ. Theory 2014, 152, 179–213. [Google Scholar] [CrossRef]
- Peski, M. Generalized risk-dominance and asymmetric dynamics. J. Econ. Theory 2010, 145, 216–248. [Google Scholar] [CrossRef]
- Pradelski, B.S.; Young, H.P. Learning efficient Nash equilibria in distributed systems. Games Econ. Behav. 2012, 75, 882–897. [Google Scholar] [CrossRef]
- Pradelski, B.S. Decentralized Dynamics and Fast Convergence in the Assignment Game. In Proceedings of the Sixteenth ACM Conference on Economics and Computation, Portland, OR, USA, 15–19 June 2015; ACM: New York, NY, USA. [Google Scholar]
- Quijano, N.; Ocampo-Martinez, C.; Barreiro-Gomez, J.; Obando, G.; Pantoja, A.; Mojica-Nava, E. The role of population games and evolutionary dynamics in distributed control systems: The advantages of evolutionary game theory. IEEE Control Syst. 2017, 37, 70–97. [Google Scholar] [CrossRef]
- Ritzberger, K.; Weibull, J.W. Evolutionary selection in normal-form games. Econometrica 1995, 63, 1371–1399. [Google Scholar] [CrossRef]
- Rivas, J. Cooperation, imitation and partial rematching. Games Econ. Behav. 2013, 79, 148–162. [Google Scholar] [CrossRef]
- Robalino, N.; Robson, A. The evolution of strategic sophistication. Am. Econ. Rev. 2016, 106, 1046–1072. [Google Scholar] [CrossRef]
- Robson, A.J. Efficiency in evolutionary games: Darwin, Nash and the secret handshake. J. Theor. Biol. 1990, 144, 379–396. [Google Scholar] [CrossRef]
- Robson, A.J. A biological basis for expected and non-expected utility. J. Econ. Theory 1996, 68, 397–424. [Google Scholar] [CrossRef]
- Rosenthal, R.W. Games of perfect information, predatory pricing and the chain-store paradox. J. Econ. Theory 1981, 25, 92–100. [Google Scholar] [CrossRef]
- Roth, A.E.; Erev, I. Learning in extensive-form games: Experimental data and simple dynamic models in the intermediate term. Games Econ. Behav. 1995, 8, 164–212. [Google Scholar] [CrossRef]
- Roth, A.E.; Postlewaite, A. Weak versus strong domination in a market with indivisible goods. J. Math. Econ. 1977, 4, 131–137. [Google Scholar] [CrossRef]
- Roth, A.E.; Vande Vate, J.H. Random Paths to Stability in Two-Sided Matching. Econometrica 1990, 58, 1475–1480. [Google Scholar] [CrossRef]
- Roughgarden, T. Intrinsic Robustness of the Price of Anarchy. J. ACM 2015, 62, 32. [Google Scholar] [CrossRef]
- Rozen, K. Conflict leads to cooperation in demand bargaining. J. Econ. Behav. Organ. 2013, 87, 35–42. [Google Scholar] [CrossRef]
- Rusch, H. The evolutionary interplay of intergroup conflict and altruism in humans: a review of parochial altruism theory and prospects for its extension. Proc. R. Soc. B Biol. Sci. 2014, 281, 20141539. [Google Scholar] [CrossRef] [PubMed]
- Rusch, H. Shared Intentions: Collaboration Evolving; MAGKS Joint Discussion Paper Series in Economics 39; University of Marburg: Marburg, Germany, 2017. [Google Scholar]
- Rustichini, A. Optimal properties of stimulus—Response learning models. Games Econ. Behav. 1999, 29, 244–273. [Google Scholar] [CrossRef]
- Samuelson, L.; Zhang, J. Evolutionary stability in asymmetric games. J. Econ. Theory 1992, 57, 363–391. [Google Scholar] [CrossRef]
- Samuelson, L. Stochastic stability in games with alternative best replies. J. Econ. Theory 1994, 64, 35–65. [Google Scholar] [CrossRef]
- Samuelson, L. Evolutionary Games and Equilibrium Selection; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Samuelson, L. Introduction to the evolution of preferences. J. Econ. Theory 2001, 97, 225–230. [Google Scholar] [CrossRef]
- Samuelson, L. Game Theory in Economics and Beyond. J. Econ. Perspect. 2016, 30, 107–130. [Google Scholar] [CrossRef]
- Sandholm, W.H.; Staudigl, M. Large deviations and stochastic stability in the small noise double limit. Theor. Econ. 2016, 11, 279–355. [Google Scholar] [CrossRef]
- Sandholm, W.H.; Izquierdo, S.S.; Izquierdo, L.R. Best Experienced Payoff Dynamics and Cooperation in the Centipede Game; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Sandholm, W.H. Population Games and Evolutionary Dynamics; Economic Learning and Social Evolution; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Sandroni, A. Do markets favor agents able to make accurate predictions? Econometrica 2000, 68, 1303–1341. [Google Scholar] [CrossRef]
- Sandroni, A. Market selection when markets are incomplete. J. Math. Econ. 2005, 41, 91–104. [Google Scholar] [CrossRef]
- Sawa, R.; Wu, J. Prospect Dynamic and Loss Dominance; SSRN Working Paper Series 2804852; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Sawa, R.; Wu, J. Reference-Dependent Preferences, Super-Dominance and Stochastic Stability; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Sawa, R.; Zusai, D. Evolutionary imitative dynamics with population-varying aspiration levels. J. Econ. Theory 2014, 154, 562–577. [Google Scholar] [CrossRef]
- Sawa, R. Coalitional Stochastic Stability in Games, Networks and Markets. Games Econ. Behav. 2014, 88, 90–111. [Google Scholar] [CrossRef]
- Sawa, R. Stochastic Stability in Coalitional Bargaining Problems; Mimeo: New York, NY, USA, 2015. [Google Scholar]
- Schlag, K.H. Cheap Talk and Evolutionary Dynamics; University of Bonn Discussion Paper b-242; University of Bonn: Bonn, Germany, 1993. [Google Scholar]
- Schlag, K.H. When Does Evolution Lead to Efficiency in Communication Games? University of Bonn Discussion Paper b-299; University of Bonn: Bonn, Germany, 1994. [Google Scholar]
- Schlag, K.H. Why imitate, and if so, how?: A boundedly rational approach to multi-armed bandits. J. Econ. Theory 1998, 78, 130–156. [Google Scholar] [CrossRef]
- Searle, J.R. The Construction of Social Reality; Simon and Schuster: New York, NY, USA, 1995. [Google Scholar]
- Selten, R.; Hammerstein, P. Gaps in Harley’s argument on evolutionarily stable learning rules and in the logic of “tit for tat”. Behav. Brain Sci. 1984, 7, 115–116. [Google Scholar] [CrossRef]
- Selten, R. Evolutionary stability in extensive two-person games. Math. Soc. Sci. 1983, 5, 269–363. [Google Scholar] [CrossRef]
- Serrano, R.; Volij, O. Mistakes in Cooperation: the Stochastic Stability of Edgeworth’s Recontracting. Econ. J. 2008, 118, 1719–1741. [Google Scholar] [CrossRef]
- Servedio, M.R. Limits to the evolution of assortative mating by female choice under restricted gene flow. Proc. R. Soc. B Biol. Sci. 2011, 278, 179–187. [Google Scholar] [CrossRef] [PubMed]
- Sethi, R.; Somanathan, E. The evolution of social norms in common property resource use. Am. Econ. Rev. 1996, 86, 766–788. [Google Scholar]
- Sethi, R.; Somanathan, E. Preference evolution and reciprocity. J. Econ. Theory 2001, 97, 273–297. [Google Scholar] [CrossRef]
- Sethi, R. Strategy-specific barriers to learning and nonmonotonic selection dynamics. Games Econ. Behav. 1998, 23, 284–304. [Google Scholar] [CrossRef]
- Sethi, R. Stability of equilibria in games with procedurally rational players. Games Econ. Behav. 2000, 32, 85–104. [Google Scholar] [CrossRef]
- Shahshahani, S. A New Mathematical Framework for the Study of Linkage and Selection; Memoirs of the American Mathematical Society; American Mathematical Society: Providence, RI, USA, 1979; Volume 211. [Google Scholar]
- Shapley, L.; Shubik, M. The assignment game I: The core. Int. J. Game Theory 1971, 1, 111–130. [Google Scholar] [CrossRef]
- Shapley, L.S. Stochastic games. Proc. Natl. Acad. Sci. USA 1953, 39, 1095–1100. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Simon, H.A. Rationality as process and as product of thought. Am. Econ. Rev. 1978, 68, 1–16. [Google Scholar]
- Skyrms, B. Signals, evolution and the explanatory power of transient information. Philos. Sci. 2002, 69, 407–428. [Google Scholar] [CrossRef]
- Sobel, J. Evolutionary stability and efficiency. Econ. Lett. 1993, 42, 301–312. [Google Scholar] [CrossRef]
- Sorin, S. Exponential weight algorithm in continuous time. Math. Programm. 2009, 116, 513–528. [Google Scholar] [CrossRef]
- Spiegler, R. Bounded Rationality and Industrial Organization; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Stahl, D.O.; Wilson, P.W. On players’ models of other players: Theory and experimental evidence. Games Econ. Behav. 1995, 10, 218–254. [Google Scholar] [CrossRef]
- Staudigl, M.; Weidenholzer, S. Constrained interactions and social coordination. J. Econ. Theory 2014, 152, 41–63. [Google Scholar] [CrossRef]
- Staudigl, M. Stochastic stability in asymmetric binary choice coordination games. Games Econ. Behav. 2012, 75, 372–401. [Google Scholar] [CrossRef]
- Strassmann, J.E.; Page Jr, R.E.; Robinson, G.E.; Seeley, T.D. Kin selection and eusociality. Nature 2011, 471, E5. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y. Long run equilibria in an asymmetric oligopoly. Econ. Theory 1999, 14, 705–715. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Thomas, B. On evolutionarily stable sets. J. Math. Biol. 1985, 22, 105–115. [Google Scholar] [CrossRef]
- Tomasello, M. A Natural History of Human Thinking; Harvard University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Traulsen, A.; Hauert, C.; De Silva, H.; Nowak, M.A.; Sigmund, K. Exploration dynamics in evolutionary games. Proc. Natl. Acad. Sci. USA 2009, 106, 709–712. [Google Scholar] [CrossRef] [PubMed]
- Trivers, R.L. The evolution of reciprocal altruism. Q. Rev. Biol. 1971, 46, 35–57. [Google Scholar] [CrossRef]
- Van Veelen, M. Group selection, kin selection, altruism and cooperation: when inclusive fitness is right and when it can be wrong. J. Theor. Biol. 2009, 259, 589–600. [Google Scholar] [CrossRef] [PubMed]
- Van Veelen, M. The replicator dynamics with n players and population structure. J. Theor. Biol. 2011, 276, 78–85. [Google Scholar] [CrossRef] [PubMed]
- Van Veelen, M. Robustness against indirect invasions. Games Econ. Behav. 2012, 74, 382–393. [Google Scholar] [CrossRef]
- Vega-Redondo, F. The evolution of Walrasian behavior. Econometrica 1997, 65, 375–384. [Google Scholar] [CrossRef]
- Vesely, F.; Yang, C.L. On Optimal and Neutrally Stable Population Equilibrium in Voluntary Partnership Prisoner’s Dilemma Games; Mimeo: New York, NY, USA, 2010. [Google Scholar]
- Vesely, F.; Yang, C.L. Breakup, Secret Handshake and Neutral Stability in Repeated Prisoner’s Dilemma with Option to Leave: A Note; Mimeo: New York, NY, USA, 2012. [Google Scholar]
- Vovk, V. Aggregating strategies. In Proceedings of the Third Annual Workshop on Computational Learning Theory, Rochester, NY, USA, 6–8 August 1990; Fulk, M., Case, J., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1990; pp. 371–383. [Google Scholar]
- Weibull, J.W.; Salomonsson, M. Natural selection and social preferences. J. Theor. Biol. 2006, 239, 79–92. [Google Scholar] [CrossRef] [PubMed]
- Weibull, J. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Williams, D. Probability with Martingales; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Wilson, D.S.; Dugatkin, L.A. Group selection and assortative interactions. Am. Nat. 1997, 149, 336–351. [Google Scholar] [CrossRef]
- Wu, J. Evolving assortativity and social conventions. Econ. Bull. 2016, 36, 936–941. [Google Scholar]
- Wu, J. Social Hierarchy and the Evolution of Behavior. Int. Game Theory Rev. 2017, 19, 1750019. [Google Scholar] [CrossRef]
- Wu, J. Political Institutions and the Evolution of Character Traits. Games Econ. Behav. 2017, 106, 260–276. [Google Scholar] [CrossRef]
- Xu, Z. Convergence of best-response dynamics in extensive-form games. J. Econ. Theory 2016, 162, 21–54. [Google Scholar] [CrossRef]
- Young, H.P.; Burke, M.A. Competition and Custom in Economic Contracts: A Case Study of Illinois Agriculture. Am. Econ. Rev. 2001, 91, 559–573. [Google Scholar] [CrossRef]
- Young, H.P. The Evolution of Conventions. Econometrica 1993, 61, 57–84. [Google Scholar] [CrossRef]
- Young, H.P. An Evolutionary Model of Bargaining. J. Econ. Theory 1993, 59, 145–168. [Google Scholar] [CrossRef]
- Young, H.P. Individual Strategy and Social Structure; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Young, H.P. Conventional Contracts. Rev. Econ. Stud. 1998, 65, 773–792. [Google Scholar] [CrossRef]
- Young, H.P. The possible and the impossible in multi-agent learning. Artif. Intell. 2007, 171, 429–433. [Google Scholar] [CrossRef]
- Young, H.P. Learning by trial and error. Games Econ. Behav. 2009, 65, 626–643. [Google Scholar] [CrossRef]
- Young, H.P. Innovation diffusion in heterogeneous populations: Contagion, social influence, and social learning. Am. Econ. Rev. 2009, 99, 1899–1924. [Google Scholar] [CrossRef]
- Young, H.P. The dynamics of social innovation. Proc. Natl. Acad. Sci. USA 2011, 108 (Suppl. 4), 21285–21291. [Google Scholar] [CrossRef] [PubMed]
- Zusai, D. Tempered best response dynamics. Int. J. Game Theory 2017, 47, 1–34. [Google Scholar] [CrossRef]
- Zusai, D. Nonaggregable Evolutionary Dynamics Under Payoff Heterogeneity; DETU Working Paper 17-02; Department of Economics, Temple University: Philadelphia, PA, USA, 2017. [Google Scholar]
- Zusai, D. Gains in Evolutionary Dynamics: Unifying Rational Framework for Dynamic Stability of ESS; Mimeo: New York, NY, USA, 2018. [Google Scholar]


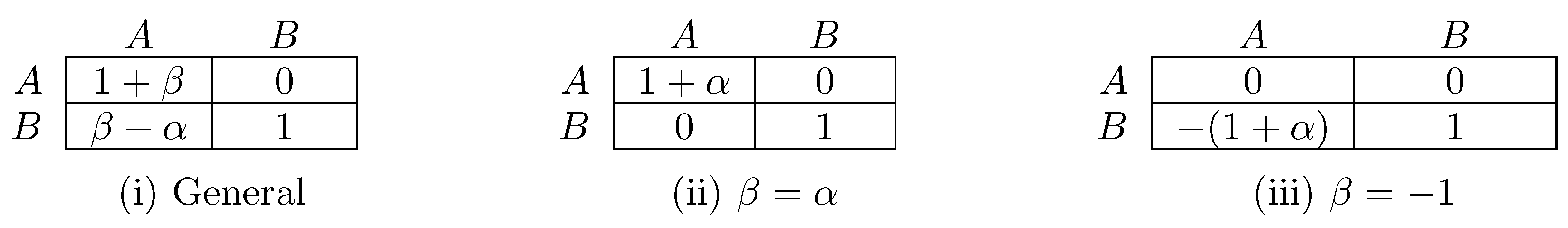

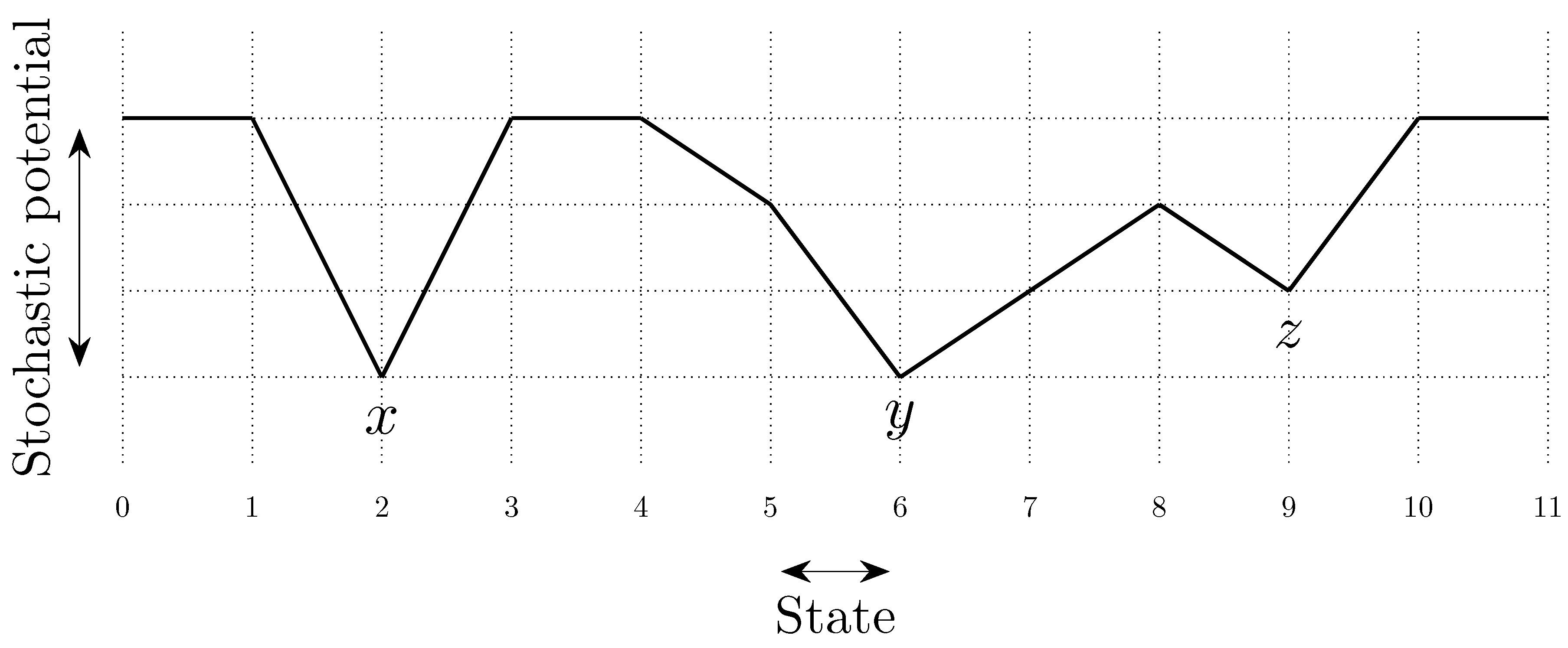
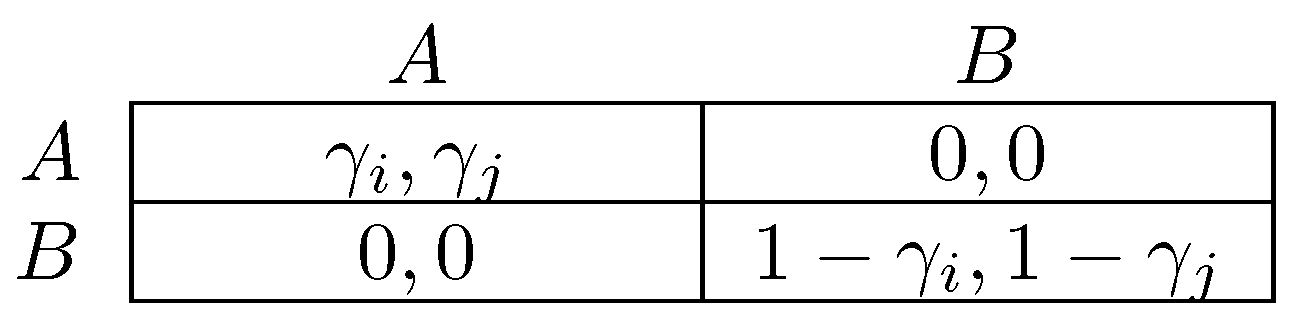
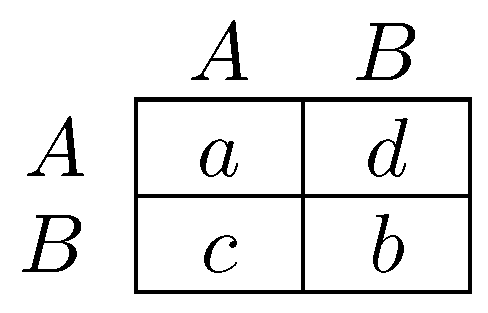
| Unintentional | Intentional | |
|---|---|---|
| Uniform | Kalai-Smorodinsky Young [364] | Nash bargaining Naidu et al. [244] |
| Logit | Logit bargaining Hwang et al. [179] | Egalitarian Hwang et al. [179] |
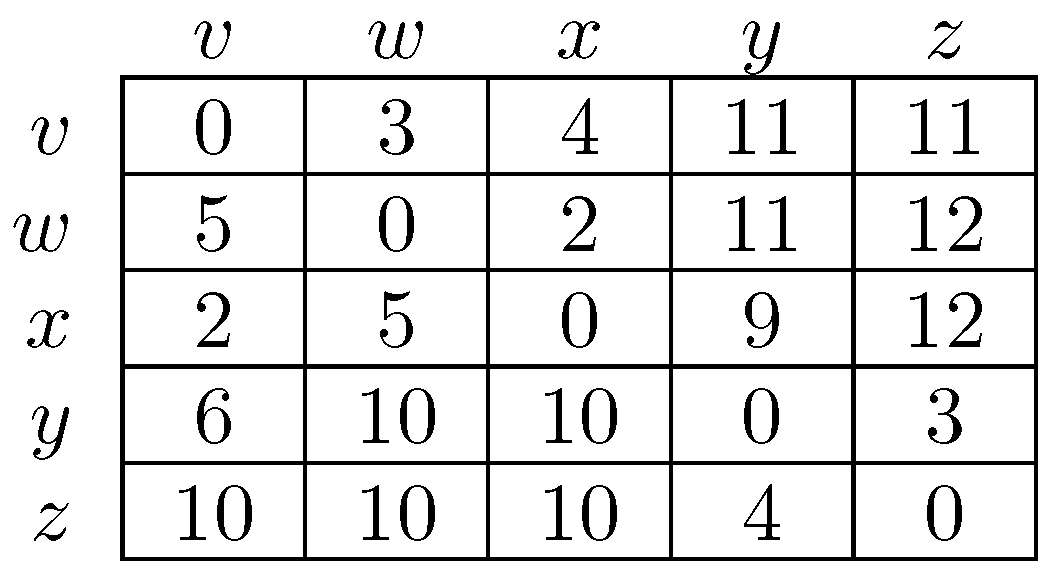
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Newton, J. Evolutionary Game Theory: A Renaissance. Games 2018, 9, 31. https://doi.org/10.3390/g9020031
Newton J. Evolutionary Game Theory: A Renaissance. Games. 2018; 9(2):31. https://doi.org/10.3390/g9020031
Chicago/Turabian StyleNewton, Jonathan. 2018. "Evolutionary Game Theory: A Renaissance" Games 9, no. 2: 31. https://doi.org/10.3390/g9020031
APA StyleNewton, J. (2018). Evolutionary Game Theory: A Renaissance. Games, 9(2), 31. https://doi.org/10.3390/g9020031




